Abstract
Counting the number of shortest paths in various graphs is an important and interesting combinatorial problem, especially in weighted graphs with various applications. We consider a specific infinite graph here, namely the honeycomb grid. Changing to its dual, the triangular grid, paths between triangle pixels (we abbreviate this term to trixels) are counted. The number of shortest weighted paths between any two trixels of the triangular grid is discussed. For each trixel, there are three different types of neighbor trixels, 1-, 2- and 3-neighbours, depending the Euclidean distance of their midpoints. When considering weighted distances, the positive values α, β and γ are assigned to the ‘steps’ to various neighbors. We gave formulae for the number of shortest weighted paths between any two trixels in various cases by the respective weight values. The results are nicely connected to various numbers well-known in combinatorics, e.g., to binomial coefficients and Fibonacci numbers.
1. Introduction
Although in Euclidean geometry the shortest path is always unique between two points, in graph theory it is not true, since in general, paths are understood as consecutive alternating sequences of vertices and edges. Graph theory has various applications in computer and social networks and shortest paths and their numbers give significant information about the network, and it is also important for various applications, e.g., sending packages through the network. Special structured (infinite) graphs are called grids/lattices, and they play important roles, e.g., in image processing, computer graphics and cellular automata. The geometry of these grids is called digital geometry [1]. In digital geometry, based on the structure of the grid, integer coordinates are used for addressing the vertices of the graph (the points of the given space). In many of these fields instead of the original graph its Voronoi dual is used, that it instead of the vertices, pixels/voxels are used. The square and cubic grids are self-dual. The honeycomb grid is dual of the triangular grid, that is instead of having vertices of the hexagons in the honeycomb (or hexagonal) grid, we may use the triangle pixels of the triangular grid keeping both the coordinate system and neighborhood structure [2,3]. In this paper we also use the triangle pixels (also called trixels) as the elements of the grid. Pixels in any grid are generally adjacent if they share at least one point on their border. In the square grid, two integer coordinates are used for addressing the pixels, and, consequently, there are two types of neighbor relations between any two adjacent pixels in the grid: cityblock and chessboard neighborhood, they are also called 1-neighbors and 2-neighbors, respectively, indicating the number of coordinates that changes the value by ±1 ‘stepping’ from a pixel to the indicated neighbor one. By using only one type of neighborhood in each step of the path, the cityblock and chessboard paths, and consequently the first studied digital distances, the cityblock (also called the Manhattan taxicab) distance and the chessboard distance were investigated [4]. Path counting as a tool for image processing was also introduced in that paper, and for these distances it was solved in [5]. Since the mentioned distances are very rough approximations of the Euclidean distance, other digital distances, namely, distances based on neighborhood sequences [6,7,8,9,10] and chamfer distances [11] were also investigated. Path counting was solved for neighborhood sequence distances in [12]. Chamfer distances actually correspond to weighted distances; for different types of neighbors, different weights can be assigned, and the shortest weighted paths are computed: for a movement from one pixel to another, weight α is used for horizontal and vertical movements, while weight β is used for diagonal movements. Formulae giving the number of shortest weighted paths are provided in [13]. The hexagonal and the triangular grids have different symmetries and properties than the square grid, they behave in a different way and there are various advantages to apply them [14,15,16]. There are three types of neighbors widely used on the triangular grid [17,18]. Thus, the triangular grid has the most complex neighborhood structure among the three regular two-dimensional grids. Digital distances based on these neighborhoods were described in [19], based on neighborhood sequences were studied in [3,18,20], chamfer distances were investigated in [21,22,23]. Because there are three types of neighbors, chamfer distances are based on three weights on the triangular grid. Some path counting results were obtained for distances based on a given neighborhood in [24,25]. In this paper we continue this line of the research by counting the number of shortest paths for various cases based on weighted distances on the triangular grid.
2. Preliminaries
Each pixel in the triangular grid (we call it a trixel from now on) is addressed uniquely by a triplet of coordinates having axes with directions x,y and z to reflect the symmetry of the grid structure. In this grid, to the sum of the coordinate values reflects the orientation of the trixels, thus we differentiate two types of trixels: even (zero sum trixels has orientation ) and odd trixels (triangle pixels having orientation are addressed by triplets with 1-sum). Figure 1 shows the origin (trixel with coordinates (0,0,0)), the axes of the coordinate system and also a part of the grid with the assigned coordinate values.
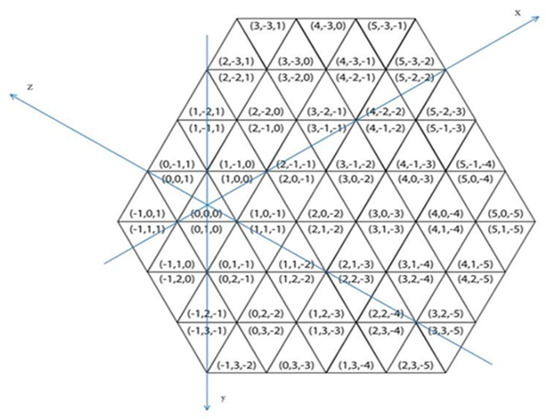
Figure 1.
Coordinate system for the triangular grid with the Origin and the axes.
Each trixel in the triangular grid has three types of neighbors: there are three 1-neighbors, each of them shares a side with the original trixel, there are six more 2-neighbors and, further, there are three more 3-neighbor trixels. All twelve neighbors share at least one point on the boundary with the original trixel (see Figure 2). One can also define formally the neighborhood relations based on the coordinates of the trixels:
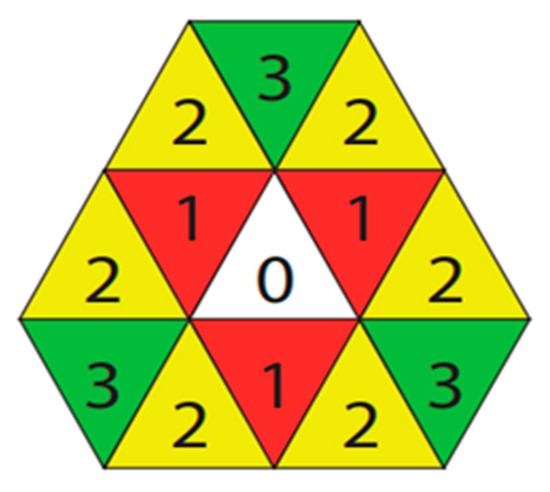
Figure 2.
Three types of neighbors of trixel 0. 1-neighbors are red, 2-neighbors are yellow and 3-neighbors are green.
- ❖
- The trixels p(p(1),p(2),p(3)) and q(q(1),q(2),q(3)) are in m-neighbor relation (m {1,2,3}) if:
- ∘
- |p(k) q(k)| for every k {1, 2, 3} and
- ∘
- .
We note here that, when working with a given neighborhood and also at neighborhood sequences, in the second condition the sign ≤ is used and the neighborhood relation is having the extensive property, that is all m-neighbors are also (m − 1)-neighbors (for m > 1). In case of equality of the last condition, the trixels are usually referred as strict m-neighbors in the literature. However, for chamfer distances, this strict neighborhood is more adequate, thus we use the definition as we have formally described above. Notice that 1- and 3-neighbors have different orientation than the original trixel (i.e., if the original trixel is even, then these neighbors are odd and vice versa), while 2-neighbors have the same orientation as the original trixel [21]. Figure 2 shows these three neighbor types for an even trixel.
In the triangular grid, the trixels that have a fixed coordinate value form a lane, i.e., if two trixels share either x, y or z coordinate, then they are in a common lane (e.g., y = −3 for the trixels of the top lane in Figure 1). If the two trixels are not is a common lane, then these two trixels can be connected by two lanes with angle between the two lanes. Shortest weighted paths are used in order to define weighted/chamfer distance in the triangular grid. According to the three types of neighbor relations, we assign three weights to the steps to adjacent trixels. Weight α is assigned to steps to 1-neighbor trixels. Weight β is used for stepping from a trixel to one of its 2-neighbors, while γ is the weight from a trixel to its 3-neighbor trixels. All these three weights are positive real values. We will also use the concepts of α-step, β-step and γ-step, accordingly, to refer to a step with the given weight. In this context chamfer distance is defined as the least total weight needed for connecting the two trixels by α-, β- and/or γ-steps. However, this value may refer not to a unique path, but many paths. (Two paths are identical if they consist the same sequence of trixels.) This is very natural, and we also use the assumption in this paper that the weights reflect the Euclidean distance of the midpoints of the trixels in such a way that closer neighbors can be reached by smaller weight, more precisely, 0 < α < β < γ holds.
Without loss of generality we discuss and find the number of shortest paths between trixels P1(0,0,0) and P2(x,y,z) with the condition x,y > 0 and z < 0 (or x > 0 and y,z < 0). Based on translations and mirroring the grid to itself (see [26] for details), any respective position of any two trixels can be mapped to P1 and P2 with this condition.
3. Number of Shortest Weighted Paths in Triangular Grid
Let p(x1,y1,z1) and q(x2,y2,z2) be two trixels in a triangular grid, and let w1, w2 and w3 be the absolute differences between the coordinates of p and q such that w1 = |x1 x2|, w2 = |y1 y2| and w3 = |z1 z2|. Let S = w1 + w2 + w3, and , and are minimum, middle (median) and maximum of respectively. The number of shortest weighted paths between p(x1,y1,z1) and q(x2,y2,z2) depends on the values of the weights α, β and γ. According to this fact, we analyze the various cases in the next subsections.
3.1. The Binomial Case: 2α < β and 3α < γ
Theorem 1.
Let,andbe the weights of steps to a 1-, 2- and a 3-neighbor, respectively, such that. Let p(x1,y1,z1) and q(x2,y2,z2) be two trixels of the triangular grid. Further, let w1 = |x1 − x2|, w2 = |y1 − y2| and w3 = |z1 − z2| be the absolute differences between the corresponding coordinates of the trixels. Then, the number of the shortest paths between p and q, denoted by f(w1,w2,w3), is computed as
Proof.
By the given conditions on the weights, every shortest path is built up only by 1-steps since each 2-steps can be substituted by two consecutive 1-steps and each 3-step can be substituted by three consecutive 1-steps with less sum of weights. The proof goes by induction on the smallest coordinate difference of the points. Let us consider the base case when , i.e., the two trixels are in the same lane:
The number of steps, i.e., the number of -steps in a shortest weighted path between the two trixels is mid + max, since min = 0. There is only 1 shortest path between any two trixels on the same lane, through the trixels ‘between’ the two trixels in the same lane. Thus, there is only one path, any by (1) we will also get = 1.
Now, let us consider the cases when the two trixels are not in the same lane:
For simplicity we will take the two trixels to be (0,0,0) and (i,j,k), and let us assume, that the sector of triangular grid that we are interested in having values, i,j > 0 and k < 0, or j,k < 0 and i > 0. As we have already mentioned, based on the transformations detailed in [26], by mirroring of these sectors, one may obtain the whole triangular grid.
Firstly, case i,j > 0 and k < 0 is considered. As we have already mentioned, we prove the Formula (1) by induction. The base case of induction is = 0, which is already proven: Formula (1) is satisfied, i.e., it gives 1 for these cases. Now, as the induction hypothesis, let us assume that Formula (1) holds for every trixel with |i| + |j| + |k| = i + j − k < M, with a positive integer M. Further, let us consider a trixel with coordinates |i| + |j| + |k| = i + j − k = M. We may also assume that > 0. Since every trixel has either 0-sum or 1-sum triplet, this condition also means that in this region of the grid, one of i and j has the value and the other has the value . Then, let us analyze, first, the case when q is an odd trixel. In this case, all shortest paths from (0,0,0) to (i,j,k) must contain, as the last step, a step either from (i − 1,j,k) or from (i,j − 1,k) the target trixel (i,j,k). However, both (i − 1,j,k) and (i,j − 1,k) are even trixels such that the sum of the absolute values of their coordinates is less than M. Thus, the number of the shortest paths to the trixels (i − 1,j,k) and (i,j − 1,k) are given by the Formula (1) by our hypothesis, i.e., and , respectively, not depending on which of i or j (or both) have the minimal value, since, e.g., . Moreover, the number of shortest paths to (i,j,k) is, then, exactly the sum of those two values, that is,
which was to be proven. Now, let us analyze the case when q is an even trixel. In this case all the shortest paths from (0,0,0) to (i,j,k) has the last step from the trixel (i,j,k + 1) = (i,j,−(|k| − 1)) to the trixel (i,j,k). Thus, the number of shortest path to the even trixel q(i,j,k) is exactly the same as the number of shortest paths to the odd trixel q′(i,j,k + 1). However, for q′ the sum of absolute coordinate values is |i| + |j| + |k + 1| = i + j + |k| − 1 = M − 1. Therefore, based on the hypothesis, the number of shortest path is . Observing that q and q′ shares the coordinates i and j, which are, in fact, and , the formula also holds for the trixel q.
Secondly, let us consider the case i > 0 and j,k < 0. Here, , since every trixel has either 0-sum or 1-sum triplet, i.e., i + j + k {0,1}. Again the induction based on the cases, where = 0, for which cases it is already proven that Formula (1) is satisfied. Now, as the induction hypothesis, let us assume that Formula (1) holds for every trixel with |i| + |j| + |k| = i − j − k < M, with a positive integer M. Further, let us consider a trixel with coordinates |i| + |j| + |k| = i − j − k = M. The number of shortest paths from trixel (0,0,0) to an even trixel (i,j,k) equals to the sum of the number of shortest paths to trixels (i,j 1,k) = (i, −(|j| − 1), −|k|) and (i,j,k 1) =(i, −|j|, −(|k| − 1)), since each the shortest path from (0,0,0) to (i,j,k) is passing through exactly one of these two trixels having the last step from there to (i,j,k). However, by the induction hypothesis, Formula (1) is correct for trixels (i,j 1,k) and (i,j,k 1) since their absolute coordinate sum is M − 1. Therefore, for trixel (i,j,k) we have
For odd trixel (i,j,k), with j,k < 0 and i > 0, the number of shortest weighted paths equals to the number of shortest weighted paths for even trixel (i 1,j,k), since in each shortest path the last step is from the even trixel (i 1,j,k) to the odd trixel (i,j,k). Here and have the values and (in an order) both for the trixels (i 1,j,k) and (i,j,k). Therefore, the number of shortest paths to both of them is given by:
The proof has been finished. □
As one may also observe in the next example, the binomial coefficients appear in the figure (hence the name of the subsection), in fact, the space is cut to six parts, and in each part one can observe the Pascal’s triangle. We also note here that in [24], based on a different approach, but, in fact, very similar results were presented (as the case of path counting for 1-neighborhood).
Example 1.
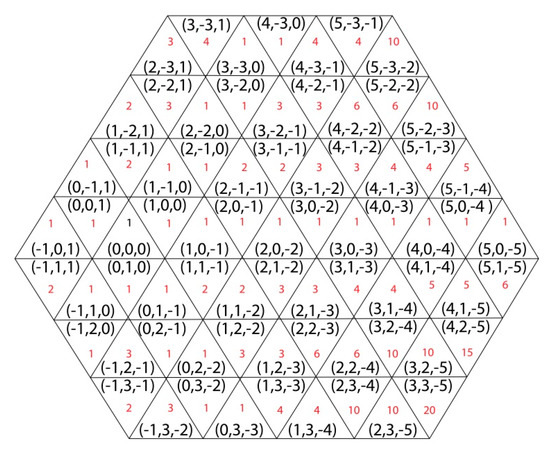
Figure 3 illustrates the number of weighted shortest paths from trixel (0,0,0) to all other trixels in case 2α < β and 3α < γ.

Figure 3.
The number of shortest weighed paths from trixel (0,0,0) to other trixels of the grid with the condition 2α < β and 3α < γ.
3.2. Case of Double-Steps: Case of 2α > β and 3α < γ
In this case the shortest path between p(x1,y1,z1) and q(x2,y2,z2) contains a number of -steps (plus one -step in case p and q are have different parities).The number of -steps is equal to , hence the subsection head. Furthermore, the number of shortest weighted paths, f(w1,w2,w3), between p(x1,y1,z1) and q(x2,y2,z2) is computed based on two sub-cases which are given by the following subsections.
3.2.1. Sub-Case (2α > β and 3α < γ) and S Is an Even Number
Theorem 2.
Let , and be the weights for movements to 1-, 2- and 3-neighbor trixels in the triangular grid, respectively, such that and . Let p(x1,y1,z1) and q(x2,y2,z2) be two trixels of the triangular grid, and w1 = |x1 − x2|, w2 = |y1 − y2| and w3 = |z1 − z2| be the absolute differences between the corresponding coordinates of the trixels such that = w1 + w2 + w3 is an even number. Then, the number of the shortest paths between p and q, denoted by f(w1,w2,w3), is computed as
Proof.
By the given values of the weights, it is clear that the number of -steps equals to in any of the shortest paths and there is no other steps are considered (any 3-step can be broken to three consecutive 1-steps, and any 2 consecutive 1-steps can be joined to a -step such that the total weight of the paths is decreasing if the path has other type of steps originally). First, we deal with the case when the two trixels are on the same lane, i.e., they share one of the coordinates values. In this case, clearly, exactly one shortest path between them, built up by 2-steps on the given common lane; and since , Formula (2) also provides this result.
Now, without loss of generality, assume that p is the origin and q does not share any lane with p. By the symmetry of the grid, there are various, but equivalent cases. Let us consider, first, the case that q(i,j,k) has coordinates with the properties i,j > 0 and k < 0. The base of the induction consists the value 1 for the cases when . We use induction on the sum of the coordinate difference, that is, in this case, i + j − k. By the induction hypothesis let us assume that Equation (2) holds also for each even trixel (i,j,k) with i + j − k < M for any given positive integer M. Then, let us consider an even trixel (i,j,k) with i + j − k = M and count the number of the shortest paths from the origin to (i,j,k). It is clear that since only 2-steps are used, each shortest path goes through only on even trixels. On the other hand, to reach (i,j,k) in a shortest path the last step could be from exactly one of the two trixels (i − 1,j,k + 1) = (i − 1,j,−(|k| − 1)) and (i,j − 1,−(|k| − 1)). However, for these two trixels, the condition that their absolute coordinate sum is less than M holds (it is actually, M − 2 for any of these two trixels). Therefore, by the hypothesis, the number of shortest paths to them can be computed by Formula (2), that is, actually, and , since the first two coordinates correspond to the minimum and to the middle coordinate differences (in one of the others). Then the number of shortest paths to the trixel (i,j,k) is exactly the sum of the previous two values, i.e., , which is the value we wanted to prove.
Now we show the proof in the case i > 0 and j,k < 0. We use induction again on the value M = |i| + |j| + |k|=i − j − k. The base of the induction gives 1 for the cases when . Now, by the induction hypothesis, let us assume that Equation (2) holds for each even trixel (i,j,k) with i + j − k < M for any given positive integer M. Let us consider the shortest paths from (0,0,0) to q(i,j,k) with M = |i| + |j| + |k|. In this case all shortest paths from (0,0,0) to q have the last step either from (i − 1,j + 1,k) = (|i| − 1,−(|j| − 1),k) or from (i − 1,j,k + 1)= (|i| − 1,j,−(|k| − 1)) to q. By the addition rule, we need the sum of the number of shortest paths to those two trixels to get the number of shortest paths between (0,0,0) and q. Observing that in this sixth of the grid, |j| = −j and |k| = −k play the role of and , we have: . That is exactly the value of Formula (2) for the number of shortest paths between (0,0,0) and q, thus the proof has been finished. □
Now, let us give a comment on the previous case, since the result is exactly the same as in the first case, when only 1-steps were used.
Remark 1.
Every two consecutive 1-steps can be joined to a 2-step and any 2-step can be broken to two consecutive 1-steps, in fact there is a bijection between the set of shortest paths used in Theorem 1 and the set of shortest paths used in Theorem 2 between the same trixels (since Theorem 2, only same parity trixels are considered here). By the used sixth of the grid one of the directions of any two consecutive 1-steps is a necessary direction step in a shortest path, while there could be two choices in the other (if the actual trixel is not in the same lane as the target trixel). Thus, by describing every second steps of a shortest path with only 1-steps (case of Theorem 1), one can still uniquely defined the whole path, and in fact, this description gives a shortest path between the same two trixels if only 2-steps are used (i.e., in the case of Theorem 2).
3.2.2. Sub-Case (2α > β and 3α < γ) and S Is an Odd Number
Theorem 3.
Let , and be the weights of the 1-, 2- and 3-steps, respectively, with the conditions . Let p(x1,y1,z1) and q(x2,y2,z2) be two trixels of the triangular grid, and let w1 = |x1 − x2|, w2 = |y1 − y2| and w3 = |z1 − z2| be the absolute differences between the corresponding coordinates of the trixels, such that = w1 + w2 + w3 is odd. Then, the number of shortest paths between p and q, denoted by f(w1,w2,w3), is computed as
Proof.
In this case the shortest path composed of -steps, and one -step. Thus, the total number of steps in any shortest path is . By Remark 1, we know that each shortest path in this case corresponds to a shortest path with only 1-steps (in the sense that only those trixels are used during the path of the actual case which are included in that shortest path with only 1-steps). However, the mapping is not a bijection in this case. There could be many actual shortest paths that correspond to the same shortest path with only 1-steps: in fact, any one of the steps can be the 1-step, and then, all others are 2-steps. This gives us the possibility to use the multiplication rule to count the number of shortest paths, first we can fix a shortest path with only 1-steps in many ways, and then, we can choose different ways the place of the 1-step in the path. Thus, the formula of (3) has been proven. □
Example 2.
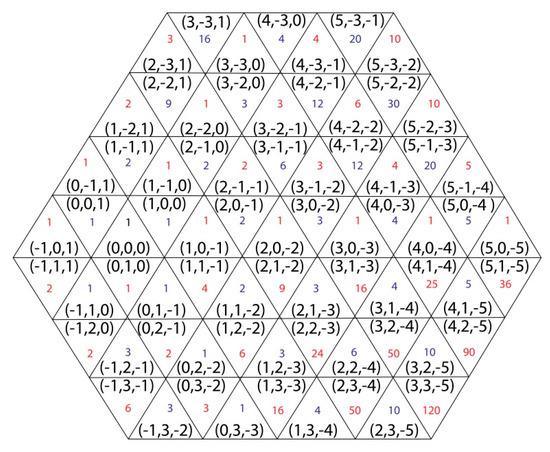
Figure 4 shows the number of shortest weighted paths from (0,0,0) to the displayed trixels of the grid in case 2α > β and 3α < γ.

Figure 4.
The number of shortest weighed paths between trixel (0,0,0) and some other trixels in the case 2α > β and 3α < γ.
3.3. Case of Triple-Steps: Case of 2α < β < γ < 3α
In this case 3-steps have the smallest relative weight, this is from where the name of the subsection comes. Moreover, two consecutive 1-steps give less sum of weights than a 2-step, thus, in this case 2-steps are not used in any shortest paths.
Theorem 4.
Let , and be the weights of 1-, 2- and 3-steps, respectively, such that the weights satisfy the conditions 2α < β < γ < 3α. Let p(x1,y1,z1) and q(x2,y2,z2) be trixels of the triangular grid, further, let w1 = |x1 − x2|, w2 = |y1 − y2| and w3 = |z1 − z2| be the absolute differences between the corresponding coordinates of the trixels. Then, the number of the shortest paths between p and q, denoted by f(w1,w2,w3), is computed as
Proof.
The proof consists of various cases. We start it with the case when the two trixels are in the same lane. Then the number of -steps (and also the number of -steps) is zero. The number of shortest paths becomes one, having exactly one path through 1-neighbors between the two trixels in their common lane. Since = 0, the Formula (4) leads also to this result:
Let us consider the cases when the two trixels are not lying on a common lane. Because of the symmetry of the grid, further we need to differentiate two cases, i.e., we do the proof for two of the sixths of the grid. The sixths of the triangular grid that we are interested in is i,j > 0 and k < 0 (2 positive coordinates and 1 negative), and i > 0 and j,k < 0 (2 negative and 1 positive coordinates). By mirroring these sixths one gets the whole triangular grid. Further, without loss of generality, we assume that p(0,0,0) is the origin and q(i,j,k) with the above properties. Let us consider the possible cases one by one.
Case 1. If the two trixels p(0,0,0) and q(i,j,k) are not in the same lane and i,j > 0 and k < 0. Further, let us assume, first that q is an even trixel and let us see how a shortest path is built up from (0,0,0) to q. The shortest path contains the possible maximum number of “-combo” steps (any of those is a -step followed by an -step, such that both of the first 2 coordinates are increased by 1 and the third coordinate is decreased by 2 during such a “combo” step). Thus, the number of these “combo” steps equals . Notice that both the order and the direction of these steps is fixed by the coordinate values of q. In case i = j, one can reach q in this way, otherwise, “double” α-steps (those are two consecutive α-steps by increasing one of the first two coordinates, the one that had the value , and by also decreasing the value of the third coordinate). The direction and the order of these α-steps is also fixed in a “double” step. Now, any of the shortest paths built up altogether by many “-combo” and “double” α-steps. The order of these combined steps, however, can be arbitrary, and of them are “-combo”. This leads to the formula that we wanted to prove. Observe that in each of the shortest paths in this case the last step, in fact, is an α-step, which decreases the third coordinate. This leads us the solution of the next case.
The next case includes the same sixth of the grid, but q is an odd trixel (i.e., i + j + k = 1). Instead of this odd trixel, let us consider the even trixel q‘(i,j,k − 1). The number of shortest paths from (0,0,0) to q is the same as the number of shortest paths to q′, in fact, there is a bijection between these sets of paths, such that to any paths to q the last α-step from q to q′ is concatenated. However, in this sixth of the grid i and j are playing the role of and (in some order), thus the Formula (4) also holds for this case.
Case 2. Let us consider the other sixth of the grid, thus let p(0,0,0) and q(i,j,k) be given such that i > 0 and j, k < 0 (two negative coordinates and one positive coordinate). First, let q be even.
A shortest path contains the possible maximum number of “-combo” steps (their number is , each of them is increasing the first coordinate by 2 and decreasing each of the other two by 1) and “double” α-steps (two consecutive α-steps, their directions are also fixed by q). Altogether the path contains number of those combined steps from which is “-combo” steps. Since the order of these combined steps is arbitrary, the number of the shortest paths is
which was to be proven.
Finally, let us consider the case in the same sixth of the grid when q(i,j,k) is odd (i + j + k = 1). In this case every shortest path from (0,0,0) will have the last step an α-step from the even trixel q′(i − 1,j,k) to q. Therefore, the number of shortest paths from the origin to q coincides to the number of shortest paths to q′. However, in this case j and k have the values − and (in some order) both for q and q′, and therefore, the Formula (4) gives also the number of the shortest paths to q. The theorem is proven. □
Example 3.
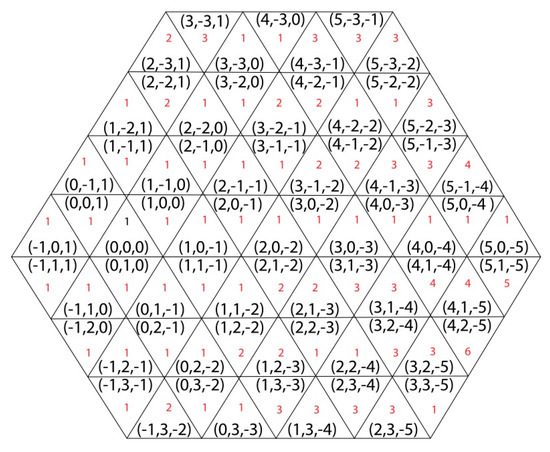
In Figure 5, one can observe the number of shortest weighted paths from the trixel (0,0,0) to some other trixels in case 2α < β < γ < 3α.

Figure 5.
The number of shortest weighed paths from trixel (0,0,0) to some other trixels with the condition 2α < β < γ < 3α.
3.4. Two-Dimensional Extension of Fibonacci Numbers: Case of 2α = β and 3α < γ
In this case every shortest path is built up by 1-steps and 2-steps, they are equally preferred, since their relative weight for changing a coordinate value is the same. Since 3-steps has a larger respective weight, they are not used in any shortest path. Moreover, every two consecutive 1-steps can be changed to a 2-step and vice versa without changing the sum of the weights in the path.
Theorem 5.
Let , and be the weights of 1-, 2- and 3-steps, respectively, such that the weights satisfy the conditions . Let p(x1,y1,z1) and q(x2,y2,z2) be two trixels of the triangular grid, further, let w1 = |x1 − x2|, w2 = |y1 − y2| and w3 = |z1 − z2| be the absolute differences between the corresponding coordinates of the trixels, and be the sum of these absolute differences. Further, let FS denote the S-th Fibonacci number, i.e., the S-th element of the Fibonacci sequence defined by F0 = F1 = 1, Fi+2 = Fi + Fi+1 (for every nonnegative integer i). Then, the number of the shortest paths between p and q, denoted by f(w1,w2,w3), is computed as
Proof.
In this case a shortest weighted path may contain only -steps, or only -steps or both of them. Each -step can be substituted by two -steps and vice versa. The number of shortest weighted paths with only -steps equals to , as we have seen in Formula (1). In each of these paths there are exactly S -steps. In each path, we can always substitute two consecutive -steps by a -step, such that the original path only 1-steps is clearly identifiable. The obtained -step can be broken down to two consecutive -steps in a unique way. Therefore, we may apply the multiplication rule, first by counting the number of base paths with only 1-steps, and then, to count the number of paths when various number of 2-steps are used in various places. That is actually, the number of the possible orders of 1′s and 2′s such that their sum is S = w1 + w2 + w3. Let, then i be the number of -steps (0 i , and each time we increase the number of -steps by 1, we decrease the number of -steps by 2. Thus, there is i 2-steps, and the path contains totally S − i steps. Therefore, we need to sum up the values to get the number of possible ways. Actually, , that is the S-th Fibonacci number: One can see it as follows. When p = q, or they are 1-neighbors, there is exactly 1 shortest path, without any steps (any number) or with a 1-step (one number 1), respectively. Also and have the value 1, as the initial values of the sequence. Now, as an induction hypothesis, let us assume that the number of possible orders of 1′s and 2′s such that their sum is S is exactly when S < M for any fixed M (where M is at least 2). Now there are exactly two ways to have such a sequence of 1′s and 2′s such that their sum is M: either the last element is a 1 or a 2 (1-step and 2-step, respectively, considering paths). However, by the assumption, the number of those sequences (paths) with sum M that have a 1 as their last element is exactly while the number of those that have a 2 as their last element is exactly . Using the addition rule, we get that , which is exactly the recursive formula for the Fibonacci sequence, thus is exactly the M-th element of this sequence. Summarizing it, we have the formula what we wanted to prove:
Example 4.
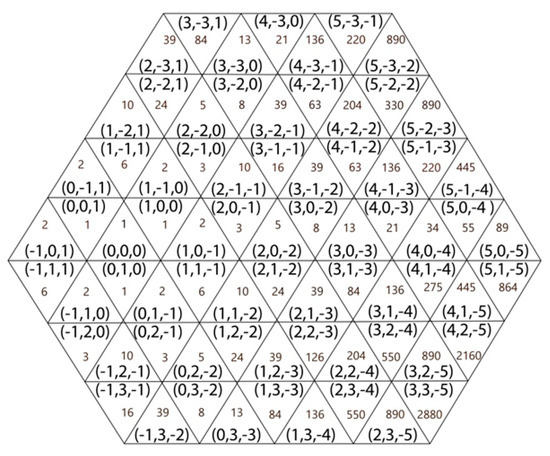
Figure 6 shows the number of shortest paths from trixel (0,0,0) to the displayed trixels in the case 2α = β and 3α < γ.

Figure 6.
The number of the shortest weighed paths from trixel the origin to some other trixels with the condition 2α = β and 3α < γ.
Observe that if the two trixels are in a common lane (i.e., ), the number of the shortest paths between them is, in fact, the S-th (i.e., ()-th) element of the Fibonacci sequence, starting with F0 = F1 = 1. (Actually, as we have shown, see also, e.g., [25], the number of {1,2}-sequences having sum S is FS, that is the S-th element of the Fibonacci sequence.) Based on that, we can see the results as a kind of two-dimensional extension of the Fibonacci sequence.
3.5. Generalising the Sequence of Odd Numbers: Case of 2α < β and 3α = γ
In this case the shortest weighted path between p(x1,y1,z1) and q(x2,y2,z2) is composed from -steps and -steps, and we will never use -steps, where the number of -steps is between 0 and in a shortest weighted path. Note that a -step can always be substituted by three consecutive -steps, but the converse does not hold. The number of shortest weighted paths between p(x1,y1,z1) and q(x2,y2,z2), f(w1,w2,w3), can be computed according to four sub-cases which are given in the next theorem.
Theorem 6.
Let , and be the weights of 1-, 2- and 3-steps, respectively, such that hold. Let p(0,0,0) and q(x,y,z) be two trixels of the triangular grid, further, let the absolute coordinate differences w1 = |x|, w2 = |y| and w3 = |z| and the sum of them be given. Then, there are the following cases for counting the number of the shortest paths, denoted by f(w1,w2,w3), between p and q: If the trixels are in a common lane, that is if , then there is exactly 1 shortest path. If the trixels are not in a common lane then, if S is even, then
If S is odd and q has 2 positive and a negative coordinate, then
If S is odd and q has 2 negative and 1 positive coordinate, then
Proof.
If the trixels are in the same lane, clearly, the shortest path built up by 1-steps including each trixel between them, and there is only 1 such path. Now, let us consider the shortest weighted paths from trixel p(0,0,0) to q(x,y,z) where none of the coordinates of q is zero, i.e., the two trixels are not in the same lane. A shortest path may contain -steps only. It may contain “-combo” steps if q has 1 negative and 2 positive coordinates or it may contain “-combo” steps if q has 2 negative coordinates and 1 positive coordinate. A shortest path may also contain many -steps and also many combo steps (based on the case as they were described above). Now, let us consider the remaining three cases one after the other.
When q is an even trixel, i.e., S is an even number, every shortest path is built up by combo steps and “double” -steps (two consecutive -steps). The type of the combo steps, i.e., either “-combo” or “-combo” depends on the number of negative and positive values among the coordinates x, y and z (as we have already described). We can partition the set of shortest paths to equivalent classes based on the number of combo steps used in them. Consequently, we will compute the number of shortest paths in each such blocks and we sum up those values. On the one hand, we may have only -steps in a shortest path, which means that 0 combo steps are used. On the other hand, the maximal number of combo steps in a shortest path (since they change all the three coordinate values), is . When only -steps are used, the number of such shortest paths is (from Theorem 1). The number of shortest paths with the maximal number of combo steps is (from Theorem 4). In one combo step the sum of the coordinate changes in absolute value is 4 (3 + 1 in and 1 + 3 in -combo), while a double -step changes 2 of the coordinates with sum 2 in absolute value, that implies that a combo step can be changed to two double -steps (although the reverse may not hold). Let i be the number of the combo steps in a shortest path where , then the number of combo and double steps in such shortest path is . It is actually, double -steps, if combo steps are not used: and of them in one direction, while of them in other direction (60 degree between the two directions). Moreover, each combo steps decrease the number of double steps by 2, i.e., by one and one both directions double -steps, and therefore the sum of all types of combined steps by 1. In any path the used combo and double -steps can be put in any order. Thus, the combination of the i combo, double -steps in one direction and double -steps in the other direction, altogether steps, gives the number of shortest paths in this block. This number can be written as . By summing up these values for the possible values of i, one gets exactly the Formula (6). The proof of this case is finished.
In the case S = |x| + |y| + |z| is odd and q(x,y,z) has 2 positive and one negative coordinate, by the symmetry of the triangular grid, we consider only x, y > 0 and z < 0. In this sixth of the grid, in the shortest paths “-combo” and “double” -steps can be used (to any even trixel). In what follows, for any even trixel q′ the shortest path finishes with an -step into the opposite direction than axis z., i.e., by decreasing the third coordinate and not changing the other two. Therefore, the number of shortest paths from the trixel (0,0,0) to the odd trixel q(x,y,z) is exactly the same as the number of shortest paths from (0,0,0) to the even trixel q′(x,y,z 1). However, the number of shortest paths to q′ is already computed in the previous case. Knowing that in this sixth of the grid, one of x and y plays the role of and the other plays the role of and for q′ the sum of the coordinate differences is one more than it is for q (it is S + 1 for q′), the number of shortest paths is proven to be:
Finally, considering the last case, because of symmetry, we use x > 0 and y,z < 0. In this sixth of the grid, all shortest paths to an even trixel q′ built up by “-combo” and “double” -steps. To reach an odd trixel q(x,y,z) every shortest path from (0,0,0) has the last step as an -step from the trixel q′(x − 1,y,z) to q(x,y,z). From this fact, it flows that the number of shortest path from (0,0,0) to q is the same as to q′. However, the latter one is already proven and it is computed by Formula (6). In this sixth of the grid −y and −z play the role of and in an order. Further, the sum of the absolute coordinate values is S for q, then it is S − 1 for q′. Therefore, one needs to modify the Formula (6) according to this and gets
which was to be proven. Thus, each case of the theorem is proven. □
Remark 2.
Observe that if , . We also know that the number of shortest paths to any odd trixel is the same as the number of shortest paths to an even neighbor trixel. To make a comment on the title of the subsection let us consider the special case when, e.g., two even trixels are located such that . Then Let denote by n. Then, S = 2n. The variable i of Formula (6) could be either 0 or 1 (the number of combo steps containing an - and a -step). Thus, we have the sum of two values, namely, and This gives, n + n − 1 = 2n − 1, which is exactly the n-th positive odd number. Hence the name of the case.
Example 5.
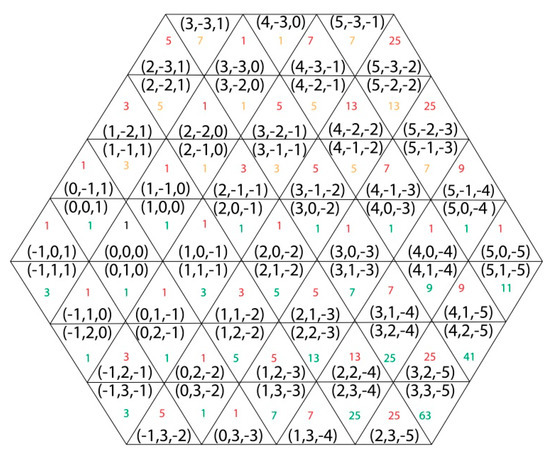
In Figure 7 the number of weighted shortest paths from the origin (0,0,0) to some trixels are presented in case of 2α < β and 3α = γ. The sequence of odd number can be seen as embedded next to the lanes containing the origin and having only 1′s.

Figure 7.
The number of shortest weighed paths from trixel (0,0,0) to all other displayed trixels in the case of 2α < β and 3α = γ.
4. Conclusions
This paper discusses five of the most popular cases for the number of shortest weighted paths between any two trixels in the triangular grid. The number of these paths depends on the weights of the movements from the trixel to its various types of neighbors. In Section 3.1 (2α < β and 3α < γ), is preferred, it has the smallest relative weight for changing a coordinate value in a path, and thus, no shortest path contains any - and -steps. In this case, clearly, binomial coefficients based on coordinate differences of the trixels provide the number of shortest paths. In Section 3.2 (2α > β and 3α < γ), -steps are preferred, has the smallest relative weight for changing a coordinate value in a path, and thus, no shortest path contain any -steps (and at most one -step is used, since we may need to change the parity when we are looking for a shortest path between an odd and an even trixel). The results are given either by binomial coefficients or by their multipliers, depending on the parities of the trixels. In contrast to this, in Section 3.3 (when the weights satisfy 2α < β < γ < 3α) -steps are not used at all, in fact -steps are preferred (even by adding also many -steps because of the parities of the trixels). The numbers of shortest paths are again described by binomial coefficients. In the case considered in Section 3.4 (2α = β and 3α < γ), -steps and -steps are equally preferred, and no -step can occur in a shortest path. We have seen that the results, in this case, can be seen as a two dimensional extension of the Fibonacci sequence. In our last studied case, with weights satisfying 2α < β and 3α = γ, -steps and -steps are equally preferred, and no -step can occur. While in some cases the computation results clearly well-known binomials, the structure of the grid gives some more interesting cases. We believe that the cases presented here are among the most basic and usual ones: we have studied the cases, when exactly one or two types of steps are not preferred, and therefore they have not appeared in any of the shortest paths. However, there are also some other interesting cases that can be discussed later on, e.g., when and , when all the three types of steps are equally preferred. Another possible future task is to consider “inhomogeneous” distribution of the weights, which involves counting the number of shortest weighted paths of one case concatenated by the shortest weighted paths of another case. A somehow connected result was discussed in [22]: “digital disks” were defined and used to approximate the Euclidean disks where the set of gridpoints having less (or equal) distance than a given radius from a given gridpoint defined the digital disk.
Author Contributions
Writing—original draft, B.K.; Supervision, Writing—review & editing, B.N. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klette, R.; Rosenfeld, A. Digital Geometry: Geometric Methods for Digital Picture Analysis; Morgan Kaufmann: Burlington, MA, USA, 2004; pp. 1–656. ISBN 978-1-55860-861-0. [Google Scholar]
- Nagy, B. A symmetric coordinate frame for hexagonal networks. In Proceedings of the Theoretical Computer Science—In the 7th International Multi-Conference on the Information Society (IS-TCS’04), Ljubljana, Slovenia, 11–15 October 2004; pp. 193–196. [Google Scholar]
- Nagy, B. Shortest Path in Triangular Grids with Neighbourhood Sequences. J. Comput. Inf. Technol. 2003, 11, 111–122. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Pfaltz, J. Distance functions on digital pictures. Pattern Recognit. 1968, 1, 33–61. [Google Scholar] [CrossRef]
- Das, P. Counting minimal paths in digital geometry. Pattern Recognit. Lett. 1991, 12, 595–603. [Google Scholar] [CrossRef]
- Yamashita, M.; Ibaraki, T. Distances defined by neighborhood sequences. Pattern Recognit. 1986, 19, 237–246. [Google Scholar] [CrossRef]
- Das, P.; Chakrabarti, P.; Chatterji, B. Generalized distances in digital geometry. Inform. Sci. 1987, 42, 51–67. [Google Scholar] [CrossRef]
- Nagy, B. Distance functions based on generalized neighbourhood sequences in finite and infinite dimensional space. In Proceedings of the 5th International Conference on Applied Informatics (ICAI’01), Eger, Hungary, 28 January–3 February 2001; pp. 183–190. [Google Scholar]
- Nagy, B. Distance functions based on neighbourhood sequences. Publ. Math. 2003, 63, 483–493. [Google Scholar]
- Nagy, B. Distance with generalized neighbourhood sequences in nD and ∞D. Discret. Appl. Math. 2008, 156, 2344–2351. [Google Scholar] [CrossRef]
- Borgefors, G. Distance transformations in digital images. Comput. Graph. Image Process. 1986, 34, 344–371. [Google Scholar] [CrossRef]
- Nagy, B. On the number of shortest paths by neighborhood sequences on the square grid. In Proceedings of the Abstract Booklet of the Joint Austrian-Hungarian Mathematical Conference, Győr, Hungary, 25–27 August 2015. [Google Scholar]
- Alzboon, L.; Khassawneh, B.; Nagy, B. On the Number of Weighted Shortest Paths in the Square Grid. In Proceedings of the IEEE 21st International Conference on Intelligent Engineering Systems (INES), Larnaca, Cyprus, 20–23 October 2017; pp. 83–90. [Google Scholar]
- Lee, M.; Jayanthi, S. Hexagonal Image Processing: A Practical Approach (Advances in Pattern Recognition); Springer: Berlin, Germany, 2005. [Google Scholar]
- Nagy, B. Application of neighborhood sequences in communication of hexagonal networks. Discret. Appl. Math. 2017, 216, 424–440. [Google Scholar] [CrossRef]
- Lukic, T.; Nagy, B. Binary tomography on the isometric tessellation involving pixel shape orientation. IET Image Process. 2020, 14, 25–30. [Google Scholar]
- Deutsch, E.S. Thinning algorithms on rectangular, hexagonal, and triangular arrays. Commun. ACM 1972, 15, 827–837. [Google Scholar] [CrossRef]
- Nagy, B. Metrics based on neighbourhood sequences in triangular grids. Pure Math. Appl. 2002, 13, 259–274. [Google Scholar]
- Nagy, B. Digital geometry of various grids based on neighbourhood structures. In Proceedings of the 6th Conference of Hungarian Association for Image Processing and Pattern Recognition (KEPAF 2007), Debrecen, Hungary, 25–27 January 2007; pp. 46–53. [Google Scholar]
- Nagy, B. Finding Shortest Path with Neighborhood Sequences in Triangular Grids. In Proceedings of the 2nd IEEE International Symposium on Image and Signal Processing and Analysis (ITI-ISPA 2001), Pula, Croatia, 19–21 June 2001; pp. 55–60. [Google Scholar]
- Nagy, B. Weighted distances on a triangular grid. In International Workshop on Combinatorial Image Analysis, Brno, Czech Republic, 28–30 May 2014; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8466, pp. 37–50. [Google Scholar]
- Nagy, B.; Mir-Mohammad-Sadeghi, H. Digital disks by weighted distances in the triangular grid. In International Conference on Discrete Geometry for Computer Imagery, Nantes, France, 18–20 April 2016; Normand, N., Guédon, J., Autrusseau, F., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9647, pp. 385–397. [Google Scholar]
- Kovács, G.; Nagy, B.; Vizvári, B. Chamfer distances on the isometric grid: A structural description of minimal distances based on linear programming approach. J. Comb. Optim. 2019, 38, 867–886. [Google Scholar] [CrossRef]
- Dutt, M.; Biswas, A.; Nagy, B. Number of Shortest Paths in Triangular Grid for 1- and 2-Neighborhoods. In International Workshop on Combinatorial Image Analysis, Kolkata, India, 24–27 November 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9448, pp. 115–124. [Google Scholar]
- Nagy, B.; Akkeleş, A. Trajectories and Traces on Non-traditional Regular Tessellations of the Plane. In International Workshop on Combinatorial Image Analysis, Plovdiv, Bulgaria, 19–21 June 2017; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10256, pp. 16–29. [Google Scholar]
- Nagy, B. Isometric transformations of the dual of the hexagonal lattice. In Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis (ISPA 2009), Salzburg, Austria, 16–18 September 2009; pp. 432–437. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).