Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations
Abstract
1. Introduction
2. The Fractional Diffusion Model and Option Pricing
2.1. Exponential Market Models
- Gaussian process: (standard Brownian motion). In this case, the stock price is said to follow a geometric Brownian motion. This is the basic hypothesis for the Black-Scholes model [40].
- Lévy process: (standardized Lévy-stable process with stability and skewness or asymmetry ). In this case, one says that follows an exponential Lévy-stable process (see the details in [43]). Exponential Lévy models generalize the Gaussian framework (because for any ), while allowing additional realistic features such as the presence of price jumps with non-zero probability. Their relevance in financial modeling has been known since the works of Mandelbrot and Fama [50,51]. For most financial applications, only the so-called Lévy-Pareto distributions, i.e., the values , are relevant (historically, Mandelbrot calibrated for the cotton market).
2.2. Generalizing Exponential Market Models: The Fractional Diffusion Model
2.2.1. Setup of the Model
2.2.2. Financial Interpretation of the Parameters
2.3. Particular Cases
2.3.1. Finite Moment Log Stable model
2.3.2. Black-Scholes Model
3. Pricing Formulas
3.1. Risk-Neutral Parameter
3.2. European Options
3.3. Binary (or Digital) Options
3.3.1. Cash-or-Nothing
- The poles of at the points , whose residues are given by the formula:
- The poles of at the points , whose residues are given by the formula:
3.3.2. Asset-or-Nothing
4. Risk Sensitivities and Portfolio Hedging
4.1. First Order Sensitivity (Delta)
4.1.1. European Call
4.1.2. Cash-or-Nothing Call
4.1.3. Cash-or-Nothing Put
4.1.4. Asset-or-Nothing Call
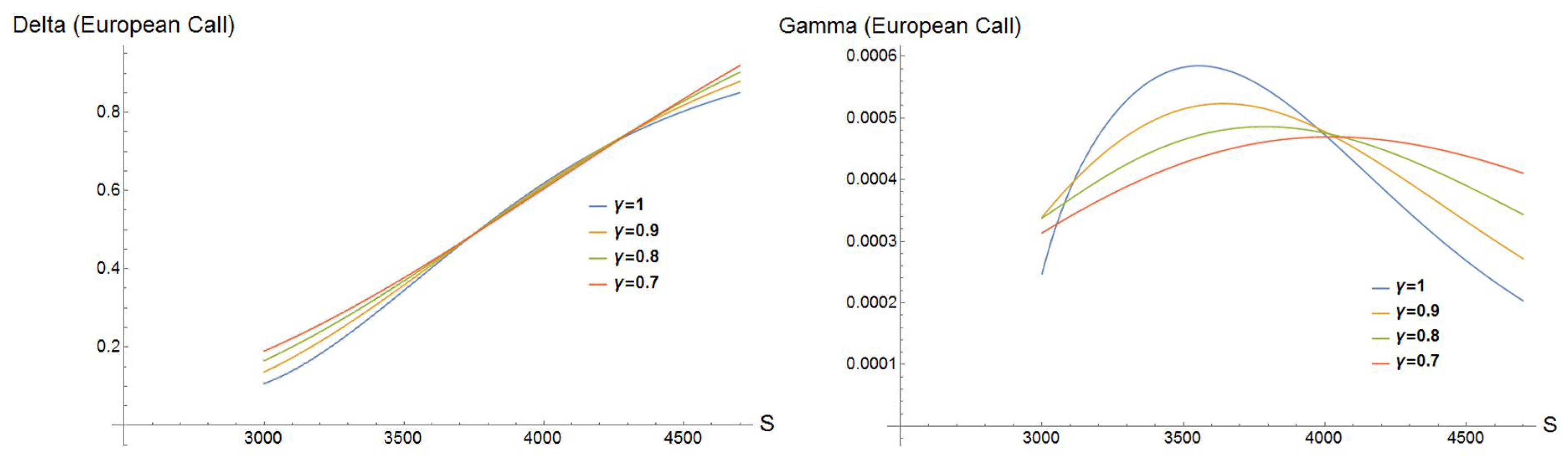
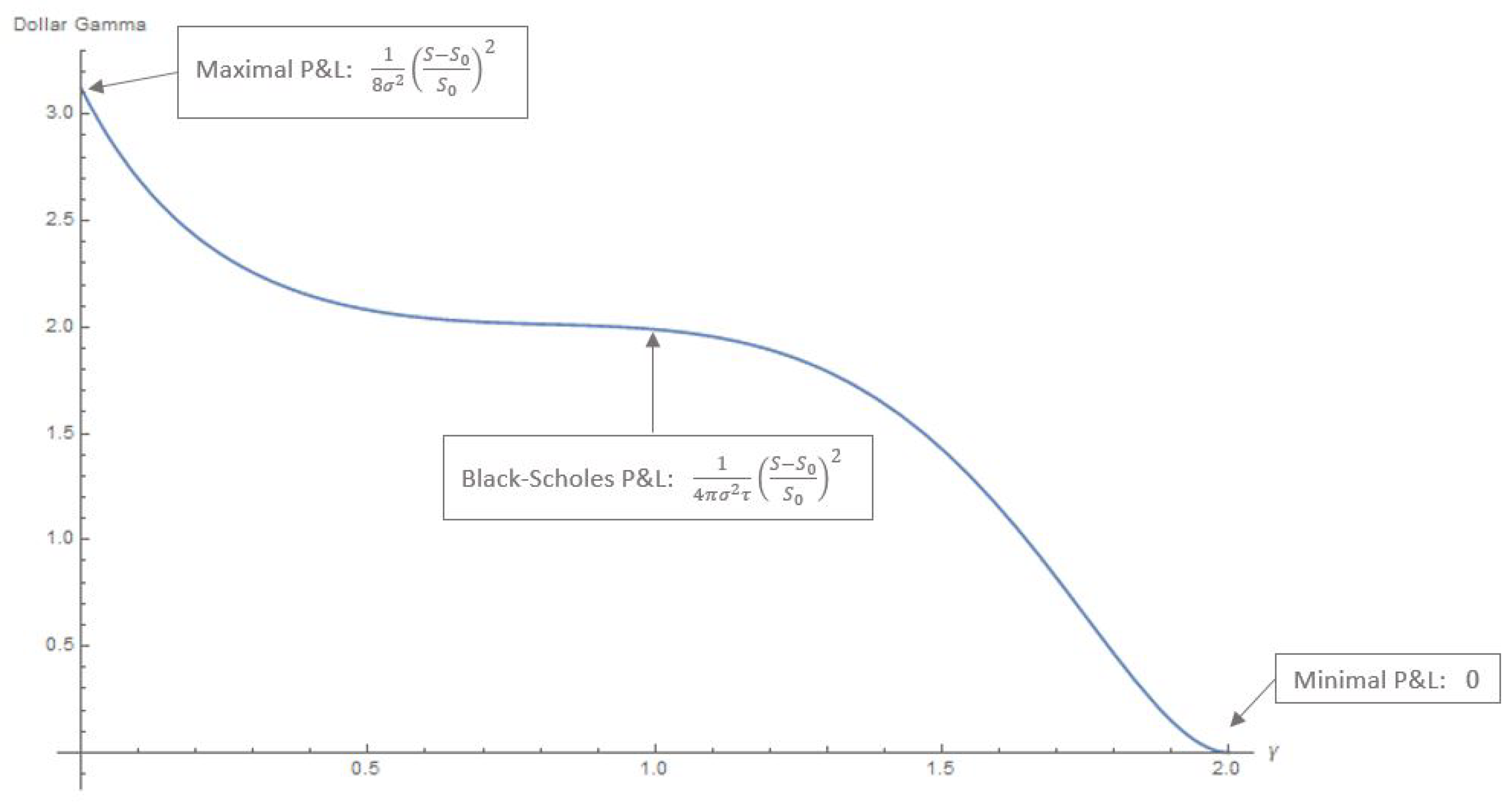
4.2. Second Order Sensitivity (Gamma, Dollar Gamma)
- If :
- If :
- If :
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Kochubei, A.; Luchko, Y. (Eds.) Handbook of Fractional Calculus with Applications. Volume 1: Basic Theory; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Kochubei, A.; Luchko, Y. (Eds.) Handbook of Fractional Calculus with Applications. Volume 2: Fractional Differential Equations; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V. (Ed.) Handbook of Fractional Calculus with Applications. Volume 4: Applications in Physics, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V. (Ed.) Handbook of Fractional Calculus with Applications. Volume 5: Applications in Physics, Part B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Petras, I. (Ed.) Handbook of Fractional Calculus with Applications. Volume 6: Applications in Control; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Baleanu, D.; Mendes Lopes, A. (Eds.) Handbook of Fractional Calculus with Applications. Volume 7: Applications in Engineering, Life and Social Sciences, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Baleanu, D.; Mendes Lopes, A. (Eds.) Handbook of Fractional Calculus with Applications. Volume 8: Applications in Engineering, Life and Social Sciences, Part B.; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; Wiley-VCH: Hoboken, NJ, USA, 2008. [Google Scholar]
- Jin, B.; Rundell, W. A tutorial on inverse problems for anomalous diffusion processes. Inverse Probl. 2015, 31, 035003. [Google Scholar] [CrossRef]
- Luchko, Y. Anomalous Diffusion: Models, Their Analysis, and Interpretation. In Advances in Applied Analysis; Rogosin, S.V., Koroleva, A.A., Eds.; Birkhäuser: Basel, Switzerland, 2012; pp. 115–146. [Google Scholar]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. Phys. A Math. Gen. 2004, 37, R161–R208. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Helbing, D.; Brockmann, D.; Chadefaux, T. Saving Human Lives: What Complexity Science and Information Systems can Contribute. J. Stat. Phys. 2015, 158, 735. [Google Scholar] [CrossRef]
- Perc, M.; Ozer, M.; Hojnik, J. Social and juristic challenges of artificial intelligence. Palgrave Commun. 2019, 5, 61. [Google Scholar] [CrossRef]
- Fallahgoul, H.; Focardi, S.; Fabozzi, F. Fractional Calculus and Fractional Processes with Applications to Financial Economics: Theory and Application; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Gorenflo, R.; Mainardi, F.; Moretti, D.; Paradisi, P. Time fractional diffusion: a discrete random walk approach. Nonlinear Dyn. 2002, 29, 129–143. [Google Scholar] [CrossRef]
- Kerss, A.; Leonenko, N.N.; Sikorskii, A. Fractional Skellam processes with applications to finance. Fract. Calc. Appl. Anal. 2014, 17, 532–551. [Google Scholar] [CrossRef]
- Scalasa, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, V.V. Macroeconomic models with long dynamic memory: Fractional calculus approach. Appl. Math. Comput. 2018, 338, 466–486. [Google Scholar] [CrossRef]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Tarasova, V.V.; Tarasov, V.E. Concept of dynamic memory in economics. Commun. Nonlinear Sci. 2018, 55, 127–145. [Google Scholar] [CrossRef]
- Tejado, I.; Pérez, E.; Valério, D. Fractional calculus in economic growth modeling of the group of seven. Fract. Calc. Appl. Anal. 2019, 22, 139–157. [Google Scholar] [CrossRef]
- Elliott, R.J.; van der Hoek, J. A general fractional white noise theory and applications to finance. Math. Financ. 2003, 13, 301–330. [Google Scholar] [CrossRef]
- Longjin, L.; Ren, F.-Y.; Qiu, W.-Y. The application of fractional derivatives in stochastic models driven by fractional Brownian motion. Phys. A 2010, 389, 4809–4818. [Google Scholar] [CrossRef]
- Vilela Mendes, R. A fractional calculus interpretation of the fractional volatility model. R. Nonlinear Dyn. 2009, 55, 395. [Google Scholar] [CrossRef]
- Necula, C. Option Pricing in a Fractional Brownian Motion Environment. 2002. Available online: https://ssrn.com/abstract=1286833 (accessed on 29 August 2019).
- Akrami, M.H.; Erjaee, G.H. Examples of analytical solutions by means of Mittag-Leffler function of fractional Black-Scholes option pricing equation. Fract. Calc. Appl. Anal. 2015, 18, 38–47. [Google Scholar] [CrossRef]
- Gong, X.; Zhuang, X. American option valuation under time changed tempered stable Lévy processes. Phys. A 2017, 466, 57–68. [Google Scholar] [CrossRef]
- Wang, X.T. Scaling and long-range dependence in option pricing I: Pricing European option with transaction costs under the fractional Black-Scholes model. Phys. A 2010, 389, 438–444. [Google Scholar] [CrossRef]
- Yavuz, M.; Necati, Ö. European Vanilla Option Pricing Model of Fractional Order without Singular Kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Cartea, A.; del-Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Phys. A 2007, 374, 749–763. [Google Scholar] [CrossRef]
- Chen, W.; Xu, X.; Zhu, S.P. Analytically pricing double barrier options based on a time-fractional Black-Scholes equation. Comput. Math. Appl. 2015, 69, 1407–1419. [Google Scholar] [CrossRef]
- Xiao, W.L.; Zhang, W.G.; Zhang, X.L.; Wang, Y.L. Pricing currency options in a fractional Brownian motion with jumps. Econ. Model. 2010, 27, 935–942. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of time-fractional Black-Scholes equation. Comput. Appl. Math. 2017, 36, 1699–1715. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black-Scholes option pricing model by finite difference method. Abstr. Appl. Anal. 2013, 2013, 194286. [Google Scholar] [CrossRef]
- Funahashi, H.; Kijima, M. A solution to the time-scale fractional puzzle in the implied volatility. Fractal Fract. 2017, 1, 14. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Heston, S.L. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Duan, J.C.; Popova, I.; Ritchken, P. Option pricing under regime switching. Quant. Financ. 2002, 2, 209. [Google Scholar] [CrossRef]
- Cont, R.; Tankov, P. Financial Modelling with Jump Processes; Chapman & Hall: New-York City, NY, USA, 2004. [Google Scholar]
- Carr, P.; Wu, L. The Finite Moment Log Stable Process and Option Pricing. J. Financ. 2003, 58, 753–778. [Google Scholar] [CrossRef]
- Kleinert, H.; Korbel, J. Option pricing beyond Black-Scholes based on double-fractional diffusion. Phys. A 2016, 449, 200–214. [Google Scholar] [CrossRef]
- Aguilar, J.-P.; Coste, C.; Korbel, J. Series representation of the pricing formula for the European option driven by space-time fractional diffusion. Fract. Calc. Appl. Anal. 2018, 21, 981–1004. [Google Scholar] [CrossRef]
- Aguilar, J.-P.; Korbel, J. Option pricing models driven by the space-time fractional diffusion: series representation and applications. Fractal Fract. 2018, 2, 15. [Google Scholar] [CrossRef]
- Aguilar, J.-P.; Korbel, J. Simple formulas for pricing and hedging European options in the Finite Moment Log Stable model. Risks 2019, 7, 36. [Google Scholar] [CrossRef]
- Korbel, J.; Luchko, Y. Modeling of financial processes with a space-time fractional diffusion equation of varying order. Fract. Calc. Appl. Anal 2016, 19, 1414–1433. [Google Scholar]
- Fama, E.F. The behavior of stock market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Wilmott, P. Paul Wilmott on Quantitative Finance; Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gerber, H.U.; Shiu, E.S.W. Option Pricing by Esscher Transforms. Trans. Soc. Actuar. 1994, 46, 99–191. [Google Scholar]
- Zolotarev, V.M. One-Dimensional Stable Distributions; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
- Flajolet, P.; Gourdon, X.; Dumas, P. Mellin transform and asymptotics: Harmonic sums. Theor. Comput. Sci. 1995, 144, 3–58. [Google Scholar] [CrossRef]
- Bateman, H. Tables of Integral Transforms (Volume I&II); McGraw & Hill: New-York, NY, USA, 1954. [Google Scholar]
- Aguilar, J.-P. On expansions for the Black-Scholes prices and hedge parameters. J. Math. Anal. Appl. 2019, 478, 9739–9989. [Google Scholar] [CrossRef]
- Brenner, M.; Subrahmanyam, M.G. A simple approach to option valuation and hedging in the Black-Scholes Model. Financ. Anal. J. 1994, 50, 25–28. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, J.-P.; Korbel, J.; Luchko, Y. Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations. Mathematics 2019, 7, 796. https://doi.org/10.3390/math7090796
Aguilar J-P, Korbel J, Luchko Y. Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations. Mathematics. 2019; 7(9):796. https://doi.org/10.3390/math7090796
Chicago/Turabian StyleAguilar, Jean-Philippe, Jan Korbel, and Yuri Luchko. 2019. "Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations" Mathematics 7, no. 9: 796. https://doi.org/10.3390/math7090796
APA StyleAguilar, J.-P., Korbel, J., & Luchko, Y. (2019). Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations. Mathematics, 7(9), 796. https://doi.org/10.3390/math7090796






