Kolmogorov-Arnold-Moser Theory and Symmetries for a Polynomial Quadratic Second Order Difference Equation

Abstract

By using the Kolmogorov-Arnold-Moser (KAM) theory, we investigate the stability of two elliptic equilibrium points (zero equilibrium and negative equilibrium) of the difference equation $t_{n+1}=\alpha t_n+\beta t_n^2-t_{n-1},n=0,1,2,\dots ,$ where are $t_{-1}$, $t_0$, $\alpha \in \mathbb{R}$, $\alpha \ne 0$, $\beta >0$. By using the symmetries we find the periodic solutions with some periods. Finally, some numerical examples are given to verify our theoretical results.

1. Introduction and Preliminaries

In this paper, we investigate the behavior of the polynomial quadratic second order difference equation

$$t_{n+1}=\alpha t_n+\beta t_n^2-t_{n-1},n=0,1,2,\dots ,$$

(1)

where is parameter $\beta >0$, parameter $\alpha \ne 0$ and the initial conditions $t_{-1}$, $t_0$ are real numbers.

In References [1,2] the global dynamics of polynomial difference equations

$$x_{n+1}=c{x}_{n-1}^2+d{x}_{n-1}+1,$$

(2)

and

$$x_{n+1}=\sum _{i=0}^3\sum _{j=0}^i{\zeta }_{ij}{x}_n^{i-j}{x}_{n-1}^j,$$

(3)

are studied, where

$$c>0,d>0,{\zeta }_{ij}\ge 0,x_{-1}\ge 0,x_0\ge 0n=0,1,2\dots .$$

(4)

In studying the global dynamics of (1) and (2), with non-negative initial conditions and non-negative parameters, the authors used the theory of monotonic maps.

There is extensive literature on polynomial difference equations in the complex domain in the last 30 years by mathematicians. First investigations on polynomial difference equations with non-negative parameters and initial conditions were for a special case

$$x_{n+1}=B{x}_n{x}_{n-1}+E{x}_{n-1}+F,n=0,1,2,\dots .$$

This difference equation was the subject of many mathematical results published in papers [3,4,5]. One of open problems in mathematics known as the 16th Hilbert problem is to find the upper limit number of periodic solutions of the system of polynomial differential equations of the forms

$$\frac{dx}{dt}=P(x,y)\mathrm{and}\frac{dy}{dt}=Q(x,y)$$

depending on the degree and coefficients of the polynomials $P(x,y)$ and $Q(x,y)$, and then determine the local character of periodic solutions. Y. Ilyashenko and J. Écalle ($1991/1992$) have shown that this number is finite in the case where $degP=degQ=2$ (see [6]).

Equation (1) is a special case of the equation

$$x_{n+1}=\sum _{i=0}^2\sum _{j=0}^i{\zeta }_{ij}{x}_n^{i-j}{x}_{n-1}^j,$$

(5)

which is equivalent to the following system of difference equations

$$\begin{array}{ccc}\hfill x_{n+1}& =& \sum _{i=0}^2\sum _{j=0}^i{\zeta }_{ij}{x}_n^{i-j}{y}_n^j,\hfill \\ \hfill y_{n+1}& =& x_n.\hfill \end{array}$$

This system is a special case of discrete version of the 16th Hilbert problem and for which, in Reference [7], the authors have shown that under certain conditions may have infinitely many periodic solutions of the period 2, which means that the discrete version of 16th Hilbert problem does not hold.

One of the most famous examples of a polynomial difference equation is the second-order Hénon difference equation

$$x_{n+1}=1+B{x}_{n-1}-A{x}_n^2,n=0,1,2,\dots .$$

(6)

The dynamics of this equation are very complex, for which the existence of a chaotic attractor has been proven ([8]).

Note that after the substitution

$$t_n=-\frac{\alpha }{2\beta }-\frac{\alpha \left(\alpha -4\right)}{4\beta }{u}_n$$

(7)

Equation (1) becomes

$$\alpha \left(\alpha -4\right)\left({\alpha }^2{u}_n^2-4\alpha u_n^2+4u_{n-1}+4u_{n+1}-4\right)=0.$$

For $\alpha \ne 0$ and $\alpha \ne 4$ we get

$$u_{n+1}=1-\frac{\alpha \left(\alpha -4\right)}{4}{u}_n^2-u_{n-1}.$$

If

$$a=\frac{\alpha \left(\alpha -4\right)}{4},b=-1,$$

we get Hénon’s mapping

$$u_{n+1}=1-a{u}_n^2+b{u}_{n-1}.$$

Equation (1) has very specific dynamics. Namely, we cannot find the invariant of this equation and we can use only Kolmogorov-Arnold-Moser (KAM) theory to investigate the dynamics of this equation. Some results about using KAM theory are given in References [9,10,11,12,13,14,15,16,17,18,19,20,21]. Other techniques have been used (not only KAM theory) to study the Lyness’ equation (see References [9,10,11,17,22,23,24,25,26,27]).

The definition of an area preserving map is given in Reference [21] (Definition 1). Also, for the basic results about Birkhoff normal forms and the KAM theory, see References [8,20,21,28,29,30,31] (especially see Theorems 1–4 and Remark 1 in [21]).

Assume that $\beta >0$. Then Equation (1) has a unique equilibrium $\overline{t}=0$ for $\alpha =2$ and two equilibrium points ${\overline{t}}_1=0$ and ${\overline{t}}_2=\frac{2-\alpha }{\beta }$, where ${\overline{t}}_2$ is positive for $\alpha <2$ and ${\overline{t}}_2$ is negative for $\alpha >2$.

Equation (1) can be transformed into the system

$$\left.\begin{array}{ccc}\hfill x_{n+1}& =& \beta x_n^2+\alpha x_n-y_n\hfill \\ \hfill y_{n+1}& =& x_n.\hfill \end{array}\right\}$$

(8)

The map T associated to System (8) takes the form

$$T\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\beta x^2+\alpha x-y\\ x\end{array}\right).$$

Jacobian matrix of map T at the point $(x,y)$ is given by

$$J_T\left(x,y\right)=\left(\begin{array}{cc}2\beta x+\alpha & -1\\ 1& 0\end{array}\right).$$

Since $det{J}_T\left(x,y\right)=1$, the map T is an area preserving map.

Remark 1.

When the equilibrium point of Equation (1) is a non-hyperbolic of elliptic type and T is an area-preserving map, we can apply KAM theory to the investigation of its stability.

Lemma 1.

Assume that $\beta >0$.

1.

For $\alpha \in \left(-\infty ,-2\right)\cup \left(2,\infty \right)$ the equilibrium $(0,0)$ is a saddle point.

2.

For $\alpha =\pm 2$ the equilibrium $(0,0)$ is non-hyperbolic of the parabolic type.

3.

For $\alpha \in \left(-2,2\right)$ the equilibrium $(0,0)$ is non-hyperbolic of the elliptic type.

Proof. 

For $\overline{x}=\overline{y}=0,\alpha \in \mathbb{R},\beta >0:$

$$J_0=J_T\left(0,0\right)=\left(\begin{array}{cc}\alpha & -1\\ 1& 0\end{array}\right).$$

The characteristic equation at $(0,0)$ is

$${\lambda }^2-\alpha \lambda +1=0,$$

(9)

and we have the following cases:

• ${\lambda }_{1,2}=\frac{\alpha \pm \sqrt{{\alpha }^2-4}}{2}$ for $\alpha \in \left(-\infty ,-2\right)\cup \left(2,\infty \right),$ and ${\lambda }_1\in \left(-1,0\right),{\lambda }_2<-1$ or ${\lambda }_1\in \left(0,1\right),{\lambda }_2>1$,
• ${\lambda }_{1,2}=-1$ for $\alpha =-2$ and ${\lambda }_{1,2}=1$ for $\alpha =2$,
• ${\lambda }_{1,2}=\frac{\alpha \pm i\sqrt{4-{\alpha }^2}}{2}$ for $\alpha \in \left(-2,2\right)$.

  □

Lemma 2.

Assume that $\beta >0$.

1.

For $\alpha \in \left(-\infty ,2\right)$ the positive equilibrium $\left(\frac{2-\alpha }{\beta },\frac{2-\alpha }{\beta }\right)$ is a saddle point.

2.

For $\alpha \in \left(2,6\right)$ the negative equilibrium $\left(\frac{2-\alpha }{\beta },\frac{2-\alpha }{\beta }\right)$ is non-hyperbolic of the elliptic type.

3.

For $\alpha =6$ the negative equilibrium $\left(\frac{2-\alpha }{\beta },\frac{2-\alpha }{\beta }\right)$ is non-hyperbolic of the parabolic type.

4.

For $\alpha >6$ the negative equilibrium $\left(\frac{2-\alpha }{\beta },\frac{2-\alpha }{\beta }\right)$ is a saddle point.

Proof. 

For $\overline{x}=\overline{y}=\frac{2-\alpha }{\beta },\alpha \in \mathbb{R},\beta >0$ we have

$$J_T\left(\overline{x},\overline{x}\right)=\left(\begin{array}{cc}4-\alpha & -1\\ 1& 0\end{array}\right).$$

The corresponding characteristic equation is:

$${\lambda }^2+\left(\alpha -4\right)\lambda +1=0.$$

So that:

• ${\lambda }_1=\frac{4-\alpha -\sqrt{\left(\alpha -2\right)\left(\alpha -6\right)}}{2}\in \left(0,1\right)$, ${\lambda }_2=\frac{4-\alpha +\sqrt{\left(\alpha -2\right)\left(\alpha -6\right)}}{2}>1$ for $\alpha \in \left(-\infty ,2\right)$.
• ${\lambda }_{1,2}=\frac{4-\alpha \pm i\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}{2}$ for $\alpha \in \left(2,6\right)$ and $\left|{\lambda }_{1,2}\right|=1$.
• ${\lambda }_{1,2}=-1$ for $\alpha =6$.
• ${\lambda }_1=\frac{4-\alpha -\sqrt{\left(\alpha -2\right)\left(\alpha -6\right)}}{2}<-1,{\lambda }_2=\frac{4-\alpha +\sqrt{\left(\alpha -2\right)\left(\alpha -6\right)}}{2}\in \left(-1,0\right)$ for $\alpha >6.$

  □

This paper is organized as follows. By using KAM theorem, in Section 2, we will prove that the equilibrium points ${\overline{t}}_1=0$ for $\alpha \in (-2,2)\backslash \left\{-1,-\frac{1}{2},0\right\}$, $\beta >0$ and ${\overline{t}}_1=\frac{2-\alpha }{\beta }$ for $\alpha \in (2,6)\backslash \left\{4,\frac{9}{2},5\right\}$, $\beta >0$ are stable. In Section 3, we will prove that there exists an infinite number of periodic solutions. Also, we will study the minimal possible period (M.P.P.) for periodic orbit in the neighborhood of the equilibrium point $\left(0,0\right)$ for $\alpha \in (-2,2)\backslash \left\{-1,-\frac{1}{2},0\right\}$, $\beta >0$. By using the symmetries, in Section 4, we will find the periodic solutions with some periods and several numerical examples are given.

2. KAM Theory Applied to Equation (1)

Theorem 1.

The equilibrium point $\overline{t}=0$ of (1) is stable for $\alpha \in (-2,2)\backslash \left\{-1,-\frac{1}{2},0\right\}$ and $\beta >0$.

Proof. 

For $\alpha \in \left(-2,2\right)$ the zero equilibrium is non-hyperbolic of the elliptic type. The characteristic Equation (9) at $(0,0)$ has the roots $\lambda =\frac{\alpha +i\sqrt{4-{\alpha }^2}}{2},\overline{\lambda }=\frac{\alpha -i\sqrt{4-{\alpha }^2}}{2}.$ So,

$$\begin{array}{cc}\hfill {\lambda }^2& =\frac{{\alpha }^2-2}{2}+\frac{\alpha \sqrt{4-{\alpha }^2}}{2}i,\hfill \\ \hfill {\lambda }^3& =\frac{\alpha ({\alpha }^2-3)}{2}+\frac{({\alpha }^2-1)\sqrt{4-{\alpha }^2}}{2}i,\hfill \end{array}$$

and

$${\lambda }^4=\frac{{\alpha }^4-4{\alpha }^2+2}{2}+\frac{\alpha ({\alpha }^2-2)\sqrt{4-{\alpha }^2}}{2}i.$$

Clearly $\left|\lambda \right|=1,{\lambda }^3\ne 1,{\lambda }^4\ne 1$ for $\alpha \in \left(-2,-1\right)\cup \left(-1,0\right)\cup \left(0,2\right)$.

Now, we will find the Birkhoff normal form of System (8) (see Theorem 1 in Reference [21]). The change of variables

$$\left[\begin{array}{c}{x}_n\\ y_n\end{array}\right]=\left[\begin{array}{cc}1& 1\\ \overline{\lambda }& \lambda \end{array}\right]\left[\begin{array}{c}{u}_n\\ v_n\end{array}\right]=\left[\begin{array}{c}{u}_n+v_n\\ \overline{\lambda }{u}_n+\lambda v_n\end{array}\right]$$

transforms System (8) into

$$\begin{array}{c}{u}_{n+1}=\lambda u_n+\sigma {\left(u_n+v_n\right)}^2,\\ v_{n+1}=\overline{\lambda }{v}_n+\overline{\sigma }{\left(u_n+v_n\right)}^2,\end{array}$$

(10)

where

$$\sigma =\frac{\lambda \beta }{\lambda -\overline{\lambda }}.$$

Also, the change of variables

$$u_n={\xi }_n+\sum _{k=0}^2\left(a_{2k}{\xi }_n^{2-k}{\eta }_n^k\right)+\sum _{k=0}^3\left(a_{3k}{\xi }_n^{3-k}{\eta }_n^k\right)$$

(11)

$$v_n={\eta }_n+\sum _{k=0}^2\left(\overline{a_{2k}}{\xi }_n^k{\eta }_n^{2-k}\right)+\sum _{k=0}^3\left(\overline{a_{3k}}{\xi }_n^k{\eta }_n^{3-k}\right)$$

(12)

reduces System (10) to the form

$$\left.\begin{array}{c}{\xi }_{n+1}=\left(\lambda {\xi }_n+{\alpha }_2{\xi }_n^2{\eta }_n\right)+O_4,\\ {\eta }_{n+1}=\left(\overline{\lambda }{\eta }_n+\overline{{\alpha }_2}{\xi }_n{\eta }_n^2\right)+O_4\end{array}\right\},$$

(13)

where (see Reference [14])

$${\alpha }_2=2\left(a_{21}+\overline{a_{21}}\right)\sigma +2\left(a_{20}+\overline{a_{22}}\right)\sigma =4Re\left(a_{21}\right)\sigma +2\left(a_{20}+\overline{a_{22}}\right)\sigma ,$$

$$a_{21}=\frac{2\sigma }{1-\lambda },a_{22}=\frac{\sigma }{{\overline{\lambda }}^2-\lambda },$$

$$\sigma =\frac{\beta }{2}\left(1-i\frac{\alpha }{\sqrt{4-{\alpha }^2}}\right).$$

Furthermore

$$a_{20}+\overline{a_{22}}=\frac{\beta }{(\alpha -2)(\alpha +1)},$$

$${\alpha }_2=\sigma \left(4Re\left(a_{21}\right)+2\left(a_{20}+\overline{a_{22}}\right)\right)=\frac{2\beta \left(\right(2\alpha +1\left)\right)}{(2-\alpha )(\alpha +1)}\sigma ,$$

$${\alpha }_2=\frac{{\beta }^2\left((2\alpha +1)\right)}{(2-\alpha )(\alpha +1)}\left(1-i\frac{\alpha }{\sqrt{4-{\alpha }^2}}\right).$$

Thus

$$Re\left({\alpha }_2\right)=\frac{{\beta }^2\left((2\alpha +1)\right)}{(2-\alpha )(\alpha +1)}.$$

By using the transformation

$${\xi }_n=r_n+i{s}_n,$$

$${\eta }_n=r_n-i{s}_n,$$

we obtain (see Theorem 1, for $l=4$, in Reference [21]):

$$cos{\gamma }_0=Re\left(\lambda \right)=\frac{\alpha }{2}\in \left(-1,1\right)\mathrm{for}\alpha \in \left(-2,2\right),$$

$${\gamma }_1=-\frac{Re\left({\alpha }_2\right)}{sin{\gamma }_0},$$

i.e.,

$${\gamma }_1=\frac{{\beta }^2(2\alpha +1)}{\left(\alpha +1\right)\left(\alpha -2\right)\sqrt{1-{\alpha }^2/4}}.$$

Since $\alpha \in (-2,2)\backslash \left\{-1,-\frac{1}{2},0\right\}$, this implies ${\gamma }_1\ne 0$.   □

Theorem 2.

The negative equilibrium point $\overline{t}=\frac{2-\alpha }{\beta }$ of (1) is stable for $\alpha \in (2,6)\backslash \left\{4,\frac{9}{2},5\right\}$ and $\beta >0$.

Proof. 

For the negative equilibrium ${\overline{t}}_2=\frac{2-\alpha }{\beta },\alpha \in (2,6),$ we use the substitution

$$\begin{array}{cc}\hfill x_n& =t_n-{\overline{t}}_2=t_n-\frac{2-\alpha }{\beta },\hfill \\ \hfill y_n& =x_{n-1},\hfill \end{array}$$

and Equation (1) can be transformed into the system

$$\left.\begin{array}{ccc}\hfill x_{n+1}& =& \beta x_n^2-\left(\alpha -4\right)x_n-x_{n-1},\hfill \\ \hfill y_{n+1}& =& x_n.\hfill \end{array}\right\}$$

(14)

The map G associated with System (14) takes the form

$$G\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\beta x^2-\left(\alpha -4\right)x-y\\ x\end{array}\right).$$

We see that

$$J_G\left(x,y\right)=\left(\begin{array}{cc}2\beta x-\alpha +4& -1\\ 1& 0\end{array}\right),$$

and $det{J}_G\left(x,y\right)=1$. So, the map G is an area preserving map and we will apply KAM theory to System (14).

Now, for $\overline{x}=\overline{y}=0,\alpha \in \left(2,6\right)$ we have

$$J_0=J_G\left(0,0\right)=\left(\begin{array}{cc}4-\alpha & -1\\ 1& 0\end{array}\right).$$

The corresponding characteristic equation at equilibrium $\left(0,0\right)$ is:

$${\lambda }^2+\left(\alpha -4\right)\lambda +1=0,$$

from which

$$\begin{array}{cc}\hfill \lambda & =\frac{4-\alpha +i\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}{2},\hfill \\ \hfill \overline{\lambda }& =\frac{4-\alpha -i\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}{2},\hfill \end{array}$$

$$\left|\lambda \right|=\left|\overline{\lambda }\right|=1,$$

$$\begin{array}{cc}\hfill {\lambda }^2& =\frac{-8\alpha +{\alpha }^2+14}{2}+\frac{\left(4-\alpha \right)i\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}{2},\hfill \\ \hfill {\lambda }^3& =-\frac{\left(\alpha -4\right)\left(-8\alpha +{\alpha }^2+13\right)}{2}+\frac{i\left(\alpha -5\right)\left(\alpha -3\right)\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}{2},\hfill \end{array}$$

$${\lambda }^4=\frac{-224\alpha +92{\alpha }^2-16{\alpha }^3+{\alpha }^4+194}{2}-\frac{\left(\alpha -4\right)\left(-8\alpha +{\alpha }^2+14\right)\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}{2}i.$$

Clearly $\left|\lambda \right|=1,{\lambda }^3\ne 1,{\lambda }^4\ne 1$ for $\alpha \in \left(2,4\right)\cup \left(4,5\right)\cup \left(5,6\right)$.

Now, the change of variables

$$\left[\begin{array}{c}{x}_n\\ y_n\end{array}\right]=\left[\begin{array}{cc}1& 1\\ \overline{\lambda }& \lambda \end{array}\right]\left[\begin{array}{c}{u}_n\\ v_n\end{array}\right]=\left[\begin{array}{c}{u}_n+v_n\\ \overline{\lambda }{u}_n+\lambda v_n\end{array}\right]$$

transforms System (14) into System (10), where

$$\sigma =\frac{\lambda \beta }{\lambda -\overline{\lambda }}.$$

Now, for $\alpha \in \left(2,4\right)\cup \left(4,5\right)\cup \left(5,6\right)$ we obtain

$$\sigma =\frac{\beta }{2}\left(1+\frac{\left(\alpha -4\right)}{\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}i\right),$$

and

$${\alpha }_2=\frac{2\beta \left(2\alpha -9\right)}{\left(\alpha -2\right)\left(\alpha -5\right)}\frac{\beta }{2}\left(1+\frac{\left(\alpha -4\right)}{\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}i\right).$$

Thus

$$Re\left({\alpha }_2\right)=\frac{{\beta }^2\left(2\alpha -9\right)}{\left(\alpha -2\right)\left(\alpha -5\right)}.$$

Now, we obtain

$$cos{\gamma }_0=Re\left(\lambda \right)=\frac{4-\alpha }{2}\in \left(-1,1\right)\mathrm{for}\alpha \in \left(2,6\right),$$

$${\gamma }_1=-\frac{Re\left({\alpha }_2\right)}{sin{\gamma }_0},$$

i.e.,

$${\gamma }_1=\frac{2{\beta }^2\left(2\alpha -9\right)}{\left(\alpha -2\right)\left(\alpha -5\right)\sqrt{\left(\alpha -2\right)\left(6-\alpha \right)}}.$$

This implies that ${\gamma }_1\ne 0$ for $\alpha \in (2,6)\backslash \left\{4,\frac{9}{2},5\right\}$ and $\beta >0$.   □

For the bifurcation diagrams (B.D.) which indicate the appearance of chaos see Figure 1, Figure 2, Figure 3 and Figure 4.

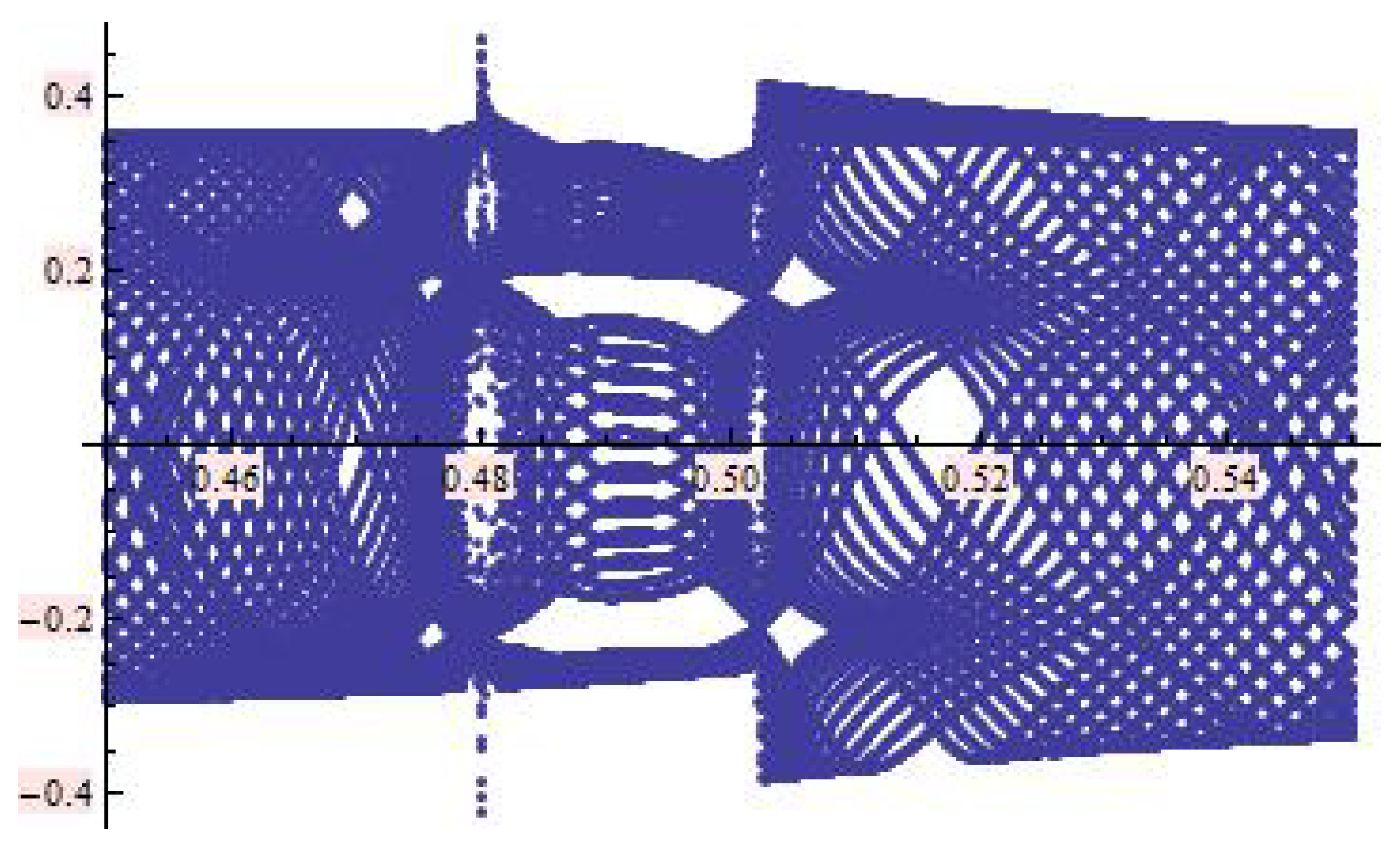
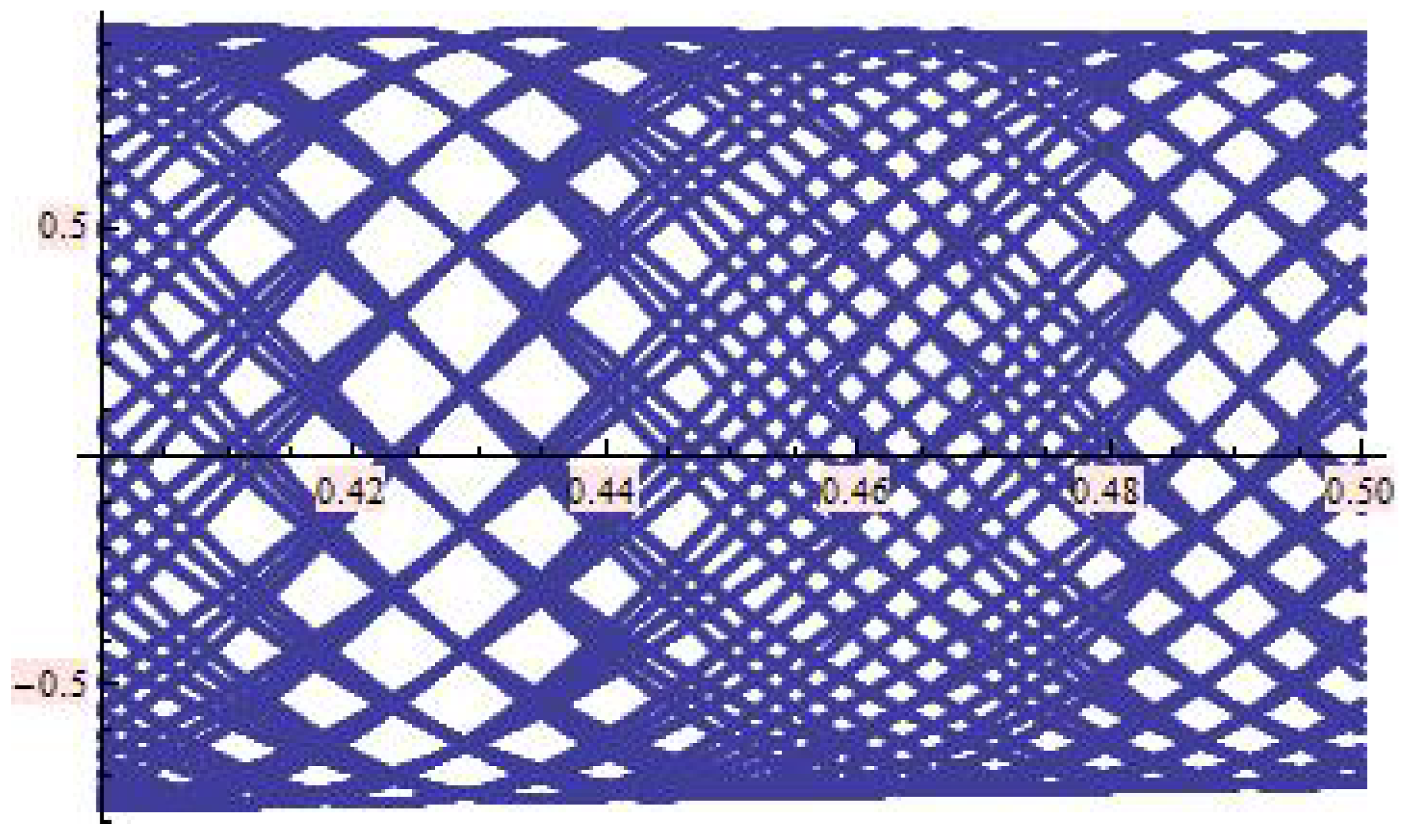
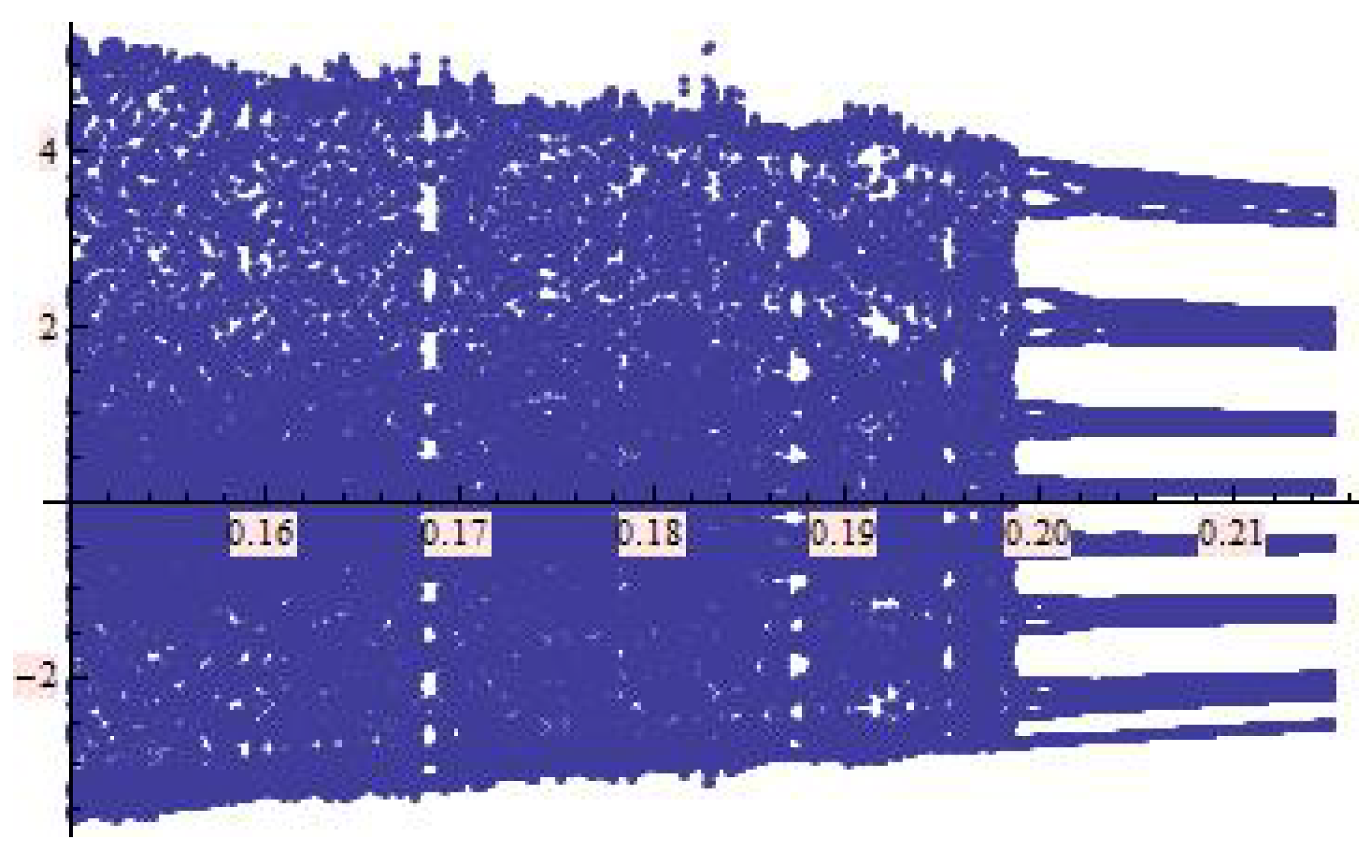
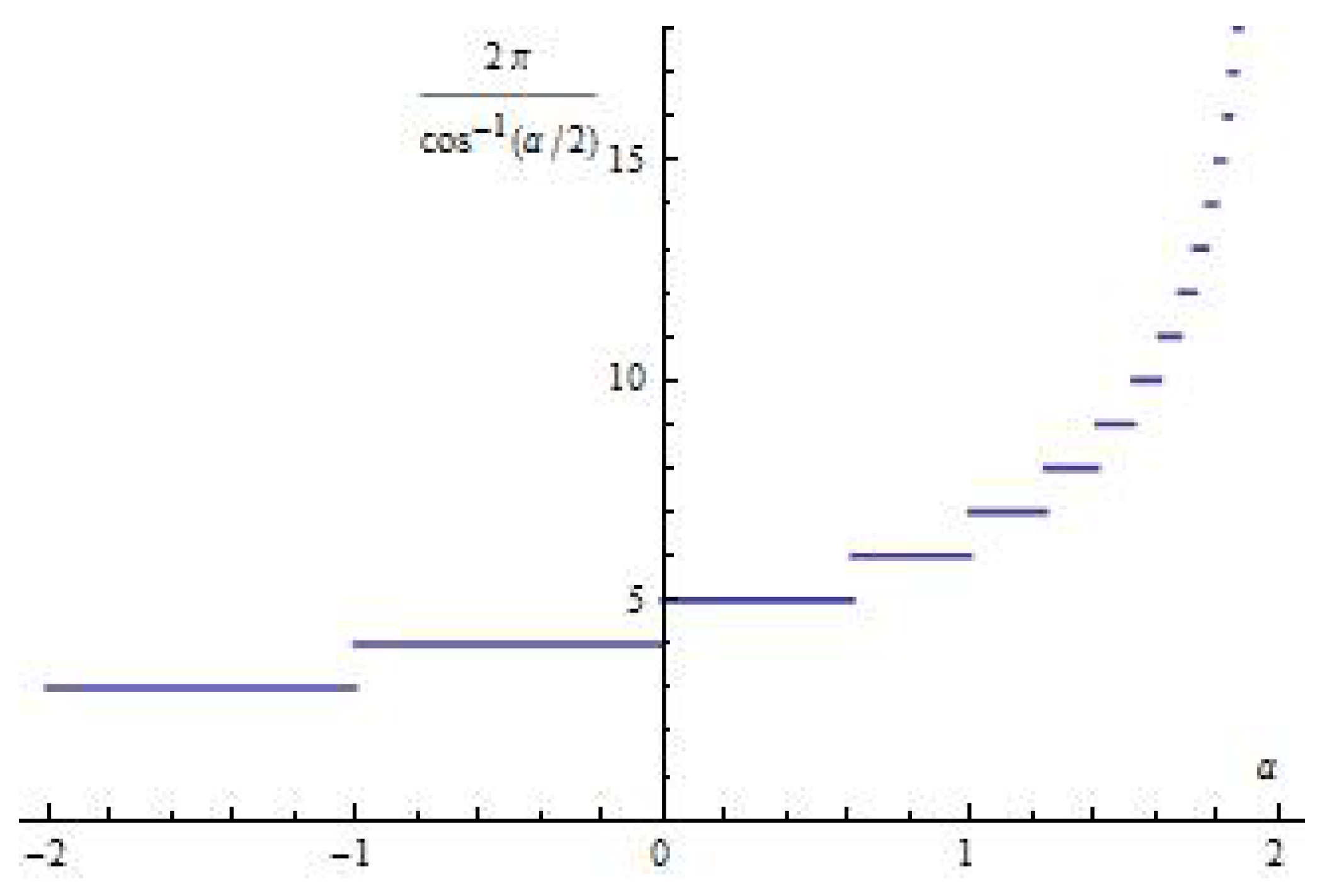
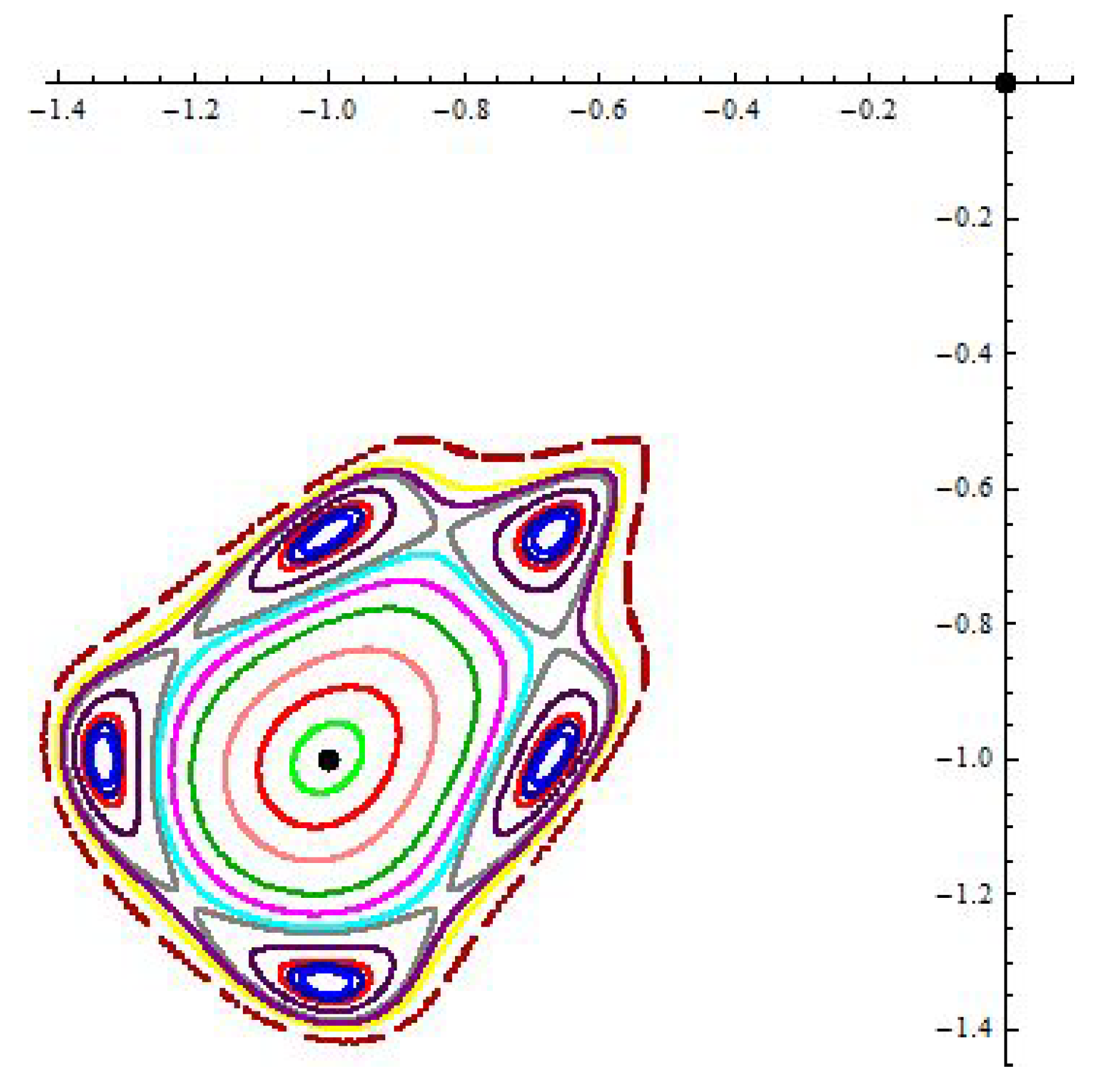
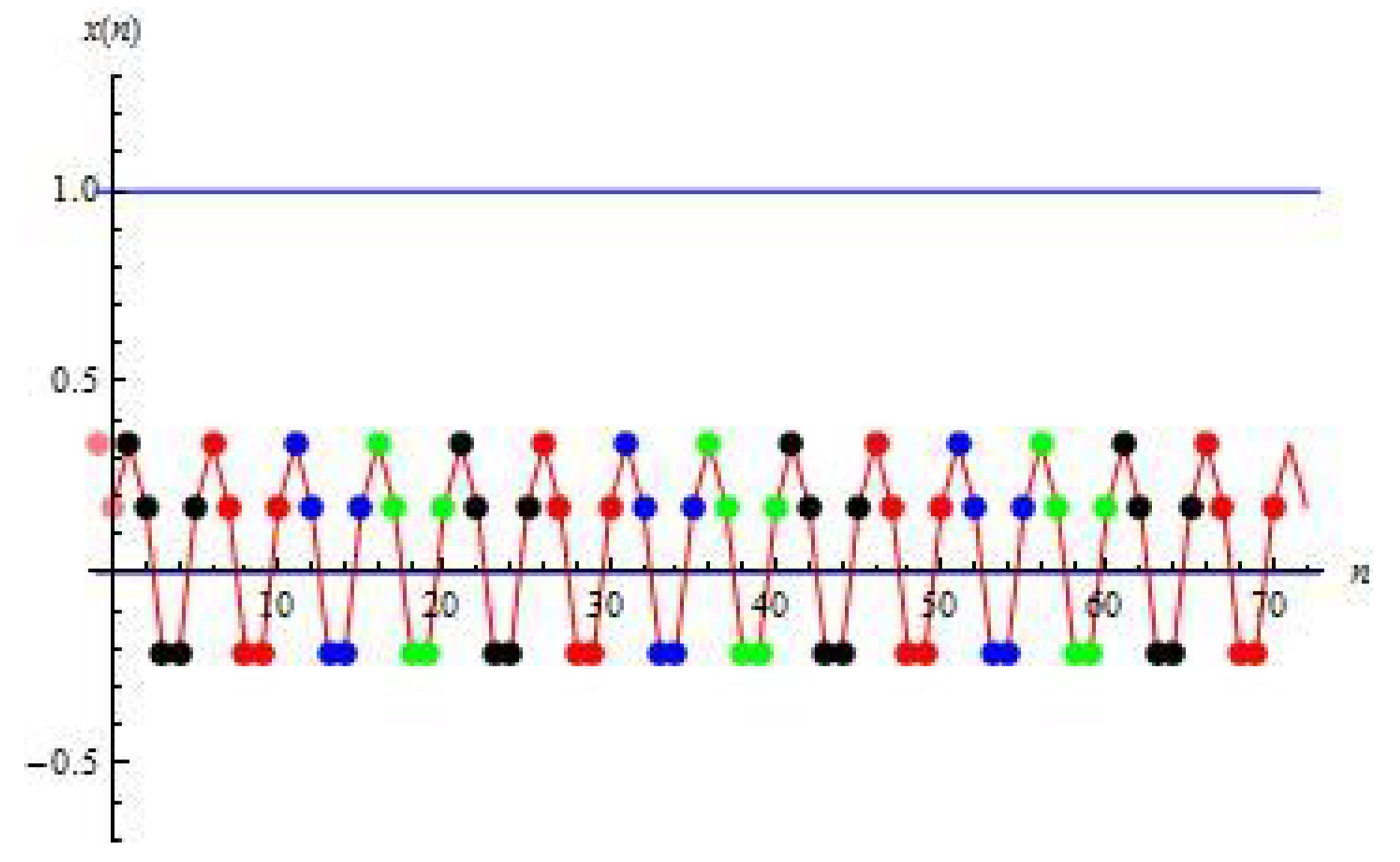
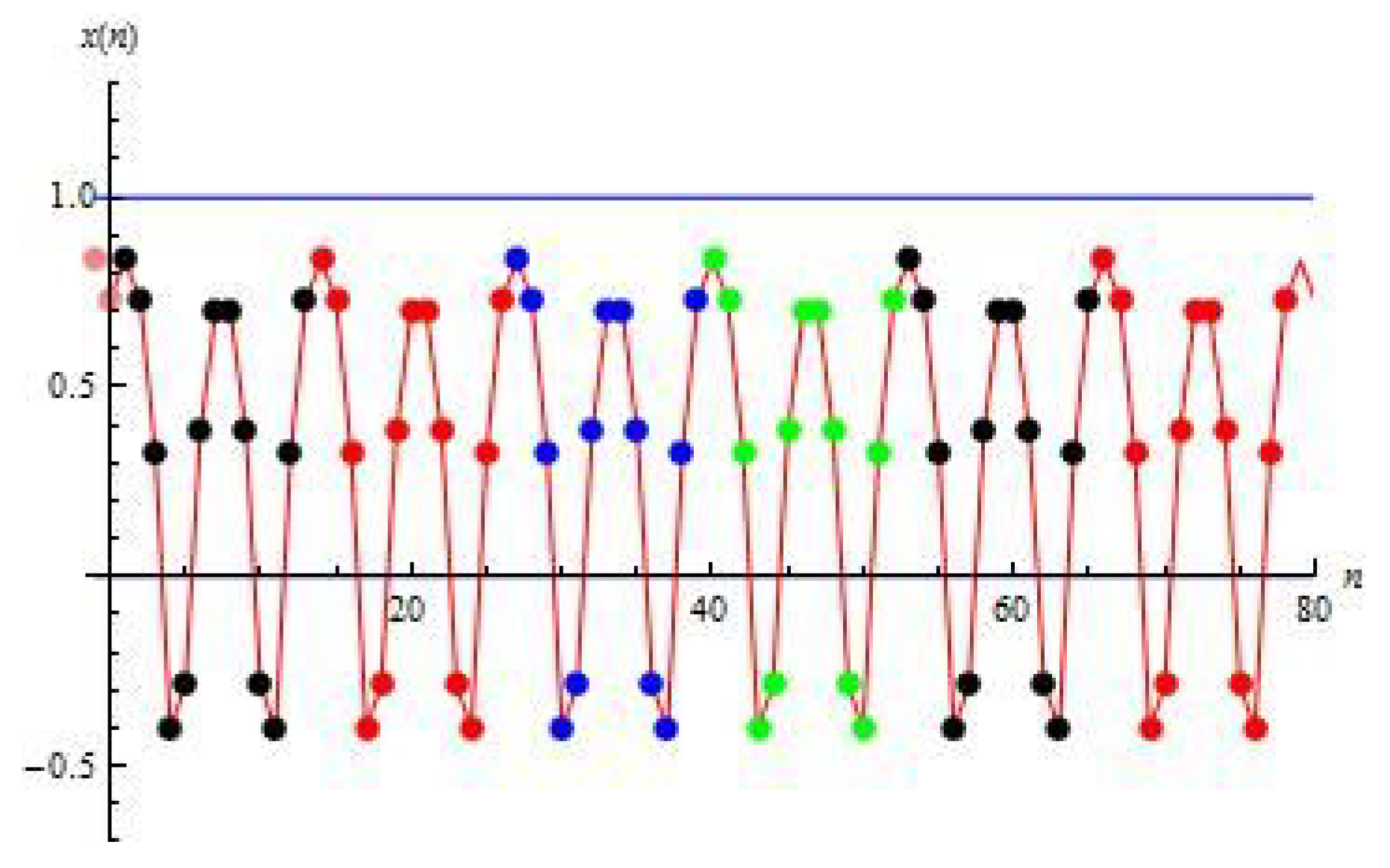
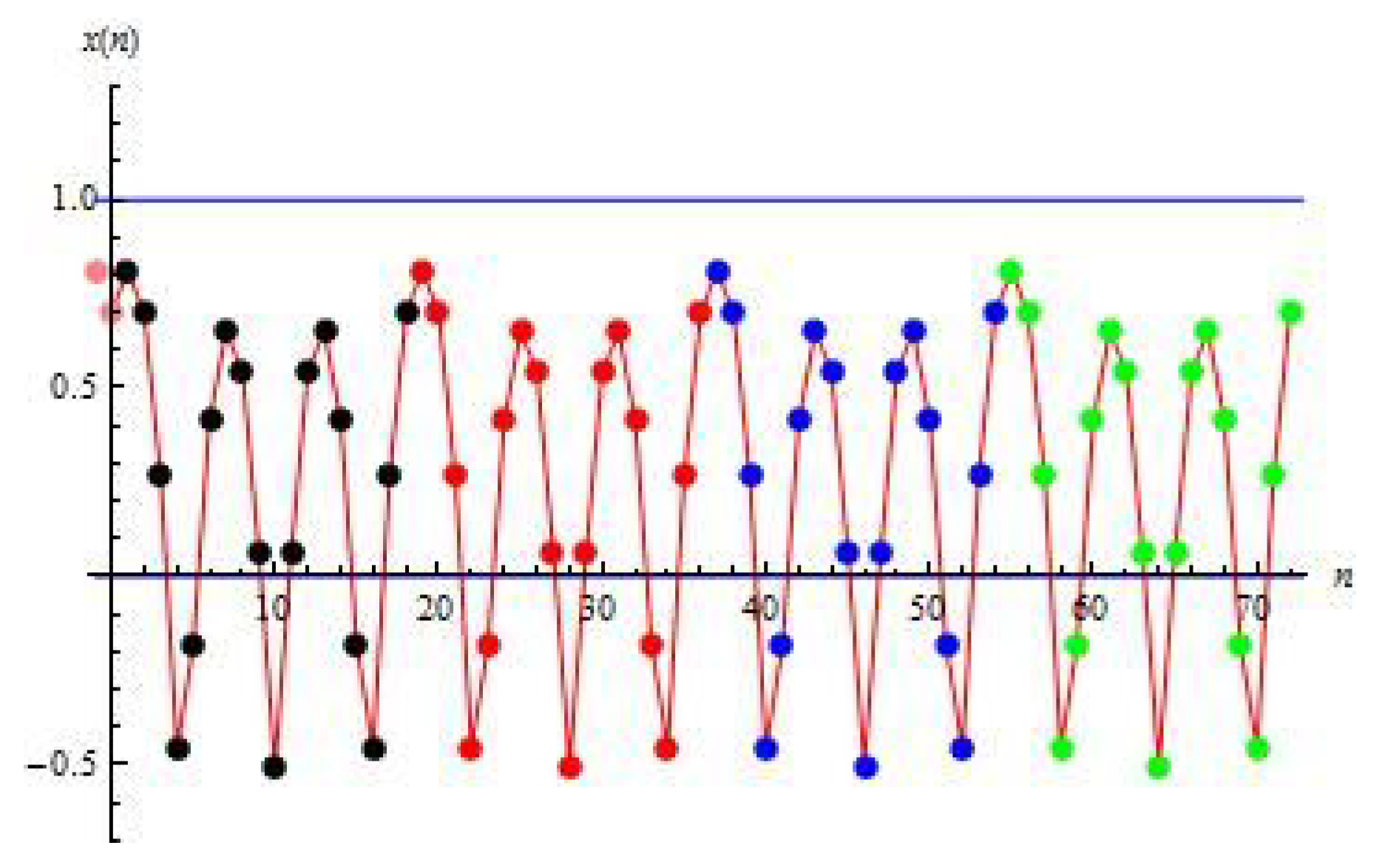
3. Periodic Points and Orbits

In this section, we study the M.P.P. for a periodic orbit in the neighborhood of the equilibrium $(0,0)$ where $\alpha \in \left(-2,-1\right)\cup \left(-1,-\frac{1}{2}\right)\cup \left(-\frac{1}{2},0\right)\cup \left(0,2\right)$ and $\beta >0$.

Lemma 3.

M.P.P. for a periodic orbit in the neighborhood of the elliptic equilibrium $(0,0)$ is 3.

Proof. 

The eigenvalues at the elliptic equilibrium are of the form $\lambda =e^{\pm i\varphi }$ with $cos\left(\varphi \right)=\frac{\alpha }{2}$, $0<\varphi <\pi$. Then the period of the motion around the equilibrium must be $q>\frac{2\pi }{\varphi }>2$. So, the map T cannot have an orbit of period less than 3 in a neighborhood of the elliptic equilibrium $(0,0)$.   □

For example, if $\alpha =0.5$, then $2\pi /\varphi \approx 4.7668$. So M.P.P. is $5.$ If $\alpha =1.5$, then $2\pi /\varphi \approx 8.6936$ and M.P.P. is $9.$ Figure 5 visualize M.P.P. as a function of parameter $\alpha$. Figure 6 gives us some possible orbits (S.P.O.) around the elliptic equilibrium $(0,0)$ for $\alpha =0.5$ and $\beta =1.5$ and Figure 7 gives us S.P.O. around the elliptic equilibrium $(-1,-1)$ for $\alpha =3.5$ and $\beta =1.5$.

Remark 2.

Equation (1) has the period-three solutions

$$\dots ,-\frac{\alpha -\sqrt{{\alpha }^2-4\alpha -4}}{2\beta },-\frac{\alpha -\sqrt{{\alpha }^2-4\alpha -4}}{2\beta },-\frac{\alpha +2-\sqrt{{\alpha }^2-4\alpha -4}}{2\beta },\dots ,$$

and

$$\dots ,-\frac{\alpha +\sqrt{{\alpha }^2-4\alpha -4}}{2\beta },-\frac{\alpha +\sqrt{{\alpha }^2-4\alpha -4}}{2\beta },-\frac{\alpha +2+\sqrt{{\alpha }^2-4\alpha -4}}{2\beta },\dots ,$$

for

$$\alpha \in \left(-\infty ,2-2\sqrt{2}\right]\cup \left[2+2\sqrt{2},+\infty \right).$$

See Figure 5.

Remark 3.

Notice that Equation (1) has a minimal period-two solution

$$\dots ,-\frac{\alpha +2-\sqrt{\left(\alpha +2\right)\left(\alpha -6\right)}}{2\beta },-\frac{\alpha +2+\sqrt{\left(\alpha +2\right)\left(\alpha -6\right)}}{2\beta },\dots$$

for

$$\alpha \in \left(-\infty ,-2\right]\cup \left[6,+\infty \right).$$

The Jacobian matrix of the map $T^2$ in the minimal period-two solutions is

$$J_{T^2}=\left(\begin{array}{cc}-{\alpha }^2+4\alpha +15& 2\pm \sqrt{{\alpha }^2-4\alpha -12}\\ -2\pm \sqrt{\left(\alpha +2\right)\left(\alpha -6\right)}& -1\end{array}\right),$$

with the eigenvalues:

$${\lambda }_{1,2}=-\frac{1}{2}{\alpha }^2+2\alpha +7\pm \frac{1}{2}\sqrt{\left(\alpha -6\right)\left(\alpha +2\right)\left(-4\alpha +{\alpha }^2-16\right)}.$$

So, the minimal period-two solution is

1.

a saddle point for $\alpha \in \left(-\infty ,2-2\sqrt{5}\right)\cup \left(2+2\sqrt{5},+\infty \right),$

2.

non-hyperbolic of the parabolic type for $\alpha =2\pm 2\sqrt{5},$

3.

non-hyperbolic of the elliptic type for $\alpha \in \left(2-2\sqrt{5},-2\right)\cup \left(6,2+2\sqrt{5}\right).$

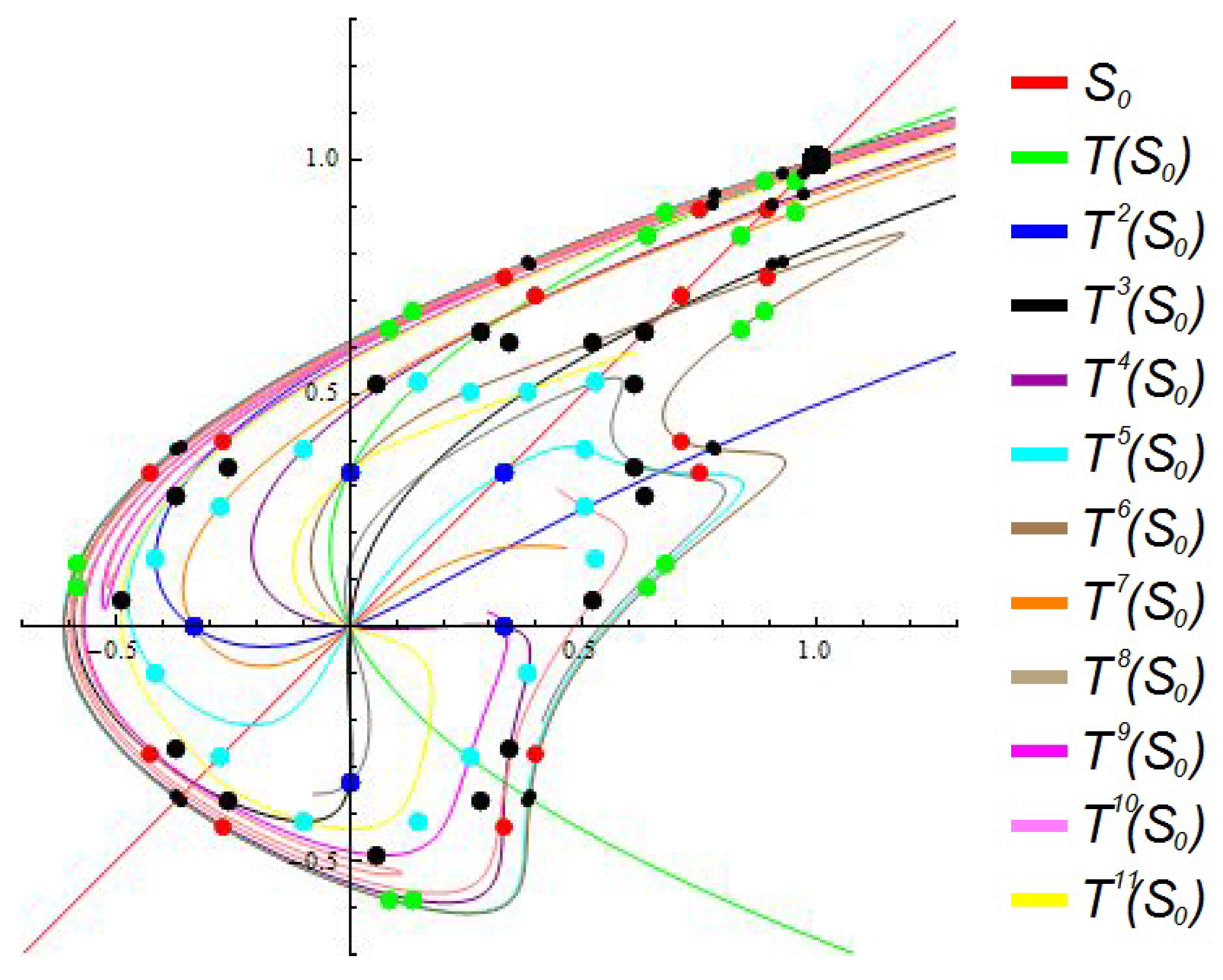
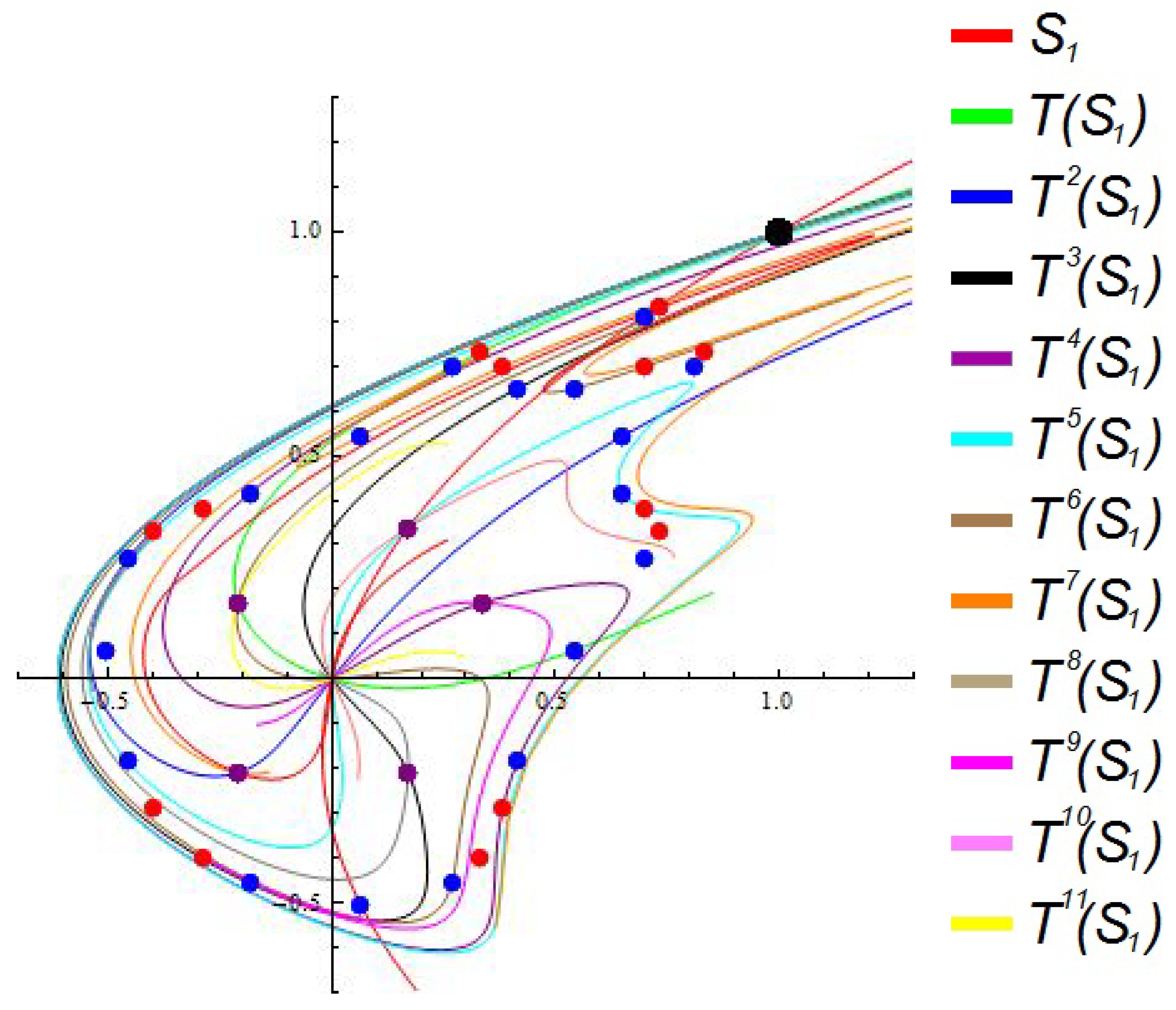
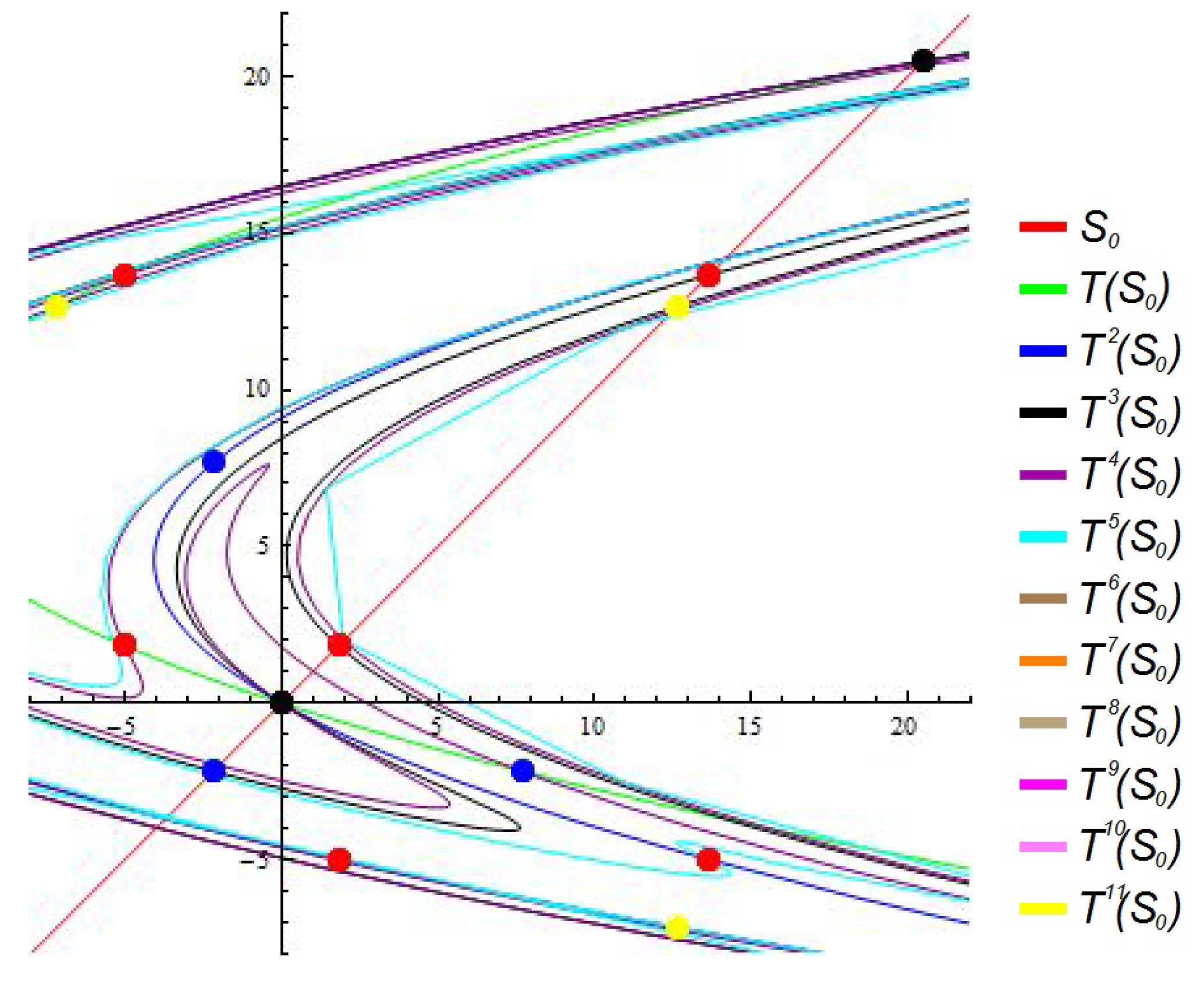
4. Symmetries

It is well known that symmetries play an important role because they have special dynamic behavior. See References [12,28] and Theorem 13 in Reference [13]. Now, the map T associated with the system (8) can be rewritten as follows:

$$T(x,y)=(\beta x^2+\alpha x-y,x),$$

and

$$T^{-1}(x,y)=(y,\beta y^2+\alpha y-x).$$

The involution $\mathcal{R}(x,y)=\left(y,x\right)$ is a reversor for the map T. Indeed,

$$\begin{array}{cc}\hfill (\mathcal{R}\circ T\circ \mathcal{R})(x,y)& =(\mathcal{R}\circ T)\left(y,x\right)=\mathcal{R}\left(\beta y^2+\alpha y-x,y\right)\hfill \\ \hfill & =(y,\beta y^2+\alpha y-x)=T^{-1}(x,y).\hfill \end{array}$$

Thus $T={\mathcal{I}}_1\circ {\mathcal{I}}_0$ where ${\mathcal{I}}_0(x,y)=\mathcal{R}(x,y)=(y,x)$ and

$${\mathcal{I}}_1(x,y)=T\circ \mathcal{R}(x,y)=\left(\beta y^2+\alpha y-x,y\right).$$

The symmetry lines corresponding to ${\mathcal{I}}_0$ and ${\mathcal{I}}_1$ are

$${\mathcal{S}}_0=\{(x,y):x=y\},{\mathcal{S}}_1=\{(x,y):(\alpha +\beta y)y=2x\}.$$

Periodic orbits on the symmetry line ${\mathcal{S}}_0$ with even period n are searched for by starting with points $(x_0,x_0)\in {\mathcal{S}}_0$ and imposing that $(x_{n/2},y_{n/2})\in {\mathcal{S}}_0,$ where

$$(x_{n/2},y_{n/2})=T^{n/2}(x_0,x_0).$$

This reduces to a one-dimensional root finding for the equation $x_{n/2}=y_{n/2},$ where the unknown is $x_0$. Also, periodic orbits on ${\mathcal{S}}_0$ with odd period n are obtained by solving for $x_0$ the equation $y_{(n+1)/2}(\alpha +\beta y_{(n+1)/2})=2x_{(n+1)/2}$ where

$$(x_{(n+1)/2},y_{(n+1)/2})=T^{(n+1)/2}(x_0,x_0).$$

Visualization of some periodic orbits can be seen in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. For example, in Figure 8, for $\alpha =0.5$ we have cyan points

$$(x_1,y_1)=\left(0.5235660872586801{}^{\prime },0.5235660872586801{}^{\prime }\right)\in {\mathcal{S}}_0\cap {\mathcal{S}}_{16},$$

$$(x_2,y_2)=\left(0.5060816278767843{}^{\prime },0.2564826010712121{}^{\prime }\right)\in {\mathcal{S}}_4\cap {\mathcal{S}}_{20},$$

$$(x_3,y_3)=\left(0.2564826010712121{}^{\prime },-0.27916534036279644{}^{\prime }\right)\in {\mathcal{S}}_2\cap {\mathcal{S}}_{18},$$

where ${\mathcal{S}}_{16}=T^8\left({\mathcal{S}}_0\right)$, ${\mathcal{S}}_4=T^2\left({\mathcal{S}}_0\right)$, ${\mathcal{S}}_{20}=T^{10}\left({\mathcal{S}}_0\right)$, ${\mathcal{S}}_2=T\left({\mathcal{S}}_0\right)$, ${\mathcal{S}}_{18}=T^9\left({\mathcal{S}}_0\right)$, and then

$$T^{16-0}(x_1,y_1)=T^{16}(x_1,y_1)=(x_1,y_1),$$

$$T^{20-4}(x_2,y_2)=T^{16}(x_2,y_2)=(x_2,y_2),$$

$$T^{18-2}(x_3,y_3)=T^{16}(x_3,y_3)=(x_3,y_3).$$

Also, for $\alpha =-2.1,$ in Figure 10, we have red point

$$(x,y)=\left(13.671359641163505{}^{\prime },-5.{}^{\prime }\right)\in {\mathcal{S}}_4\cap {\mathcal{S}}_{10},$$

where ${\mathcal{S}}_4=T^2\left({\mathcal{S}}_0\right)$, ${\mathcal{S}}_{10}=T^5\left({\mathcal{S}}_0\right)$, and then

$$T^{10-4}(x,y)=T^6(x,y)=(x,y).$$

Remark 4.

All Figures are generated by Dynamica 3 [8].

5. Conclusions

By using KAM theory, under certain conditions on parameter $\alpha$, we proved the stability of the zero equilibrium and the negative equilibrium of the difference Equation (1). Also, by using symmetries we proved the existence of periodic solutions with certain periods.