A New Class of 2q-Point Nonstationary Subdivision Schemes and Their Applications
Abstract
1. Introduction
2. Preliminaries
3. The Even-Point ANSSs
- Using in (17) and (18), we get a new 2-point symmetric binary ANSS with free parameterwhereIn fact, the sum of the stencils of scheme at the jth level areNow for , we define the normalized ANSS (corresponding to (18)). Observe thatThe corresponding normalized SS can be obtained by dividing the stencils at the jth iteration of SS (18) by their sum.whereLemma 3.If f is the limit function of ANSS (18), then is the limit function of the corresponding normalized SS.Proof.Note that□
4. Smoothness and Convergence of ANSSs
- Using in (21), our four-point NSS becomes a nonstationary counterpart B-spline of degree 6.
5. Results and Discussion
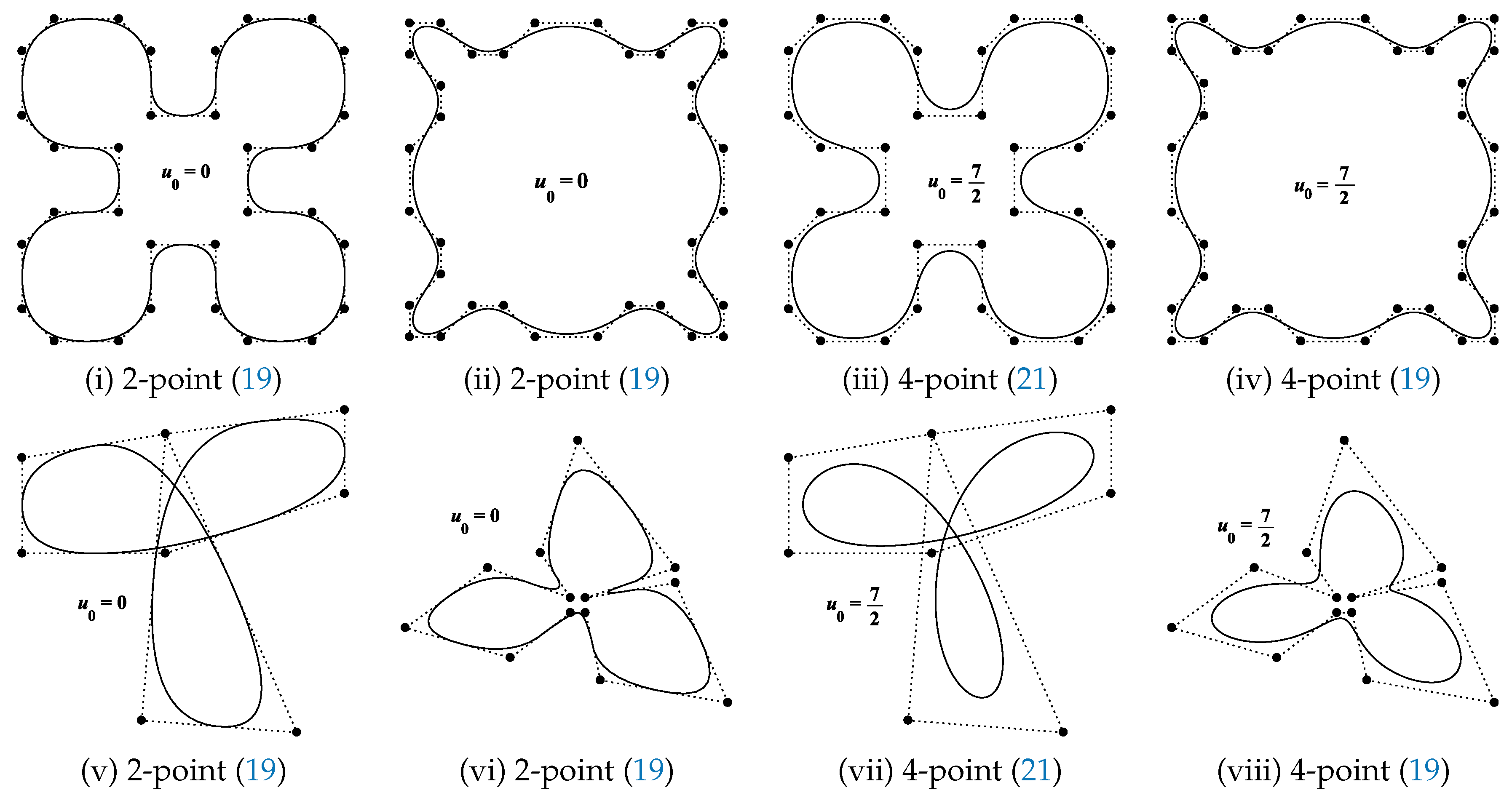
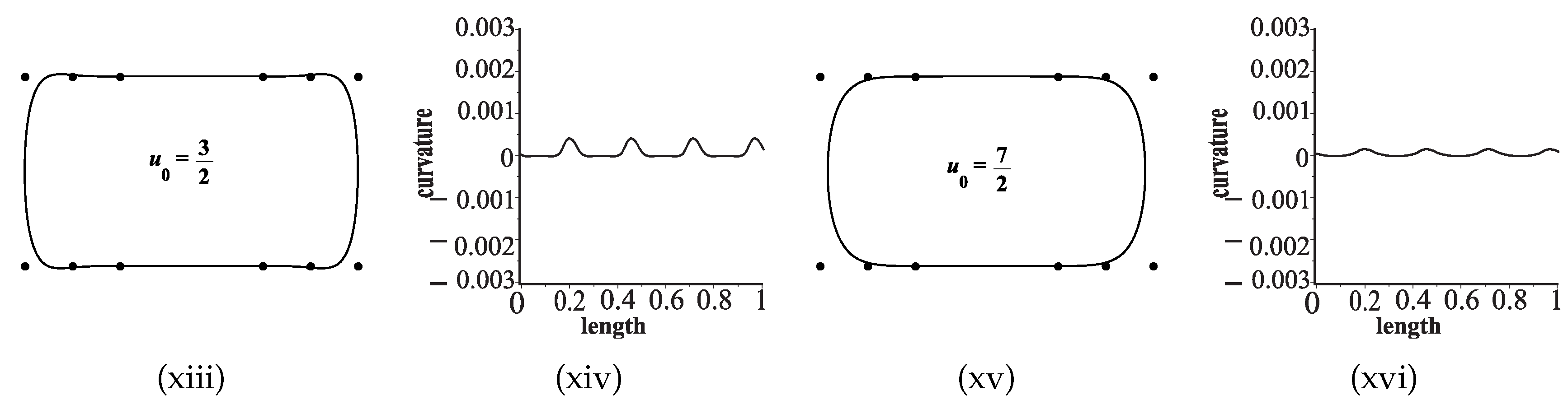
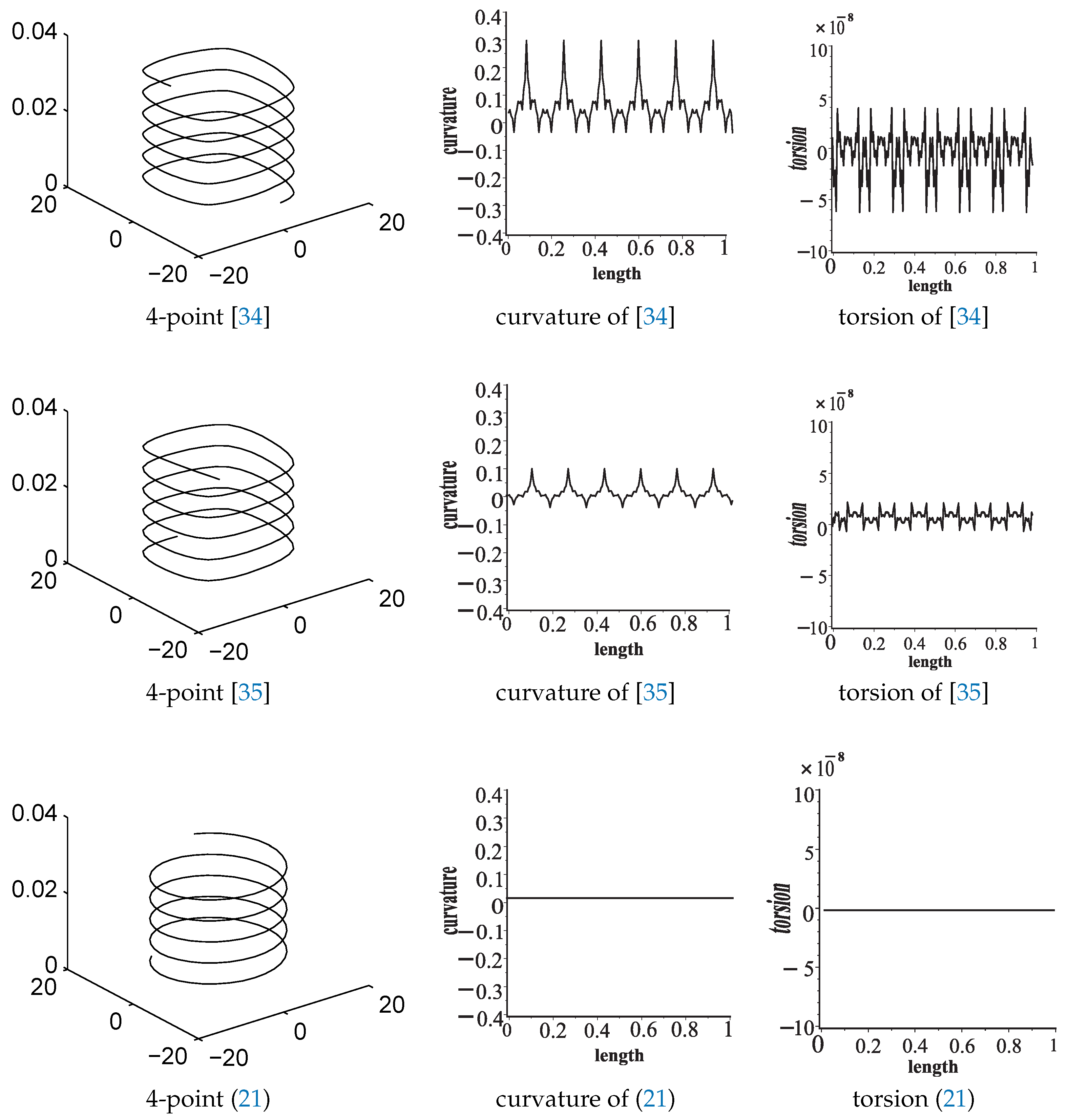
- Figure 1 demonstrates the visual performance of the proposed ANSSs. The limit curves, obtained by our ANSSs, are more rational as compared to other famous existing NSSs. In Figure 2, two examples are given to illustrate the behavior of the parameter . The proposed ANSSs gives considerable variations in the results, which is a useful mechanism in geometric modeling.
6. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- De Rham, G. Sur une courbe plane. J. Math. Pures Appl. 1956, 35, 25–42. [Google Scholar]
- Chaikin, G.M. An algorithm for high-speed curve generation. Comput. Graph. Image Process. 1974, 3, 346–349. [Google Scholar] [CrossRef]
- Deslauriers, G.; Dubuc, S. Symmetric iterative interpolation processes. Constr. Approx. 1989, 5, 49–68. [Google Scholar] [CrossRef]
- Dyn, N.; Levin, D. Stationary and non-stationary binary subdivision scheme. In Mathematical Methods in Computer Aided Geometric Design II; Lyche, T., Schumaker, L.L., Eds.; Academic Press: New York, NY, USA, 1992; pp. 209–216. [Google Scholar]
- Jena, M.K.; Shunmugaraj, P.; Das, P.C. A subdivision algorithm for trigonometric spline curves. Comput. Aided Geom. Des. 2002, 19, 71–88. [Google Scholar] [CrossRef]
- Wallner, J.; Dyn, N. Convergence and C1 analysis of subdivision schemes on manifolds by proximity. Comput. Aided Geom. Des. 2005, 22, 593–622. [Google Scholar] [CrossRef]
- Beccari, C.; Casciola, G.; Romani, L. A nonstationary uniform tension controlled interpolating 4-point scheme reproducing conics. Comput. Aided Geom. Des. 2007, 24, 1–9. [Google Scholar] [CrossRef]
- Beccari, C.; Casciola, G.; Romani, L. An interpolating 4-point C2 ternary non- stationary subdivision scheme with tension control. Comput. Aided Geom. Des. 2007, 24, 210–219. [Google Scholar] [CrossRef]
- Daniel, S.; Shunmugaraj, P. An interpolating 6-point C2 non-stationary subdivision scheme. J. Comput. Appl. Math. 2009, 230, 164–172. [Google Scholar] [CrossRef]
- Daniel, S.; Shunmugaraj, P. Three point stationary and non-stationary subdivision schemes. In Proceedings of the 3rd International Conference on Geometric Modeling & Imaging, London, UK, 9–11 July 2008. [Google Scholar] [CrossRef]
- Conti, C.; Romani, L. A new family of interpolatory non-stationary subdivision schemes for curve design in geometric modeling. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics, Rhodes, Greece, 19–25 September 2010. [Google Scholar] [CrossRef]
- Dyn, N.; Floater, M.S.; Hormann, K. Four-point curve subdivision based on iterated chordal and centripetal parameterizations. Comput. Aided Geom. Des. 2009, 26, 279–286. [Google Scholar] [CrossRef]
- Li, B.-J.; Yu, Z.-L.; Yu, B.-W.; Su, Z.-X.; Liu, X.-P. Non-stationary subdivision for exponential polynomials reproduction. Acta Math. Appl. Sin. Engl. Ser. 2013, 29, 567–578. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Younis, M. Ternary approximating non-stationary subdivision schemes for curve design. Cent. Eur. J. Eng. 2014, 4, 371–378. [Google Scholar] [CrossRef][Green Version]
- Conti, C.; Dyn, N.; Manni, C.; Mazure, M.L. Convergence of univariate non-stationary subdivision schemes via asymptotic similarity. Comput. Aided Geom. Des. 2015, 37, 1–8. [Google Scholar] [CrossRef]
- Salam, W.; Siddiqi, S.S.; Rehan, K. Chaikins perturbation subdivision scheme in non-stationary forms. Alex. Eng. J. 2016, 55, 2855–2862. [Google Scholar] [CrossRef][Green Version]
- Tan, J.; Sun, J.; Tong, G. A non-stationary binary three-point approximating subdivision scheme. Appl. Math. Comput. 2016, 276, 37–43. [Google Scholar] [CrossRef]
- Hameed, R.; Mustafa, G. Family of a-point b-ary subdivision schemes with bell-shaped mask. Appl. Math. Comput. 2017, 309, 289–302. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, H.; Tang, S.; Tan, J. A combined approximating and interpolating ternary 4-point subdivision scheme. J. Comput. Appl. Math. 2018, 350, 37–49. [Google Scholar] [CrossRef]
- Ghaffar, A.; Ullah, Z.; Bari, M.; Nisar, K.S.; Baleanu, D. Family of odd point non-stationary subdivision schemes and their applications. Adv. Differ. Equ. 2019, 1, 171. [Google Scholar] [CrossRef]
- Akram, G.; Bibi, K.; Rehan, K.; Siddiqi, S.S. Shape preservation of 4-point interpolating non-stationary subdivision scheme. J. Comput. Appl. Math. 2017, 319, 480–492. [Google Scholar] [CrossRef]
- Mustafa, G.; Ghaffar, A.; Khan, F. The Odd-Point Ternary Approximating Schemes. Am. J. Comput. Math. 2011, 1, 111–118. [Google Scholar] [CrossRef]
- Mustafa, G.; Ghaffar, A.; Aslam, M. A subdivision-regularization framework for preventing over fitting of data by a model. Appl. Appl. Math. Int. J. 2013, 8, 178–190. [Google Scholar]
- Mustafa, G.; Khan, F.; Ghaffar, A. The m-point approximating subdivision scheme. Lobachevskii J. Math. 2009, 30, 138–145. [Google Scholar] [CrossRef]
- Barton, M.; Shi, L.; Kilian, M.; Wallner, J.; Pottmann, H. Circular arc snakes and kinematic surface generation. Comput. Graph. Forum 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Song, X.; Aigner, M.; Chen, F.; Jüttler, B. Circular spline fitting using an evolution process. J. Comput. Appl. Math. 2009, 231, 423–433. [Google Scholar] [CrossRef]
- Aslam, M.; Mustafa, G.; Ghaffar, A. The (2n−1)-point ternary approximating and interpolating subdivision schemes. J. Appl. Math. 2011, 2011, 13. [Google Scholar] [CrossRef]
- Ghaffar, A.; Mustafa, G. The family of even-point ternary approximating schemes. ISRN Appl. Math. 2012, 1, 1–14. [Google Scholar] [CrossRef]
- Dyn, N.; Levin, D. Analysis of asymptotically equivalent binary subdivision schemes. J. Math. Anal. Appl. 1995, 193, 594–621. [Google Scholar] [CrossRef]
- Dyn, N.; Levin, D. Subdivision scheme in geometric modelling. Acta Numer. 2002, 11, 73–144. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Ahmad, N. An approximating C4 stationary subdivision scheme. Eur. J. Sci. Res. 2006, 15, 97–102. [Google Scholar]
- Zheng, H.; Hu, M.; Peng, G. P-ary subdivision seneralizing B-splines. In Proceedings of the 2009 Second International Conference on Computer and Electrical Engineering (ICCEE 2009), Dubai, UAE, 28–30 December 2009. [Google Scholar] [CrossRef]
- Daniel, S.; Shunmugaraj, P. An approximating C2 non-stationary subdivision scheme. Comput. Aided Geom. Des. 2009, 26, 810–821. [Google Scholar] [CrossRef]
- Daniel, S.; Shunmugaraj, P. Some interpolating non-stationary subdivision schemes. In Proceedings of the 2011 International Symposium on Computer Science and Society, Kota Kinabalu, Malaysia, 16–17 July 2011. [Google Scholar] [CrossRef]
- Jena, M.K.; Shunmugaraj, P.; Das, P.C. A non-stationary subdivision scheme for curve interpolation. ANZIAM J. 2003, 44, 216–235. [Google Scholar] [CrossRef]

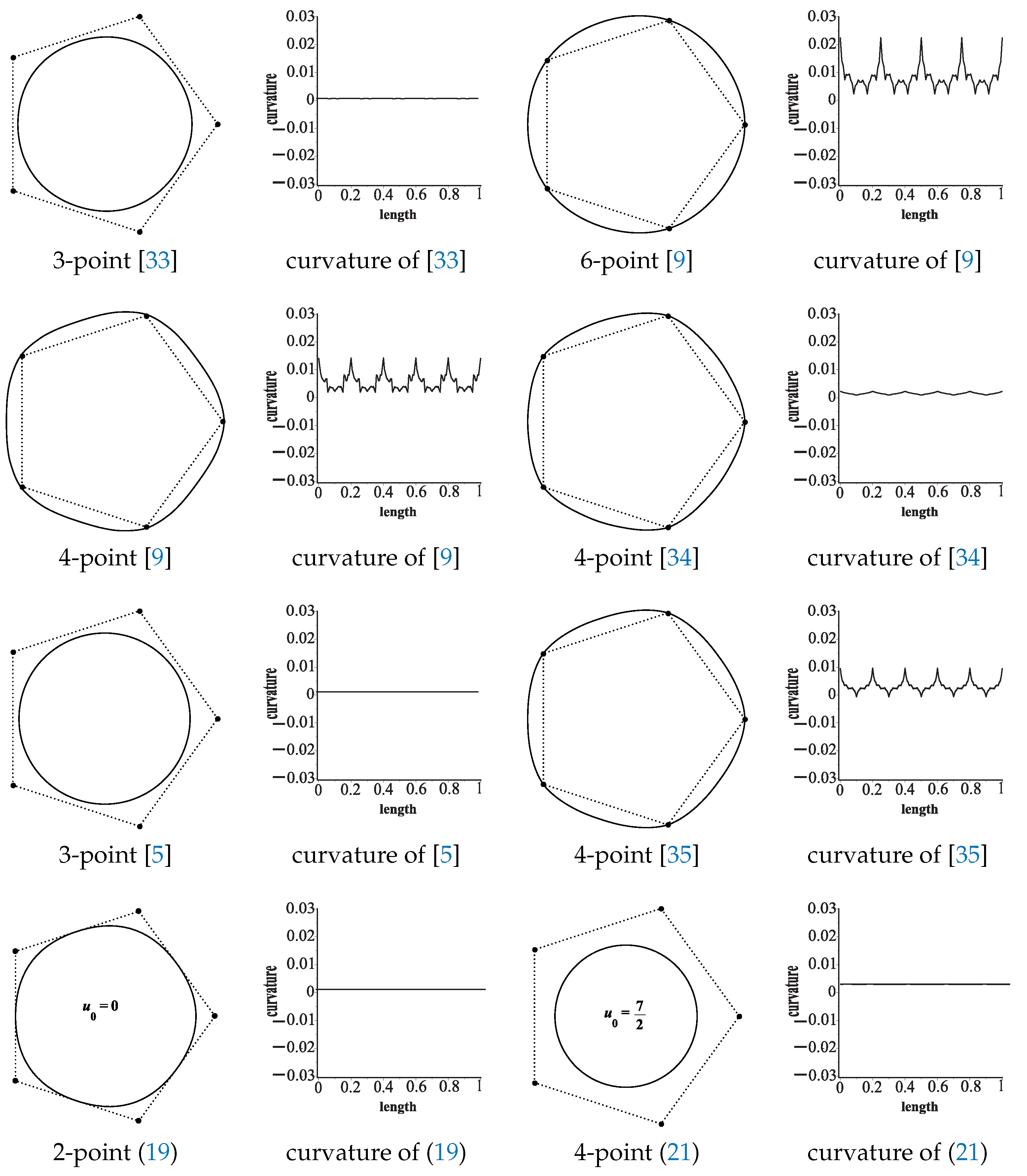
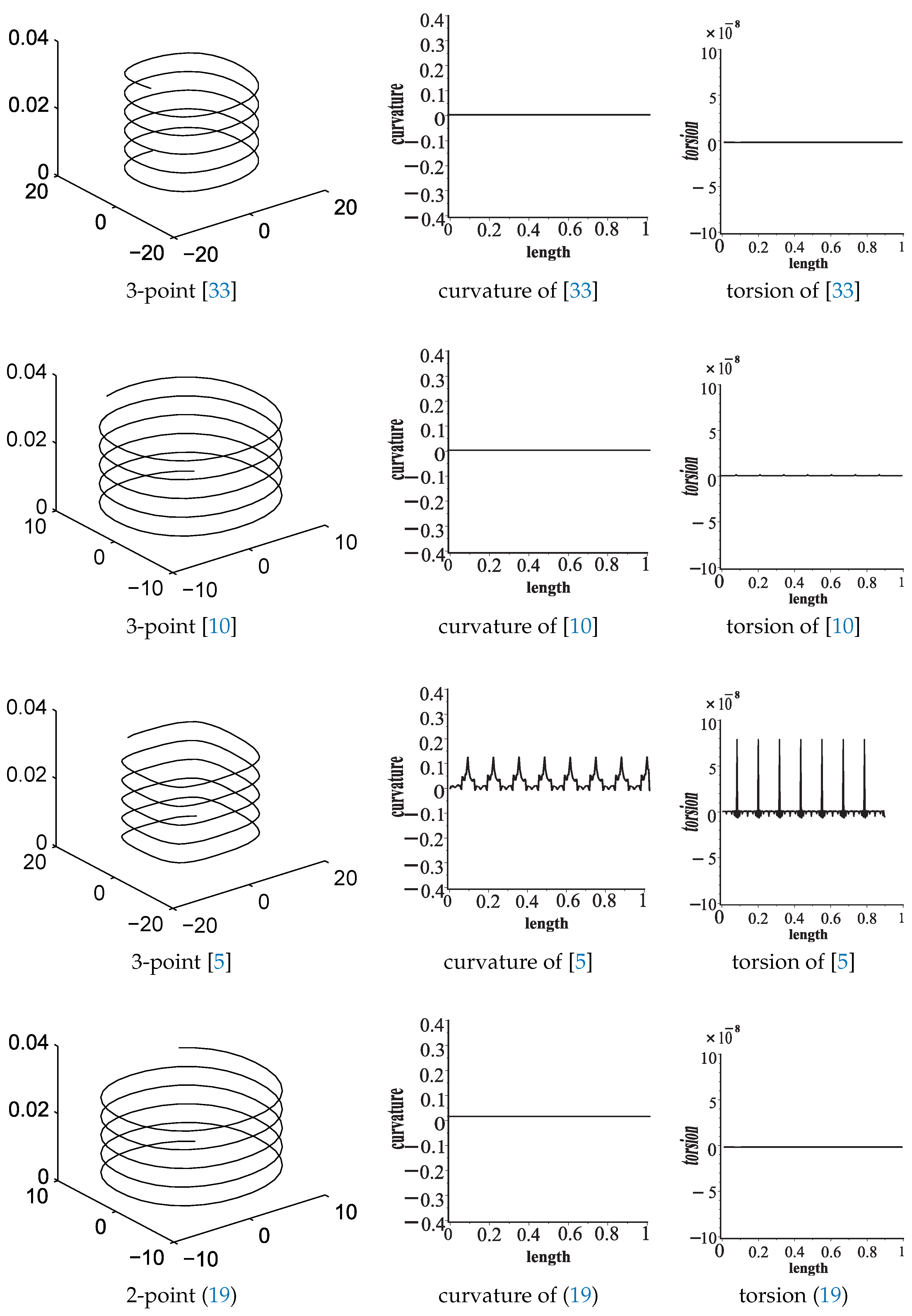
| Scheme | Type | Scheme | Type | Scheme | Type | |||
|---|---|---|---|---|---|---|---|---|
| 2-point [33] | ANSS | 4-point [11] | INSS | 4-point [7] | INSS | |||
| 2-point [5] | ANSS | 4-point [35] | INSS | 4-point [8] | INSS | |||
| 3-point [33] | ANSS | 4-point [9] | INSS | 2-point (19) | ANSS | |||
| 3-point [10] | ANSS | 6-point [11] | INSS | 4-point (21) | ANSS | |||
| 3-point [5] | ANSS | 6-point [34] | INSS |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaffar, A.; Bari, M.; Ullah, Z.; Iqbal, M.; Nisar, K.S.; Baleanu, D. A New Class of 2q-Point Nonstationary Subdivision Schemes and Their Applications. Mathematics 2019, 7, 639. https://doi.org/10.3390/math7070639
Ghaffar A, Bari M, Ullah Z, Iqbal M, Nisar KS, Baleanu D. A New Class of 2q-Point Nonstationary Subdivision Schemes and Their Applications. Mathematics. 2019; 7(7):639. https://doi.org/10.3390/math7070639
Chicago/Turabian StyleGhaffar, Abdul, Mehwish Bari, Zafar Ullah, Mudassar Iqbal, Kottakkaran Sooppy Nisar, and Dumitru Baleanu. 2019. "A New Class of 2q-Point Nonstationary Subdivision Schemes and Their Applications" Mathematics 7, no. 7: 639. https://doi.org/10.3390/math7070639
APA StyleGhaffar, A., Bari, M., Ullah, Z., Iqbal, M., Nisar, K. S., & Baleanu, D. (2019). A New Class of 2q-Point Nonstationary Subdivision Schemes and Their Applications. Mathematics, 7(7), 639. https://doi.org/10.3390/math7070639








