1. Introduction
Understanding spatial distributions of animal species is a key concern for ecology, being of fundamental importance for a wide range of applications including conservation efforts [
1], quantifying biodiversity [
2], and invasive species research [
3,
4]. For mobile animals, decisions about where to move drive their individual locations. Consequently there has been a huge amount of effort in recent years to understand the causes and consequences of animal movement [
5,
6,
7]. However, these movement decisions have an effect not only on individuals’ locations but also on the spatial distribution of the whole population [
8]. To understand this individual-to-population upscaling in a non-speculative way requires mathematical models that are built from the underlying movement processes of individuals [
9]. Such models exhibit emergent phenomena on the population level that can be then quantified and related concretely to the underlying mechanisms of individual movement (e.g., [
10,
11]).
One recent study in this general area examines how the movement responses between individuals from
different animal populations can drive spatio-temporal distribution patterns on temporal scales whereby births and deaths are negligible [
12]. This takes spatial ecology in a slightly different direction to its tradition trajectory, whereby the combination of nonlinear birth-and-death terms (a.k.a. kinetics) combine with diffusive or cross-diffusive movement to drive spatio-temporal patterns [
13,
14,
15,
16,
17]. Instead, the study of [
12] shows that inter-population taxis (a form of cross-diffusion) can drive a wide range of complex patterns on its own, without the need for nonlinear kinetics.
However, the study by [
12] assumes that individuals move diffusively in the absence of interactions. While this may be a reasonable approximation in many cases, in reality animals will always display some directional correlation in movement [
18,
19], if only due to the significant energetic costs of turning [
20]. For some organisms, this correlation may only persist over quite small spatio-temporal scales, in which case diffusion is a reasonable model [
21,
22]. However, if the spatial scale of correlation is at a similar order of magnitude to the scale over which animals move in the time between successive interactions, diffusive assumptions may be less valid [
23].
Here, I address this issue of directional correlation by extending the model of [
12] from a diffusion-taxis system to a telegrapher-taxis system in 1D. The telegrapher’s equation accurately models random movement with directional correlation in a 1D setting [
24,
25]. Moreover, it is a direct generalisation of the diffusion equation, simply requiring the introduction of a characteristic time-scale parameter,
T, which is set to
in the diffusion limit.
The aim of this study is to examine the effect of introducing
on the linear pattern formation properties of the model in [
12]. These patterning properties separate parameter space into three well-known categories [
26]. First, patterns may not form at all from small non-constant perturbations of the steady state, i.e., the system is
stable to such perturbations. Second, small non-constant perturbations of the steady state may grow over small times in a non-oscillatory fashion. This is classically known as a
Turing instability after [
27]. Third, these perturbations may both grow in magnitude and oscillate, which is sometimes known as a
Turing-Hopf instability.
I give general criteria for when an increase
T can cause a shift from one of these three patterning regions to another. When this shift occurs, it holds for all
where
is a threshold persistence time, which is quantified. As an example, I examine in detail the case
in the absence of self-aggregation. Here, the diffusion-taxis model (
) can either be stable to non-constant perturbations or exhibit a Turing instability, dependent on the parameter values of the model. Furthermore, the parameter regimes where the system falls into these two patterning regions is known precisely [
12]. However, the
and
case is never susceptible to a Turing-Hopf instability unless a self-aggregation process is in play [
28]. I show that when
T is increased sufficiently high, Turing-Hopf instabilities are possible without self-aggregation. Furthermore, they occur when the populations are engaged in a “pursuit-and-avoid” situation, with one population exhibiting taxis towards the other, and the latter exhibiting taxis away from the first. In contrast, for
, this pursuit-and-avoid situation is always linearly stable to non-constant perturbations.
2. The Modelling Framework and General Results
This work focusses on a system of
N populations, each of fixed size (i.e., no births or deaths). Individuals from each population move on a 1D landscape as biased, correlated random walkers (i.e., those where there is both persistence in movement and bias in a particular direction). This bias depends on the density of the various populations in the system, and is represented by a taxis term up or down the density gradient of the various populations. The correlated aspect of movement is modelled using a telegrapher’s equation formalism [
24,
25].
Denoting by
the spatial probability density function of population
i at time
t, the study system is given by the following telegrapher-taxis equation for each population
i (
)
where
,
,
, and one can assume, without loss of generality, that the units are dimensionless and
. The case where
and
for all
i was studied in [
12], and the reader is referred there for details of the non-dimensionalisation process. The dynamics take place on a unit line segment,
, with periodic boundary conditions
so locations,
x, live in the quotient space
. In Equation (
1),
is an integrable function, symmetric about
on the domain
, and
is the following spatial convolution
The inter-population taxis term, in the right-hand summand of Equation (
1), can come about through different biological mechanisms. The simplest is for the organisms in population
i to sense directly the gradient of population density,
, a mechanism that may be valid for very small individuals such as single-celled organisms or swarming insects. However, for larger organisms, this population gradient is more likely to be observed indirectly. For example, the deposition of marks in the environment from population
j (e.g., through scenting; [
29,
30]) may indicate the population density,
, across space. Similarly, memory of past interactions with individuals from population
j can act as a proxy for sensing the population density gradient [
31,
32]. In [
12], the authors showed how all of these biological mechanism can be modelled via the same taxis term, given in Equation (
1).
The linear pattern formation properties of Equation (
1) are analysed by perturbing the system about the constant steady-state solution,
for all
. Specifically, let
, where
,
and
are constants, and
denotes matrix transpose. By neglecting non-linear terms, Equation (
1) becomes
where
is an
matrix with
and
is the Fourier transform of
on
.
Let
be the eigenvalues of
(which are not necessarily distinct). If
then
gives a solution to Equation (
4) for some non-trivial vector
. From the perspective of pattern formation, there are three regimes of interest. These are well-documented [
26] but it is valuable to summarise them briefly, for the purposes of introducing the key concepts and nomenclature used throughout this work:
Stable. All eigenvalues have negative real part: Re for all , ,
Turing instability. The dominant eigenvalue (i.e., the one with the largest real part) is positive and real, i.e., ,
Turing-Hopf instability. The dominant eigenvalue is not real but has positive real part, i.e., .
The first of these states that the linear perturbation, , will decay back to the homogeneous steady state, the second that will grow at small times for certain wavenumbers, , in a non-oscillatory fashion, and the third that will grow and oscillate at small times. These regimes give an indication for the pattern formation properties of the system. In the Stable region, the expectation is that spatial patterns do not form. In the Turing instability region, stationary patterns are predicted to form, which are fixed over time. If there is a Turing-Hopf instability, patterns that are in perpetual flux are expected to emerge. However, it is important to note that these are merely predictions, arising from a linearisation of the system, and that it is possible for the non-linear terms to cause different pattern formation properties asymptotically.
The main aim of this work is to examine how the demarcation into the above three regimes changes as
T is increased from 0. When
, for each
, there are up to two values of
such that
. Thus I define
for each
, and note that
solves Equation (
4) for each
i. The main results from this work are given in the following three theorems.
Theorem 1. In the case where the system is linearly stable for (i.e., Re for all , ) one of two situations can occur:
- 1
If for all , then Re for all , so the system stays in the Stable regime for all .
- 2
If there exist i and κ such that then there exists some such that for all , there is a Turing-Hopf instability. In other words, for this value of i and κ, for all . Furthermore, is the minimum such that there exist with Re.
Proof. For part (1), if for all then, since Re, the inequality holds, so Re for all .
For part (2), let and such that . Assume, without loss of generality, that Im (otherwise, pick the complex conjugate of ). Then if Re, the inequality Re holds, so that there is a Turing-Hopf instability.
I now show that if
T is arbitrarily large, the criterion Re
is always satisfied. Here,
Now, arg
arg
. Since Im
and Re
, the following holds
Therefore
so that Re(
. Hence Re
whenever
T is sufficiently large. Furthermore, Re
as
, so there exists some
such that Re
for all
. There may be more than one
and
such that
. Thus let
be the minimum of
over such
j and all
. Then
satisfies the requirements of the theorem. □
Theorem 2. Consider the Turing instability case for (i.e., ). For a given κ, let be the dominant eigenvalue of . Then one of two situations can occur:
- 1
If Re for all j then there is a Turing instability at wavenumber κ and persistence time T.
- 2
If there is some j such that Re then there is a Turing-Hopf instability at wavenumber κ and persistence time T. Let be the minimum such that Re for some j. Then there is a Turing-Hopf instability for all .
Proof. For part (1), let . If Re for all j then is the dominant eigenvalue. Since , so so there is a Turing instability for these values of T and .
For part (2), suppose there exist with Re and suppose Re for all k. Then is the dominant eigenvalue. It is necessary to show that is not real. Therefore, for a contradiction, suppose . Then . However, , since is the dominant eigenvalue of , so , which contradicts the assumption. Hence so there is a Turing-Hopf instability for these values of T and . □
Corollary. If there is some j such that Re then there is a Turing-Hopf instability at wavenumber for sufficiently large T.
Theorem 3. Consider the case where there is a Turing-Hopf instability for . Then there is a Turing-Hopf instability for all .
Proof. Let
i be such that
is the dominant eigenvalue of
for some
where there is a Turing-Hopf instability for
. Assume, without loss of generality, that Im
(otherwise choose the complex conjugate of
). Since Re
, the inequality Re
holds, so
. Since
has positive real and imaginary part,
. The latter follows from the following general calculation for
and
The inequality in (
9) requires
, which follows from
.
It follows that
, and thus from Equation (
6) that Re
for all
. To show that this is within the Turing-Hopf instability region, it is necessary to check that there does not exist
j such that both
and
, since otherwise this is the Turing instability region. For a contradiction, suppose such a
exists. Then
so
so
, which contradicts the fact that
is the dominant eigenvalue for the
case. □
3. The Case of Two Interacting Populations ()
In this section, I look in detail at the specific example where
and
for all
, to show how persistent movement can drive qualitative changes in pattern formation properties even in this simple situation. In the case
(studied by [
12]), the following holds
and it follows that the system for
is linearly stable to wave perturbations whenever
. When
, the system can have a Turing instability, and always does in the limit
, where the spatial averaging given by
is arbitrarily small. The system never exhibits a Turing-Hopf instability for
[
12].
In the Turing instability case for
, both the eigenvalues are real, so the conditions of Theorem 2, part 2, are met. Thus there is a Turing instability for all
. The case where
, however, is more interesting. Here, Theorem 1 states that a Turing-Hopf instability will occur for sufficiently large
T as long as
, that is
The first thing to notice about the condition given by (
12) is that
and
need to be of opposite signs. This means that one population tends to advect up the density gradient of the other, while the second population retreats down the gradient of the first. This is termed a ‘pursuit-and-avoid’ situation in [
12]. In this situation, for
, no patterns form: the populations each settle to a steady-state distribution whereby they are uniformly distributed on the terrain. However, if
is defined to be the minimum positive real number such that there exists
with Re
, then Theorem 1 implies there is a Turing-Hopf instability whenever
.
To understand how
depends on the parameters, I fix
and set
. (Notice that
since
and
are of opposite signs.) It is also necessary to pick a particular functional form for
. This is a slightly delicate matter as it is not necessarily the case that the pattern formation problem is well-posed for an arbitrary
. For example, if
is used, where
is the Dirac delta function, then, by Equation (
6), the dominant eigenvalue is
If T is fixed and is arbitrarily large, then ReRe as . Hence patterns can form for arbitrarily high wavenumbers, meaning the pattern formation problem is ill-posed.
However, suppose instead that
for some
, so that
The case of interest is where
is small, in which case the following approximation can be made
Now, notice that if
T is fixed and
is arbitrarily large, then
as
. Therefore, with the Gaussian averaging kernel from Equation (
14), the pattern formation problem is well-posed, in the sense that patterns cannot form at arbitrarily high wavenumbers.
By Theorem 1, there is some
such that there is a Turing-Hopf instability for all
. Furthermore, this Theorem states that
is the minimum
T such that the following holds for some
In
Figure 1a,
is plotted against
for
,
, and varying values of
T. This reveals that
T not only affects whether patterns form, but the range of wavenumbers for which patterns may form. In this example, there is a Turing-Hopf bifurcation for value of
somewhere between
and
.
The precise values of
for a range of
- and
-values are plotted in
Figure 1b,c. The
parameter encodes the strength of attraction/avoidance.
Figure 1b,c shows that
decays for increasing
and grows with the width of spatial averaging,
.
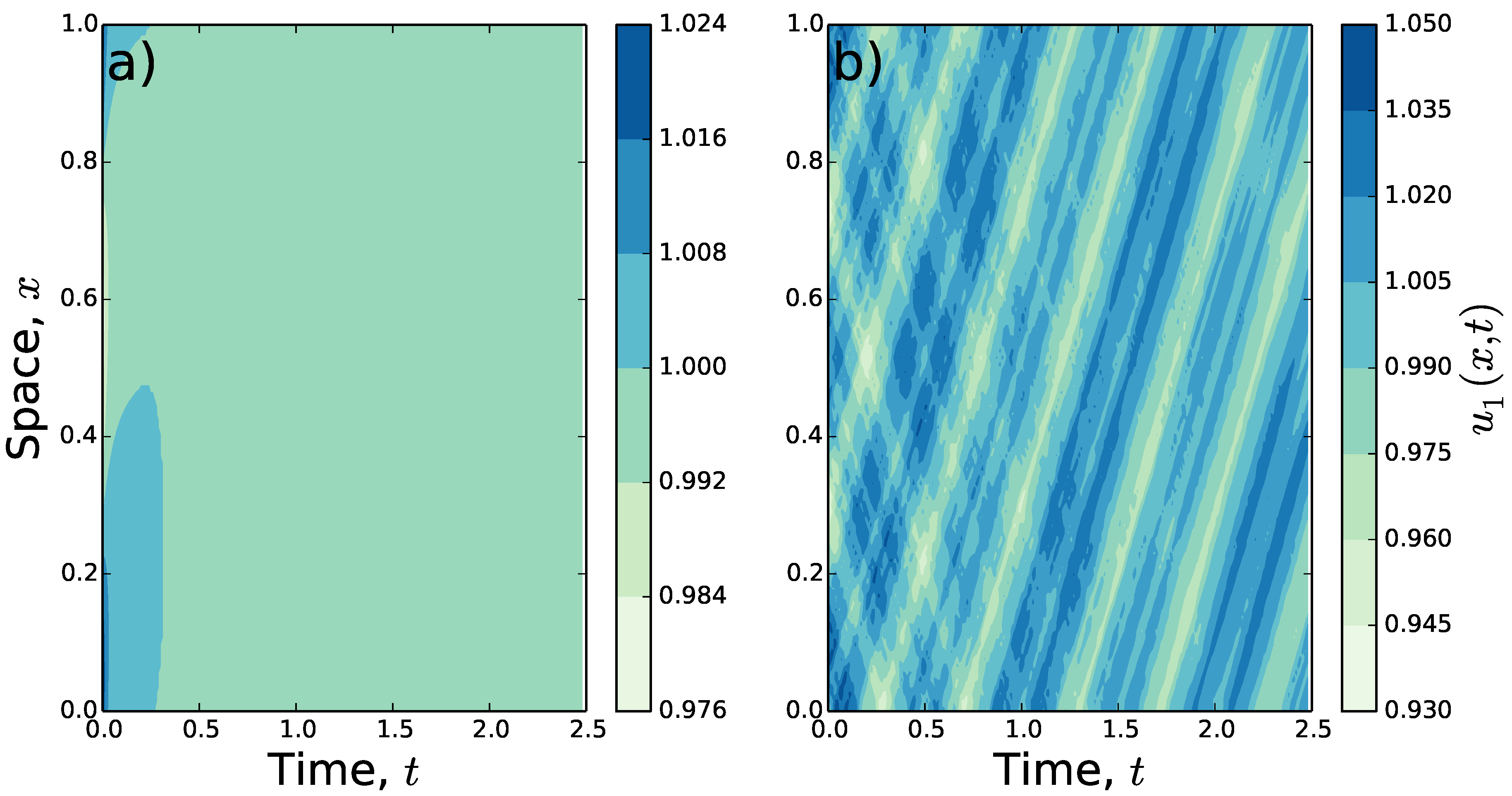
To understand the qualitative properties of the patterns that emerge from increasing
past the Turing-Hopf bifurcation point, the system in Equations (
1)–(
3) is solved numerically, with
,
,
, and the Gaussian spatial averaging from Equation (
14). In
Figure 2, the results of these numerics are shown for certain values of
,
and
T. Here, rather than decaying to the homogeneous steady state (
), for higher
T the populations move across the landscape while maintaining a non-constant population distribution.
4. Discussion
This study examines a telegrapher-taxis system of
N populations to demonstrate how directional correlation can drive pattern formation in systems of between-population taxis. General criteria are given for switches in pattern formation regime driven by directional correlation and the
case is examined in detail. These results demonstrate the importance of considering directional correlation when seeking to understanding the spatio-temporal population distributions of moving organisms. As our ability to capture data on animal movement is becoming increasingly sophisticated, better understanding of how the details of animal movement can affect population dynamics is becoming an ever-more pertinent question [
6], with implications for a diverse range of ecological areas such as connectivity dynamics [
33] and conservation [
34].
The model of [
12], on which the present model is based, is closely related to aggregation and chemotaxis models inspired by cell biology [
35,
36,
37,
38]. Although many such models only examine a single population, there are various examples of two-population models [
28,
39], and some that incorporate an arbitrary number of populations [
40,
41]. In the latter examples, the diffusion-taxis equations are coupled via interactions with a diffusive chemical, different to the model studied here. While cells lack the momentum of much larger organisms, directional correlation is known to be a factor in the movement of cells in certain circumstances [
42,
43,
44]. Therefore the results presented here suggest that it is worth exploring how directional correlation may affect the pattern formation properties of such aggregation and chemotaxis models.
Here, ecosystems are modelled on a constrained timescale whereby births and deaths are negligible. However, it would be valuable to extend the model presented here to incorporate such effects, via competition and/or predation terms (i.e., kinetics), and so explore the effect of directional persistence over longer timescales. Adding directional persistence to models that incorporate kinetics is non-trivial, though, and does not simply involve adding a second temporal derivative to a reaction-diffusion-taxis model [
45].
Nonetheless, building such a system of reaction-telegrapher-taxis equations would enable connection with cross-diffusion models (e.g., [
16,
17,
46,
47]). These are generalisations of reaction-diffusion systems, whereby terms are added that allow for motion driven by the presence of foreign populations. These terms include, but are not limited to, the taxis terms observed in the model from Equation (
1). However, incorporating directional correlation via a telegrapher’s term into a cross-diffusive setting is much rarer (but see [
48]) and the pattern formation properties of such systems are not well-explored. Given the results presented here, it may be interesting to extend cross-diffusive models in this way, to show how directional correlation may affect pattern formation in such models.
In summary, the simple but general results shown here demonstrate that directional correlation of individuals’ movement can have a great effect on the spatio-temporal distribution of species. While I have demonstrated this in a model of ecosystems relevant over relatively short timescales, where births and deaths are minimal, it highlights a general principle that is little-studied and may have much wider implications.