A Meta-Model-Based Multi-Objective Evolutionary Approach to Robust Job Shop Scheduling

Abstract

In the real-world manufacturing system, various uncertain events can occur and disrupt the normal production activities. This paper addresses the multi-objective job shop scheduling problem with random machine breakdowns. As the key of our approach, the robustness of a schedule is considered jointly with the makespan and is defined as expected makespan delay, for which a meta-model is designed by using a data-driven response surface method. Correspondingly, a multi-objective evolutionary algorithm (MOEA) is proposed based on the meta-model to solve the multi-objective optimization problem. Extensive experiments based on the job shop benchmark problems are conducted. The results demonstrate that the Pareto solution sets of the MOEA are much better in both convergence and diversity than those of the algorithms based on the existing slack-based surrogate measures. The MOEA is also compared with the algorithm based on Monte Carlo approximation, showing that their Pareto solution sets are close to each other while the MOEA is much more computationally efficient.

1. Introduction

Production scheduling is of great significance in both scientific study and engineering applications [1,2,3,4,5]. Generally, the aim of the job shop scheduling problem (JSS) is to find a schedule that minimizes certain performance objective, given a set of machines and a set of jobs. However, in practice, the execution of a schedule is usually confronted with disruptions and unforeseen events, such as random machine breakdowns (RMDs), which make the actual performance of a schedule hard to predict. Against this background, we will focus on the multi-objective robust JSS under RMDs with the goal of optimizing the makespan and the robustness simultaneously.

In the last few decades, the JSS problems have been extensively studied, most of which have addressed the JSS with makespan as the objective [6,7,8], such as the hybrid genetic algorithm [9], the genetic algorithm [10] with search area adaptation [11], the global optimization technique which combines tabu search with the ant colony optimization [12], and the memetic algorithm conditioned on a limited set of human operators [13]. However, it is often assumed that the problem parameters about jobs and machines are known and deterministic. This makes it difficult to generate a good schedule for a real-world job shop which is subjected to various uncertainties [14], such as machine breakdowns, variable processing times, and due date changes. Mehta et al. [15] had classified the uncertainties in the practical manufacturing into three main categories: complete unknowns, suspicions about the future, and known uncertainties. Complete unknowns are those unpredictable events, e.g. a sudden strike, about which no a-priori information is available, while suspicions about the future arise from the intuition and experience of the human scheduler. On the other hand, known uncertainties are those events about which some information is available in advance, such as machine breakdowns [16,17,18] whose frequency and duration may be characterized by probability distributions. Under these uncertainties, a schedule will be difficult to execute as planned, and finally the actual performance of the schedule will deteriorate.

Recently, robust optimization has gained intensive interest [19], where most of existing studies focus on addressing the scheduling problems under known uncertainties. The robustness of a schedule indicates the ability of the schedule to preserve a specified level of solution quality in the presence of uncertainties [20], which is generally measured by the expected deviation of the performance from its initial performance under uncertainties [21]. Liu et al. [22] defined the robust schedule as a schedule that is insensitive to uncertainties, such as that a schedule may degrade its performance to a very small degree under disruptions. Thus, in addition to the makespan, the robustness of a schedule will also be taken as one of the objectives in the robust scheduling. Xiao et al. [23] addressed the stochastic JSS problem with uncertain processing times, and the robustness took the expected relative deviation between the realized makespan and the predictive makespan. Zuo et al. [24] considered both the expectation and standard deviation of the performance of a schedule. Ahmadi et al. [25] defined the robustness of a schedule as the expected deviation of starting and completion time of each job between preschedule and realized schedule under RMD.

With simultaneous consideration of the performance and the robustness of a schedule, the JSS under uncertainties holds a multi-objective nature. Usually, the two objectives are combined by the weight sum, and then the problem with two objectives will be transferred into a single-objective problem, such as that described in [26,27]. However, providing a wide range of solutions to decision-makers might be more useful [20], since decision-makers can make a better trade-off between the performance and the robustness for their schedules. The multi-objective evolutionary algorithm (MOEA), such as NSGA II [28,29,30], has been successfully solved the classic JSS without considering uncertainties [31]. In addition, Hosseinabadi, et al. [32] proposed a TIME_GELS algorithm that uses the gravitational emulation local search [33] for solving the multiobjective flexible dynamic job-shop scheduling problem. But, when the robustness is considered, a MOEA should further be able to solve the problems in the presence of uncertainties [34].

Because of the intractable complexity of JSS with uncertainties, it is difficult to evaluate the effects of uncertainties on a schedule, and thus the robustness is not available in a closed form. In this case, approximation methods should be applied for fitness evaluation in the MOEA. The simplest way is to employ the Monte Carlo method [35,36] to estimate the robustness, by averaging the objective values over a few randomly sampled uncertainty scenarios. The Monte Carlo method is based on random sampling and has been proven to be a powerful method for estimation [37,38,39]. However, it may cause potentially expensive fitness evaluations and reduce the computing efficiency. For this reason, the problem approximation that tends to replace the original statement of a problem by one which is simple but easier to solve, has been applied. Mirabi, et al. [40] simplified the machine breakdown by assuming the repair time is constant, while Liu et al. [41] assumed that all possible machine breakdowns during a scheduling horizon are aggregated as one. However, this may lead to a large mismatch between the model and the actual problem. In contrast, the meta-model which is an approximate function of the real fitness, also known as the surrogate measure, may be preferred. However, the design of a meta-model for the robustness is challenging. So far, the available surrogate measures for the robustness measured by the expected makespan delay (EMD) only include the average total slack time of operations in [42] and the sum of free slack times of operations in [26]. Since these surrogate measures ignored uncertainties, their estimation accuracy will be reduced [43].

In comparison with the existing research, the main contributions of our approach are as follows:

• The robustness of a schedule is considered jointly with the makespan and is defined as EMD, for which a meta-model is designed by using a data-driven response surface method.
• A MOEA is proposed based on the meta-model, gaining excellent performance and efficiency.

The remainder of this paper is organized as follow. The multi-objective optimization model for the JSS under RMD is defined in the next section. In Section 3, a meta-model-based MOEA is proposed. The performance of the proposed algorithm is presented in Section 4, with comparison with the Monte Carlo method. In Section 5, we conclude the whole study.

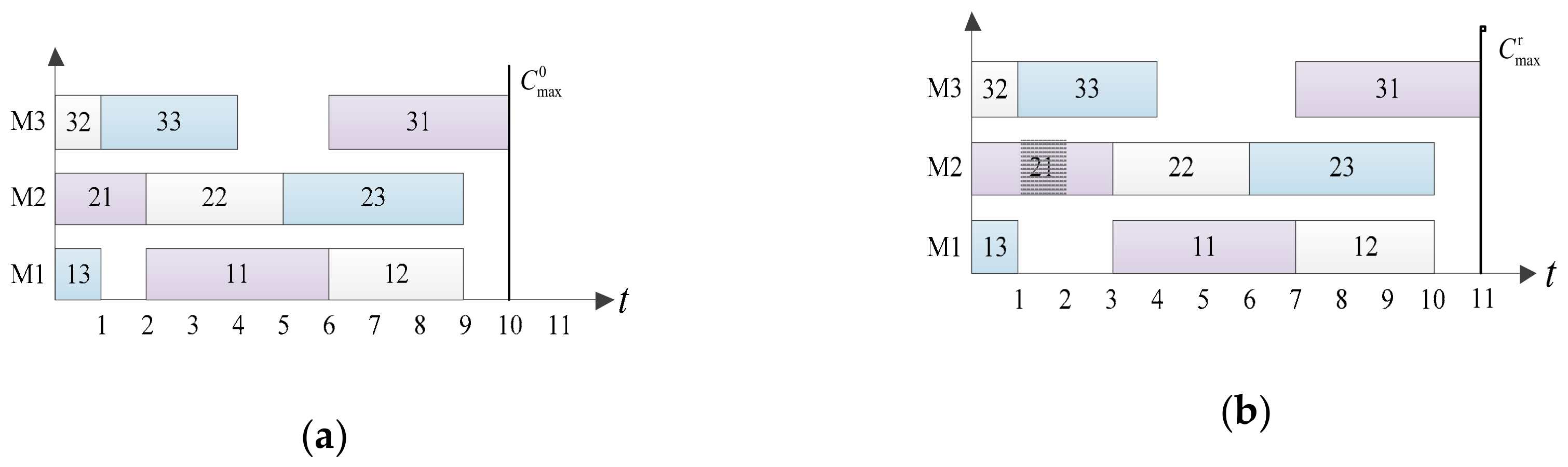
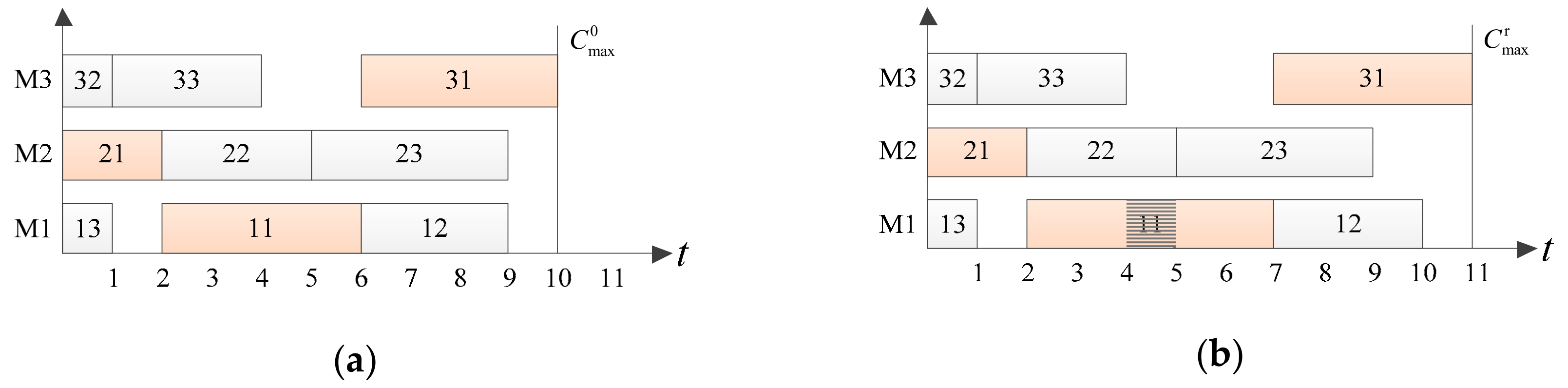
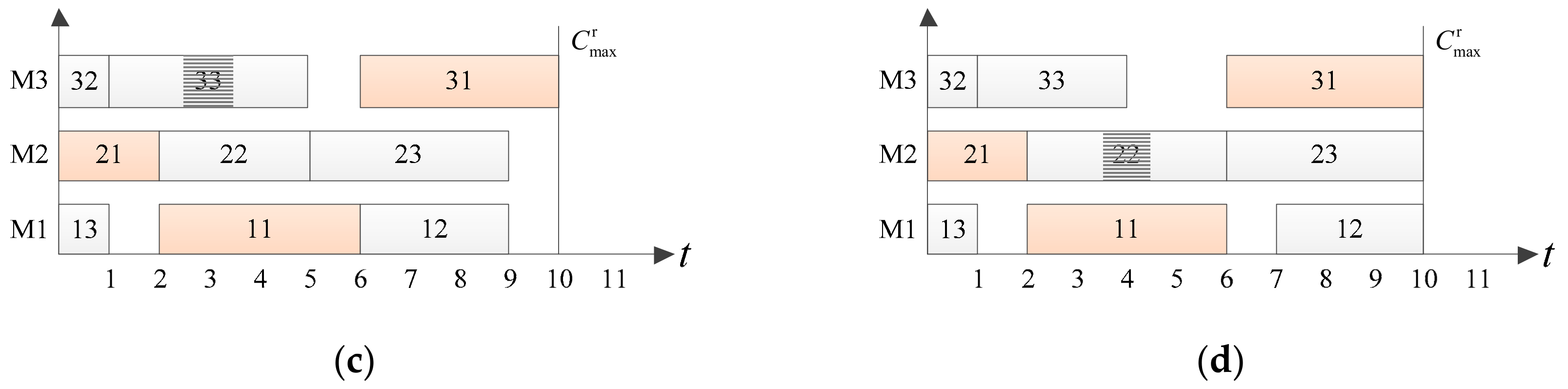
2. Problem Definition

We consider the JSS problem with n jobs ($\mathit{J}=\left\{J_j\right|j=1,2,\dots ,n\}$) to be processed on m machines ($\mathit{M}=\left\{M_i\right|i=1,2,\dots ,m\}$). All jobs and machines are available at time zero. The processing of job $j$ on machine $i$ is called operation $O_{ij}, i\in [1,m],j\in [1,n]$, and its processing time $p_{ij}$ is constant and known. Each job includes m operations (${\mathit{O}}_j=\left\{O_{ij}\right|i=1,2,\dots ,m\}$, $j\in [1,n]$) that must be processed in a specified sequence through each machine. A feasible schedule that specifies the starting and completion time of all operations should satisfy the constraints: (1) job splitting is not allowed; (2) an operation is not allowed to be preempted by the others; (3) each operation is performed only once on one machine; and (4) each machine performs only one operation at a time.

In this study, the operation-based machine breakdown model presented in [21] will be applied. More specifically, the machine breakdown is modeled by two parameters: the downtime required to repair the machine after its breakdown, and the breakdown probability during a time interval. The machine breakdown probability ${\mathrm{Pr}}_{ij}$ when processing operation $O_{ij}$ can be calculated by Equation (1), where ${\lambda }_0$ is the machine failure rate of each machine.

$${\mathrm{Pr}}_{ij}=\min \{{\lambda }_0{p}_{ij},1\}$$

(1)

The downtime $D_{ij}$ of a machine after a breakdown when processing operation $O_{ij}$ is modeled as an exponential distribution, as shown in Equation (2), where ${\beta }_0$ is the expectation of the downtime.

$$f(D_{ij})=\left\{\begin{array}{ll}\frac{1}{{\beta }_0}{e}^{-\frac{1}{{\beta }_0}{D}_{ij}}& D_{ij}>0\\ 0& D_{ij}\le 0\end{array}\right.$$

(2)

In the classic JSS problems without considering uncertainties, the aim of scheduling is generally to find a schedule that minimizes the makespan. The makespan of a schedule is equal to the maximum completion time of all operations in the schedule, which can be determined by Equation (3), where $c{t}_{ij}^{}$ is the completion time of operation $O_{ij}$.

$$C_{\max }^0=\underset{i\in \mathit{M}}{\max }\{\underset{j\in \mathit{J}}{\max }\{c{t}_{ij}^{}\}\}$$

(3)

However, the makespan of a schedule will be affected by RMDs in practice [16,17,18]. Since RMDs postpone the completion time of operations, the actual makespan $C_{\max }^{\mathrm{r}}$ of a schedule will be delayed. As shown in Figure 1a, the makespan $C_{\max }^0$ of the schedule before execution is equal to 10. If a machine breakdown with one unit of downtime occurring on the operation $O_{21}$, as shown in Figure 1b, its completion time is directly postponed by one unit of time. Then, all the completion times of its subsequent operations {$O_{22}$, $O_{11}$, $O_{23}$, $O_{12}$, $O_{31}$} are also delayed by one unit of time. Finally, the actual makespan $C_{\max }^{\mathrm{r}}$ of the schedule is equal to 11, which has been delayed by one unit of time.

According to the analysis above, the influence of machine breakdowns on the makespan of a schedule can be given by the makespan delay ${\delta }_{\mathrm{c}}$ in Equation (4).

$${\delta }_{\mathrm{c}}=\max (C_{\max }^{\mathrm{r}}-C_{\max }^0, 0)$$

(4)

Since machine breakdowns take place randomly, the makespan delay of a schedule will vary with the actual scenario of machine breakdowns, which makes the actual makespan very instability. The stochastic change of the actual makespan will reduce the performance of a schedule, such as that it may lead to the products cannot be delivered on time and lose the customer good will. Therefore, it is preferred that the makespan of a schedule is robust under RMDs. To measure the robustness of makespan, the EMD will further be applied, as the ${\Delta }_{\mathrm{c}}$ shown in Equation (5).

$${\Delta }_{\mathrm{c}}=E({\delta }_{\mathrm{c}})={\displaystyle {\int }_0^{+\infty }{\delta }_{\mathrm{c}}f({\delta }_{\mathrm{c}})d\delta }$$

(5)

However, a schedule with the minimum makespan is generally very compact, which means that it may be very sensitive to RMD and with a large EMD. Thus, the makespan $C_{\max }^0$ of a schedule will conflict with the EMD. Since different decision-makers have various preferences for the makespan and the makespan delay, it is worth providing a wide range of schedules for decision-makers to make the best trade-off. When consider the makespan and the EMD of a schedule at the same time, the JSS under RMD can be modeled as a multi-objective optimization problem. Let A be the set of precedence constraints (O_ij, O_kj) that require job j to be processed on machine i before it is processed on machine k, the multi-objective optimization model can be provided as follows:

Minimize:

$$\mathit{F}=(C_{\max }^0, {\Delta }_{\mathrm{c}})$$

(6)

Subject to:

$$s{t}_{kj}^{}-s{t}_{ij}^{}\ge p_{ij} , \mathrm{for} \mathrm{all} (O_{ij}, O_{kj})\in A$$

(7)

$$s{t}_{ij}^{}-s{t}_{il}^{}\ge p_{il} \mathrm{or} s{t}_{il}^{}-s{t}_{ij}^{}\ge p_{ij}, \mathrm{for} \mathrm{all} O_{ij} \mathrm{and} O_{il}$$

(8)

$$s{t}_{ij}^{}\ge 0, \mathrm{for} \mathrm{all} O_{ij}$$

(9)

$${\lambda }_i={\lambda }_0, \mathrm{for} \mathrm{all} i\in M$$

(10)

$$D_{ij}\sim Exp(1/{\beta }_0), \mathrm{for} \mathrm{all} O_{ij}$$

(11)

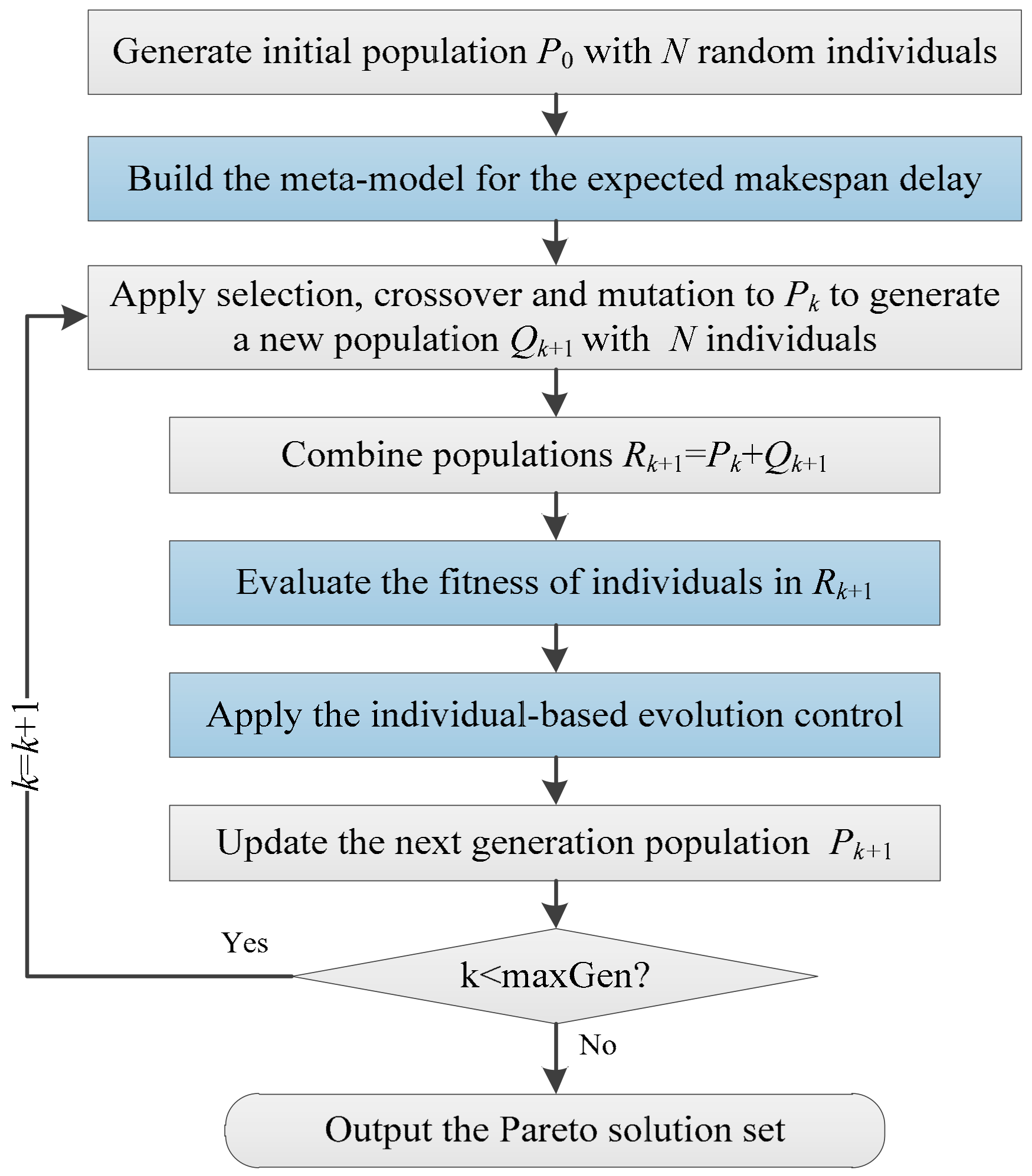
3. The Meta-Model Based MOEA

When solving the multi-objective optimization model in Section 2 by a MOEA, the primary task is to evaluate the fitness of each individual in a population. However, the EMD in Equation (5) cannot be analytically calculated for the intractable complexity of JSS under RMD. Although the commonly-used Monte Carlo simulation can be used to approximate the EMD, it will make the MOEA inefficient for it is very time-consuming to evaluate each single individual, especially for the problems with larger scales. In view of this, a meta-model-based MOEA will be proposed to solve the multi-objective optimization model for the robust JSS.

3.1. Framework of The Algorithm

The meta-model-based MOEA is designed according to the basic framework of the classic NSGA-II [28]. As shown in Figure 2, the algorithm begins with an initial population P₀ with N randomly generated individuals. Before executing the following genetic operators, the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ of the ${\Delta }_{\mathrm{c}}$ will be constructed based on the initial population P₀. Then, the selection, crossover, and mutation operators will be applied on the current population P_k to generate new individuals and construct a combined population R_k+1. The fitness of individuals in the combined population R_k+1 will first be evaluated by the makespan $C_{\max }^0$ and the proposed meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$, and then the individual-based evolution control will be applied to update the fitness of some individuals. Finally, the next generation population P_k+1 will be generated according to the ranks of individuals. When the maximum generation number is reached, the algorithm will stop and return the obtained Pareto solution set.

3.2. Meta-Model of The EMD

The meta-model for the EMD will be constructed based on the response surface methodology. As shown in Equation (12), this method applies a quadratic polynomial $\widehat{f}(\mathit{x})$ to approximate the function relation between the input $\mathit{x}$ and the output $y$ of a system,

$$y\approx \widehat{f}(\mathit{x})=a_0+\mathit{Bx}+\mathit{xC}{\mathit{x}}^{\mathrm{T}},$$

(12)

where, $\mathit{x}$ is the input variant vector with $v$ variables as shown in Equation (13), $a_0$ is the constant term, $\mathit{B}$ is the coefficient vector of the linear term as shown in Equation (14), and $\mathit{C}$ is the coefficient matrix of the quadratic term as shown in Equation (15).

$$\mathit{x}=(x_1,x_2,\dots ,x_v)$$

(13)

$$\mathit{B}=(b_1,b_2,\dots ,b_v)$$

(14)

$$\mathit{C}=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1v}\\ & c_{22}& \cdots & c_{2v}\\ & & \ddots & ⋮\\ & & & c_{vv}\end{array}\right]$$

(15)

However, a schedule cannot be directly taken as an input variant of the EMD, since it cannot be quantified. Therefore, to construct a meta-model by the response surface method for the EMD, the primary task is to extract features related to the EMD from the schedule. To this end, we will further analyze how RMDs affect the makespan of a schedule. As we all know, a feasible job shop schedule is decided by the process constraints and the resource constraints. As a result, machines may have some idle time during a schedule period, as shown in Figure 3a. In the classic JSS problems, we are devoted to reducing the idle time to minimize the makespan for improving the utilities of machines. However, when RMDs are considered, the idle time may be useful for an operation to control the influence of machine breakdowns on the makespan of a schedule and then improve the robustness of the makespan.

The available idle time of operations in a schedule can be classified into two types: the free slack time and the total slack time. The former is the time that an operation can be delayed without delaying the starting of its very next operations, while the latter is the difference between the earliest and latest starting times of an operation without delaying the makespan. Take the schedule in Figure 3a as an example, the free slack time of operations {$O_{13}$, $O_{11}$, $O_{12}$, $O_{21}$, $O_{22}$, $O_{23}$, $O_{32}$, $O_{33}$, $O_{31}$} are {0, 0, 1, 0, 0, 1, 0, 1, 0}, respectively. The earliest and latest starting time of operations {$O_{13}$, $O_{11}$, $O_{12}$, $O_{21}$, $O_{22}$, $O_{23}$, $O_{32}$, $O_{33}$, $O_{31}$} without delaying the makespan is {0, 2, 6, 0, 2, 5, 0, 1, 6} and {1, 2, 7, 0, 3, 6, 2, 3, 6}, respectively. Therefore, the total slack time of each operation is {1, 0, 1, 0, 1, 1, 2, 2, 0}, respectively.

It is clear that not all operations have the free/total slack time. For an operation without slack time, the makespan of a schedule will be directly delayed, when an RMD takes place on it. As shown in Figure 3b, when a RMD with one unit of downtime takes places on the operation $O_{11}$, the actual makespan $C_{\max }^{\mathrm{r}}$ is changed to 11, which is directly delayed by one unit of time. However, when an RMD takes places on an operation with slack time, the makespan will not be delayed until the slack time of this operation is used up. As shown in Figure 3c, after a RMD with one unit of downtime takes place on the operation $O_{33}$ with two units of free slack time, the makespan is still equal to 10, for the free slack time of this operation is larger than the downtime of the breakdown. On the other hand, although the operation $O_{22}$ has no free slack time, the makespan can also be protected by the total slack time of the operation, as shown in Figure 3d.

According to the analysis above, it can be found that the makespan delay of a schedule depends on the machine breakdown level, the free slack time and total slack time of each operation. In view of this, we will extract the mathematical features for the schedule under RMDs from these three aspects: the RMDs, the set ${\mathit{O}}_y$ of operations with slack time and the set ${\mathit{O}}_{\mathrm{n}}$ of operations without slack time. For the RMDs, the machine failure rate ${\lambda }_0$ and the expected downtime ${\beta }_0$ after a breakdown will be taken. For the operations in the set ${\mathit{O}}_y$, all their processing time $p_{ij}$, free slack time $f{s}_{ij}$ and total slack time $t{s}_{ij}$ will be taken. As for the operations in the set ${\mathit{O}}_{\mathrm{n}}$, only their processing time $p_{ij}$ will be taken.

However, it is practically impossible to consider all the processing time, free slack time, and total slack time of operations as the input variants of the EMD. To reduce the number of input variants, we will further generalize these basic features into some comprehensive features. Formally, the sum of processing time $p_{\mathrm{s}}^{\mathrm{y}}$ and $p_{\mathrm{s}}^{\mathrm{n}}$ will be used to represent the processing time of operations in the sets ${\mathit{O}}_y$ and ${\mathit{O}}_{\mathrm{n}}$, respectively. For the slack time, the average free slack time $f{s}_{\mathrm{a}}$ and the average total slack time $t{s}_{\mathrm{a}}$ of operations in the set ${\mathit{O}}_y$ will be applied.

Finally, the input variants of the EMD can be listed as follows: the machine failure rate ${\lambda }_0$, the expected downtime ${\beta }_0$, the sum of processing time $p_{\mathrm{s}}^{\mathrm{n}}$, the sum of processing time $p_{\mathrm{s}}^{\mathrm{y}}$, the average free slack time $f{s}_{\mathrm{a}}$, and the average total slack time $t{s}_{\mathrm{a}}$. Then, the input variant vector $\mathit{x}$ of the EMD can be set as $\mathit{x}=(x_1,x_2,x_3,x_4,x_5,x_6)$ $=({\lambda }_0,{\beta }_0,p_{\mathrm{s}}^{\mathrm{n}},p_{\mathrm{s}}^{\mathrm{y}},f{s}_{\mathrm{a}},t{s}_{\mathrm{a}})$, and then the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ of ${\Delta }_{\mathrm{c}}$ can be defined by Equation (16).

$${\Delta }_{\mathrm{c}}\approx {\Delta }_{\mathrm{c}}^{\mathrm{a}}=a_0+{\displaystyle \sum _{i=1}^6{b}_i{x}_i}+{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^6{c}_{ij}{x}_i{x}_j}}$$

(16)

Then, the coefficients should further be determined to finalize the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$. As shown in Algorithm 1, it takes the initial population P₀ and the input variant vector x as the inputs, and outputs the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ with the determined coefficients. First, a training data set ${\mathit{D}}_{\mathrm{c}}$ which includes N data instances will first be generated based on the initial population P₀. A data instance ${\mathit{I}}_i=({\mathit{x}}_i,{\Delta }_{\mathrm{c}}^i)$ is composed of the values of the input variant vector ${\mathit{x}}_i$ and the corresponding ${\Delta }_{\mathrm{c}}^i$. The values of the input variant vector ${\mathit{x}}_i$ can be determined once a schedule $s_i$ is generated based on the ith individual in the initial population P₀. Since the EMD cannot be analytically calculated, it will be evaluated by the Monte Carlo approximation ${\Delta }_{\mathrm{c}}^{\mathrm{sim}}$ as shown in Equation (17). After the training data set ${\mathit{D}}_{\mathrm{c}}$ is constructed, the Multiple Linear Regression will be used to determine the coefficients of the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ for the EMD,

$${\Delta }_{\mathrm{c}}^{\mathrm{sim}}=\frac{1}{N_{\mathrm{s}}}{\displaystyle \sum _{i=1}^{N_{\mathrm{s}}}(C_{\max }^i-C_{\max }^0)},$$

(17)

where $N_{\mathrm{s}}$ is the simulation times and $C_{\max }^i$ is the makespan of a schedule under the ith simulation.

Algorithm 1 The pseudo-code to finalize the meta-model.

Inputs: the initial population P0 and the input variant vector x Outputs: the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ with the determined coefficients

1: Set the training data set ${\mathit{D}}_{\mathrm{c}}=\varnothing$; 2: Generate Ns machine breakdown scenarios with the machine failure rate ${\lambda }_0$ and the expected downtime ${\beta }_0$; 3: for $i=1$ to $N$ 4:   Generate the schedule $s_i$ based on the ith individual in P0; 5:   Determine the makespan $C_{\max }^0$ of the schedule $s_i$ by Equation (3); 6:   Calculate the free slack time $f{s}_{ij}$ and the total slack time $t{s}_{ij}$ in schedule $s_i$; 7:   Calculate the sum of processing time $p_{\mathrm{s}}^{\mathrm{n}}$ and $p_{\mathrm{s}}^{\mathrm{y}}$; 8:   Calculate the average free slack time $f{s}_{\mathrm{a}}$ and the average total slack time $t{s}_{\mathrm{a}}$; 9:   Determine the values ${\mathit{x}}_i$ of the input variant vector $\mathit{x}=({\lambda }_0,{\beta }_0,p_{\mathrm{s}}^{\mathrm{n}},p_{\mathrm{s}}^{\mathrm{y}},f{s}_{\mathrm{a}},t{s}_{\mathrm{a}})$; 10:   Determined the EMD ${\Delta }_{\mathrm{c}}^i={\Delta }_{\mathrm{c}}^{\mathrm{sim}}$ by Equation (17); 11:   Generate the ith data instance ${\mathit{I}}_i=({\mathit{x}}_i,{\Delta }_{\mathrm{c}}^i)$; 12:   Update the training data set ${\mathit{D}}_{\mathrm{c}}={\mathit{D}}_{\mathrm{c}}\cup {\mathit{I}}_i$; 13: end for 14: Based on the training data set ${\mathit{D}}_{\mathrm{c}}$, apply the multiple linear regression to determine the coefficients of the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ in Equation (16); 15: Return the finalized meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$.

3.3. Fitness Evaluation

To compare the fitness of different individuals, the makespan and the EMD of each individual in a population should be evaluated. Once a schedule is generated, the makespan can be directly determined by Equation (3). However, the EMD cannot be analytically calculated for the complexity of the JSS. Although it can be effectively approximated by the time-consuming Monte Carlo approximation in Equation (17), the efficiency of the algorithm will be significantly reduced. In view of this, we will apply the proposed meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ in Equation (16) to approximate the EMD. The basic motivation for using the meta-model in the fitness evaluation is to reduce the number of expensive fitness evaluations without degrading the quality of the obtained optimal solution.

Based on the proposed meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$, Algorithm 2 can be used to provide the fitness set ${\mathit{F}}_{k+1}=\{(C_{\max }^0(s_0),{\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_0)),\dots ,(C_{\max }^0(s_i),{\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_i)),\dots ,(C_{\max }^0(s_i),{\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_i))\}$ of the individuals in the combined population P_k+1, where ${\mathit{F}}_{k+1}^i=(C_{\max }^0(s_i),{\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_i))$ represents the fitness of the ith individual in the combined population P_k+1 with the makespan ${\mathit{F}}_{k+1}^i(1)=C_{\max }^0(s_i)$ and the EMD ${\mathit{F}}_{k+1}^i(2)={\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_i)$.

Algorithm 2 Fitness evaluation for the combined population

Inputs: the combined population Rk+1 Outputs: the fitness set ${\mathit{F}}_{k+1}$ of the individuals in Rk+1

1: Set the fitness set ${\mathit{F}}_{k+1}=\varnothing$; 2: for $i=1$ to $2N$ 3:   Select the ith individual $ch{m}_i$ from the population Rk+1; 4:   Generate the schedule $s_i$ based on the individual $ch{m}_i$; 5:   Evaluate the makespan $C_{\max }^{0,i}$ of the schedule $s_i$ by Equation (3); 6:   Get machine failure rate ${\lambda }_0$ and expected downtime ${\beta }_0$; 7:   Calculate the free slack time $f{s}_{ij}$ and the total slack time $t{s}_{ij}$ in the schedule $s_i$; 8:   Calculate the sum of processing time $p_{\mathrm{s}}^{\mathrm{n}}$ and $p_{\mathrm{s}}^{\mathrm{y}}$; 9:   Calculate the average free slack time $f{s}_{\mathrm{a}}$ and the average total slack time $t{s}_{\mathrm{a}}$; 10:   Determine the values ${\mathit{x}}_i$ of the input variant vector $\mathit{x}=({\lambda }_0,{\beta }_0,p_{\mathrm{s}}^{\mathrm{n}},p_{\mathrm{s}}^{\mathrm{y}},f{s}_{\mathrm{a}},t{s}_{\mathrm{a}})$ 11:   Evaluate the EMD by ${\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_i)$ in Equation (16) with the values of ${\mathit{x}}_i$; 12:   Update the fitness set ${\mathit{F}}_{k+1}={\mathit{F}}_{k+1}\cup {\mathit{F}}_{k+1}^i={\mathit{F}}_{k+1}\cup (C_{\max }^0(s_i),{\Delta }_{\mathrm{c}}^{\mathrm{a}}(s_i))$; 13: end for 14: Return the fitness set ${\mathit{F}}_{k+1}$;

3.4. Individual-Based Evolution Control

Generally, the approximate model is assumed to be of high fidelity and, therefore, the real fitness function will be not at all used in the evolution [20]. However, an evolutionary algorithm using meta-models without controlling the evolution using the real fitness function can run the risk of an incorrect convergence [28]. For this reason, the meta-model is combined with the real fitness function in our algorithm, which is often known as evolution control or model management.

As shown in Algorithm 3, the individual-based evolution control framework will be applied, which chooses the best individuals according to the pre-evaluation using the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ for reevaluation using the real fitness function. For this purpose, the fitness set ${\mathit{F}}_{k+1}$ will first be ranked by the fast non-dominated sorting. And then, the individuals with the rank $rank({\mathit{F}}_{k+1}^i)=1$ will further be reevaluated by the Monte Carlo approximation ${\Delta }_{\mathrm{c}}^{\mathrm{sim}}$ in Equation (17). In addition, to avoid the unnecessary simulation computational time, the repeated individuals will only be evaluated once.

Algorithm 3 Individual-based evolution control framework

Inputs: the fitness set ${\mathit{F}}_{k+1}$ of the combined population Rk+1 Outputs: the modified fitness set ${\widehat{\mathit{F}}}_{k+1}$

1: Generate Ns scenarios with the machine failure rate ${\lambda }_0$ and the expected downtime ${\beta }_0$; 2: Rank the fitness set ${\mathit{F}}_{k+1}$ by the fast non-dominated sorting; 3: Sort the fitness set ${\mathit{F}}_{k+1}$ in the ascending lexicographic order of the rank, the makespan and the EMD; 4: Set ${\widehat{\mathit{F}}}_{k+1}={\mathit{F}}_{k+1}$; 5: for $i=1$ to $2N$ 6:   if $rank({\mathit{F}}_{k+1}^i)>1$ 7:     Break; 8:   else if ${\mathit{F}}_{k+1}^i\left(1\right)={\mathit{F}}_{k+1}^{i-1}(1)$ and ${\mathit{F}}_{k+1}^i\left(2\right)={\mathit{F}}_{k+1}^{i-1}(2)$ 9:     Update the fitness ${\widehat{\mathit{F}}}_{k+1}^i$ by ${\widehat{\mathit{F}}}_{k+1}^i\left(2\right)={\widehat{\mathit{F}}}_{k+1}^{i-1}(2)$; 10:   else 11:     Generate the schedule $s_i$ of the individual associated by ${\mathit{F}}_{k+1}^i$ in the Rk+1; 12:     Evaluate the EMD by the Monte Carlo method ${\Delta }_{\mathrm{c}}^{\mathrm{sim}}$ in Equation (17); 13:     Update the fitness ${\widehat{\mathit{F}}}_{k+1}^i$ by ${\widehat{\mathit{F}}}_{k+1}^i(2)={\Delta }_{\mathrm{c}}^{\mathrm{sim}}$; 14:   end if 15: end for 16: Return the modified fitness set ${\widehat{\mathit{F}}}_{k+1}$.

3.5. Evolutionary Operators

In our algorithm, the preference list representation is applied to code the chromosomes. The chromosome built by this coding method is made up of m substrings corresponding to m machines. Every substring is a preference list of n jobs on the corresponding machine. Supposing the chromosome is [(2 3 1) (1 3 2) (2 1 3)], the substring (2 3 1) is the preference list for machine 1, the substring (1 3 2) for machine 2 and the substring (2 1 3) for machine 3. When decoding, the job the first to appear in every precedence list will be selected firstly. If a selected operation meets the process constraint, the operation will be scheduled, and then it is removed from corresponding preference list. If there are more than one operation can be scheduled, then select one randomly.

The main genetic operators include selection, crossover and mutation. The usual binary tournament selection is used to select parent individuals for generating child solutions. Namely, randomly select two individuals from the population, and choose one of them with better fitness for the subsequent genetic operators. In the crossover operator, the substring crossover which exchanges the substrings of parents between two randomly selected machine numbers is applied. For the mutation operator, the swap-mutation operator to a randomly selected substring is applied.

Before updating the next generation population, the fast non-dominated sorting approach is applied to ranking the solutions in the combined population. Then, the population will be updated by choosing the individuals in the order of their ranks. Since all the previous and current population members are included in the combined population, the elitism can also be ensured.

4. Experimental Analysis

In this section, the performance of the meta-model in evaluating the EMD will first be presented, and then the meta-model-based MOEA will be used to solve the robust JSS problem.

4.1. Experiment Setting

The algorithm is implemented using C++ and run on a 2.8 GHz PC with an Intel Pentium dual-core CPU and 2 GB of RAM. The parameters are listed as follows: the population size is 1024; the generation number is 64; the crossover rate is 0.95; the mutation rate is 0.05; the machine breakdown ratio is 0.005; the expected downtime is 20; and the simulation times are 600.

In the literature, many benchmark problems have been generated by different researchers to test the performance of different algorithms, which are also very useful for this research for they include a wide range of problem instances. In this study, the problem instances La01-La40 with sizes from $10\times 5$ to $30\times 10$ in the benchmark problem set LA (Lawrence in 1984) and the problem instances Ta01-Ta40 with sizes from $15\times 15$ to $30\times 15$ in the benchmark problem set TA (Taillard in 1994) will be applied. In total, there are 80 benchmark problem instances will be used to test the performance of the proposed algorithm.

4.2. Evaluation Performance of The Proposed Mete-Model

To distinguish the robustness of different schedules, an effective meta-model must have high evaluation accuracy and perform a strong linear correlation to the real value of the robustness. To show the accuracy of the proposed meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ in evaluating the EMD, the average $\overline{\chi }$ in Equation (18) and standard variance $\sigma (\chi )$ in Equation (19) of the absolute relative deviation $\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})$ from the Monte Carlo approximation ${\Delta }_{\mathrm{c}}^{\mathrm{sim}}$ will be applied. In addition, a correlation study will be conducted using IBM SPSS. For each test problem, the $R^2$ statistic and the significance level $Sig.$ of the linear model ANOVA are recorded. The value of $R^2$ is used to measure the fitting degree of the meta-model, while the significance level $Sig.$ is used to test whether there is a significant linear correlation between the meta-model and the EMD. Therefore, a good meta-model should be with a large value of $R^2$ and a small value of $Sig.$ for each test problem.

$$\overline{\chi }=\frac{1}{N}{\displaystyle \sum _{i=1}^N\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|\frac{{\Delta }_{\mathrm{c}}^{\mathrm{a}}-{\Delta }_{\mathrm{c}}^{\mathrm{sim}}}{{\Delta }_{\mathrm{c}}^{\mathrm{sim}}}\right|}$$

(18)

$$\sigma (\chi )=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^N{(\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})-\overline{\chi })}^2}}{N-1}}$$

(19)

The experimental results have been processed and recorded in

Table 1. The experimental results of the meta-model in the problem set LA.

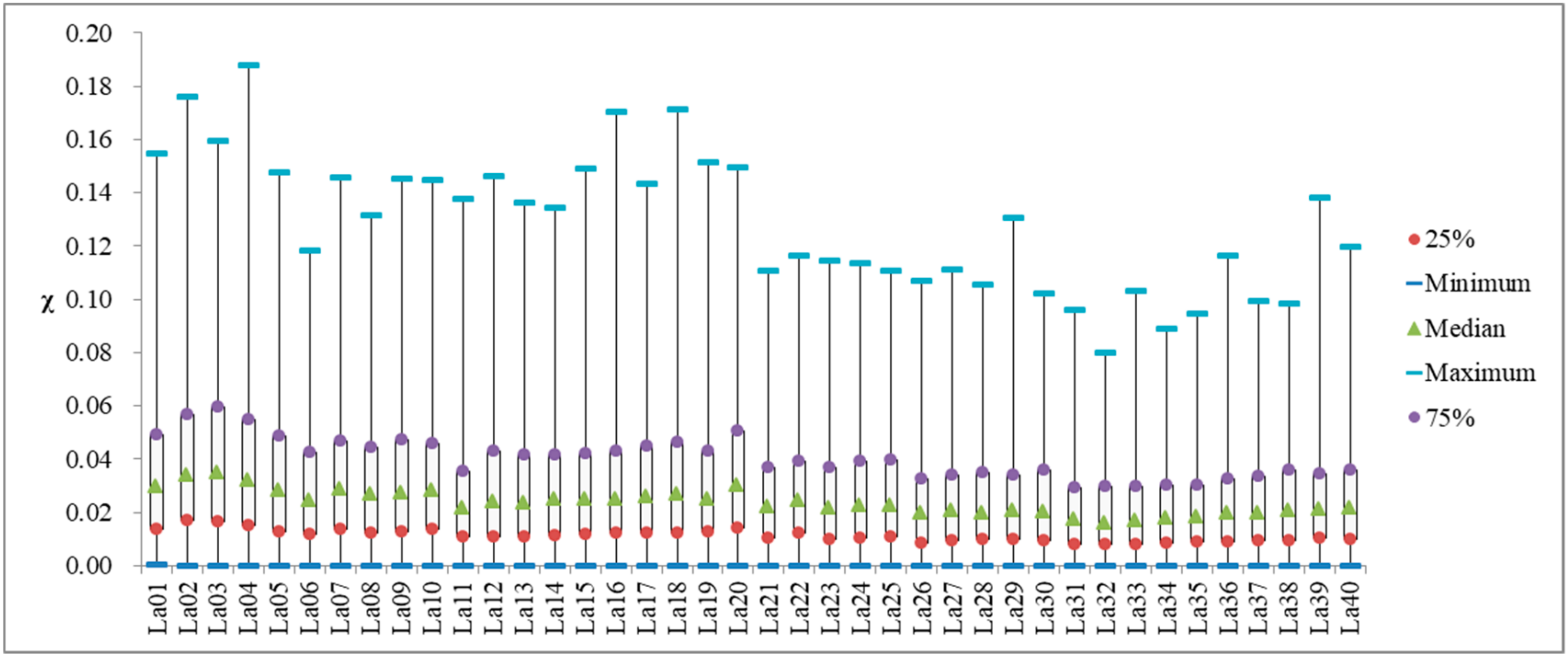
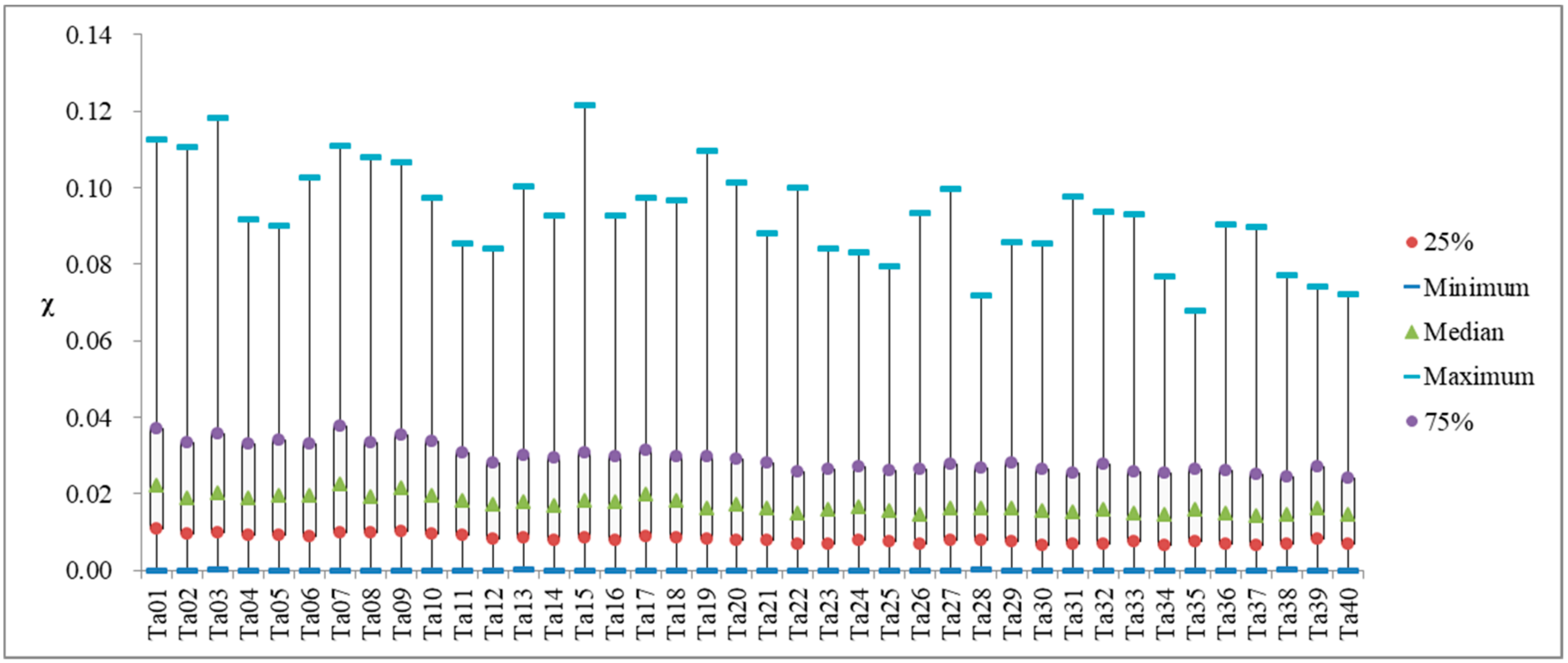
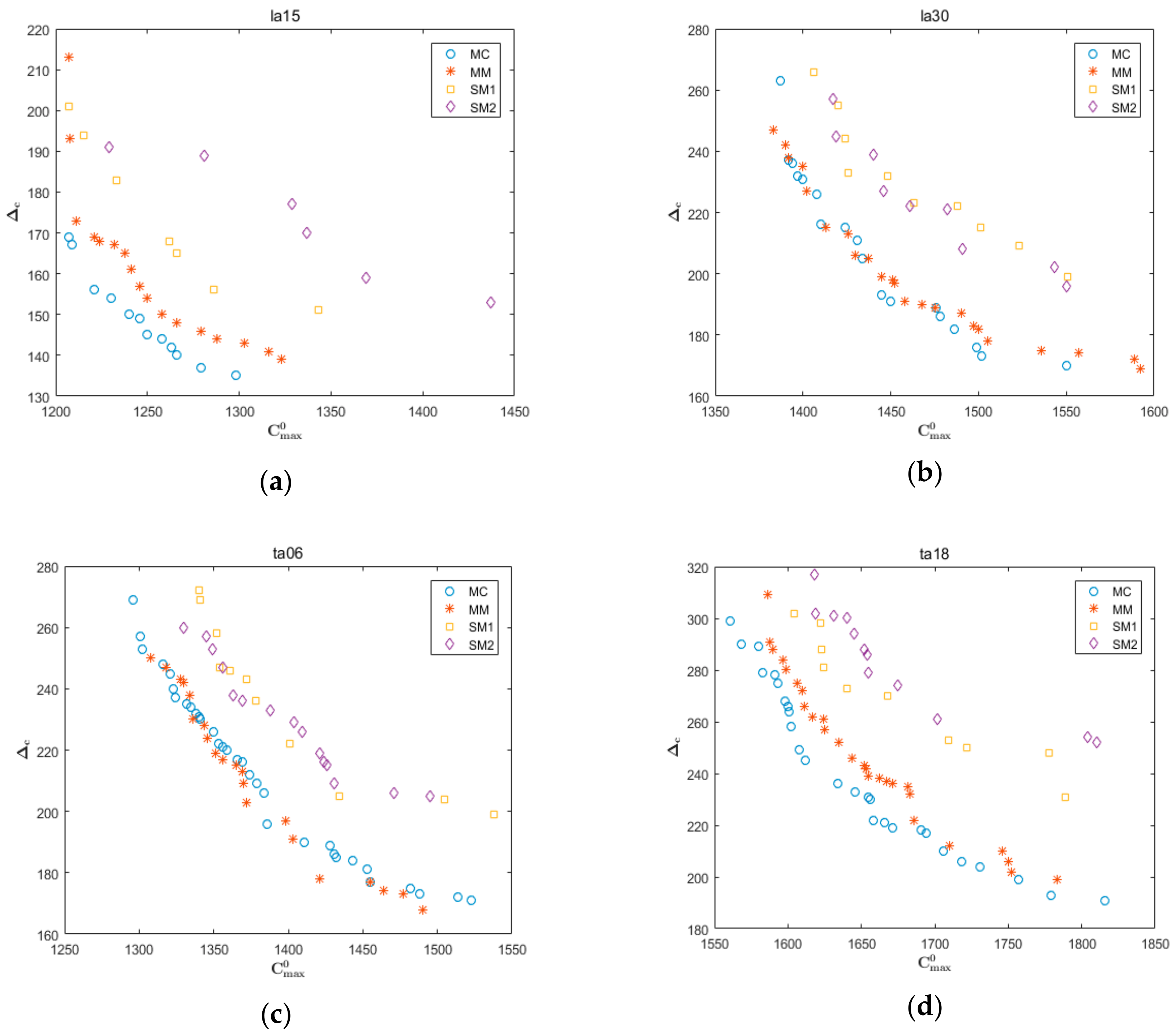
Cases	n × m	$\overline{\mathit{\chi }}$	$\mathit{\sigma }\mathbf{(}\mathit{\chi }\mathbf{)}$	${\mathit{R}}^{\mathbf{2}}$	Sig.	Cases	n × m	$\overline{\mathit{\chi }}$	$\mathit{\sigma }\mathbf{(}\mathit{\chi }\mathbf{)}$	${\mathit{R}}^{\mathbf{2}}$	Sig.
La01	10 × 5	0.035	0.027	0.74	<0.01	La21	15 × 10	0.026	0.019	0.77	<0.01
La02	10 × 5	0.040	0.029	0.59	<0.01	La22	15 × 10	0.028	0.021	0.74	<0.01
La03	10 × 5	0.041	0.031	0.53	<0.01	La23	15 × 10	0.026	0.020	0.78	<0.01
La04	10 × 5	0.038	0.028	0.71	<0.01	La24	15 × 10	0.027	0.021	0.76	<0.01
La05	10 × 5	0.034	0.026	0.78	<0.01	La25	15 × 10	0.028	0.021	0.75	<0.01
La06	15 × 5	0.029	0.022	0.80	<0.01	La26	20 × 10	0.023	0.018	0.76	<0.01
La07	15 × 5	0.033	0.024	0.71	<0.01	La27	20 × 10	0.024	0.018	0.74	<0.01
La08	15 × 5	0.032	0.024	0.72	<0.01	La28	20 × 10	0.024	0.019	0.73	<0.01
La09	15 × 5	0.033	0.026	0.68	<0.01	La29	20 × 10	0.024	0.018	0.75	<0.01
La10	15 × 5	0.033	0.024	0.76	<0.01	La30	20 × 10	0.025	0.019	0.74	<0.01
La11	20 × 5	0.026	0.020	0.76	<0.01	La31	30 × 10	0.020	0.016	0.75	<0.01
La12	20 × 5	0.029	0.023	0.76	<0.01	La32	30 × 10	0.020	0.015	0.75	<0.01
La13	20 × 5	0.029	0.023	0.70	<0.01	La33	20 × 10	0.020	0.015	0.76	<0.01
La14	20 × 5	0.029	0.023	0.76	<0.01	La34	30 × 10	0.021	0.016	0.76	<0.01
La15	20 × 5	0.029	0.023	0.71	<0.01	La35	30 × 10	0.022	0.017	0.82	<0.01
La16	10 × 10	0.031	0.024	0.74	<0.01	La36	15 × 15	0.023	0.018	0.80	<0.01
La17	10 × 10	0.031	0.024	0.74	<0.01	La37	15 × 15	0.023	0.018	0.75	<0.01
La18	10 × 10	0.032	0.025	0.72	<0.01	La38	15 × 15	0.025	0.019	0.74	<0.01
La19	10 × 10	0.030	0.023	0.72	<0.01	La39	15 × 15	0.025	0.018	0.75	<0.01
La20	10 × 10	0.035	0.026	0.65	<0.01	La40	15 × 15	0.025	0.019	0.71	<0.01
Aver.	/	0.032	0.025	0.71	<0.01	Aver.	/	0.024	0.018	0.76	<0.01

and

Table 2. The experimental results of the meta-model in the problem set TA.

Cases	n × m	$\overline{\mathit{\chi }}$	$\mathit{\sigma }\mathbf{(}\mathit{\chi }\mathbf{)}$	${\mathit{R}}^{\mathbf{2}}$	Sig.	Cases	n × m	$\overline{\mathit{\chi }}$	$\mathit{\sigma }\mathbf{(}\mathit{\chi }\mathbf{)}$	${\mathit{R}}^{\mathbf{2}}$	Sig.
Ta01	15 × 15	0.026	0.019	0.73	<0.01	Ta21	20 × 20	0.019	0.015	0.78	<0.01
Ta02	15 × 15	0.023	0.018	0.76	<0.01	Ta22	20 × 20	0.018	0.014	0.79	<0.01
Ta03	15 × 15	0.025	0.019	0.74	<0.01	Ta23	20 × 20	0.018	0.014	0.76	<0.01
Ta04	15 × 15	0.023	0.018	0.77	<0.01	Ta24	20 × 20	0.019	0.014	0.77	<0.01
Ta05	15 × 15	0.023	0.018	0.78	<0.01	Ta25	20 × 20	0.018	0.014	0.79	<0.01
Ta06	15 × 15	0.023	0.017	0.76	<0.01	Ta26	20 × 20	0.018	0.014	0.78	<0.01
Ta07	15 × 15	0.026	0.020	0.73	<0.01	Ta27	20 × 20	0.019	0.015	0.75	<0.01
Ta08	15 × 15	0.024	0.018	0.76	<0.01	Ta28	20 × 20	0.019	0.014	0.77	<0.01
Ta09	15 × 15	0.025	0.018	0.74	<0.01	Ta29	20 × 20	0.019	0.015	0.76	<0.01
Ta10	15 × 15	0.023	0.018	0.77	<0.01	Ta30	20 × 20	0.018	0.014	0.79	<0.01
Ta11	20 × 15	0.022	0.016	0.76	<0.01	Ta31	30 × 15	0.018	0.014	0.77	<0.01
Ta12	20 × 15	0.020	0.016	0.78	<0.01	Ta32	30 × 15	0.019	0.015	0.77	<0.01
Ta13	20 × 15	0.021	0.016	0.78	<0.01	Ta33	30 × 15	0.018	0.014	0.74	<0.01
Ta14	20 × 15	0.020	0.016	0.77	<0.01	Ta34	30 × 15	0.017	0.014	0.78	<0.01
Ta15	20 × 15	0.021	0.016	0.73	<0.01	Ta35	30 × 15	0.018	0.014	0.80	<0.01
Ta16	20 × 15	0.021	0.015	0.78	<0.01	Ta36	30 × 15	0.018	0.014	0.76	<0.01
Ta17	20 × 15	0.023	0.017	0.74	<0.01	Ta37	30 × 15	0.018	0.014	0.76	<0.01
Ta18	20 × 15	0.021	0.016	0.75	<0.01	Ta38	30 × 15	0.018	0.014	0.79	<0.01
Ta19	20 × 15	0.021	0.017	0.76	<0.01	Ta39	30 × 15	0.019	0.013	0.81	<0.01
Ta20	20 × 15	0.021	0.016	0.79	<0.01	Ta40	30 × 15	0.017	0.013	0.78	<0.01
Aver.	/	0.023	0.017	0.76	<0.01	Aver.	/	0.018	0.014	0.77	<0.01

for the problem sets LA and TA, respectively. It can be found that the maximum and minimum values of $\overline{\chi }$ for all problems in LA are equal to 0.041 and 0.020, respectively. And, the maximum and minimum values of $\overline{\chi }$ for all problems in TA are equal to 0.026 and 0.017, respectively. That is, the values of $\overline{\chi }$ for all test problems are less than 0.05 in average. Therefore, the values of the meta-model are very close to that of the Monte Carlo approximation, which indicate that the proposed meta-model have high accuracy in evaluating the EMD for the JSS under RMD. On the other hand, the maximum and minimum values of $\sigma (\chi )$ for all problems in LA are equal to 0.031 and 0.015, respectively. The maximum and minimum values of $\sigma (\chi )$ for all problems in TA are equal to 0.020 and 0.013, respectively. All these results show that the meta-model have a small variance in the absolute relative deviation, which indicate that the performance of the meta-model is also robust in evaluating the EMD.

The results can also be clearly presented by the quartile graphs of the absolute relative deviation $\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})$, as shown in Figure 4 and Figure 5. In Figure 4, the maximum value of the absolute relative deviations $\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})$ for all problems in LA is about 0.19, but more than 75% of the values are less than 0.06 for all the problems in the problem set LA. Especially, when the problem scale is larger, such as the problems LA21-LA40, more than 75% of the values of $\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})$ are less than 0.04. As for the problem set TA in Figure 5, the maximum value of the absolute relative deviation $\chi ({\Delta }_{\mathrm{c}}^{\mathrm{a}},{\Delta }_{\mathrm{c}}^{\mathrm{sim}})$ for all problems is only about 0.12, and more than 75% of the values are less than 0.04 for all the test problems. Therefore, it can be concluded that the proposed meta-model has a very small estimation error for the EMD.

On the other hand, the results of the linear model ANOVA have also been provided in Table 1 and Table 2. For the results in Table 1, except for the problems La02, La03, La09, and La20, we can find that all the values of $R^2$ are larger than 0.70. Especially for the problems La21-La40 with larger problem scales, the average of $R^2$ even reaches to 0.76. All the values of $R^2$ are larger than 0.70 for the problems in TA and the average value is about 0.76 as shown in Table 2. In addition, for all the problems in LA and TA, the significance level $Sig.$ is less than 0.01. All these results show that the proposed meta-model have a significant linear correlation with the expected makespan.

In summary, the proposed meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ have high evaluation accuracy and holds a strong linear correlation to the EMD. This means that the meta-model ${\Delta }_{\mathrm{c}}^{\mathrm{a}}$ is able to effectively distinguish the robustness of different schedules in the evolutionary algorithm.

4.3. Optimization Performance of The Proposed Algorithm

In this section, the performance of the proposed meta-model (MM)-based MOEA in optimizing the makespan and the EMD for the JSS under RMD will be presented. To show the performance of the algorithm, the Monte Carlo approximation in Equation (17)-based MOEA (MC) will be applied. In addition, the proposed meta-meta will also be compared with the existing surrogate measures, and thus the results on the MOEAs with the average total slack time (SM1) in [42] and the sum of free slack time (SM2) in [26] will also be provided. By implementing these algorithms with various approximations of EMD, four Pareto solution sets can be obtained for each problem.

To investigate the performance of MOEAs, many metrics have been developed and applied in the related research [44]. Since a single metric can only provide some specific but incomplete of performance, to comprehensively evaluate the performance of the proposed algorithm, both the average distance and the number of distinct choices will be used in our experiments to measure the convergence and diversity of the algorithm, respectively.

Average distance metric $A_{\mathrm{d}}$ in Equation (20) evaluates the closeness of the obtained Pareto solution set $P{F}_{\mathrm{find}}$ to the true Pareto solution set $P{F}_{\mathrm{true}}$, where $d(z_i,a_j)$ denotes the Euclidean distance between $z_i$ in $P{F}_{\mathrm{find}}$ and all points $a_j$ in $P{F}_{\mathrm{true}}$.

$$A_{\mathrm{d}}=\frac{1}{\left|P{F}_{\mathrm{find}}\right|}{\displaystyle \sum _{i=1}^{\left|P{F}_{\mathrm{find}}\right|}\underset{j=1}{\overset{\left|P{F}_{\mathrm{true}}\right|}{\min }}} d(z_i,a_j)$$

(20)

Number of distinct choices $N_{\mu }$ in Equation (21) focuses on the distribution of solutions, which defines the number of distinct choices for a pre-specified value of $\mu , 0<\mu <1$. In this metric, an m-dimensional objective space will be divided into $1/{\mu }^m$ number of small grids, where any solutions within the same grid are considered similar to one another. If there are individuals in the obtained Pareto set $P{F}_{\mathrm{find}}$ that fall into the region $T(l_m,\dots ,l_2,l_1)$, $NT(l_m,\dots ,l_2,l_1)$ is equal to one, otherwise zero. In our experiments, the value of $\mu$ for the metric $N_{\mu }$ is taken as 0.05.

$$N_{\mu }(P{F}_{\mathrm{find}})={\displaystyle \sum _{l_m=0}^{1/\mu -1}\dots }{\displaystyle \sum _{l_2=0}^{1/\mu -1}{\displaystyle \sum _{l_1=0}^{1/\mu -1}NT(l_m,\dots ,l_2,l_1)}}$$

(21)

Since the NP-hard nature of the JSS under RMD, the true Pareto set $P{F}_{\mathrm{true}}$ is not available for all test problems. In view of this, the approximate Pareto solution set which is provided by all comparison algorithms will be used to represent the true one. That is, under the obtained Pareto fronts $(P{F}_{\mathrm{find}}^1,P{F}_{\mathrm{find}}^2,\dots ,P{F}_{\mathrm{find}}^{n_p})$ by different algorithms for a test problem, the true Pareto solution set can be approximated by Equation (22), where $a_j\prec b_i$ implies that $a_j$ dominates $b_i$. Besides, in order to reduce the scale difference between different objectives, all Pareto fronts will be normalized by $P{F}_{\mathrm{find}}=(P{F}_{\mathrm{find}}-P{F}_{\mathrm{true}}^{\min })/(P{F}_{\mathrm{true}}^{\max }-P{F}_{\mathrm{true}}^{\min })$ based on the maximum and minimum of objectives of the true Pareto set $P{F}_{\mathrm{true}}$.

$$P{F}_{\mathrm{true}}\approx \left\{b_i\right|\forall b_i,\neg \exists a_j\in (P{F}_{\mathrm{find}}^1\cup P{F}_{\mathrm{find}}^2\cup \dots \cup P{F}_{\mathrm{find}}^{n_{\mathrm{p}}})\prec b_i\}$$

(22)

The results on the metric $A_{\mathrm{d}}$ of the algorithms MC, MM, SM1, and SM2 have been provided in

Table 3. The values of $A_{\mathrm{d}}$ for the algorithms Monte Carlo approximation-based MOEA (MC), meta-model (MM), total slack time (SM1), and free slack time (SM2) in the problem set LA.

Cases	n × m	MC	MM	SM1	SM2	Cases	n × m	MC	MM	SM1	SM2
La01	10 × 5	0.01	0.07	0.99	1.57	La21	15 × 10	0.00	0.10	0.31	0.34
La02	10 × 5	0.01	0.04	0.26	0.50	La22	15 × 10	0.03	0.01	0.19	0.13
La03	10 × 5	0.01	0.05	0.08	0.10	La23	15 × 10	0.00	0.14	0.19	0.31
La04	10 × 5	0.07	0.00	0.16	0.36	La24	15 × 10	0.04	0.03	0.20	0.12
La05	10 × 5	0.00	0.00	0.00	0.00	La25	15 × 10	0.00	0.07	0.19	0.30
La06	15 × 5	0.00	0.92	3.96	7.19	La26	20 × 10	0.02	0.02	0.23	0.17
La07	15 × 5	0.52	0.00	1.55	1.22	La27	20 × 10	0.06	0.02	0.26	0.06
La08	15 × 5	0.00	0.33	3.70	2.95	La28	20 × 10	0.00	0.11	0.18	0.15
La09	15 × 5	0.00	0.35	2.89	1.45	La29	20 × 10	0.01	0.07	0.17	0.08
La10	15 × 5	0.00	0.00	0.00	0.00	La30	20 × 10	0.02	0.04	0.26	0.24
La11	20 × 5	0.00	0.66	6.06	4.84	La31	30 × 10	0.15	0.00	0.21	0.25
La12	20 × 5	0.04	0.03	1.38	0.92	La32	30 × 10	0.00	0.18	0.24	0.24
La13	20 × 5	0.06	0.05	1.34	1.22	La33	20 × 10	0.00	0.17	0.24	0.09
La14	20 × 5	0.00	0.00	0.00	0.00	La34	30 × 10	0.00	0.10	0.27	0.08
La15	20 × 5	0.00	0.30	0.63	1.12	La35	30 × 10	0.01	0.16	0.18	0.26
La16	10 × 10	0.09	0.14	1.09	0.36	La36	15 × 15	0.00	0.12	0.19	0.38
La17	10 × 10	0.00	0.08	0.20	0.16	La37	15 × 15	0.00	0.12	0.22	0.25
La18	10 × 10	0.00	0.15	0.30	0.46	La38	15 × 15	0.00	0.04	0.18	0.27
La19	10 × 10	0.01	0.02	0.34	0.13	La39	15 × 15	0.00	0.13	0.04	0.20
La20	10 × 10	0.02	0.09	0.40	0.55	La40	15 × 15	0.00	0.05	0.24	0.31
Aver.	/	0.04	0.16	1.27	1.26	Aver.	/	0.02	0.08	0.21	0.21

and

Table 4. The values of $A_{\mathrm{d}}$ for the algorithms MC, MM, SM1 and SM2 in the problem set TA.

Cases	n × m	MC	MM	SM1	SM2	Cases	n × m	MC	MM	SM1	SM2
Ta01	15 × 15	0.00	0.08	0.19	0.20	Ta21	20 × 20	0.02	0.05	0.23	0.31
Ta02	15 × 15	0.00	0.08	0.22	0.33	Ta22	20 × 20	0.00	0.17	0.28	0.34
Ta03	15 × 15	0.00	0.04	0.17	0.09	Ta23	20 × 20	0.09	0.01	0.14	0.19
Ta04	15 × 15	0.01	0.12	0.21	0.17	Ta24	20 × 20	0.02	0.01	0.17	0.16
Ta05	15 × 15	0.00	0.15	0.15	0.24	Ta25	20 × 20	0.00	0.22	0.29	0.24
Ta06	15 × 15	0.04	0.01	0.23	0.22	Ta26	20 × 20	0.00	0.07	0.30	0.22
Ta07	15 × 15	0.00	0.14	0.24	0.26	Ta27	20 × 20	0.00	0.09	0.18	0.38
Ta08	15 × 15	0.01	0.02	0.08	0.11	Ta28	20 × 20	0.03	0.05	0.30	0.21
Ta09	15 × 15	0.06	0.03	0.27	0.30	Ta29	20 × 20	0.02	0.06	0.31	0.34
Ta10	15 × 15	0.06	0.10	0.29	0.22	Ta30	20 × 20	0.02	0.05	0.24	0.24
Ta11	20 × 15	0.00	0.22	0.29	0.30	Ta31	30 × 15	0.02	0.04	0.16	0.17
Ta12	20 × 15	0.01	0.04	0.24	0.19	Ta32	30 × 15	0.05	0.05	0.13	0.14
Ta13	20 × 15	0.00	0.08	0.14	0.29	Ta33	30 × 15	0.03	0.05	0.34	0.26
Ta14	20 × 15	0.01	0.12	0.10	0.17	Ta34	30 × 15	0.00	0.13	0.33	0.39
Ta15	20 × 15	0.00	0.21	0.26	0.37	Ta35	30 × 15	0.00	0.09	0.21	0.14
Ta16	20 × 15	0.00	0.06	0.23	0.21	Ta36	30 × 15	0.02	0.03	0.15	0.18
Ta17	20 × 15	0.03	0.06	0.14	0.33	Ta37	30 × 15	0.03	0.02	0.17	0.08
Ta18	20 × 15	0.00	0.07	0.24	0.30	Ta38	30 × 15	0.00	0.27	0.24	0.35
Ta19	20 × 15	0.09	0.00	0.30	0.34	Ta39	30 × 15	0.07	0.16	0.01	0.13
Ta20	20 × 15	0.00	0.14	0.17	0.19	Ta40	30 × 15	0.00	0.13	0.19	0.18
Aver.	/	0.02	0.09	0.21	0.24	Aver.	/	0.02	0.09	0.22	0.23

for the problem sets LA and TA, respectively. The results show that the algorithms SM1 and SM2 have the similar performance in the convergence, for the values of $A_{\mathrm{d}}$ of the algorithms SM1 and SM2 are always close to each other. For example, in Table 3, their average values of $A_{\mathrm{d}}$ in the problems La01–La20 are 1.27 and 1.26, and the average values of $A_{\mathrm{d}}$ in the problems La21–La40 are 0.21 and 0.21, respectively. The similar results can also be found in Table 4, the average values of $A_{\mathrm{d}}$ in the problems Ta01–Ta20 are 0.21 and 0.24, while they are 0.22 and 0.23 in the problems Ta21–Ta40.

By comparison, the proposed algorithm MM performs better in the convergence than the algorithms SM1 and SM2. This is because that, except for the problems La39, Ta14, and Ta39, all the values of $A_{\mathrm{d}}$ for the algorithm MM in the problem sets LA and TA are less than that of the algorithms SM1 and SM2. In average, the values of $A_{\mathrm{d}}$ for the algorithm MM in the problems La01–La20 and La21–La40 are 0.16 and 0.08, while the corresponding values of $A_{\mathrm{d}}$ for the algorithms SM1 and SM2 are about 1.26 and 0.21, respectively. And, in the problem set TA, the average values of $A_{\mathrm{d}}$ for the algorithm MM in the problems La01–La20 and La21–La40 are both 0.09, while the average values of $A_{\mathrm{d}}$ for the algorithms SM1 and SM2 are about 0.22.

On the other hand, the results also indicate that the convergence of the algorithm MM can even be very close to that of the algorithm MC. As shown in Table 3, the results show that the proposed algorithm MM can have the best convergence in the problems La04, La05, La07, La10, La12, La13, La14, La22, La24, La26, La27, and La31 from the problem set LA and Ta06, Ta09,Ta19, Ta23, Ta24, Ta37, and Ta37 from the problem set TA. In addition, the average of $A_{\mathrm{d}}$ for the algorithm MM in the problems La01–La21 with smaller problem scales is 0.16, which is 0.12 larger than that of the algorithm MC. But, in the problems with larger problem scales, such as the problems La21–La40 and Ta01–Ta40, the average of $A_{\mathrm{d}}$ for the algorithm MM is only 0.06 larger that of the algorithm MC. Therefore, we conclude that the proposed algorithm MM is better than the algorithms SM1 and SM2 and similar to the algorithm MC in convergence.

The results on the metric $N_{\mu }$ of the algorithms MC, MM, SM1 and SM2 are presented in

Table 5. The values of $N_{\mu }$ for the algorithms MC, MM, SM1, and SM2 in the problem set LA.

Cases	n × m	MC	MM	SM1	SM2	Cases	n × m	MC	MM	SM1	SM2
La01	10 × 5	11	12	2	4	La21	15 × 10	15	15	8	13
La02	10 × 5	12	9	5	4	La22	15 × 10	16	17	10	9
La03	10 × 5	11	8	2	6	La23	15 × 10	13	18	6	12
La04	10 × 5	9	8	4	4	La24	15 × 10	12	12	10	15
La05	10 × 5	1	1	2	3	La25	15 × 10	14	15	11	9
La06	15 × 5	3	3	3	6	La26	20 × 10	15	15	10	10
La07	15 × 5	11	6	4	8	La27	20 × 10	12	14	10	13
La08	15 × 5	5	7	3	9	La28	20 × 10	14	18	8	7
La09	15 × 5	7	9	9	7	La29	20 × 10	13	14	7	11
La10	15 × 5	1	2	4	2	La30	20 × 10	13	16	10	9
La11	20 × 5	4	5	6	5	La31	30 × 10	15	12	9	8
La12	20 × 5	11	8	5	7	La32	30 × 10	13	12	7	12
La13	20 × 5	12	7	7	6	La33	20 × 10	11	13	8	9
La14	20 × 5	1	1	3	1	La34	30 × 10	13	16	11	10
La15	20 × 5	12	16	7	6	La35	30 × 10	11	16	10	7
La16	10 × 10	9	8	2	2	La36	15 × 15	12	16	11	11
La17	10 × 10	10	11	7	7	La37	15 × 15	14	17	8	9
La18	10 × 10	12	14	8	4	La38	15 × 15	15	18	14	13
La19	10 × 10	12	12	6	6	La39	15 × 15	18	14	8	12
La20	10 × 10	12	14	4	7	La40	15 × 15	14	17	10	11
Aver.	/	8.3	8.1	4.7	5.2	Aver.	/	13.7	15.3	9.3	10.5

and

Table 6. The values of $N_{\mu }$ for the algorithms MC, MM, SM1, and SM2 in the problem set TA.

Cases	n × m	MC	MM	SM1	SM2	Cases	n × m	MC	MM	SM1	SM2
Ta01	15 × 15	16	18	9	9	Ta21	20 × 20	17	14	10	9
Ta02	15 × 15	14	10	10	12	Ta22	20 × 20	13	15	6	8
Ta03	15 × 15	15	19	12	10	Ta23	20 × 20	15	11	11	11
Ta04	15 × 15	14	19	11	11	Ta24	20 × 20	13	13	11	9
Ta05	15 × 15	17	15	9	11	Ta25	20 × 20	14	12	11	9
Ta06	15 × 15	16	14	9	10	Ta26	20 × 20	16	12	10	10
Ta07	15 × 15	15	17	12	10	Ta27	20 × 20	14	8	12	9
Ta08	15 × 15	17	11	13	9	Ta28	20 × 20	15	17	7	9
Ta09	15 × 15	15	14	10	8	Ta29	20 × 20	17	12	12	10
Ta10	15 × 15	15	14	11	12	Ta30	20 × 20	17	10	7	7
Ta11	20 × 15	13	15	10	10	Ta31	30 × 15	13	13	9	10
Ta12	20 × 15	12	14	8	7	Ta32	30 × 15	13	12	7	8
Ta13	20 × 15	16	13	8	10	Ta33	30 × 15	13	11	6	5
Ta14	20 × 15	13	14	9	10	Ta34	30 × 15	14	13	10	9
Ta15	20 × 15	17	18	12	11	Ta35	30 × 15	10	14	9	7
Ta16	20 × 15	19	13	8	8	Ta36	30 × 15	15	10	9	6
Ta17	20 × 15	15	11	10	9	Ta37	30 × 15	13	11	6	8
Ta18	20 × 15	16	15	10	9	Ta38	30 × 15	9	15	8	10
Ta19	20 × 15	10	13	12	8	Ta39	30 × 15	11	14	7	6
Ta20	20 × 15	16	17	11	10	Ta40	30 × 15	13	13	9	7
Aver.	/	15.1	14.7	10.2	9.7	Aver.	/	13.8	12.5	8.9	8.4

for the problem sets LA and TA, respectively. The results show that the algorithms SM1 and SM2 also have the similar performance in the diversity. From the results in Table 5, we can found that the average values of $N_{\mu }$ for the algorithms SM1 and SM2 in the problems La01–La20 are 4.7 and 5.2, and the average values of $A_{\mathrm{d}}$ for the problems La21–La40 are 9.3 and 10.5, respectively. That is, the average difference of $A_{\mathrm{d}}$ between the algorithms SM1 and SM2 is only about 1.0 in average. The similar results can also be found in Table 6, the average values of $N_{\mu }$ for the problems Ta01–Ta20 are 10.2 and 9.7, while they are 8.9 and 8.4 in the problems Ta21–Ta40.

Compared with the algorithms SM1 and SM2, the proposed algorithm MM performs better in diversity. This is because that the values of $A_{\mathrm{d}}$ for the algorithm MM are larger than that of the algorithms SM1 and SM2 for most of the problems in the problem sets LA and TA as shown in Table 5 and Table 6. In addition, the results have also shown the algorithm MM have the similar performance in diversity to that of the algorithm MC. For example, the average values of $A_{\mathrm{d}}$ for the algorithms MM and MC in the problems La01–La20 are about 8.1 and 8.3, while the average values of $A_{\mathrm{d}}$ are 15.3 and 13.7 in the problems La21–La40, respectively. Similar results can be found in Table 6 for the problem set TA. Therefore, we can conclude that the proposed algorithm MM is very close to the algorithm MC in diversity, but it is much better than the algorithms SM1 and SM2.

Taking the problems instances La06, La15, Ta15, and Ta36 as examples, the performance of the algorithms MC, MM, SM1, and SM2 can also be clearly illustrated by the Pareto fronts. As shown in Figure 6, the Pareto front of the algorithm MM is very close to that of the algorithm MC, while the Pareto fronts of the algorithms SM1 and SM2 are very far from that of the algorithm MC. On the other hand, the number of solutions in the Pareto front of the algorithm MM is approximately equal to that of the algorithm MC, while the number of solutions in the Pareto fronts of the algorithms SM1 and SM2 are much less in comparison.

However, as indicated earlier, the algorithm based on the Monte Carlo approximation will be very time-consuming. To investigate computational efforts for each algorithm, the average $T_{\mathrm{a}}$ and the relative value $T_{\mathrm{r}}$ of CPU time have been recorded, where $T_{\mathrm{r}}$ is the ratio of the average $T_{\mathrm{a}}$ of an algorithm (MC, MM, SM1, or SM2) to that of the algorithm MC. In this experiment, the simulation times for the Monte Carlo approximation are set as 30, which is generally the required minimum number of samples in statistical estimation [20]. As the results shown in

Table 7. Results on the CPU time (in seconds) of algorithms MC, MM, SM1, and SM2.

Cases	n × m	MC		MM		SM1		SM2
		${\mathit{T}}_{\mathit{a}}$	${\mathit{T}}_{\mathit{r}}$	${\mathit{T}}_{\mathit{a}}$	${\mathit{T}}_{\mathit{r}}$	${\mathit{T}}_{\mathit{a}}$	${\mathit{T}}_{\mathit{r}}$	${\mathit{T}}_{\mathit{a}}$	${\mathit{T}}_{\mathit{r}}$
La01–La05	10 × 5	66	1.00	53	0.80	50	0.76	50	0.76
La06–La10	15 × 5	83	1.00	54	0.65	52	0.63	50	0.60
La11–La15	20 × 5	113	1.00	55	0.49	55	0.49	52	0.46
La16–La20	10 × 10	102	1.00	54	0.53	54	0.53	51	0.50
La21–La25	15 × 10	153	1.00	56	0.37	55	0.36	54	0.35
La26–La30	20 × 10	220	1.00	60	0.27	59	0.27	57	0.26
La31–La35	30 × 10	398	1.00	73	0.18	70	0.18	68	0.17
La36–La40	15 × 15	238	1.00	65	0.27	62	0.26	60	0.25
Ta01–Ta10	15 × 15	231	1.00	63	0.27	61	0.26	59	0.26
Ta11–Ta20	20 × 15	351	1.00	75	0.21	70	0.20	68	0.19
Ta21–Ta30	20 × 20	543	1.00	85	0.16	82	0.15	83	0.15
Ta31–Ta40	30 × 15	733	1.00	95	0.13	92	0.13	89	0.12
Aver.	/	269.3	1.00	65.7	0.24	63.5	0.24	61.8	0.23

, the algorithms SM1 and SM2 always consume the least time, while the algorithm MC consumes the most. By comparison, the time consumption of the proposed algorithm MM is almost equal to that of the algorithms SM1 and SM2, but it is much less than that of the algorithm MC. What is more, the time consumption of the algorithm MC increases significantly with the problem scale. For example, the average $T_{\mathrm{a}}$ of the algorithm MC in the problems La01-La05 is 66, which is close to that of the algorithm MM with the value 53. But, in the problems Ta31-Ta40, the time consumption of the algorithm MC is about 8 times of that of the algorithm MM. In more complex problems or uncertain scenarios, a larger sample size may be needed for the algorithm MC, which will result in a computational time that is unacceptable.

5. Conclusions

In this study, we have addressed the robust JSS with RMDs, in which the makespan and the EMD are considered simultaneously. To improve the efficiency of the MOEA, a meta-model has been constructed by using the data-driven response surface method. Then, with the individual-based evolution control, the meta-model-based MOEA has been proposed to solve this problem. The results have shown that regarding the convergence and diversity, the proposed algorithm yields better Pareto solution sets than the algorithms with the existing slack time-based surrogate measures. Moreover, the meta-model has high accuracy in evaluating the EMD similar to the Monte Carlo approximation. Overall, the proposed meta-model-based MOEA can effectively and efficiently solve the robust JSS with RMDs.