Back to Basics: Meaning of the Parameters of Fractional Order PID Controllers
Abstract
1. Introduction
- the proportional action is simply proportional to the current control error;
- the integral action is related to the past values of the control error, so represents the accumulated error, i.e., the area under the error curve;
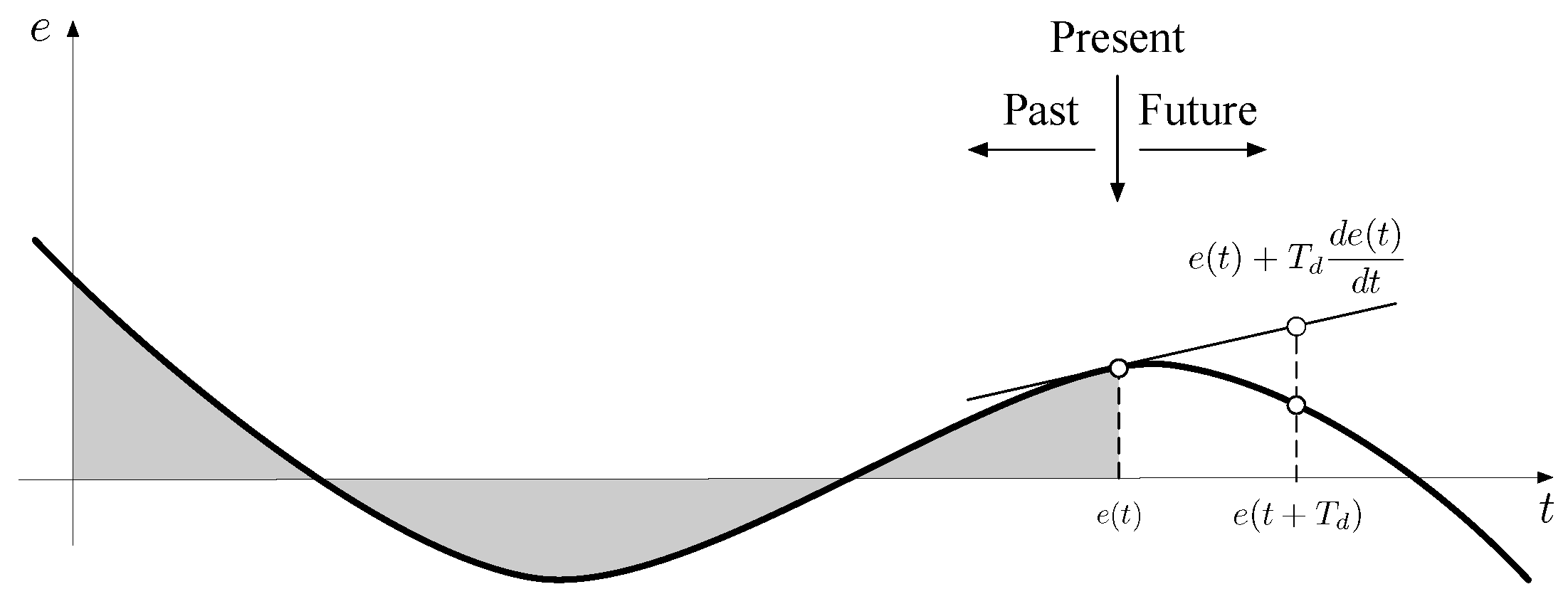
- the derivative action predicts future values of the error or, in other words, corrects based on the rate of change of the deviation from the set-point.
2. Generalities
2.1. Classical PID Controller
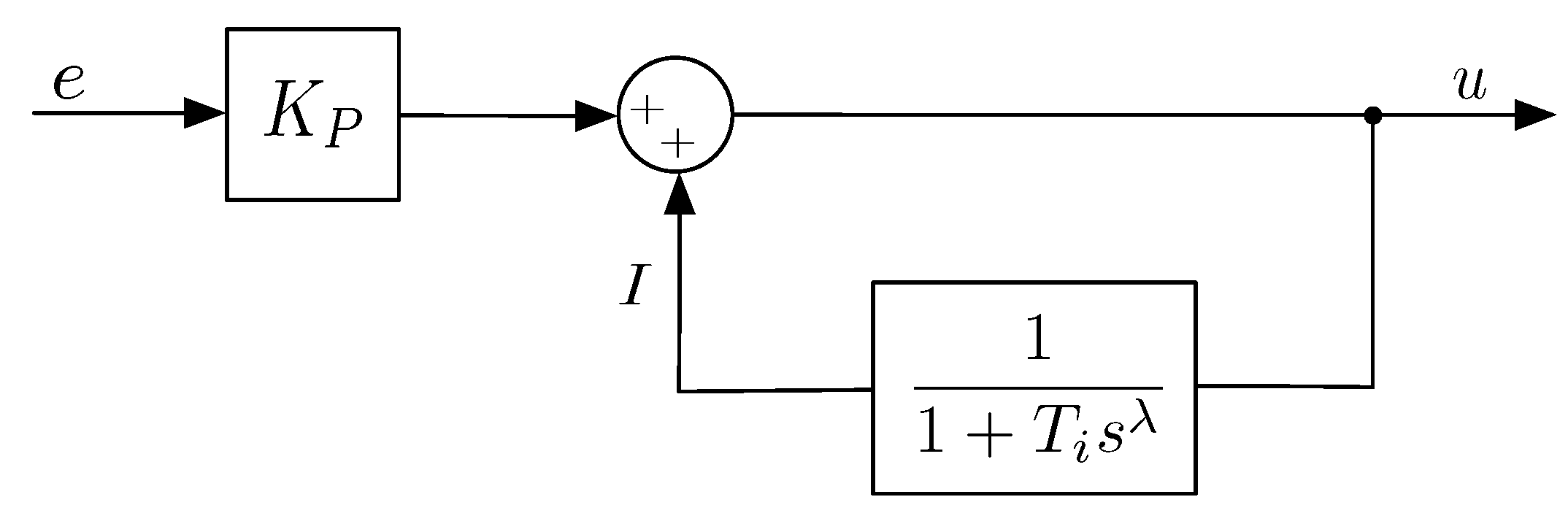
2.2. Fractional Order PID Controller
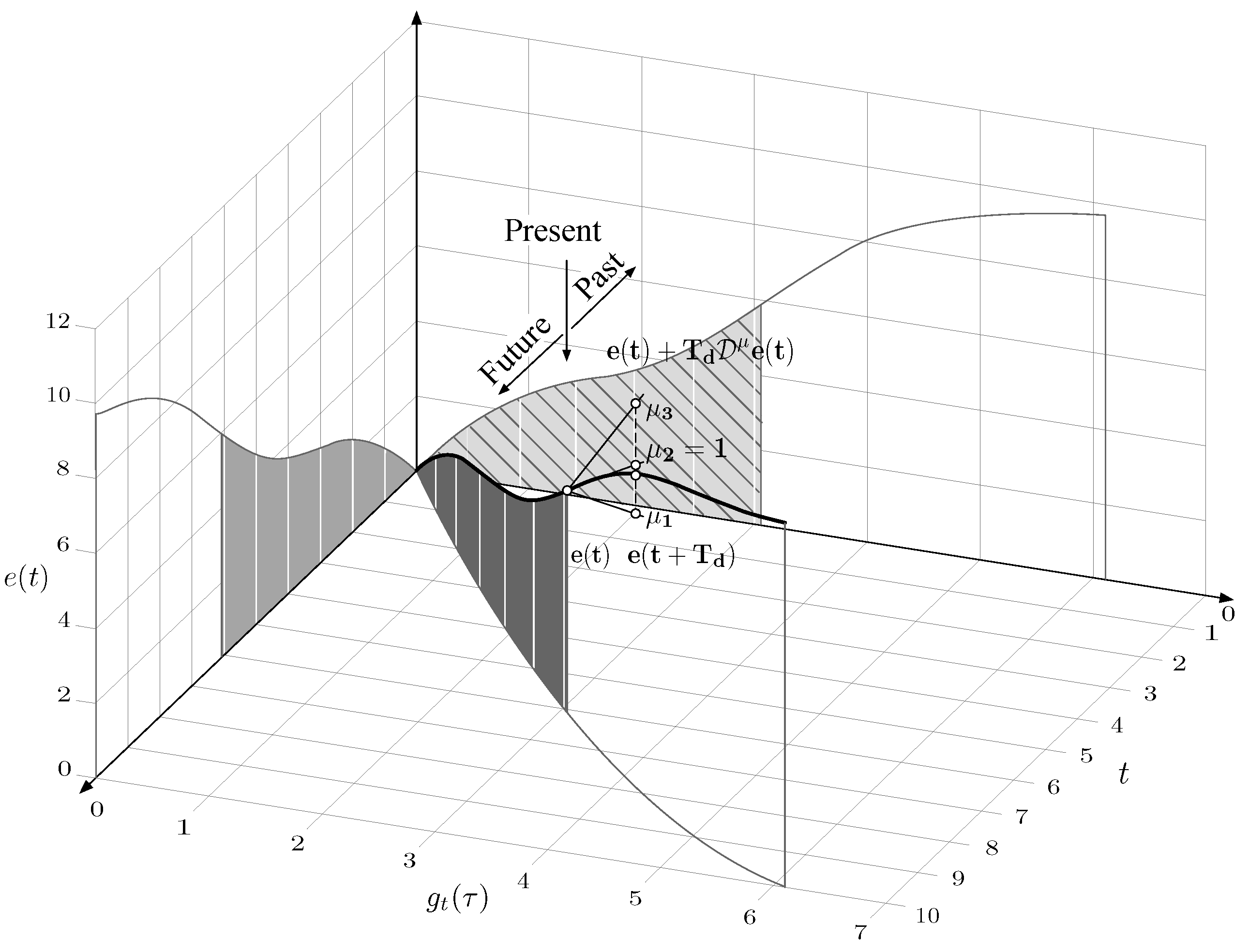
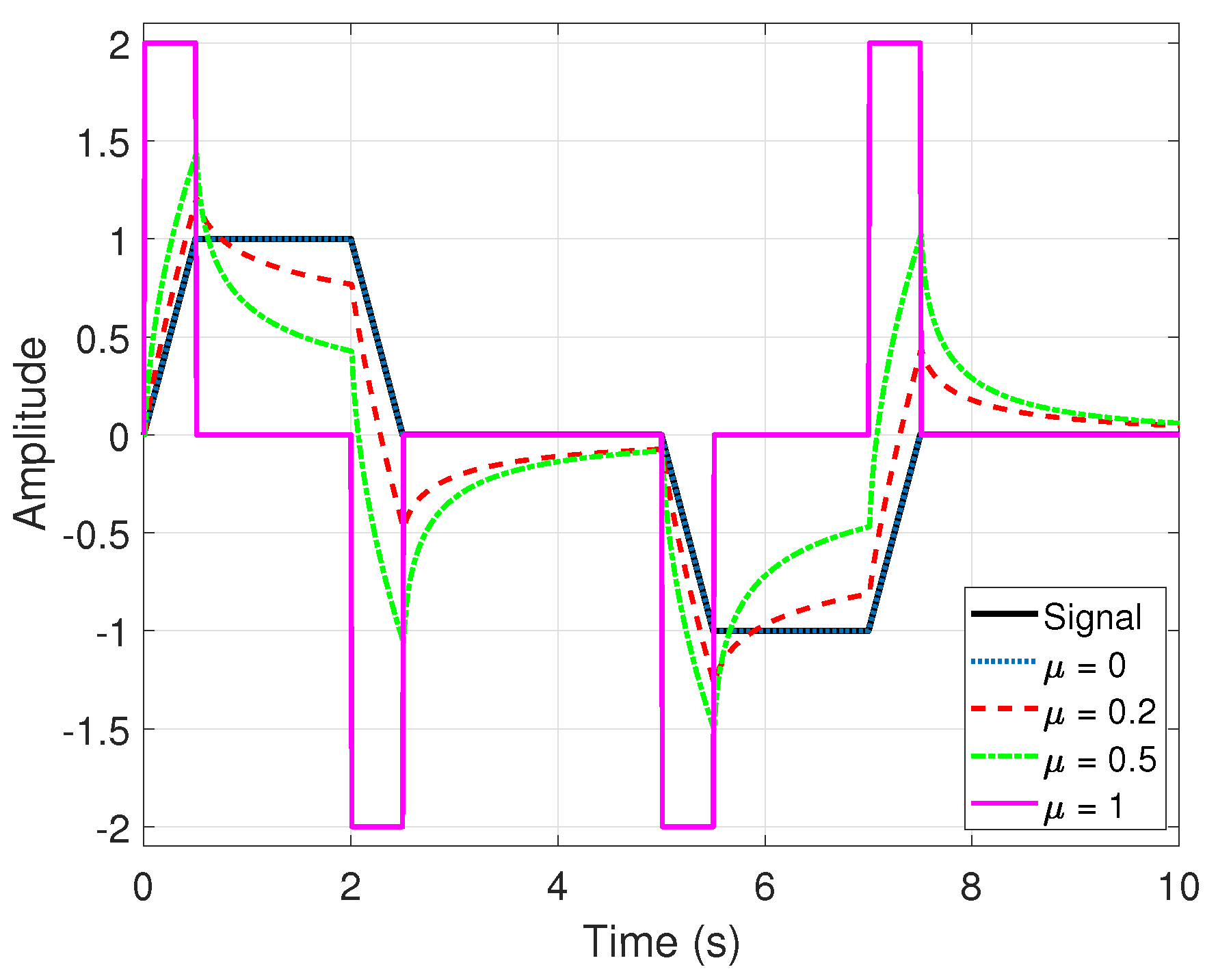
- For integral action, left-side Riemann-Liouville fractional integral of the error was considered as:whereThen, taking the axes , and e, function was plotted in the plane for . Along the obtained curve, a “fence” was plotted varying , so the top edge of the “fence” is a 3D line for . The area of the projection of this “fence” onto the plane corresponds to the value of the integer order integral of the error (i.e., the classical area under the curve), whereas that of the projection onto the plane corresponds to the value of fractional order integral (4). All this reasoning was adapted from [51].
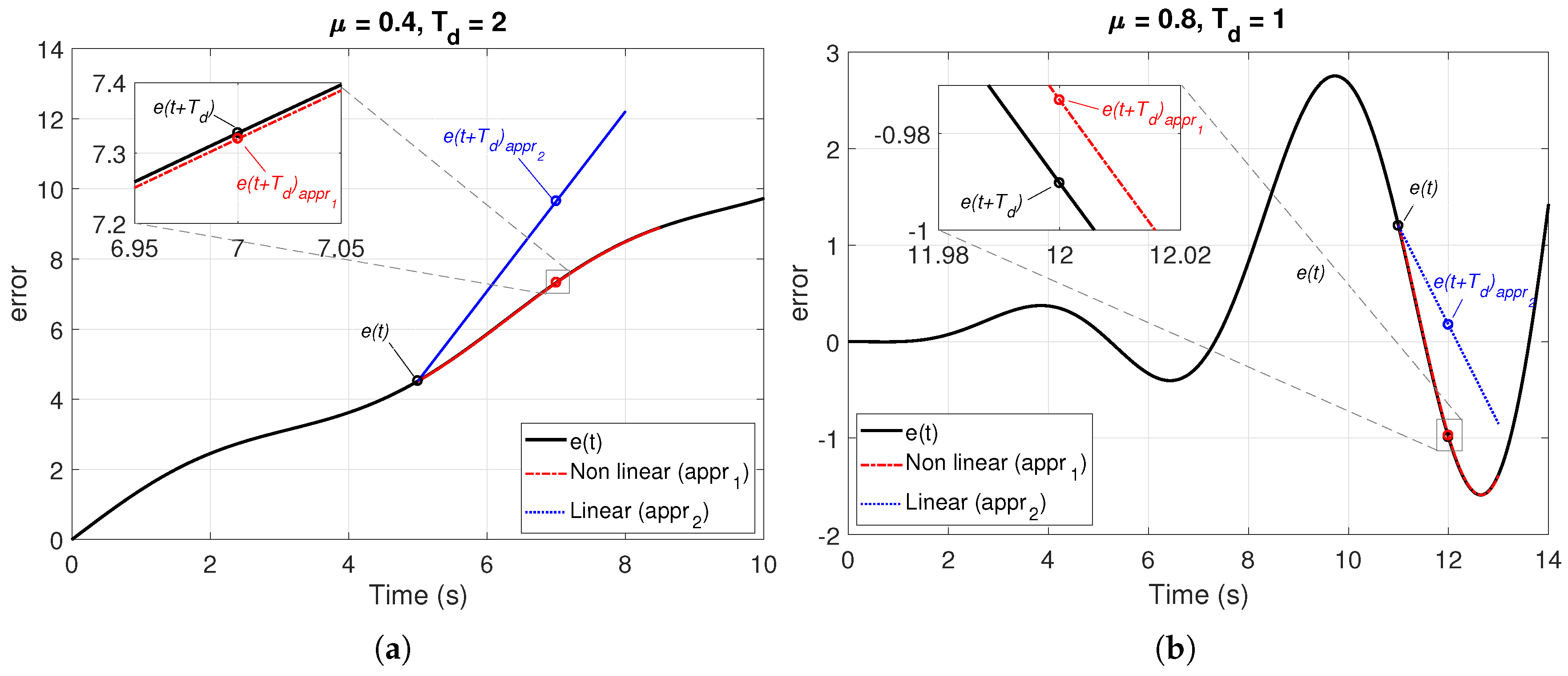
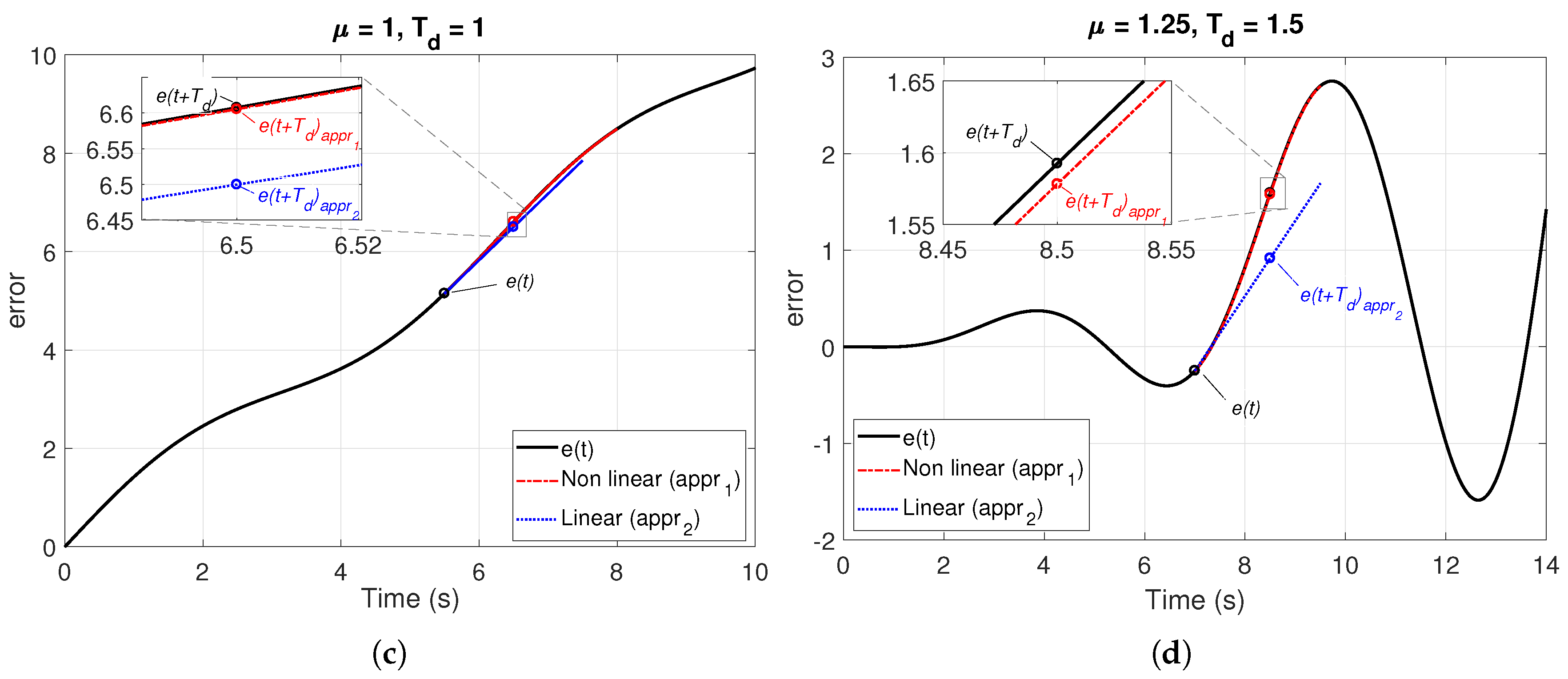
- For derivative action, straight lines that pass through the point and whose slope matches the value of the differentiation of order of the error curve at that point were plotted.
3. Going Into Detail About Parameters
3.1. Proportional Action
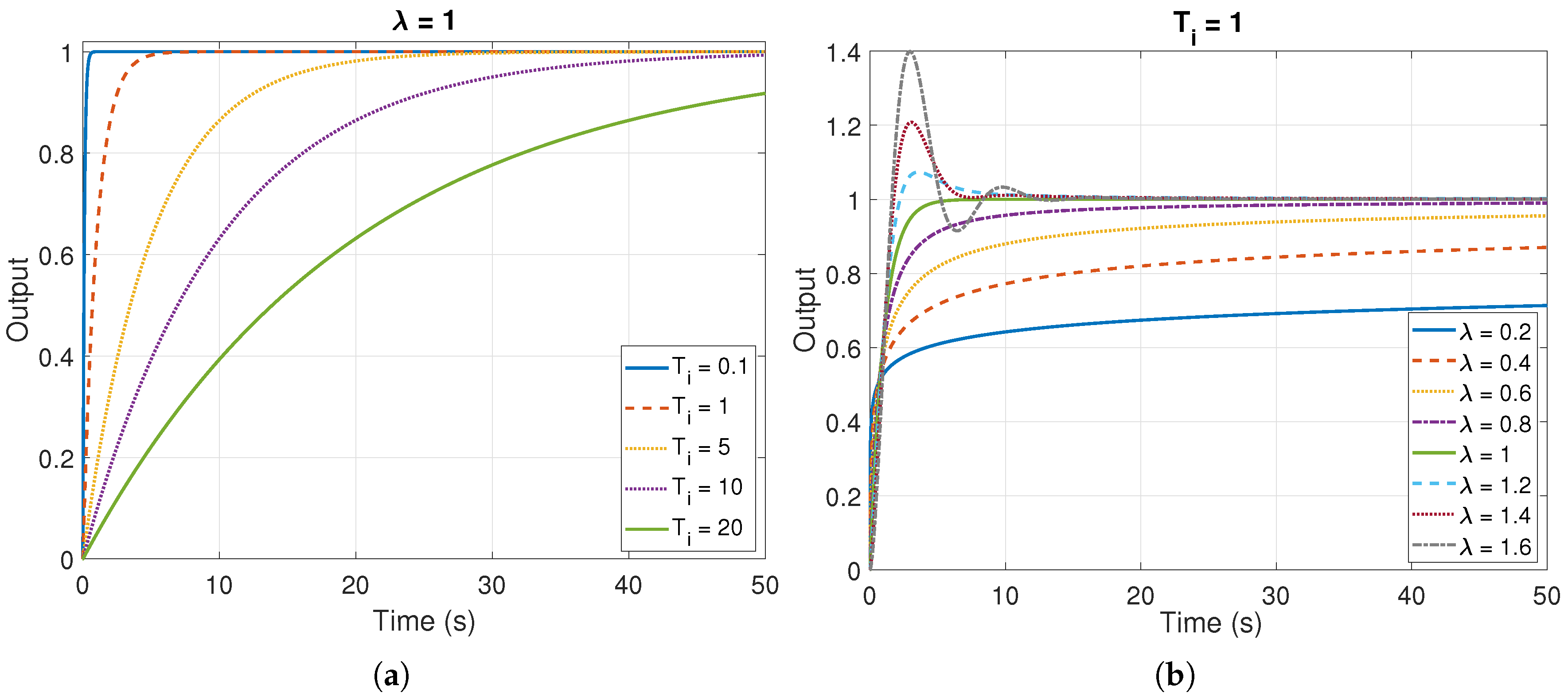
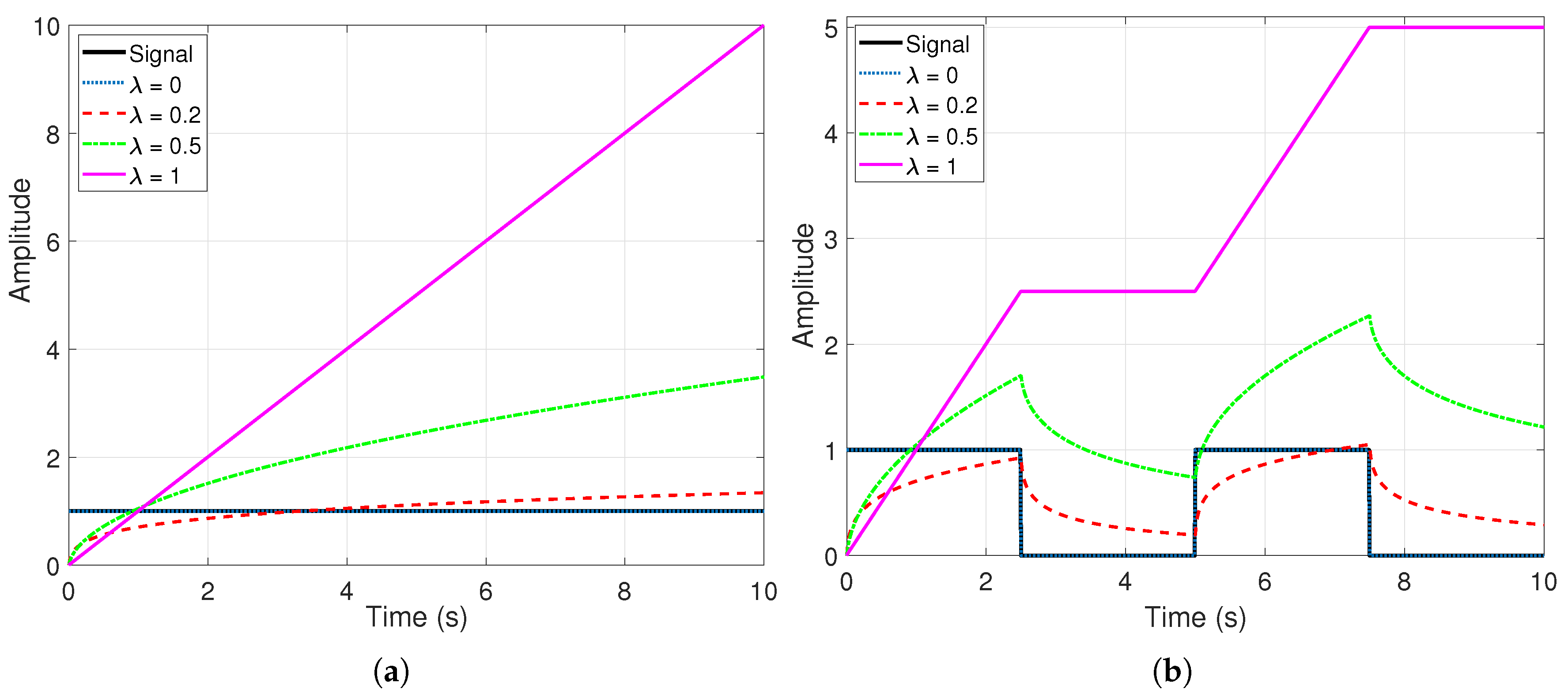
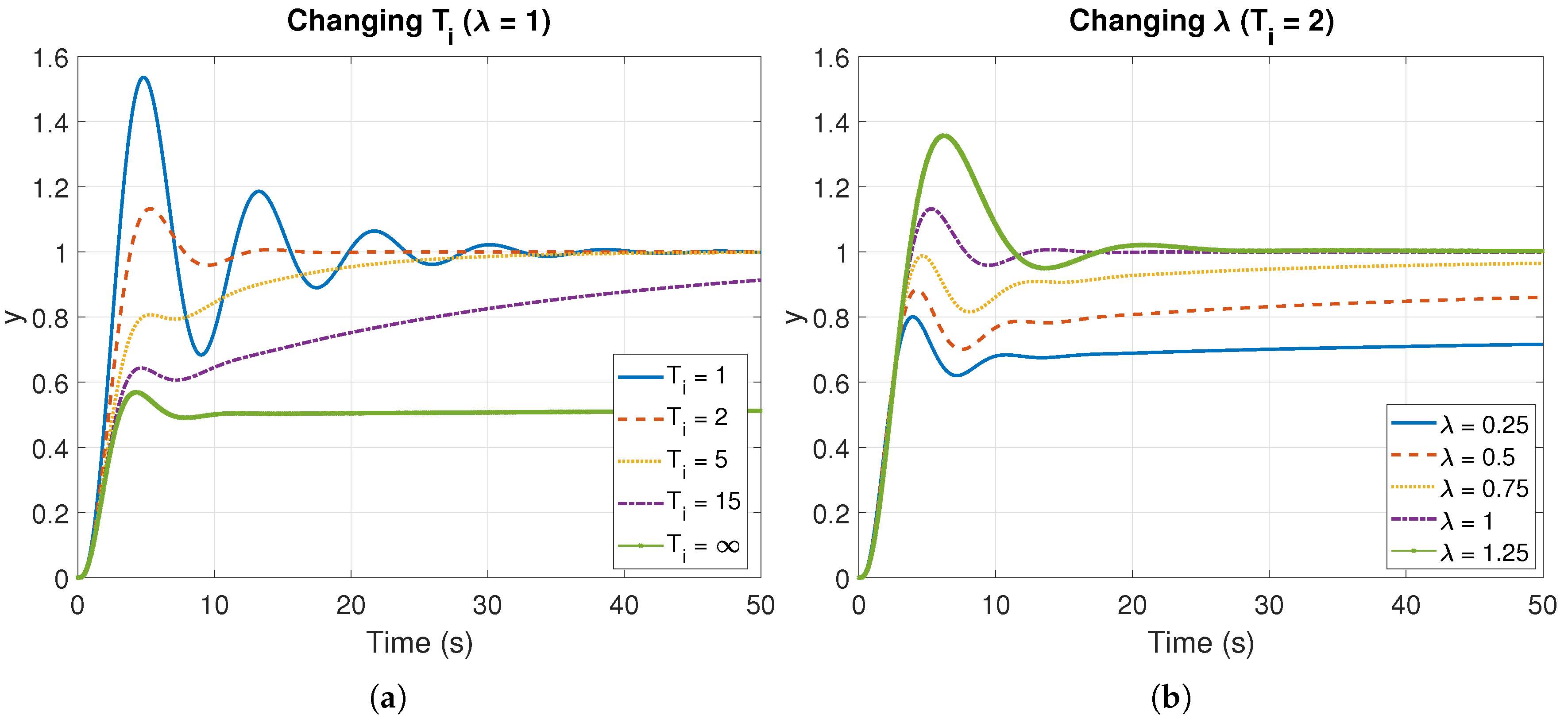
3.2. Integral Action
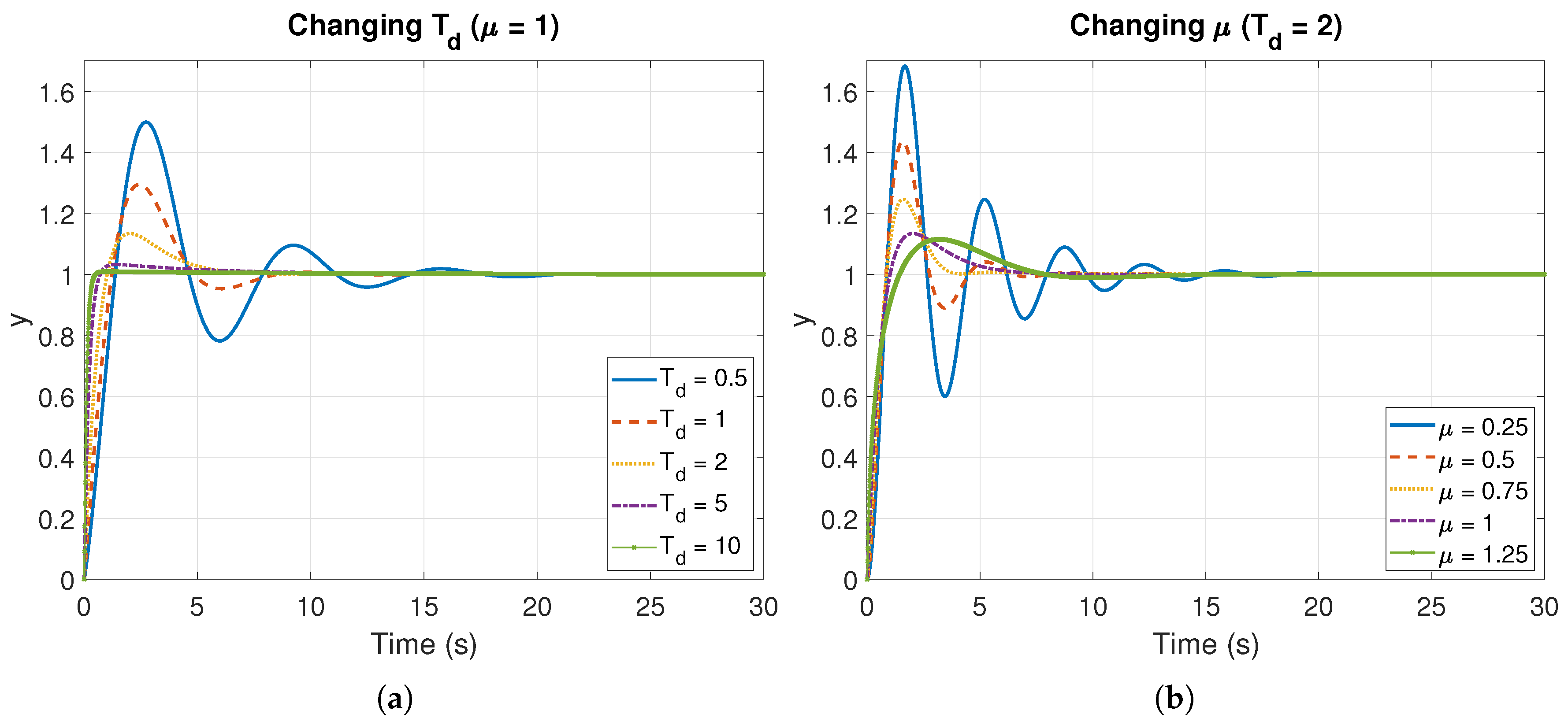
3.3. Derivative Action
4. Classical Versus Fractional PIDs
4.1. Integral Part
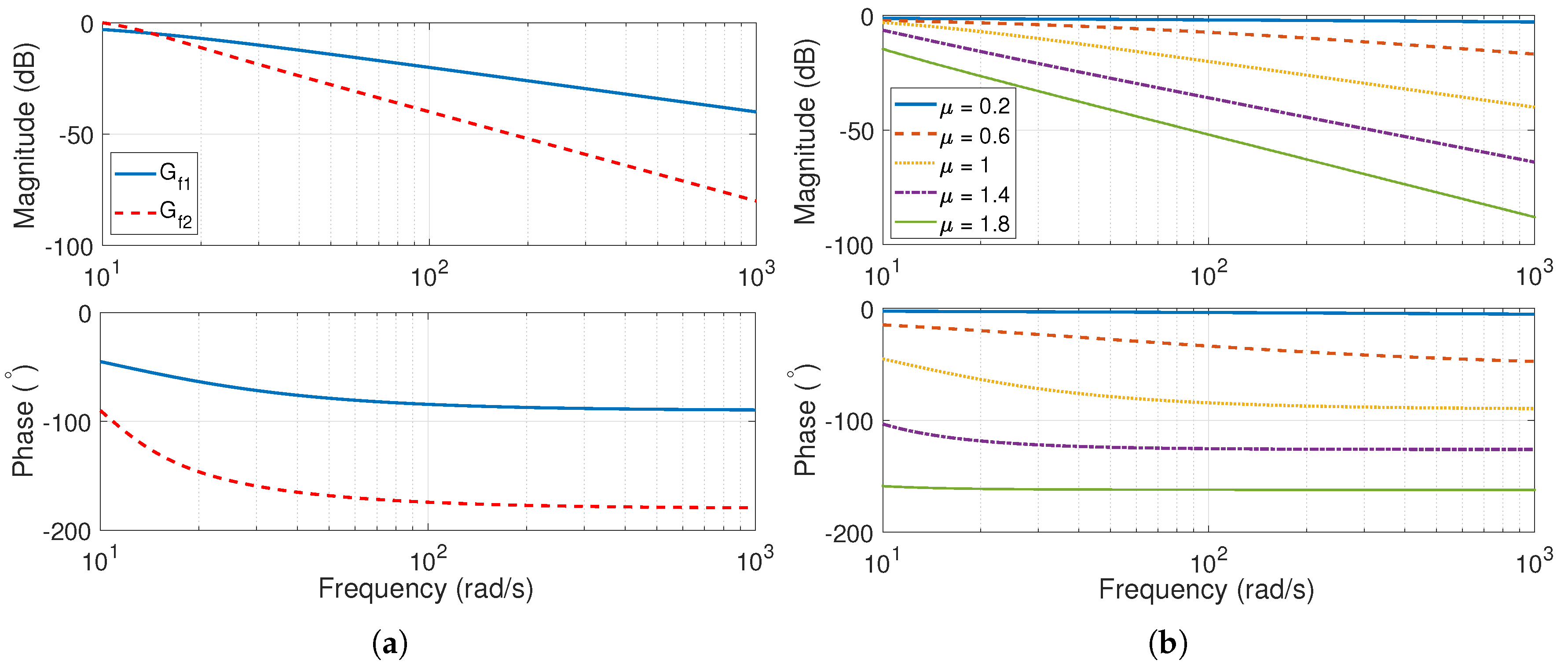
4.2. Derivative Part
5. Illustrative Examples
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Analysis of Prediction Horizon
References
- Aström, K.J.; Hägglund, T. PID Controllers: Theory, Design and Tuning, 2nd ed.; ISA—The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Aström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Aström, K.J.; Hägglund, T. Advanced PID Control; Chapter PID Control; ISA—The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006; pp. 64–94. [Google Scholar]
- Visioli, A. Practical PID Control; Advances in Industrial Control; Chapter Basics of PID Control; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–18. [Google Scholar]
- Li, Y.; Heong, K.; Chong, G.C.Y. PID Control System Analysis and Design. Problems, Remedies, and Future Directions. IEEE Control Syst. Mag. 2006, 26, 32–41. [Google Scholar]
- Vinagre, B.M.; Feliu-Batlle, V.; Tejado, I. Fractional Control: Fundamentals and User Guide. Revista Iberoamericana de Automática e Informática Industrial 2016, 13, 265–280. [Google Scholar] [CrossRef]
- Valério, D.; Sá da Costa, J. An Introduction to Fractional Control; IET Control Engineering, The Institution of Engineering and Technology: Stevenage, UK, 2013. [Google Scholar]
- Vinagre, B.M.; Monje, C.A. PID Control in the Third Millennium. Lessons Learned and New Approaches; Advances in Industrial Control; Chapter Fractional-Order PID; Springer: Berlin/Heidelberg, Germany, 2012; pp. 465–494. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls. Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lorenzini, C.; Bazanella, A.S.; Alves Pereira, L.F.; Goncalves da Silva, G.R. The generalized forced oscillation method for tuning PID controllers. ISA Trans. 2019, 87, 68–87. [Google Scholar] [CrossRef] [PubMed]
- Tajjudin, M.; Rahiman, M.H.F.; Arshad, N.M.; Adnan, R. Robust Fractional-Order PI Controller with Ziegler-Nichols Rules. Int. J. Electr. Comput. Eng. 2013, 7, 1034–1041. [Google Scholar]
- Gude, J.J.; Kahoraho, E. Modified Ziegler-Nichols method for fractional PI controllers. In Proceedings of the 2010 IEEE 15th Conference on Emerging Technologies & Factory Automation (ETFA 2010), Bilbao, Spain, 13–16 September 2010. [Google Scholar]
- Valério, D.; Sá da Costa, J. Tuning of fractional PID controllers with Ziegler-Nichols-type rules. Signal Process. 2006, 10, 2771–2784. [Google Scholar] [CrossRef]
- Hekimoglu, B. Optimal Tuning of Fractional Order PID Controller for DC Motor Speed Control via Chaotic Atom Search Optimization Algorithm. IEEE Access 2019, 7, 38100–38114. [Google Scholar] [CrossRef]
- Kesarkar, A.A.; Selvaganesan, N. Tuning of optimal fractional-order PID controller using an artificial bee colony algorithm. Syst. Sci. Control Eng. 2015, 3, 99–105. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Biswas, A.; Das, S.; Abraham, A.; Dasgupta, S. Design of fractional-order PIλDμ controllers with an improved differential evolution. Eng. Appl. Artif. Intell. 2009, 22, 343–350. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S. Robust Fractional-Order PID Controller Tuning Based on Bode’s Optimal Loop Shaping. Complexity 2018, 2018, 6570560. [Google Scholar] [CrossRef]
- HosseinNia, S.H.; Tejado, I.; Vinagre, B.M. A Method for the Design of Robust Controllers Ensuring the Quadratic Stability for Switching Systems. J. Vib. Control 2014, 20, 1085–1098. [Google Scholar] [CrossRef]
- Monje, C.A.; Calderón, A.J.; Vinagre, B.M.; Chen, Y.Q.; Feliu, V. On fractional PIλ controllers: Some tuning rules for robustness to plant uncertainties. Nonlinear Dyn. 2004, 38, 369–381. [Google Scholar] [CrossRef]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. A novel auto-tuning method for fractional order PI/PD controllers. ISA Trans. 2016, 62, 268–275. [Google Scholar] [CrossRef] [PubMed]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. Tuning and auto-tuning of fractional order controllers for industry applications. Control Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Chevalier, A.; Francis, C.; Copot, C.; Ionescu, C.M.; De Keyser, R. Fractional-order PID design: Towards transition from state-of-art to state-of-use. ISA Trans. 2019, 84, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Feliu-Batlle, V.; Rivas-Perez, R.; Castillo-Garcia, F.J. Simple Fractional Order Controller Combined with a Smith Predictor for Temperature Control in a Steel Slab Reheating Furnace. Int. J. Control Autom. Syst. 2013, 11, 533–544. [Google Scholar] [CrossRef]
- Feliu-Battle, V.; Rivas Pérez, R.; Castillo García, F.J.; Sánchez Rodríguez, L. Smith predictor based robust fractional order control: Application to water distribution in a main irrigation canal pool. J. Process Control 2009, 19, 506–519. [Google Scholar] [CrossRef]
- Luan Vu, T.N.; Lee, M. Smith predictor based fractional-order PI control for time-delay processes. Korean J. Chem. Eng. 2014, 31, 1321–1329. [Google Scholar]
- Lakshmanaprabu, S.K.; Banu, U.S.; Hemavathy, P.R. Fractional order IMC based PID controller design using Novel Bat optimization algorithm for TITO Process. Energy Proc. 2017, 117, 1125–1133. [Google Scholar] [CrossRef]
- Muresan, C.I.; Dutta, A.; Dulf, E.H.; Pinar, Z.; Maxim, A.; Ionescu, C.M. Tuning algorithms for fractional order internal model controllers for time delay processes. Int. J. Control 2016, 89, 579–593. [Google Scholar] [CrossRef]
- Maamar, B.; Rachid, M. IMC-PID-fractional-order-filter controllers design for integer order systems. ISA Trans. 2014, 53, 1620–1628. [Google Scholar] [CrossRef] [PubMed]
- HosseinNia, S.H.; Tejado, I.; Vinagre, B.M.; Milanés, V.; Villagrá, J. Experimental Application of Hybrid Fractional Order Adaptive Cruise Control at Low Speed. IEEE Trans. Control Syst. Technol. 2014, 22, 2329–2336. [Google Scholar] [CrossRef]
- Ahmed, M.F.; Dorrah, H.T. Design of gain schedule fractional PID control for nonlinear thrust vector control missile with uncertainty. Automatika 2018, 59, 357–372. [Google Scholar] [CrossRef]
- Tejado, I.; Milanés, V.; Villagrá, J.; Vinagre, B.M. Fractional Network-based Control for Vehicle Speed Adaptation via vehicle-to-infrastructure Communications. IEEE Trans. Control Syst. Technol. 2013, 21, 780–790. [Google Scholar] [CrossRef]
- Tejado, I.; HosseinNia, S.H.; Vinagre, B.M.; Chen, Y.Q. Efficient control of a SmartWheel via Internet with compensation of variable delays. Mechatronics 2013, 23, 821–827. [Google Scholar] [CrossRef]
- Tejado, I.; HosseinNia, S.H.; Vinagre, B.M. Adaptive gain-order fractional control for network-based applications. Fract. Calc. Appl. Anal. 2014, 17, 462–482. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Intelligent Fractional Order Systems and Control; Chapter Gain and Order Scheduling for Fractional Order Controllers; Springer: Berlin/Heidelberg, Germany, 2013; pp. 147–157. [Google Scholar]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.Q.; HosseinNia, S.H. Linear fractional order controllers; A survey in the frequency domain. Ann. Rev. Control 2019. [Google Scholar] [CrossRef]
- Birs, I.; Muresan, C.; Nascu, I.; Ionescu, C. A Survey of Recent Advances in Fractional Order Control for Time Delay Systems. IEEE Access 2019, 7, 30951–30965. [Google Scholar] [CrossRef]
- Petrás, I. Handbook of Fractional Calculus with Applications; Chapter Modified Versions of the Fractional-Order PID Controller; De Gruyter: Berlin, Germany, 2019; Volume 6, pp. 57–72. [Google Scholar]
- Dastjerdi, A.A.; Saikumar, N.; HosseinNia, S.H. Tuning guidelines for fractional order PID controllers: Rules of thumb. Mechatronics 2018, 56, 26–36. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID Controllers and Their Industrial Applications: A Survey of Recent Results. In Proceedings of the 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; Volume 51, pp. 25–30. [Google Scholar]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Apte, A.; Thakar, U.; Joshi, V. Disturbance Observer Based Speed Control of PMSM Using Fractional Order PI Controller. IEEE-CAA J. Autom. Sin. 2019, 6, 316–326. [Google Scholar] [CrossRef]
- AbouOmar, M.S.; Zhang, H.J.; Su, Y.X. Fractional Order Fuzzy PID Control of Automotive PEM Fuel Cell Air Feed System Using Neural Network Optimization Algorithm. Energies 2019, 12, 1435. [Google Scholar] [CrossRef]
- Copot, D.; Ghita, M.; Ionescu, C.M. Simple Alternatives to PID-Type Control for Processes with Variable Time-Delay. Processes 2019, 7, 146. [Google Scholar] [CrossRef]
- Deng, Y. Fractional-order fuzzy adaptive controller design for uncertain robotic manipulators. Int. J. Adv. Robot. Syst. 2019, 16, 1–10. [Google Scholar] [CrossRef]
- Feliu-Talegon, D.; Feliu-Batlle, V.; Tejado, I.; Vinagre, B.M.; HosseinNia, S.H. Stable force control and contact transition of a single link flexible robot using a fractional-order controller. ISA Trans. 2019, 89, 139–157. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.P.; Fan, J.T.; Kaynak, O. Optimal Design of a Fractional-Order Proportional-Integer-Differential Controller for a Pneumatic Position Servo System. IEEE Trans. Ind. Electr. 2019, 66, 6220–6229. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, C.; Zhou, X.; Gui, W. Optimal Setting and Control Strategy for Industrial Process Based on Discrete-Time Fractional-Order (PID mu)-D-lambda. IEEE Access 2019, 7, 47747–47761. [Google Scholar] [CrossRef]
- Mystkowski, A.; Kierdelewicz, A. Fractional-order water level control based on PLC: hardware-in-the-loop simulation and experimental validation. Energies 2018, 11, 2928. [Google Scholar] [CrossRef]
- Podlubny, I. Geometric and Physical Interpretation of Fractional Integration and Fractional Differentiation. Fract. Calc. Appl. Anal. 2004, 5, 367–386. [Google Scholar]
- Tavassoli, M.H.; Tavassoli, A.; Rahimi, M.R.O. The geometric and physical interpretation of fractional order derivatives of polynomial functions. Differ. Geom. Dyn. Syst. 2013, 15, 93–104. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering; Academic Press: Cambridge, MA, USA, 1999; Volume 198. [Google Scholar]
- Hägglund, T. A unified discussion on signal filtering in PID control. Control Eng. Pract. 2013, 21, 994–1006. [Google Scholar] [CrossRef]
- Isaksson, A.; Graebe, S. Derivative filter is an integral part of PID design. IEE Proc. Control Theor. Appl. 2002, 149, 41–45. [Google Scholar] [CrossRef]
- Fractional Taylor Series for Caputo Fractional Derivatives. Construction of Numerical Schemes. Available online: http://www.fdi.ucm.es/profesor/lvazquez/calcfrac/docs/paper_Usero.pdf (accessed on 22 April 2019).


| Action | Domain | Effect on | Integer | Fractional |
|---|---|---|---|---|
| I | Time | Steady-state error | Elimination | |
| u with respect to the sign of e | If , u grows linearly with time | The same but the growing or the decrease is not linear with time | ||
| If , u decreases linearly with time | ||||
| Automatic reset | The velocity of reset can be changed | Both the velocity and the shape of reset can be changed | ||
| Frequency | Frequency response | The magnitude curve decreases with a slope of 20 dB/dec | The magnitude curve decreases with a slope of dB/dec | |
| Decrease of rad in the phase curve | Decrease of rad in the phase curve | |||
| D | Time | Constant errors | Does not response, so the derivative term needs to be combined with, at least, the proportional term | Does response, so the derivative term can be used individually |
| Prediction horizon | Time ahead over the tangent to the error curve at | Time ahead over a curve (non-linear extrapolation) or over a straight line (linear extrapolation) that passes through the point and whose slope matches the value of the fractional differentiation of order of the error curve at that point | ||
| Frequency | Frequency response | The magnitude curve grows with a slope of 20 dB/dec | The magnitude curve grows with a slope of dB/dec | |
| Increment of rad in the phase curve | Increment of rad in the phase curve | |||
| Filtering | Low-pass filters up to second order | Low-pass filter of order | ||
| Usually needs two parameters to be tuned, i.e., (filter time constant) and N (ratio between and ) | Parameter allows to have different frequency responses, ranged between those of the two integer filters, and consequently, have different filtering effects on the error signal. | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tejado, I.; Vinagre, B.M.; Traver, J.E.; Prieto-Arranz, J.; Nuevo-Gallardo, C. Back to Basics: Meaning of the Parameters of Fractional Order PID Controllers. Mathematics 2019, 7, 530. https://doi.org/10.3390/math7060530
Tejado I, Vinagre BM, Traver JE, Prieto-Arranz J, Nuevo-Gallardo C. Back to Basics: Meaning of the Parameters of Fractional Order PID Controllers. Mathematics. 2019; 7(6):530. https://doi.org/10.3390/math7060530
Chicago/Turabian StyleTejado, Inés, Blas M. Vinagre, José Emilio Traver, Javier Prieto-Arranz, and Cristina Nuevo-Gallardo. 2019. "Back to Basics: Meaning of the Parameters of Fractional Order PID Controllers" Mathematics 7, no. 6: 530. https://doi.org/10.3390/math7060530
APA StyleTejado, I., Vinagre, B. M., Traver, J. E., Prieto-Arranz, J., & Nuevo-Gallardo, C. (2019). Back to Basics: Meaning of the Parameters of Fractional Order PID Controllers. Mathematics, 7(6), 530. https://doi.org/10.3390/math7060530







