Non-Parametric Threshold Estimation for the Wiener–Poisson Risk Model
Abstract
:1. Introduction
2. Estimation of Survival Probability
3. Asymptotic Properties
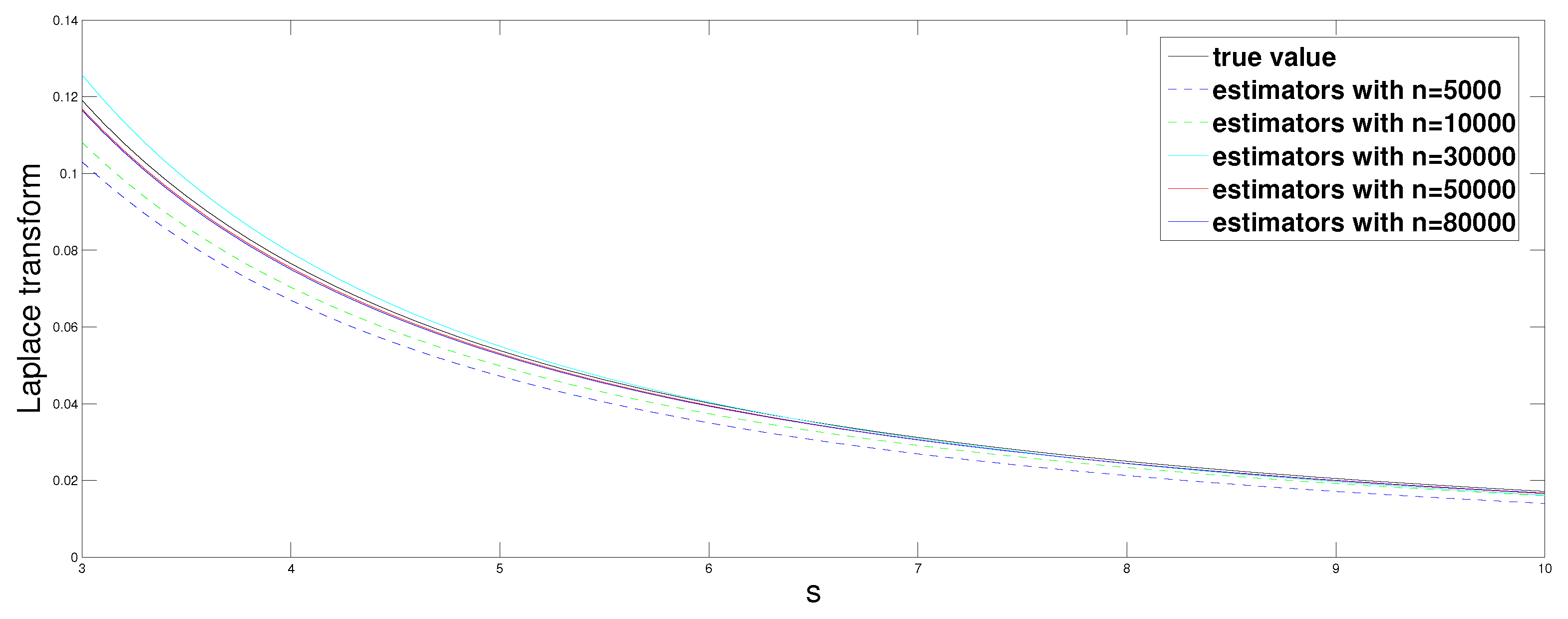
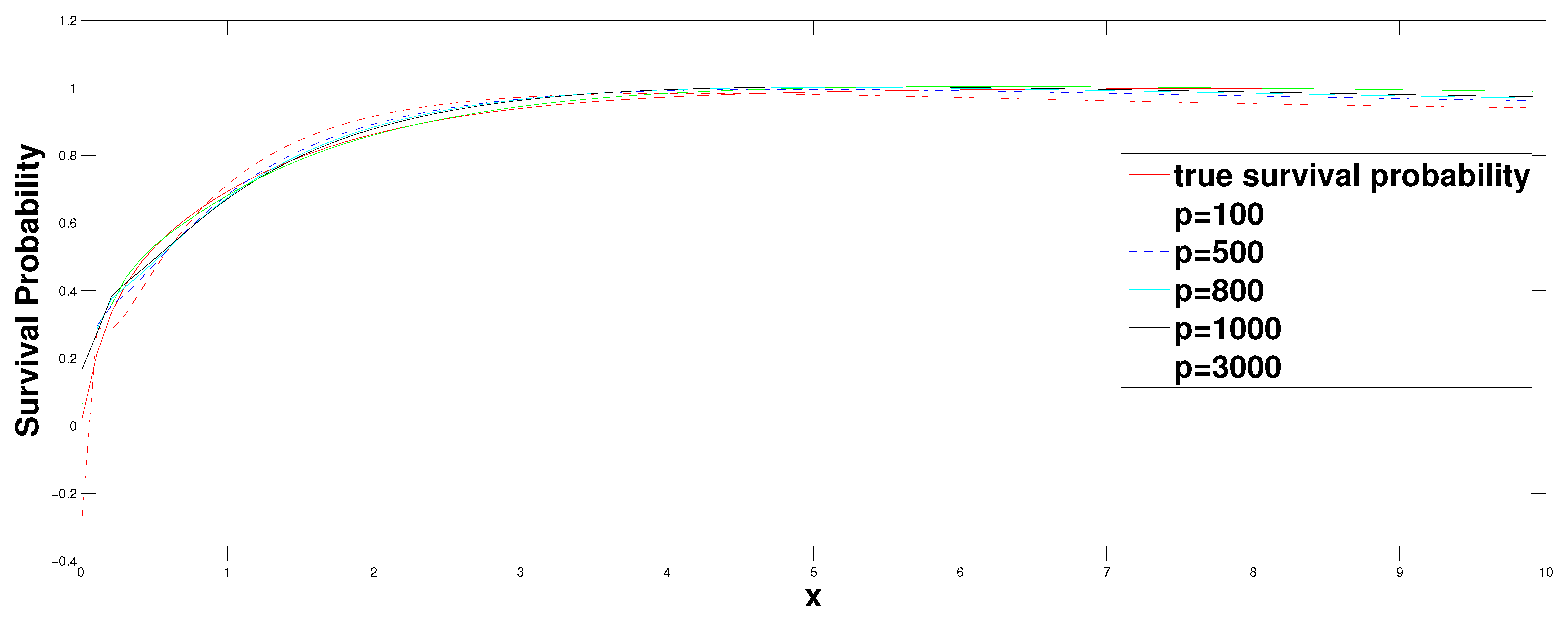
4. Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Theorems
References
- Gerber, H.U. An extension of the renewal equation and its application in the collective theory of risk. Scand. Actuar. J. 1970, 1970, 205–210. [Google Scholar] [CrossRef]
- Dufresne, F.; Gerber, H.U. Risk theory for the compound Poisson process that is perturbed by diffusion. Insur. Math. Econ. 1991, 10, 51–59. [Google Scholar] [CrossRef]
- Furrer, H.J.; Schimidli, H. Exponential inequalities for ruin probabilities of risk process perturbed by diffusion. Insur. Math. Econ. 1994, 15, 23–36. [Google Scholar] [CrossRef]
- Gatto, R.; Mosimann, M. Four approaches to compute the probability of ruin in the compound Poisson risk process with diffusion. Math. Comput. Modell. 2012, 55, 1169–1185. [Google Scholar] [CrossRef]
- Gatto, R.; Baumgartner, B. Saddlepoint Approximations to the Probability of Ruin in Finite Time for the Compound Poisson Risk Process Perturbed by Diffusion. Methodol. Comput. Appl. Probab. 2014, 18, 1–19. [Google Scholar] [CrossRef]
- Gatto, R. Importance sampling approximations to various probabilities of ruin of spectrally negative Lévy risk processes. Appl. Math. Comput. 2014, 243, 91–104. [Google Scholar] [CrossRef]
- Schimidli, H. Cramer-Lundberg approximations for ruin probabilites of risk processes perturbed by diffusion. Insur. Math. Econ. 1995, 16, 135–149. [Google Scholar] [CrossRef]
- Veraverbeke, N. Asymptotic estimates for the probability of ruin in a Poisson model with diffusion. Insur. Math. Econ. 1993, 13, 57–62. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, C. Approximation for the ruin probabilities in a discrete time risk model with dependent risks. Stat. Probab. Lett. 2010, 80, 1335–1342. [Google Scholar] [CrossRef]
- Bening, V.E.; Korolev, V.Y. Nonparametric estimation of the ruin probability for generalized risk processes. Theory Probab. Its Appl. 2002, 47, 1–16. [Google Scholar] [CrossRef]
- Croux, K.; Veraverbeke, N. Non-parametric estimators for the probability of ruin. Insur. Math. Econ. 1990, 9, 127–130. [Google Scholar] [CrossRef]
- Frees, E.W. Nonparametric estimation of the probability of ruin. Astin Bull. 1986, 16, 81–90. [Google Scholar] [CrossRef]
- Hipp, C. Estimators and bootstrap confidence intervals for ruin probabilities. Astin Bull. 1989, 19, 57–70. [Google Scholar] [CrossRef]
- Mnatsakanov, R.; Ruymgaart, L.L.; Ruymgaart, F.H. Nonparametric estimation of ruin probabilities given a random sample of claims. Math. Methods Stat. 2008, 17, 35–43. [Google Scholar] [CrossRef]
- Pitts, S.M. Nonparametric estimation of compound distributions with applications in insurance. Ann. Inst. Stat. Math. 1994, 46, 537–555. [Google Scholar]
- Politis, K. Semiparametric estimation for non-ruin probabilities. Scand. Actuar. J. 2003, 2003, 75–96. [Google Scholar] [CrossRef]
- Shimizu, Y. Non-parametric estimation of the Gerber-Shiu function for the Wiener-Poisson risk model. Scand. Actuar. J. 2012, 2012, 56–69. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H. Nonparametric estimate of the ruin probability in a pure-jump lévy risk model. Insur. Math. Econ. 2013, 53, 24–35. [Google Scholar] [CrossRef]
- Mancini, C. Estimation of the characteristics of the jump of a general Poisson-diffusion model. Scand. Actuar. J. 2004, 1, 42–52. [Google Scholar] [CrossRef]
- Mancini, C. Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps. Scand. J. Stat. 2009, 36, 270–296. [Google Scholar] [CrossRef]
- Shimizu, Y. A new aspect of a risk process and its statistical inference. Insur. Math. Econ. 2009, 44, 70–77. [Google Scholar] [CrossRef]
- Shimizu, Y. Functional estimation for lévy measures of semimartingales with Poissonian jumps. J. Multivar. Anal. 2009, 100, 1073–1092. [Google Scholar] [CrossRef]
- Morales, M. On the expected discounted penalty function for a perturbed risk process driven by a subordinator. Insur. Math. Econ. 2007, 40, 293–301. [Google Scholar] [CrossRef]
- Chauveau, D.E.; Vanrooij, A.C.M.; Ruymgaart, F.H. Regularized inversion of noisy Laplace transforms. Adv. Appl. Math. 1994, 15, 186–201. [Google Scholar] [CrossRef]
- Asmussen, S.; Albrecher, H. Ruin Probabilities, 2nd ed.; World Scientific: Singapore, 2010. [Google Scholar]
- Cai, C.; Chen, N.; You, H. Nonparametric estimation for a spectrally negative Lévy process based on low–frequency observation. J. Comput. Appl. Math. 2018, 328, 432–442. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, H.; Gao, Y. Non-Parametric Threshold Estimation for the Wiener–Poisson Risk Model. Mathematics 2019, 7, 506. https://doi.org/10.3390/math7060506
You H, Gao Y. Non-Parametric Threshold Estimation for the Wiener–Poisson Risk Model. Mathematics. 2019; 7(6):506. https://doi.org/10.3390/math7060506
Chicago/Turabian StyleYou, Honglong, and Yuan Gao. 2019. "Non-Parametric Threshold Estimation for the Wiener–Poisson Risk Model" Mathematics 7, no. 6: 506. https://doi.org/10.3390/math7060506
APA StyleYou, H., & Gao, Y. (2019). Non-Parametric Threshold Estimation for the Wiener–Poisson Risk Model. Mathematics, 7(6), 506. https://doi.org/10.3390/math7060506




