Statistical Tests for Extreme Precipitation Volumes
Abstract
:1. Introduction
2. Mathematical Models to Derive Statistical Tests for Precipitation Volume to Be Anomalous Large
2.1. The Tempered Snedecor–Fisher Distribution as an Asymptotic Approximation to the Maximum Daily Precipitation Volume Within a Wet Period
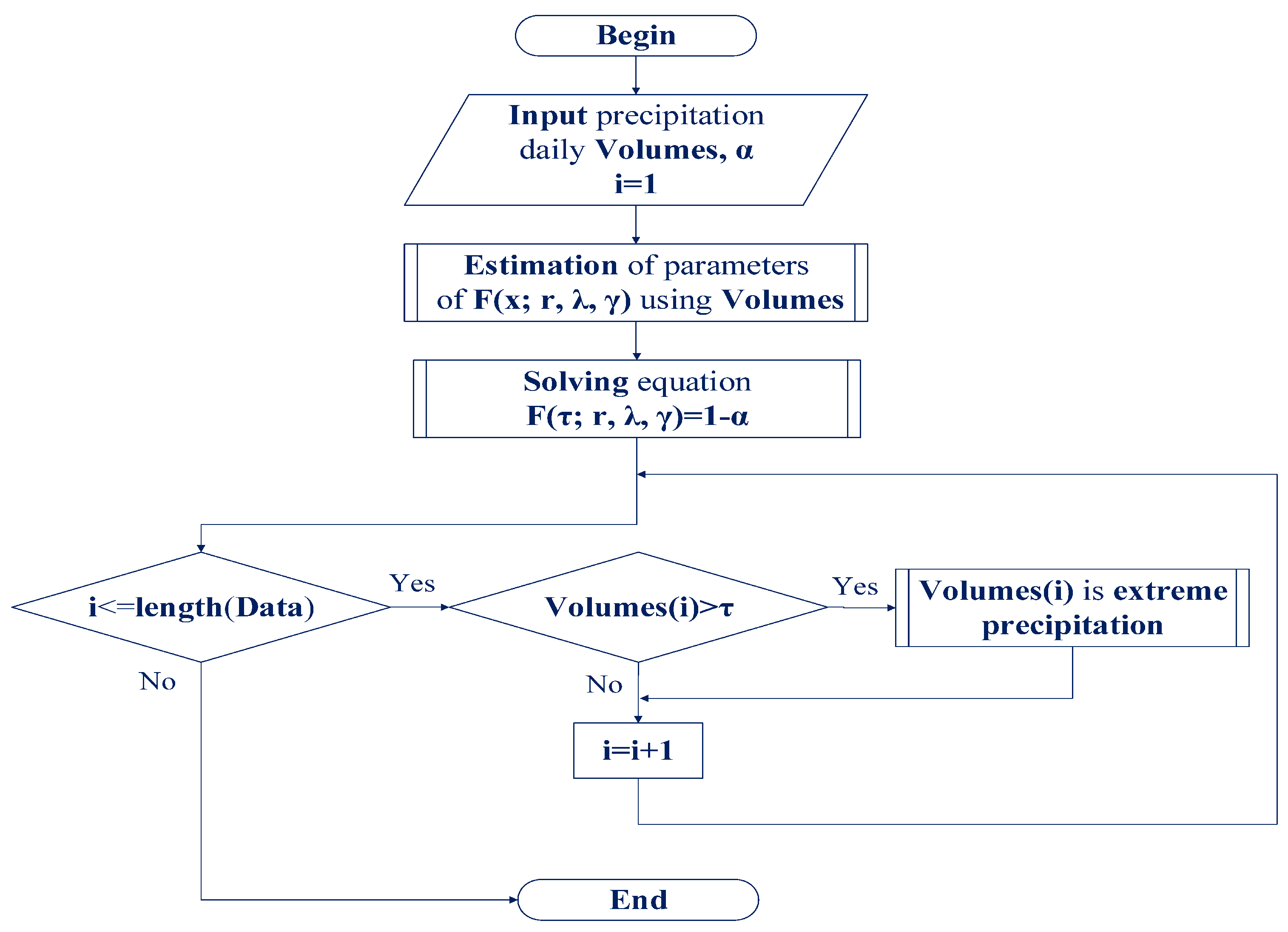
2.2. The Algorithms of Statistical Fitting of the Tempered Snedecor-Fisher Distribution Model
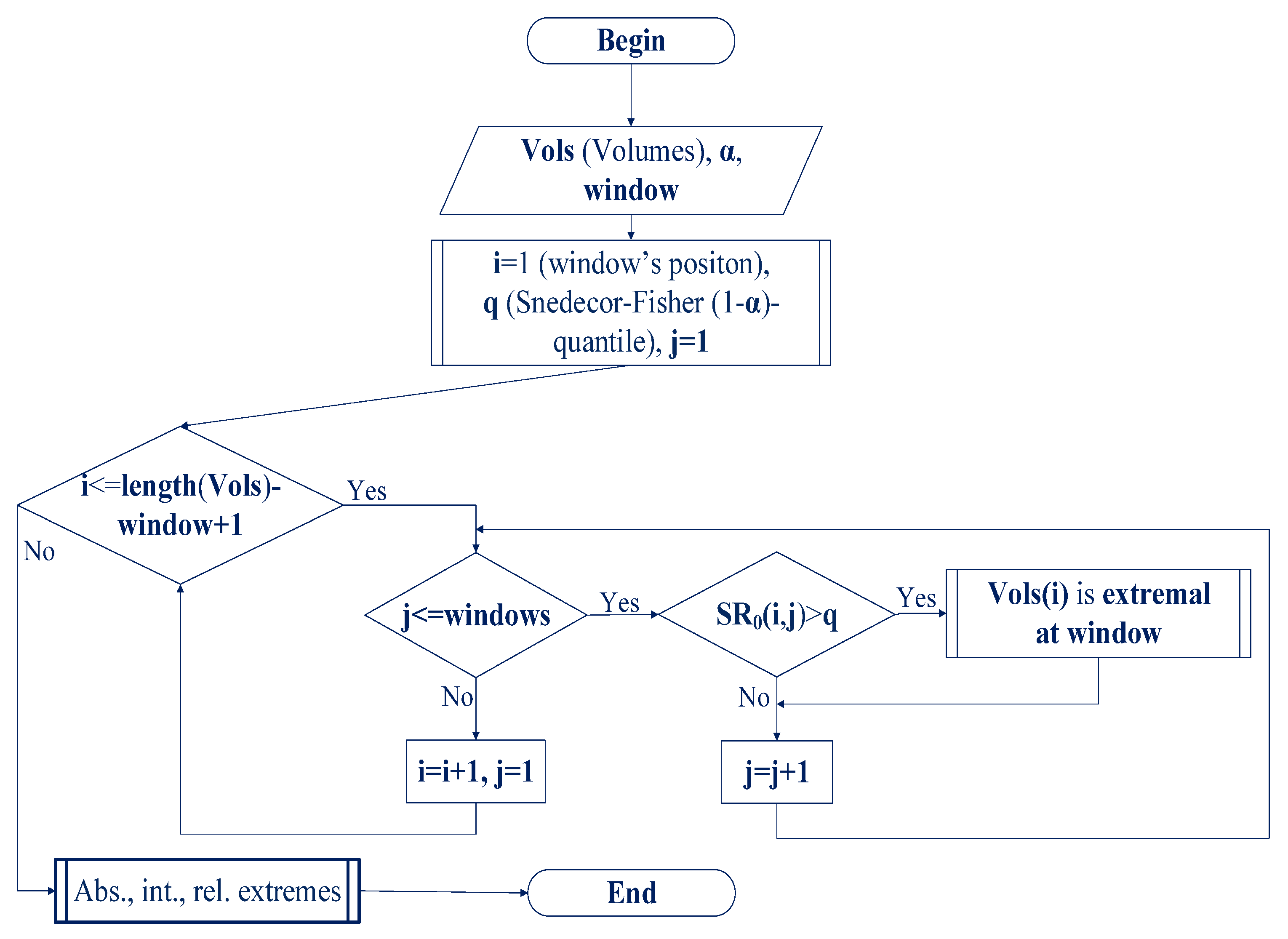
2.3. The Tests for a Total Precipitation Volume to Be Anomalously Extremal Based on the Homogeneity Test of a Sample From the Gamma Distribution
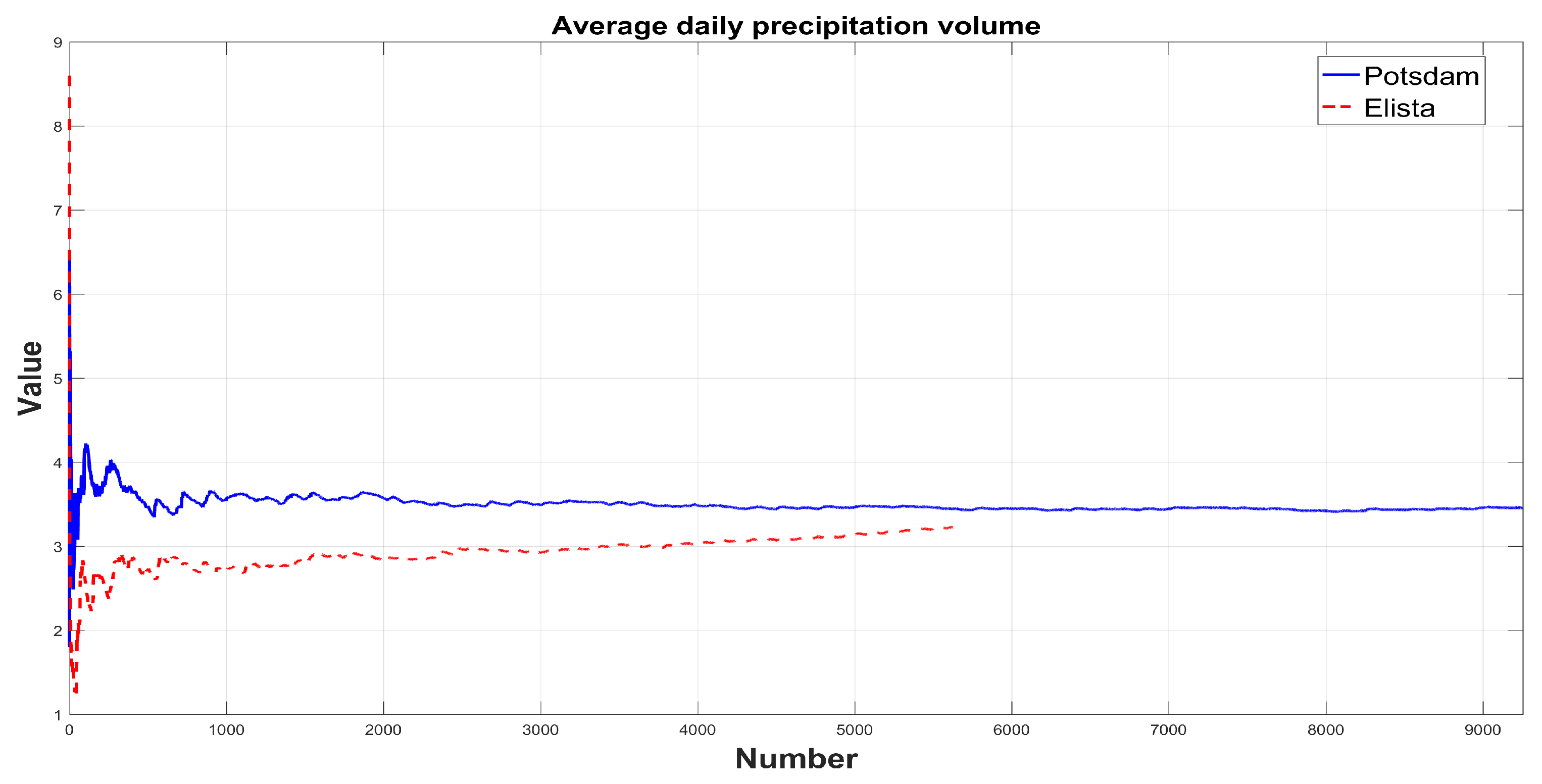
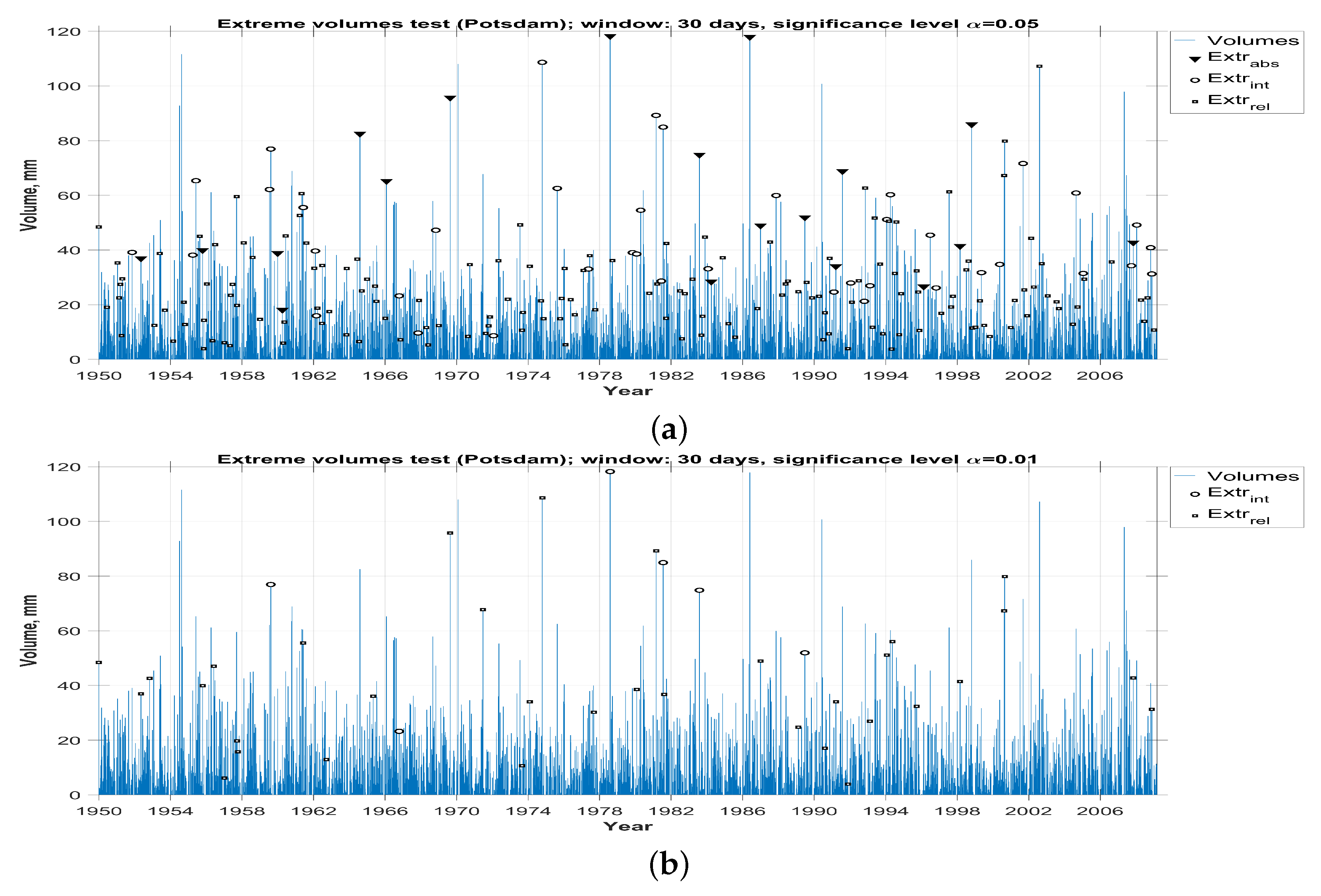
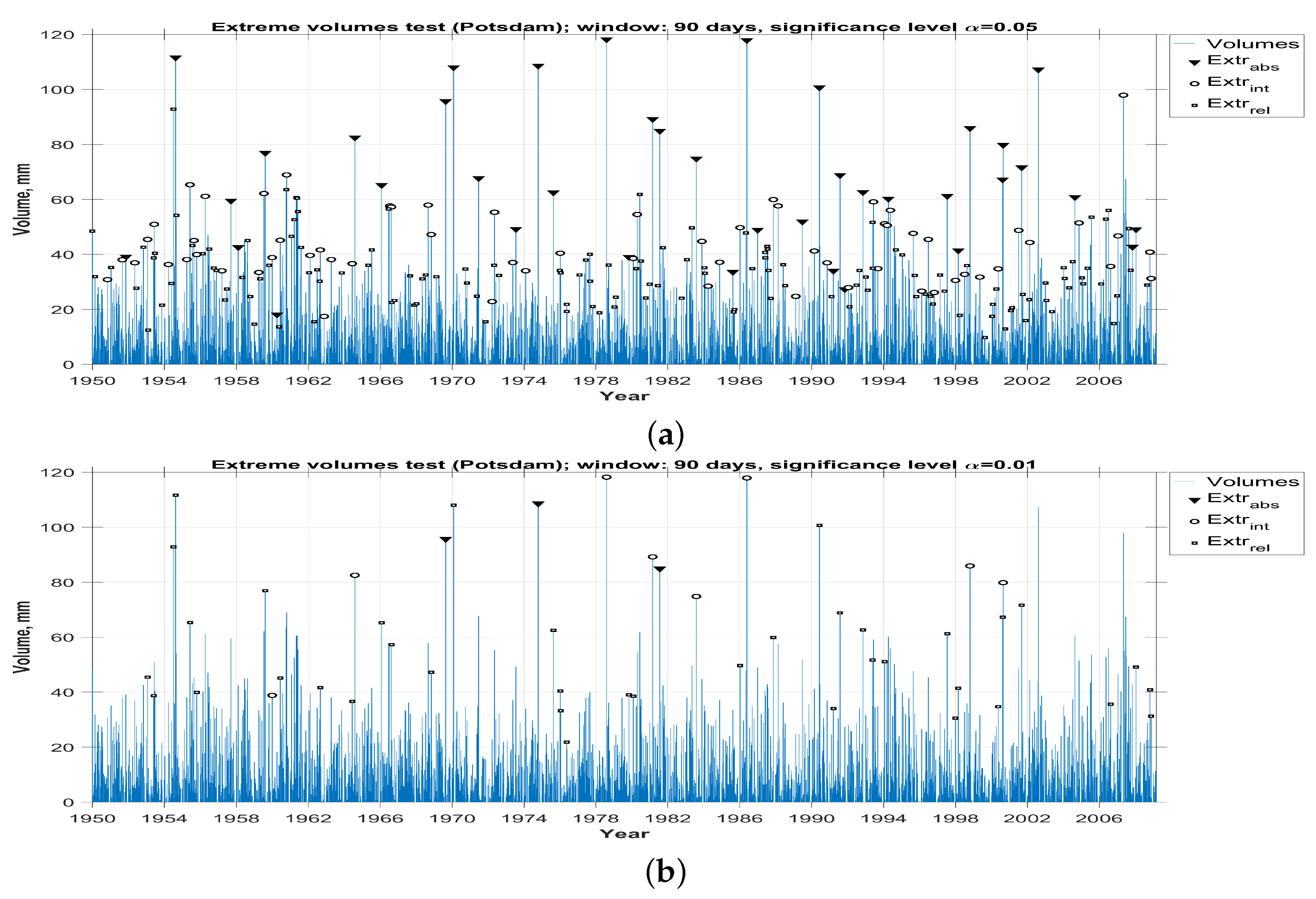
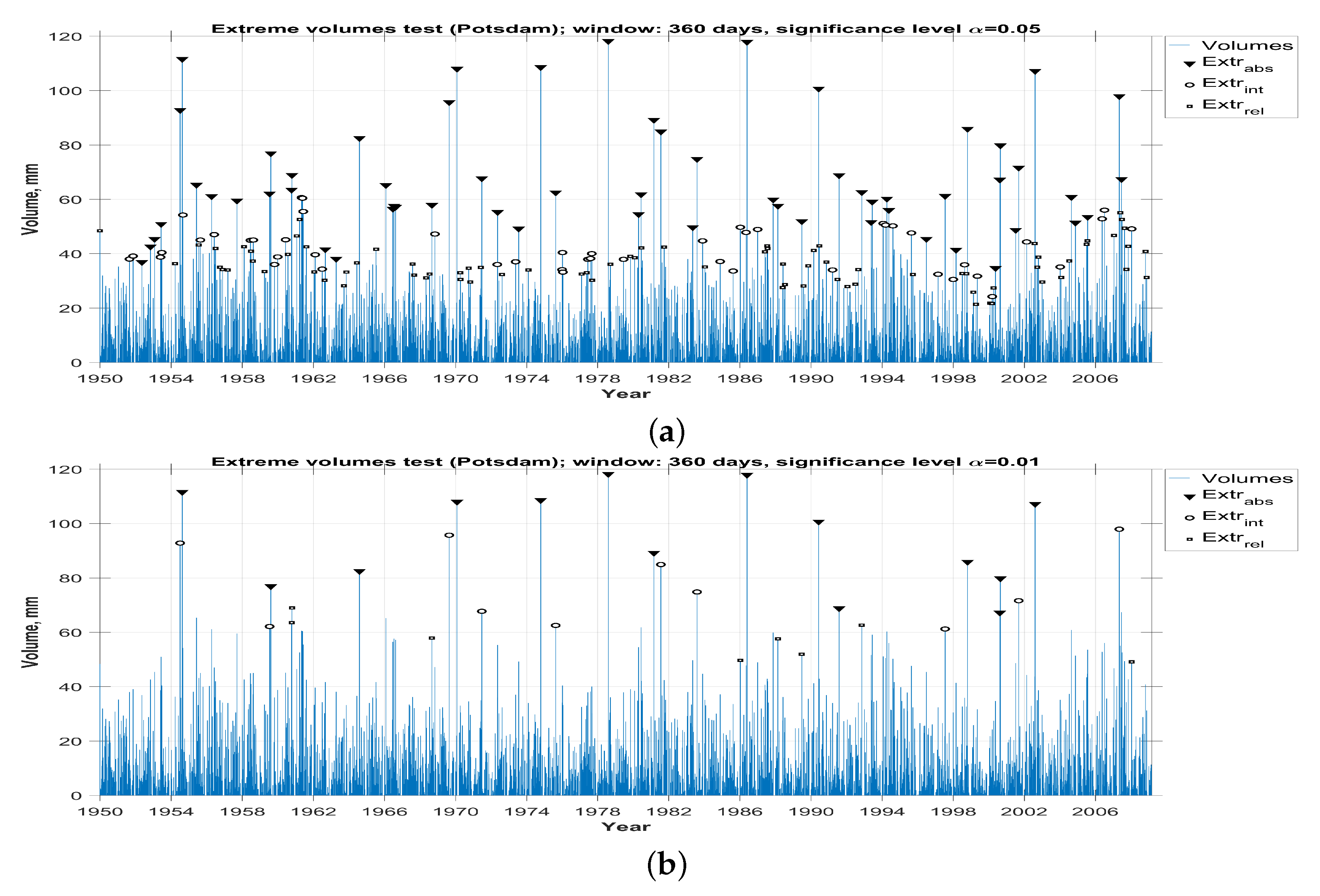
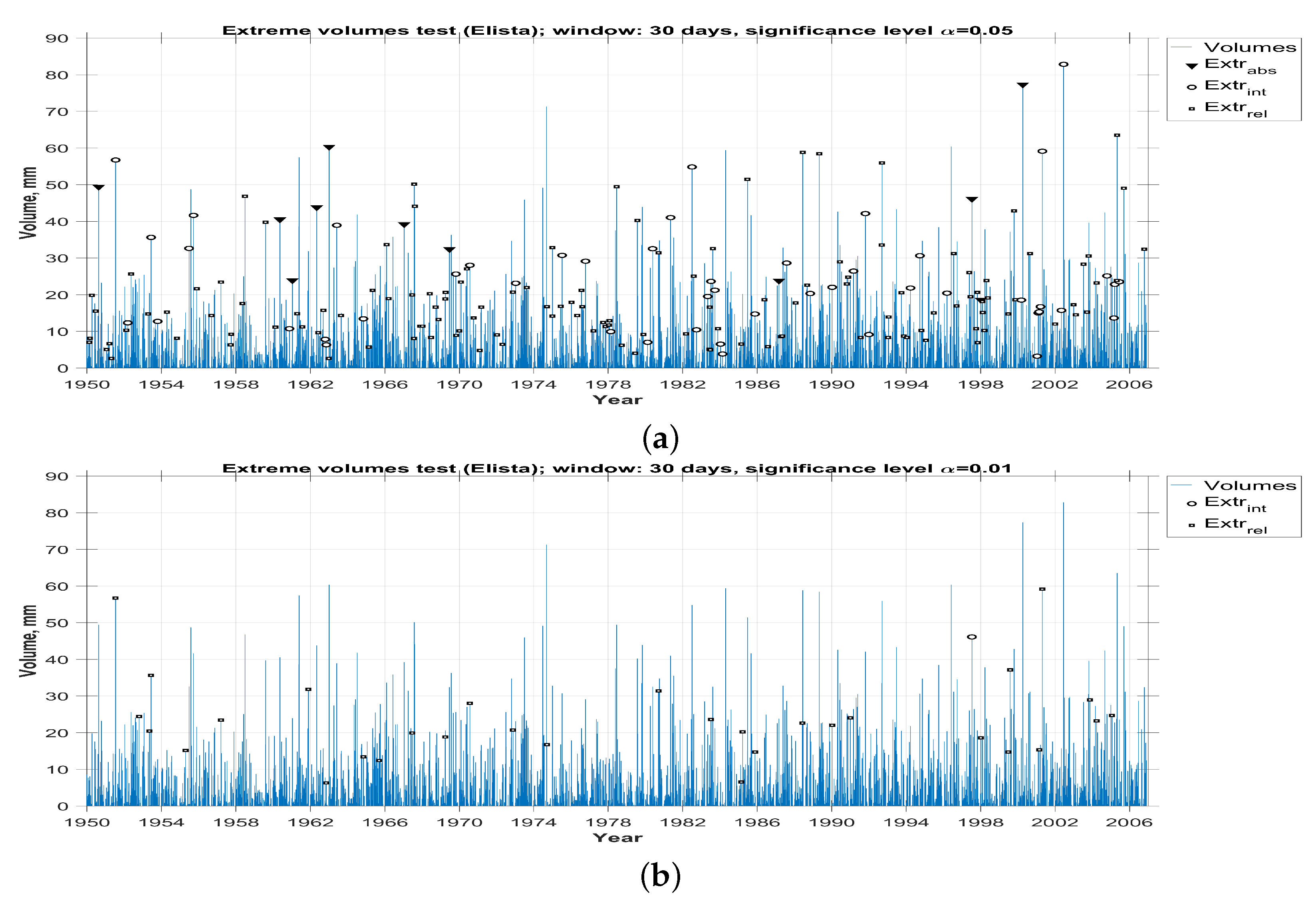
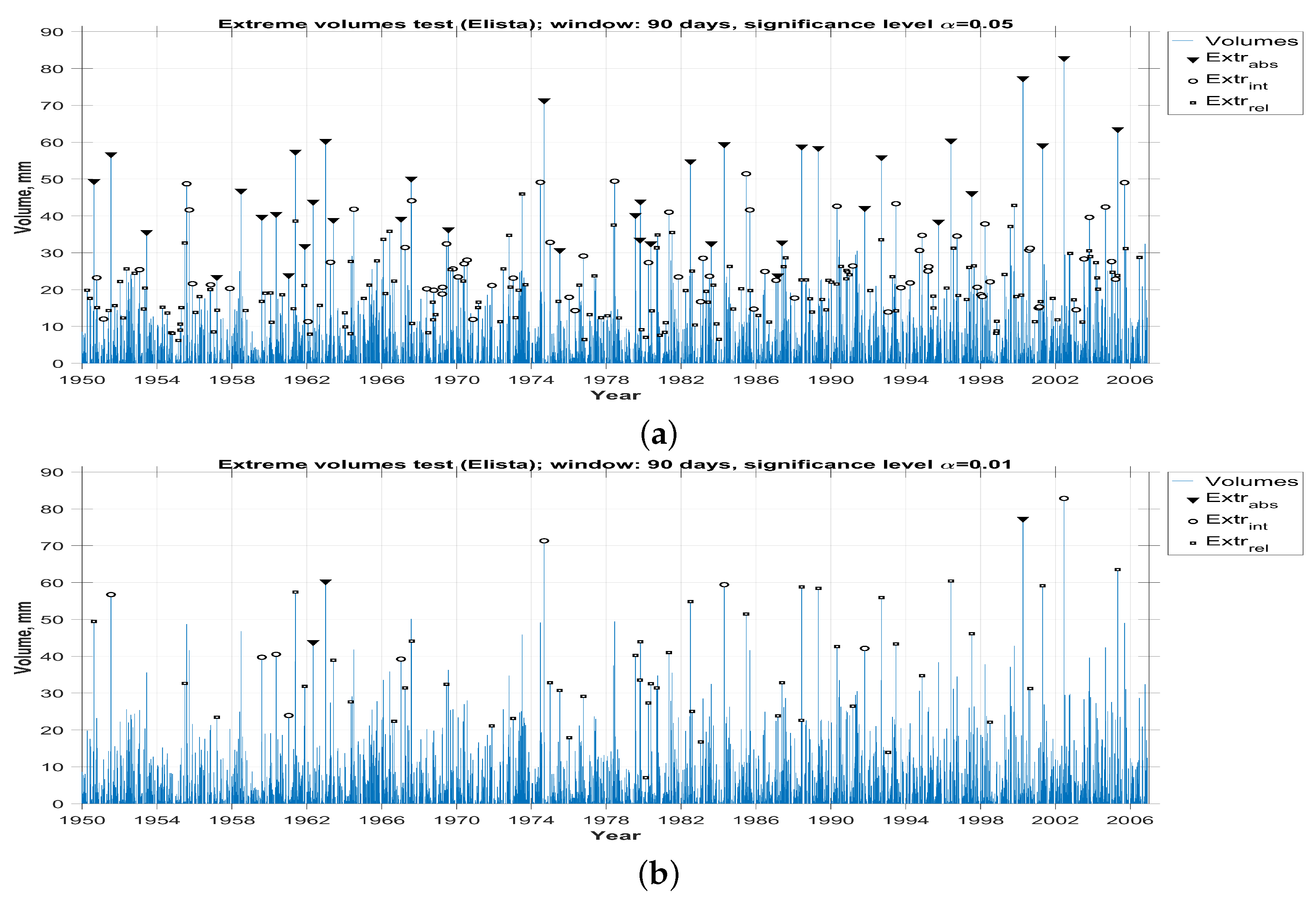
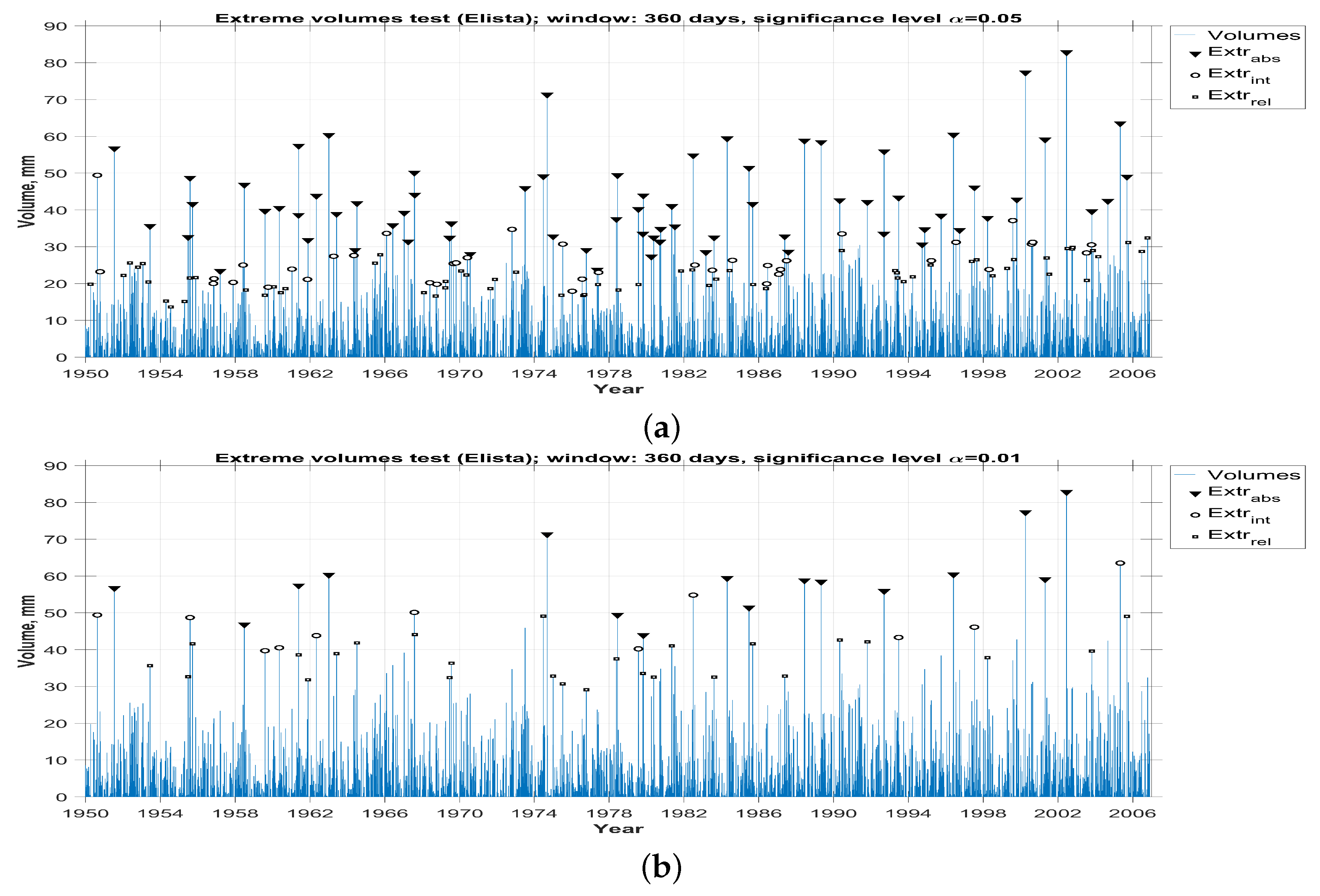
3. The Results of the Analysis of Real Data
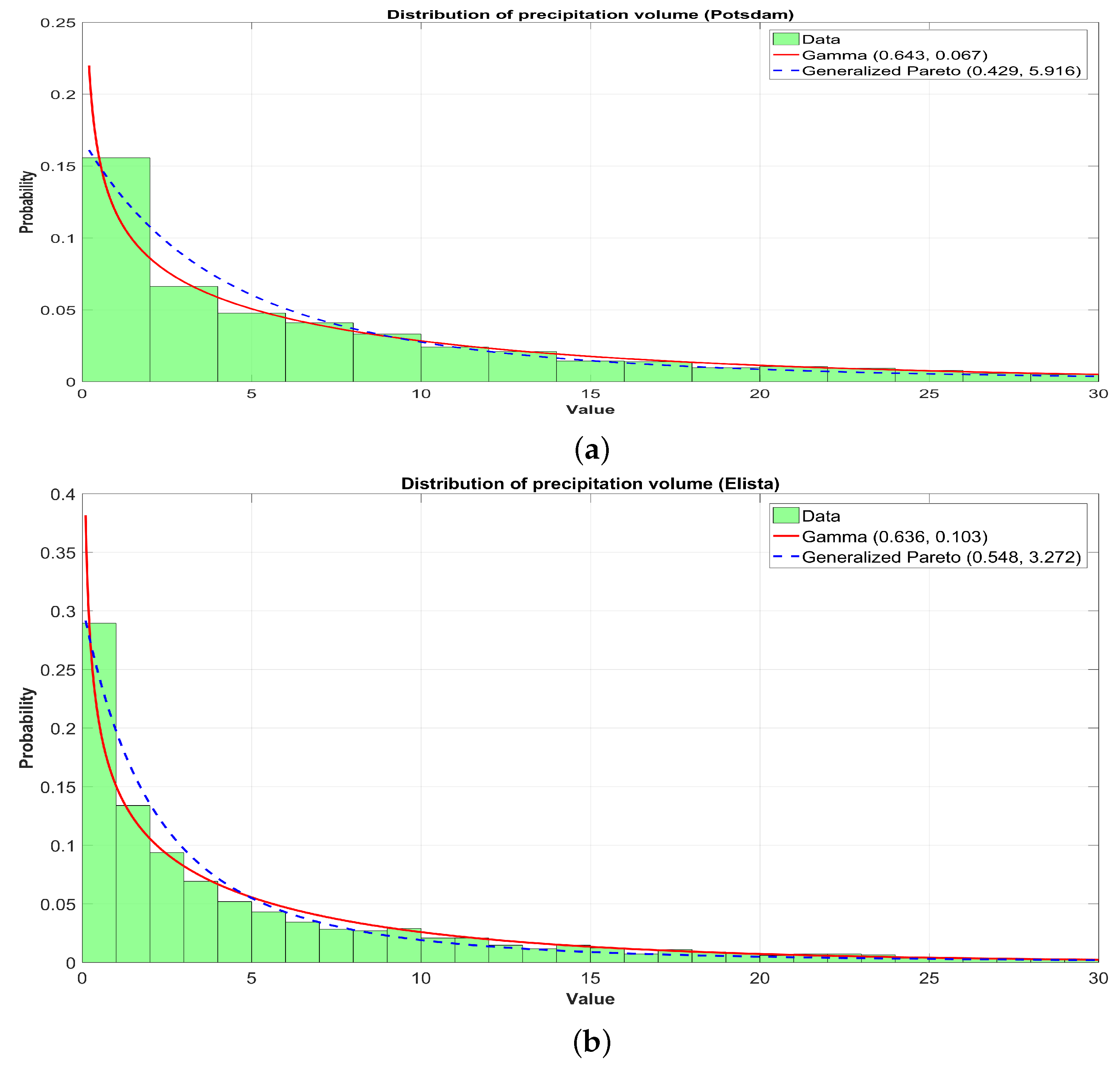
3.1. Statistical Fitting of the Tempered Snedecor-Fisher Distribution Model to Real Data
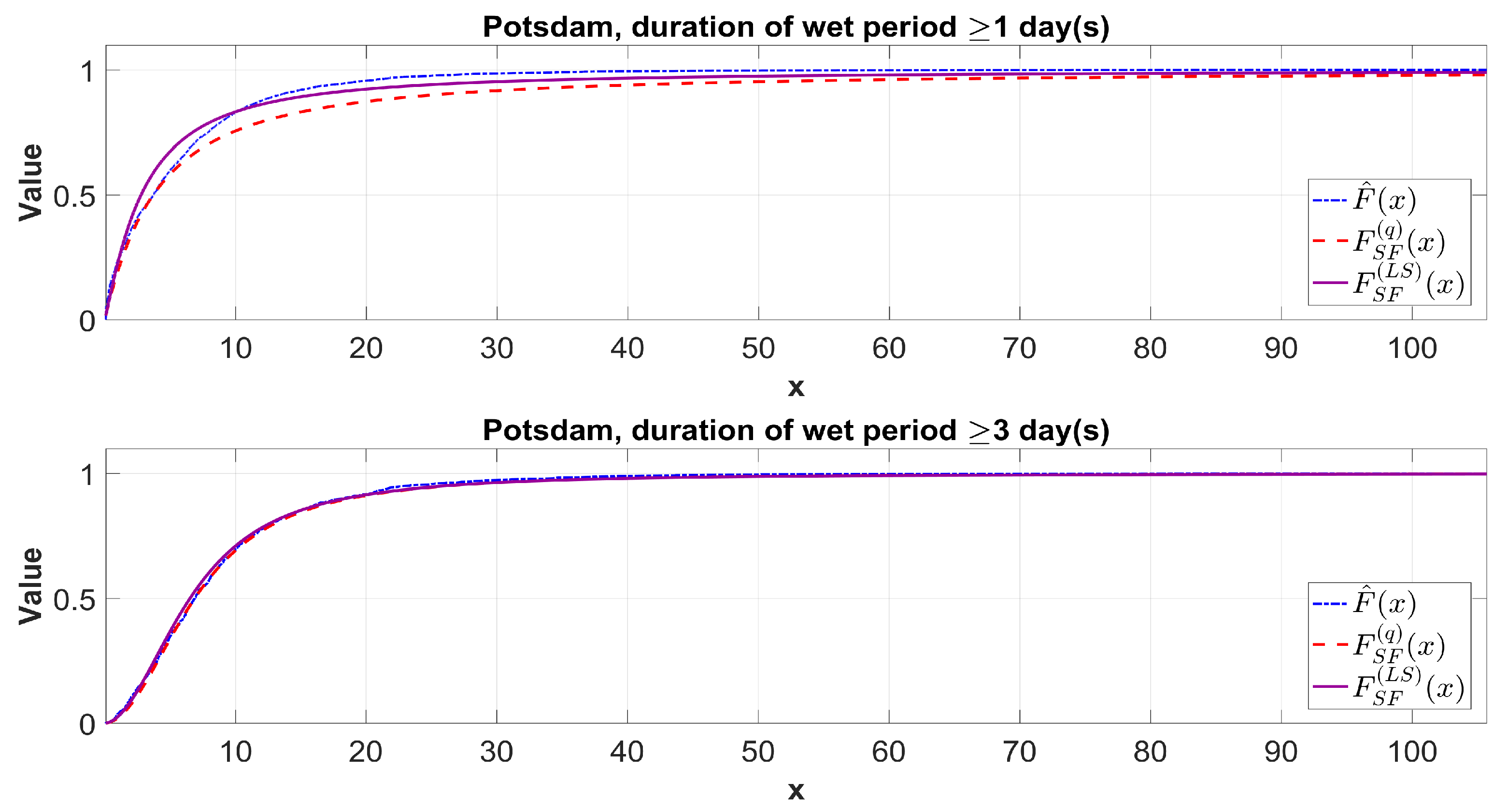
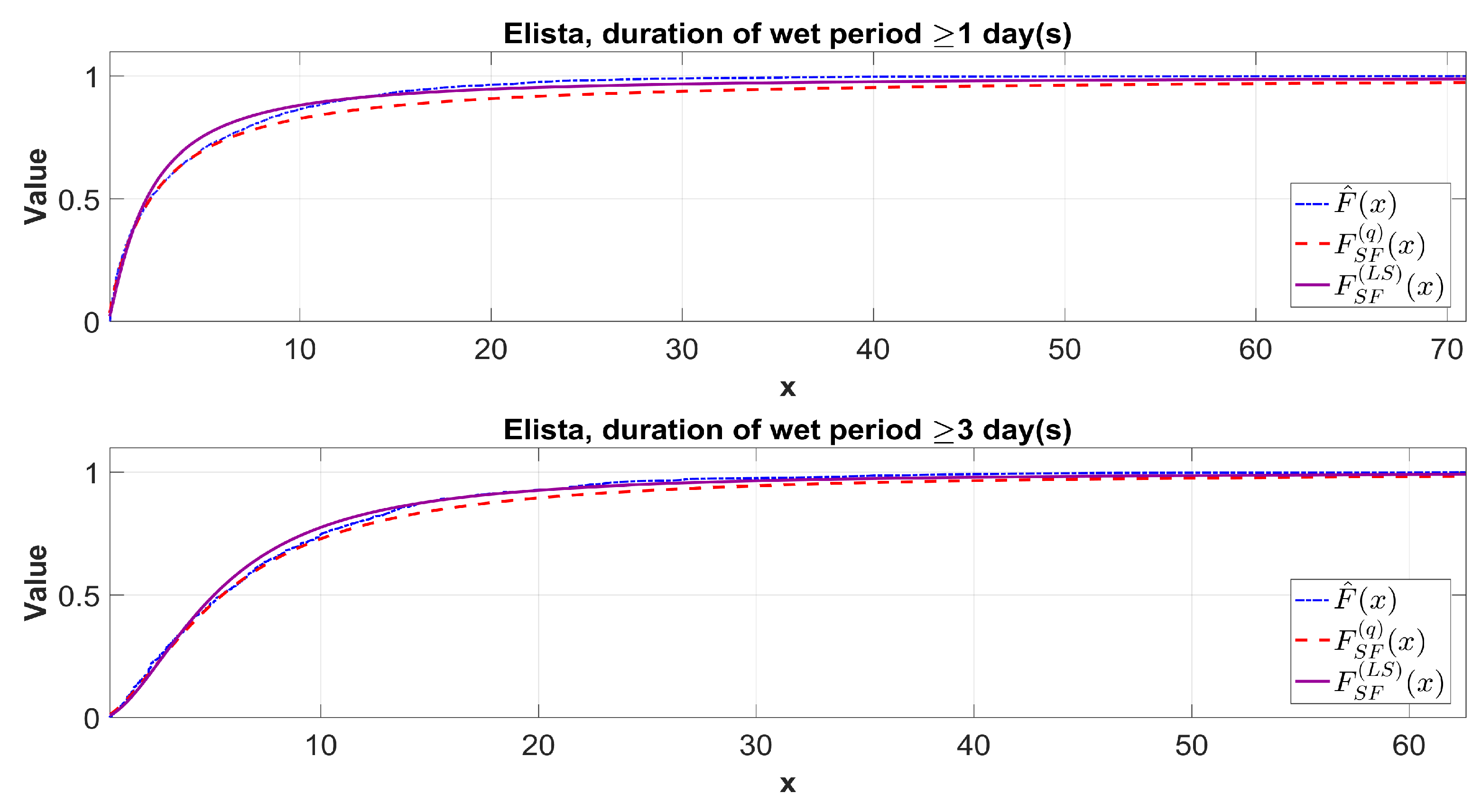
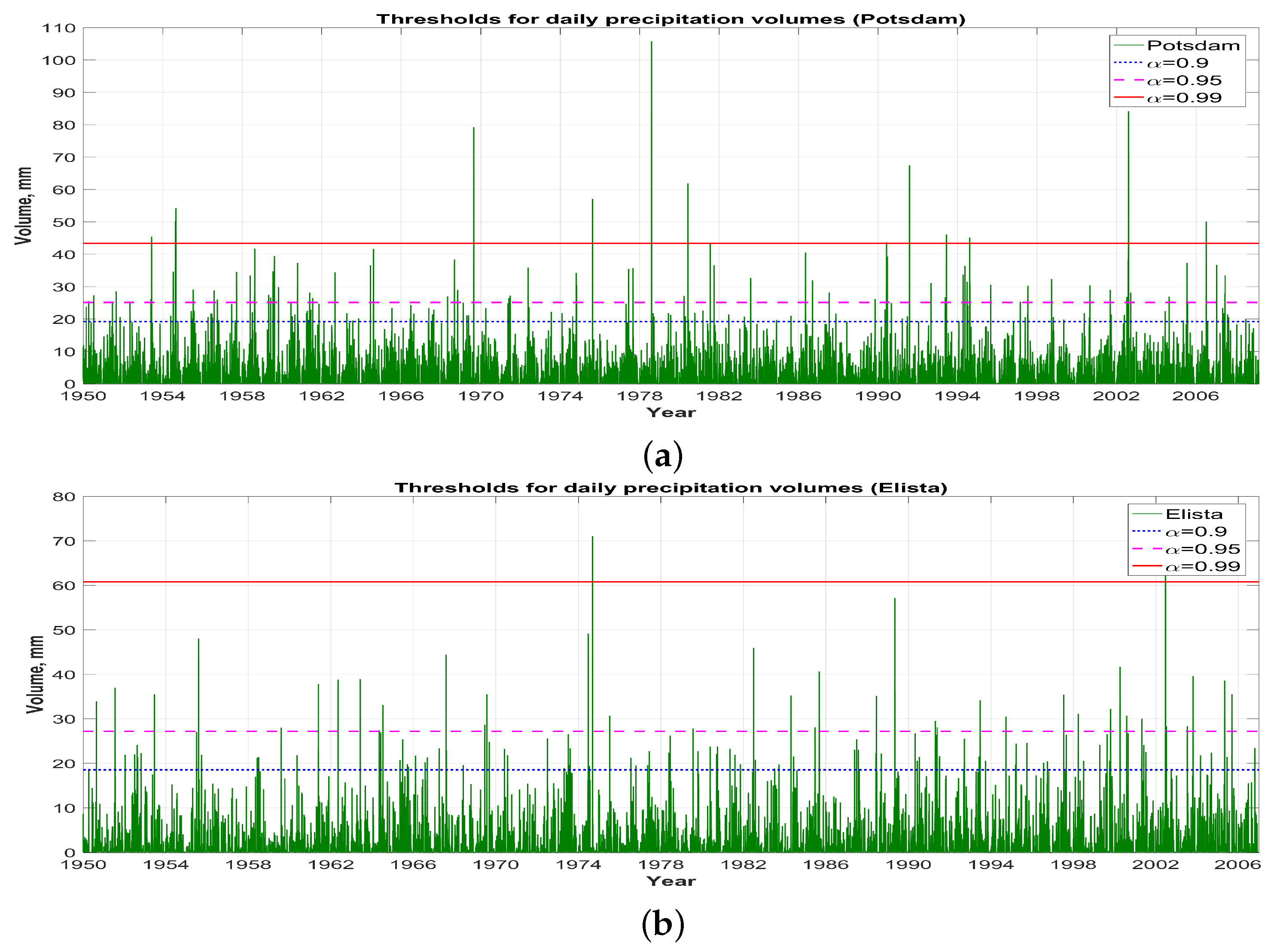
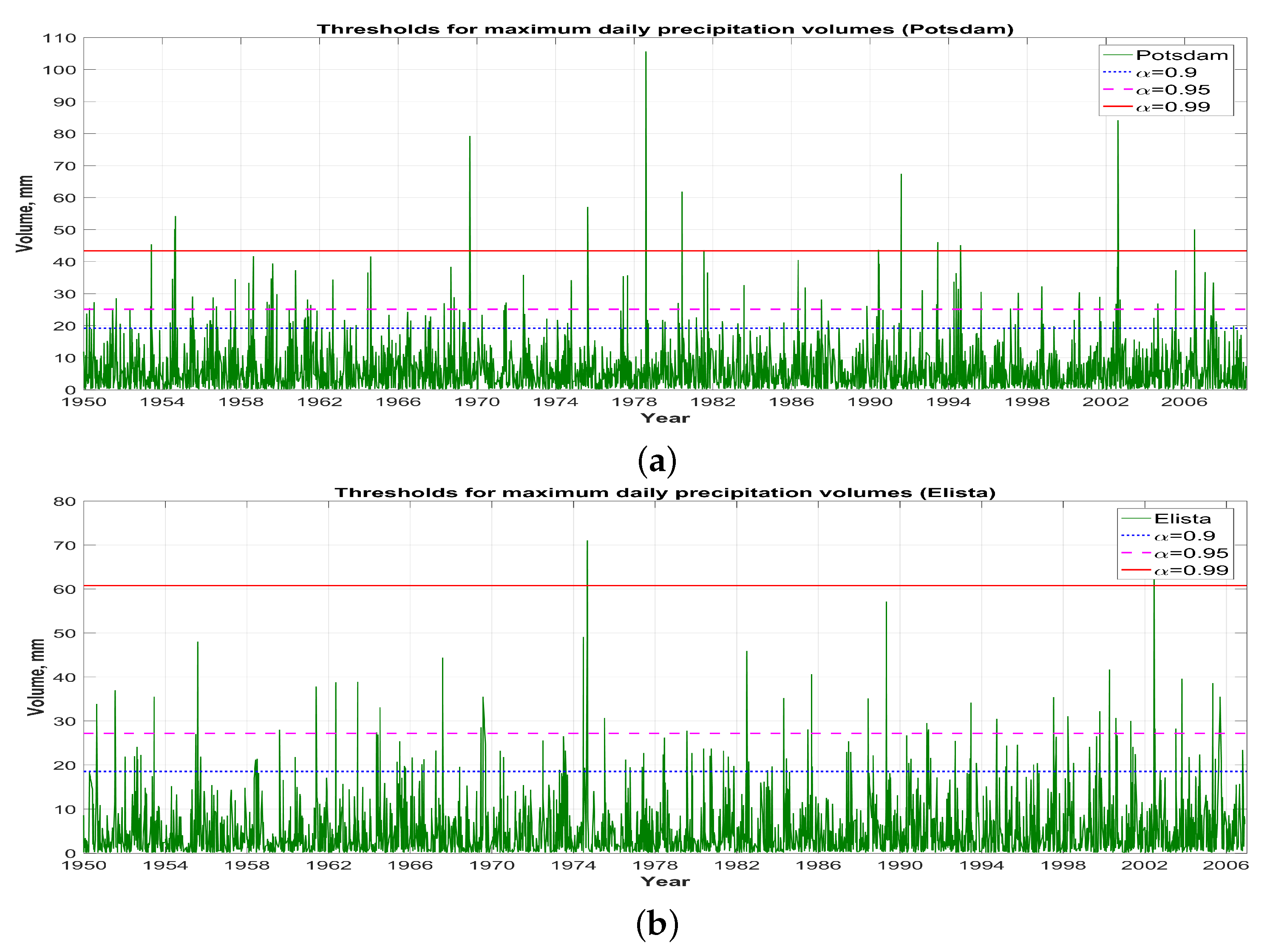
3.2. Determining an Extreme Daily Precipitation Volume Based on Quantiles of the Tempered Snedecor-Fisher Distribution
3.3. Comparison With the Extreme Precipitation Detected by the Beta-Distributed Tests
3.4. Determination Of Abnormalities Types Based on the Results of the Statistical Analysis
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Groisman, P.; Legates, D. Documenting and detecting long-term precipitation trends: Where we are and what should be done. Clim. Chang. 1995, 31, 601–622. [Google Scholar] [CrossRef]
- Groisman, P.; Karl, T.; Easterling, D.; Knight, R.; Jamason, P.; Hennessy, K.; Suppiah, R.; Page, C.; Wibig, J.; Fortuniak, K.; et al. Changes in the probability of heavy precipitation: Important indicators of climatic change. Clim. Chang. 1999, 42, 243–283. [Google Scholar] [CrossRef]
- Lockhoff, M.; Zolina, O.; Simmer, C.; Schulz, J. Evaluation of Satellite-Retrieved Extreme Precipitation over Europe using Gauge Observations. J. Clim. 2014, 27, 607–623. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Belyaev, K.; Kapala, A.; Gulev, S.; Koltermann, P. Multidecadal trends in the duration of wet spells and associated intensity of precipitation as revealed by a very dense observational German network. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Belyaev, K.; Kapala, A.; Gulev, S.; Koltermann, P. Changes in the duration of European wet and dry spells during the last 60 years. J. Clim. 2013, 26, 2022–2047. [Google Scholar] [CrossRef]
- Mo, C.; Ruan, Y.; He, J.; Jin, J.; Liu, P.; Sun, G. Frequency analysis of precipitation extremes under climate change. Int. J. Climatol. 2019, 39, 1373–1387. [Google Scholar] [CrossRef]
- Donat, M.; Angelil, O.; Ukkola, A. Intensification of precipitation extremes in the world’s humid and water-limited regions. Environ. Res. Lett. 2019, 14. [Google Scholar] [CrossRef]
- Bezak, N.; Auflic, M.J.; Mikos, M. Application of hydrological modelling for temporal prediction of rainfall-induced shallow landslides. Landslides 2019, 16, 1273–1283. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; van Asch, T.; Wang, C.; Li, Q. Study on the combined threshold for gully-type debris flow early warning. Nat. Hazards Earth Syst. Sci. 2019, 19, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Bliznak, V.; Kaspar, M.; Muller, M.; Zacharov, P. Sub-daily temporal reconstruction of extreme precipitation events using NWP model simulations. Atmos. Res. 2019, 224, 65–80. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Belyaev, K.; Kapala, A.; Gulev, S. Improving estimates of heavy and extreme precipitation using daily records from European rain gauges. J. Hydrometeorol. 2009, 10, 701–716. [Google Scholar] [CrossRef]
- Balkema, A.; de Haan, L. Residual life time at great age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Pickands, J. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar] [CrossRef]
- Begueria, S.; Vicente-Serrano, S. Mapping the hazard of extreme rainfall by peaks over threshold extreme value analysis and spatial regression techniques. J. Appl. Meteorol. Climatol. 2006, 45, 108–124. [Google Scholar] [CrossRef]
- Kyselỳ, J.; Picek, J.; Beranova, R. Estimating extremes in climate change simulations using the peaks-over-threshold method with a non-stationary threshold. Glob. Planet. Chang. 2010, 72, 55–68. [Google Scholar] [CrossRef]
- Begueria, S.; Angulo-Martinez, M.; Vicente-Serrano, S.; Lopez-Moreno, I.; El-Kenawy, A. Assessing trends in extreme precipitation events intensity and magnitude using non-stationary peaks-over-threshold analysis: A case study in northeast Spain from 1930 to 2006. Int. J. Climatol. 2011, 31, 2102–2114. [Google Scholar] [CrossRef]
- Gorshenin, A.; Korolev, V. Determining the extremes of precipitation volumes based on a modified “Peaks over Threshold”. Inform. Primenen. 2018, 12, 16–24. [Google Scholar] [CrossRef]
- Huang, W.; Nychka, D.; Zhang, H. Estimating precipitation extremes using the log-histospline. Environmetrics 2019, 30. [Google Scholar] [CrossRef]
- Gorshenin, A. Pattern-based analysis of probabilistic and statistical characteristics of precipitations. Inform. Primenen. 2017, 11, 38–46. [Google Scholar] [CrossRef]
- Gorshenin, A. On some mathematical and programming methods for construction of structural models of information flows. Inform. Primenen. 2017, 11, 58–68. [Google Scholar] [CrossRef]
- Korolev, V.; Gorshenin, A.; Gulev, S.; Belyaev, K.; Grusho, A. Statistical Analysis of Precipitation Events. AIP Conf. Proc. 2017, 1863. [Google Scholar] [CrossRef]
- Vasilieva, M.; Gorshenin, A.; Korolev, V. Statistical analysis of probability characteristics of precipitation in different geographical regions. Adv. Intell. Syst. Comput. 2020, 902, 629–639. [Google Scholar] [CrossRef]
- Zolotarev, V. One-Dimensional Stable Distributions; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Kotz, S.; Ostrovskii, I. A mixture representation of the Linnik distribution. Stat. Probab. Lett. 1996, 26, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Korolev, V.; Gorshenin, A. The probability distribution of extreme precipitation. Dokl. Earth Sci. 2017, 477, 1461–1466. [Google Scholar] [CrossRef]
- Gorshenin, A.; Korolev, V. Scale mixtures of Frechet distributions as asymptotic approximations of extreme precipitation. J. Math. Sci. 2018, 234, 886–903. [Google Scholar] [CrossRef]
- Korolev, V. Convergence of random sequences with independent random indexes. I. Theory Probab. Appl. 1994, 39, 313–333. [Google Scholar] [CrossRef]
- Korolev, V. Convergence of random sequences with independent random indexes. II. Theory Probab. Appl. 1995, 40, 770–772. [Google Scholar] [CrossRef]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Embrechts, P.; Klüppelberg, K.; Mikosch, T. Modeling Extremal Events; Springer: Berlin, Germany, 1998. [Google Scholar]
| Minimum Duration | Sample Size | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 3323 | ||||||
| 2 | 2066 | ||||||
| 3 | 1282 | ||||||
| 4 | 862 | ||||||
| 6 | 384 | ||||||
| 8 | 163 | ||||||
| 10 | 73 | ||||||
| 15 | 12 |
| Minimum Duration | Sample Size | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2937 | ||||||
| 2 | 1374 | ||||||
| 3 | 656 | ||||||
| 4 | 319 | ||||||
| 6 | 77 | ||||||
| 7 | 42 | ||||||
| 8 | 22 | ||||||
| 10 | 10 |
| City | Volume | Ratio | Decision | ||
|---|---|---|---|---|---|
| Potsdam | Yes/Yes | ||||
| 16 | Yes/No | ||||
| Elista | Yes/Yes | ||||
| No/No |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korolev, V.; Gorshenin, A.; Belyaev, K. Statistical Tests for Extreme Precipitation Volumes. Mathematics 2019, 7, 648. https://doi.org/10.3390/math7070648
Korolev V, Gorshenin A, Belyaev K. Statistical Tests for Extreme Precipitation Volumes. Mathematics. 2019; 7(7):648. https://doi.org/10.3390/math7070648
Chicago/Turabian StyleKorolev, Victor, Andrey Gorshenin, and Konstatin Belyaev. 2019. "Statistical Tests for Extreme Precipitation Volumes" Mathematics 7, no. 7: 648. https://doi.org/10.3390/math7070648







