1. Introduction and Preliminary Results
Graph theory has provided chemists with a variety of useful tools, such as topological indices. Molecules and molecular compounds are often modeled by molecular graph. A molecular graph is a representation of the structural formula of a chemical compound in terms of graph theory, whose vertices correspond to the atoms of the compound and edges correspond to chemical bonds. Cheminformatics is new subject which is a combination of chemistry, mathematics, and information science. It studies quantitative structure–activity (QSAR) and structure–property (QSPR) relationships that are used to predict the biological activities and properties of chemical compounds. Biological indicators such as the Randi Index, Zagreb Index, Wiener Index, and Balaban index are used to predict and study the physical and chemical properties of chemical structures. The topological index is a numeric quantity associated with chemical constitutions purporting the correlation of chemical structures with many physicochemical properties, chemical reactivity or biological activity. Topological indices are made on the grounds of the transformation of a chemical network into a number that characterizes the topology of the chemical network. Some of the major types of topological indices of graphs are distance-based topological indices, degree-based topological indices, and counting-related topological indices.
Recently, many researchers have found topological indices vital for the study of structural properties of molecular graph or network or chemical tree. An acyclic connected graph is called a tree graph. The degree 3 or greater of every vertex of a tree is called the branching point of the tree. A chemical tree is a connected acyclic graph having maximum degree 4. The first and second Zagreb index of star-like trees and sun-like graphs and also caterpillar trees containing the hydrocarbons, especially ethane, propane, and butane, was studied and computed in Reference [
1]. Imran et al. [
2] also computed the topological indices of fractal and cayley tree type dendrimers.
For any graph, where V is be the vertex set and E to be the edge set of . The degree of vertex x is the amount of edges of episode with x. A graph can be spoken by a polynomial, a numerical esteem or by network shape.
In the present paper, we consider the topological indices of hex-derived networks which are derived from a hexagonal graph that include molecular graphs of unbranched benzenoid hydrocarbons [
3]. Graphs of hexagonal systems consist of mutually fused hexagons. Since this class of chemical compounds is attracting the great attention of theoretical chemists, the theory of the topological index of the respective molecular graphs have been intensively developed in the last 4 decades. Benzenoid hydrocarbons are important raw materials of the chemical industry (used, for instance, for the production of dyes and plastics) but are also dangerous pollutants [
3,
4,
5]. A hexagonal mesh was derived by Chen et al. [
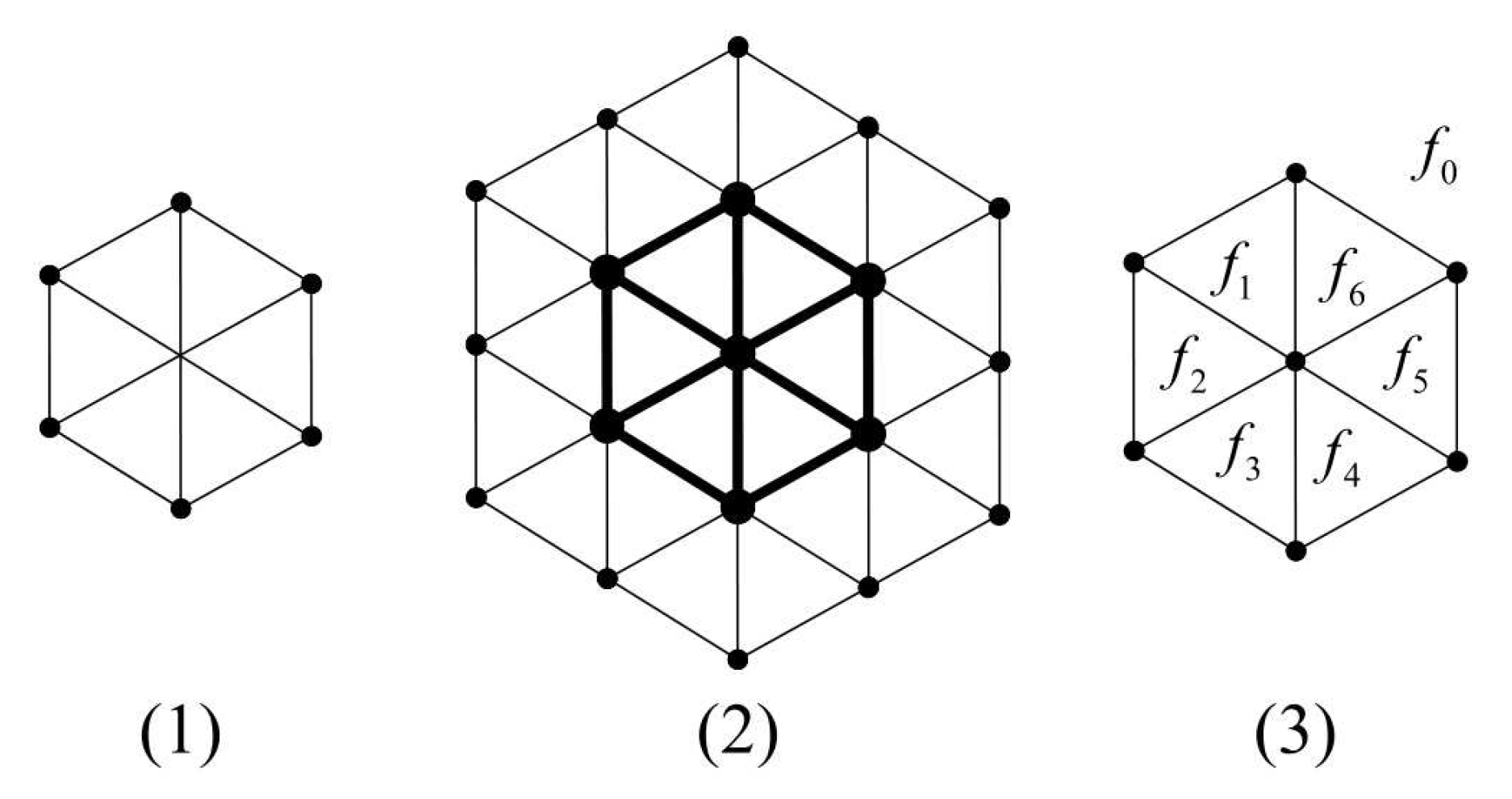
6]. A set of triangles made a
hexagonal mesh, as shown in
Figure 1. No hexagonal mesh with dimension 1 exists. A composition of six triangles made a 2-dimensional hexagonal mesh
(see
Figure 1 (1)). By adding a new layer of triangles around the boundary of
, we have a 3-dimensional hexagonal mesh
(see
Figure 1 (2)). Similarly, we formed
by adding
n layers around the boundary of each proceeding hexagonal mesh.
Drawing algorithm of networks
- Step-1:
First, we draw a hexagonal network of dimension r.
- Step-2:
Replace all
subgraphs into a planar octahedron
once. The resulting graph is called an
(see
Figure 2) network.
- Step-3:
From the
network, we can easily form
(see
Figure 3),
(see
Figure 4), and
(see
Figure 5).
In this article, we consider as a network, with as the set of vertices and edge set ; the degree of any vertex is denoted by .
The Estrada index is a graph–spectrum-based topological index, which is defined as [
7]:
In full analogy with the Estrada index, Fath-Tabar et al. [
8] proposed the Laplacian Estrada index, which is defined as:
The
Randić index [
9] was denoted by
and acquainted by Milan Randić and written as:
The general Randić index
is the sum of
over all edges
, defined as:
Gutman and Trinajstić were acquainted with a substantial topological index, which is the
Zagreb index denoted by
and formalised as:
The augmented Zagreb index was presented by Furtula et al. [
10], and it is defined as:
The harmonic index was presented by Zhong [
11], and it is defined as:
The
Atom-bond connectivity index is one of the famous degree-based topological indices denoted by Estrada et al. in Reference [
12] and formalised as:
The
Geometric-arithmetic index is another famous connectivity topological descriptor, which was introduced by Vukičević et al. in Reference [
13] and written as:
By taking , the general Randić index is the second Zagreb index for any graph .
2. Main Results for Third Type of Hex-Derived Networks
Simonraj et al. [
14] derived a new third type of hex-derived networks and found the metric dimension of
and
. In this work, we discuss the newly derived third type of hex-derived networks and compute the exact results for degree-based topological indices. At present, there is an extensive research activity on these topological indices and their variants, see [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26]. For basic definitions and notations, see [
27,
28,
29,
30,
31].
2.1. Results for Third Type of Hex-Derived Network
In this section, we discuss the newly derived third type of hex-derived network and compute the exact results for Randi, Zagreb, Harmonic, augmented Zagreb, atom–bond connectivity and geometric–arithmetic indices for the very first time.
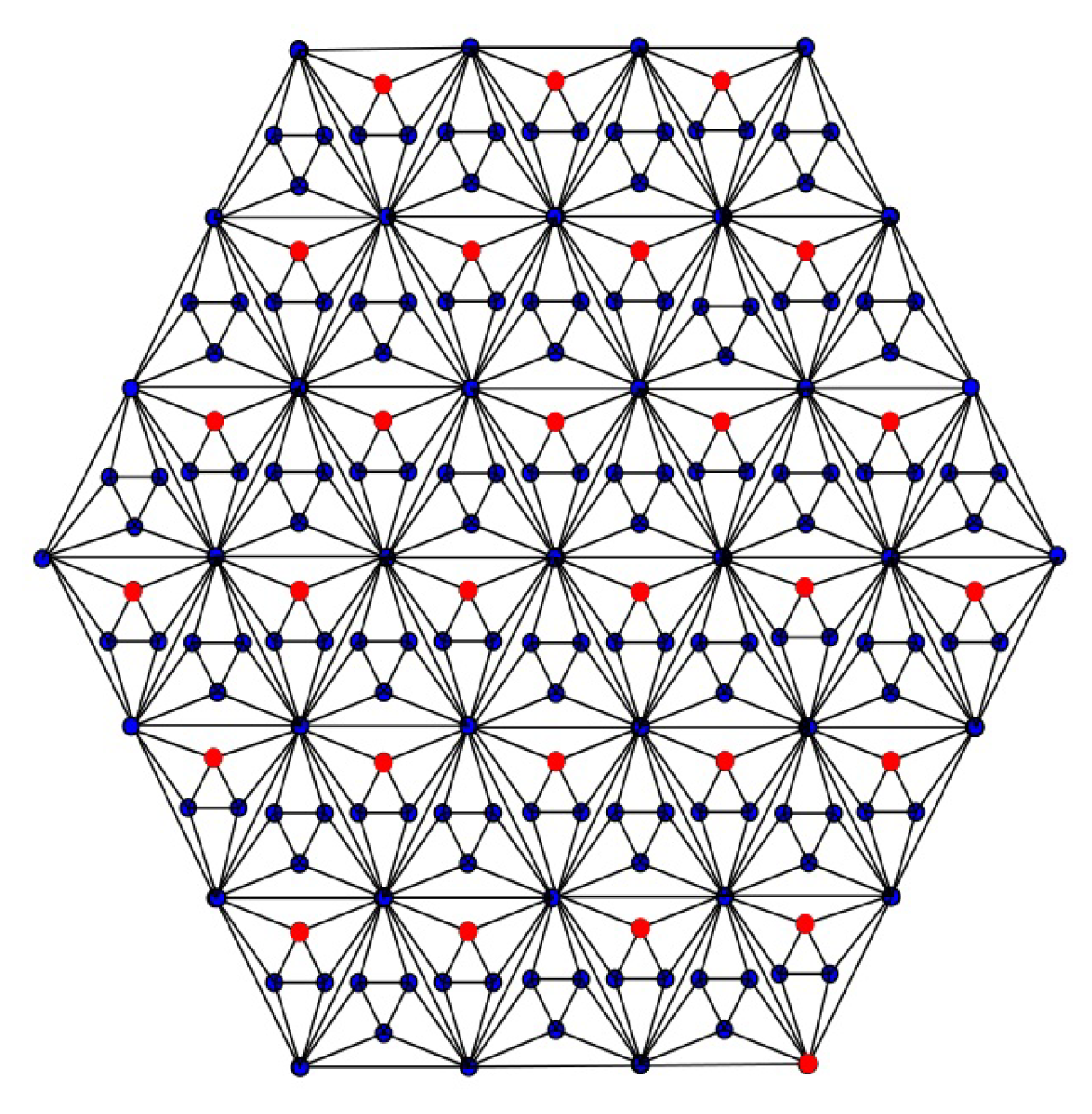
Theorem 1. Consider the hex-derived network of type 3 , the general Randić index is equal to: Proof. Let
be the hex-derived network of type 3,
shown in
Figure 2, where
. The hex-derived network
has
vertices, and the edge set of
is divided into nine partitions based on the degree of end vertices. The first edge partition
contains
edges
, where
. The second edge partition
contains 24 edges
, where
and
. The third edge partition
contains
edges
, where
and
. The fourth edge partition
contains
edges
, where
and
. The fifth edge partition
contains 12 edges
, where
and
. The sixth edge partition
contains 6 edges
, where
and
. The seventh edge partition
contains
edges
, where
, the eighth edge partition
contains
edges
, where
and
, and the ninth edge partition
contains
edges
, where
.
Table 1 shows such an edge partition of
. Thus, from Equation (3), it follows that:
For The general Randi
index
can be computed as follows:
Using the edge partition given in
Table 1, we get:
For We apply the formula of
:
Using the edge partition given in
Table 1, we get:
For We apply the formula of
:
For We apply the formula of
:
□
In the following theorem, we compute the first Zagreb index of hex-derived network .
Theorem 2. For hex-derived network , the first Zagreb index is equal to: Proof. Let
be the hex-derived network
. Using the edge partition from
Table 1, the result follows. The Zagreb index can be calculated using Equation (
5) as follows:
By doing some calculations, we get:
□
Now, we compute H, , , and indices of the third type of hex-derived network .
Theorem 3. Let be the third type of hex-derived network, then:
= ;
= ;
= ;
= .
Proof. Using the edge partition given in
Table 1, The Harmonic index can be calculated using Equation (7) as follows:
By doing some calculations, we get:
The augmented Zagreb index can be calculated from Equation (
6) as follows:
By doing some calculations, we get:
The atom–bond conectivity index can be calculated from Equation (
8) as follows:
By doing some calculations, we get:
The geometric–arithmetic index can be calculated from Equation (9) as follows:
By doing some calculations, we get:
□
2.2. Results for Third Type of Triangular Hex-Derived Network
In this section, we calculate certain degree-based topological indices of a triangular hex-derived network of type 3, of dimension r. We compute general Randić index with , , H, , and indices in the coming theorems of .
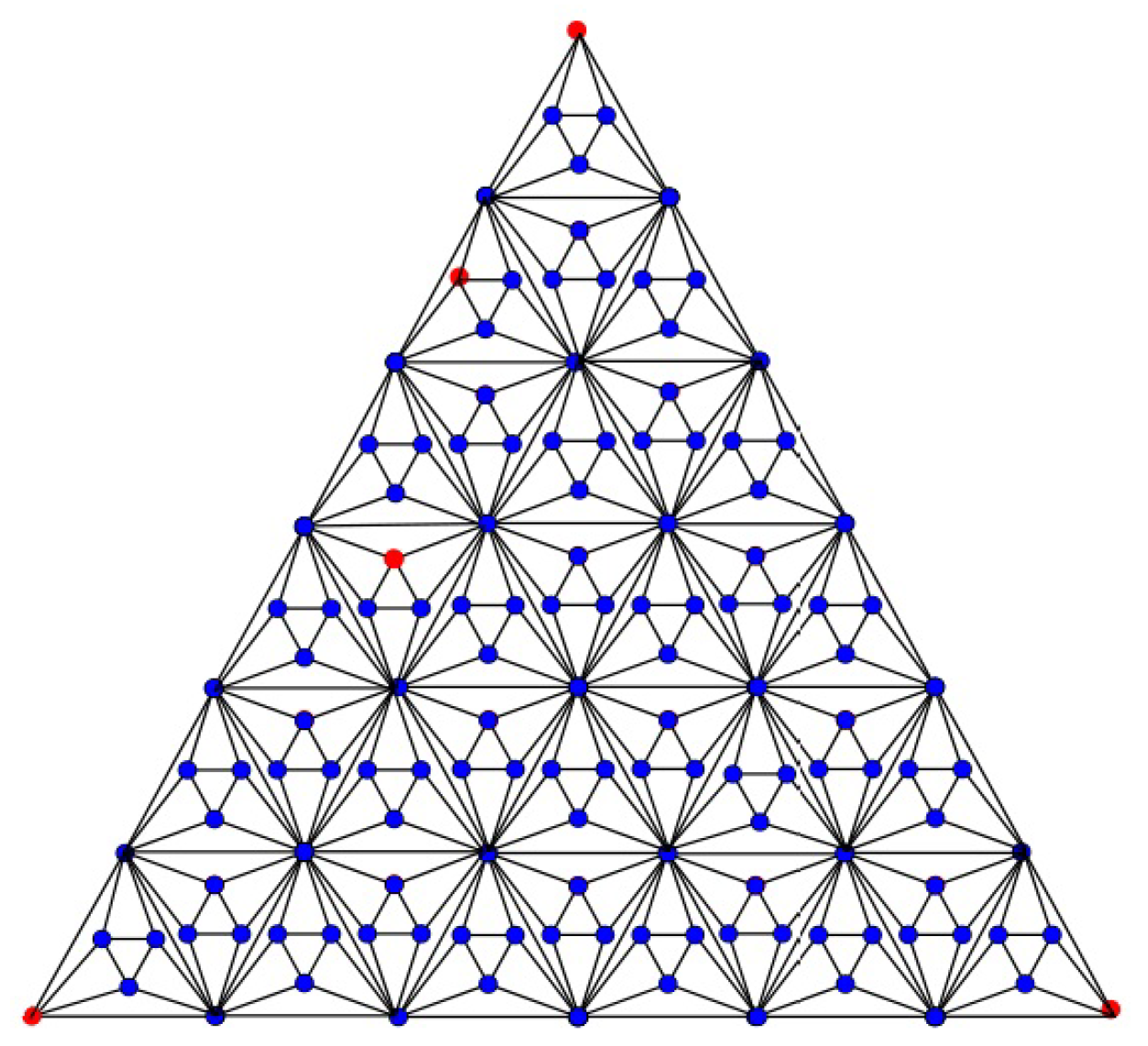
Theorem 4. Consider the triangular hex-derived network of type 3, , the general Randić index is equal to: Proof. Let
be the third type of a triangular hex-derived network of type 3,
shown in
Figure 3, where
. The triangular hex-derived network
has
vertices and the edge set of
is divided into six partitions based on the degree of end vertices. The first edge partition
contains
edges
, where
. The second edge partition
contains
edges
, where
and
. The third edge partition
contains
edges
, where
and
. The fourth edge partition
contains
edges
, where
. The fifth edge partition
contains
edges
, where
and
, and the sixth edge partition
contains
edges
, where
.
Table 2 shows such an edge partition of
. Thus, from Equation
, it follows that:
For The general Randi
index
can be computed as follows:
Using the edge partition given in
Table 2, we get:
For We apply the formula of
:
Using the edge partition given in
Table 2, we get:
For We apply the formula of
:
For We apply the formula of
:
□
In the following theorem, we compute the first Zagreb index of the third type of triangular hex-derived network .
Theorem 5. For the third type of triangular hex-derived network , the first Zagreb index is equal to: Proof. Let
be the triangular hex-derived network
. Using the edge partition from
Table 2, the result follows. The first Zagreb index can be calculated using Equation (
5) as follows:
By doing some calculations, we get:
□
Now, we compute the H, , , and indices of the third type of triangular hex-derived network .
Theorem 6. Let be the third type of a triangular hex-derived network, then:
=;
= ;
= ;
= .
Proof. Using the edge partition given in
Table 2, The Harmonic index can be calculated using Equation (7) as follows:
By doing some calculations, we get:
The augmented Zagreb index can be calculated from Equation (6) as follows:
By doing some calculations, we get:
The atom–bond connectivity index can be calculated from Equation (8) as follows:
By doing some calculations, we get:
The geometric–arithmetic index can be calculated from Equation (
9) as follows:
By doing some calculations, we get:
□
2.3. Results of the Third Type of Rectangular Hex-Derived Network
In this section, we compute certain degree-based topological indices of the third type of rectangular hex-derived network of dimension . We compute general Randić index with the , , H, , and indices in the coming theorems of .
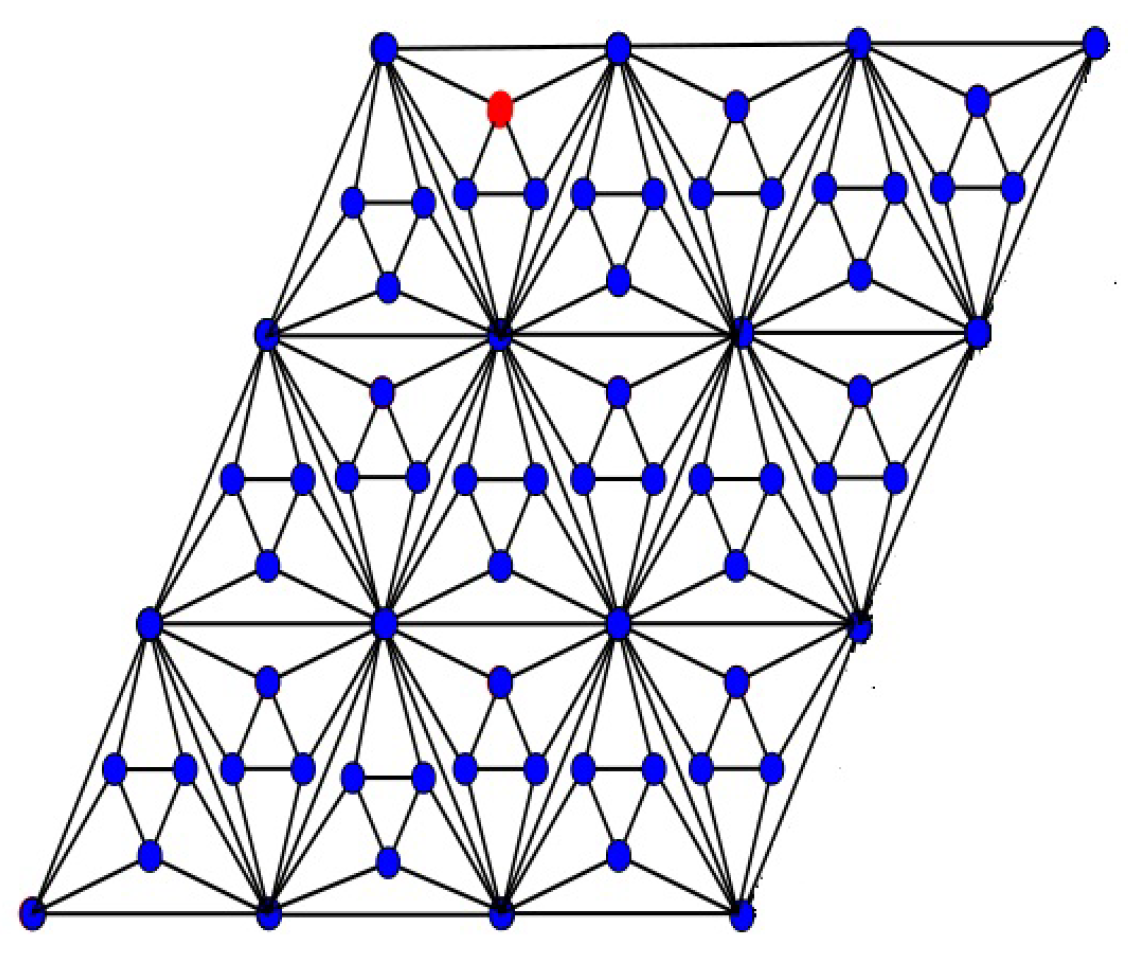
Theorem 7. Consider the rectangular hex-derived network of type 3, , the general Randić index is equal to: Proof. Let
be the rectangular hex-derived network of type 3,
shown in
Figure 4, where
. The rectangular hex-derived network
has
vertices and the edge set of
is divided into nine partitions based on the degree of end vertices. The first edge partition
contains
edges
, where
. The second edge partition
contains 8 edges
, where
and
. The third edge partition
contains
edges
, where
and
. The fourth edge partition
contains
edges
, where
and
. The fifth edge partition
contains 4 edges
, where
and
. The sixth edge partition
contains 2 edges
, where
and
. The seventh edge partition
contains
edges
, where
, the eighth edge partition
contains
edges
, where
and
, and the ninth edge partition
contains
edges
, where
,
Table 3 shows such an edge partition of
. Thus, from Equation (3), it follows that:
For The general Randi
index
can be computed as follows:
Using the edge partition given in
Table 3, we get:
For We apply the formula of
:
Using the edge partition given in
Table 3, we get:
For We apply the formula of
:
For We apply the formula of
:
□
In the following theorem, we compute the first Zagreb index of rectangular hex-derived network .
Theorem 8. For the third type of rectangular hex-derived network , the first Zagreb index is equal to: Proof. Let
be the hex-derived network
. Using the edge partition from
Table 3, the result follows. The Zagreb index can be calculated using Equation (5) as follows:
By doing some calculations, we get:
□
Now, we compute the H, , , and indices of the third type of rectangular hex-derived network .
Theorem 9. Let be the third type of rectangular hex-derived network, then:
= ;
= ;
= ;
= .
Proof. Using the edge partition given in
Table 3, The Harmonic index can be calculated using Equation (7) as follows:
By doing some calculations, we get:
The augmented Zagreb index can be calculated from Equation (
6) as follows:
By doing some calculations, we get:
The atom–bond connectivity index can be calculated from Equation (
8) as follows:
By doing some calculations, we get:
The geometric–arithmetic index can be calculated from Equation (
9) as follows:
By doing some calculations, we get:
□
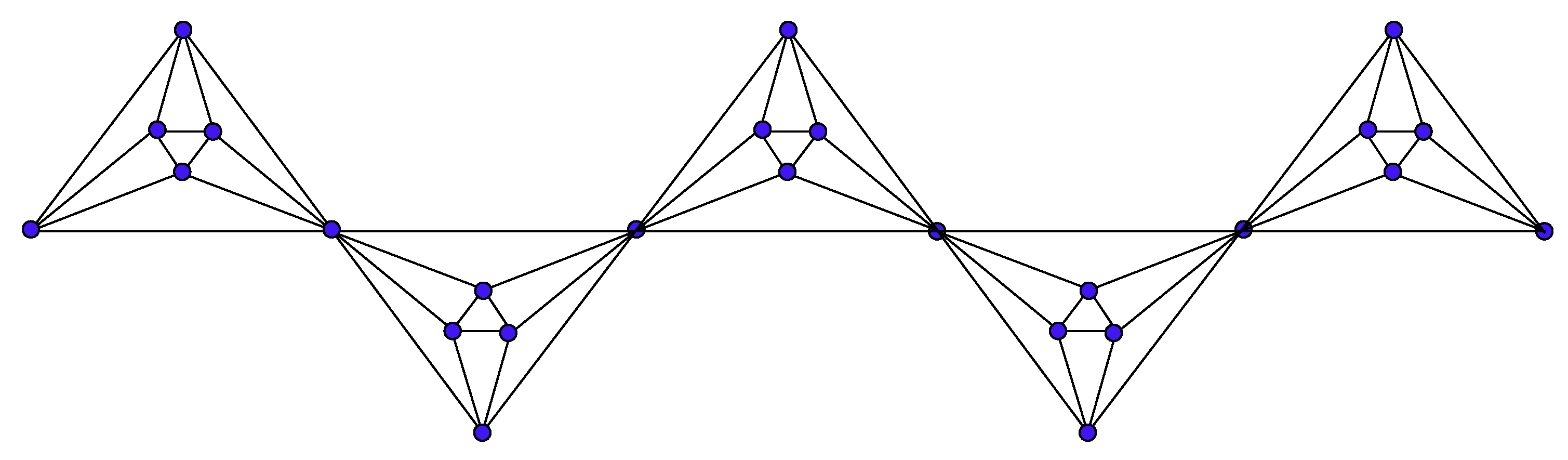
2.4. Results of the Third Type of Chain Hex-Derived Network,
In this section, we compute certain degree-based topological indices of the third type of chain hex-derived network, of dimension r. We compute general Randić index with the , , H, , and indices in the coming theorems of .
Theorem 10. Consider the chain hex-derived network of type 3, , the general Randić index is equal to: Proof. Let
be the chain hex-derived network of type 3,
shown in
Figure 5, where
. The chain hex-derived network
has
vertices, and the edge set of
is divided into three partitions based on the degree of end vertices. The first edge partition
contains
edges
, where
. The second edge partition
contains
edges
, where
and
, and the third edge partition
contains
edges
, where
.
Table 4 shows such an edge partition of
. Thus, from Equation
, it follows that:
For The general Randi
index
can be computed as follows:
Using the edge partition given in
Table 4, we get:
For We apply the formula of
:
Using the edge partition given in
Table 4, we get:
For We apply the formula of
:
For We apply the formula of
:
□
In the following theorem, we compute the first Zagreb index of chain hex-derived network .
Theorem 11. For the third type of chain hex-derived network , the first Zagreb index is equal to: Proof. Let
be the hex-derived network
. Using the edge partition from
Table 4, the result follows. The Zagreb index can be calculated using Equation (5) as follows:
By doing some calculations, we get:
□
Now, we compute the H, , and indices of the third type of chain hex-derived network .
Theorem 12. Let be the third type of rectangular hex-derived network, then:
= ;
= ;
= ;
= .
Proof. Using the edge partition given in
Table 4, the Harmonic index can be calculated using Equation (7) as follows:
By doing some calculations, we get:
The augmented Zagreb index can be calculated from Equation (6) as follows:
By doing some calculations, we get:
The atom–bond connectivity index can be calculated from Equation (8) as follows:
By doing some calculations, we get:
The geometric–arithmetic index can be calculated from Equation (
9) as follows:
By doing some calculations, we get:
□
For the comparison of topological indices numerically for
,
,
, and
, we computed all indices for different values of
r. From
Table 5,
Table 6,
Table 7 and
Table 8, we can easily see that all indices are in increasing order as the values of
r increases.
The Zagreb and augmented Zagreb indices were found to occur for the computation of the total
-electron energy of molecules [
30]. Thus, the total
-electron energy is in increasing order in the case of all networks.