Abstract
Probabilistic evolution theory (PREVTH) forms a framework for the solution of explicit ODEs. The purpose of the paper is two-fold: (1) conversion of multinomial right-hand sides of the ODEs to purely second degree multinomial right-hand sides by space extension; (2) decrease the computational burden of probabilistic evolution theory by using the condensed Kronecker product. A first order ODE set with multinomial right-hand side functions may be converted to a first order ODE set with purely second degree multinomial right-hand side functions at the expense of an increase in the number of equations and unknowns. Obtaining purely second degree multinomial right-hand side functions is important because the solution of such equation set may be approximated by probabilistic evolution theory. A recent article by the authors states that the ODE set with the smallest number of unknowns can be found by searching. This paper gives the details of a way to search for the optimal space extension. As for the second purpose of the paper, the computational burden can be reduced by considering the properties of the Kronecker product of vectors and how the Kronecker product appears within the recursion of PREVTH: as a Cauchy product structure.
MSC:
34A45; 65L05; 68T20
1. Introduction
Probabilistic evolution theory (PREVTH) is for the solution of the initial value problem of explicit ODEs with multinomial right-hand side functions. Probabilistic evolution theory represents the sum as an infinite series. Truncating the series creates an approximation for the solution of the ODE assuming that the series is convergent (there are also ways to improve the convergence).
In this paper, we show how to obtain purely second degree right-hand side functions from any multinomial right-hand side functions by using space extension. The way to perform the space extension is given by branch and bound search with an admissible heuristic. Obtaining purely second degree right-hand side functions is important because PREVTH can solve these kinds of ODEs. Space extension methods have been used widely in the past ten years. Up to now, the utilization of space extension was intuitive: a manual trial and error effort where it is not possible to see if the newly-formed ODE set has the minimum number of equations and therefore unknowns. This paper gives a very concrete algorithm for space extension. The algorithm gives the space extension with the minimum number of equations and therefore unknowns, using branch and bound with an admissible heuristic. The second purpose of the paper is to reduce the computational burden of PREVTH. This is achieved through defining the condensed Kronecker product operation.
Probabilistic evolution theory resembles B-series methods and generalizations of B-series methods [1,2]. Although there is a certain resemblance, probabilistic evolution theory is not a variant of B-series methods. Probabilistic evolution theory is formed from a totally different perspective: it makes use of Kronecker power series. Furthermore, by the use of space extension, it is possible to apply probabilistic evolution theory to a large variety of problems. Certain works such as [3,4] build upon B-series to form a Taylor series expansion of the solution. These works rely on the definition of many binary operators defined on certain manifolds. On the other hand, we are interested in forming a method using linear algebraic tools instead of properties of manifolds. We also believe that improvements such as recursion of squarification have potential applications beyond PREVTH and may also be used from B-series perspective.
Parker–Sochacki methods (PSM) also focus on ODEs with multinomial right- hand side functions [5,6]. Just like PREVTH, PSM is based on Picard iteration, and it also incorporates space extension to put the original ODE into another form. PSM also follows the traditional approach of trial and error to put the ODE set into a more suitable form. Although PSM does not have purely second degree multinomials at its focus, it may benefit from branch and bound for the space extension.
Recursion of squarification and condensation are closely related to combinatorial identities. Works such as [7,8] focused on Catalan numbers, rooted trees, and Dyck paths. A rooted tree may be used to represent a single term of a Taylor expansion [9]. In this sense, there is a relation between enumerative combinatorics and the solution of ODEs with multinomial right-hand side functions.
Here, the focus is optimal space extension. In this paper, we propose a novel algorithm for space extension using branch and bound with an admissible heuristic. The secondary focus is using probabilistic evolution theory with less effort through certain simplifications.
A detailed survey of probabilistic evolution theory is [10]. We will try to avoid any repetition; therefore, we focus on the works that are directly related to this paper. There are several introductory articles on the subject [11,12]. Constancy adding space extension takes second degree multinomial right-hand side functions to purely second degree multinomial right-hand side functions [13]. Squarification is a way to prevent the rapid growth of matrices and vectors in probabilistic evolution theory [14]. PREVTH is successfully applied to certain systems [15,16]. Squarification is facilitated by the recursion of squarification [9,17,18]. It is also possible to obtain single monomial right-hand side functions from multinomial right-hand side functions through space extension [19].
Other works that are not on probabilistic evolution theory, but form a basis for this paper are as follows. Single monomial PREVTH also forms a theoretical background for obtaining second degree right-hand side functions from more general right-hand side functions through space extension [20,21]. Details on branch and bound optimization can be found in artificial intelligence textbooks [22]. Branch and bound methods are popular in many application areas, especially in scheduling [23,24].
Structure of the Paper
The second section shows how to obtain purely second degree right-hand side functions from multinomial right-hand side functions. The third section details probabilistic evolution theory. The third section also gives all the surrounding details of condensed Kronecker product operation and the simplifications arising from the use of this operation. We finalize the paper with the Conclusions section.
2. Optimal Space Extension through Branch and Bound Optimization
The purpose of putting so much effort into obtaining purely-second degree multinomials is because probabilistic evolution theory can work on ordinary differential equation sets with purely second degree multinomial right-hand side functions. The third section is devoted to probabilistic evolution theory.
Consider the initial value problem of the system of explicit first order ordinary differential equations. The purpose is to define new unknowns that are functionally dependent on the original unknowns so that the right-hand side functions become purely second degree multinomials. In space extension, not only the space, but also the equation set is extended. The newly-obtained ordinary differential equation set represents a wider family of equation sets: the original ordinary differential equation set is only a part within this family. Assume that we have a linear vector space spanned by two linearly-independent functions: and . Furthermore, assume that a new unknown function, for example , is defined as , and a differential equation on is formed and appended to the ordinary differential equation set. Now, in this new ordinary differential equation set, it is possible to put in place of and show that the set becomes the original ordinary differential equation set. The fact that is utilized as if it was independent of is compensated by considering a larger space: a space spanned by , , and instead of just and . Since we want to work in a linear vector space, linear independence should be in play. That is already the case, since and are linearly independent: their functional dependence is constructed nonlinearly. The equality defines a region within the space spanned by , , and .
In addition, space extension is not unique. According to the choice, different structures may be attained. This is not problematic: the inverse of the actions performed in the space extension may be performed in reverse order to obtain the original ordinary differential equation set.
The right-hand side functions may be considered as a linear combination of basis functions. The basis functions are defined as follows:
where it is possible to notice that if two us have a different superindex (different sequence of ℓs), they are linearly independent. Then, the original ODE set is:
where s are given constants. In (2), we utilized the short-hand notation for the sums: on the right-hand side, there is a nested sum structure. In this structure, goes from 0–, and so forth, up to going from 0–. is the highest power of appearing in the original ODE set where i goes from 1–n. By using (1), it is possible to observe that:
giving the possibility of rewriting the left-hand sides of (2) also in us: the left-hand sides are the temporal derivatives of us. Space extension extends the equation set by introducing new equations for the us that appear at least once on right-hand side, but do not appear on left-hand side. The new equations are formed through:
by using the chain rule. Derivatives of us with respect to xs are:
The temporal derivatives of xs may be substituted by the corresponding right-hand side of the ODE set. Consequently,
appears. Equation (6) may be used as many times as necessary: until there is a corresponding equation for all us appearing on the right-hand side.
2.1. Branch and Bound Optimization
The purpose is to obtain two us (different or the same) in each term on the right-hand side. The reason is that PREVTH can easily find solutions for ODEs with purely second degree multinomial right-hand side functions. Space extension is utilized in order to obtain a purely second degree multinomial structure from higher degree multinomial structure. Furthermore, the minimal extension (minimum number of equations) is a desired property since it means working with the smallest possible matrices and vectors. In a previous paper, we proposed checking all possible space extensions to find the minimal extension. We also stated that it was necessary to search only within a certain region. Here, we focus on a powerful search method for the optimal (minimal) space extension. This search is branch and bound search with an admissible heuristic.
Finding the optimal space extension is similar to finding the minimum distance between two points on a map. Branch and bound search keeps track of all partial paths and extends the shortest one. Branch and bound search may be improved by adding an admissible heuristic. An admissible heuristic is an underestimate for the distance remaining. If all estimates are guaranteed to be underestimates (admissible heuristic), one cannot blunder [22]. Therefore, at each node (each space extension), we extend the path with the minimum score (sum of partial path already traveled and an underestimate for the distance to the goal).
For brevity, we limit ourselves to the case where we start with two unknown functions. The algorithm may be generalized without much effort. In order to represent the ODEs on the computer efficiently, we propose the use of a list of lists. The outer list is the whole ODE set. Each inner list (element of the outer list) corresponds to a single equation. If corresponding to a single term, the inner list has three pairs. The first pair shows the superscripts of u on the left-hand side. The middle pair and the right pair represent the superscripts of us in a certain term. As the convention, the middle pair is chosen numerically smaller than the right pair: this eliminates reconsideration. There is a semicolon separating left-hand side-related entities and right-hand side-related entities. When there is more than one term in a single right-hand side, the new terms are appended to the inner list after a semicolon. There is also another list to keep track of the coefficients. The two lists are related: their corresponding order is important to keep track of which term has which coefficient.
As an example, consider the representation of one of the equations of classical quartic anharmonic oscillator. Assuming that and are the first and second unknown functions, respectively, the equation and the representation is:
The right-hand side of the ODE in (7) can be considered as a purely second degree multinomial: space extension dictates to us to consider as if it was an unknown function.
2.2. Classical Quartic Anharmonic Oscillator as an Illustrative Example
This subsection shows how to perform optimal space extension on classical quartic anharmonic oscillator. The ODE set for classical quartic anharmonic oscillator is given by:
and this can be rewritten as:
where is used. The coefficients on the right-hand side of (9) are:
where it may be observed that the equations are kept a bit more general than is necessary. The way to extend the equation set is through:
using (6). The equation set after optimal space extension is:
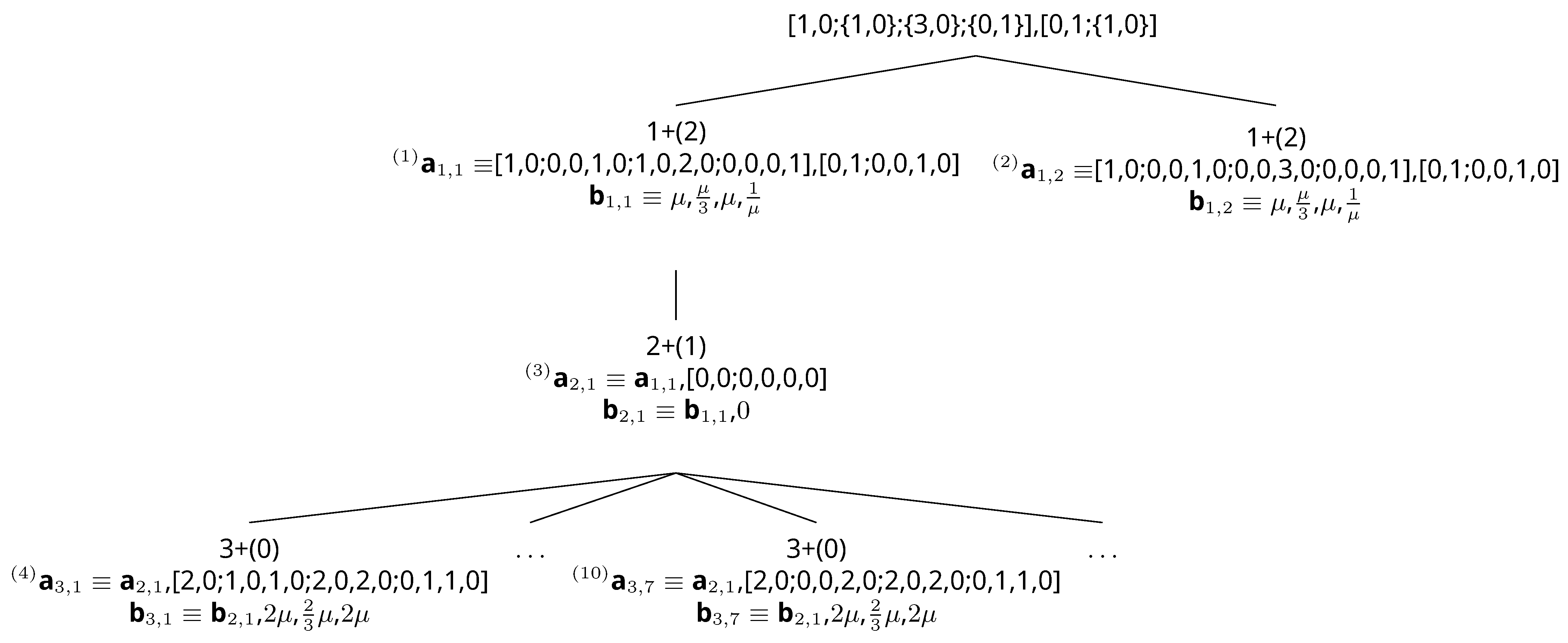
having four equations and four unknown functions. The way to obtain (12) from (9) is given in Figure 1. Note that, in the beginning, we have an empty tree: as we perform space extension, we are adding nodes to the tree. The root represents (9), and it has numbers in curly braces: this notation is peculiar to the root node. It represents the sum of the corresponding superscripts of adjacent us, which will be rewritten as a product of two us. The order in which the nodes are created is given as a left superscript of the term lists: s. The coefficient lists shown by are given right below s. Note that three can be written as a sum of two nonnegative numbers in two ways: 0 + 3 and 1 + 2. This is the reason why the root has two nodes extending from it. Therefore, we need to consider integer partitioning in all possible ways. The coefficient lists in Node (1) and Node (2) come directly from the equation set shown in (9).
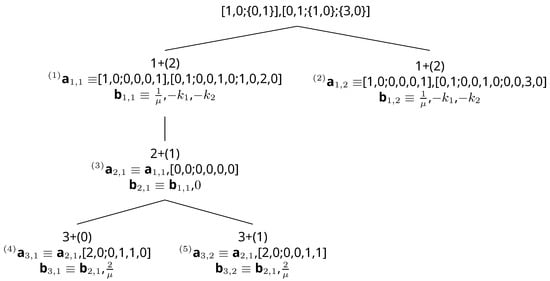
Figure 1.
Branch and bound with an admissible heuristic and reverse numerical tie-break for the classical quartic anharmonic oscillator ODE set.
Above each term list, the score is given. The first additive term of the score is the distance traveled, whereas the second additive term within parentheses is the heuristic distance to the goal. The heuristic distance is chosen as the number of us appearing on the right-hand side, but not on the left-hand side: this will always be an underestimate and therefore an admissible heuristic. In Node (1), there is no equation for 0,0 and 2,0: 0,0 and 2,0 appear on the right, but not on the left. Therefore, the heuristic distance of Node (1) is two.
We assume that all the child nodes of a node are formed at the same time. Therefore, we have Node (1) and Node (2) as leaves at this point. We want to extend the node with the smallest score, but the nodes have the same score. In this situation, a tie-break is needed. We always use reverse numerical tie-break: we extend the node where the term list is smaller reverse numerically. Therefore, we look at the elements within the term lists. Once we know which node to extend, we use (11) to introduce the new equation. Therefore, Node (3) is created. The new equation is formed for the leftmost pair on the right-hand side, which does not exist on the left-hand side: in this case, 0,0. After extending, we have traveled a distance of two from the root: the equation set is extended by two. The heuristic distance to the goal is one because the only pair appearing on the right-hand side, but not on the left-hand side, is 2,0. Using (11) on Node (3), it is possible to see that the resulting set can be written in two ways: Node (4) and Node (5). Observing Node (4), its heuristic distance is zero. For the heuristic distance used here, zero distance means we have reached the goal. Therefore, Node (4) is the goal: the optimal space extension. One may observe that Node (4) is the representation of (12). Once the goal is reached, we can stop searching: it is always guaranteed that we have found the optimal space extension.
In the case that there is more than one optimal space extension, a branch and bound can find all optimal space extensions one by one. For practical purposes, this is not necessary: finding one of the optimal space extensions is enough. Therefore, in the algorithm proposed here, if there is more than one optimal space extension, we do not try to find all of them.
2.3. Van Der Pol ODE as an Illustrative Example
The van der Pol ODE is given by:
and after optimal space extension, the newly-formed ODE has four equations and four unknowns. The structure of the tree is given in Figure 2. There are two leaves with zero heuristic distance: any one of them may be chosen as the optimal space extension. The leaves not shown in the figure are shown explicitly in Table 1.
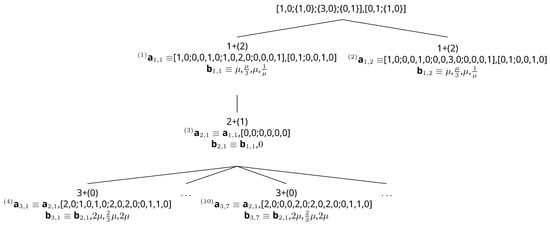
Figure 2.
Branch and bound with an admissible heuristic and reverse numerical tie-break for the van der Pol ODE set.

Table 1.
Node values and scores for the child nodes of in branch and bound with an admissible heuristic for van der Pol ODE.
2.4. Remarks on the Admissible Heuristic and Tie-Break
Counting the number of unknowns appearing on the right-hand side, but not on the left-hand side provides a handy admissible heuristic. For this heuristic, zero heuristic distance means we have reached the goal. We want the heuristic distance to be as close to the actual distance to the goal as possible. As heuristic distance is closer to the actual distance, the number of nodes we need to extend will decrease: therefore, less computational effort will be needed. However, if the heuristic distance is difficult to calculate, it will form an overhead: in the extreme case, following the path to the goal may be easier than trying to form an underestimate for the distance to the goal. Therefore, finding a better heuristic is an open question.
The rationale behind using reverse numerical tie-break is as follows. The intuition is to decrease the powers as fast as possible. The way to do that is to divide the powers in almost equal amounts each time. The reverse numerical ordering corresponds to this situation. It may be argued that the algorithm puts as much emphasis on tie-break as on the admissible heuristic, but our aim is to formulate an algorithm that is easy to use. This combination of admissible heuristic and tie-break produces little computational overhead: finding out whether we have reached the goal is incorporated into the admissible heuristic.
2.5. Implementation
Drawing trees is an efficient way of finding the optimal space extension manually. We can use queues when implementing optimal space extension using a computer. All the node creation and tree traversals are actually about how we are using the queue. The flow chart of the algoritm is given in Figure 3. It is an adaptation from [22]. The way to check if the goal is reached is by looking at the first path in the queue. If the first path in the queue terminates at the goal node, then it is the optimal path. We also assume that it is always possible to reach the goal, and that is why the program will always announce success. This is a valid assumption because it is always possible to obtain purely second degree multinomial right-hand side functions from multinomial right-hand side functions. Second degree multinomial functions may be formed from multinomial functions [20,21]. Single monomial functions may be formed from multinomial functions [19,25,26]: obtaining purely second degree multinomials from second degree multinomials is a special case of this. Putting it together, it is always possible to obtain purely second degree multinomial functions from multinomial functions. The algorithm presented in this paper guarantees finding the optimal space extension: the space extension with the minimum number of equations.
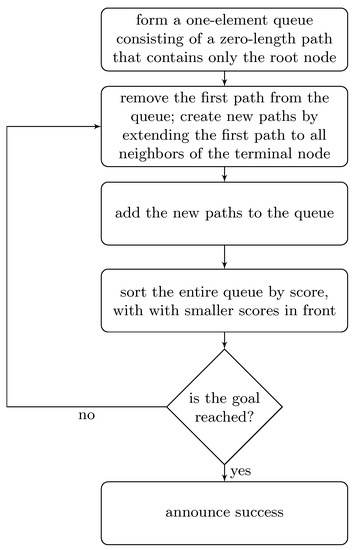
Figure 3.
Branch and bound with an admissible heuristic (as an implementation detail, we assume that we do not start from the goal and there exists a path to the goal).
The application of the algorithm to the classical quartic anharmonic oscillator is given in Table 2. In the table, the queue is also shown: the outer lists are separated by a semicolon, whereas the inner lists are separated by a comma.

Table 2.
Optimal space extension for the classical quartic anharmonic oscillator ODE set using branch and bound with an admissible heuristic.
We focused on two specific examples. It is important to emphasize that the algorithm works for all first order explicit ODEs with multinomial right-hand side functions. For all such ODE sets, there exists an optimal space extension, and branch and bound can find it. Branch and bound can always find the optimal space extension because it performs an exhaustive search.
Performing an exhaustive search is time consuming; therefore, for higher degrees, the search will not end in a reasonable amount of time. To overcome this problem, one may try to parallelize the search. There are papers about generic parallelizations of branch and bound [27]. Space extension may also benefit from parallelization. One simpler approach is by a certain trade-off: instead of making an exhaustive search, take the best n cases at each step. Compromises built upon such ideas yield faster results. Although such an alternative approach does not guarantee optimality and even convergence, it has practical importance.
2.6. Coping with Negative Integer Powers of Unknown Functions
If negative integer powers of the unknown functions appear on the right-hand side functions, it is still possible to use branch and bound with an admissible heuristic. Equation (6) is still valid in this case. Attention should be paid when the coefficient shown by ℓ in (6) becomes zero, causing that additive term to be dropped.
Furthermore, the branch and bound does not need to start with the original ODE set. Starting with multiplicative inverses of the unknown functions is also possible. That corresponds to accompanying algebraic identities to the ODE set. The main idea is to form the algebraic identities in such a way that using them requires little effort. The way to choose the starting ODE set is an open question: it requires some intuition. Therefore, we do not force optimality (the smallest number of equations and unknowns). If the final ODE set is close to being optimal, it will serve the purpose.
For this case, we avoid the discussion of the existence of solution and optimality on purpose. Branch and bound helps us search for a space extension, and it is very useful.
Furthermore, it is important to find the range of the search. An integer can be written as a sum of two integers in infinitely many ways. Therefore, each node may have infinitely many children. In order to overcome this difficulty and make each node have a finite number of children, the idea is as follows. A positive integer is written as the sum of two nonnegative integers smaller than or equal to the original positive integer. A negative integer is written as the sum of two nonpositive integers greater than or equal to the original negative integer. Zero is written as sum of two zeroes. Under these limitations, branch and bound will take us to a local minimum. Finding out if the local minimum is also the global minimum requires a rigorous analysis. Here, we are interested in a space extension that is optimal or close to being optimal: we do not force the optimality. In branch and bound terminology, we are interested in finding a path that is either the optimal path or a path that is not the optimal path, but still a very good one.
For the tie-break, the reverse numerical ordering is still valid: it corresponds to the situation where the powers are taken to smaller values in absolute value as fast as possible (keeping in mind the convention of making the middle pair numerically smaller than the right pair).
Gravitational Two-Body Problem As an Illustrative Example
The ODE for the gravitational two-body problem is:
where is a positional entity and is the radial momentum [15,18]. Equation (14) can be rewritten using the basis functions:
in the form:
It is possible to rewrite (16) as a list of lists so that we can perform branch and bound with an admissible heuristic. We only give the terms: the coefficients need to be stored in a separate list. The list corresponding to (16) is:
where we need to partition the pairs in curly braces in all possible ways. Although it is possible to go in this direction, it may be better to start off with another set of ODEs. The right-hand sides of (16) contain powers of the first function as and , whereas powers of the second function as one. If we start off with an equation with the power for the first function, we may find a better space extension. Therefore, the right-hand sides tell us with which ODE set to start. We may accompany the algebraic identities and with the equation set. Therefore, once we know and , we can easily find the solution of the original ODE set. For brevity, the dependence of u functions on and is not shown. Having this mind, it is possible to start off with:
using (6). Then, it is necessary to partition all the pairs in curly braces to obtain:
where the different choices are shown between dashed lines. There are 90 combinations in total. For this example, it is possible to eyeball the best choice, but the general idea is to sort the choices according to the score where the smallest score is in the front of the queue. If there is a tie, it is possible to use the reverse numerical tie-break. For this problem, if we choose the bottommost choices, and we acquire a heuristic distance to the goal that is one. That is smaller compared to the heuristic distance to the goal of the other 89 possibilities. Therefore, we obtain:
where the lists not containing multiple choices are shown with a superscript. Equation (20) is not a closed set: does not appear on the left-hand side. Augmenting the list by using (6), we obtain:
with four options. The bottommost one has zero heuristic distance to the goal. For this heuristic, zero heuristic distance means we reached the goal; therefore, we found the space extension we were looking for. The result is:
which corresponds to the ODE set:
We have not shown the calculation of the coefficients in (23). The method is the same as in the other previous examples.
3. Probabilistic Evolution Theory Using the Condensed Kronecker Product
Certain introductory content of this section was presented at an international conference and is available as an extended abstract [28].
3.1. Brief Recall of Probabilistic Evolution Theory
Optimal space extension has taken us to:
where the right-hand side functions are purely second degree multinomials. is just us obtained from optimal space extension stacked together to form a vector. is an matrix. The Kronecker product symbol on the exponent is the Kronecker power symbol. The Kronecker power two is the Kronecker square operation: the Kronecker product of an entity (vector) with itself. The elements of can be found by observing the coefficients. is not unique due to the linear dependence of the elements of the Kronecker squared vector. Uniqueness may be attained by dividing the contributions equally between the elements corresponding to the linearly-dependent elements of the Kronecker squared vector [11]. The vector of unknowns may be written as:
where Kronecker squaring appears on the right-hand side under an integral. As usual, as an inspiration from measure theory, we prefer to write the differential right after the integration symbol instead of writing it after the integrand. In this way, it is clear that integration is the application of an operator. It is possible to propose:
by substituting in place of in (24). We will try to find the value of the matrix. Equation (26) may be rewritten as:
where the Leibniz rule is utilized to manipulate the left-hand side of the ordinary differential equation. Using the mixed product rule (the Kronecker product can be distributed over product and vice versa), can be observed to be:
also keeping in mind that (24) holds. Both sides of (26) may be integrated, and the result may be substituted in (25) to form:
Integration by parts may be utilized for the integral in (29) to yield:
The process may be repeated over and over. matrices appear in the form:
where the zeroth Kronecker power of a vector is one. The ordered multiplication of s is named telescope matrices shown by . They are:
and the formal solution of the ordinary differential equation is:
which is an infinite series. is an matrix. The growth in size as the index of summation increases is undesirable. To prevent the growth, it is possible to propose matrices that satisfy:
and try to solve for . In this situation, the formal solution is:
where there is no growth in size of the matrix coefficients as j increases. It is necessary to make the following definitions in order to find the matrices. can be considered to be a horizontal concatenation of n square matrices; therefore,
is the structure of the horizontally-rectangular matrix . A squarification is an operation that takes two operands: an matrix and a vector with n elements. For the definition and properties from (37)–(42), assume that and are arbitrary matrices, and are arbitrary vectors with n elements, and is an arbitrary scalar. Squarification of with is defined to be:
where is the ith Cartesian unit vector and is the ith square block of . There is a strong connection between squarification and the Kronecker product. It is shown below.
Squarification has interesting properties. It can be distributed over the sum of vectors as follows:
and a scalar can penetrate to become a coefficient for the vector as follows:
Thus, squarification is linear with respect to its vector operand. Furthermore, it is also possible to show that:
and:
Thus, squarification is also linear with respect to its matrix operand.
The calculation of each in (35) is through the following quadratic recursion:
where is squarification of with . The proof of the recursion can be found in [18]. It is a direct proof using the definition of squarification and the properties of Cauchy products.
3.2. Simplifying the Factorials
The goal is to perform simplifications so that computational burden is reduced. Both sides of (43) may be multiplied by to give:
and the binomial coefficient on the right-hand side may be written explicitly to form:
where there are many factorials on the right-hand side. Using (40) and the fact that the scalar is commutative with the matrix,
may be formed. Defining a vector:
and rewriting (46) using (47),
appears. Furthermore, using (47) in (35),
may be acquired. The quadratic recursion in (48) can be used with (49) to give the solution of the problem in (24). Truncations from the series in (49) will be approximations for the solution.
3.3. Cauchy Product Folding
The Kronecker product of two vectors is not commutative. Nevertheless, the Kronecker product of two vectors with the same size is related to the Kronecker product of the same vectors in reverse order, through a permutation matrix. For arbitrary and with n elements,
where Π is a permutation matrix. This property can be seen for the case where n is two as follows:
and the general structure of the permutation matrix can be observed to be:
where the Cartesian unit vectors shown by have elements. Using this property, it is possible to change the order of s. We have:
and using (38) in (53):
appears. There is a Cauchy product structure on the right-hand side of (48): as the index of summation increases, one subindex is incremented, whereas the other subindex is decremented. Instead of having the two subindices going all the way in opposite directions, it is possible to have them go only half the way in opposite directions, until the subindices reach (or bypass) each other. This is possible as a consequence of (54). If j is odd, the subindices bypass each other. If j is even, the subindices reach each other. The two cases will be handled separately. If j is odd, by folding the Cauchy product,
appears using (54). In (55), the finite sum goes up to . Using (41) in (55),
may be obtained. Using (38) in (56), the recursion becomes:
in Kronecker product form. For the case where j is even, the two subindices reach each other. Therefore, attention should be paid in order not to count twice the term where the subindices are the same. If j is even, by folding the Cauchy product in (48),
appears. Using (41) and rewriting the rightmost term,
appears where both of the terms on the right-hand side involve . Using (38) in (59), the recursion is:
in Kronecker product form. For brevity, the definition:
is utilized. Then, the squarification form of the recursion is:
for even integers and:
for odd integers. The two recursions should be used alternatingly. Equations (62) and (63) are:
in the Kronecker product form. The squarification form and Kronecker product form are both useful. The squarification form is more efficient in terms of space complexity: it avoids the growth of size by the Kronecker product. The Kronecker product form is more efficient in terms of time complexity: the matrix is factored out of the sum.
As a result of Cauchy product folding, we are able to use as the matrix in the recursion. The matrix has certain properties that bring about further simplifications.
3.4. Condensed Kronecker Product
3.4.1. The Two by Four Matrix as a Special Case
In order to investigate the properties of , it is possible to first consider the case where n is two and then generalize the resulting simplifications. The matrix is:
in its most general form, and the resulting is:
which is more explicitly:
The second and the third columns of are equal. Therefore, it may be possible to remove one of these columns and also manipulate the vector on which this matrix acts. Then, consistency is acquired. It is possible to remove the repeating column by:
to form the matrix: the condensed form of . Assume that acts on the Kronecker product of two vectors. That is:
where and are any two-element vectors. Then, consistency may be achieved by making sure that:
holds. That may be done through condensing the Kronecker product of vectors by summing the corresponding cross terms. That is by considering an element where the subindices are not all the same (second and third elements of the vector) and then summing the element with the other element where the subindices are in reverse order to create a single element. This operation is:
which may be named as the condensation of the Kronecker product of vectors.
3.4.2. Generalization
It is observed in (69) that condensation of is by postmultiplication by a certain matrix, which may be named as to form:
as the expression for : the condensed matrix. When n is two, is:
by observing (69). The type of is given as the right subscript of so that we can observe the size of the condensed matrix: will be a matrix. When n is three, is:
forming a that is . When n is four, is:
forming a that is . The general structure is:
forming a that is . It is important to observe the pattern in (77). After , one index is skipped to go to . After , two indices are skipped to go to . After , three indices will be skipped to go to . This will go up to . For the asymptotic behavior with respect to n, it is possible to say that condensation removes half of the columns: as n goes to infinity, the number of elements in goes to half of the number of elements in the corresponding .
The other issue is the condensation of vectors. For vectors, condensation corresponds to merging pairs of elements together by summing them. This is a linear operation. Therefore, condensation can be distributed over the sum of the Kronecker product of vectors as follows:
where the vectors in (78) are any n-element vectors. Furthermore, a scalar can penetrate into a condensation to form:
where is any scalar. Using (71) in (64) and (65):
is obtained. Furthermore, using (78) and (79) in (80) and (81):
appears. (82) and (83) may be used alternatingly as the recursion for probabilistic evolution theory. is formed through (73) using (52) and (77). The only remaining issue is to generalize the condensation of the Kronecker product of vectors, which is given for the case where n is two in (72). Instead of performing the Kronecker product operations and merging pairs of elements, it is possible to consider a new operation: the condensed Kronecker product operation. The condensed Kronecker product operation avoids the unnecessary growth and shrinking of the vector: it embeds merging of the pairs within the Kronecker product. The condensed Kronecker product operation is shown by the Kronecker product symbol with the letter c as the right subscript. For any n-element vector and :
holds. Using (84) in (82) and (83):
is obtained as the recursion within probabilistic evolution theory. Equations (85) and (86) together are the final form of the recursion. The condensed Kronecker product of two three-element vectors is:
where the result has six elements. By observing (87), it is possible to notice that changing the places of and does not change the result. This also applies to the n-element case. The condensed Kronecker product is a commutative operation. Therefore:
holds. We prefer to show the operation as a function written in the Maxima programming language. It is given in Listing 1. The idea is to merge the pairs of elements where the subindex sequence of one is equal to the reverse of the subindex sequence of the other (that is done when the two subindices in an element are not the same).
Listing 1. Maxima function for the condensed Kronecker product of two vectors.
- conKronProd (a, b) :=
- block ([i, j, c:[]],
- for i : 1 thru length (a) do
- (
- c : append (c, [a [i] ∗ b [i]]),
- for j : i + 1 thru length (a) do
- (
- c : append (c, [a [i] ∗ b [j]+b [i] ∗ a [j]])
- )
- ),
- return (c)
4. Conclusions
The concluding remarks are itemized as follows.
- The purpose of the paper is neither introducing probabilistic evolution theory, nor showing numerical implementations. That is done in certain previous works. Here, the focus is on space extension.
- Probabilistic evolution theory is not a simplified variant of B-series. The trees used in this work are for space extension; they are not for the expansion of the solution. Probabilistic evolution theory uses Kronecker power series for the solution. Combined with space extension, probabilistic evolution theory may be applied to a large set of problems. Probabilistic evolution theory has certain general aspects that make it applicable to both classical dynamical systems and quantum dynamical systems.
- For symbolic computation, we represent each multinomial right-hand side function as two lists of integers: one list for the terms (excluding the coefficients) and one list for the coefficients.
- By list manipulations, we find the optimal space extension by using branch and bound with an admissible heuristic.
- Up to now, space extension for obtaining purely second degree multinomials from multinomials (any degree) was intuitive: a manual trial and error effort. Although [18] was an important step in the formation of an algorithm, this paper gives the algorithm for performing space extension. The algorithm is based on branch and bound with an admissible heuristic.
- Branch and bound guarantees the minimum number of equations (optimal space extension), because it performs an exhaustive search.
- If there is more than one ODE set having the minimum number of equations, it is possible to obtain them one by one by using branch and bound search. It is enough to obtain one of the optimal (minimum number of equations) ODE sets for many applications.
- Branch and bound search is used in order to convert ODE with a multinomial (any degree) right-hand side to ODE with a purely second degree multinomial right-hand side. Therefore, the method is quite general.
- It is possible to use branch and bound search on ODEs having also negative integer powers of unknown functions in the right-hand sides. In this situation, we are a little more flexible in the search: we do not force optimality; we are interested in finding a very good space extension with small effort.
- When negative integer powers appear, the starting ODE set may become important. It is possible to use branch and bound for several obvious choices and to try to find the optimal space extension. Finding the ODE set to start the branch and bound is intuitive. This does not pose a problem: the gain acquired by choosing a better starting set is small.
- Branch and bound search may be improved by using a better heuristic. This is left for future works.
- Factorials appearing within the formulation of probabilistic evolution theory are simplified. Factorial behavior is embedded inside the recursion. This is a computational gain.
- The Cauchy product folding operation is defined. By using this operation, we are able to halve the number of terms to be summed to find a single . This is also an important computational gain.
- Cauchy product folding results in further simplifications because it puts a specific structure into the core matrix. It is possible to remove certain columns of this matrix and manipulate the vectors upon which the matrix acts. This does not change the numerical result. Instead of working with the matrix and n-element vectors, we can now work with the matrix and -element vectors. This is also an important computational gain.
- Calculation of these -element vectors is through the condensed Kronecker product: this is an operation proposed in this paper. It is a commutative operation. It takes two n-element vectors and forms a vector with elements. This operation is expected to be useful in areas other than probabilistic evolution theory, as well.
Author Contributions
Conceptualization, C.G. and M.D.; methodology, C.G. and M.D.; software, C.G.; validation, C.G. and M.D.; formal analysis, C.G. and M.D.; investigation, C.G. and M.D.; resources, C.G. and M.D.; data curation, C.G. and M.D.; writing, original draft preparation, C.G.; writing, review and editing, C.G. and M.D.; visualization, C.G.; supervision, C.G. and M.D.; project administration, C.G. and M.D.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; Wiley Online Library: New York, NY, USA, 2008. [Google Scholar]
- Munthe-Kaas, H.Z.; Lundervold, A. On Post-Lie Algebras, Lie–Butcher Series and Moving Frames. Found. Comput. Math. 2013, 13, 583–613. [Google Scholar] [CrossRef]
- McLachlan, R.I.; Modin, K.; Munthe-Kaas, H.; Verdier, O. B-series methods are exactly the affine equivariant methods. Numer. Math. 2016, 133, 599–622. [Google Scholar] [CrossRef]
- Carothers, D.C.; Parker, G.E.; Sochacki, J.S.; Warne, P.G. Some properties of solutions to polynomial systems of differential equations. Electron. J. Differ. Equ. 2005, 2005, 1–17. [Google Scholar]
- Warne, P.; Warne, D.P.; Sochacki, J.; Parker, G.; Carothers, D. Explicit A-Priori error bounds and Adaptive error control for approximation of nonlinear initial value differential systems. Comput. Math. Appl. 2006, 52, 1695–1710. [Google Scholar] [CrossRef]
- Krattenthaler, C. Permutations with Restricted Patterns and Dyck Paths. Adv. Appl. Math. 2001, 27, 510–530. [Google Scholar] [CrossRef]
- Stanley, R.P. Enumerative Combinatorics. In Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1999; Volume 2. [Google Scholar]
- Gözükırmızı, C.; Kırkın, M.E.; Demiralp, M. Probabilistic evolution theory for the solution of explicit autonomous ordinary differential equations: Squarified telescope matrices. J. Math. Chem. 2017, 55, 175–194. [Google Scholar] [CrossRef]
- Demiralp, M. Probabilistic evolution theory in its basic aspects, and, its fundamental progressive stages. J. MESA 2018, 9, 245–275. [Google Scholar]
- Gözükırmızı, C.; Demiralp, M. Probabilistic evolution approach for the solution of explicit autonomous ordinary differential equations. Part 1: Arbitrariness and equipartition theorem in Kronecker power series. J. Math. Chem. 2014, 52, 866–880. [Google Scholar] [CrossRef]
- Gözükırmızı, C.; Demiralp, M. Probabilistic evolution approach for the solution of explicit autonomous ordinary differential equations. Part 2: Kernel separability, space extension, and, series solution via telescopic matrices. J. Math. Chem. 2014, 52, 881–898. [Google Scholar] [CrossRef]
- Gözükırmızı, C.; Demiralp, M. Constancy adding space extension for ODE sets with second degree multinomial right-hand side functions. AIP Conf. Proc. 2014, 1618, 875–878. [Google Scholar] [CrossRef]
- Demiralp, M. Squarificating the Telescope Matrix Images of Initial Value Vector in Probabilistic Evolution Theory (PET). In Proceedings of the 19th International Conference on Applied Mathematics (AMATH); WSEAS Press: Istanbul, Turkey, 2014; pp. 99–104. [Google Scholar]
- Gözükırmızı, C.; Tataroğlu, E. Squarification of telescope matrices in the probabilistic evolution theoretical approach to the two particle classical mechanics as an illustrative implementation. AIP Conf. Proc. 2017, 1798, 020062. [Google Scholar] [CrossRef]
- Gözükırmızı, C.; Kırkın, M.E. Classical symmetric fourth degree potential systems in probabilistic evolution theoretical perspective: Most facilitative conicalization and squarification of telescope matrices. AIP Conf. Proc. 2017, 1798, 020061. [Google Scholar] [CrossRef]
- Kırkın, M.E.; Demiralp, M. A Case Study on Squarification in Probabilistic Evolution Theory (PREVTH) for Henon-Heiles Systems. J. Comput. 2016, 1, 158–165. [Google Scholar]
- Gözükırmızı, C.; Demiralp, M. Probabilistic evolution theory for explicit autonomous ordinary differential equations: Recursion of squarified telescope matrices and optimal space extension. J. Math. Chem. 2018, 56, 1826–1848. [Google Scholar] [CrossRef]
- Demiralp, M. Promenading in the enchanted realm of Kronecker powers: Single monomial probabilistic evolution theory (PREVTH) in evolver dynamics. J. Math. Chem. 2018, 56, 2001–2023. [Google Scholar] [CrossRef]
- Demiralp, M.; Rabitz, H. Lie algebraic factorization of multivariable evolution operators: Definition and the solution of the canonical problem. Int. J. Eng. Sci. 1993, 31, 307–331. [Google Scholar] [CrossRef]
- Demiralp, M.; Rabitz, H. Lie algebraic factorization of multivariable evolution operators: Convergence theorems for the canonical case. Int. J. Eng. Sci. 1993, 31, 333–346. [Google Scholar] [CrossRef]
- Winston, P.H. Artificial Intelligence, 2nd ed.; Addison-Wesley Series in Computer Science; Addison-Wesley: Reading, PA, USA, 1984. [Google Scholar]
- Graham, R.; Lawler, E.; Lenstra, J.; Kan, A. Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey. In Discrete Optimization II; Hammer, P., Johnson, E., Korte, B., Eds.; Annals of Discrete Mathematics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar] [CrossRef]
- Lawler, E.L.; Wood, D.E. Branch-and-Bound Methods: A Survey. Oper. Res. 1966, 14, 699–719. [Google Scholar] [CrossRef]
- Kalay, B.; Demiralp, M. Somehow emancipating Probabilistic Evolution Theory (PREVTH) from singularities via getting single monomial PREVTH. J. Math. Chem. 2018, 56, 2024–2043. [Google Scholar] [CrossRef]
- Bayat Özdemir, S.; Demiralp, M. Using enchanted features of Constancy Adding Space Extension (CASE) to reduce the dimension of evolver dynamics: Single Monomial Probabilistic Evolution Theory. J. Math. Chem. 2018, 56, 2044–2068. [Google Scholar] [CrossRef]
- Eckstein, J.; Phillips, C.A.; Hart, W.E. Pico: An Object-Oriented Framework for Parallel Branch and Bound. In Inherently Parallel Algorithms in Feasibility and Optimization and their Applications; Butnariu, D., Censor, Y., Reich, S., Eds.; Studies in Computational Mathematics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 8, pp. 219–265. [Google Scholar] [CrossRef]
- Gözükırmızı, C. Probabilistic evolution theory for explicit autonomous ODEs: Simplifying the factorials, Cauchy product folding and Kronecker product decomposition. AIP Conf. Proc. 2018, 2046, 020034. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).