Abstract
Springs are critical components in mining vibrating screen elastic supports. However, long-term alternating loads are likely to lead to spring failures, likely resulting in structural damages to the vibrating screen and resulting in a lower separation efficiency. Proper dynamic models provide a basis for spring failure diagnosis. In this paper, a six-degree-of-freedom theoretical rigid body model of a mining vibrating screen is proposed, and a dynamic equation is established in order to explore the dynamic characteristics. Numerical simulations, based on the Newmark-β algorithm, are carried out, and the results indicate that the model proposed is suitable for revealing the dynamic characteristics of the mining vibrating screen. Meanwhile, the mining vibrating screen amplitudes change with the spring failures. Therefore, six types of spring failure are selected for simulations, and the results indicate that the spring failures lead to an amplitude change for the four elastic support points in the x, y, and z directions, where the changes depend on certain spring failures. Hence, the key to spring failure diagnosis lies in obtaining the amplitude change rules, which can reveal particular spring failures. The conclusions provide a theoretical basis for further study and experiments in spring failure diagnosis for a mining vibrating screen.
1. Introduction
Mining vibrating screens are important equipment for mine washing and processing, and are widely used for mine grading, dehydration, and desliming in China [1,2], working as a forced vibration system under alternating loads [3,4,5]. The SLK3661W double-deck linear mining vibrating screen is shown in Figure 1, and its main structures include a screen box and four elastic supports, designed using principles of symmetry. As shown in Figure 2, the screen box is assembled from an exciter, a lateral plate, an exciting beam, reinforcing beams, upper-bearing beams, under-bearing beams, an upper-screen deck, and an under-screen deck. Additionally, each elastic support is composed of several metal helical springs. These springs are critical components in a mining vibrating screen’s elastic supports, which directly affect the working performance of the mining vibrating screen [6,7]. However, long-term alternating loads are highly likely to lead to spring failure through spring stiffness decrease [8], causing a negative influence on the mining vibrating screen. On one hand, spring failures could lead to structural damages, such as beam fracture or lateral plate cracks [9,10,11]. On the other hand, spring failures could produce a loss of particle separation efficiency, thus hardly meeting practical process demands [12,13]. Therefore, it is necessary to diagnose the spring failures of a mining vibrating screen for routing maintenance, which can help to ensure safety and reliability.

Figure 1.
The SLK3661W double-deck linear mining vibrating screen, unloading side view.
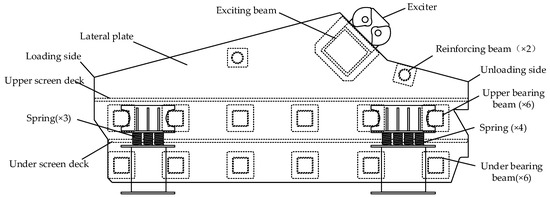
Figure 2.
Structures of the SLK3661W double-deck linear mining vibrating screen.
Proper dynamic models provide a basis for diagnosing spring failures. In recent years, even though many studies have reported vibrating screen dynamic models on optimization [14,15,16], separation [17,18], and particle motion [19], there has been very little research reported on spring failure diagnosis. Aimed at spring failure diagnosis, Rodriguez et al. developed a two-dimensional, three-degree-of-freedom nonlinear model that considered one angular motion and damping, which allowed for the prediction of the behavior of a vibrating screen when there was a reduction in spring stiffness, and they used this model to determine a limit on spring failures before separation efficiency was affected [20]. Peng et al. presented a three-degree-of-freedom rigid plate structure to describe the isolation system, and they also proposed the method of stiffness identification by stiffness matrix disassembly; the numerical simulation results demonstrated the feasibility of the developed method [21]. However, each elastic support of a mining vibrating screen could have spring failures with spring stiffness decreases. The mining vibrating screen operating mode becomes spatial motion with very complicated dynamic characteristics, including multiple degrees of freedom.
The purpose of the present study is to explore the mining vibrating screen dynamic characteristics with spring failures, providing a theoretical basis for spring failure diagnosis. In this paper, a theoretical rigid body of a mining vibrating screen is proposed, the dynamic equation is established, and the steady-state solutions are obtained. Numerical simulations were carried out, and the results showed that the proposed model is feasible. In addition, spring failure simulations were also carried out, and the results indicated that the x, y, and z direction amplitude change rules for all the elastic supports were strongly related to spring failures. Hence, the key for spring failure diagnosis lies in obtaining the amplitude change rules, which can reveal the certain spring failures.
2. Theoretical Rigid Body Model
2.1. The Model
As shown in Figure 3, a six-degree-of-freedom theoretical rigid body model of spatial motion considering three rotations (Roll, Pitch, and Yaw) is proposed for exploring the mining vibrating screen dynamic characteristics with spring failures. The list of symbols is shown in abbreviations section.
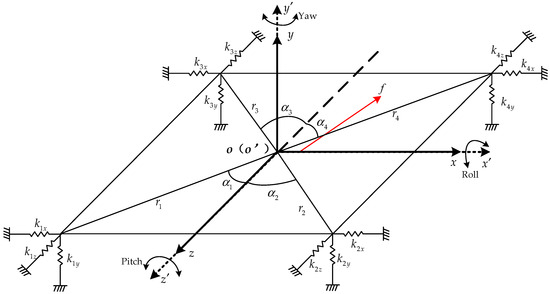
Figure 3.
Spatial motion dynamic model of the mining vibrating screen, including three translational degrees of freedom and three rotational degrees of freedom.
The screen box is simplified to a rigid body, and the four elastic support points are individually simplified as three mutually perpendicular springs , (where i is the elastic support point number, i = 1, 2, 3, 4). The movement of a rigid body is expressed by the position of a body frame o’x′y′z′ relative to the inertial frame oxyz. The ox-axis and oz-axis are mutually perpendicular and located in the horizontal plane, and the oy-axis is perpendicular to the horizontal plane. The origin o’ of the body frame is located at the mass center of the rigid body, at all times. The o’x′-axis and o’z′-axis are mutually perpendicular and located in the rigid body plane, and the o’y′-axis is perpendicular to the rigid body plane. Initially, the origin o of the inertial frame and the origin o’ of the body frame are coincident. The distances between the mass center of the rigid body and the four elastic support points of spring are and, furthermore, the angles between them and oz-axis are . Suppose that the rigid body′s mass is m, and the moments of inertia are Jx, Jy, Jz. Define x, y, z as the translation displacements of the rigid body and as the angular displacements in the inertial frame. The exciting force f is exerted on the rigid body as an alternating load, with included angles between exciting force and the o’x′-axis, o’y′-axis, and o’z′-axis, respectively.
The dynamic equation is established by adopting the Lagrange method, and the processes are as follows. The three rotation angles are small, define , , , and .
2.2. System Potential Energy
The dynamic system includes three translation motions and three rotation motions. According to the Tait–Bryan angles in the literature [22], the rotation matrix between the body frame and the inertial frame was derived using the rotation system shown in Figure 4.
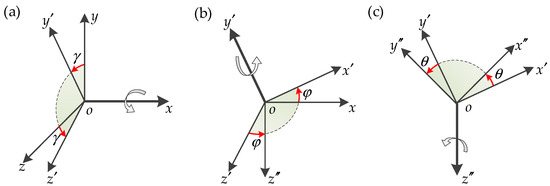
Figure 4.
(a) Rotation of the inertial frame oxyz around the ox-axis by angle ; (b) Rotation of the instantaneous system around the oy′-axis by angle ; (c) Rotation of the instantaneous system around the oz′′-axis by angle .
As the three rotation angles of the rigid body are small, they can be simplified as rotations around the oxyz axis. When rotating the rigid body around the ox-axis by the new angle of roll , the moment of inertia is , and the rotation matrix is written as:
When rotating the rigid body around the oy′-axis by the new angle of yaw , the moment of inertia is , and the rotation matrix is written as:
When rotating the rigid body around the oz′′-axis by the new angle of pitch θ, the moment of inertia is , and the rotation matrix is written as:
When rotating the rigid body in the sequence oz-oy-ox, the rotation matrix between the body frame and the inertial frame is obtained as:
Supposing that the coordinate of the mass center is (x, y, z) in an inertial frame, and any point of the rigid body is (x′, y′, z′) in the body frame, the coordinate of any point of the rigid body in an inertial frame is written as:
Moreover, the coordinates of the four spring support points in the body frame can be written as:
In (6), , , , , , , , and .
In the initial state, the coordinate of the mass center is (0, 0, 0) in the inertial frame, and the rotation matrix is . Thus, the coordinates of the four spring support points in the inertial frame can be written as:
In a motion state, the coordinate of the mass center is () in the inertial frame. Thus, the coordinates of the four spring support points in the inertial frame can be written as:
The results in (8) are equivalent to the spring compression and, therefore, the system potential energy is obtained as:
2.3. System Kinetic Energy
According to the literature [23,24], there is a relation expressing a rigid body′s spatial motion, which is written as:
Therefore, the system’s kinetic energy is obtained as:
2.4. System Force Vector
The mining vibrating screen in this study is equipped with two groups of counter-rotating vibrators, with each group having two pairs of eccentric blocks. Due to manufacturing errors and installation errors, the resultant force f typically does not pass through the center of mass of the screen box in practice. The resultant force f can be equivalent to a force vector. In the body frame, the force vector is written as:
On account of the force vector changing with the rigid body motion, the force vector in a body frame is written as:
Meanwhile, supposing that the coordinate of the point exerting force is () in a body frame, the coordinate of the point exerting force in an inertial frame can be written as:
According to the literature [23,24], there is a relation expressing a rigid body′s spatial motion, which is written as:
In an inertial frame, the system’s force vector is obtained as:
2.5. Dynamic Equation
After linearizing, the dynamic equation can be written as:
In (17), is the acceleration column vector:
is the displacement column vector:
is the mass matrix:
and is the stiffness matrix:
In (21), ,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Additionally, F is the force column vector:
According to the dynamic theory [20], the steady-state solutions of a forced vibration system can be written as:
In (23), is the angular speed. It should be noted that the relations are valid for a constant rotational velocity of counter-rotating vibrators, for which there exists a resultant force acting along a straight line towards the body of vibrating screen. Taking the derivative of both sides of (23), the acceleration can be written as:
Bringing Equations (23) and (24) into Equation (22), the steady-state solutions can be obtained as:
The dynamic equation of a mining vibrating screen in spatial motion, shown above, gives the dynamic characteristics. In the following section, numerical simulations are carried out to verify the proposed model.
3. Simulations
3.1. Numerical Simulations Results
In this paper, numerical simulations are carried out using Matlab, and the programs are available in supplementary materials online. In order to ensure the physical significance of the dynamic equation, the damping is significant. Generally, the damping matrix can be regarded as a linear combination of the mass matrix (Equation (20)) and the stiffness matrix (Equation (21)) in a mechanical system dynamics equation, and can be written as:
After inserting the damping matrix (Equation (26)) into the dynamic Equation (17), the system dynamic equation can be written as:
In (27), is the velocity vector:
This paper intends to use the SLK3661W double-deck linear mining vibrating screen as an exploration object, which has certain parameters, such as screen box mass (18,944 kg), spring stiffness of each unloading side (1,242,400 N/m), spring stiffness of each loading side (931,800 N/m), screen deck dimension (3.6 × 6.1 m), processing capacity (350–400 t/h), motor speed (1480 r/min), and electric power (55 kW). Numerical simulations were carried out, based on the Newmark-β algorithm, and the main parameters used in the simulation are shown in Table 1. Additionally, the coordinate of force action point was (−0.2, 0, 0) in the body frame. The total time of the simulation was tm, while the time step was dt.

Table 1.
Simulation parameters table.
Under normal conditions, the system vibrations included x, y, and θ, while z = φ = γ = 0. The displacement curves of the mass center are shown in Figure 5.

Figure 5.
Displacement curves of the mass center under normal conditions, including two translational displacements (x, y) and one angular displacement (θ). Additionally, z = φ = γ = 0.
As shown in Figure 5, the displacements are large initially, then gradually decrease to a stable range. The stable state amplitudes (peak to peak values of displacement) are as follows:
x = 7.82 mm, y = 7.80 mm, θ = 4.79 × 10−4 rad.
Under spring failure conditions, the value of was decreased to 652,260 N/m and the simulation was run again. The system vibrations include x, y, and z, as well as γ, φ, and θ. The displacement curves of the mass center are shown in Figure 6.
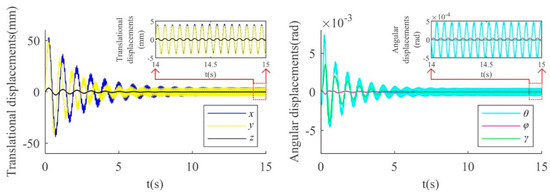
Figure 6.
Displacement curves of the rigid body mass center under spring failure conditions, including three translational displacements (x, y, z) and three angular displacements (γ, φ, θ).
As shown in Figure 6, the displacements are large initially, then gradually decrease to a stable range. The stable state amplitudes (peak to peak values of displacement) are as follows:
x = 7.82 mm, y = 7.79 mm, z = 0.96 mm, γ = 0.2 × 10−4 rad, φ = 0.75 × 10−4 rad, θ = 9.40 × 10−4 rad.
According to the analysis of the simulations above, the results showed that the four elastic supports of the whole system were symmetric on the x-y plane under normal conditions. The system vibrations included two translations and one rotation; namely, the rigid body only moved in the x–y plane. In addition, the system vibrations changed into a very complicated spatial motion with spring stiffness decrease, which included three translations and three rotations. Meanwhile, the amplitudes changed at the same time.
Therefore, the proposed six-degree-of-freedom model is feasible for exploring the mining vibrating screen dynamic characteristics with spring stiffness decrease caused by spring failures, and vice versa.
3.2. Spring Failure Simulations Results
Under normal conditions, the four elastic support points were symmetrical (point 1 = point 3, point 2 = point 4) in the proposed model. However, this symmetry broke under spring failure conditions, and hence six types of failure were selected for the simulation analysis, as shown in Table 2. Aimed at obtaining the influence rule of the spring failures, only the spring stiffness in the y direction was changed in the simulations.

Table 2.
Types of spring failure.
Due to the difference of each spring’s stiffness and stiffness change, the stiffness variation coefficient (SVC) for normalization was defined as:
In (29), i is the elastic support point sequence number, j is the stiffness sequence number, is the normal spring stiffness in the y direction (as shown in Table 2), and is the various spring stiffness in the y direction.
Setting the value of as 89° in Table 2, the amplitudes of the four elastic support points in all directions were selected to be normal amplitudes. Due to the difference of each amplitude and amplitude change, the amplitude variation coefficient (AVC) for normalization was defined as:
In (30), i is the elastic support point sequence number, d is one of the three directions, is the normal amplitude of one elastic support point, and is the various amplitudes of the same elastic support point.
3.2.1. Single Spring Failure Simulations Results
In the case of failures, the spring stiffness variation coefficient () was changed from 0 to 30%, and hence the amplitude variation coefficients of the four elastic support points in all directions changed together.
As shown in Figure 7, if the spring stiffness variation coefficient () increased, the amplitude variation coefficients of all elastic support points in the x direction decreased, while all amplitude variation coefficients in the z direction increased. In the y direction, the amplitude variation coefficients of points 2 and 4 increased, while the amplitude variation coefficients of points 1 and 3 decreased.
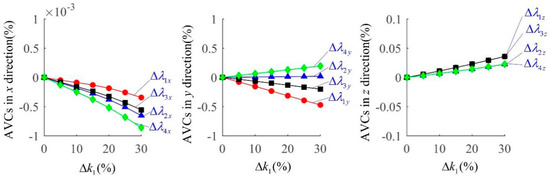
Figure 7.
The amplitude variation coefficient curves of four elastic support points, including the amplitude variation coefficients in the x, y, and z directions.
3.2.2. Double Spring Failures Simulations Results
In the case of and failures, the spring stiffness variation coefficient ( and ) was changed from 0% to 30%, and hence the amplitude variation coefficients of four elastic support points in all directions changed together.
As shown in Figure 8, if the spring stiffness variation coefficient increased, the amplitude variation coefficients of the four elastic support points in the x direction decreased, increased, or stayed the same (i.e., indeterminate) under the coupling action of and failures. The amplitude variation coefficients of all elastic support points in the x direction decreased, increased, or stayed the same (i.e., indeterminate) under the coupling action of and failures as well. Meanwhile, the amplitudes of variation coefficients in the z direction always increased, as well as and .
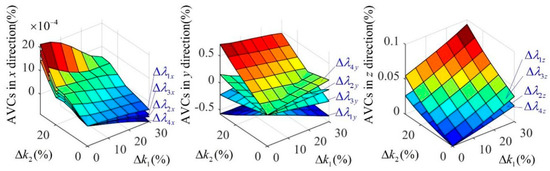
Figure 8.
The amplitude variation coefficient surfaces of four elastic support points, including the amplitude variation coefficients in the x, y, and z directions.
3.3. Discussion
Many simulations were carried out with differing failure types, as shown in Table 2, and the change rules between the spring stiffness coefficient and the amplitude variation coefficient were obtained, as shown in Table 3.

Table 3.
The change rules between the spring stiffness coefficient and the amplitude variation coefficient.
As shown in Table 3, the amplitude variation coefficient probably increased, decreased or was indeterminate under different spring failures. The change rules of the amplitude variation coefficient are the same as the change rules of the amplitudes, according to Formula (30). Hence, the change rules of the amplitudes of four elastic support points in the x, y, and z directions can be summarized, as follows:
- In the case of spring failure, the amplitudes of all points in the x direction will decrease, while all amplitudes increase in the z direction. In the y direction, the amplitudes of points 2 and 4 increase, while the amplitudes of points 1 and 3 decrease.
- In the case of spring failure, all amplitudes will increase in both the x and z directions. In the y direction, the amplitudes of points 1 and 3 increase, while the amplitudes of points 2 and 4 decrease.
- In the case of spring and spring failure, all amplitudes will increase in the z direction. In the other directions, the change rules of all amplitudes are indeterminate.
- In the case of spring and spring failure, all amplitudes will decrease in the x direction. In the y direction, the amplitudes of points 3 and 4 increase, while the change rules of the amplitudes of points 1 and 2 are indeterminate. In the z direction, the change rules of all amplitudes are indeterminate.
- In the case of spring and spring failure, the change rules of all amplitudes are indeterminate in all directions.
- In the case of spring and spring failure, all amplitudes will increase in the x direction. In the y direction, the amplitudes of points 1 and 3 increase, while the amplitudes of points 2 and 4 decrease. In the z direction, the change rules of all amplitudes are indeterminate.
The change rules for amplitudes, obtained above, indicated that the spring failures would lead to amplitude change of the four elastic support points in the x, y, and z directions, and the amplitude change rules can reveal certain spring failures. Hence, the amplitude change rules can provide useful information for spring failure diagnosis.
4. Conclusions
The proposed theoretical rigid body model can reveal the dynamic characteristics of a mining vibrating screen, with or without spring failures. From the numerical simulation results, using the Newmark-β method, there are certain relationships between the system amplitudes and different spring failures, which can be used for spring failure diagnosis. This information is useful for operations and maintenance staff, to determine whether it is necessary to change one or more springs. However, further study and experiments need to be done to verify the accuracy of this approach.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-7390/7/3/246/s1, Matlab Program for dynamic equation establishments and simulations with spring failures.m, Matlab Program for dynamic equation establishments and simulations without spring failures.m.
Author Contributions
Conceptualization, Y.L. and G.M.; Methodology. S.S., L.B., and D.S.; Validation, Y.L. and J.S.; Writing—Original Draft Preparation, Y.L.; Writing—Review & Editing, G.M.; and Visualization, J.S.
Funding
This research was funded by the National key research and development program of China, grant number 2016YFC0600900; the National Natural Science Foundation of China, grant number U13611151; and the Yue Qi Distinguished Scholar Project, China University of Mining & Technology, Beijing.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The list of symbols is as follows:
| Spring of the elastic support point 1 in y direction | |
| Spring of the elastic support point 2 in y direction | |
| Spring of the elastic support point 3 in y direction | |
| Spring of the elastic support point 4 in y direction | |
| Spring stiffness of the elastic support point 1 in x direction | |
| Spring stiffness of the elastic support point 1 in y direction | |
| Spring stiffness of the elastic support point 1 in z direction | |
| Spring stiffness of the elastic support point 2 in x direction | |
| Spring stiffness of the elastic support point 2 in y direction | |
| Spring stiffness of the elastic support point 2 in z direction | |
| Spring stiffness of the elastic support point 3 in x direction | |
| Spring stiffness of the elastic support point 3 in y direction | |
| Spring stiffness of the elastic support point 3 in z direction | |
| Spring stiffness of the elastic support point 4 in x direction | |
| Spring stiffness of the elastic support point 4 in y direction | |
| Spring stiffness of the elastic support point 4 in z direction | |
| i | Elastic support points number |
| o | Origin of the inertial frame |
| x | x-axis |
| x | Translation displacement of the rigid body in x direction |
| x | Coordinate of the mass center in the inertial frame |
| xd | Coordinate of one point of the rigid body in the inertial frame |
| Displacement column vector | |
| Velocity column vector | |
| Acceleration column vector | |
| y | y-axis |
| y | Translation displacement of the rigid body in y direction |
| y | Coordinate of the mass center in the inertial frame |
| yd | Coordinate of one point of the rigid body in the inertial frame |
| z | z-axis |
| z | Translation displacement of the rigid body in z direction |
| z | Coordinate of the mass center in the inertial frame |
| zd | Coordinate of one point of the rigid body in the inertial frame |
| o’ | Origin of the body frame |
| x′ | x′-axis |
| x′ | Coordinate of the mass center in the body frame |
| y′ | y′-axis |
| y′ | Coordinate of the mass center in the body frame |
| z′ | z′-axis |
| z′ | Coordinate of the mass center in the body frame |
| Distance between the mass center of the rigid body and the elastic support point 1 | |
| Distance between the mass center of the rigid body and the elastic support point 2 | |
| Distance between the mass center of the rigid body and the elastic support point 3 | |
| Distance between the mass center of the rigid body and the elastic support point 4 | |
| Angle between and z-axis | |
| Angle between and z-axis | |
| Angle between and z-axis | |
| Angle between and z-axis | |
| m | Mass of rigid body |
| Moment of inertia of the rigid body rotation around ox-axis | |
| Moment of inertia of the rigid body rotation around oy-axis | |
| Moment of inertia of the rigid body rotation around oz-axis | |
| Angular of the rigid body rotation around ox-axis | |
| Angular of the rigid body rotation around oy-axis | |
| Angular of the rigid body rotation around oz-axis | |
| f | Exciting force |
| F | System force vector |
| Angle between exciting force vector and o’x′-axis | |
| Angle between exciting force vector and o’y′-axis | |
| Angle between exciting force vector and o’z′-axis | |
| Rotation matrix of the rigid body rotation around ox-axis | |
| Rotation matrix of the rigid body rotation around oy-axis | |
| Rotation matrix of the rigid body rotation around oz-axis | |
| Rotation matrix of the rigid body in the sequence of oz-oy-ox | |
| U | System potential energy |
| E | System kinetic energy |
| Mass matrix | |
| Stiffness matrix | |
| C | Damping matrix |
| Circular frequency of exciting force | |
| Angular velocity of the rigid body rotation around ox-axis | |
| Angular velocity of the rigid body rotation around oy-axis | |
| Angular velocity of the rigid body rotation around oz-axis | |
| Steady state solution of the forced vibration system | |
| Steady state solution of the forced vibration system | |
| Steady state solution of the forced vibration system | |
| Steady state solution of the forced vibration system | |
| Steady state solution of the forced vibration system | |
| Steady state solution of the forced vibration system | |
| tm | Total time of simulation |
| dt | Time step of simulation |
| Spring stiffness variation coefficient of spring k1 | |
| Spring stiffness variation coefficient of spring k2 | |
| Spring stiffness variation coefficient of spring k3 | |
| Spring stiffness variation coefficient of spring k4 | |
| Spring stiffness variation coefficient of spring k1 | |
| Spring stiffness variation coefficient of spring k2 | |
| Spring stiffness variation coefficient of spring k3 | |
| Spring stiffness variation coefficient of spring k4 | |
| Amplitude variation coefficient of elastic support point 1 in x direction | |
| Amplitude variation coefficient of elastic support point 1 in y direction | |
| Amplitude variation coefficient of elastic support point 1 in z direction | |
| Amplitude variation coefficient of elastic support point 2 in x direction | |
| Amplitude variation coefficient of elastic support point 2 in y direction | |
| Amplitude variation coefficient of elastic support point 2 in z direction | |
| Amplitude variation coefficient of elastic support point 3 in x direction | |
| Amplitude variation coefficient of elastic support point 3 in y direction | |
| Amplitude variation coefficient of elastic support point 3 in z direction | |
| Amplitude variation coefficient of elastic support point 4 in x direction | |
| Amplitude variation coefficient of elastic support point 4 in y direction | |
| Amplitude variation coefficient of elastic support point 4 in z direction |
References
- Liu, C.S.; Zhang, S.M.; Zhou, H.P.; Li, J.; Xia, Y.F.; Peng, L.P.; Wang, H. Dynamic analysis and simulation of four-axis forced synchronizing banana vibrating screen of variable linear trajectory. J. Cent. South Univ. 2012, 19, 1530–1536. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.S.; Peng, L.P.; Jiang, X.W.; Ji, L.Q. Dynamic analysis of elastic screen surface with multiple attached substructures and experimental validation. J. Cent. South Univ. 2012, 19, 2910–2917. [Google Scholar] [CrossRef]
- Song, B.C.; Liu, C.S.; Peng, L.P.; Li, J. Dynamic analysis of new type elastic screen surface with multi degree of freedom and experimental validation. J. Cent. South Univ. 2015, 22, 1334–1341. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhao, C.Y.; Wen, B.C. Theoretical and experimental study on synchronization of the two homodromy exciters in a non-resonant vibrating system. Shock Vib. 2013, 20, 327–340. [Google Scholar] [CrossRef]
- Zhang, Z.R.; Wang, Y.Y.; Fan, Z.M. Similarity Analysis between Scale Model and Prototype of Large Vibrating Screen. Shock Vib. 2015. [Google Scholar] [CrossRef]
- Dong, K.J.; Wang, B.; Yu, A.B. Modeling of Particle Flow and Sieving Behavior on a Vibrating Screen: From Discrete Particle Simulation to Process Performance Prediction. Ind. Eng. Chem. Res. 2013, 52, 11333–11343. [Google Scholar] [CrossRef]
- Makinde, O.A.; Ramatsetse, B.I.; Mpofu, K. Review of vibrating screen development trends: Linking the past and the future in mining machinery industries. Int. J. Miner. Process. 2015, 145, 17–22. [Google Scholar] [CrossRef]
- Peng, L.; Liu, C.; Wang, H. Health identification for damping springs of large vibrating screen based on stiffness identification. J. China Coal Soc. 2016, 41, 1568–1574. [Google Scholar]
- Jiang, H.S.; Zhao, Y.M.; Duan, C.L.; Yang, X.L.; Liu, C.S.; Wu, J.D.; Qiao, J.P.; Diao, H.R. Kinematics of variable-amplitude screen and analysis of particle behavior during the process of coal screening. Powder Technol. 2017, 306, 88–95. [Google Scholar] [CrossRef]
- Peng, L.P.; Liu, C.S.; Song, B.C.; Wu, J.D.; Wang, S. Improvement for design of beam structures in large vibrating screen considering bending and random vibration. J. Cent. South Univ. 2015, 22, 3380–3388. [Google Scholar] [CrossRef]
- Zhang, Z.R. Strain modal analysis and fatigue residual life prediction of vibrating screen beam. J. Meas. Eng. 2016, 4, 217–223. [Google Scholar] [CrossRef]
- Li, Z.; Tong, X. Modeling and parameter optimization for vibrating screens based on AFSA-SimpleMKL. Chin. J. Eng. Des. 2016, 23, 181–187. [Google Scholar]
- Xiao, J.; Tong, X. Characteristics and efficiency of a new vibrating screen with a swing trace. Particuology 2013, 11, 601–606. [Google Scholar] [CrossRef]
- Baragetti, S. Innovative structural solution for heavy loaded vibrating screens. Miner. Eng. 2015, 84, 15–26. [Google Scholar] [CrossRef]
- Baragetti, S.; Villa, F. A dynamic optimization theoretical method for heavy loaded vibrating screens. Nonlinear Dyn. 2014, 78, 609–627. [Google Scholar] [CrossRef]
- Peng, L.P.; Fang, R.X.; Fen, H.H.; Zhang, L.; Ma, W.D.; He, X.D. A more accurate dynamic model for dual-side excitation large vibrating screens. J. Vibroeng. 2018, 20, 858–871. [Google Scholar]
- Du, C.L.; Gao, K.D.; Li, J.P.; Jiang, H. Dynamics Behavior Research on Variable Linear Vibration Screen with Flexible Screen Face. Adv. Mech. Eng. 2014, 12. [Google Scholar] [CrossRef]
- Trumic, M.; Magdalinovic, N. New model of screening kinetics. Miner. Eng. 2011, 24, 42–49. [Google Scholar] [CrossRef]
- Dong, K.J.; Yu, A.B.; Brake, I. DEM simulation of particle flow on a multi-deck banana screen. Miner. Eng. 2009, 22, 910–920. [Google Scholar] [CrossRef]
- Rodriguez, C.G.; Moncada, M.A.; Dufeu, E.E.; Razeto, M.I. Nonlinear Model of Vibrating Screen to Determine Permissible Spring Deterioration for Proper Separation. Shock Vib. 2016. [Google Scholar] [CrossRef]
- Peng, L.P.; Liu, C.S.; Wu, J.D.; Wang, S. Stiffness identification of four-point-elastic-support rigid plate. J. Cent. South Univ. 2015, 22, 159–167. [Google Scholar] [CrossRef]
- Baranowski, L. Equations of motion of a spin-stabilized projectile for flight stability testing. J. Theor. Appl. Mech. 2013, 51, 235–246. [Google Scholar]
- Bai, L.; Dong, Z.F.; Ge, X.S. The closed-loop kinematics modeling and numerical calculation of the parallel hexapod robot in space. Adv. Mech. Eng. 2017, 9, 15. [Google Scholar] [CrossRef]
- Bai, L.; Ma, L.H.; Dong, Z.F.; Ge, X.S. Kinematics, Dynamics, and Optimal Control of Pneumatic Hexapod Robot. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).