Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning
Abstract
1. Introduction
2. Neural Network Model and Application
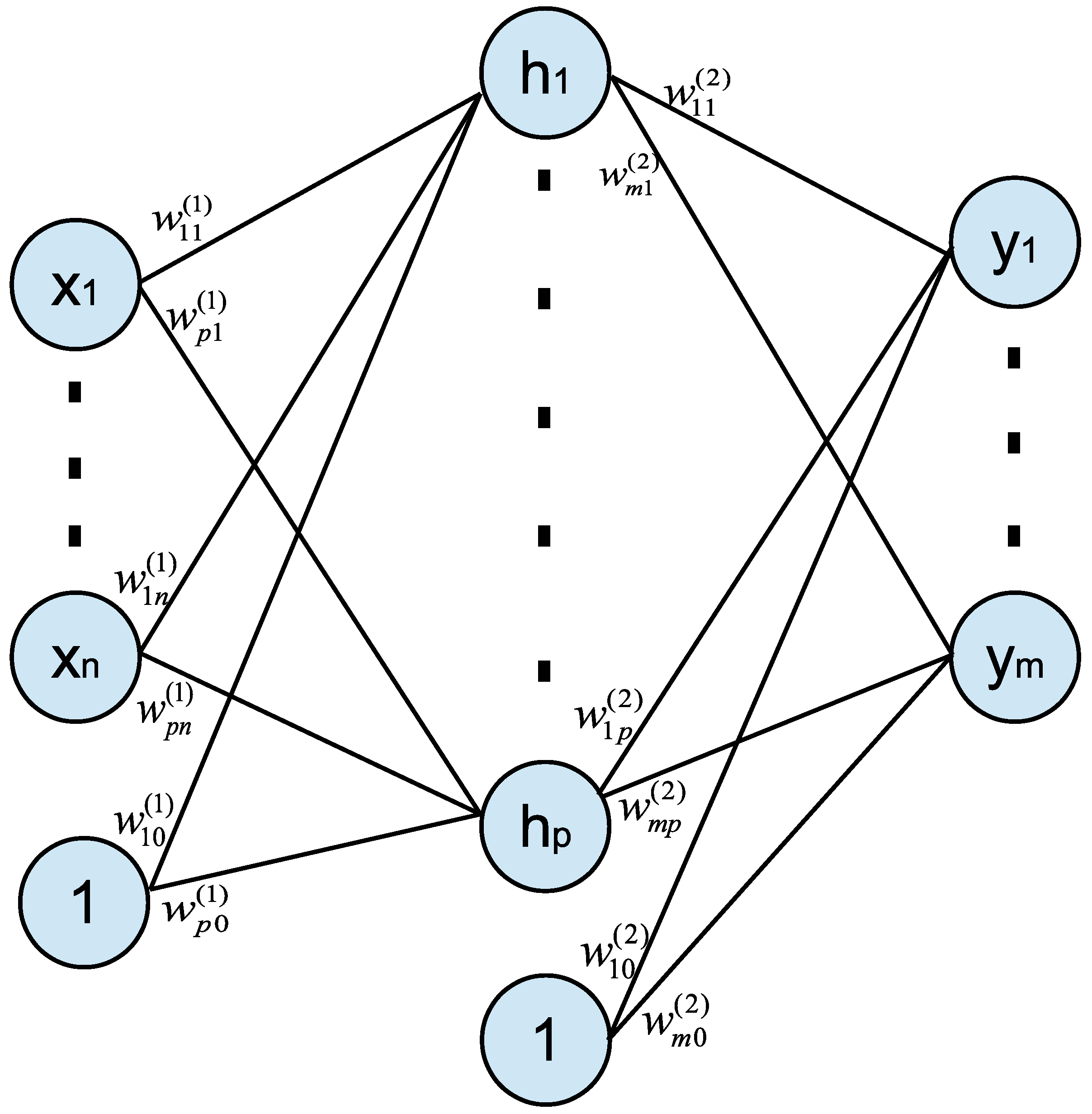
2.1. Neural Network Model
2.2. Application of Neural Network Models in RTO and MPC
2.2.1. RTO with the Neural Network Model
2.2.2. MPC with Neural Network Models
3. Application to a Chemical Reactor Example
3.1. Process Description and Simulation
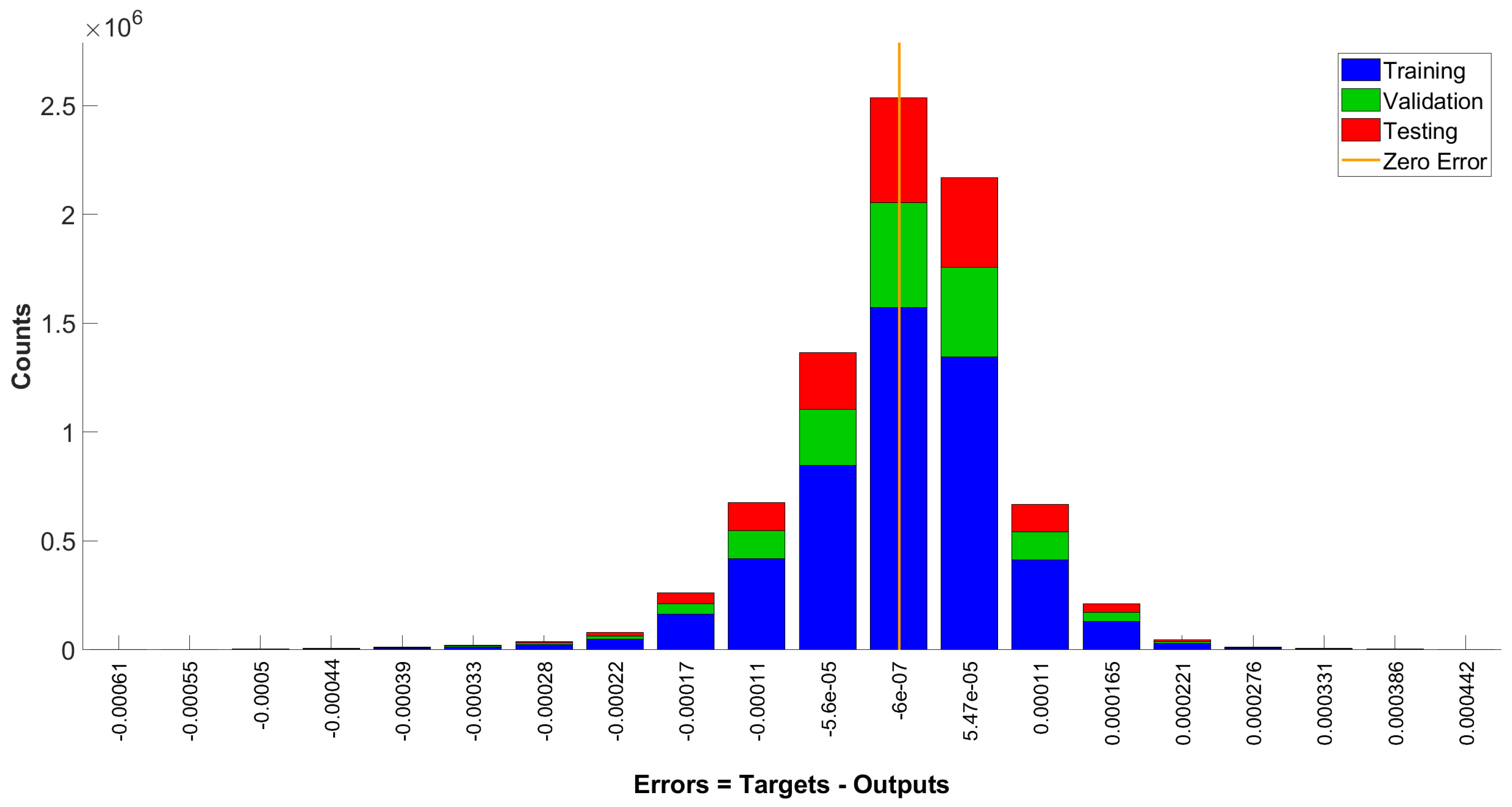
3.2. Neural Network Model
3.3. RTO and Controller Design
3.3.1. RTO Design
3.3.2. Controller Design
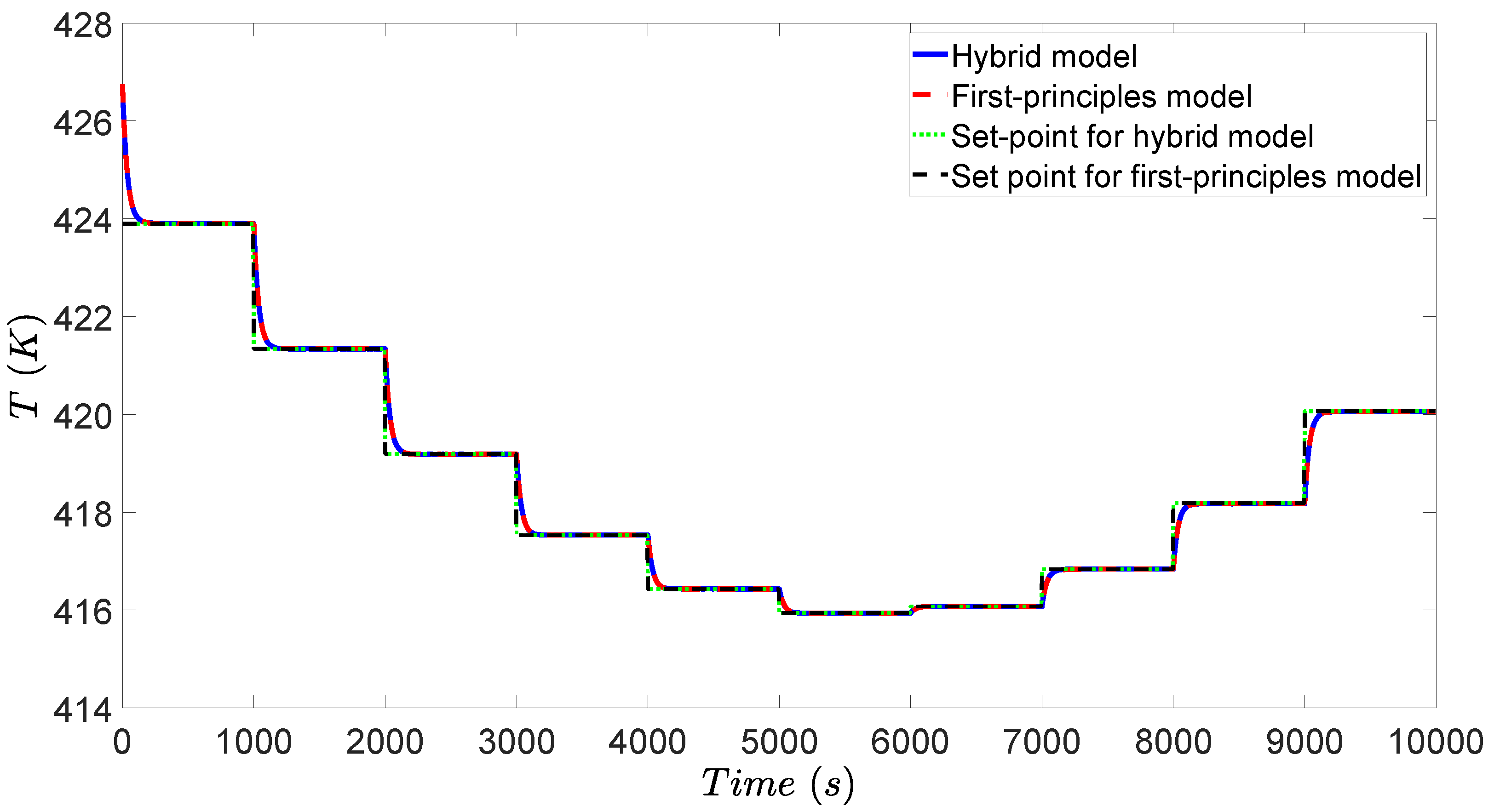
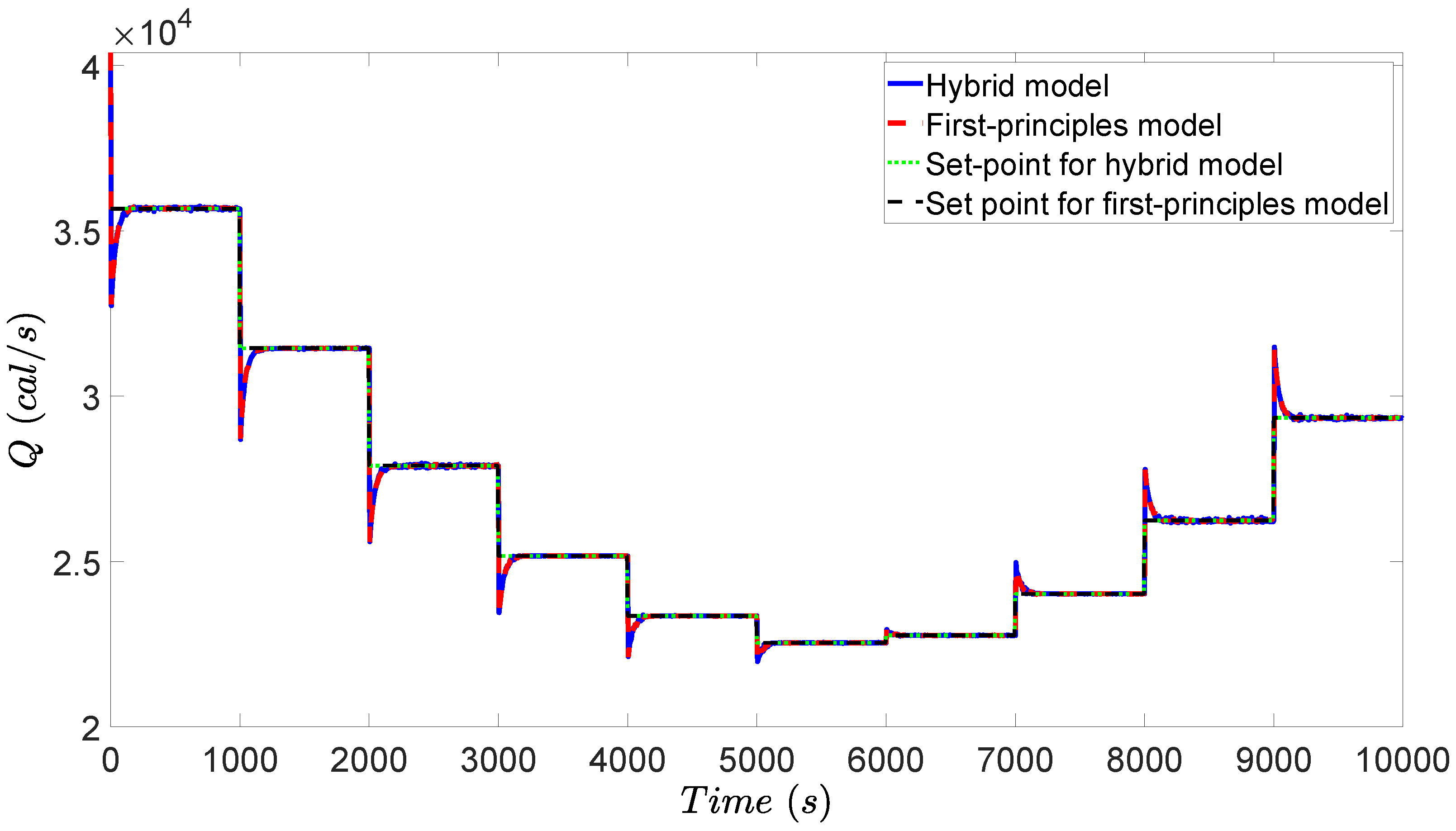
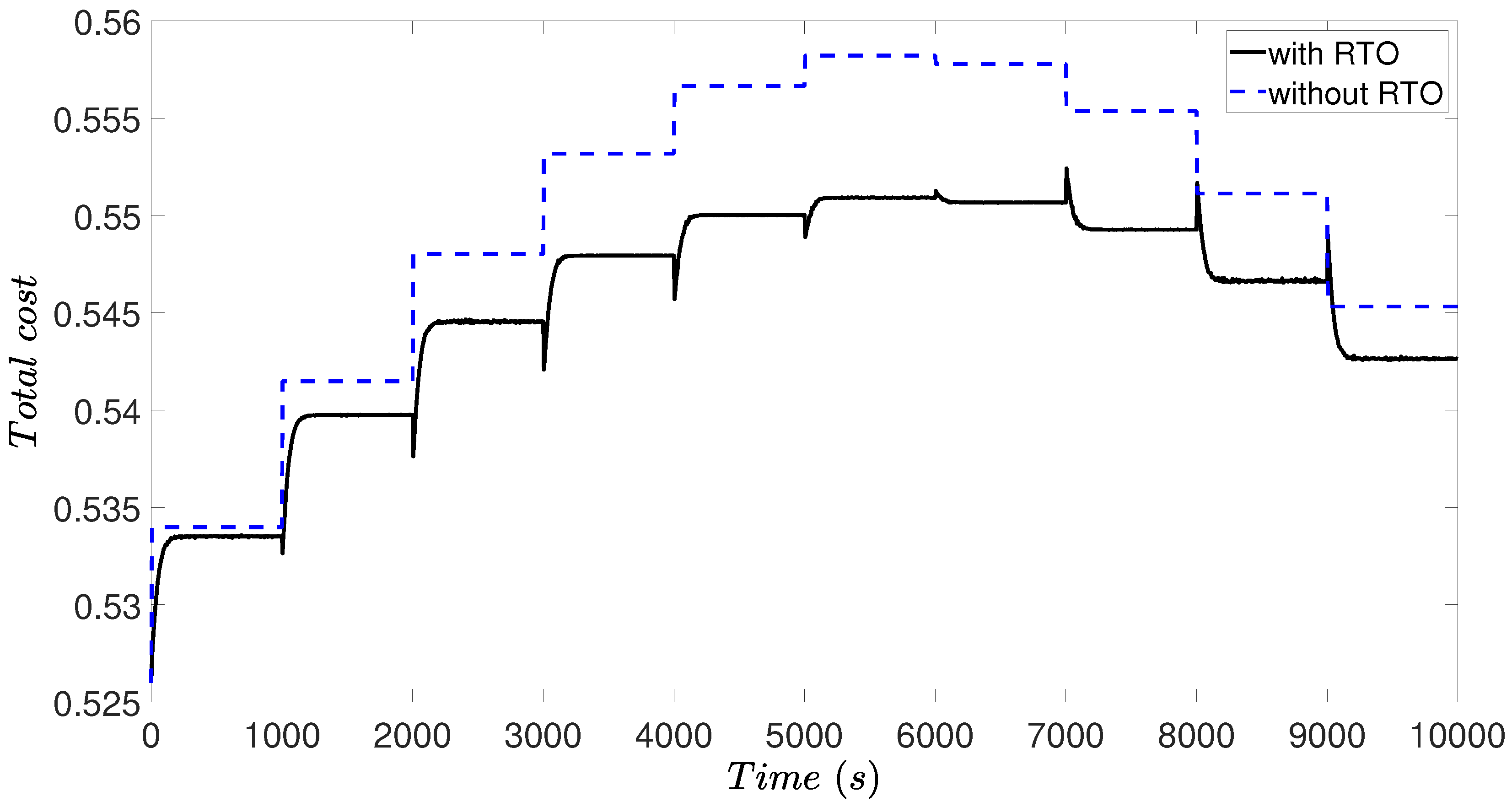
3.4. Simulation Results
4. Application to a Distillation Column
4.1. Process Description, Simulation, and Model
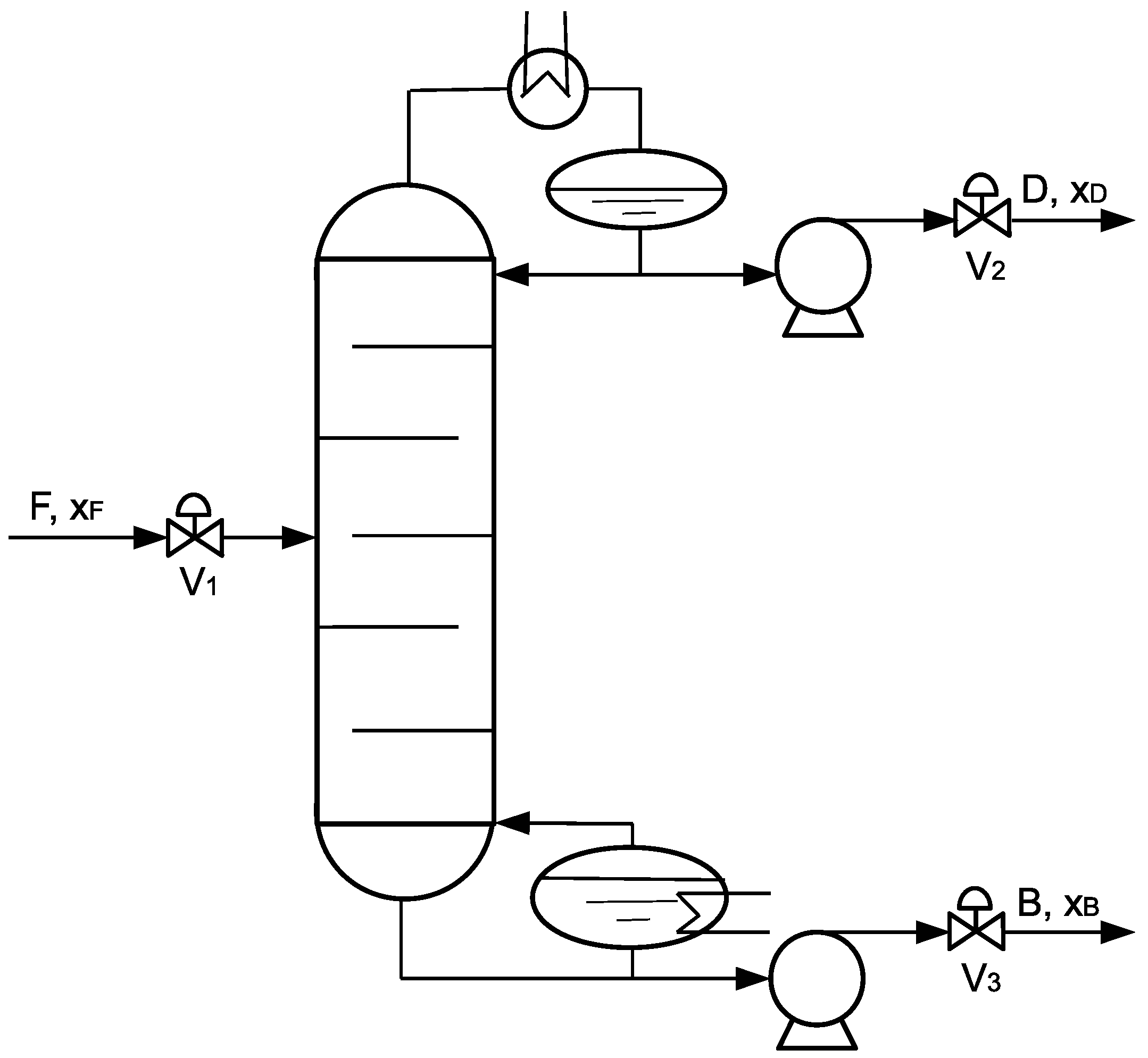
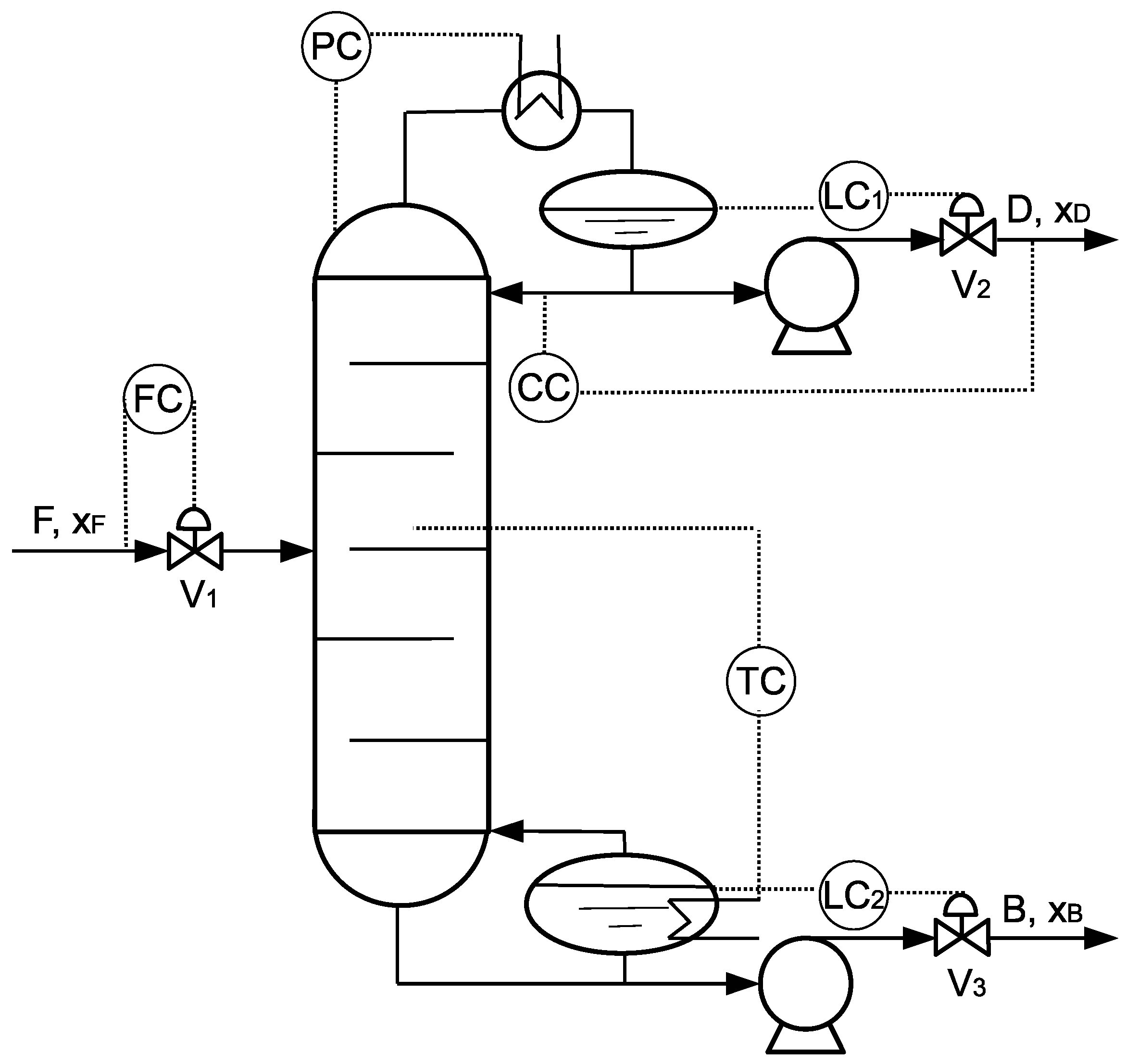
4.1.1. Process Description
4.1.2. Process Model
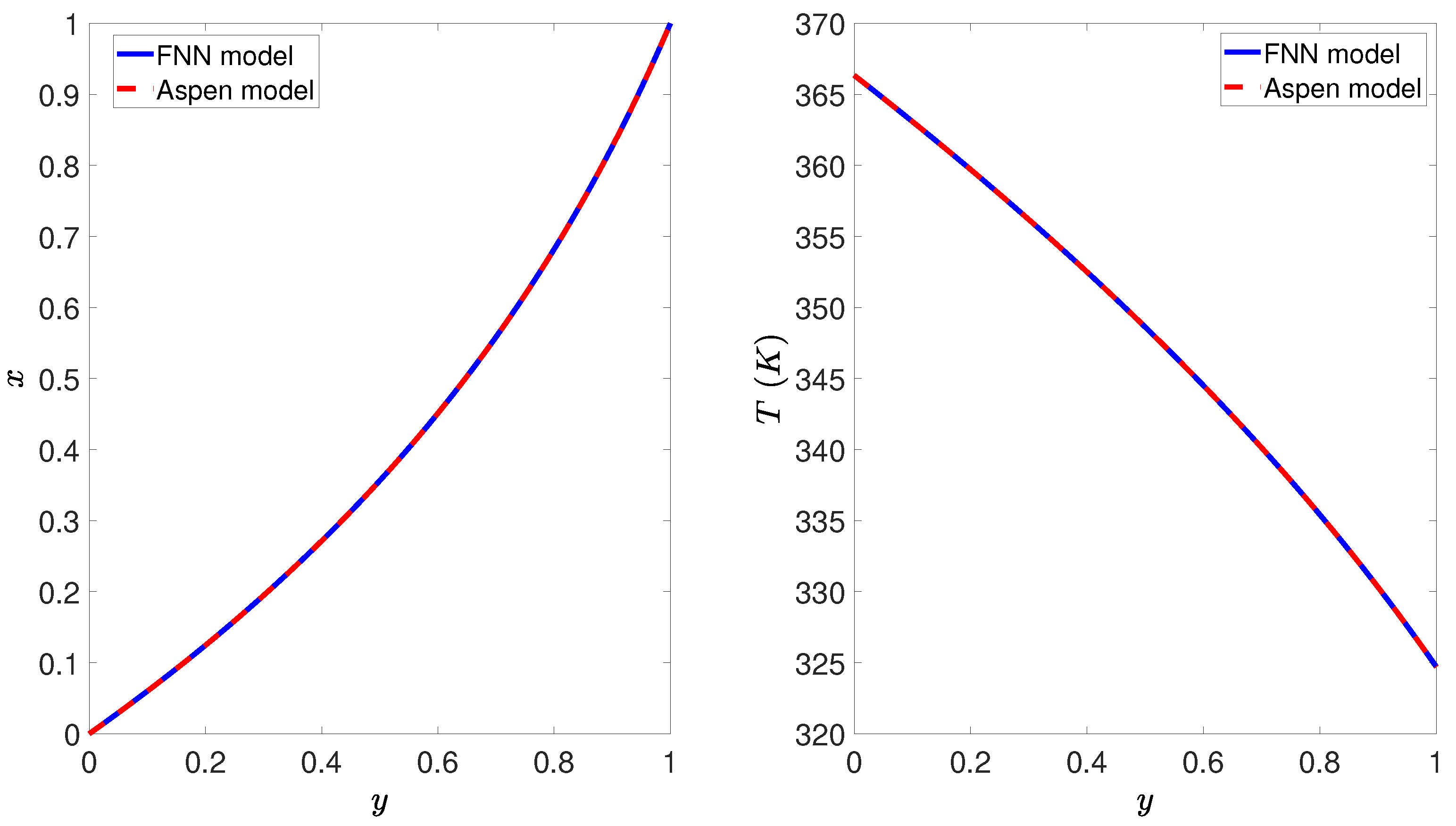
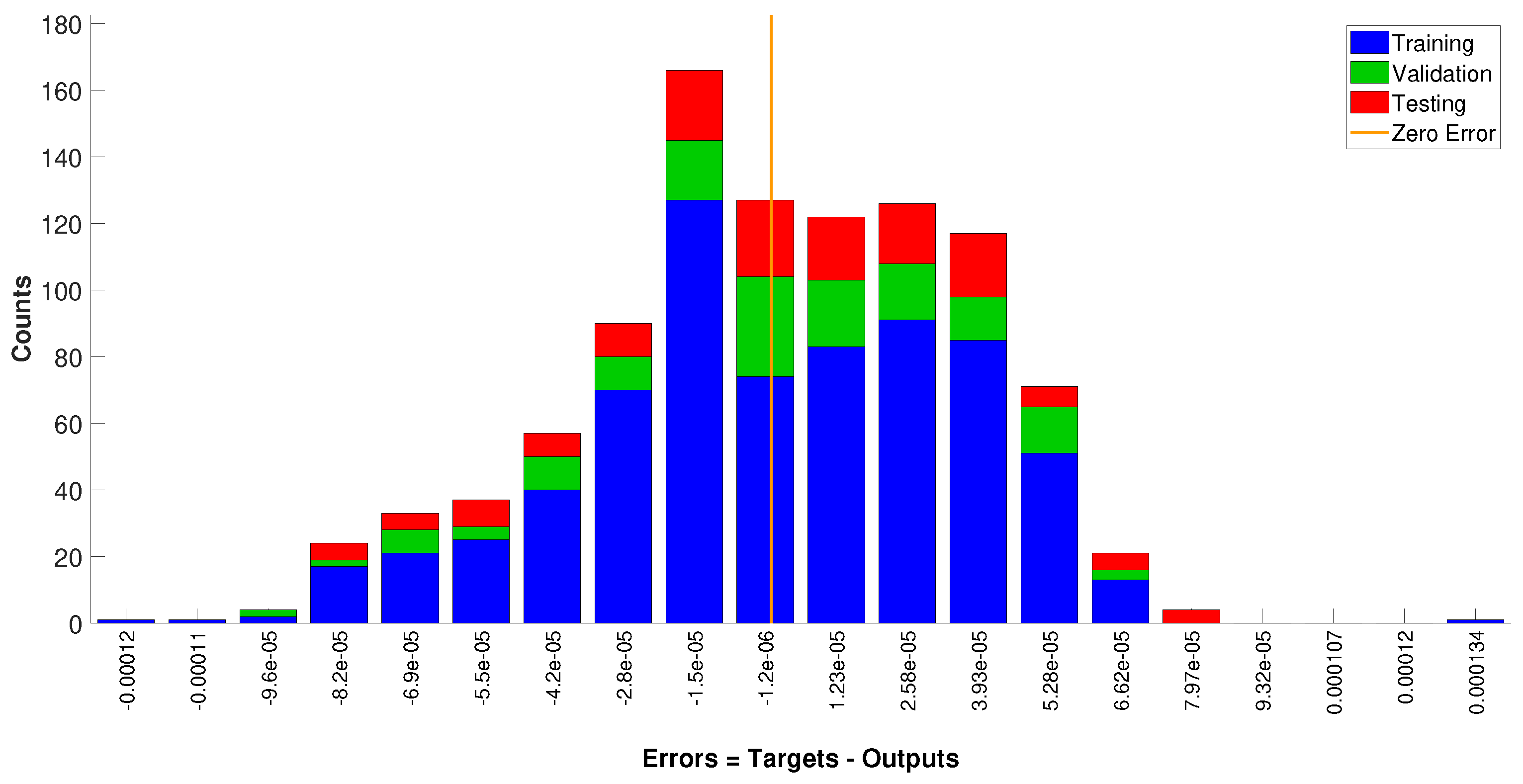
4.2. Neural Network Model
4.3. RTO and Controller Design
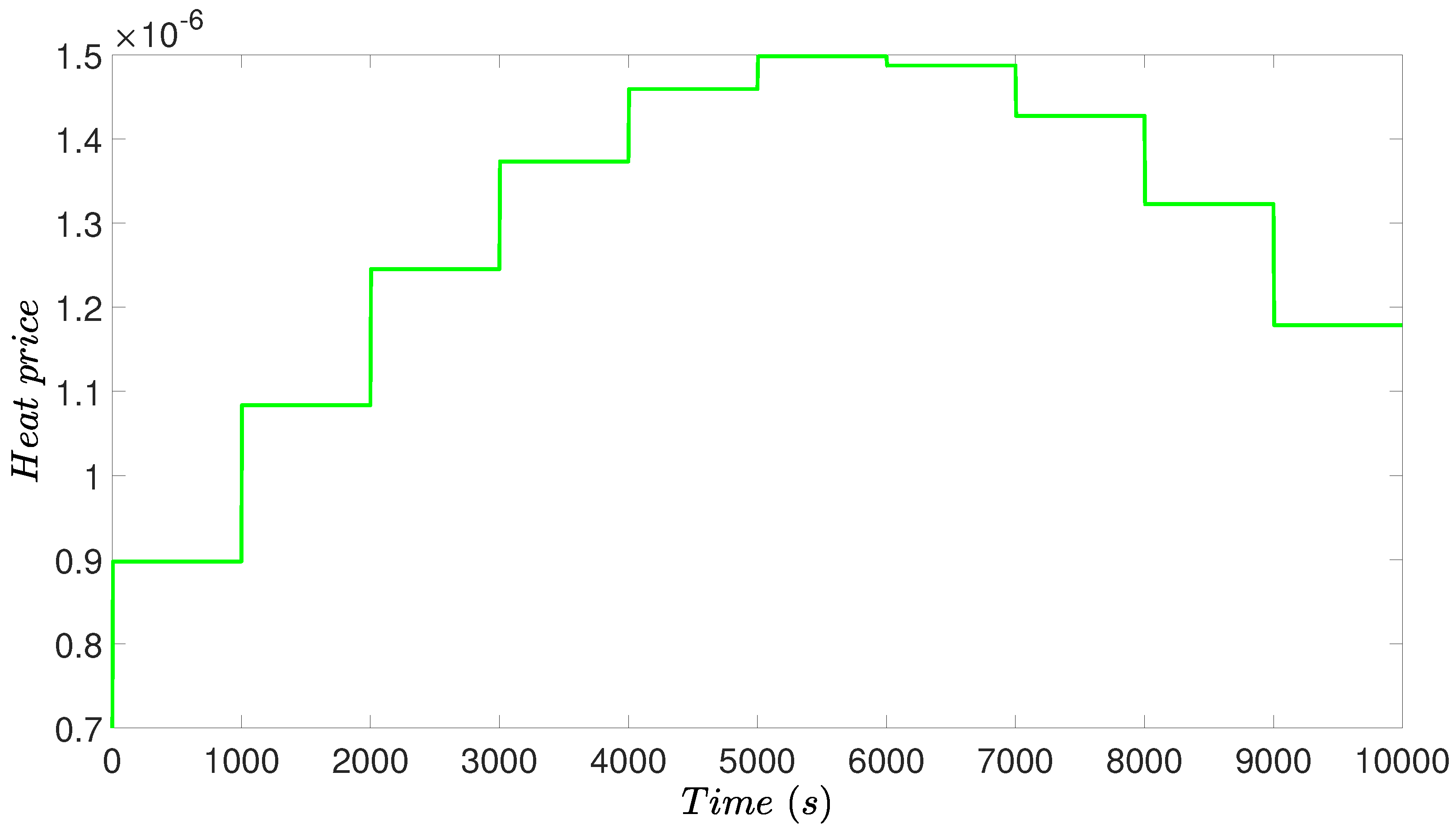
4.3.1. RTO Design
4.3.2. Controller Design
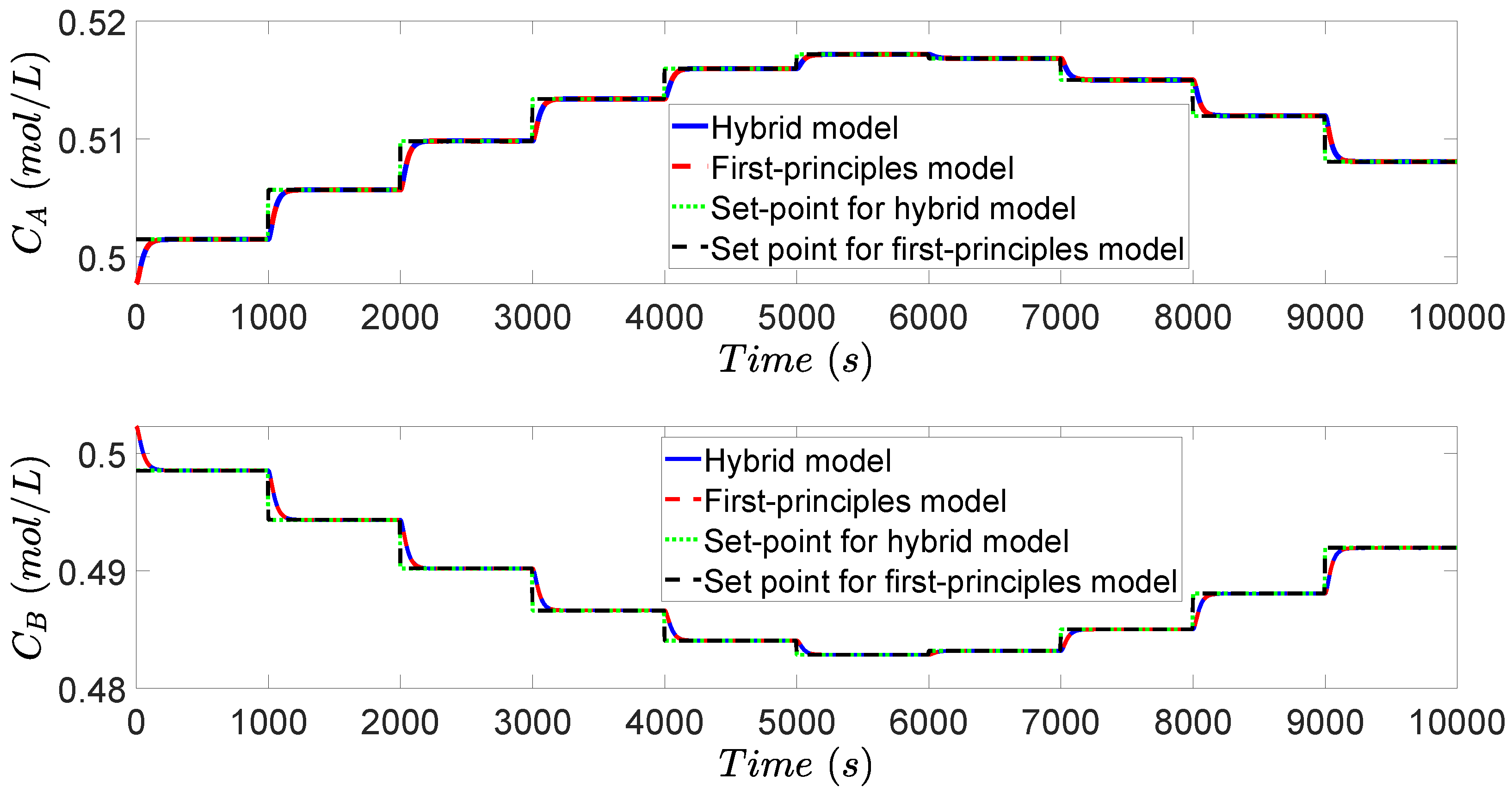
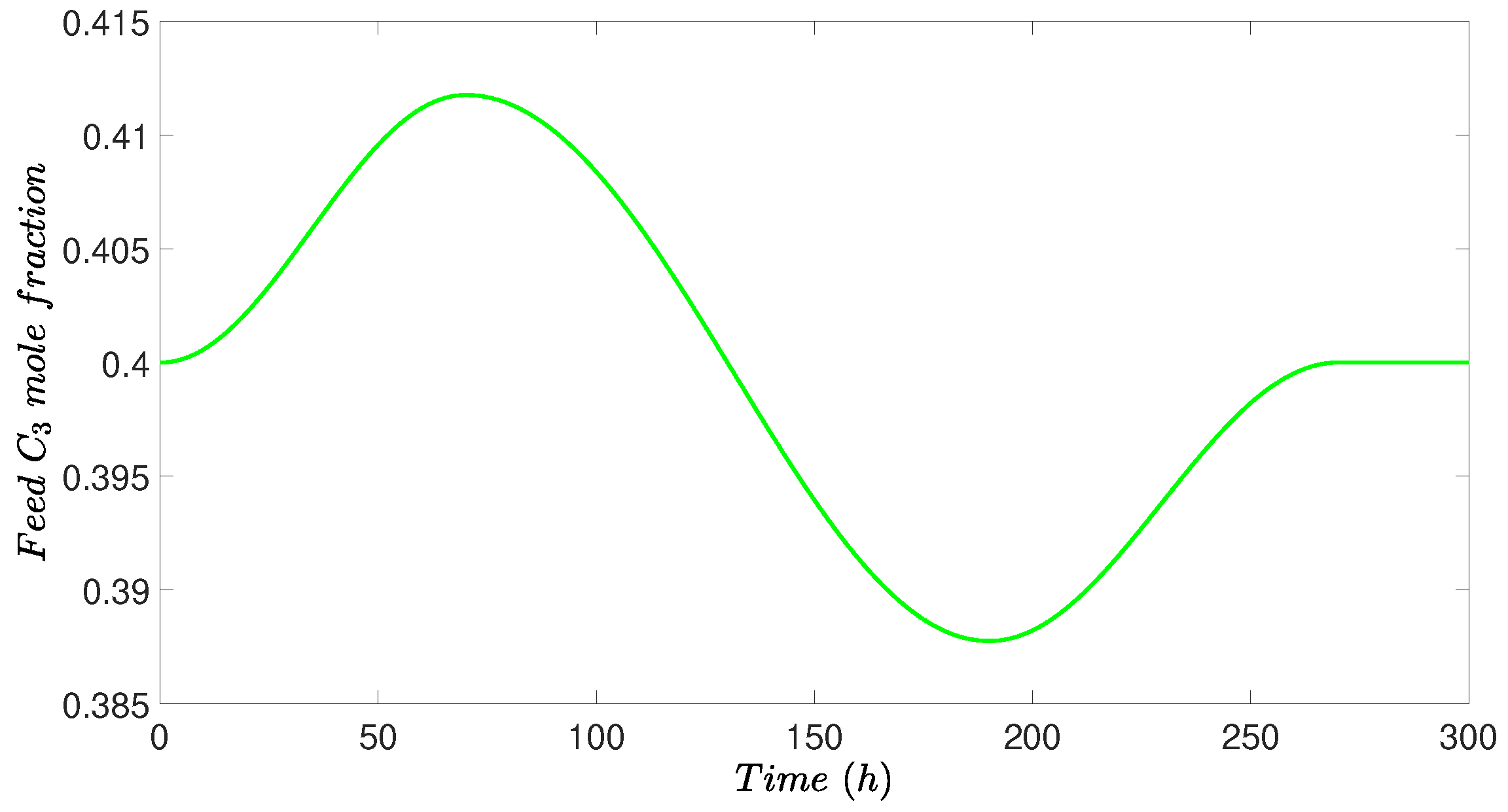
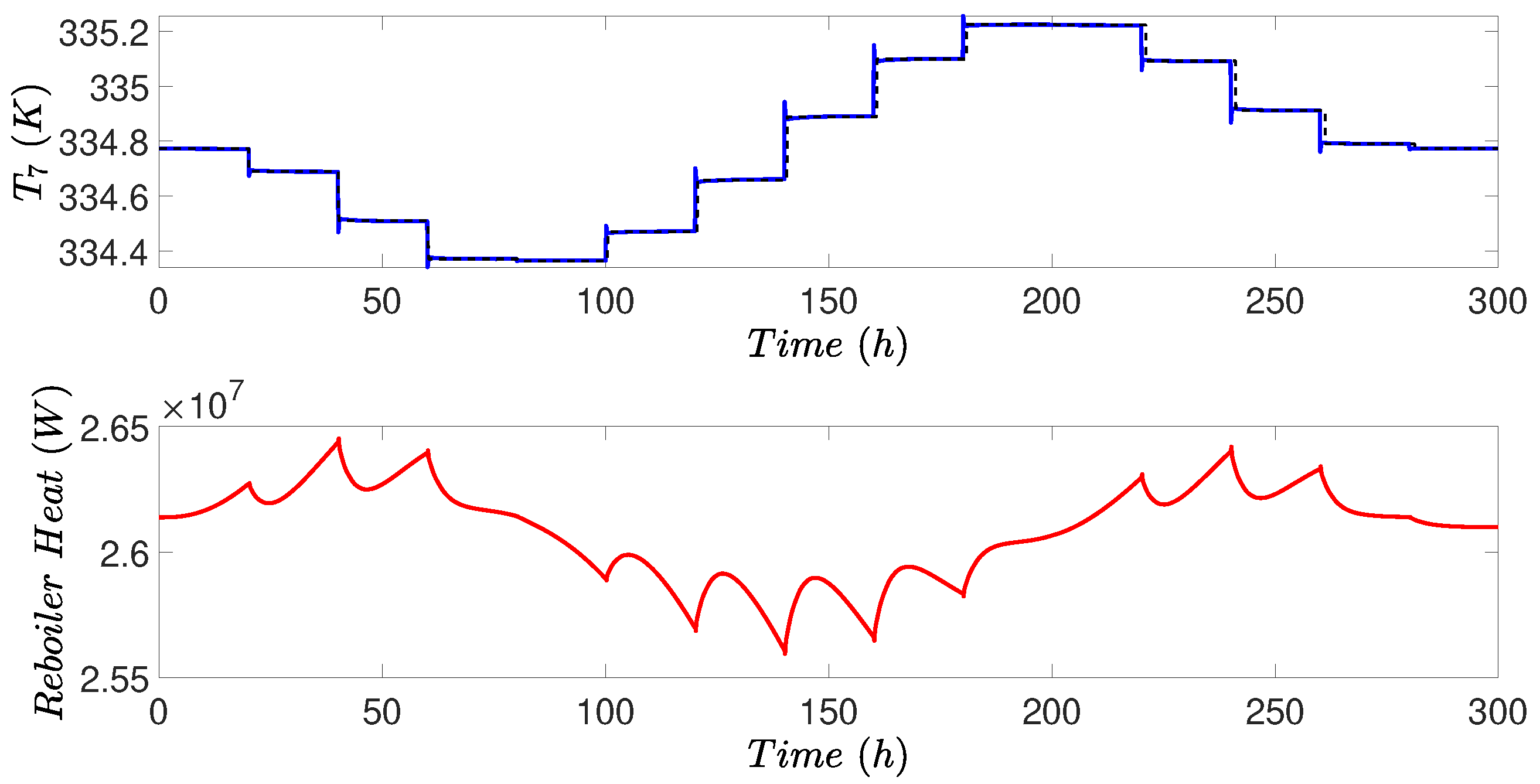
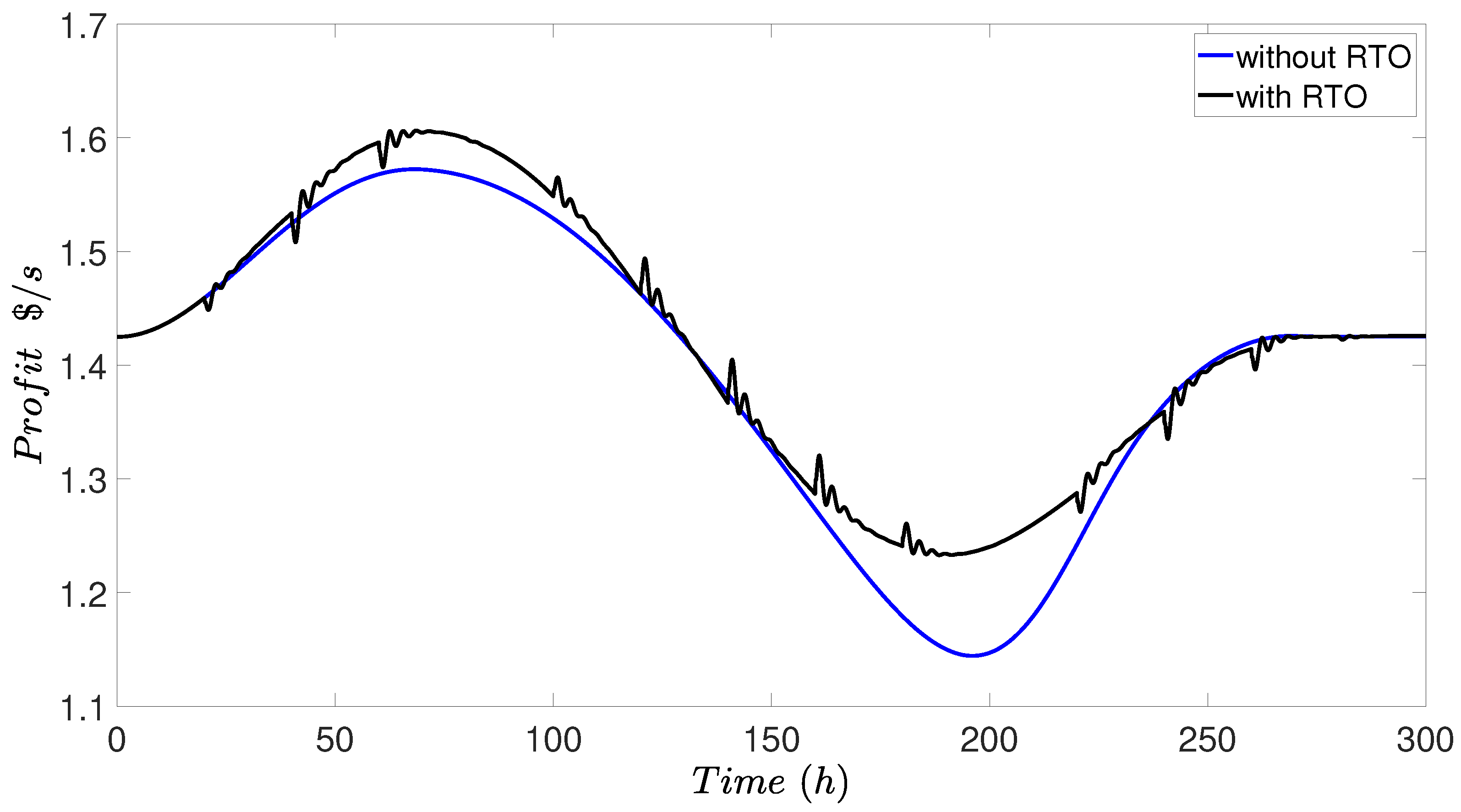
4.4. Simulation Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bhutani, N.; Rangaiah, G.; Ray, A. First-principles, data-based, and hybrid modeling and optimization of an industrial hydrocracking unit. Ind. Eng. Chem. Res. 2006, 45, 7807–7816. [Google Scholar] [CrossRef]
- Pantelides, C.C.; Renfro, J. The online use of first-principles models in process operations: Review, current status and future needs. Comput. Chem. Eng. 2013, 51, 136–148. [Google Scholar] [CrossRef]
- Quelhas, A.D.; de Jesus, N.J.C.; Pinto, J.C. Common vulnerabilities of RTO implementations in real chemical processes. Can. J. Chem. Eng. 2013, 91, 652–668. [Google Scholar] [CrossRef]
- Wu, Z.; Tran, A.; Rincon, D.; Christofides, P.D. Machine Learning-Based Predictive Control of Nonlinear Processes. Part I: Theory. AIChE J. 2019, 65, e16729. [Google Scholar] [CrossRef]
- Wu, Z.; Tran, A.; Rincon, D.; Christofides, P.D. Machine Learning-Based Predictive Control of Nonlinear Processes. Part II: Computational Implementation. AIChE J. 2019, 65, e16734. [Google Scholar] [CrossRef]
- Lee, M.; Park, S. A new scheme combining neural feedforward control with model-predictive control. AIChE J. 1992, 38, 193–200. [Google Scholar] [CrossRef]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally? AIChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- Himmelblau, D. Applications of artificial neural networks in chemical engineering. Korean J. Chem. Eng. 2000, 17, 373–392. [Google Scholar] [CrossRef]
- Chouai, A.; Laugier, S.; Richon, D. Modeling of thermodynamic properties using neural networks: Application to refrigerants. Fluid Phase Equilib. 2002, 199, 53–62. [Google Scholar] [CrossRef]
- Galván, I.M.; Zaldívar, J.M.; Hernandez, H.; Molga, E. The use of neural networks for fitting complex kinetic data. Comput. Chem. Eng. 1996, 20, 1451–1465. [Google Scholar] [CrossRef]
- Faúndez, C.A.; Quiero, F.A.; Valderrama, J. Phase equilibrium modeling in ethanol+ congener mixtures using an artificial neural network. Fluid Phase Equilib. 2010, 292, 29–35. [Google Scholar] [CrossRef]
- Fu, K.; Chen, G.; Sema, T.; Zhang, X.; Liang, Z.; Idem, R.; Tontiwachwuthikul, P. Experimental study on mass transfer and prediction using artificial neural network for CO2 absorption into aqueous DETA. Chem. Eng. Sci. 2013, 100, 195–202. [Google Scholar] [CrossRef]
- Bakshi, B.; Koulouris, A.; Stephanopoulos, G. Wave-Nets: Novel learning techniques, and the induction of physically interpretable models. In Wavelet Applications; International Society for Optics and Photonics: Orlando, FL, USA, 1994; Volume 2242, pp. 637–648. [Google Scholar]
- Lu, Y.; Rajora, M.; Zou, P.; Liang, S. Physics-embedded machine learning: Case study with electrochemical micro-machining. Machines 2017, 5, 4. [Google Scholar] [CrossRef]
- Psichogios, D.C.; Ungar, L.H. A hybrid neural network-first principles approach to process modeling. AIChE J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Oliveira, R. Combining first principles modelling and artificial neural networks: A general framework. Comput. Chem. Eng. 2004, 28, 755–766. [Google Scholar] [CrossRef]
- Chen, L.; Bernard, O.; Bastin, G.; Angelov, P. Hybrid modelling of biotechnological processes using neural networks. Control Eng. Pract. 2000, 8, 821–827. [Google Scholar] [CrossRef]
- Georgieva, P.; Meireles, M.; de Azevedo, S. Knowledge-based hybrid modelling of a batch crystallisation when accounting for nucleation, growth and agglomeration phenomena. Chem. Eng. Sci. 2003, 58, 3699–3713. [Google Scholar] [CrossRef]
- Schuppert, A.; Mrziglod, T. Hybrid Model Identification and Discrimination with Practical Examples from the Chemical Industry. In Hybrid Modeling in Process Industries; CRC Press: Boca Raton, FL, USA, 2018; pp. 63–88. [Google Scholar]
- Qin, S.; Badgwell, T. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Câmara, M.; Quelhas, A.; Pinto, J. Performance evaluation of real industrial RTO systems. Processes 2016, 4, 44–64. [Google Scholar] [CrossRef]
- Lee, W.J.; Na, J.; Kim, K.; Lee, C.; Lee, Y.; Lee, J.M. NARX modeling for real-time optimization of air and gas compression systems in chemical processes. Comput. Chem. Eng. 2018, 115, 262–274. [Google Scholar] [CrossRef]
- Agbi, C.; Song, Z.; Krogh, B. Parameter identifiability for multi-zone building models. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 6951–6956. [Google Scholar]
- Yen-Di Tsen, A.; Jang, S.S.; Wong, D.S.H.; Joseph, B. Predictive control of quality in batch polymerization using hybrid ANN models. AIChE J. 1996, 42, 455–465. [Google Scholar] [CrossRef]
- Klimasauskas, C.C. Hybrid modeling for robust nonlinear multivariable control. ISA Trans. 1998, 37, 291–297. [Google Scholar] [CrossRef]
- Chang, J.; Lu, S.; Chiu, Y. Dynamic modeling of batch polymerization reactors via the hybrid neural-network rate-function approach. Chem. Eng. J. 2007, 130, 19–28. [Google Scholar] [CrossRef]
- Noor, R.M.; Ahmad, Z.; Don, M.M.; Uzir, M.H. Modelling and control of different types of polymerization processes using neural networks technique: A review. Can. J. Chem. Eng. 2010, 88, 1065–1084. [Google Scholar] [CrossRef]
- Wang, J.; Cao, L.L.; Wu, H.Y.; Li, X.G.; Jin, Q.B. Dynamic modeling and optimal control of batch reactors, based on structure approaching hybrid neural networks. Ind. Eng. Chem. Res. 2011, 50, 6174–6186. [Google Scholar] [CrossRef]
- Chaffart, D.; Ricardez-Sandoval, L.A. Optimization and control of a thin film growth process: A hybrid first principles/artificial neural network based multiscale modelling approach. Comput. Chem. Eng. 2018, 119, 465–479. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Mitsos, A. Deterministic global optimization with artificial neural networks embedded. J. Opt. Theory Appl. 2019, 180, 925–948. [Google Scholar] [CrossRef]
- Wu, Z.; Christofides, P.D. Economic Machine-Learning-Based Predictive Control of Nonlinear Systems. Mathematics 2019, 7, 494. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Naysmith, M.; Douglas, P. Review of real time optimization in the chemical process industries. Dev. Chem. Eng. Miner. Process. 1995, 3, 67–87. [Google Scholar] [CrossRef]
- Rawlings, J.; Amrit, R. Optimizing process economic performance using model predictive control. In Nonlinear Model Predictive Control; Springer: Berlin, Germany, 2009; pp. 19–138. [Google Scholar]
- Ellis, M.; Durand, H.; Christofides, P. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Bonné, D.; Jørgensen, J.B.; Venkat, A.N.; Jørgensen, S.B. Unreachable setpoints in model predictive control. IEEE Transa. Autom. Control 2008, 53, 2209–2215. [Google Scholar] [CrossRef]
- Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Stabilization of nonlinear systems with state and control constraints using Lyapunov-based predictive control. Syst. Control Lett. 2006, 55, 650–659. [Google Scholar] [CrossRef]
- Wang, L. Continuous time model predictive control design using orthonormal functions. Int. J. Control 2001, 74, 1588–1600. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Cotorruelo, A.; Limon, D.; Garone, E. Constrained Control of Linear Systems Subject to Combinations of Intersections and Unions of Concave Constraints. IEEE Control Syst. Lett. 2019, 3, 571–576. [Google Scholar] [CrossRef]
- Daoutidis, P.; Kravaris, C. Dynamic output feedback control of minimum-phase multivariable nonlinear processes. Chem. Eng. Sci. 1994, 49, 433–447. [Google Scholar] [CrossRef][Green Version]
- Economou, C.; Morari, M.; Palsson, B. Internal model control: Extension to nonlinear system. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 403–411. [Google Scholar] [CrossRef]
- Lin, Y.; Sontag, E. A universal formula for stabilization with bounded controls. Syst. Control Lett. 1991, 16, 393–397. [Google Scholar] [CrossRef]
- Luyben, W.L. Distillation Design and Control Using Aspen Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Al-Malah, K.I. Aspen Plus: Chemical Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Aspen Technology, Inc. Aspen Plus User Guide; Aspen Technology, Inc.: Cambridge, MA, USA, 2003. [Google Scholar]


| K | s |
| /s | /s |
| cal/mol | cal/mol |
| cal/(mol K) | cal/mol |
| kg/L | cal/(kg K) |
| mol/L | L |
| mol/L | mol/L |
| K | cal/s |
| F = 1 kmol | = 0.4 |
| K | atm |
| q = 1.24 | = 14 |
| = 30 | m |
| m | m |
| m | |
| steady-state condition: | R = 3.33 |
| atm | atm |
| B = 0.61 kmol/L | D = 0.39 kmol/L |
| W | W |
| KC | τI/min | |
|---|---|---|
| FC | 0.5 | 0.3 |
| PC | 15 | 12 |
| LC1 | 2 | 150 |
| LC2 | 4 | 150 |
| CC | 0.1 | 20 |
| TC | 0.6 | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wu, Z.; Rincon, D.; Christofides, P.D. Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning. Mathematics 2019, 7, 890. https://doi.org/10.3390/math7100890
Zhang Z, Wu Z, Rincon D, Christofides PD. Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning. Mathematics. 2019; 7(10):890. https://doi.org/10.3390/math7100890
Chicago/Turabian StyleZhang, Zhihao, Zhe Wu, David Rincon, and Panagiotis D. Christofides. 2019. "Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning" Mathematics 7, no. 10: 890. https://doi.org/10.3390/math7100890
APA StyleZhang, Z., Wu, Z., Rincon, D., & Christofides, P. D. (2019). Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning. Mathematics, 7(10), 890. https://doi.org/10.3390/math7100890





