Convergence Theorems for Generalized Viscosity Explicit Methods for Nonexpansive Mappings in Banach Spaces and Some Applications
Abstract
1. Introduction
2. Preliminaries
- (1)
- E is uniformly convex.
- (2)
- There is a strictly-increasing, continuous, and convex function such that and:for all .
- (i)
- ;
- (ii)
- or .
3. The Main Results
- (C1)
- and ;
- (C2)
- .
- (1)
- (2)
- (3)
- We give new control conditions and techniques to prove our results.
- (4)
- (5)
- Our results are applicable for the family of nonexpansive mappings, for example -mapping, a countable family of nonexpansive mappings, and nonexpansive semigroups.
Open Problem
4. Convergence Theorems for a Strict Pseudo-Contraction Mapping
5. Some Applications
5.1. Periodic Solution of a Nonlinear Evolution Equation
- (1)
- and ;
- (2)
- and ;
- (3)
- There exists a mild solution u of the Equation (31) on for each initial value ;
- (4)
- There exists some such that for all with and .
5.2. Nonlinear Fredholm Integral Equation
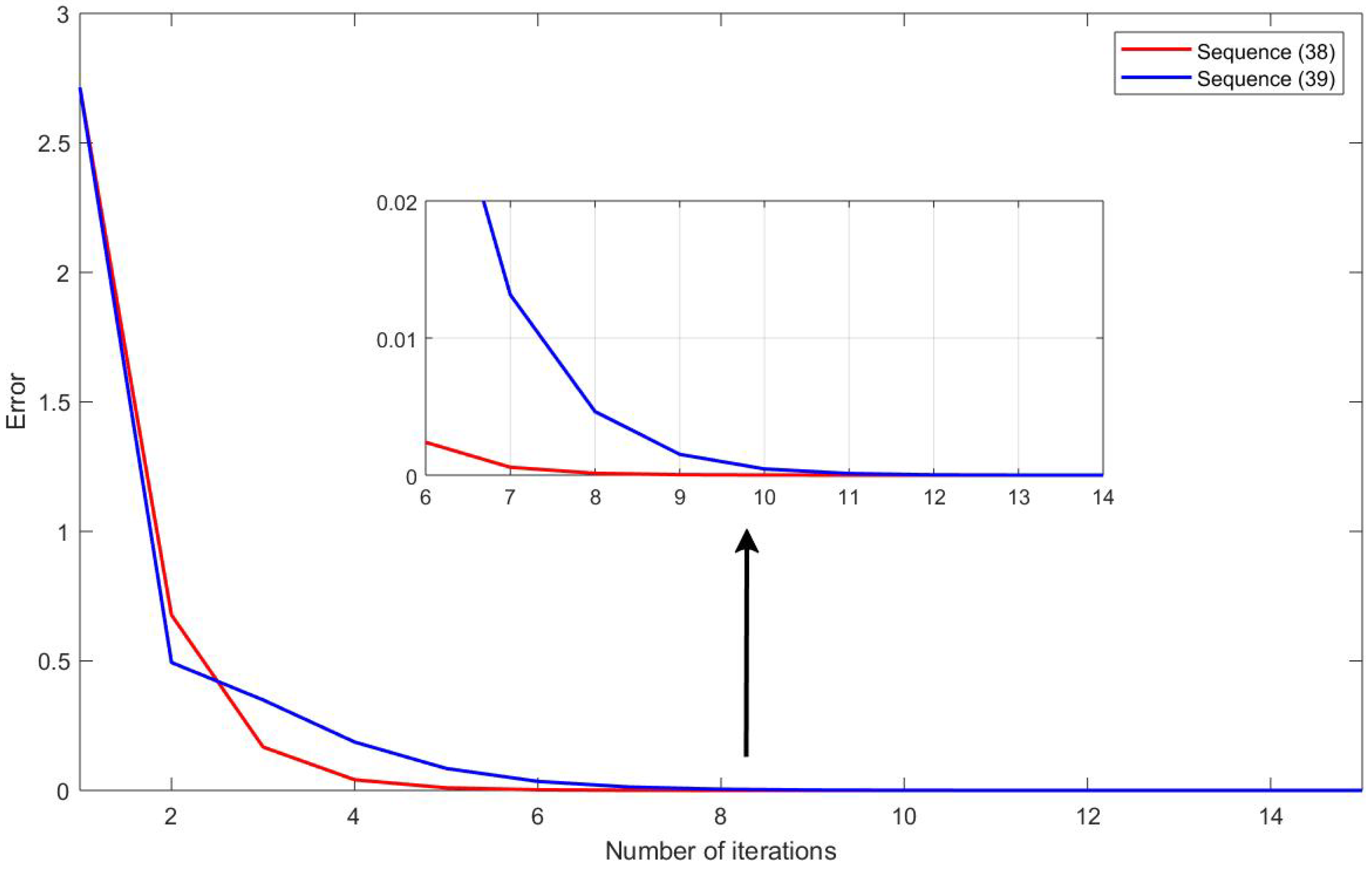
6. Numerical Examples
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Auzinger, W.; Frank, R. Asymptotic error expansions for stiff equations: an analysis for the implicit midpoint and trapezoidal rules in the strongly stiff case. Numer. Math. 1989, 56, 469–499. [Google Scholar] [CrossRef]
- Bader, G.; Deuflhard, P. A semi-implicit mid-point rule for stiff systems of ordinary differential equations. Numer. Math. 1983, 41, 373–398. [Google Scholar] [CrossRef]
- Deuflhard, P. Recent progress in extrapolation methods for ordinary differential equations. SIAM Rev. 1985, 27, 505–535. [Google Scholar] [CrossRef]
- Schneider, C. Analysis of the linearly implicit mid-point rule for differential-algebra equations. Electron. Trans. Numer. Anal. 1993, 1, 1–10. [Google Scholar]
- Somalia, S. Implicit midpoint rule to the nonlinear degenerate boundary value problems. Internat. J. Comput. Math. 2002, 79, 327–332. [Google Scholar] [CrossRef]
- Veldhuxzen, M.V. Asymptotic expansions of the global error for the implicit midpoint rule (stiff case). Computing 1984, 33, 185–192. [Google Scholar] [CrossRef]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd ed.; Springer Series in Computational Mathematics; Springer: Berlin, Germany, 1993. [Google Scholar]
- Xu, H.K.; Alghamdi, M.A.; Shahzad, N. The viscosity technique for the implicit midpoint rule of nonexpansive mappings in Hilbert spaces. Fixed Point Theory Appl. 2015, 2015, 41. [Google Scholar] [CrossRef]
- Moudafi, A. Viscosity approximation methods for fixed point problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef]
- Cho, Y.J.; Qin, X. Viscosity approximation methods for a finite family of m-accretive mappings in reflexive Banach spaces. Positivity 2008, 12, 483–494. [Google Scholar] [CrossRef]
- Qin, X.; Cho, Y.J.; Kang, S.M. Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Anal. 2010, 72, 99–112. [Google Scholar] [CrossRef]
- Wang, S.H.; Zhao, M.; Kumam, P.; Cho, Y.J. A viscosity extragradient method for an equilibrium problem and fixed point problem in Hilbert spaces. J. Fixed Point Theory Appl. 2018, 20, 19. [Google Scholar] [CrossRef]
- Eshita, K.; Takahashi, W. Approximating zero points of accretive operators in general Banach spaces. J. Fixed Point Theory Appl. 2007, 2, 105–116. [Google Scholar]
- Chen, R.; Song, Y.; Zhou, H. Convergence theorems for implicit iteration process for a finite family of continuous pseudocontractive mappings. J. Math. Anal. Appl. 2006, 314, 701–709. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Fixed Point Theory for Lipschitzian-Type Mappings with Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Censor, Y.; Elfving, T. A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Byrne, C. A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 2008, 20, 103–120. [Google Scholar] [CrossRef]
- Xu, H.K. A variable Krasnoselskii–Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 2006, 22, 2021–2034. [Google Scholar] [CrossRef]
- Censor, Y.; Bortfeld, T.; Martin, B.; Trofimov, A. A unified approach for inversion problems in intensity-modulated radiation therapy. Phys. Med. Biol. 2006, 51, 2353–2365. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Shahzad, N.; Xu, H.K. The implicit midpoint rule for nonexpansive mappings. Fixed Point Theory Appl. 2014, 2014, 96. [Google Scholar] [CrossRef]
- Ke, Y.; Ma, C. The generalized viscosity implicit rules of nonexpansive mappings in Hilbert spaces. Fixed Point Theory Appl. 2015, 2015, 190. [Google Scholar] [CrossRef]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Palais, R.S.; Palais, R.A. Differential Equations, Mechanics and Computation; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Moaveni, S. Finite Element Analysis Theory And Application With Ansys, 3rd ed.; Pearson Education: London, UK, 2008. [Google Scholar]
- Marino, G.; Scardamaglia, B.; Zaccone, R. A general viscosity explicit midpoint rule for quasi-nonexpansive mappings. J. Nonlinear Convex Anal. 2017, 18, 137–148. [Google Scholar]
- Takahashi, W. Nonlinear Functional Analysis; Yokohama Publishers: Yokohama, Japan, 2000. [Google Scholar]
- Liu, L.S. Ishikawa and Mann iterative processes with errors for nonlinear strongly accretive mappings in Banach spaces. J. Math. Anal. Appl. 1995, 194, 114–125. [Google Scholar] [CrossRef]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Xu, H.K. Viscosity approximation methods for nonexpansive mappings. J. Math. Anal. Appl. 2004, 298, 279–291. [Google Scholar] [CrossRef]
- Reich, S. Strong convergence theorems for resolvents of accretive operators in Banach spaces. J. Math. Anal. Appl. 1980, 75, 287–292. [Google Scholar] [CrossRef]
- Kopecka, E.; Reich, S. Approximating fixed points in the Hilbert ball. J. Nonlinear Convex Anal. 2014, 15, 819–829. [Google Scholar]
- Song, Y.; Chen, R.; Zhou, H. Viscosity approximation methods for nonexpansive mapping sequences in Banach spaces. Nonlinear Anal. 2007, 66, 1016–1024. [Google Scholar] [CrossRef]
- Xu, H.K. Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66, 240–256. [Google Scholar] [CrossRef]
- Reich, S. Constructive Techniques for Accretive and Monotone Operator. In Applied Nonlinear Analysis; Academic Press: Cambridge, MA, USA, 1979; pp. 335–345. [Google Scholar]
- Maingé, P.E. Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 2008, 16, 899–912. [Google Scholar] [CrossRef]
- Yao, Y.; Shahzad, N.; Liou, Y.C. Modified semi-implicit midpoint rule for nonexpansive mappings. Fixed Point Theory Appl. 2015, 2015, 166. [Google Scholar] [CrossRef]
- Luo, P.; Cai, G.; Shehu, Y. The viscosity iterative algorithms for the implicit midpoint rule of nonexpansive mappings in uniformly smooth Banach spaces. J. Inequal. Appl. 2017, 2017, 154. [Google Scholar] [CrossRef]
- Zhou, H. Convergence theorems for λ-strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Anal. 2008, 69, 3160–3173. [Google Scholar] [CrossRef]
- Browder, F.E. Existence of periodic solutions for nonlinear equations of evolution. Proc. Natl. Acad. Sci. USA 1965, 53, 1100–1103. [Google Scholar] [CrossRef] [PubMed]
- Goebel, K.; Reich, S. Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings; Series of Monographs and Textbooks in Pure and Applied Mathematics; Dekker: New York, NY, USA, 1984. [Google Scholar]
- Nieto, J.J.; Xu, H.K. Solvability of nonlinear Volterra and Fredholm equations in weighted spaces. Nonlinear Anal. 1995, 24, 1289–1297. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Cho, Y.J.; Kumam, P. General iterative algorithms approach to variational inequalities and minimum-norm fixed point for minimization and split feasibility problems. OPSEARCH 2014, 51, 400–415. [Google Scholar] [CrossRef]
| Number of Iterates | ||
|---|---|---|
| 1 | (1.0000000, −2.0000000, 3.0000000, 0, 0, 0, …) | 2.7144176 |
| 2 | (0.2327849, −0.4480184, 0.7292703, 0, 0, 0, …) | 0.6771823 |
| 3 | (0.0526107, −0.0931765, 0.1750471, 0, 0, 0, …) | 0.1675113 |
| 4 | (0.0118323, −0.0180499, 0.0418631, 0, 0, 0, …) | 0.0410437 |
| 5 | (0.0026730, −0.0031216, 0.0099981, 0, 0, 0, …) | 0.0099602 |
| 6 | (0.0006105, −0.0004172, 0.0023865, 0, 0, 0, …) | 0.0023955 |
| 7 | (0.0001418, −9.9203 × , 0.0005694, 0, 0, 0, …) | 5.7233 × |
| 8 | (3.3678 × , 2.2004 × , 0.0001358, 0, 0, 0, …) | 1.3688 × |
| 9 | (8.2042 × , 1.1855 × , 3.2365 × , 0, 0, 0, …) | 3.3056 × |
| 10 | (2.0542 × , 4.6141 × , 7.7051 × , 0, 0, 0, …) | 8.2639 × |
| ⋮ | ⋮ | ⋮ |
| 15 | (2.8321 × , 1.3627 × , 5.6702 × , 0, 0, 0, …) | 1.3986 × |
| Number of Iterates | ||
|---|---|---|
| 1 | (1.0000000, −2.0000000, 3.0000000, 0, 0, 0, …) | 2.7144176 |
| 2 | (−0.0470355, 0.3985926, 0.3853261, 0, 0, 0, …) | 0.4938371 |
| 3 | (0.0337876, 0.3481921, 0.0732708, 0, 0, 0, …) | 0.3493757 |
| 4 | (0.0344241, 0.1863456, 0.0570267, 0, 0, 0, …) | 0.1867381 |
| 5 | (0.0196135, 0.0844269, −0.0054563, 0, 0, 0, …) | 0.0847707 |
| 6 | (0.0091690, 0.0345417, −0.0045213, 0, 0, 0, …) | 0.0347302 |
| 7 | (0.0038295, 0.0130688, −0.0024315, 0, 0, 0, …) | 0.0131499 |
| 8 | (0.0014729, 0.0046081, −0.0011026, 0, 0, 0, …) | 0.0046371 |
| 9 | (5.2742 × , 0.0015100, −4.5084 × , 0, 0, 0, …) | 0.0015180 |
| 10 | (1.7573 × , 4.5282 × , −1.7034 × , 0, 0, 0, …) | 4.5360 × |
| ⋮ | ⋮ | ⋮ |
| 15 | (−1.7307 × , −1.6353 × , −3.0799 × , 0, 0, 0, …) | 8.1981 × |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunthrayuth, P.; Pakkaranang, N.; Kumam, P.; Thounthong, P.; Cholamjiak, P. Convergence Theorems for Generalized Viscosity Explicit Methods for Nonexpansive Mappings in Banach Spaces and Some Applications. Mathematics 2019, 7, 161. https://doi.org/10.3390/math7020161
Sunthrayuth P, Pakkaranang N, Kumam P, Thounthong P, Cholamjiak P. Convergence Theorems for Generalized Viscosity Explicit Methods for Nonexpansive Mappings in Banach Spaces and Some Applications. Mathematics. 2019; 7(2):161. https://doi.org/10.3390/math7020161
Chicago/Turabian StyleSunthrayuth, Pongsakorn, Nuttapol Pakkaranang, Poom Kumam, Phatiphat Thounthong, and Prasit Cholamjiak. 2019. "Convergence Theorems for Generalized Viscosity Explicit Methods for Nonexpansive Mappings in Banach Spaces and Some Applications" Mathematics 7, no. 2: 161. https://doi.org/10.3390/math7020161
APA StyleSunthrayuth, P., Pakkaranang, N., Kumam, P., Thounthong, P., & Cholamjiak, P. (2019). Convergence Theorems for Generalized Viscosity Explicit Methods for Nonexpansive Mappings in Banach Spaces and Some Applications. Mathematics, 7(2), 161. https://doi.org/10.3390/math7020161