A Numerical Study on the Crack Development Behavior of Rock-Like Material Containing Two Intersecting Flaws
Abstract
1. Introduction
2. Numerical Simulation Procedure
3. Results and Discussion
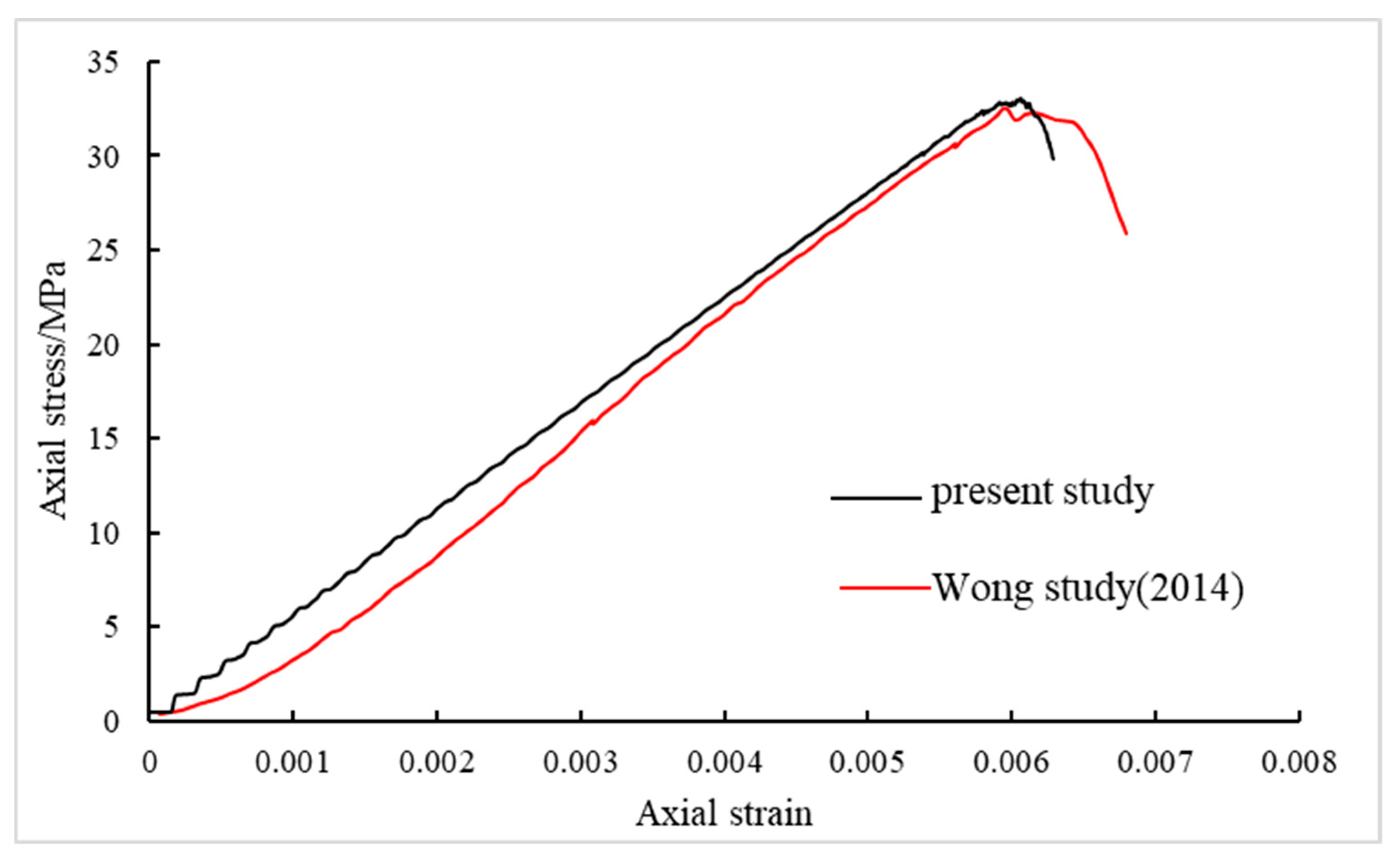
3.1. Mechanical Properties of Intact Models
3.2. Mechanical Behavior of Specimens Containing Flaws
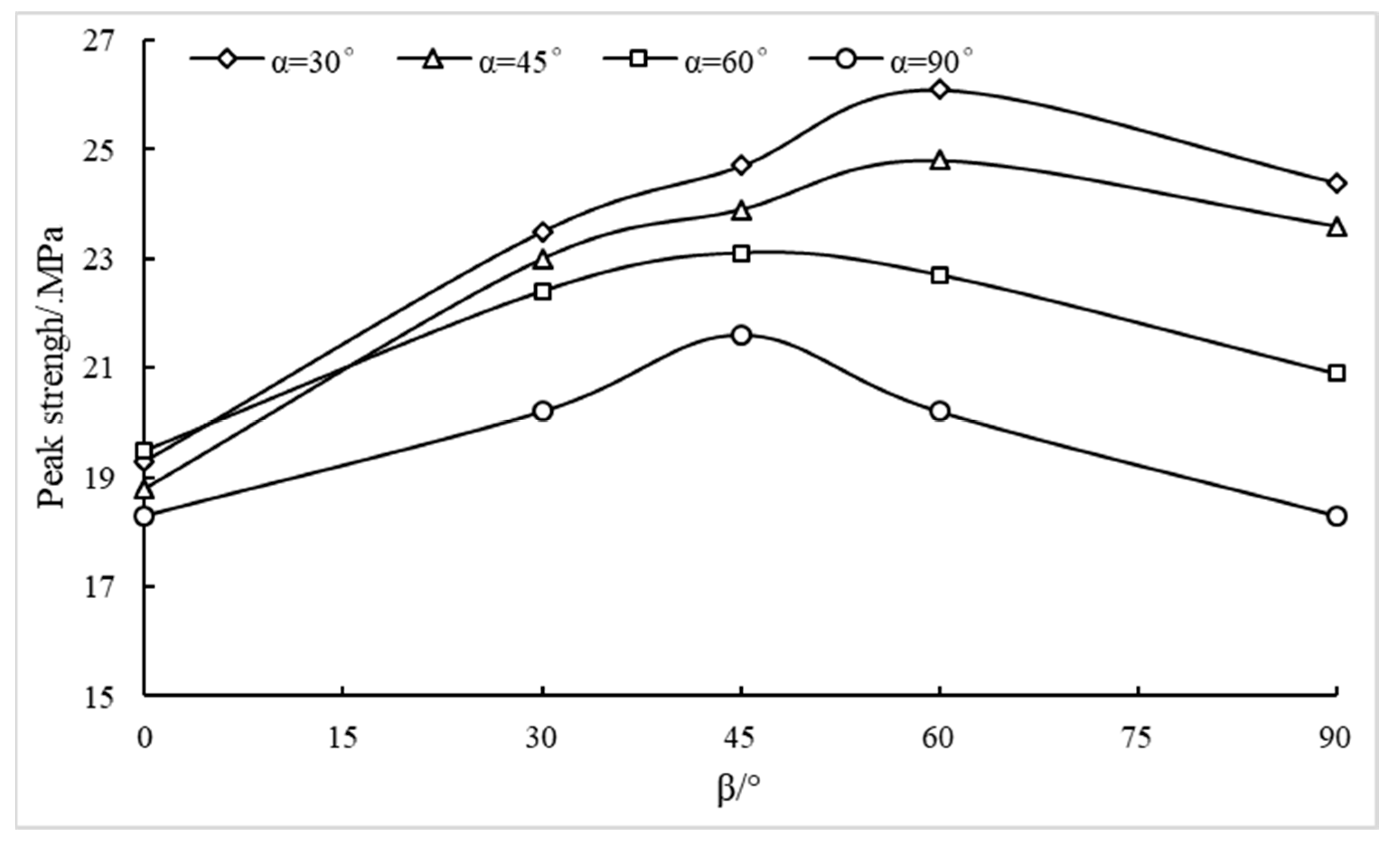
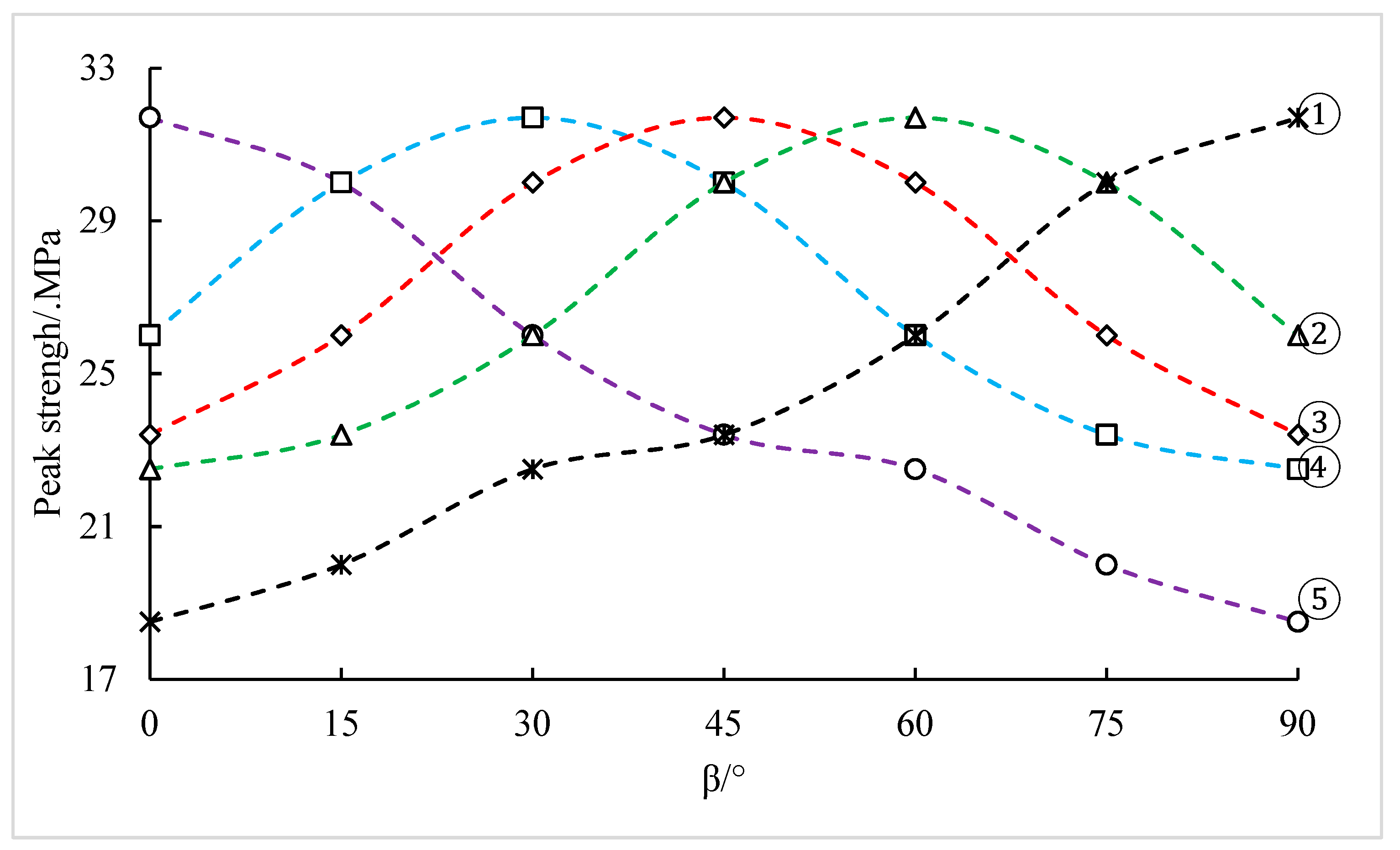
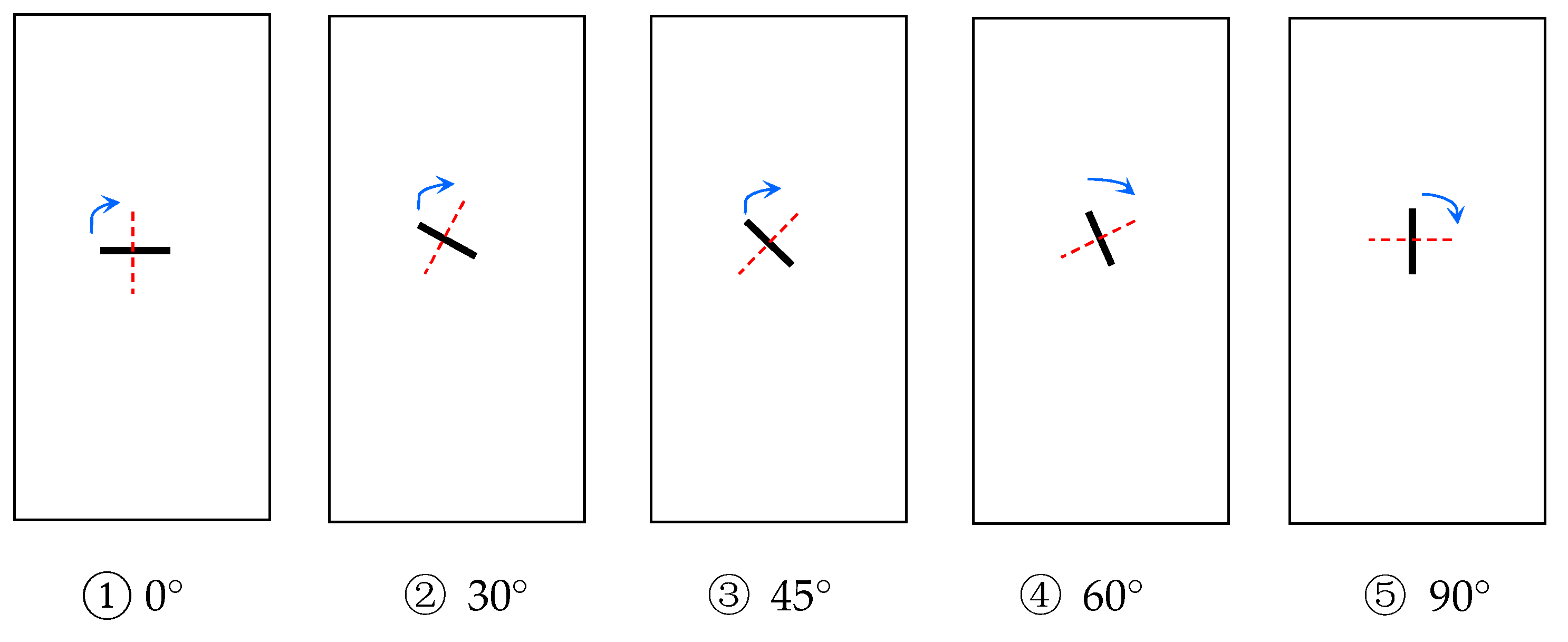
3.2.1. Effect of the Flaw Geometries on Peak Strength
- (1)
- For low values of α (below app. 50°), the peak strength first increases up to about β = 60° and then decreases.
- (2)
- For higher values of α (above app. 50°), the peak strength first increased up to about β = 45° and then decreased.
- (3)
- For the values of β (above app. 15°), the peak strength decreased with increasing α.
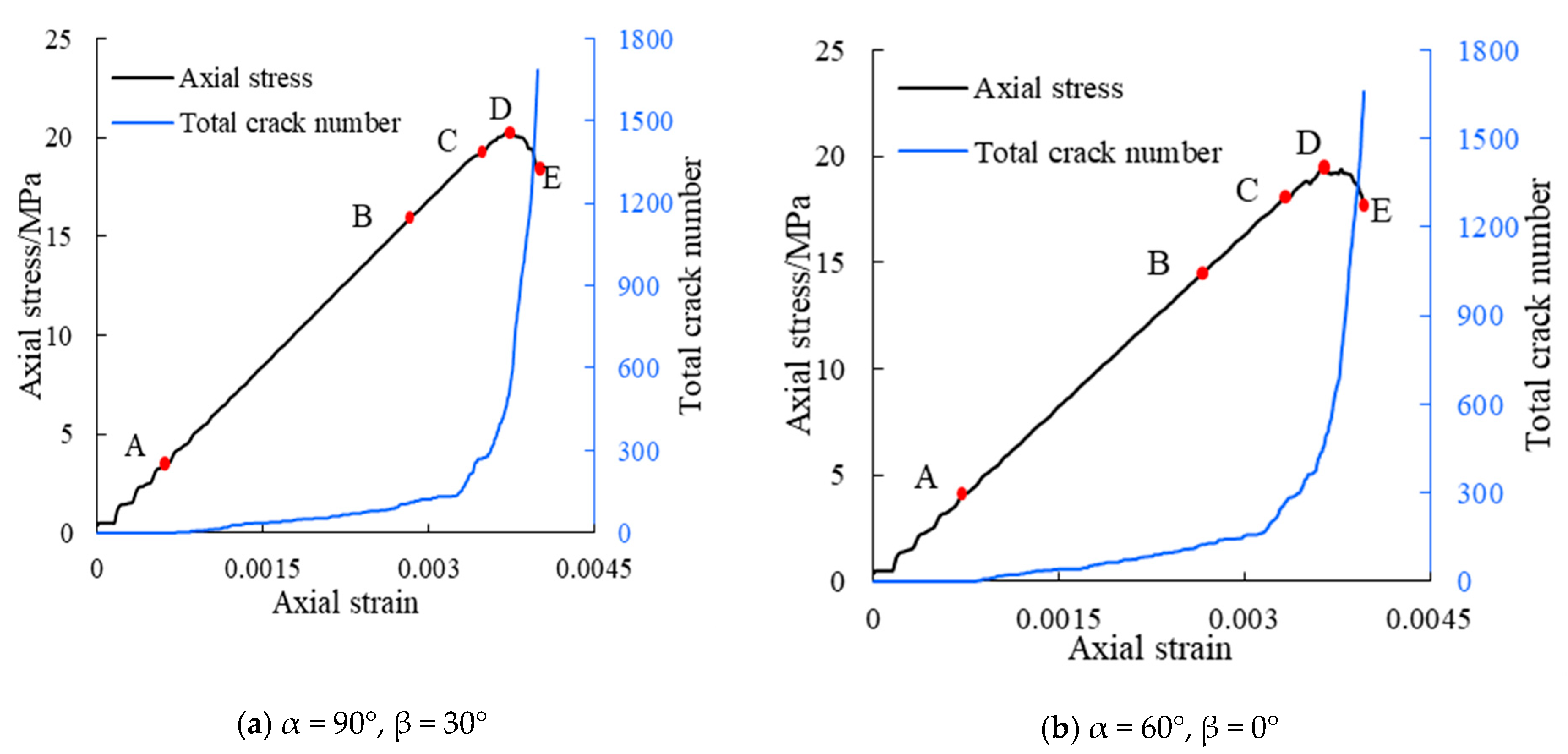
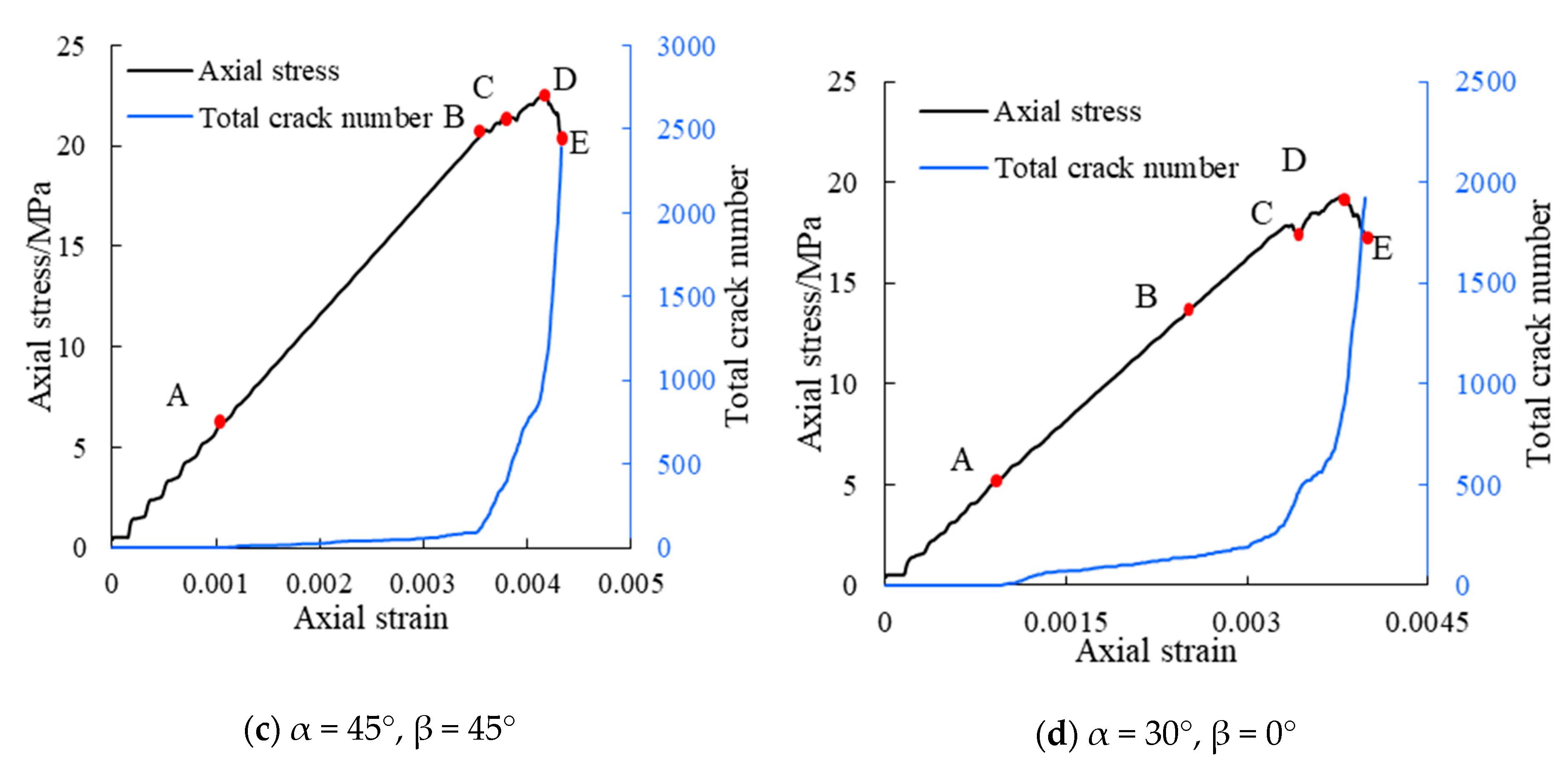
3.2.2. Crack Initiation and Coalescence Behavior
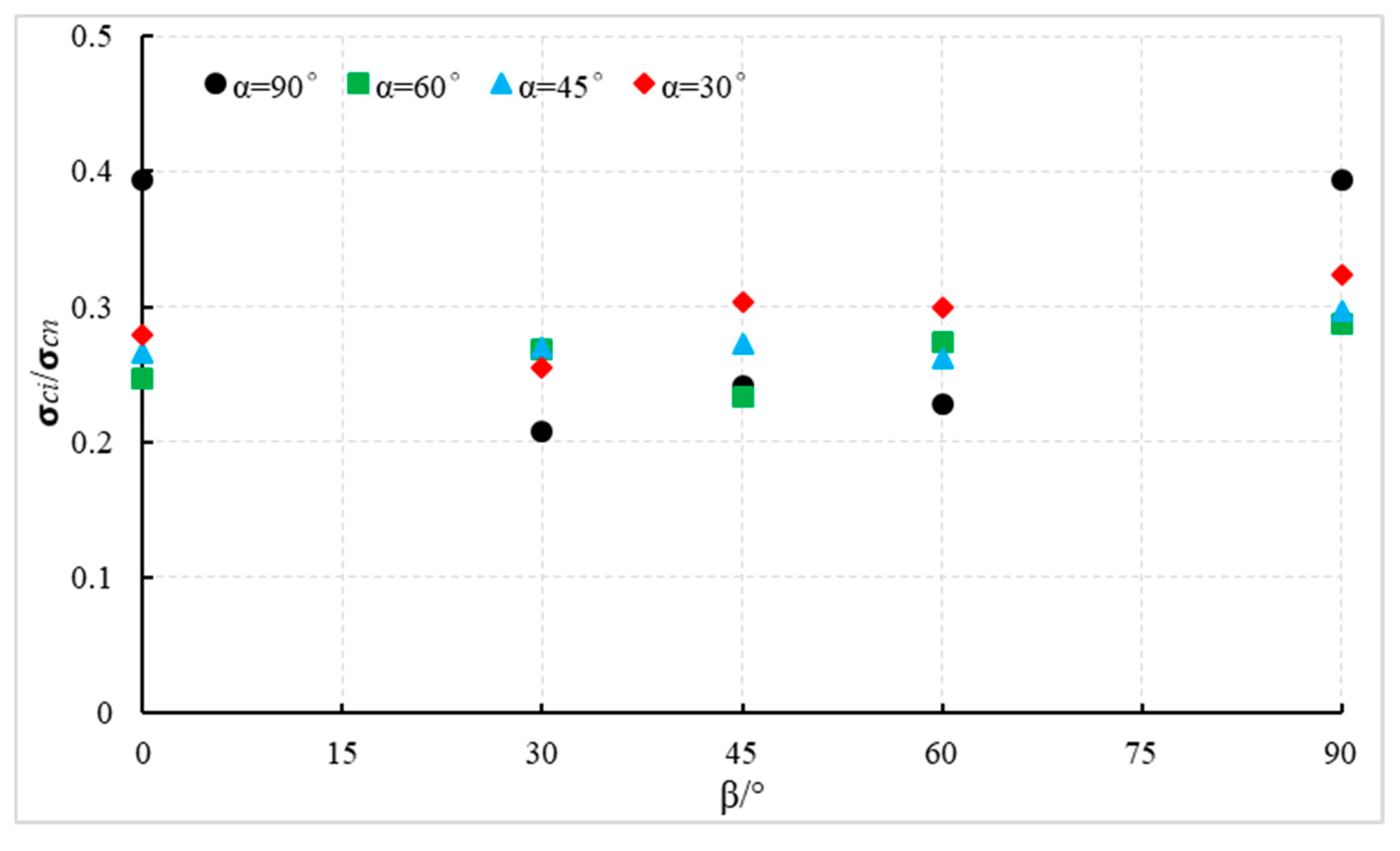
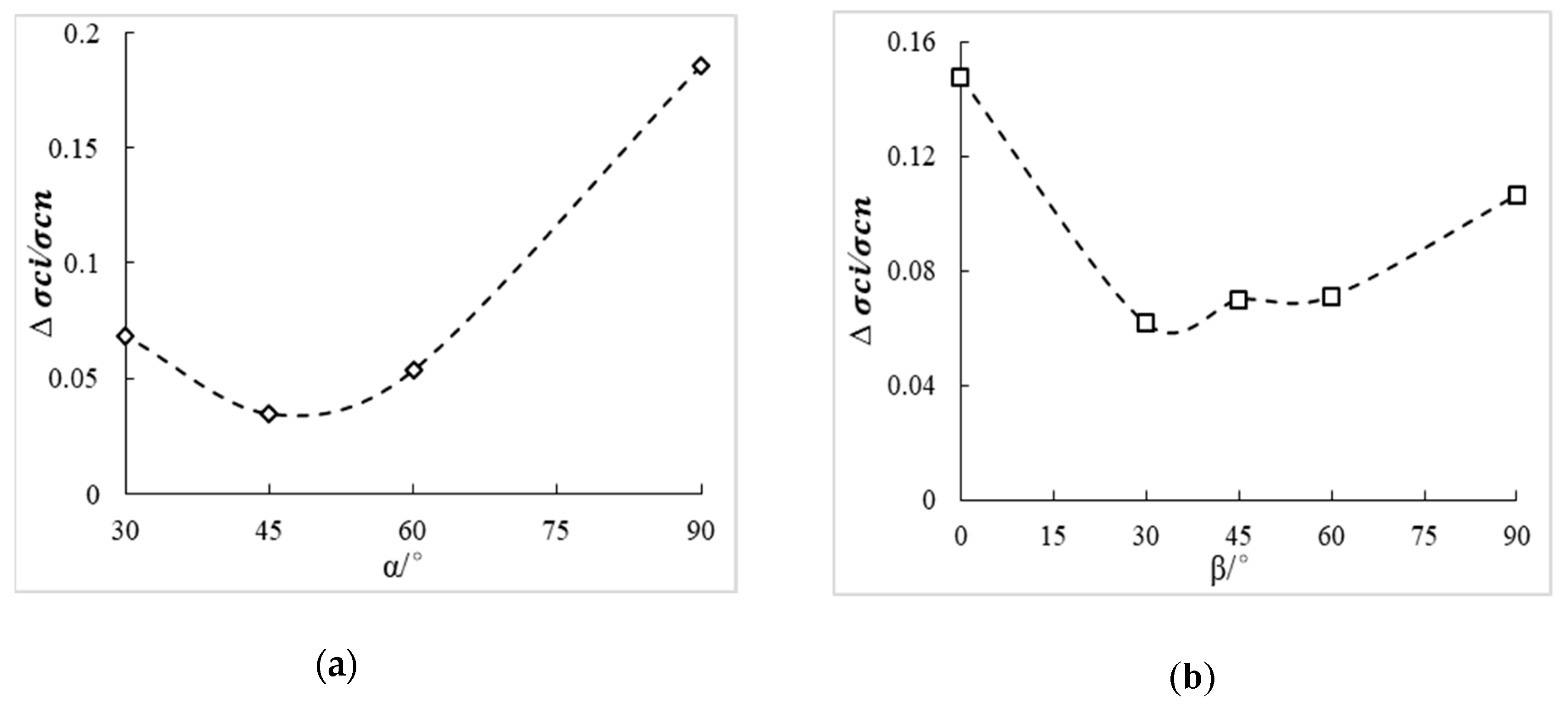
3.3. Crack Initiation Stress
- The ration varies between 0.2 and 0.4.
- For the same values of α, the minimum values of are observed at β = 30°, which means that the first crack initiates more easily (except α = 60°, β = 45°). For four cases of β = 90° and one case of β = 0°, α = 90° is the maximum value of observed.
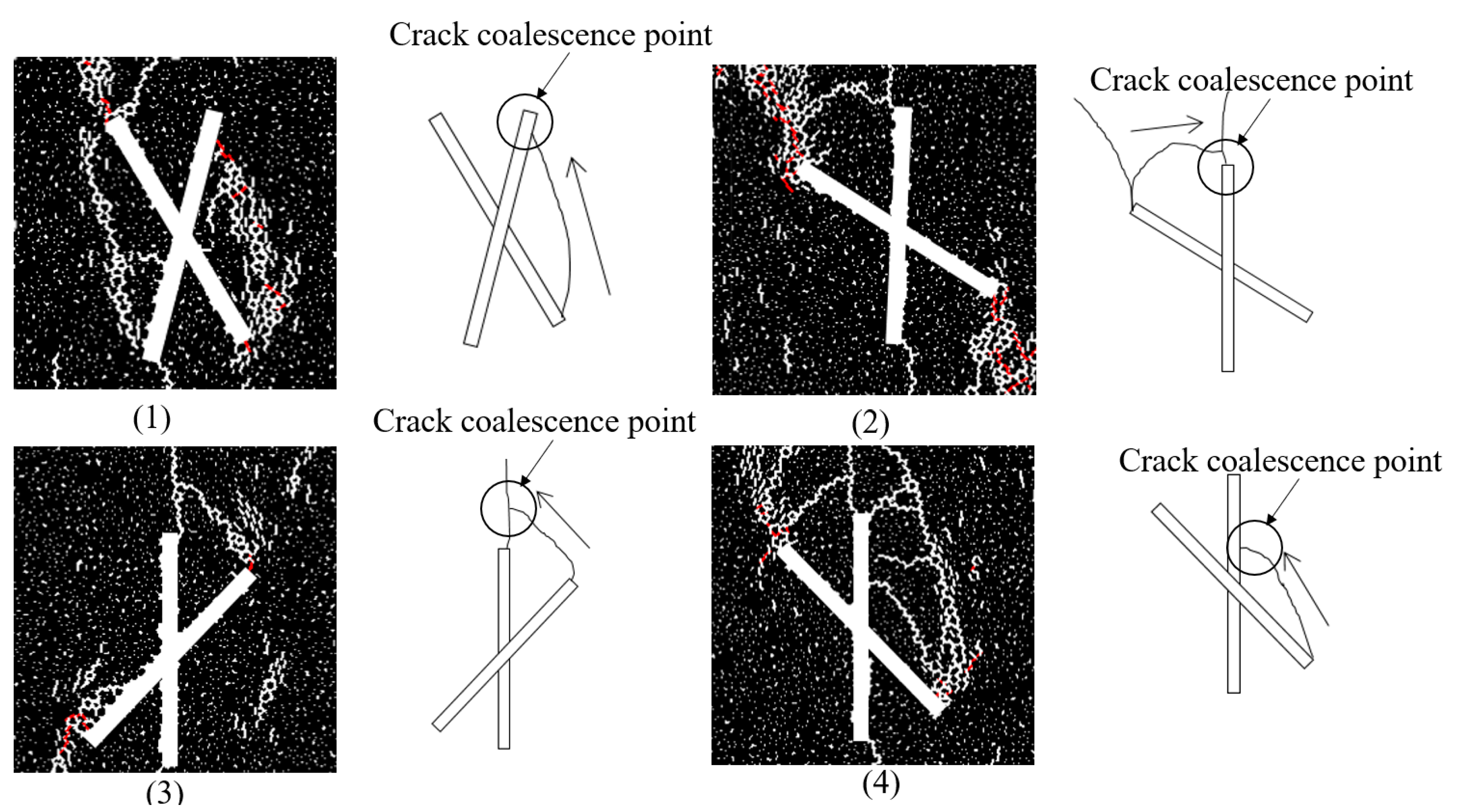
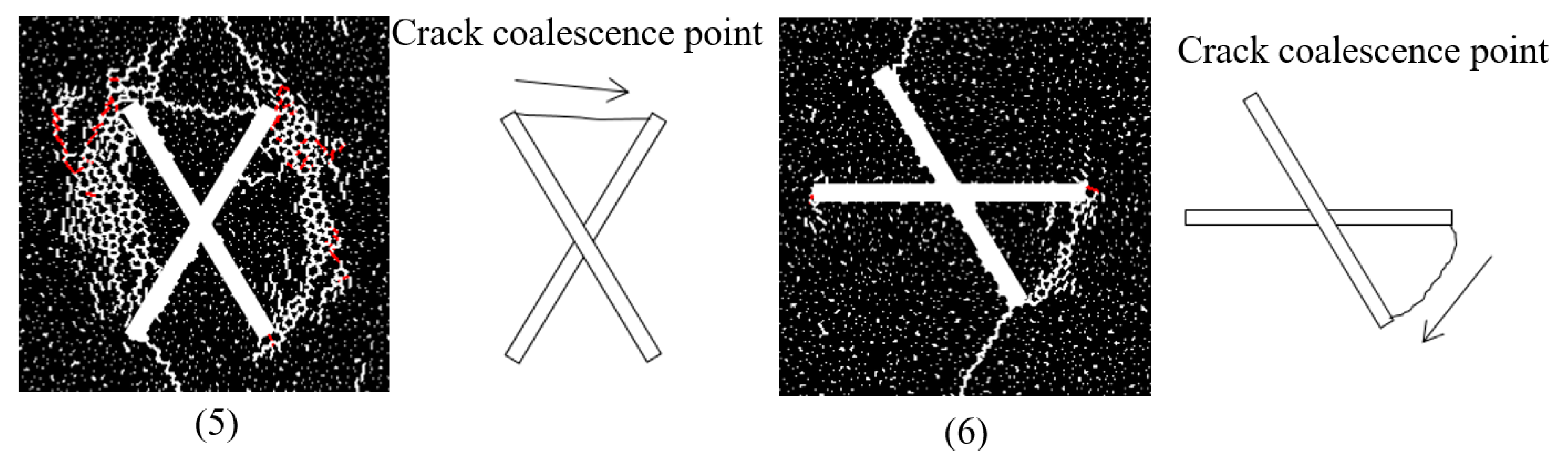
3.4. Crack Coalescence
- A macroscopic tensile crack initiated from the tip of one of the flaws extends upwards or downwards to the other flaw but does not reach the tip and some microscopic shear or mixed tensile-shear cracks participate at coalescence. This is classified as one-tip-linkage. According to the coalescence position, the one-tip-linkage mechanism contains three sub-types: Coalescence position near the tip (Figure 11(1),(2)), coalescence position at the flaw, but far away from the tip (Figure 11(4)), or coalescence position outside the flaw with a certain distance from the tip (Figure 11(3)).
- A macroscopic tensile crack initiated from the tip of one flaw extends upwards or downwards to the tip of the other flaw. The coalescence occurred by the linkage of tensile cracks and is classified as two-tips-linkage. The two tips linkage has two sub-types: Straight linkage (Figure 11(5)) and arc linkage (Figure 11(6)).
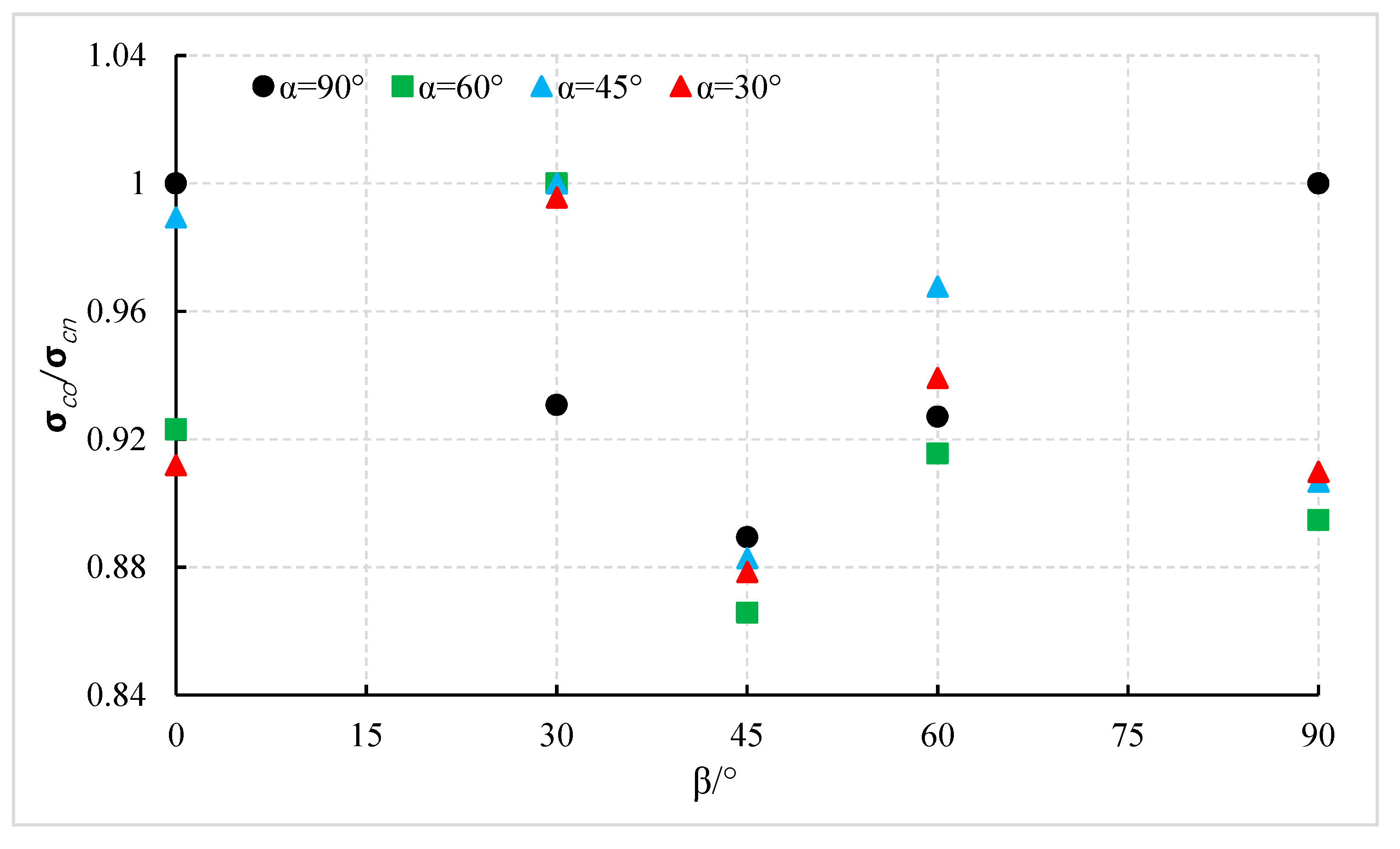
3.5. Crack Coalescence Stress
4. Conclusions
- For any intersection angle α, the strength is increases for flaw inclination angle β, ranging from 0° to about 45°. For intersection angle α up to about 45°, the strength is further slightly increased for inclination angle β, bigger than 45°. For intersection angle α, it is bigger than about 45° and the strength is strongly decreased for inclination angle β, bigger than 45°.
- The macro-crack initiated from the tips of two intersect flaws that did not occur simultaneously. The crack initial stress σ_ci of the first crack, obtained at the tip of flaw (A flaw or B flaw), normalized by the respective specimen peak strength , which changed between 0.2 and 0.4 with different flaw geometries.
- Two major crack coalescence patterns were observed: (a) One-tip-linkage (either near the crack tip, at the flaw but far away from the crack tip or outside the flaw at a certain distance from the tip) and (b) two-tips-linkage (straight or arc linkage). The geometry of flaws governed the coalescence type.
Author Contributions
Funding
Conflicts of Interest
References
- Bobet, A.; Einstein, H.H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Peng, K.; Zhou, J.; Zou, Q.; Yan, F. Deformation characteristics of sandstones during cyclic loading and unloading with varying lower limits of stress under different confining pressures. Int. J. Fatigue 2019, 127, 82–100. [Google Scholar] [CrossRef]
- Hoek, E.; Martin, C.D. Fracture initiation and propagation in intact rock–a review. J. Rock Mech. Geotech. Eng. 2014, 6, 287–300. [Google Scholar] [CrossRef]
- Peng, K.; Zhou, J.; Zou, Q.; Zhang, J.; Wu, F. Effects of stress lower limit during cyclic loading and unloading on deformation characteristics of sandstones. Constr. Build. Mater. 2019, 217, 202–215. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, G.; Wang, X.; Zhao, J.; Ma, C. Assessing the rockburst risk for deep shafts via distance-based multi-criteria decision making approaches with hesitant fuzzy information. Eng. Geol. 2019, 260, 105211. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Yao, J.; Gong, F.; Li, X.; Du, K.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Adams, M.; Sines, G. Crack extension from flaws in a brittle material subjected to compression. Tectonophysics 1978, 49, 97–118. [Google Scholar] [CrossRef]
- Peng, K.; Liu, Z.; Zou, Q.; Zhang, Z.; Zhou, J. Static and dynamic mechanical properties of granite from various burial depths. Rock Mech. Rock Eng. 2019, 52, 3545–3566. [Google Scholar]
- Camones, L.A.M.; do Amaral Vargas, E.; de Figueiredo, R.P.; Velloso, R.Q. Application of the discrete element method for modeling of rock crack propagation and coalescence in the step-path failure mechanism. Eng. Geol. 2013, 153, 80–94. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Sahouryeh, E.; Jewell, R.J.; Joer, H.; Ustinov, K.B. Influence of shape and locations of initial 3-D cracks on their growth in uniaxial compression. Eng. Fract. Mech. 2003, 70, 2115–2136. [Google Scholar] [CrossRef]
- Peng, K.; Wang, Y.; Zou, Q.; Liu, Z.; Mou, J. Effect of crack angles on energy characteristics of sandstones under a complex stress path. Eng. Fract. Mech. 2019, 218, 106577. [Google Scholar] [CrossRef]
- Li, Y.P.; Chen, L.Z.; Wang, Y.H. Experimental research on pre-cracked marble under compression. Int. J. Solids Struct. 2005, 42, 2505–2516. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.; Fantuzzi, N.; Zhao, Y.; Liu, Y.-B.; Peng, B.; Chen, J. Investigation of the Flow Properties of CBM Based on Stochastic Fracture Network Modeling. Materials 2019, 12, 2387. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Crack coalescence in molded gypsum and Carrara marble: Part 1. Macroscopic observations and interpretation. Rock Mech. Rock Eng. 2009, 42, 475–511. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Crack coalescence in molded gypsum and Carrara marble: Part 2—Microscopic observations and interpretation. Rock Mech. Rock Eng. 2009, 42, 513–545. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T.; Tang, C.A.; Lin, P. Analysis of crack coalescence in rock-like materials containing three flaws—Part I: Experimental approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 909–924. [Google Scholar] [CrossRef]
- Yang, S.Q. Crack coalescence behavior of brittle sandstone samples containing two coplanar fissures in the process of deformation failure. Eng. Fract. Mech. 2011, 78, 3059–3081. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wong, L.N.Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on parallel bonded-particle model approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Ko, T.Y.; Einstein, H.; Kemeny, J. Crack coalescence in brittle material under cyclic loading. In Proceedings of the Golden Rocks 2006, The 41st US Symposium on Rock Mechanics (USRMS), Golden, CO, USA, 17–21 June 2006; American Rock Mechanics Association: Alexandria, VA, USA, 2006. [Google Scholar]
- Park, C.H.; Bobet, A. Crack coalescence in specimens with open and closed flaws: A comparison. Int. J. Rock Mech. Min. Sci. 2009, 46, 819–829. [Google Scholar] [CrossRef]
- Sagong, M.; Bobet, A. Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2002, 39, 229–241. [Google Scholar] [CrossRef]
- Tang, C.A.; Lin, P.; Wong, R.H.C.; Chau, K.T. Analysis of crack coalescence in rock-like materials containing three flaws—Part II: Numerical approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 925–939. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, S.; Li, Y.; Guo, P.; Yang, H.; Yang, T. Effect of moisture content on methane adsorption- and desorption- induced deformation of tectonically deformed coal. Adsorpt. Sci. Technol. 2018, 36, 1648–1668. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Li, H.Q. Numerical study on coalescence of two pre-existing coplanar flaws in rock. Int. J. Solids Struct. 2013, 50, 3685–3706. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, S.; Li, Y.; Zhang, Z.; Guo, P.; Yang, H.; Zhang, S.; Pan, R. The occurrence state of moisture in coal and its influence model on pore seepage. RSC Adv. 2018, 8, 5420–5432. [Google Scholar] [CrossRef]
- Wong, R.H.; Chau, K.T. Crack coalescence in a rock-like material containing two cracks. Int. J. Rock Mech. Min. Sci. 1998, 35, 147–164. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jing, H.W. Strength failure and crack coalescence behavior of brittle sandstone samples containing a single fissure under uniaxial compression. Int. J. Fract. 2011, 168, 227–250. [Google Scholar] [CrossRef]
- Yang, S.Q. Strength, Failure and Crack Evolution Behavior of Rock Material Containing Pre-Existing Fissures; Springer: Cham, Switzerland, 2015; p. 246. [Google Scholar]
- Pollard, D.D.; Aydin, A. Progress in understanding jointing over the past century. GSA Bull. 1988, 100, 1181–1204. [Google Scholar] [CrossRef]
- Lee, H.; Jeon, S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. Int. J. Solids Struct. 2011, 48, 979–999. [Google Scholar] [CrossRef]
- Li, H.; Wong, L.N.Y. Influence of flaw inclination angle and loading condition on crack initiation and propagation. Int. J. Solids Struct. 2012, 49, 2482–2499. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, J.; An, X.; Ma, G. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework. Comput. Geotech. 2011, 38, 40–49. [Google Scholar] [CrossRef]
- Wu, Z.; Wong, L.N.Y. Frictional crack initiation and propagation analysis using the numerical manifold method. Comput. Geotech. 2012, 39, 38–53. [Google Scholar] [CrossRef]
- Amarasiri, A.; Kodikara, J. Use of material interfaces in DEM to simulate soil fracture propagation in Mode I cracking. Int. J. Geomech. 2010, 11, 314–322. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Chen, W.; Konietzky, H.; Tan, X.; Frühwirt, T. Pre-failure damage analysis for brittle rocks under triaxial compression. Comput. Geotech. 2016, 74, 45–55. [Google Scholar] [CrossRef]
- Chen, W.; Konietzky, H.; Abbas, S.M. Numerical simulation of time-independent and-dependent fracturing in sandstone. Eng. Geol. 2015, 193, 118–131. [Google Scholar] [CrossRef]
- Gui, Y.L.; Zhao, Z.Y.; Kodikara, J.; Bui, H.H.; Yang, S.Q. Numerical modelling of laboratory soil desiccation cracking using UDEC with a mix-mode cohesive fracture model. Eng. Geol. 2016, 202, 14–23. [Google Scholar] [CrossRef]
- Gui, Y.L.; Bui, H.H.; Kodikara, J.; Zhang, Q.B.; Zhao, J.; Rabczuk, T. Modelling the dynamic failure of brittle rocks using a hybrid continuum-discrete element method with a mixed-mode cohesive fracture model. Int. J. Impact Eng. 2016, 87, 146–155. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wong, L.N.Y.; Wang, S. Effects of the ratio of flaw size to specimen size on cracking behavior. Bull. Eng. Geol. Environ. 2015, 74, 181–193. [Google Scholar] [CrossRef]
- Turco, E. In-plane shear loading of granular membranes modeled as a Lagrangian assembly of rotating elastic particles. Mech. Res. Commun. 2018, 92, 61–66. [Google Scholar] [CrossRef]
- Turco, E.; dell’Isola, F.; Misra, A. A nonlinear Lagrangian particle model for grains assemblies including grain relative rotations. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1051–1079. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Zhang, X.P. Size effects on cracking behavior of flaw-containing specimens under compressive loading. Rock Mech. Rock Eng. 2014, 47, 1921–1930. [Google Scholar] [CrossRef]
- Shen, B.; Stephansson, O.; Einstein, H.H.; Ghahreman, B. Coalescence of fractures under shear stresses in experiments. J. Geophys. Res. Ser. 1995, 100, 5975. [Google Scholar] [CrossRef]
- Vesga, L.F.; Vallejo, L.E.; Lobo-Guerrero, S. DEM analysis of the crack propagation in brittle clays under uniaxial compression tests. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1405–1415. [Google Scholar] [CrossRef]
- Bray, J.W. A study of jointed and fractured rock. Rock Mech. Eng. Geol. 1967, 5, 117–136. [Google Scholar]
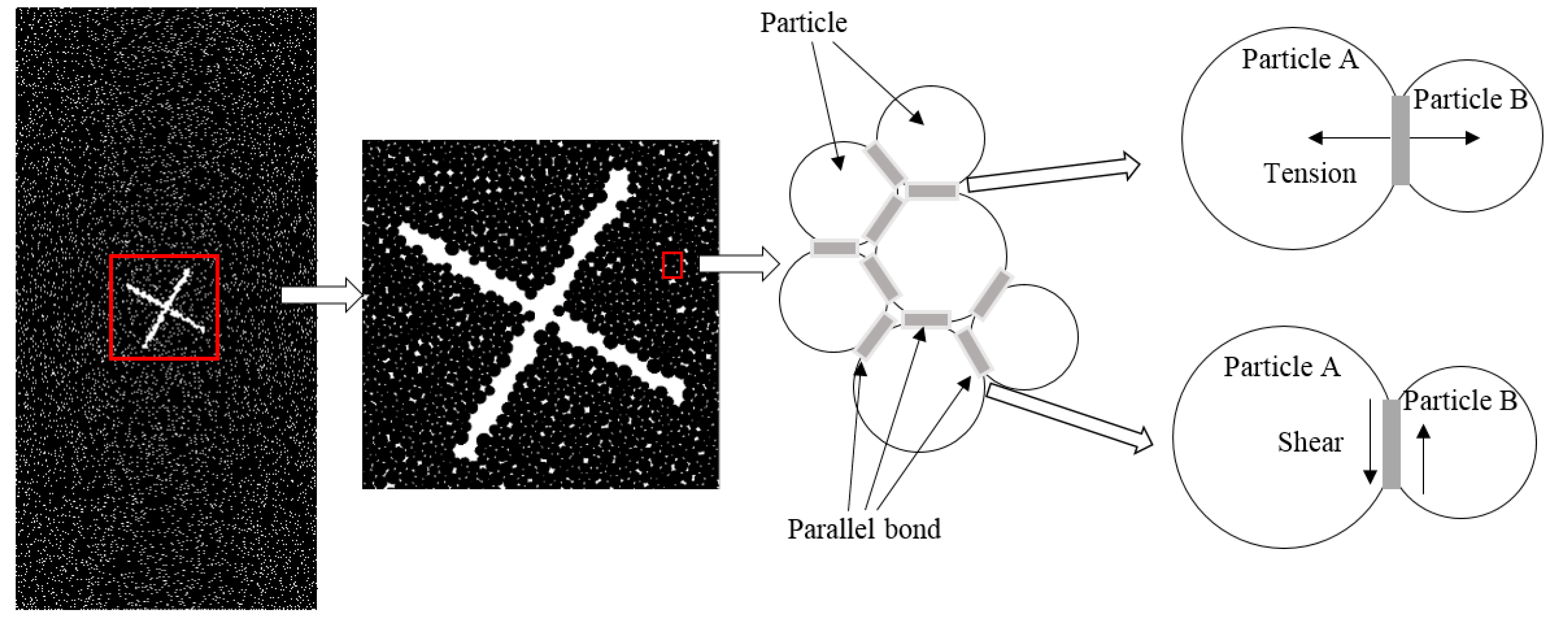

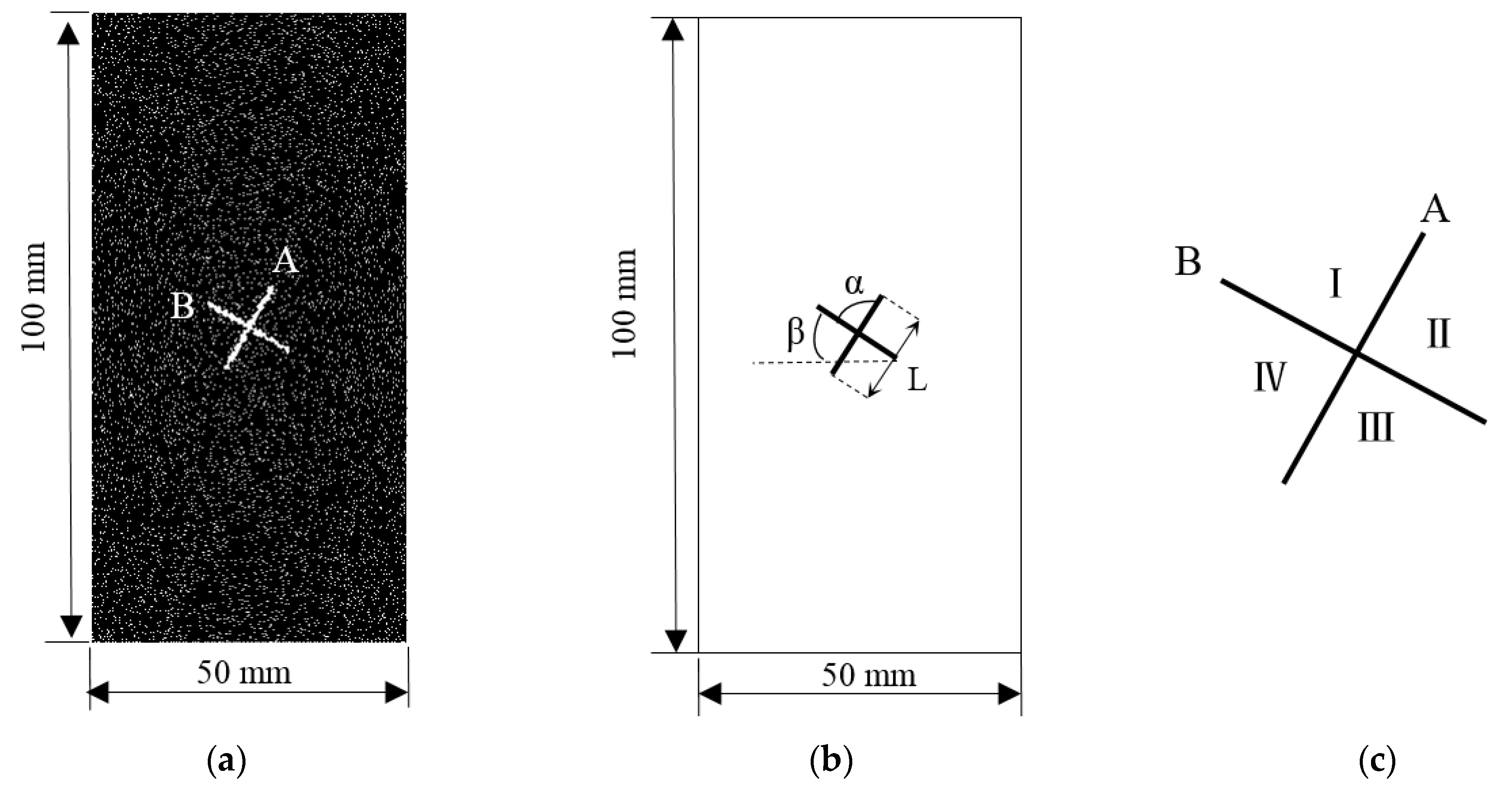
| Particle Parameters | Value | Parallel Bond Parameters | Value |
|---|---|---|---|
| Ec Young’s modulus of the particle | 2.5 GPa | Young’s modulus of the parallel bond | 2.5 GPa |
| kn/ks ratio of normal to shear stiffness of the particle | 1 | ratio of normal to shear stiffness of the parallel bond | 1 |
| Grain friction coefficient, | 0.01 | tensile strength of the parallel bond | 6 MPa |
| Rmax/Rmin ratio of max particle radius to min particle radius | 1.66 | cohesion of the parallel bond | 15 MPa |
| Rmin Lower bound of particle radius | 0.21 mm | radius multiplier | 1 |
| ρ particle density | 1.83 g/m3 | Friction angle of the parallel bond | 0 |
| Parameter | Experimental Tests | BPM |
|---|---|---|
| Density (g/cm3) | 1.54 | 1.54 |
| Young’s modulus (GPa) | 5.96 | 6.09 |
| Poisson’s ratio | 0.15 | 0.15 |
| Uniaxial compressive strength (MPa) | 33.85 | 34.2 |
| Tensile strength (MPa) | 3.2 | 4.8 |
| Flaw Geometry | Crack Evolution Pattern at Different Stages of Loading | ||||
|---|---|---|---|---|---|
| (A) | (B) | I | (D) | I | |
| α = 90° β = 30° |  |  |  |  |  |
| α = 60° β = 0° |  |  |  |  |  |
| α = 45° β = 45° |  |  |  |  |  |
| α = 30° β = 0° |  |  |  |  |  |
| Flaw Geometry | The Crack Coalescence Patterns of Loading | ||||
|---|---|---|---|---|---|
| β = 0° | β = 30° | β = 45° | β = 60° | β = 90° | |
| α = 90° |  |  |  |  |  |
| α = 60° |  |  |  |  |  |
| α = 45° |  |  |  |  |  |
| α = 30° |  |  |  |  |  |
| Angle/° | Coalescence Types of Different Geometries | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0° | β = 30° | β = 45° | β = 60° | β = 90° | ||||||
| Type | Zone | Type | Zone | Type | Zone | Type | Zone | Type | Zone | |
| α = 90° | (3) | II | (6) | II IV | (6) | II IV | (3) (6) | II III | (3) | II |
| α = 60° | (6) | III | (2) (3) | I III | (1) (2) (3) (4) (5) | I II IV | (1) (5) (6) | I Ⅱ IV | (3) | I III |
| α = 45° | (3) | II | (2) (6) | I III | (2) (3) (4) (6) | I II | (1) (4) (6) | II IV | (3) (6) | I II |
| α = 30° | (5) (6) | I III | (5) (6) | I III | (2) (3) | I II | (2) (3) (4) | I III IV | (3) (4) (6) | I III |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, B.; Chen, Y.; Zhao, G.; Liang, W.; Wu, H. A Numerical Study on the Crack Development Behavior of Rock-Like Material Containing Two Intersecting Flaws. Mathematics 2019, 7, 1223. https://doi.org/10.3390/math7121223
Dai B, Chen Y, Zhao G, Liang W, Wu H. A Numerical Study on the Crack Development Behavior of Rock-Like Material Containing Two Intersecting Flaws. Mathematics. 2019; 7(12):1223. https://doi.org/10.3390/math7121223
Chicago/Turabian StyleDai, Bing, Ying Chen, Guoyan Zhao, Weizhang Liang, and Hao Wu. 2019. "A Numerical Study on the Crack Development Behavior of Rock-Like Material Containing Two Intersecting Flaws" Mathematics 7, no. 12: 1223. https://doi.org/10.3390/math7121223
APA StyleDai, B., Chen, Y., Zhao, G., Liang, W., & Wu, H. (2019). A Numerical Study on the Crack Development Behavior of Rock-Like Material Containing Two Intersecting Flaws. Mathematics, 7(12), 1223. https://doi.org/10.3390/math7121223






