1. Introduction
Fractional calculus has received much attention due to the fact that several real-world phenomena can be demonstrated successfully by developing mathematical models using fractional calculus. More specifically, fractional differential equations (FDEs) are the generalized form of integer order differential equations. The applications of the FDEs have been emerging in many fields of science and engineering such as diffusion processes [
1], thermal conductivity [
2], oscillating dynamical systems [
3], rheological models [
4], quantum models [
5], etc. However, one of the interesting issues for the FDEs is a fractional Burgers’ equation. It appears in many areas of applied mathematics and can describe various kinds of phenomena such as mathematical models of turbulence and shock wave traveling, formation, and decay of nonplanar shock waves at the velocity fluctuation of sound, physical processes of unidirectional propagation of weakly nonlinear acoustic waves through a gas-filled pipe, and so on, see [
6,
7,
8]. In order to understand these phenomena as well as further apply them in the practical life, it is important to find their solutions. Some powerful numerical methods had been developed for solving the fractional Burgers’ equation, such as finite difference methods (FDM) [
9], Adomian decomposition method [
10], and finite volume method [
11]. Moreover, in 2015, Esen and Tasbozan [
12] gave a numerical solution of time fractional Burgers’ equation by assuming that the solution
can be approximated by a linear combination of products of two functions, one of which involves only
x and the other involves only
t. Recently, Yokus and kaya [
13] used the FDM to find the numerical solution for time fractional Burgers’ equation, however, their results contained less accuracy. In 2017, Cao et al. [
14] studied solution of two-dimensional time-fractional Burgers’ equation with high and low Reynolds numbers using discontinuous Galerkin method, however, the method involves the triangulations of the domain which usually gives difficulty in terms of devising a computational program. There are more numerical studies on time- and/or space-fractional Burgers’ equations which can be found in many researches.
In this article, we present the numerical technique based on the finite integration method (FIM) for solving time-fractional Burger’ equations and time-fractional coupled Burgers’ equations. The FIM is one of the interesting numerical methods in solving partial differential equations (PDEs). The idea of using FIM is to transform the given PDE into an equivalent integral equation and apply numerical integrations to solve the integral equation afterwards. It is known that the numerical integration is very insensitive to round-off errors, while numerical differentiation is very sensitive to round-off errors. It is because the manipulation task of numerical differentiation involves division by small step-size but the process of numerical integration involves multiplication by small step-size.
Originally, the FIM has been firstly proposed by Wen et al. [
15]. They constructed the integration matrices based on trapezoidal rule and radial basis functions for solving one-dimensional linear PDEs and then Li et al. [
16] continued to develop it in order to overcome the two-dimensional problems. After that, the FIM was improved using three numerical quadratures, including Simpson’s rule, Newton-Cotes, and Lagrange interpolation, presented by Li et al. [
17]. The FIM has been successfully applied to solve various kinds of PDEs and it was verified by comparing with several existing methods that it offers a very stable, highly accurate and efficient approach, see [
18,
19,
20]. In 2018, Boonklurb et al. [
21] modified the original FIM via Chebyshev polynomials for solving linear PDEs which provided a much higher accuracy than the FDM and those traditional FIMs. Unfortunately, the modified FIM in [
21] has never been studied for the Burgers’ equations and coupled Burgers’ equations involving fractional order derivatives with respect to time. This became the major motivation to carry out the current work.
In this paper, we improve the modified FIM in [
21] by using the shifted Chebyshev polynomials (FIM-SCP) to devise the numerical algorithms for finding the decent approximate solutions of time-fractional Burgers’ equations both in one- and two-dimensional domains as well as time-fractional coupled Burgers’ equations. Their time-fractional derivative terms are described in the Caputo sense. We note here that the FIM in [
21] is applicable for solving linear differential equations. With our improvement in this paper, we propose the numerical methods that are applicable for solving time-fractional Burgers’ equations. It is well known that Chebyshev polynomial have the orthogonal property which plays an important role in the theory of approximation. The roots of the Chebyshev polynomial can be found explicitly and when the equidistant nodes are so bad, we can overcome the problem by using the Chebyshev nodes. If we sample our function at the Chebyshev nodes, we can have best approximation under the maximum norm, see [
22] for more details. With these advantages, our improved FIM-SCP is constructed by approximating the solutions expressed in term of the shifted Chebyshev expansion. We use the zeros of the Chebyshev polynomial of a certain degree to interpolate the approximate solution. With our work, we obtain the shifted Chebyshev integration matrices in one- and two- dimensional spaces which are used to deal with the spatial discretizations. The temporal discretizations are approximated by the forward difference quotient.
The rest of this paper is organized as follows. In
Section 2, we provide the basic definitions and the necessary notations used throughout this paper. In
Section 3, the improved FIM-SCP of constructing the shifted Chebyshev integration matrices, both for one and two dimensions are discussed. In
Section 4, we derive the numerical algorithms for solving one-dimensional time-fractional Burgers’ equations, two-dimensional time-fractional Burgers’ equations, and time-fractional coupled Burgers’ equations. The numerical results are presented, which are also shown to be more computationally efficient and accurate than the other methods with CPU time(s) and rate of convergence. The conclusion and some discussion for the future work are provided in
Section 5.
4. The Numerical Algorithms for Time-Fractional Burgers’ Equations
In this section, we derive the numerical algorithms based on our improved FIM-SCP for solving time-fractional Burgers’ equations both in one and two dimensions. The numerical algorithm for solving time-fractional coupled Burgers’ equations is also proposed. To demonstrate the effectiveness and the efficiency of our algorithms, some numerical examples are given. Moreover, we find the time convergence rates and CPU times(s) of each example in order to demonstrate the computational cost. We note here that we implemented our numerical algorithms in MatLab R2016a. The experimental computer system is configured as: Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz. Finally, the graphically numerical solutions of each example are also depicted.
4.1. Algorithm for One-Dimensional Time-Fractional Burgers’ Equation
Let
L and
T be positive real numbers and
. Consider the time-fractional Burgers’ equation with a viscosity parameter
as follows.
subject to the initial condition
and the boundary conditions
where
,
,
, and
are given functions. Let us first linearize (
7) by determining the iteration at time
, where
is the time step and
. Then, we have
where
is the numerical solution at the
iteration. For the Caputo time-fractional derivative term defined in Definition 2, we have
Using the first-order forward difference quotient to approximate the derivative term in (
11), we get
where
. Thus, (
10) becomes
In order to eliminate the derivative terms in (
13), we apply the modified FIM by taking the double layer integration. Then, for each shifted Chebyshev node
,
, we obtain
where
and
are the arbitrary constants of integration. Next, we consider the nonlinear term in (
14). By using the technique of integration by parts, we have
where
. Thus, for
, (
15) can be expressed in matrix form as
For computational convenience, we reduce the above equation into the matrix form:
where
,
, and
Consequently, for
by hiring (
16) and the idea of Boonklurb et al. [
21], we can convert (
14) into the matrix form as
where
is the
identity matrix,
,
,
,
and
. For the boundary conditions (
9), we can change them into the vector forms by using the linear combination of the shifted Chebyshev polynomial at the
iteration as follows.
where
and
.
From (
18)–(
20), we can construct the following system of iterative linear equations that contains
unknowns
where
for
, and
if
. Thus, starting from the initial condition
, the approximate solution
can be obtained by solving the system (
21). We note here that, for any fixed
, the approximate solution
for each arbitrary
can be computed from
where
and
is the final iterative solution of (
21).
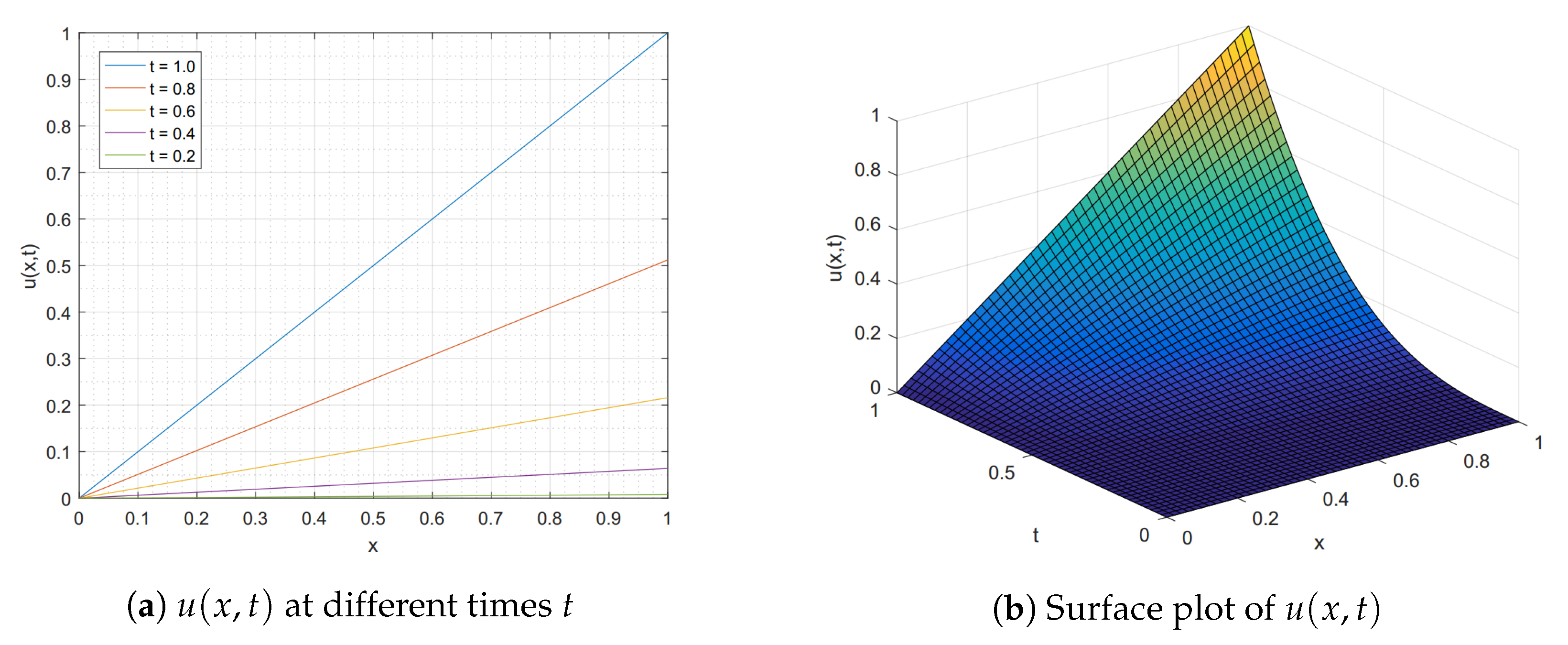
Example 1. Consider the time-fractional Burgers’ Equation (7) for and withsubject to the initial conditionand the boundary conditionsThe exact solution given by Esen and Tasbozan [12] is . In the numerical test, we choose the kinematic viscosity , and . Table 1 presents the exact solution , the numerical solution by using our FIM-SCP in Algorithm 1, and the solution obtained by the quadratic B-spline finite element Galerkin method (QBS-FEM) proposed by Esen and Tasbozan [12]. The comparison between the absolute errors (as the difference in absolute value between the approximate solution and the exact solution) of the two methods shows that our FIM-SCP is more accurate than QBS-FEM for and similar accuracy for other M. Algorithm 1 acquires the significant improvement in accuracy with less computational nodal points M and regardless the time steps and the fractional order derivatives α. With the selection of and , Table 2 shows the comparison between the exact solution and the numerical solution using Algorithm 1 for various values of . Table 3 illustrates the comparison between the exact solution and the numerical solution by our method for , , and . Moreover, the convergence rates are estimated by using our FIM-SCP with the discretization points and step sizes for . In Table 4, we observe that these time convergence rates for the norm indeed are almost for the different . Then, we also find the computational cost in term of CPU time(s) in Table 4. Finally, the graph of our approximate solutions, , for different times, t, and the surface plot of the solution under the parameters , , and , are provided in Figure 2.| Algorithm 1 The numerical algorithm for solving one-dimensional time-fractional Burgers’ equation |
| Input:, and . |
| Output: An approximate solution . |
| 1: | Set for . |
| 2: | Compute and . |
| 3: | Set and . |
| 4: | whiledo |
| 5: | Set . |
| 6: | Set . |
| 7: | Set . |
| 8: | for to do |
| 9: | Compute . |
| 10: | Compute . |
| 11: | end for |
| 12: | Compute . |
| 13: | Find by solving the iterative linear system (21). |
| 14: | end while |
| 15: | return. |
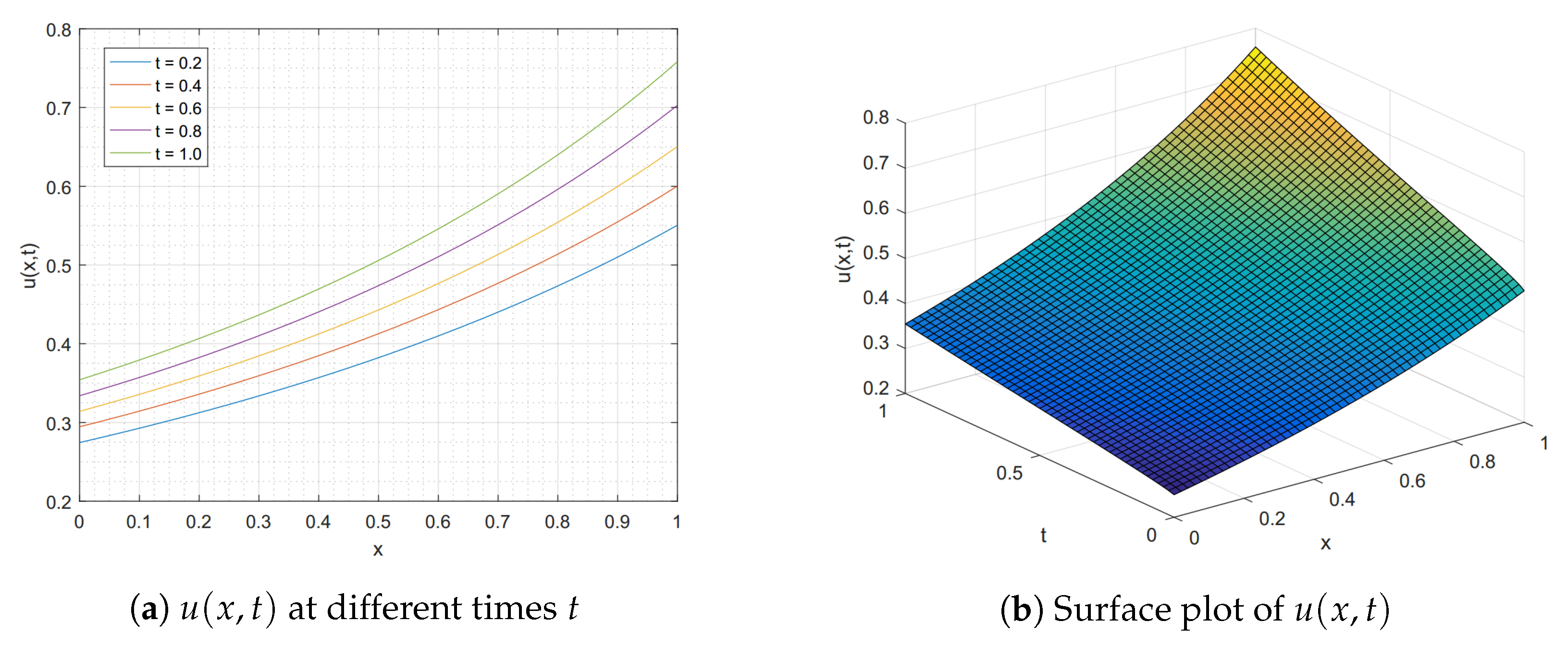
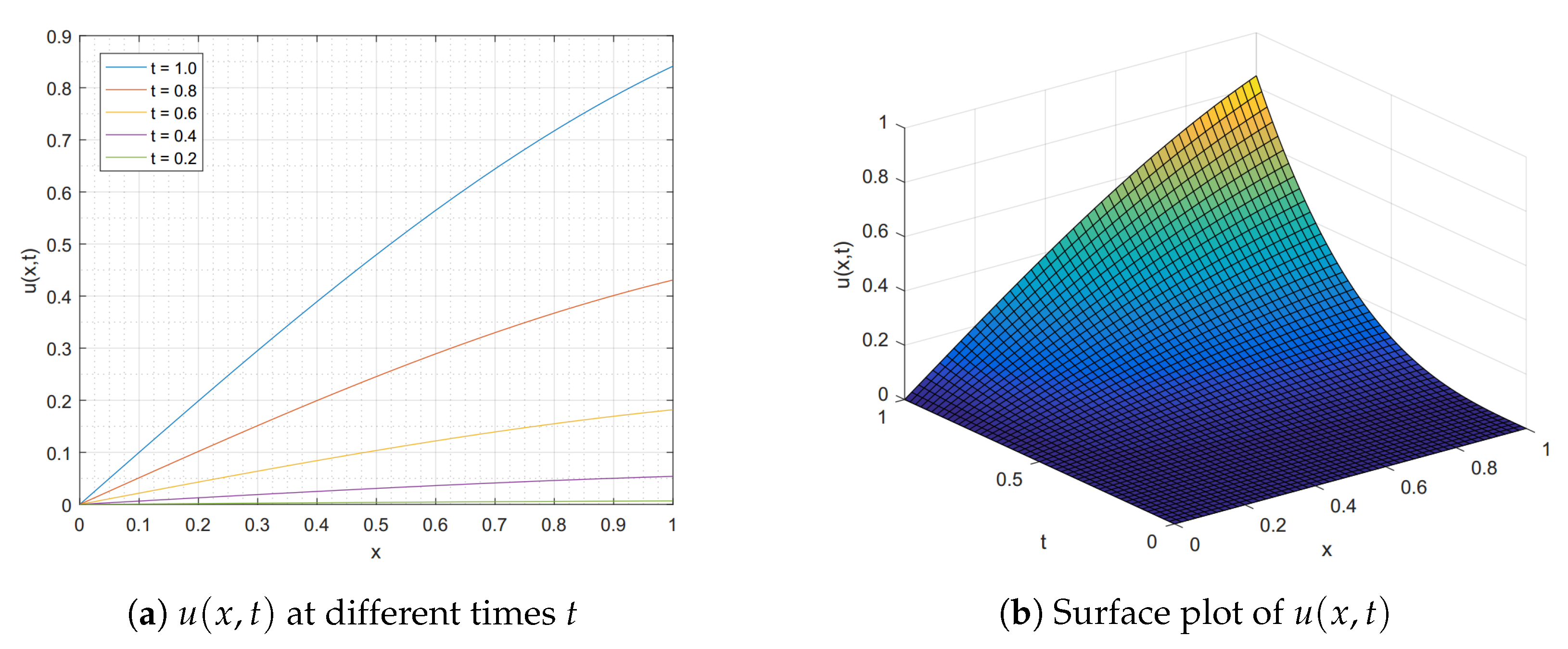
Example 2. Consider the time-fractional Burgers’ Equation (7) over with , subject to the initial conditionand the boundary conditionsThe exact solution given by Yokus and Kaya [13] is . In our numerical test, we choose the kinematic viscosity , , and . Table 5 presents the exact solution , the numerical solution by using our FIM-SCP in Algorithm 1, and the solution obtained by using the expansion method and the Cole–Hopf transformation (EPM-CHT) proposed by Yokus and Kaya in [13]. The error norms and of this problem between our FIM-SCP and EPM-CHT with for the various values of nodal grid points and step size are illustrated in Table 6. We see that our Algorithm 1 achieves improved accuracy with less computational cost. Furthermore, we estimate the convergence rates of time for this problem by using our FIM-SCP with the discretization nodes and step sizes for which are tabulated in Table 7. We observe that these rates of convergence for the norm indeed are almost linear convergence for the different values . Then, we also calculate the computational cost in term of CPU time(s) as shown in Table 7. Figure 3a,b depict the numerical solutions at different times t and the surface plot of , respectively. 4.2. Algorithm for Two-Dimensional Time-Fractional Burgers’ Equation
Let
and
be positive real numbers,
, and
. Consider the two-dimensional time-fractional Burgers’ equation with a viscosity
,
subject to the initial condition
and the boundary conditions
where
f,
,
,
, and
are given functions. As
and
, we can transform (
22) to
Let us linearize (
25) by imposing the iteration at time
for
and
is an arbitrary time step. Thus, we have
where
and
is the numerical solution at the
iteration. Next, consider the fractional order derivative in the Caputo sense as defined in Definition 2, by using (
12), then (
26) becomes
where
. The above equation can be transformed to the integral equation by taking twice integrations over both
x and
y, we have
where
,
,
, and
are the arbitrary functions emerged in the process of integration which can be approximated by the shifted Chebyshev polynomial interpolation. For
, define
where
and
, for
and
, are the unknown values of these interpolated points. Next, we divide the domain
into a mesh with
M nodes by
N nodes along
x- and
y-directions, respectively. We denote the nodes along the
x-direction by
and the nodes along the
y-direction by
. These nodes along the
x- and
y-directions are the zeros of shifted Chebyshev polynomials
and
, respectively. Thus, the total number of grid points in the system is
, where each point is an entry in the set of Cartesian product
ordering as global type system, i.e.,
for
. By substituting each node in (
27) and hiring
and
in
Section 3.2, we can change (
27) to the matrix form as
Simplifying the above equation yields
where each parameter contained in (
29) can be defined as follows.
| = | , |
| = | , |
| = | , |
| = | , |
| = | for , |
| = | for , |
| = | , |
| = | . |
From (
28), we obtain
and
, where
For the boundary conditions (
24), we can transform them into the matrix form, similar the idea in [
21], by employing the linear combination of the shifted Chebyshev polynomials as follows,
Left & Right boundary conditions: For each fixed
, then
Bottom & Top boundary conditions: For each fixed
, then
where
and
are, respectively, the
and
identity matrices,
and
are, respectively, the
and
matrices defined in Lemma 1,
is defined in (
6), and the other parameters are
| = | , |
| = | , |
| = | , |
| = | , |
| = | for , |
| = | for . |
Finally, we can construct the system of iterative linear equations from Equations (
29)–(
33) for a total of
unknowns, including
,
,
,
and
, as follows,
Thus, the approximate solutions
can be reached by solving (
34) in conjunction with the initial condition (
23), that is,
, where for all
. Therefore, an arbitrary solution
at any fixed time
t can be estimated from
where
and
.
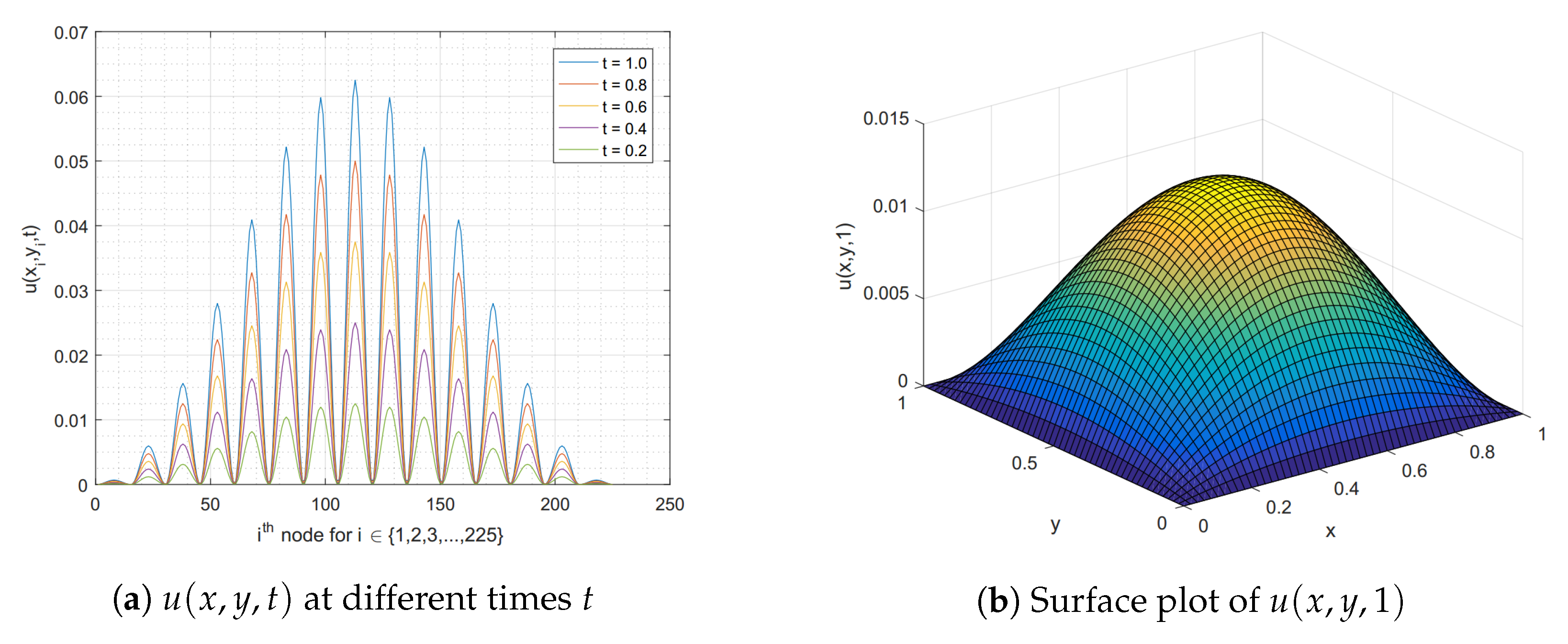
Example 3. Consider the 2D time-fractional Burgers’ Equation (22) for and with the forcing termsubject to the both homogeneous of initial and boundary conditions. The analytical solution of this problem is . For the numerical test, we pick , , , and . In Table 8, the solutions approximated by our FIM-SCP Algorithm 2 are presented in the space domain Ω for various times t. We test the accuracy of our method by measuring it with the absolute error . In addition, we seek the rates of convergence via norm of our Algorithm 2 with the nodal points and different step sizes for , we found that these convergence rates approach to the linear convergence as shown in Table 9 together with the CPU times(s). Also, the graphically numerical solutions are provided in Figure 4.| Algorithm 2 The numerical algorithm for solving two-dimensional time-fractional Burgers’ equation |
| Input: and . |
| Output: An approximate solution . |
| 1: | Set for . |
| 2: | Set for . |
| 3: | Compute and . |
| 4: | Calculate the total number of grid points . |
| 5: | Construct and in the global numbering system for . |
| 6: | Set and . |
| 7: | whiledo |
| 8: | Set . |
| 9: | Set . |
| 10: | Set . |
| 11: | for to do |
| 12: | Compute . |
| 13: | Compute . |
| 14: | end for |
| 15: | Compute and . |
| 16: | Find by solving the iterative linear system (34). |
| 17: | end while |
| 18: | return. |
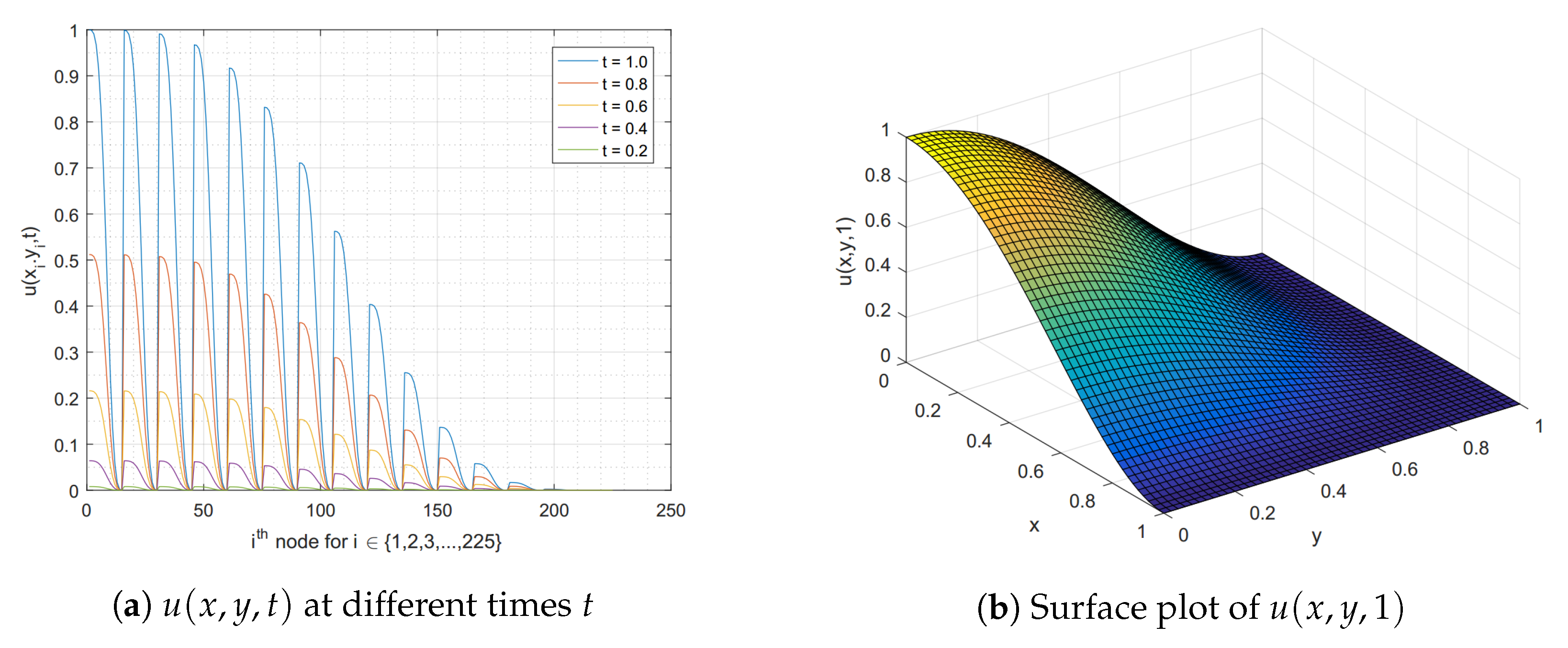
Example 4. Consider the 2D Burgers’ Equation (22) for and with the homogeneous initial condition and the forcing termsubject to the boundary conditions corresponding to the analytical solution given by Cao et al. [14] is . By picking the parameters , , and , the comparison of error norm between our FIM-SCP via Algorithm 2 and the discontinuous Galerkin method combined with finite different scheme (DGM-FDS) presented by Cao et al. [14] are displayed in Table 10 at time . We can see that our method gives a higher accuracy than the DGM-FDS at the same step size . Next, we provide the CPU times(s) and time convergence rates based on norm of our algorithm for this problem in Table 11. Then, we see that they converge to the linear rate . Finally, the graphical solutions of this Example 4 are provided in Figure 5. 4.3. Algorithm for Time-Fractional Coupled Burgers’ Equation
Consider the following coupled Burgers’ equation with fractional time derivative for
subject to the initial conditions
and the boundary conditions
where
,
,
,
and
are the given functions. The procedure of using our FIM for solving
u and
v are similar, we only discuss here the details in finding the approximate solution
u.
We begin with linearizing the system (
35) by taking the an iteration of time
for
, where
is a time step. We obtain
where
and
are numerical solutions of
u and
v in the
iteration, respectively. Next, let us consider the fractional time derivative for
in the Caputo sense by using the same procedure as in (
12), by taking the double layer integration on both sides, we obtain
where
for
, and
,
,
, and
are arbitrary constants of integration. For the nonlinear terms in (
38) and (
39), by using the same process as in (
15), we let
For computational convenience, we express
and
into matrix forms as
where
is defined in (
17) and other parameters obtained on (
40) and (
41) are
| = | , |
| = | , |
| = | , |
| = | , |
| = | for . |
Consequently, using (
40), (
41), and the procedure in
Section 3.1, we can convert both (
38) and (
39) into the matrix forms as
Rearranging the above system yields
where
is the
identity matrix and other parameters are defined by
| = | , |
| = | , |
| = | , |
| = | . |
The boundary conditions (
37) are transformed into the vector forms by using the same process as in (
19) and (
20), that is,
where
and
. Finally, starting from the initial guesses
We can construct the system of the
iterative linear equations for finding numerical solutions. The approximate solutions of
u can be obtained from (
42) and (
44) while the approximate solutions of
v can be reached by using (
43) and (
45):
and
For any fixed t, the approximate solutions of and on the space domain can be obtained by computing and , where .
Example 5. Consider the time-fractional coupled Burgers’ Equation (35) for and with the forcing termssubject to the homogeneous initial conditions and the boundary conditions corresponding to the analytical solution given by Albuohimad and Adibi [25] is . For the numerical test, we choose the kinematic viscosity , and . Table 12 presents the exact solution and the numerical solutions together with by using our FIM-SCP through Algorithm 3. The accuracy is measured by the absolute error . Table 13 displays the comparison of the error norms of our approximate solutions and the approximate solutions obtained by using the collocation method with FDM (CM-FDM) introduced by Albuohimad and Adibi in [25]. As can be seen from Table 13, our FIM-SCP Algorithm 3 is more accurate. Next, the time convergence rates based on and CPU times(s) of this problem that solved by Algorithm 3 are demonstrated in Table 14. Since the approximate solutions u and v are the same, we only present the graphical solution of u in Figure 6.| Algorithm 3 The numerical algorithm for solving 1D time-fractional coupled Burgers’ equation |
| Input: and . |
| Output: The approximate solutions and . |
| 1: | Set for . |
| 2: | Compute and . |
| 3: | Set and . |
| 4: | whiledo |
| 5: | Set . |
| 6: | Set . |
| 7: | Set and . |
| 8: | for to do |
| 9: | Compute . |
| 10: | Compute . |
| 11: | Compute . |
| 12: | Compute . |
| 13: | end for |
| 14: | Calculate , , and . |
| 15: | Find by solving the iterative linear system (46). |
| 16: | Find by solving the iterative linear system (47). |
| 17: | end while |
| 18: | return and . |
Example 6. Consider the time-fractional coupled Burgers’ Equation (35) for and with the forcing termssubject to the homogeneous initial conditions and the boundary conditions corresponding to the analytical solution given by Albuohimad and Adibi [25] is . For the numerical test, we choose the viscosity , and . Table 15 provides the comparison of error norms between our FIM-SCP and the CM-FDM in [25] for various values of and M, it show that our method is more accurate. Moreover, Table 16 illustrates the rates of convergence and CPU times(s) for . Figure 7a,b show the numerical solutions at different times t and the surface plot of , respectively. Note that we only show the graphical solution of since the approximate solutions and are the same. 5. Conclusions and Discussion
In this paper, we applied our improved FIM-SCP to develop the decent and accurate numerical algorithms for finding the approximate solutions of time-fractional Burgers’ equations both in one- and two-dimensional spatial domains and time-fractional coupled Burgers’ equations. Their fractional-order derivatives with respect to time were described in the Caputo sense and estimated by forward difference quotient. According to Example 1, even though, we obtain similar accuracy, however, it can be seen that our method does not require the solution to be separable among the spatial and temporal variables. For Example 2, the results confirm that even with nonlinear FDEs, the FIM-SCP provides better accuracy than FDM. For two dimensions, Example 4 shows that even with the small kinematic viscosity , our method can deal with a shock wave solution, which is not globally continuously differentiable as that of the classical Burgers’ equation under the same effect of small kinematic viscosity . We can also see from Examples 5 and 6 that our proposed method can be extended to solve the time-fractional Burgers’ equation and we expect that it will also credibly work with other system of time-fractional nonlinear equation. We notice that our method provides better accuracy even when we use a small number of nodal points. Evidently, when we decrease the time step, it furnishes more accurate results. Also, we illustrated the time convergence rate of our method based on norm, we observe that it approaches to the linear convergence . Finally, we show the computational cost in terms of CPU time(s) for each example. An interesting direction for our future work is to extend our technique to solve space-fractional Burgers’ equations and other nonlinear FDEs.