Abstract
In the framework of 2D circular membrane Micro-Electric-Mechanical-Systems (MEMS), a new non-linear second-order differential model with singularity in the steady-state case is presented in this paper. In particular, starting from the fact that the electric field magnitude is locally proportional to the curvature of the membrane, the problem is formalized in terms of the mean curvature. Then, a result of the existence of at least one solution is achieved. Finally, two different approaches prove that the uniqueness of the solutions is not ensured.
1. Introduction to the Problem
In recent years, a growing demand for embedded engineering applications has convinced researchers to develop low cost micro- to nano-sized components, in which actuators and transducers play important roles. This presents a link between the physical nature of the problem under study and the need to use machine languages to manage interfaces with other devices [1]. The interest of the scientific community in MEMS (Micro-Electro-Mechanical Systems) technology, which was born when Nathanson et al. produced the first batch device in 1964 [1,2], has been growing exponentially. At present, MEMS technology is fully part of the multi-disciplinary field of mathematical physics, allowing for highly varied engineering applications [1,3]. This is mainly due to the fact that it has been supported by sophisticated theoretical models, both static and dynamic [4,5]. However, even if these models appear to adhere to reality, they are often structured in an implicit form that does not provide explicit solutions (except in particular cases), for which numerical solutions must be necessarily sought [6], or analytical conditions, which ensure the existence, uniqueness, and regularity (up to the desired order) of the solution must be derived [7,8]. Analytical and numerical approaches can be used to obtain numerical solutions that do not represent ghost solutions [9,10,11]. In the field of MEMS technologies, the scientific community has been actively engaged both in the development of theoretical models and in technology transfer. In particular, some important models for coupled problems have been developed: ranging from magnetically actuated systems [1,12,13] to thermo-elastic models [14], and from electro-elastic models [15] to micro-fluid models [16], featuring highly complex formulations for the management of different MEMS devices (with plates, membranes, and so on). These theoretical models have had excellent feedback in technology transfer, through the design, realization, and distribution of the MEMS devices used in the various applications [17]. Biomedical diagnostics increasingly require efficient, low-cost, and reliable micro-components, which can be of help to health-care personnel both in on-line and off-line modes [18,19]. Many mathematical models have been theoretically conceived of in special functional spaces, in order to provide the conditions of the existence and uniqueness of the solutions, which are otherwise difficult to detect [20,21]. Cassani et al. [22] built a sophisticated mathematical model of a MEMS device constituted of two metallic plates (one fixed and one deformable), which was clumped at the edges and subjected to a drop voltage, which deformed the deformable plate towards the other one. Obviously, determining a solution for this model is very difficult, and some simplifications were necessarily required. In particular, neglecting the inertial and non-local effects, Cassani et al. obtained a simplified model in [23], which was studied using Steklov boundary conditions to achieve Dirichlet and Navier boundary conditions. Starting from this simplified model, the authors studied a new elliptical semi-linear dimensionless model for a 1D membrane MEMS, based on the proportionality between the electric field magnitude and the curvature of the membrane, achieving results of the existence and uniqueness for the solution. In particular, in [7], the algebraic condition ensuring the uniqueness of the solution did not depend on the electro-mechanical properties of the material constituting the membrane. Consequently, in [10], the authors achieved a new algebraic condition depending on these properties, ensuring the uniqueness of the solution.
In this work, for applicative reasons, the authors focus their attention on a 2D circular membrane MEMS device, which is useful in several industrial and/or biomedical applications [1,19]. In addition, the authors consider to be proportional to the mean curvature of the membrane of the device, in order to achieve a non-linear second-order differential model with singularity in the steady-state case. Finally, an algebraic condition, depending on both the mechanical and electrical properties of the membrane, guarantees the existence of at least one solution to the proposed model. However, the uniqueness of the solution is not ensured.
The paper is structured as follows. After presenting how the proposed model was achieved in Section 2, Section 3 describes the 2D circular membrane MEMS from two points of view: as an actuator and as a transducer. In the latter case, starting from the theory of the elasticity of the plates, the most important elasticity formulas of the membrane are presented, which will be useful in the following. Moreover, an important link between mechanical pressure and electrostatic pressure is detailed for our purposes. The formulation of the problem under study is detailed in Section 4. From the geometry of the problem, the model is formulated in terms of the mean curvature of the membrane, obtaining a non-linear second-order differential equation with singularity (Section 5). Once the problem under study is formulated in a general manner in Section 6, and after presenting some preliminary Lemmas in Section 7, a result of the existence of at least one solution to the problem (5) is detailed in Section 8. However, although the existence of at least one solution is ensured, uniqueness is not guaranteed, as is proven by means of two different approaches in Section 9. Finally, some conclusions and perspectives complete this work.
2. From the Cassani Model to the Proposed Model
As mentioned above, Cassani et al. [22] proposed a detailed mathematical model of a MEMS device consisting of two metallic plates, where one is fixed (the lower plate) and the other is deformable (the upper plate), but anchored at the boundary of a region and subjected to a drop voltage, which deforms the lower plate (at ) towards the upper plate (at ). This steady-state model assumes the following structure [22]:
where is a bounded function depending on the dielectric properties of the material constituting the deformable plate and the positive parameters , , , and are related to the mechanical and electrical properties of the system. In addition, is the Coulomb exponent, such that takes into account higher order Coulombian behaviors. Obviously, obtaining a solution to the problem (1) is a difficult task, as the choice of boundary conditions is an extremely delicate task [22,23]. From the model (1), by neglecting the inertial and non-local effects and setting and , one obtains the following simplified model:
Model (2) has also been studied by Cassani et al. [23], in which the existence of a solution was studied, using Steklov boundary conditions, to obtain Dirichlet and Navier boundary conditions when or . In the past, starting from (2), the authors studied the following new elliptical semi-linear dimensionless model for a 1D membrane MEMS:
where the membrane replaces the deformable lower plate and is considered to be proportional to the curvature, K, of the membrane. Interesting results of the existence and uniqueness for the solution to the problem (3) were achieved in [7]. In particular, the uniqueness condition was independent of the electro-mechanical properties of the material constituting the membrane; thus, in [10], the authors obtained a new condition of the uniqueness for the solution to Problem (3), which took into account these properties. Moreover, Model (3) was solved numerically (using the shooting approach) in both [9,24], highlighting the range of , which ensured convergence of the numerical procedure in the absence of ghost solutions. Finally, in [25], the shooting procedure and the Keller-box scheme were compared to achieve an optimal range of without ghost solutions. It is worth noting that takes into account the applied voltage V and that takes into account the electro-mechanical properties of the material constituting the membrane [9,10].
In this paper, we focus our attention on 2D circular membrane MEMS actuators, which are useful in industrial and/or biomedical applications [1,19]. First, we observe an axial symmetry in the geometry of the membrane. Then, considering the z axis as the rotation axis, the profile u of the circular membrane can be considered as the surface generated by rotating a curve C around z on the vertical plane located in the first quadrant, with . Then, u is only dependent on the radial co-ordinate r, such that the 2D problem here can be considered as a 1D problem in which the independent variable x is replaced by r. Then, only considering the radial part of the Laplace operator, the model (2) can be written as follows:
where and is a singularity. In addition, in (4), is represented by , as in [7]. Then, we consider to be proportional to the curvature of the membrane itself (with ). Finally, we exploit the expression of mean curvature to achieve, from Model (4), the following model:
where is the critical security distance, which ensures that the deflection of the membrane does not produce contact between the membrane itself and the fixed upper plate. Then, we prove a theorem of the existence of the solution to the model (5). However, as we will prove below, the uniqueness of the solution to the problem (5) is not guaranteed.
3. An Overview of Circular Membrane MEMS Devices
3.1. The Circular Membrane MEMS Actuator
Let us consider a circular membrane MEMS device, which is constituted of two parallel disks with radius R and with mutual distance d (see Figure 1). A circular membrane of the same radius is clumped on the edge of the lower disk. The membrane is free to deform towards the upper disk (which is fixed). Applying an external electrical voltage V, the membrane deforms as it approaches the upper disk without touching it. When V is externally applied (the lower disk can be considered to be at ), the field between the disks generates an electrostatic pressure [3] (where is the permittivity of free space), which deflects the membrane. While the membrane deflects, the direction of is always locally orthogonal to the tangent line of the membrane, and depends on the local distance between the membrane itself and the upper disk [3]. Moreover, when the membrane deforms, the capacitance of the device varies as the distance between the membrane and the upper disk locally varies. It is evident that, the bigger is, the bigger the curvature of the membrane will be. Hence, can be locally considered to be proportional to the curvature of the membrane.
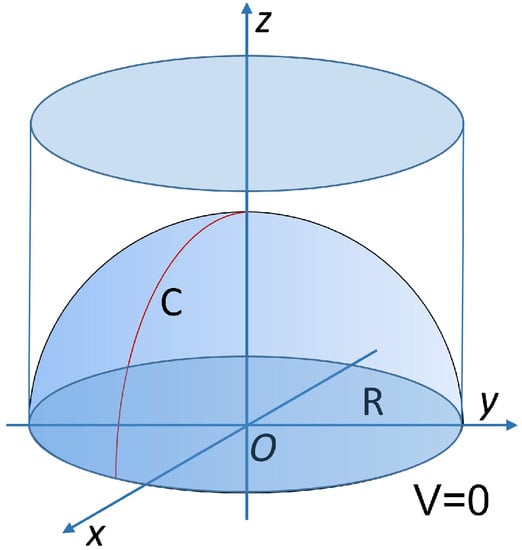
Figure 1.
Representation of a circular membrane MEMS actuator when its membrane is deformed.
3.2. The Circular Membrane MEMS Transducer
To study our model, we will utilize some analogies with the model of a circular plate MEMS transducer subjected to a mechanical pressure p.
Remark 1.
Although the terms sensor and transducer are often considered synonymous, it is imperative to specify their correct meanings. A sensor is a sensitive element that converts an input quantity into an output (physical) quantity, which can be acquired as an electrical signal. A transducer is a device that transforms the physical quantity to be measured into an electrical signal. In general, a transducer consists of an input interface, a sensor, and an output interface. For our purposes, we consider a MEMS transducer, rather than a MEMS sensor, to take also into account both of the interfaces.
3.2.1. Circular Plate MEMS Transducer: Behavior under the Effect of p
As has been shown, when a plate is subjected to a mechanical pressure p, it deforms with deflection u satisfying (in the dynamical case) the equation [1], where is the density of the material constituting the plate, h is the thickness of the plate, and T and D are the mechanical tension in the plate and the flexural stiffness of the plate, respectively. As is well known, D is defined as:
in which Y is Young’s modulus and is the Poisson ratio. In addition, for a circular plate, u only depends on the radial co-ordinate r under the assumption of radial symmetry. Then, in the steady-state case, can be calculated as , , for the z-directed displacement u, according to [26]. Obviously, if , one obtains the displacement at the center of the plate:
Thus, . In other words, in contrast with the behavior of an actuator, the device behaves as a transducer because p generates , with consequent variation of the electrostatic capacitance [1,26]:
In addition, as h and D have finite values, is very small, such that the distance between the plates can be regarded as equal to d. Exploiting the Taylor series (with three terms retained) and setting (equilibrium capacitance; ), (8) can be written as follows:
By (9), we can achieve the co-energy function of the capacitance system, ; the charge on the membrane, ; and the electrical force, . It can be noted that the capacitance is a non-linear function of , according to (9). In addition, is proportional to p through ; that is, [1,26]. Finally, if , then [1,26].
Remark 2.
All of , , q, , and depend on d. This is due to the fact that the circular plate has a relevant value of D, such that is not accentuated (). Thus, it follows that the electrical quantities only depend on d and do not depend on [3].
3.2.2. Circular Membrane MEMS Transducer: Behavior under the Effect of p
As we are interested in a circular MEMS membrane device with radius R, we need to modify the relations presented in Section 3.2.1. In particular, for circular membranes, the thickness h is very small, and so, the flexural stiffness D is lower than when a circular plate MEMS is considered (see (6)). Obviously, the lower the value of D is, the more flexible the membrane will be. Then, (as given by (7)) grows, such that the membrane is closer to the upper disk. In this case, the condition does not hold, and thus, it is necessary to consider the term in the denominator of (9). If the membrane is subjected to p, assumes the following form [1]:
where:
and T is the mechanical tension of the membrane. In addition, [1,26]. Then, is justified as:
We observe that, to calculate and , we approximate the surface of the membrane as even when the membrane deforms. This approximation is justified by the fact that , such that the surface of the deformed membrane is almost equal to the surface of the membrane in the resting position.
3.3. Link between p and
As specified above, the actuator, when subjected to V, produces , which, consequently, generates . This pressure deforms the membrane, achieving . It is clear that there exists a link between p and . However, linearly depends on p. In fact, from (11), we can write:
where is constant. Moreover, in the absence of further causes, p arises exclusively from the electrostatic pressure due to . Then, p can be considered to be dependent on , such that the following chain of equalities holds:
where and k are constants. By (12), we can write:
Remark 3.
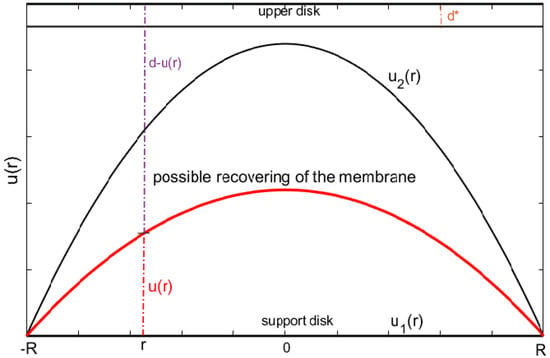
In (15), represents the distance between the profile of the membrane and the upper disk. Considering that the profile of the membrane does not touch the upper disk and that, when the deformation occurs, it is far from the upper disk with a distance , it makes sense to write , from which we obtain:
For details, see Figure 2.

Figure 2.
The functions and for the problem under study.
Remark 4.
The link between p and forms the dual transducer–actuator model. In other words, the behavior of the transducer, as we have seen in this subsection, helps us to understand how an actuator operates (and vice versa).
4. Formulation of the Problem
The Proposed Model
As shown above, the term in Model (4) is considered to be proportional to . Thus, it makes sense to rewrite model (4) as follows:
Appealing to the evident physical motivation, we can suppose to be a continuous function depending on r on . Moreover, indicating by the curvature of the deformed membrane, the proportionality between and can be expressed by , in which represents the proportionality function. Then, if we pose , where is a continuous function proportional to the tension V, Model (18) can be rewritten as follows:
with and To define the proposed model completely, we need to find the curvature K in (19) explicitly, which, in this paper, is expressed as the mean curvature [27].
5. Formulation of the Proposed Model in Terms of Mean Curvature
Let us consider a surface S generated by rotating, around the vertical axis z, a curve C located in a plane orthogonal to the plane forming an angle t with the plane (see Figure 1) [27]. To simplify our calculations, we suppose that C is parametrized with a generic parameter r differing from the curvilinear co-ordinate s, such that , , where and are regular functions satisfying:
for each . The parametrization of the surface S is then:
we observe that , as a natural parametrization, ensures that C is regular everywhere, and so, by rotation, S is regular. Then, we easily obtain:
Thus, the coefficients of the first fundamental form are:
As everywhere, the co-ordinate lines are everywhere orthogonal. Then, we can write:
Finally, we have:
and the unit normal vector to S in is:
Then, the coefficients of the second fundamental form are:
To achieve the principal curvatures and , it is sufficient to solve the following algebraic equation:
from which we can easily obtain:
Thus, the mean curvature becomes:
Taking into account (32), the model (19) can be written as follows:
we observe that, in (33), if . In fact, let us suppose that:
then, the equation of Model (34) admits the trivial solution , which cannot be considered a solution to the problem (34). In fact, let us suppose absurdly that a solution to the model (33) also satisfies from which , and again, . Taking into account that , we easily achieve:
which is a solution for the equation of the model (33) that also satisfies the equation of the model (34). However, although both Equations (33) and (34) are satisfied by the solution (35), this does not satisfy the condition . Then, in (34), . Thus, we can divide both sides of the differential equation of Model (33) by , obtaining:
6. General Formulation of the Problem
7. Preliminary Lemmas
We first present the following well known result, which will be exploited to prove the existence of a solution to the problem (5).
Lemma 1.
We consider the problem (37). Let and be twice continuously differentiable functions, such that:
and:
for . Let be a continuous function and satisfying the following Lipschitz condition:
in , where
and and () are continuous functions in . If with then the problem (37) has at least one solution, , such that in holds.
For details, see [28]. Furthermore, we will use the following Lemmas to prove that the uniqueness of the solution to the problem (5) is not ensured.
Lemma 2.
Let us suppose that the conditions of Lemma 1 are satisfied and that and satisfy the given boundary conditions. If the differential equation:
has a nontrivial solution satisfying zero boundary conditions on any sub-interval of , then the given boundary value problem has only one solution such that .
Again, see [28]. Before we present Lemma 3, we need to introduce the following definition:
Definition 1.
A point is a regular singular point if only if:
where and are functions depending on r.
Lemma 3.
Let us consider the second-order ordinary differential equation (for details, see [29]):
in which , , and are functions depending on r. As , setting and , we have:
in which is a regular singular point. As it is well known that and are both analytic functions at with convergent power series expansions:
and:
for , and as is the minimum of the radii of convergence of the power series for and , considering and as the roots of the following indicial equation:
we have that:
- If and are real, then, in either the interval or the interval , there exists a solution of the form:in which can be obtained by the following recurrence relation:with and .
8. A Result of the Existence of at Least One Solution to the Problem (5)
We now reveal and prove our principal goal, regarding the existence of at least one solution for the problem (5).
Theorem 1.
Let us consider the problem (5), and let and be two functions defined in and twice continuously differentiable, such that and:
for . In addition, let be a continuous function (except for ) satisfying the Lipschitz condition in , where . If , and:
then there exists at least one solution for the problem (5).
Proof.
To prove Theorem 1, we exploit Lemma 1. We assume the following expressions as and :
and:
as derived from (17). Figure 2 depicts both and , as well as a possible recovery of the membrane. Clearly, , and both are twice continuously differentiable functions. Now, we must verify Inequalities (54) and (55); that is:
To verify (59), we observe that, for , we trivially have . Then, if we assume that:
then (59) is verified. To verify (60) (see (58)), with , we have:
and:
We note that, in Inequality (64), the quantity , such that, if we impose , which implies that:
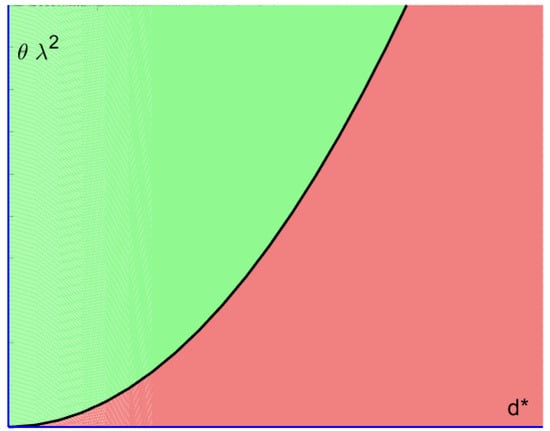
it follows that the inequality (65) automatically satisfies Inequality (61). As mentioned above, is a parameter proportional to the applied voltage V and takes into account the electro-mechanical properties of the material constituting the membrane. Figure 3 depicts the zone of existence, in the plane , of at least one solution for the problem (5). In particular, the line of equation , shown in Figure 3 as a black line, separates the area of existence of at least one solution to Model (5) (light green area) from the area where at least a solution to the model (5) is not guaranteed (light red area). As Lemma 1 requires, we also need to prove that satisfies the Lipschitz condition (42). Then, we easily prove that:

In addition,
As , then there exists a constant Z such that . Finally, Lemma 1 requires that . For this purpose, as , we obtain . In addition, Moreover, . Thus, the proof of the theorem is complete. □
Remark 5.
Condition (65) has an important physical meaning. In fact, taking into account (14), (65) can be written as follows:
Thus, the greater is, the lower the value of will be, and so, in the problem under study (5), will be smaller; that is, the concavity of the membrane will rise. In other words, the greater the value of , the greater the influence of the electrostatic pressure. Then, the mechanical pressure will rise (as ), with a consequent increase of deformation in the membrane.
9. On the Uniqueness of the Solution to the Problem (5)
Although the problem (5) admits at least one solution such that with and verifying Theorem 1, its uniqueness has not been ensured. This section proves this fact through two alternative approaches.
Theorem 2.
Consider the problem (5). Let us suppose that the conditions of Theorem 1 are satisfied and that and satisfy the given boundary conditions. Then, the uniqueness of the solution such that is not guaranteed.
Proof.
As specified in (67), we can write:
Thus, exploiting Lemma 2, we consider the ordinary differential equation:
which can be considered as a particular case of the following Bessel equation:
with and . In fact, from the above equation, we can write:
from which (in our case, assuming and ), Equation (73) becomes:
Then, if , it follows that , and so, we obtain:
Finally, setting , we obtain Equation (71).
As is known from Bessel theory [29,30], the general solution for (71) can be written as a linear combination of two linearly independent Bessel functions of the first and second kind of zeroth order, respectively; and :
where and are constants [29,30]. It is known that and , in which is the Euler–Mascheroni constant (with a value of 0.5772). Moreover, . From the above relations, we obtain the general solution for Equation (71) as:
Obviously, as , we have . Meanwhile, due to the presence of , presents a logarithmic singularity as . However, taking a linear combination, with and , we find that the general integral of the differential equation assumes the form:
We have also found a non-trivial solution for the ordinary differential Equation (71), which differs from the trivial one . By Lemma 2, we deduce that the uniqueness of the solution to the problem (5) is not guaranteed.
Alternatively, we study an approach to search for a non-trivial solution for the differential Equation (71). In fact, multiplying Equation (71) by r, we obtain:
where . Equation (79) can be considered to be a particular case of the following equation:
in which we can write , , and Moreover, we define:
In our case , and so (see Definition 1):
from which we can deduce that is a regular singular point for (79). In addition, Equation (80), taking into account (81), can be easily written as follows:
such that Lemma 3 can be applied [29]. By (48), we can write , from which and . Again, , such that and . Then, the indicial Equation (50) becomes , whose roots are . Then, applying Lemma 3, we obtain To achieve , it is sufficient to substitute the series solution for u in (83). Then, we can finally conclude that:
such that may turn out to be zero, in which case there is no logarithmic term in the solution. As Equation (71) admits solutions different from the trivial one, we deduce that the uniqueness of the solution to the problem (5) is not guaranteed.
10. Conclusions and Perspectives
In this work, a 2D non-linear second-order differential model for a electrostatic circular membrane MEMS actuator was presented and studied. In particular, a brief Introduction opened the paper, introducing the reader to the proposed 2D model based on the proportionality between and the mean curvature of the membrane. After presenting some interesting mathematical models of MEMS actuators which are well known in the literature, the membrane MEMS device under study was detailed both from the point of view of the actuator and from the point of view of the transducer. Moreover, the link between mechanical pressure p and electrostatic pressure , here exploited, was given the opportunity to consider the dual transducer–actuator model. Then, the proposed model was detailed in terms of the mean curvature of the membrane, exploiting both the first and second differential forms (as differential geometry suggests). After presenting some preliminary lemmas exploited in the following work, the authors proved the existence of at least one solution for the proposed model. In addition, in a suitable 2D plane, exploiting an achieved algebraic condition depending on both mechanical and electrical parameters, the area where the existence of at least one solution was ensured and the area where at least one solution was not guaranteed were depicted. However, as detailed at the end of the paper, the uniqueness of the solution was not ensured. In other words, while the existence of at least one solution was ensured, its uniqueness was not guaranteed. Although the achieved results were encouraging, it makes sense to classify the problem as ill-posed, according to Hadamard’s second statement (that is, a problem is ill-posed if the uniqueness of the solution is not guaranteed) and ask, as a future perspective, if there exists any additional condition that can make it a well-posed problem.
Author Contributions
The contributions of the authors are to be considered equal.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MEMS | Micro-Electro-Mechanical Systems |
References
- Pelesko, J.A.; Bernstein, D.H. Modeling MEMS and NEMS; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2003. [Google Scholar]
- Nathanson, N.H.; Newell, W.E.; Wickstrom, R.A.; Lewis, J.R. The Resonant Gate Transistor. IEEE Trans. Electr. Dev. 1964, 14, 117–119. [Google Scholar] [CrossRef]
- Di Barba, P.; Wiak, S. MEMS: Field Models and Optimal Design; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Feng, J.; Liu, C.; Zhang, W.; Hao, S. Static and Dynamic Mechanical Behaviors of Electrostatic MEMS Resonator with Surface Processing Error. Micromachines 2018, 9, 34. [Google Scholar] [CrossRef] [PubMed]
- Daeichin, M.; Ozdogan, M.; Twfighian, S.; Miles, R. Dynamic Response of a Tunable MEMS Accelerometer Based on Repulsive Force. Sens. Actuators A Phys. 2019, 289, 34–43. [Google Scholar] [CrossRef]
- Javaheri, H.; Ghanati, P. A Case Study on the Numerical Solution and Reduced Order Model of MEMS. Sens. Imaging 2018, 19, 22–31. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic Field in Terms of Geometric Curvature in Membrane MEMS Devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar] [CrossRef]
- Mashinchi Joubari, R.; Asghari, R. Analytical Solution for Nonlinear Vibration of Micro-Electro-Mechanical System (MEMS) by Frequency-Amplitude Formulation Method. J. Math. Comput. Sci. 2012, 4, 371–379. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the Membrane Detection of a 1D Electrostatic-Driven MEMS Device by the Shooting Method: Convergence Analysis and Ghost Solutions Identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the Uniqueness of the Solution for a Semi-Linear Elliptic Boundary Value Problem of the Membrane MEMS Device for Reconstructing the Membrane Profile in Absence of Ghost Solutions. Int. J. Non-Linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Fattorusso, L.; Versaci, M. A New One-Dimensional Electrostatic Model for Membrane MEMS Devices. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2018; Volume 35. [Google Scholar]
- Herrera-May, A.; Aguilera-Cortes, L.; Garcia-Ramirez, P. Resonant Magnetic Field Sensors Based on MEMS Technology. Sensors 2009, 9, 1691–1695. [Google Scholar] [CrossRef] [PubMed]
- Imai, S.; Tsukioka, T. A Magnetic MEMS Actuator Using a Permanent Magnet and Magnet Fluid Enclosed in a Cavity Sandwiched by Polymer Diaphrams. Precis. Eng. 2014, 38, 548–554. [Google Scholar] [CrossRef]
- Mohammadi, A.K.; Ali, N.A. Effect of High Electrostatic Actuation on Thermoelastic Damping in Thin Rectangular Microplate Resonators. J. Theor. Appl. Mech. 2015, 53, 317–329. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, L.; Li, L.; Wiao, Z.; Cao, Q. Design and Analysis of the Elastic-Beam Delaying Mechanism in a Micro-Mechanical Systems Device. Micromachines 2018, 9, 567. [Google Scholar] [CrossRef] [PubMed]
- Takayama, Y. Developing a MEMS Device with Built-In Microfluidics for Biophysical Single Cell Characterization. Micromachines 2018, 9, 275. [Google Scholar] [CrossRef] [PubMed]
- Karumuri, S.R. Micro-Electro-Mechanical-Systems (MEMS) Technology. Arch. Appl. Sci. Res. 2012, 4, 307–314. [Google Scholar]
- Ciuti, G.; Ricotti, L.; Menciassi, A.; Dario, P. MEMS Sensor Technologies for Human Centered Applications in Healthcare, Physical Activities, Safety and Environmental Sensing: A Review on Research Activities in Italy. Sensors 2015, 15, 6441–6468. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y. Silicon-Based Sensors for Biomedical Applications: A Review. Sensors 2019, 19, 2908. [Google Scholar] [CrossRef] [PubMed]
- Di Barba, P.; Lorenzi, A. A Magneto-Thermo-Elastic Identification Problem with a Moving Boundary in a Micro-Device. Milan J. Math. 2013, 81, 347–383. [Google Scholar] [CrossRef]
- Esposito, P.; Ghoussoub, N.; Guo, Y. Mathematical Analysis of Partial Differential Equations Modeling Electrostatic MEMS; American Mathematical Society/Courant Institute of Mathematical Sciences (AMS): Providence, RI, USA, 2010. [Google Scholar]
- Cassani, D.; Fattorusso, L.; Tarsia, A. Non-local Dynamic Problems with Singular Nonlinearities and Application to MEMS. Prog. Nonlinear Differ. Equ. Appl. 2014, 85, 185–206. [Google Scholar]
- Cassani, D.; d’O, J.M.; Ghossoub, N. On a Fourth Order Elliptic Problem with a Singular Nonlinearity. Adv. Nonlinear Stud. 2009, 9, 177–197. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Membrane Micro Electro-Mechanical Systems for Industrial Applications. In Handbook of Research on Advanced Mechatronic Systems and Intelligent Robotics; IGI Global: Hershey, PA, USA, 2019. [Google Scholar]
- Versaci, M.; Angiulli, G.; Calcagno, S.; Di Barba, P.; Jannelli, A. Recovering the Membrane Profile of an Electrostatic MEMS Device: A Comparison of Numerical Approaches. In Proceedings of the Eighteenth Biennial IEEE Conference on Electromagnetic Field Computation (CEFC 2018), Hangzhou, China, 28–31 October 2018; Volume 9. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Tu Lorin, W. Differential Geometry—Connections, Curvature, and Characteristic Classes; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bailey, P.B.; Shampine, L.F.; Waltman, P.E. Nonlinear Two Point Boundary Value Problems; Academic Press: Cambridge, MA, USA, 1968. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bowman, F. Introduction to Bessel Functions; Dover Pubblications: Mineola, NY, USA, 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).