On the Wiener Complexity and the Wiener Index of Fullerene Graphs

Abstract

Fullerenes are molecules that can be presented in the form of cage-like polyhedra, consisting only of carbon atoms. Fullerene graphs are mathematical models of fullerene molecules. The transmission of a vertex v of a graph is a local graph invariant defined as the sum of distances from v to all the other vertices. The number of different vertex transmissions is called the Wiener complexity of a graph. Some calculation results on the Wiener complexity and the Wiener index of fullerene graphs of order $n\le 232$ and IPR fullerene graphs of order $n\le 270$ are presented. The structure of graphs with the maximal Wiener complexity or the maximal Wiener index is discussed, and formulas for the Wiener index of several families of graphs are obtained.

1. Introduction

A fullerene is a spherically shaped molecule consisting of carbon atoms in which every carbon ring forms a pentagon or a hexagon. Every atom of a fullerene has bonds with exactly three neighboring atoms. The molecule may be a hollow sphere, ellipsoid, tube, or many other shapes and sizes. Fullerenes are the subject of intense research in chemistry, and they have found promising technological applications, especially in nanotechnology and materials science [1,2].

Molecular graphs of fullerenes are called fullerene graphs. A fullerene graph is a 3-connected planar graph in which every vertex has degree 3, and every face has size 5 or 6. By Euler’s polyhedral formula, the number of pentagonal faces is always 12. It is known that fullerene graphs having n vertices exist for all even $n\ge 24$ and for $n=20$. The number of all non-isomorphic fullerene graphs can be found in [3,4,5]. The set of fullerene graphs with n vertices will be denoted as $F_n$. The number of faces of graphs in $F_n$ is $f=n/2+2$ and, therefore, the number of hexagonal faces is $n/2-10$. Despite the fact that the number of pentagonal faces is very small compared to the number of hexagonal faces, their location is crucial to the shape and properties of fullerene molecules. Fullerene graphs without adjacent pentagons, i.e., each pentagon is surrounded only by hexagons, satisfy the isolated pentagon rule (IPR), and are called IPR fullerene graphs. They are considered as molecular graphs of thermodynamic stable fullerene compounds. The number of all non-isomorphic IPR fullerene graphs was reported, for example, in [5,6]. Mathematical studies of fullerenes include applications of topological and graph theory methods, information theory approaches, design of combinatorial and computational algorithms, etc. (see selected articles [3,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]). A comprehensive bibliography on mathematical methods and its applications can be found in [1,2,4,12,28,29]. The set of IPR fullerene graphs with n vertices will be denoted as $F_n^{*}$.

The vertex set of a graph G is denoted by $V\left(G\right)$. The number of vertices of G is called its order. The distance $d(u,v)$ between vertices $u,v\in V\left(G\right)$ is the number of edges in a shortest path connecting u and v in G. The maximal distance between vertices of a graph G is called the diameter $D\left(G\right)$ of G. Vertices are diametrical if the distance between them is equal to the diameter of a graph. By transmission of $v\in V\left(G\right)$, we mean the sum of distances from vertex v to all the other vertices of G, $tr\left(v\right)={\sum }_{u\in V\left(G\right)}d(v,u)$. Transmissions of vertices are used for the design of many distance-based topological indices [30]. Usually, a topological index is a graph invariant that maps a family of graphs to a set of numbers such that values of the invariant coincide for isomorphic graphs. The Wiener index is a topological index defined as a half of the sum of vertex transmissions:

$$W\left(G\right)=\sum _{\{u,v\}\subseteq V\left(G\right)}d(u,v)=\frac{1}{2}\sum _{v\in V\left(G\right)}tr\left(v\right).$$

It was introduced as a structural descriptor for tree-like organic molecules by Harold Wiener [31]. The definition of the index in terms of distances between vertices of a graph was given by Haruo Hosoya [32]. The Wiener index that has found important applications in chemistry (see books and reviews [33,34,35,36,37,38,39,40,41]). Various aspects of the theory and practice of the Wiener index of fullerene graphs are discussed in many works [7,8,11,12,13,15,16,17,18,19,20,22,24,42].

The number of different vertex transmissions in a graph G is known as the Wiener complexity [43] (or the Wiener dimension [7]), $C_W\left(G\right)$. This graph invariant can be regarded as a measure of transmission variety. A graph is called transmission irregular if all vertices of the graph have pairwise different transmissions, i.e., it has the largest possible Wiener complexity. It is obvious that a transmission irregular graph has the identity automorphism group. Various properties of transmission irregular graphs were studied in [43,44,45]. It was shown that almost all graphs are not transmission irregular. Several infinite families of transmission irregular graphs were constructed for trees, 2-connected graphs, and 3-connected cubic graphs in [44,46,47,48,49].

In this paper, we present some results of studies of the Wiener complexity and the Wiener index of fullerene graphs. In particular, we are interested in two questions: does a transmission irregular fullerene graph exist and can a graph with the maximal Wiener complexity has the maximal Wiener index?

2. Wiener Complexity of Fullerene Graphs

The Wiener complexity of fullerene graphs was examined for fullerene and IPR-fullerene graphs with $n\le 232$ and $n\le 270$ vertices, respectively. A typical distribution of the numbers of fullerene graphs with fixed number of vertices with respect to values of $C_W$ is shown in Figure 1. The number of graphs of $F_{196}$ (100 faces) is 177,175,687. Denote by $C_n$ the maximal Wiener complexity among all fullerene graphs with n vertices, i.e., $C_n=\max \left\{C_W\left(G\right)\right|G\in F\}$, where $F=F_n$ or $F=F_n^{*}$. Let $g_n$ be a difference between order and the Wiener complexity, $g_n=n-C_n$. If a transmission irregular graph exists, then $g_n=0$. It is obvious that a transmission irregular graph has the identity automorphism group. The behavior of $g_n$ when the number of vertices n increases is shown in Figure 2. The bottom and top lines correspond to all fullerene graphs and to IPR fullerene graphs, respectively. Explicit values of $C_n$ can be found in Table 1 and Table 2.

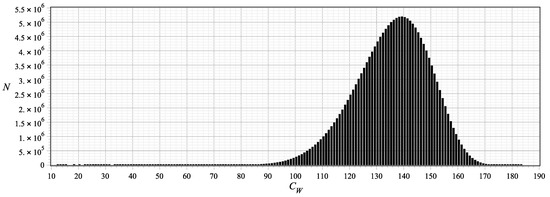
Figure 1. Distribution of fullerene graphs of $F_{196}$ with respect to their Wiener complexity $C_W$ (N is the number of graphs).

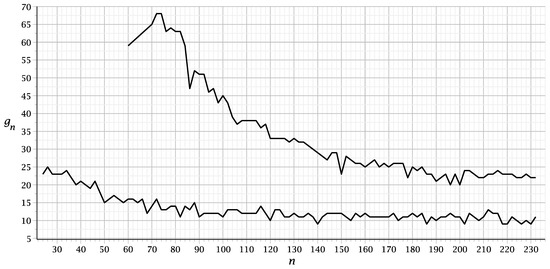
Figure 2. Difference $g_n$ between order and the maximal Wiener complexity of fullerene graphs (bottom line) and IPR fullerene graphs (top line) of order $n\le 232$.

Table 1. Maximal Wiener complexity and Wiener indices of fullerene graphs.

n	${\mathit{C}}_{\mathit{n}}$	W	D	${\mathit{W}}_{\mathit{n}}$	${\mathit{C}}_{\mathit{W}}$	D	t		n	${\mathit{C}}_{\mathit{n}}$	W	D	${\mathit{W}}_{\mathit{n}}$	${\mathit{C}}_{\mathit{W}}$	D	t
20	1	500	5	500	1	5			84	70	19,939	13	21,754	21	15	$c1$
24	2	804	5	804	2	5					20,076	13
26	2	987	6	987	2	6	b		86	73	21,404	13	23,467	8	16	b
28	5	1198	6	1198	5	6					21,521	13
30	7	1431	6	1435	3	6	a				21,593	13
32	9	1688	6	1696	3	7	b		88	73	22,359	13	24,714	21	16	$c2$
34	10	1973	7	1978	10	7					22,421	13
		1978	7								22,604	13
36	14	2288	7	2298	8	7	$c1$				22,616	13
38	18	2627	7	2651	4	8	b				22,619	13
40	19	3001	7	3035	4	8	a				22,750	14
42	22	3397	8	3415	19	8	$d1$				22,939	14
44	25	3830	8	3888	4	9	b		90	79	23,923	14	27,155	9	17	a
46	25	4285	8	4322	19	9	$d2$		92	80	25,731	15	28,256	8	17	b
		4289	8						94	82	26,793	14	28,910	44	17	$d2$
		4289	8						96	84	28,274	14	31,418	24	17	$c1$
		4291	8								28,317	15
48	30	4795	9	4858	12	9	$c1$		98	86	30,068	15	33,651	9	18	b
50	35	5310	9	5455	5	9	a		100	89	31,196	15	36,580	10	19	a
52	36	5876	9	5994	13	10	$c2$		102	89	32984	15	36,206	47	18	$d1$
54	37	6475	9	6558	22	10	$d1$				33,070	15
56	40	7114	10	7352	5	11	b				33,226	15
58	43	7782	10	7910	25	11	$d2$				33,505	15
		7822	10						104	91	34,402	15	39,688	9	19	b
60	44	8437	10	8880	6	11	a				34,529	15
		8466	10								36,801	17
		8490	10						106	93	36,648	16	40,278	47	19	$d2$
62	46	9202	10	9651	6	12	b				36,664	16
		9220	11								37,594	17
		9250	11						108	96	38,033	15	43,578	27	19	$c1$
64	49	9988	11	10,410	15	12	$c2$		110	98	40,154	16	48,005	11	21	a
		9993	11								41,419	17
		10,003	11						112	100	41,940	17	48,234	27	20	$c2$
		10,013	11						114	102	43,885	16	49,318	52	20	$d1$
		10,016	11						116	102	45,437	16	53,832	10	21	b
66	50	10,814	11	11,126	30	12	$d1$				46,632	17
		10,842	11								46,798	17
68	56	11,714	11	12,376	6	13	b				47,927	18
70	56	12,589	11	13,505	7	13	a		118	106	47,059	15	54,310	50	21	$d2$
72	56	13,407	11	14,298	18	13	$c1$				47,489	16
		13,448	11								47,697	16
		13,453	11						120	110	49,143	16	61,630	12	23	a
		13,567	12								49,606	17
		13,578	12						122	109	51,344	16	62,011	11	22	b
		13,766	12								51,456	16
74	61	14,521	12	15,563	7	14	b				51,933	17
76	63	15,867	13	16,554	18	14	$c2$				52,974	17
78	64	16,834	13	17,398	37	14	$d1$				53,070	17
		16,877	13						124	111	54,105	17	64,170	30	22	$c2$
80	66	17,727	13	19,530	8	15	a				55,050	18
		17,832	13								55,789	18
82	71	19,075	13	19,918	38	15	$d2$				57,358	19
											57,473	19
126	115	57,238	18	65,286	57	22	$d1$		186	177	167,300	26	198,046	82	32	$d1$
128	117	60,434	18	70,976	11	23	b		188	177	154,868	21	211,776	16	33	b
130	118	63,736	19	77,655	13	25	a		190	180	169,849	24	235,405	19	37	a
		63,922	19						192	181	163,370	22	222,778	48	33	$c1$
		65,396	20						194	183	187,947	27	231,763	17	34	b
132	121	62,917	17	76,538	33	23	$c1$				191,290	27
134	123	64,935	17	80,763	12	24	b		196	184	174,774	23	236,394	48	34	$c2$
		65,225	17								178,192	24
		68,161	19								178,529	25
136	124	69,838	19	83,274	33	24	$c2$				179,284	25
138	127	72,311	19	84,398	62	24	$d1$				184,011	24
		73,771	19						198	187	177,296	23	237,198	87	34	$d1$
140	131	73,644	19	96,280	14	27	a				189,530	25
142	131	79,852	20	91,518	56	25	$d2$		200	189	180,683	23	273,830	20	39	a
144	132	77,934	18	97,914	36	25	$c1$				192,365	25
		78,924	18						202	193	210,388	28	251,318	71	35	$d2$
146	134	86,095	20	102,947	13	26	b		204	192	189,450	22	265,274	51	35	$c1$
		86,287	21						206	195	221,909	28	275,427	18	36	b
		87,298	21								221,995	28
		87,442	21								222,097	28
148	136	86,432	20	105,834	36	26	$c2$		208	198	201,644	23	280,554	51	36	$c2$
150	138	87,886	19	117,705	15	29	a		210	199	238,572	29	316,255	21	41	a
		88,860	19						212	199	207,617	23	299,176	18	37	b
		92,732	21								207,975	23
		93,898	21								209,707	23
152	141	92,988	20	115,416	13	27	b				211,942	24
154	144	97,359	21	115,270	59	27	$d2$				215,779	24
156	144	95,579	19	122,938	39	27	$c1$				228,285	26
		96,997	19								228,507	26
		98,864	21								228,922	26
158	147	100,055	19	128,851	14	28	b		214	202	226,652	25	297,030	74	37	$d2$
160	148	103,952	20	142,130	16	31	a				247,352	29
		108,170	22								250,978	29
162	151	104,909	19	133,206	72	28	$d1$		216	204	220,131	23	312,858	54	37	$c1$
		116,278	23								226,928	25
164	153	110,088	20	143,288	14	29	b				240,920	27
166	155	117,531	21	142,838	62	29	$d2$				270,770	33
		119,485	23						218	209	260,324	30	324,251	19	38	b
168	157	114,316	18	151,898	42	29	$c1$		220	211	233,711	25	362,880	22	43	a
		126,632	23						222	211	240,755	26	330,406	97	38	$d1$
170	159	123,193	22	169,755	17	33	a				273,605	30
		130,548	24								273,701	30
172	160	129,708	22	162,474	42	30	$c2$				273,813	30
174	164	131,354	23	163,478	77	30	$d1$		224	214	248,633	27	350,688	19	39	b
176	165	130,105	20	175,312	15	31	b		226	217	288,789	31	347,998	77	39	$d2$
178	167	141,743	23	174,510	65	31	$d2$		228	218	258,913	25	365,818	57	39	$c1$
		150,696	25						230	221	269,286	27	413,905	23	45	a
180	168	139,697	21	200,780	18	35	a				295,719	31
182	171	144,410	21	192,971	16	32	b		232	221	292,719	28	384,714	57	40	$c2$
184	172	146,581	22	197,130	45	32	$c2$
		147,054	21
		153,615	23
		154,923	23

Table 2. Maximal Wiener complexity and Wiener indices of IPR fullerene graphs.

n	${\mathit{C}}_{\mathit{n}}$	W	D	${\mathit{W}}_{\mathit{n}}$	${\mathit{C}}_{\mathit{W}}$	D	t		n	${\mathit{C}}_{\mathit{n}}$	W	D	${\mathit{W}}_{\mathit{n}}$	${\mathit{C}}_{\mathit{W}}$	D	t
60	1	8340	9	8340	1	9			156	130	94,028	17	95,340	37	18	c
70	5	12,375	10	12,375	5	10			158	132	97,061	17	98,238	72	18	d
72	4	13,284	10	13,284	5	10			160	135	100,031	17	103,500	9	19	$a2$
74	6	14,275	10	14,275	6	10			162	136	103,213	17	104,799	72	18	d
76	13	15,248	10	15,294	4	10					103,842	18
78	14	16,305	11	16,365	8	11			164	137	106,920	18	108,598	40	19	c
80	17	17,412	11	17,600	1	11	$a2$		166	141	109,926	18	111,660	77	18	d
82	19	18,533	11	18,633	7	11			168	142	113,094	17	116,100	18	19	$b3$
84	25	19,664	11	19,734	10	11					113,725	18
86	39	20,864	11	21,007	14	11			170	145	116,472	17	121,575	10	20	$a1$
88	36	22,097	11	22,244	14	11					116,713	18
90	39	23,406	12	23,546	15	11	$a1$				117,141	19
		23,445	12						172	146	120,328	18	123,010	41	20	c
92	41	24,761	12	24,890	13	11					120,379	18
94	48	26,111	12	26,262	21	12					120,404	18
96	49	27,589	12	27,738	6	11					120,859	18
98	55	29,016	12	29,164	24	12			174	148	123,729	18	126,254	78	19	d
100	55	30,567	12	30,770	10	13	$a2$				123,765	18
		30,590	12								123,767	18
		30,551	13								124,309	19
102	59	32,133	13	32,275	28	12			176	150	127,275	18	130,684	44	20	c
104	65	33,677	12	33,946	7	13					127,354	18
106	69	35,406	13	35,547	32	13					127,583	18
108	70	37,097	13	37,296	26	13			178	156	131,619	19	134,008	82	20	d
110	72	38,849	13	39,055	7	14	$a1$		180	155	135,137	19	141,540	10	21	$a2$
112	74	40,689	13	40,878	10	13					135,577	19
114	76	42,494	13	42,753	17	13			182	158	138,427	19	142,031	78	20	d
		42,500	13						184	159	142,077	18	146,918	45	21	c
116	80	44,426	14	44,616	9	13					142,114	18
		44,434	13						186	163	146,825	19	151,887	20	21	$b1$
118	81	46,334	13	46,629	33	13					147,381	20	151,887	26	21	$b2$
120	87	48,386	14	48,820	7	15	$a2$		188	165	150,899	20	155,512	46	21	c
122	89	50,445	14	50,691	26	14			190	169	154,949	20	163,615	11	22	$a1$
		50,473	14						192	170	158,798	19	164,434	47	22	c
124	91	52,593	14	52,830	11	13			194	171	162,674	19	168,005	88	21	d
		52,635	14								162,770	19
126	93	54,737	14	54,950	52	14			196	176	167,808	20	173,708	46	22	c
128	96	57,026	15	57,240	32	15	c		198	175	171,657	20	177,339	92	22	d
130	97	59,208	14	60,095	8	16	$a1$		200	180	176,651	20	187,780	11	23	$a2$
		59,221	15						202	178	180,593	20	186,984	94	22	d
		59,328	15								180,818	21
132	100	61,579	15	62,097	14	16	$b3$				181,279	21
		61,609	15	62,097	20	16	$b4$				182,321	20
134	102	63,929	15	64,270	57	16	d		204	180	185,306	20	194,376	22	23	$b3$
		64,087	15								185,306	20	194,376	28	23	$b4$
136	105	66,439	16	66,880	33	16	c				185,410	21
138	108	68,859	15	69,285	57	16	d		206	183	188,946	20	196,937	92	22	d
		68,865	15						208	186	196,192	21	203,528	50	23	c
		68,911	16						210	188	199,403	21	214,255	12	24	$a1$
		69,075	16								199,484	21
140	111	71,543	16	72,860	8	17	$a2$		212	189	203,781	20	214,178	51	24	c
142	114	74,058	16	74,558	64	16	d				204,706	21
144	117	76,661	16	77,480	34	17	c				205,041	21
146	117	79,350	16	80,068	65	17	d		214	191	209,844	21	217,915	95	23	d
148	119	82,141	16	83,160	35	17	c				209,858	21
150	127	85,249	17	87,335	9	18	$a1$				209,885	21
152	124	88,004	17	89,106	38	18	c				210,112	21
154	127	90,792	16	91,921	68	18	d		216	192	213,004	20	225,212	51	24	c
		90,969	17								213,920	21
		91,173	17
218	195	218,701	21	228,952	102	23	d		244	223	294,943	23	313,078	58	27	c
		219,051	21						246	225	298,839	23	316,562	117	26	d
		219,302	21						248	228	310,038	25	327,240	60	27	c
		219,702	22						250	228	313,548	24	344,535	14	28	$a1$
220	197	223,863	21	243,020	12	25	$a2$		252	231	323,180	25	341,826	63	28	c
		224,835	21								328,878	26
		226,742	22						254	233	324,097	23	345,088	121	26	d
222	199	230,922	22	244,209	24	25	$b1$		256	235	328,374	23	356,860	63	28	c
				244,209	28	25	$b2$				328,471	23
224	202	235,105	21	248,358	55	25	c				329,926	24
226	204	237,981	21	252,089	101	24	d		258	237	336,694	24	368,499	30	29	$b1$
228	205	246,587	22	260,504	53	25	c						368,499	26	29	$b2$
230	208	252,526	23	274,295	13	26	$a1$		260	240	348,484	25	383,700	14	29	$a2$
232	210	260,165	23	273,042	57	26	c		262	242	349,765	24	374,298	123	27	d
		262,089	23						264	242	357,069	24	388,198	65	29	c
234	213	262,982	23	276,696	107	25	d				358,221	24
236	215	267,862	22	285,996	58	26	c				360,379	24
238	216	275,410	23	289,583	111	25	d				362,260	25
		276,644	23						266	246	364,584	25	391,052	127	28	d
240	219	282,476	23	308,060	13	27	$a2$		268	247	380,916	26	404,536	67	29	c
242	222	292,194	25	302,885	114	26	d		270	250	375,313	24	425,775	15	30	$a1$

Proposition 1.

There do not exist transmission irregular fullerene graphs with $n\le 232$ vertices and IPR fullerene graphs with $n\le 270$ vertices.

Since the almost all fullerene graphs have no symmetries, we believe that transmission irregular graphs exist for a large number of vertices (when the interval of possible values of transmissions will be sufficiently large with respect to the number of vertices).

Problem 1.

Does there exist a transmission irregular fullerene graph (IPR fullerene graph)? If yes, then what is the smallest order of such graphs?

3. Graphs with the Maximal Wiener Complexity

In this section, we study the following problem: can the Wiener index of a fullerene graph with the maximal Wiener complexity be maximal? Denote by $W_n$ the maximal Wiener index among all fullerene graphs with n vertices, i.e., $W_n=\max \left\{W\left(G\right)\right|G\in F\}$, where $F=F_n$ or $F=F_n^{*}$.

Numerical data for the Wiener indices of fullerene graphs in Table 1 and Table 2 show that Wiener indices of graphs with maximal $C_n$ are not maximal. Here, three columns $C_n$, W, and D contain the maximal Wiener complexity, the Wiener index, and the diameter of graphs with $C_n$, respectively. Three columns $W_n$, $C_W$, and D contain the maximal Wiener index of graphs with n vertices, the Wiener complexity, and the diameter of graphs with $W_n$. Based on data of the tables, one can make the following observations for the corresponding graphs:

• Values of the maximal Wiener complexity $C_n$ of all fullerene graphs do not decrease except for one case: $C_{202}=193$ and $C_{204}=192$. For IPR fullerene graphs, we have four exceptions (see pairs $C_{86},C_{88}$; $C_{150},C_{152}$; $C_{196},C_{198}$, and $C_{200},C_{202}$).
• Wiener indices of fullerene and IPR fullerene graphs with maximal $C_n$ ($|F_n|>1$) are not maximal except graphs of order $n=28$ with $W=1198$ ($|F_{28}|=2$).
• Several fullerene or IPR fullerene graphs of fixed n may have the maximal complexity $C_n$.
• Almost all fullerene graphs with fixed $C_n$ have distinct Wiener indices except for two graphs of order 46 with $C_n=25$ and $W=4289$ and two IPR fullerene graphs of order 204 with $C_n=180$ and $W=$ 185,306.
• Given n, only one fullerene graph has the maximal Wiener index while there are pairs of IPR fullerene graphs with the same maximal W (see graphs of order 132, 186, 204, 222, and 258).
• The diameter D of graphs with fixed $C_n$ is less than or equal to the diameter of graphs with a maximal Wiener index for all fullerene graphs (with seven exceptions for IPR fullerene graphs of order 90, 92, 96, 100, 102, 116, and 124).
• Fullerene graphs with the maximal Wiener index $W_n$ have the maximal diameter among all fullerenes. The values of the Wiener complexity of these graphs $C_W$ can vary greatly. This can be partially explained by the appearance of symmetries in graphs with $W_n$.

It is of interest how the pentagons are distributed among hexagons for fullerene graphs of $F_n$ with the maximal Wiener complexity $C_n$, $n\le 232$. Does there exist any regularity in the distribution of pentagons? Table 3 gives some information on the occurrence of pentagonal parts of a particular size in these graphs (an isolated pentagon forms a part). Here, N is the number of graphs in which pentagons form $N_p$ isolated connected parts. The considered fullerene graphs contain at most eight isolated parts.

Table 3. The number of graphs with $N_p$ isolated pentagonal parts.

$N_p$	1	2	3	4	5	6	7	8
N	9	8	27	66	45	42	9	1

Table 4 shows how many fullerene graphs with the maximal Wiener complexity have isolated pentagons. Here, N is the number of graphs having $N_i$ isolated pentagons. These fullerene graphs contain at most five isolated pentagons.

Table 4. The number graphs with $N_i$ isolated pentagons.

$N_i$	0	1	2	3	4	5
N	23	56	50	47	26	5

Does there exist an IPR fullerene graph with maximal Wiener complexity $C_n$ (lines of Figure 2 will have an intersection for $g_n\ne 0$)? We believe that the answer to this question will be positive for sufficiently large n.

4. Fullerene Graphs with the Maximal Wiener Index

The Wiener index of fullerene graphs was studied in [7,8,12,13,15,16,17,18,19,20,42]. A class of fullerene graphs of tubular shapes is called nanotubical fullerene graphs. They have cylindrical shape with the two ends capped by subgraphs containing six pentagons and possibly some hexagons called caps (see an illustration in Figure 3).

Figure 3. Construction of a nanotubical fullerene graph with two caps.

Consider fullerene graphs with the maximal Wiener indices (see Table 1). Five graphs of $F_{20}$–$F_{28}$ and $F_{34}$ contain one pentagonal part and the other 102 graphs possess two pentagonal parts. Two pentagonal parts of every fullerene graph are the same and contain diametrical vertices. Therefore, such graphs are nanotubical fullerene graphs with caps containing identical pentagonal parts. All diagrams of the parts are depicted in Figure 4. Cap of types a–c have symmetries. The number of fullerene graphs having a given part is shown near diagrams.

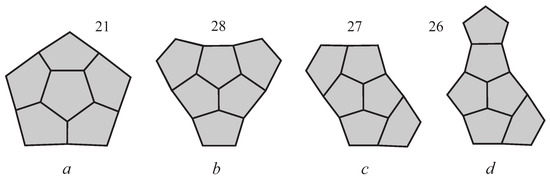
Figure 4. Pentagonal parts of caps for nanotubical fullerene graphs with the maximal Wiener index.

Characteristics of the corresponding nanotubes are reported in [9]. We assume that a type of a cap is determined by the type of its pentagonal part. Types of caps of fullerene graphs are presented in column t of Table 1. Constructive approaches for enumeration of various caps were proposed in [25,26]. Consider every kind of cap type.

1. Type a. Caps of type a define (5,0)-nanotubical fullerene graphs. The structure of graphs of this infinite family $T_a$ is clear from an example in Figure 5a. Analytical formulas for diameter and the Wiener index of such fullerene graphs were obtained in [7,18]. To indicate the order of graph G, we will use notation $G_n$. We rewrite the formulas in terms of n.

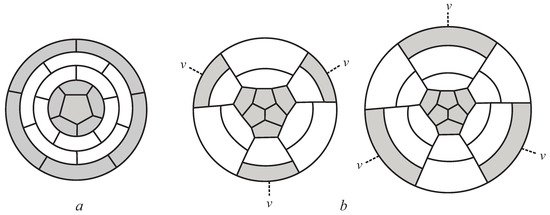
Figure 5. Structure of fullerene graphs with caps of types (a) and (b).

Proposition 2

([7,18]). Let $G_n$ be a nanotubical fullerene graph with caps of type a. It has $n=10k$ vertices, $k\ge 2$. Then, $C_W\left(G_n\right)=k$, $D\left(G_n\right)=2k-1$, and $W\left(G_{20}\right)=500$, $W\left(G_{30}\right)=1435$, $W\left(G_{40}\right)=3035$, and for $n\ge 50$,

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{30}\left(n^3+1175n-\mathrm{20,100}\right).\hfill \end{array}$$

Based on numerical data of Table 1, the similar results have been obtained for fullerene graphs of order $n\le 232$ with caps of the other three types.

2. Type b. Caps of type b define (3,3)-nanotubical fullerene graphs. The structure of graphs of the corresponding family $T_b$ is clear from examples of Figure 5b. Vertices marked by v should be identified in every graph. Table 1 contains 28 such graphs.

Proposition 3.

Let $G_n$ be a nanotubical fullerene graph with caps of type b. It has $n=6k-4\le 232$ vertices, $k\ge 5$. Then, $C_W\left(G_n\right)=\lceil k/2\rceil$, $D\left(G_n\right)=k+1$, and for $n\ge 26$,

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{36}\left(n^3+27n^2+156n-4352\right).\hfill \end{array}$$

Two caps of type b have adjacent pentagonal rings only for $k=5$. If fullerene graphs with caps of types a and b have the same number of vertices ($n=10k$), then the graph with caps of type a has the maximal Wiener index.

3. Type c. Caps of type c define (4,2)-nanotubical fullerene graphs. Fullerene graphs with caps of type c will be splitted into two disjoint families, $T_c=T_{c1}\cup T_{c2}$. The corresponding graphs are marked in column t of Table 1 by $c1$ (14 graphs) and $c2$ (13 graphs). The numbers of vertices of graphs of $T_{c1}$ and $T_{c2}$ are given in Table 5. The orders of graphs of $T_c$ do not coincide with the orders of graphs from the set $T_a\cup T_b$. By analysis of 3D-models of fullerene graphs, it is possible to determine the mutual position of their pentagonal parts. As an example, fragments of graphs with $n=84$ (case $c1$) and $n=88$ (case $c2$) vertices are depicted in Figure 6.

Table 5. Parameters of fullerene graphs with $n\le 232$ vertices and caps of types c and d ($k\ge 0$).

Family${\mathit{T}}_{\mathit{c}\mathbf{1}}$			Family${\mathit{T}}_{\mathit{c}\mathbf{2}}$
n	$C_W$	D	n	$C_W$	D
$60k+96$	$15k+24$	$10k+17$	$60k+76$	$15k+18$	$10k+14$
$60k+48$	$15k+12$	$10k+9$	$60k+88$	$15k+21$	$10k+16$
$60k+72$	$15k+18$	$10k+13$	$60k+112$	$15k+27$	$10k+20$
$60k+84$	$15k+21$	$10k+15$	$60k+64$	$15k+15$	$10k+12$
Family ${\mathit{T}}_{\mathit{d}\mathbf{1}}$			Family ${\mathit{T}}_{\mathit{d}\mathbf{2}}$
n	$C_W$	D	n	$C_W$	D
$60k+126$	$25k+57$	$10k+12$	$60k+106$	$15k+47$	$10k+19$
$60k+78$	$25k+37$	$10k+4$	$60k+118$	$15k+50$	$10k+21$
$60k+102$	$25k+47$	$10k+8$	$60k+142$	$15k+56$	$10k+25$
$60k+114$	$25k+52$	$10k+10$	$60k+94$	$15k+44$	$10k+17$

Figure 6. Mutual position of pentagonal parts for caps of types c and d.

Proposition 4.

(a) 

Let $G_n$ be a nanotubical fullerene graph of family $T_{c1}$. Then, for $36\le n\le 232$,

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{36}\left(n^3+24n^2+336n-7128\right).\hfill \end{array}$$

(b) 

Let $G_n$ be a nanotubical fullerene graph of family $T_{c2}$. Then, for $52\le n\le 232$,

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{36}\left(n^3+24n^2+336n-7192\right).\hfill \end{array}$$

The Wiener complexity and the diameter of $G_n$ are shown in Table 5.

4. Type d. Caps of type d define (5,1)-nanotubical fullerene graphs. Such graphs will be also splitted into two disjoint families, $T_d=T_{d1}\cup T_{d2}$. The both families have 13 members (see graphs with marks $d1$ and $d2$ in column t of Table 1). The numbers of vertices of graphs of $T_{d1}$ and $T_{d2}$ are shown in Table 5. The orders of graphs of $T_d$ do not coincide with the orders of graphs from the set $T_a\cup T_b\cup T_c$. An example of the mutual position of pentagonal parts of graphs from these families with $n=78$ and $n=82$ vertices are shown in Figure 6.

Proposition 5.

(a) 

Let $G_n$ be a nanotubical fullerene graph of family $T_{d1}$. Then, $W\left(G_{42}\right)=3415$ and for $54\le n\le 232$,

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{36}\left(n^3+15n^2+1068n-\mathrm{22,788}\right).\hfill \end{array}$$

(b) 

Let $G_n$ be a nanotubical fullerene graph of family $T_{d2}$. Then, $W\left(G_{46}\right)=4322$ and for $58\le n\le 232$,

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{36}\left(n^3+15n^2+1068n-\mathrm{22,756}\right).\hfill \end{array}$$

The Wiener complexity and the diameter of $G_n$ are shown in Table 5.

The above considerations of fullerene graphs with $n\le 232$ vertices lead to the following conjectures for all fullerene graphs.

Conjecture 1.

If a fullerene graph of an arbitrary sufficiently large order has the maximal Wiener index, then it is a nanotubical fullerene graph with caps of types a–d and its Wiener index is given by Propositions 2–5.

Conjecture 2.

The Wiener complexity and the diameter of fullerene graphs of an arbitrary sufficiently large order having the maximal Wiener index are given in Propositions 2–5.

5. IPR Fullerene Graphs with the Maximal Wiener Index

Numerical data for the Wiener indices of IPR fullerene graphs of order $n\le 270$ are presented in Table 2. The structure of the table is the same as for fullerene graphs. Graphs with maximal Wiener index (column $W_n$) are nanotubical fullerene graphs with two identical caps. All caps are defined by four fragments shown in Figure 7. Caps of type a–c have no symmetries. The number of fullerene graphs having a given cap is shown near diagrams. Note that it is difficult to separate caps from each other when IPR fullerene graphs have a shape close to spherical one. Therefore, caps of types $b,c,d$ can be recognized only for fullerene graphs of a sufficiently large number of vertices when graphs became nanotubical. A type of cap is indicated in column t of Table 2. Consider graphs with these caps.

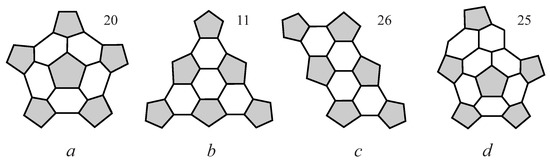
Figure 7. Pentagonal parts of caps in nanotubical IPR fullerene graphs with the maximal Wiener index.

1. Type a. Caps of type a define (5,5)-nanotubical fullerene graphs. Caps of this type can be positioned relative to each other in two ways. The structure of the corresponding graphs of this infinite families $T_a=T_{a1}\cup T_{a2}$ is described by examples in Figure 8. Analytical formulas for the Wiener index of these graphs are presented in [17]. We rewrite the formulas in terms of n.

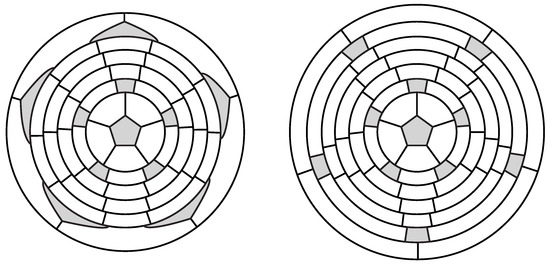
Figure 8. IPR fullerene graphs $G_{110}\in T_{a1}$ (left) and $G_{120}\in T_{a2}$ (right) with caps of type a.

Proposition 6

([17]).

(a) Let $G_n$ be a nanotubical IPR fullerene graph of family $T_{a1}$. It has $n=10k$ vertices, $k\ge 11$ and k is odd. Then, $C_W\left(G_n\right)=(k+3)/2$, $D\left(G_n\right)=k+3$, and

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{60}\left(n^3+75n^2+1820n-\mathrm{95,400}\right).\hfill \end{array}$$

(b) Let $G_n$ be a nanotubical IPR fullerene graph of family $T_{a2}$. It has $n=10k$ vertices, $k\ge 12$ and k is even. Then, $C_W\left(G_n\right)=(k+2)/2$, $D\left(G_n\right)=k+3$, and

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{60}\left(n^3+75n^2+1820n-\mathrm{97,200}\right).\hfill \end{array}$$

2. Type b. Caps of type b define (9,0)-nanotubical fullerene graphs. The caps can be positioned relative to each other in four ways $b_1-b_4$ as shown in Figure 9. Since graphs with fragments of cases $b_1,b_2$ and $b_3,b_4$ almost always have the same Wiener index, we split graphs into two infinite families. Graphs having structures $b_1,b_2$ and $b_3,b_4$ form family $T_{b12}$ and $T_{b34}$, respectively. Each family contains two graphs with the same maximal Wiener index for fixed n. Table 6 shows the number of vertices of the families. The difference between n of the neighboring graphs is 36. The numbers in table’s sells are the number of hexagonal rings (k) in the fragments connecting two caps (see Figure 9). The graph of order 168 with caps of type $b_4$ has almost maximal Wiener index, $W=$ 116,097, while the maximal Wiener index is $W=$ 116,100. Remember that the graph of order 150 with the maximal Wiener index, $W=$ 87,335, has caps of type a. The graph of order 150 with caps of type $b_1$ has the second maximal Wiener index, $W=$ 86,379, and the graph of type $b_2$ has the third maximal Wiener index, $W=$ 86,373. The graphs of order 240 with caps of types $b_3$ and $b_4$ have the second maximal Wiener index, $W=$ 302,034 (the graph with the caps of type a gives maximum W).

Figure 9. Mutual positions of caps of type b in IPR fullerene graphs.

Table 6. IPR fullerene graphs with caps of type b.

	${\mathit{T}}_{\mathit{b}12}$				${\mathit{T}}_{\mathit{b}34}$
n	150	186	222	258	132	168	204	240	276
$b_1$	2	3	4	5
$b_2$	2	3	4	5
$b_3$					2	3	4	5	6
$b_4$					2	3	4	5	6

Proposition 7.

(a) 

Let $G_n$ be a nanotubical IPR fullerene graph of family $T_{b12}$. It has $n=36k+150\le 270$ vertices, $k\ge 0$. Then, $D\left(G_n\right)=4k+17$ and

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{\mathrm{46,656}}\left(859n^3+3330n^2+\mathrm{10,767,924}n-\mathrm{559,139,976}\right).\hfill \end{array}$$

(b) 

Let $G_n$ be a nanotubical IPR fullerene graph of family $T_{b34}$. It has $n=168+36k\le 270$ vertices, $k\ge 0$. Then, $D\left(G_n\right)=4k+19$ and

$$\begin{array}{ccc}\hfill W\left(G_n\right)& =& \frac{1}{\mathrm{46,656}}\left(863n^3+720n^2+\mathrm{11,329,200}n-\mathrm{598,893,696}\right).\hfill \end{array}$$

3. Types c and d. Caps of types c and d generate many cases of their mutual arrangement. By analyzing the structure of fullerene graphs, we have preliminarily identified several families. The number of vertices of eight families of graphs with the caps of type c can be written as $n=n_0+36k$, $k\ge 0$, where $n_0\in \{128,136,140,144,148,152,156,160\}$. For nine families of graphs with the caps of type d, we have $n=n_0+44k$, $k\ge 0$, where $n_0\in \{130,134,138,146,150,154,158,162,166\}$.

Conjecture 3.

If an IPR fullerene graph of an arbitrary sufficiently large order has the maximal Wiener index, then it is a nanotubical fullerene graph with caps of types a–d and its Wiener index is given by Propositions 6 and 7 for graphs of types a and b.

6. Conclusions

Problems of finding fullerene graphs with the maximal Wiener complexity and Wiener index are studied. Numerical data show that graphs with the maximal Wiener complexity may exist for quite a large number of vertices. Some basic properties of fullerene graphs having the maximal Wiener index are established. We hope that the presented considerations will stimulate further study of the extremal fullerene graphs with respect to the Wiener index.

It is worth noting that, according to experimental studies, it was observed that there are no theoretically well founded correlations between the Wiener index and the predicted energetic stability of fullerene isomers in some cases [11,22]. In order to improve the prediction accuracy, Ori et al. defined a topological efficiency index $\rho$ derived from the Wiener index [24].