Some Root Level Modifications in Interval Valued Fuzzy Graphs and Their Generalizations Including Neutrosophic Graphs
Abstract
1. Introduction
- (1)
- It is observed that the concept of IVFG [28] has some limitations which lead us to some undefined results. The lower and upper values of the edge interval in IVFG are defined as and . According to this definition for two adjacent vertices and , we obtained an undefined edge value of by the above approach. The same type of problem occurs in the framework of IVIFG [40] in membership as well as non-membership intervals. Further, the existing definition of IVIFG is not a generalization of IFG; therefore, one must develop a definition for IVIFG which clearly generalizes IFG. These types of flaws in the existing literature lead us to develop some new definitions for IVFG and IVIFG;
- (2)
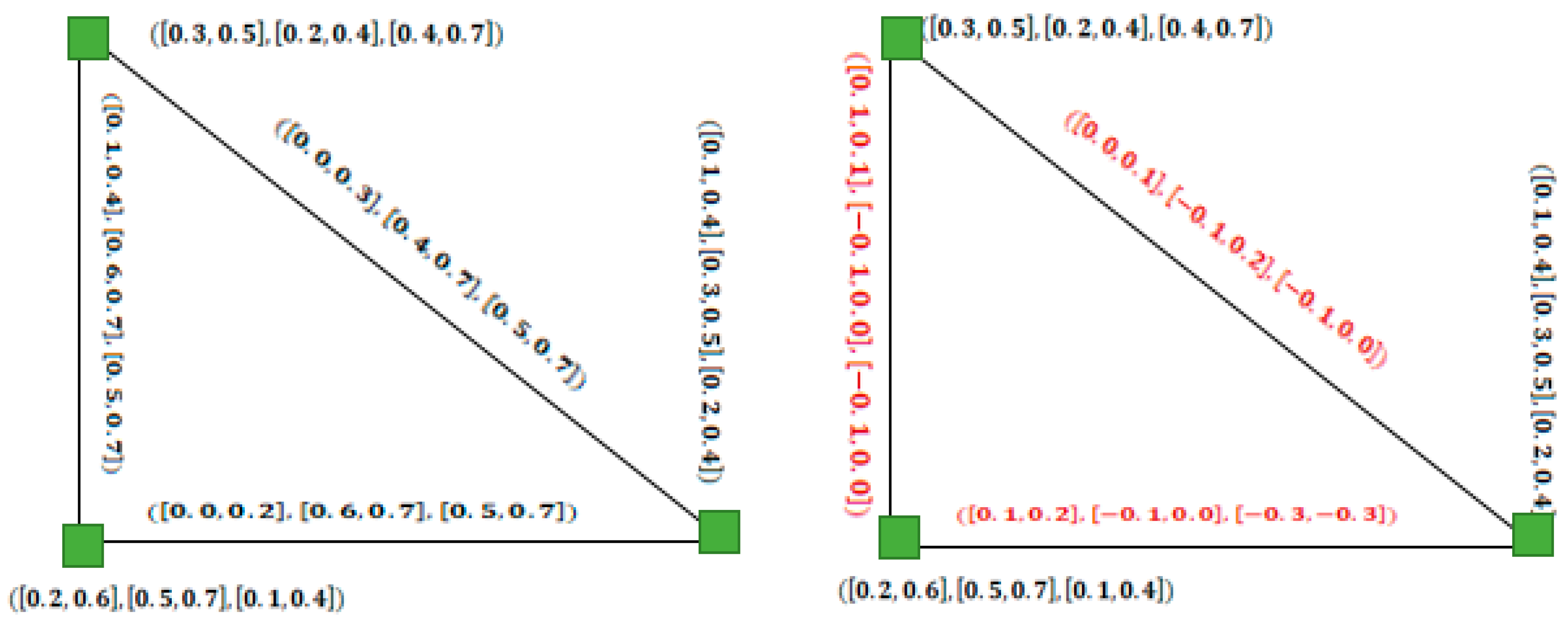
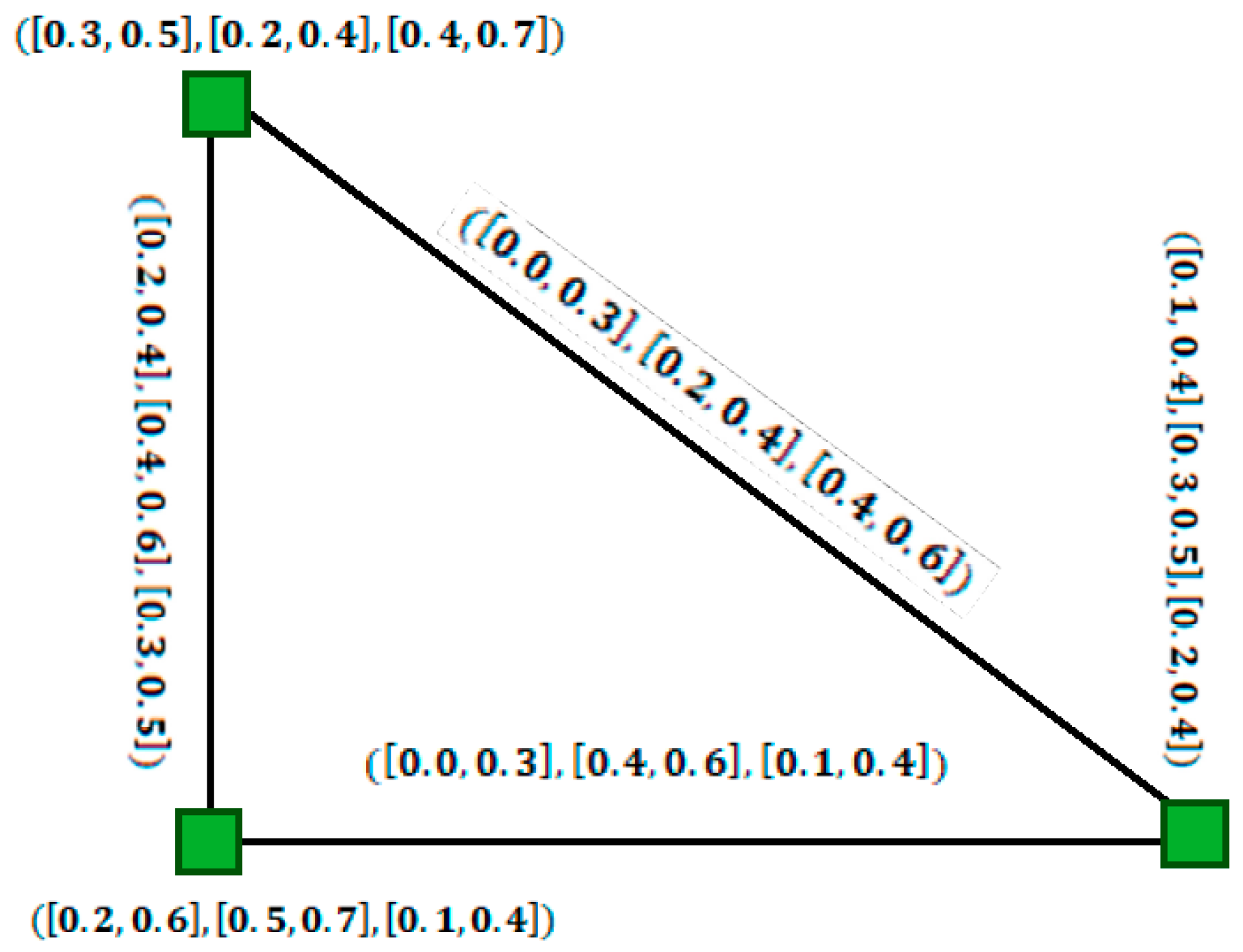
- The lower and upper values of edges in the complement of an IVFG are defined as and . Let and be two vertices and their edge. Then, upon calculating the complement, we get the corresponding edge value which is an undefined interval. Similar types of flaws exist in the existing definitions of complements of IVIFGs, therefore leading us to develop some new definitions for the complement of IVFG as well as of IVIFG.;
- (3)
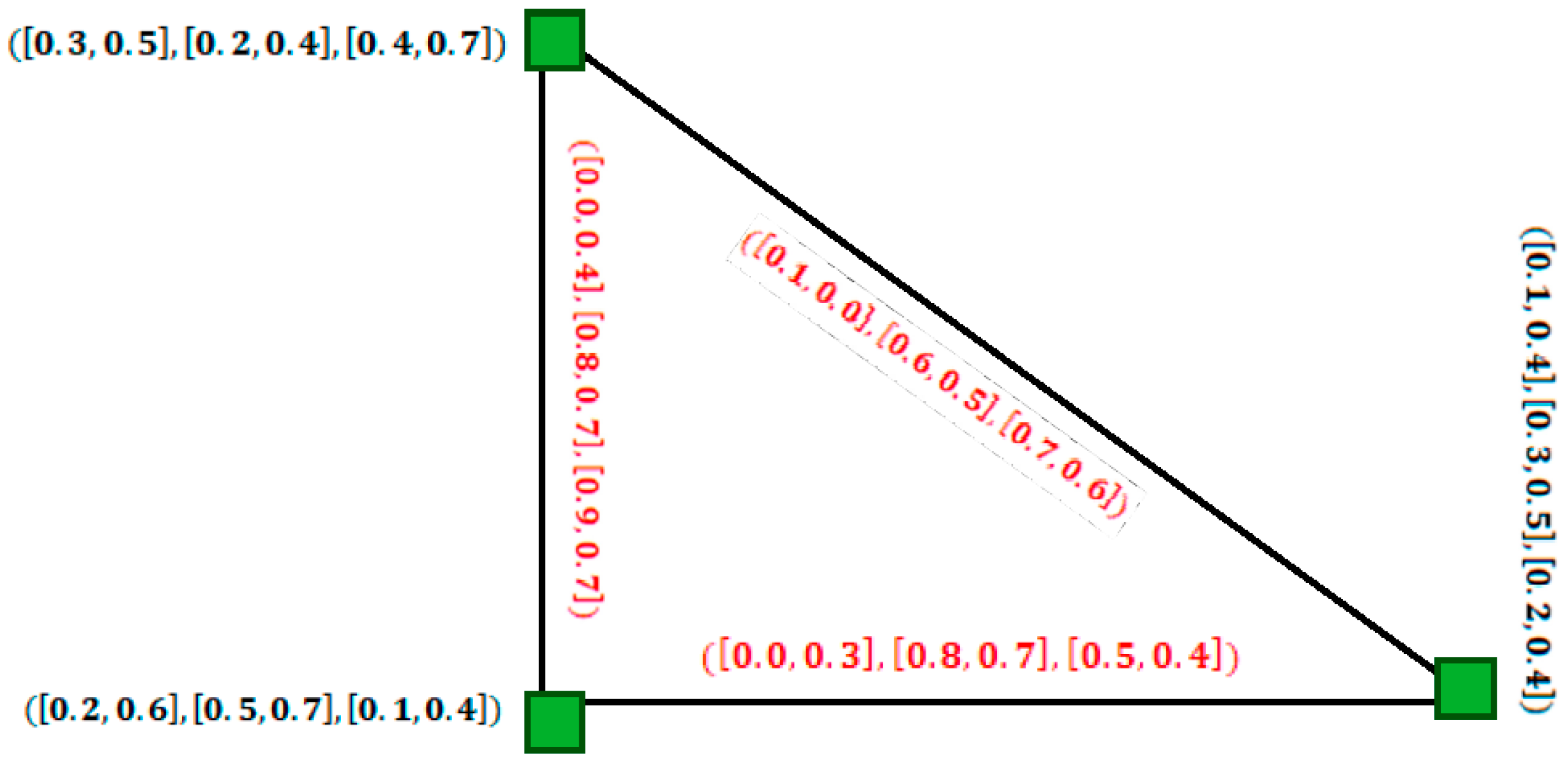
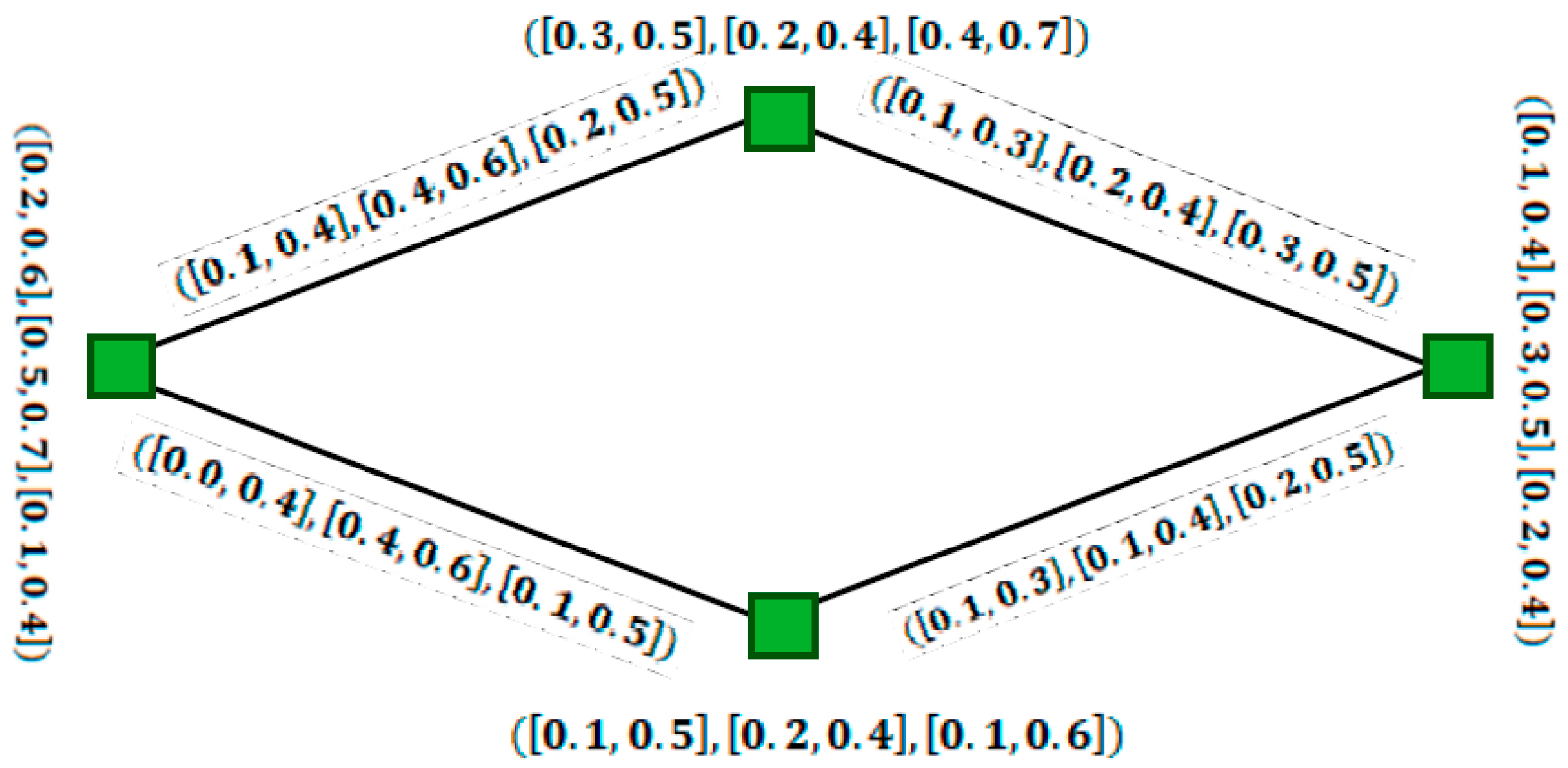
- It is observed that the existing definition of SVNG [43] is not a generalization of IFG as claimed in the existing literature. Also, the existing notion of the SVNG and of its complement as defined in [43] is not well posed, as after taking the complement of a SVNG, the resulting graph obtained is not a SVNG. Further, the existing definition of a complement does not satisfy the property . These facts are described briefly in Section 5, and based on these defects, a new definition for SVNG and its complement have been developed and their validity is proved;
- (4)
- Finally, we improve the definition of the IVNG as the existing definition contradicts the fact that IVNG is a generalization of IVIFG and IVFG. Further, the existing definition of the complement of IVNG is not well defined, which is described with the help of examples, and a new definition for complements is proposed and validated with examples.
2. Basic Concepts
- (1)
- Everyis characterized by a functiondenoting the degree of membership of;
- (2)
- Everyis characterized by a functiondenoting the degree of membershipsatisfying the condition.
- (1)
- Everyis characterized by two functionsanddenoting the membership and non-membership degree ofwhich satisfies the condition that. Moreover, the termdefined bydenotes the hesitancy level of;
- (2)
- Everyis characterized by two functionsanddenoting the membership and non-membership degree ofsatisfying the conditions:with a condition that. Moreover, the termdenotes the hesitancy level ofsuch that.
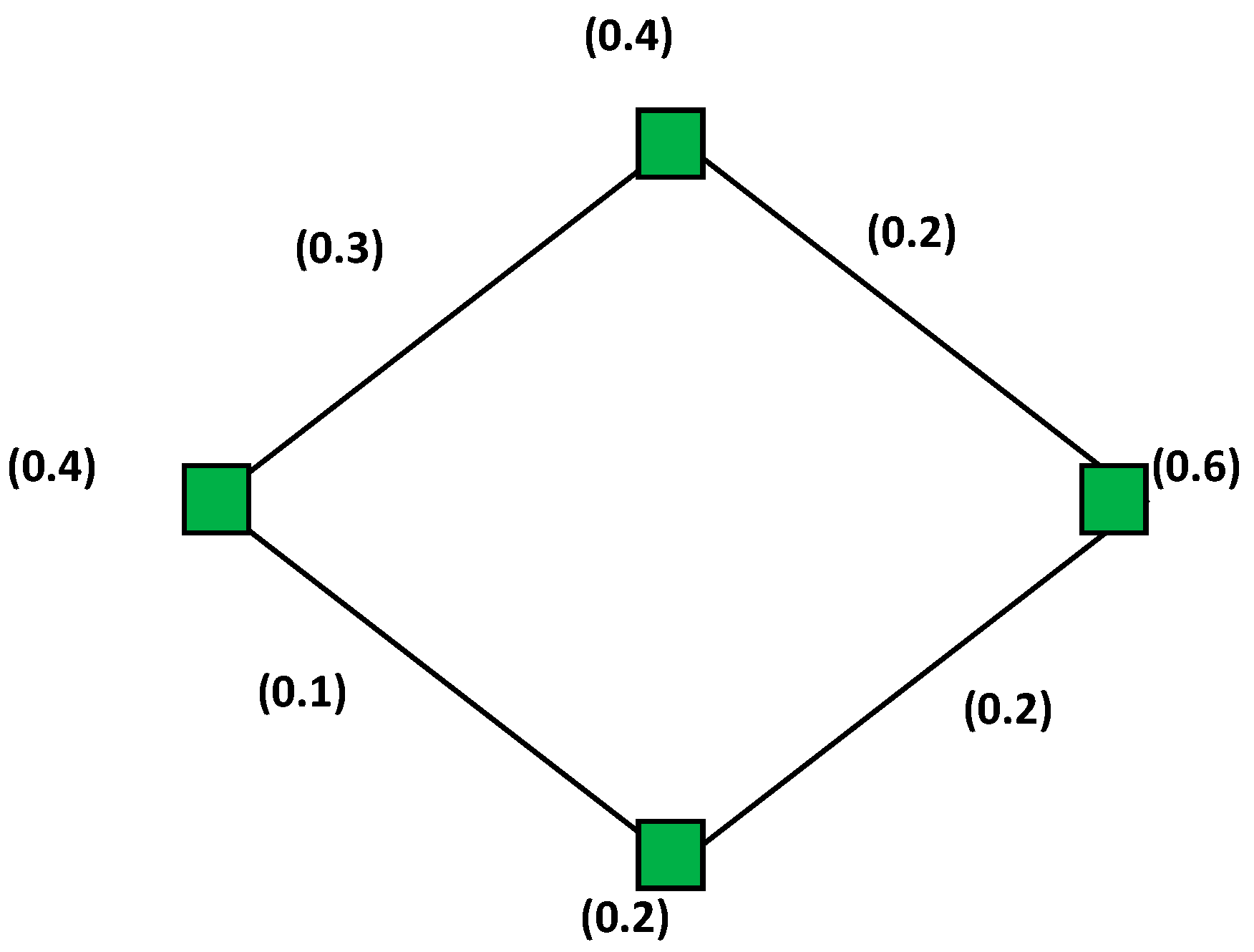
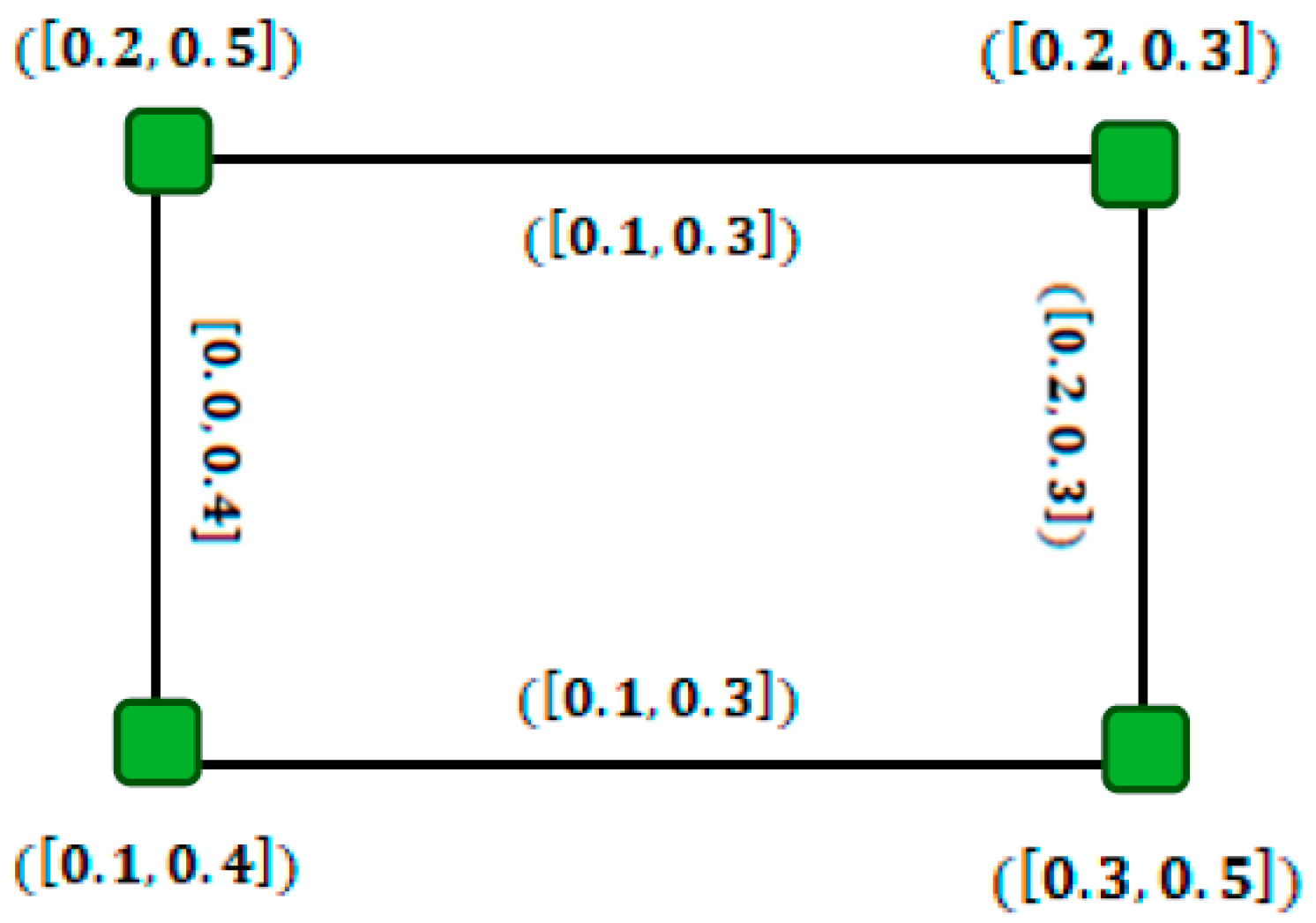
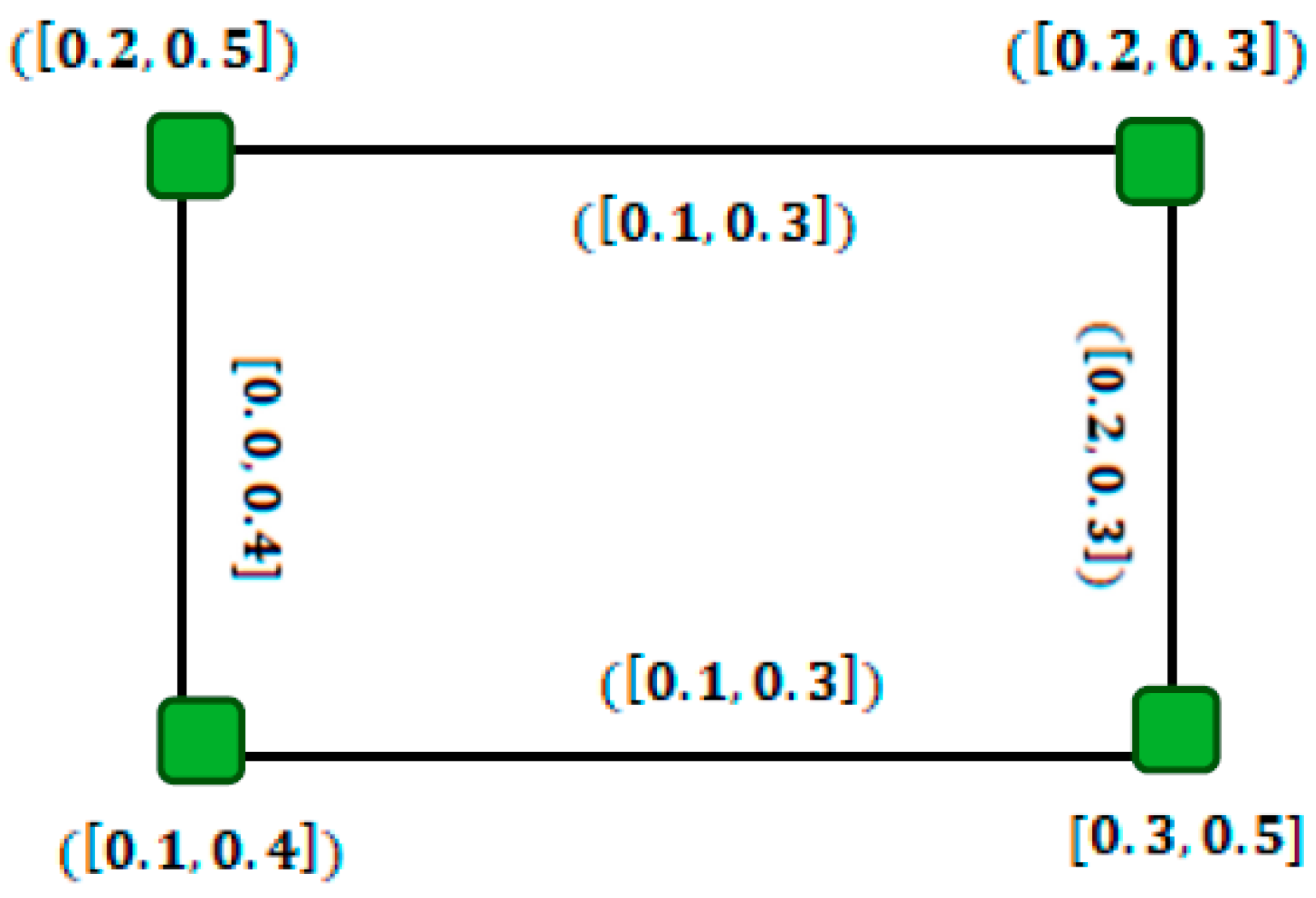
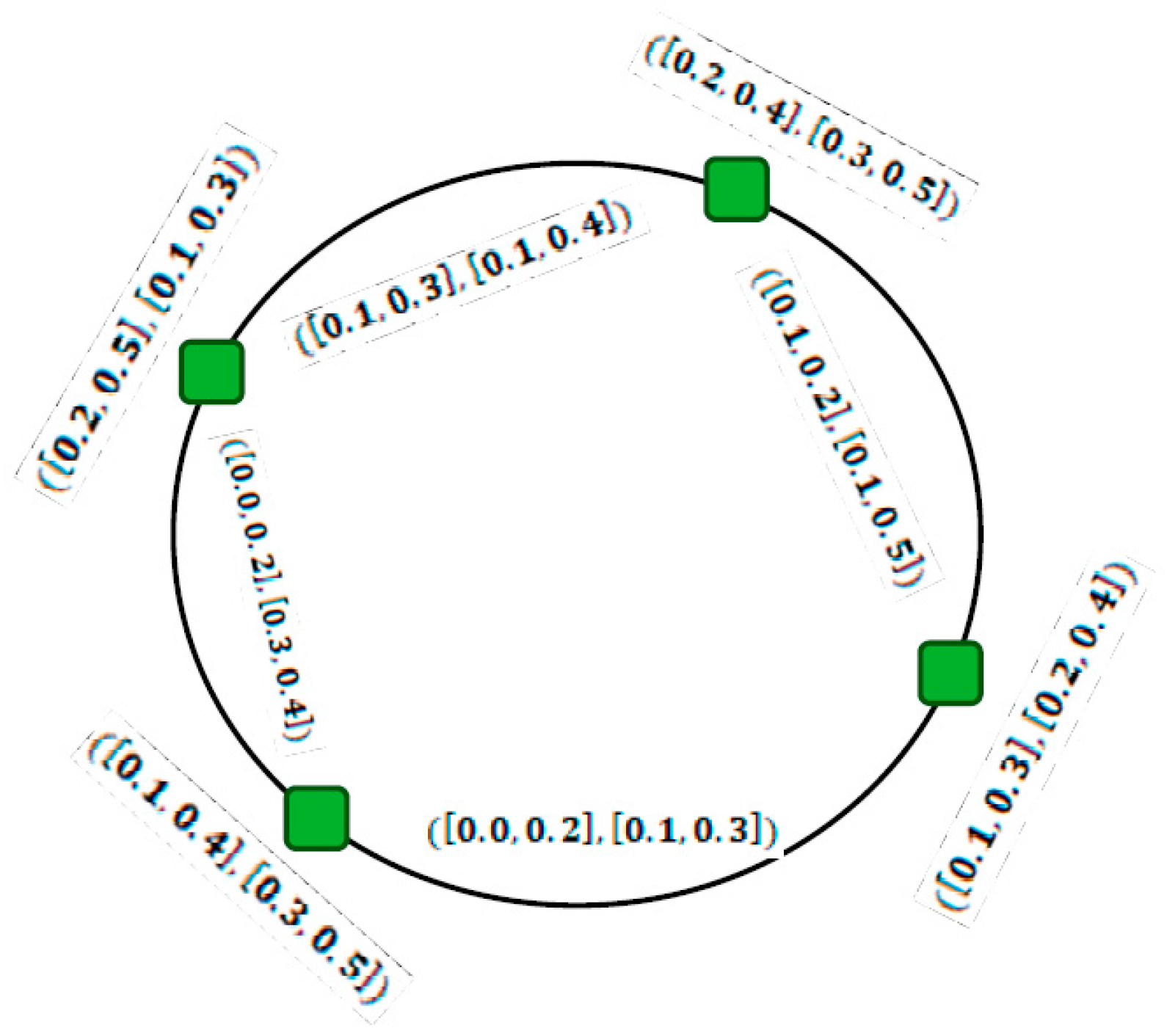
3. Improvements in Interval-Valued Fuzzy Graphs and Interval-Valued Intuitionistic Fuzzy Graphs
- (1)
- Everyis characterized by a functionrepresenting the membership degree of. Basically,is a closed subinterval [0, 1];
- (2)
- Everyis characterized by a functiondenoting the degree of membership. Basically,satisfying the conditions:
- (1)
- Everyis characterized by a functionrepresenting the membership grade of. Basically,is a closed subinterval of the unit interval [0, 1];
- (2)
- Everyis characterized by a functiondenoting the membership grade of. The closed subintervalsatisfying the conditions:
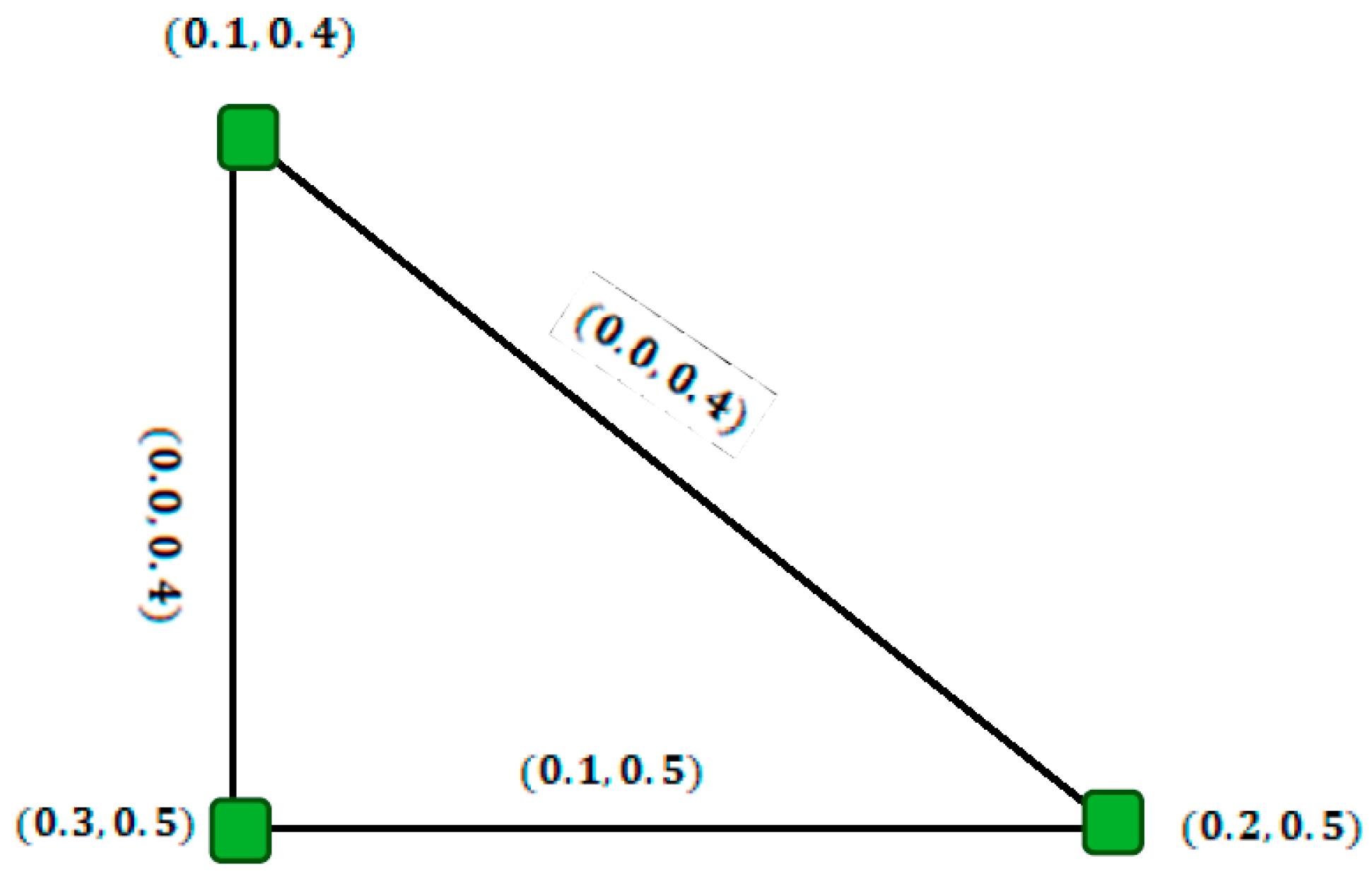
- (1)
- Everyis characterized by two functionsanddenoting the membership and non-membership grades of. Basically,andare closed subintervals of the unit interval [0, 1] with a condition that. Moreover, the termdenote the hesitancy level ofsuch thatand.
- (2)
- Everyis characterized by two functionsanddenoting the membership and non-membership grades of. Basically,andsatisfying the conditions:provided that. Moreover, the termdenote the hesitancy level ofsuch thatand.
- (1)
- Everyis characterized by two functionsanddenoting the membership and non-membership grades of. Basically,andare closed subintervals of the unit interval [0, 1] with a condition that. Moreover, the termdenote the hesitancy level ofsuch thatand;
- (2)
- Everyis characterized by two functionsanddenoting the membership and non-membership grades of. Basically,andare such thatprovided that. Moreover, the termdenote the hesitancy level ofsuch thatand.
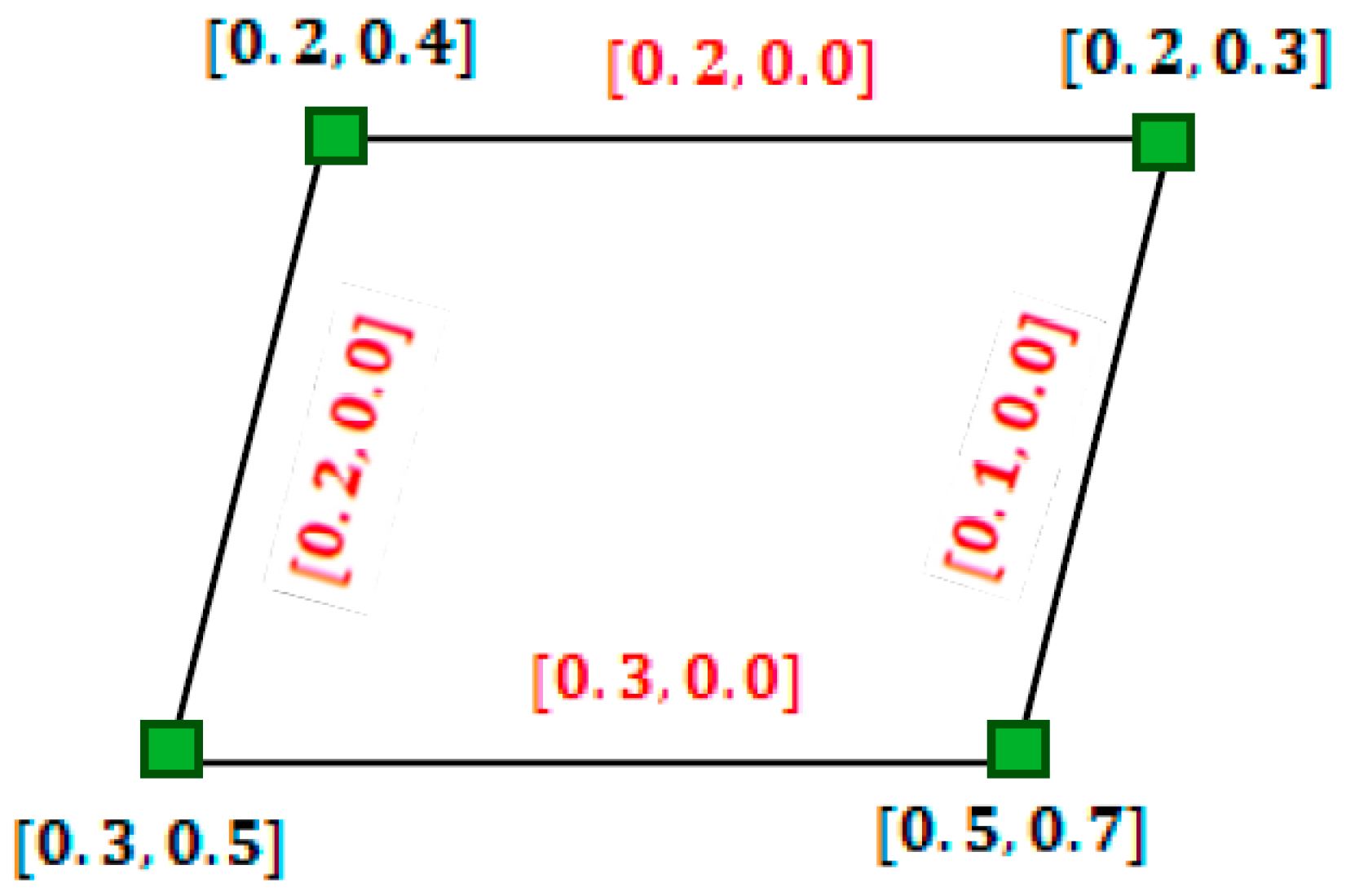
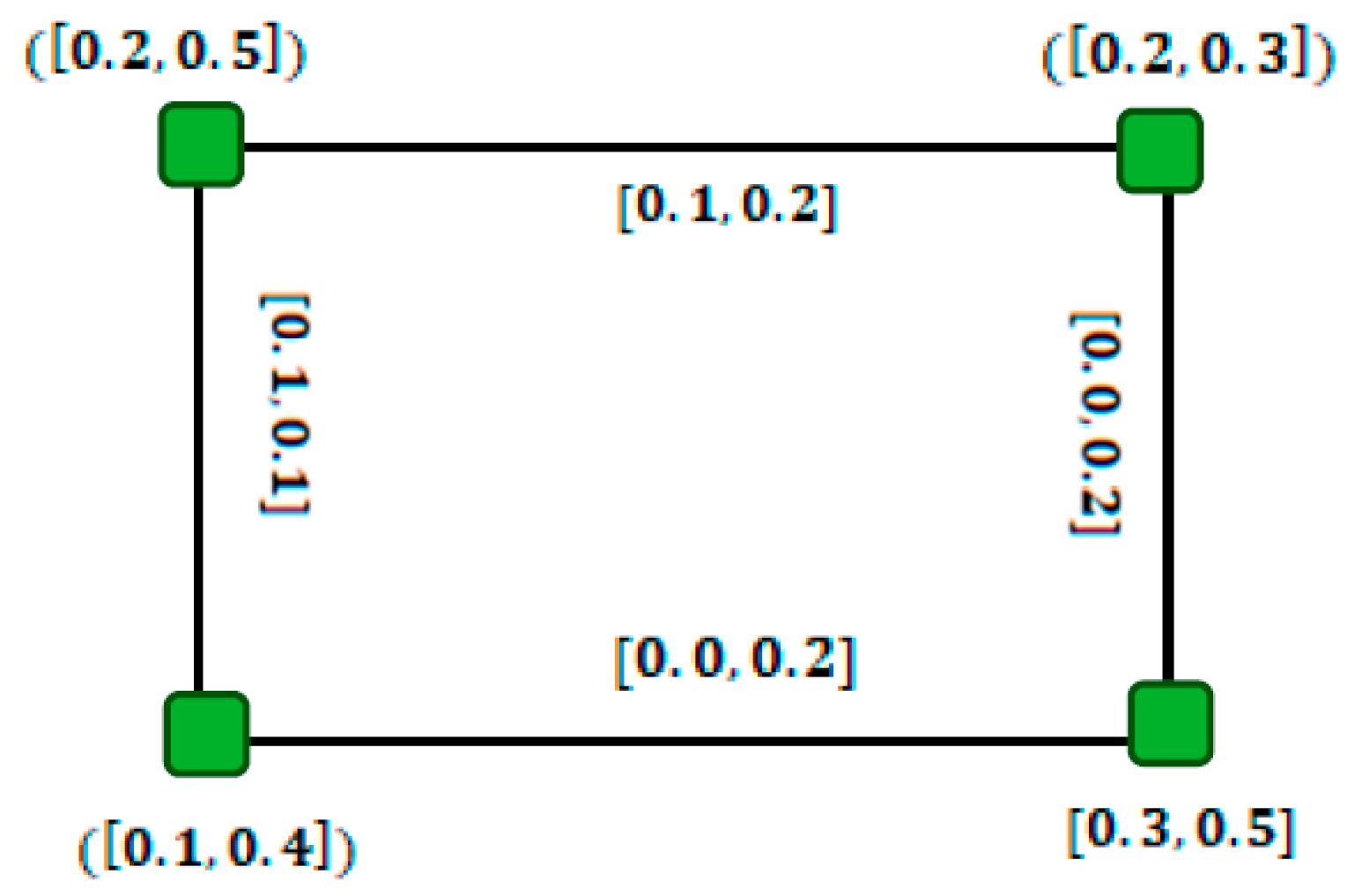
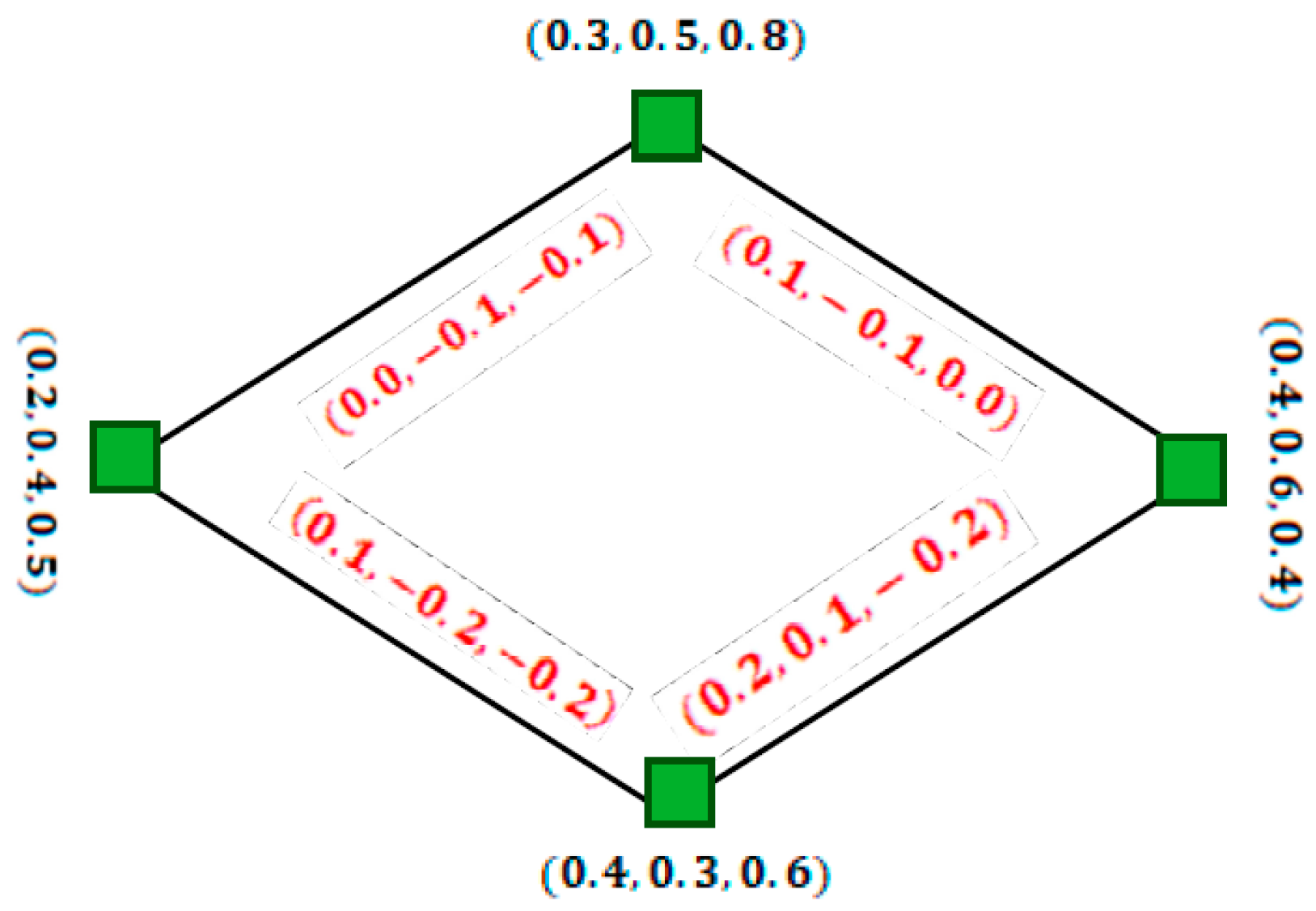
4. New Definitions for the Complement of the Interval-Valued Fuzzy Graph and Interval-Valued Intuitionistic Fuzzy Graph
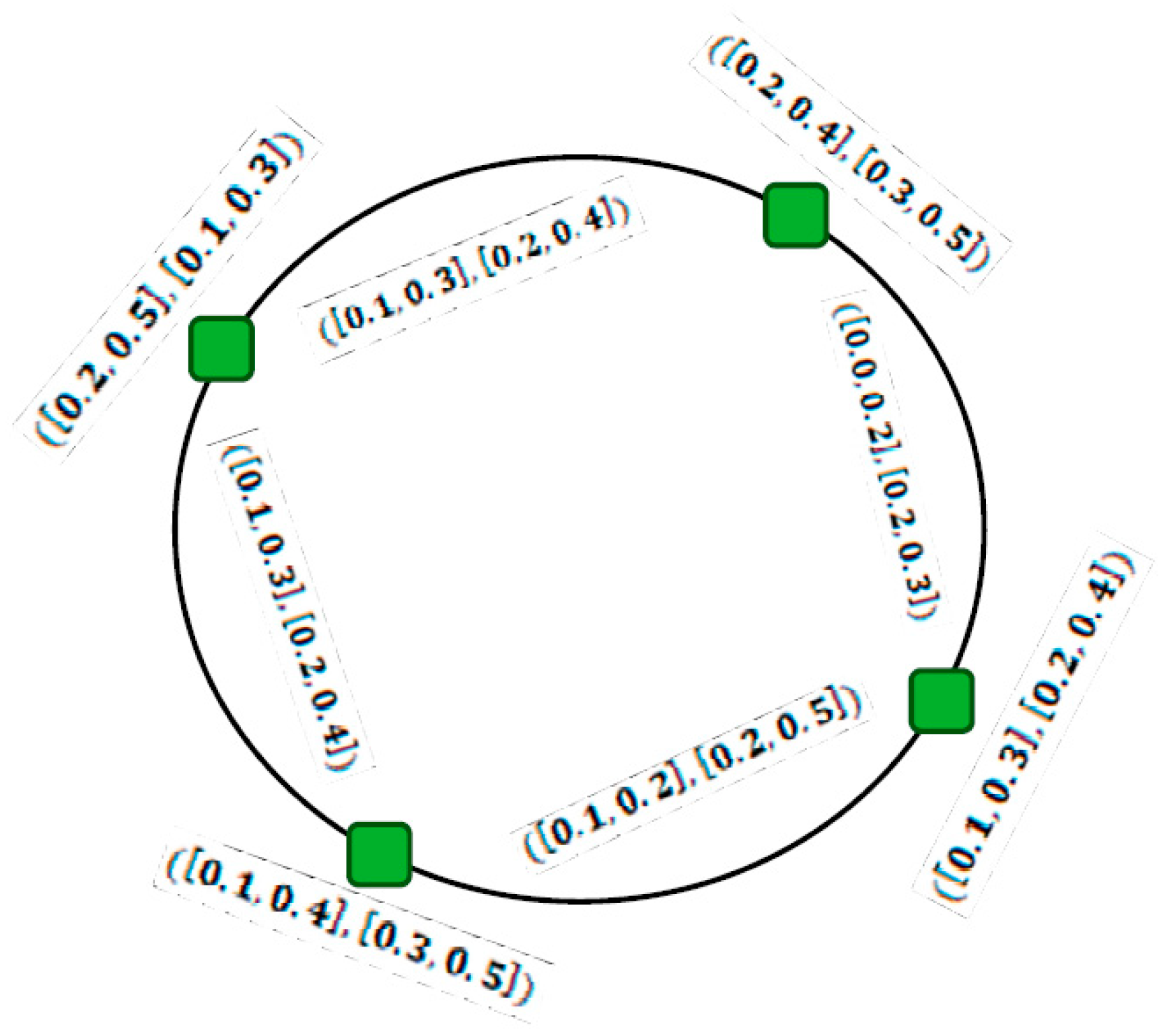
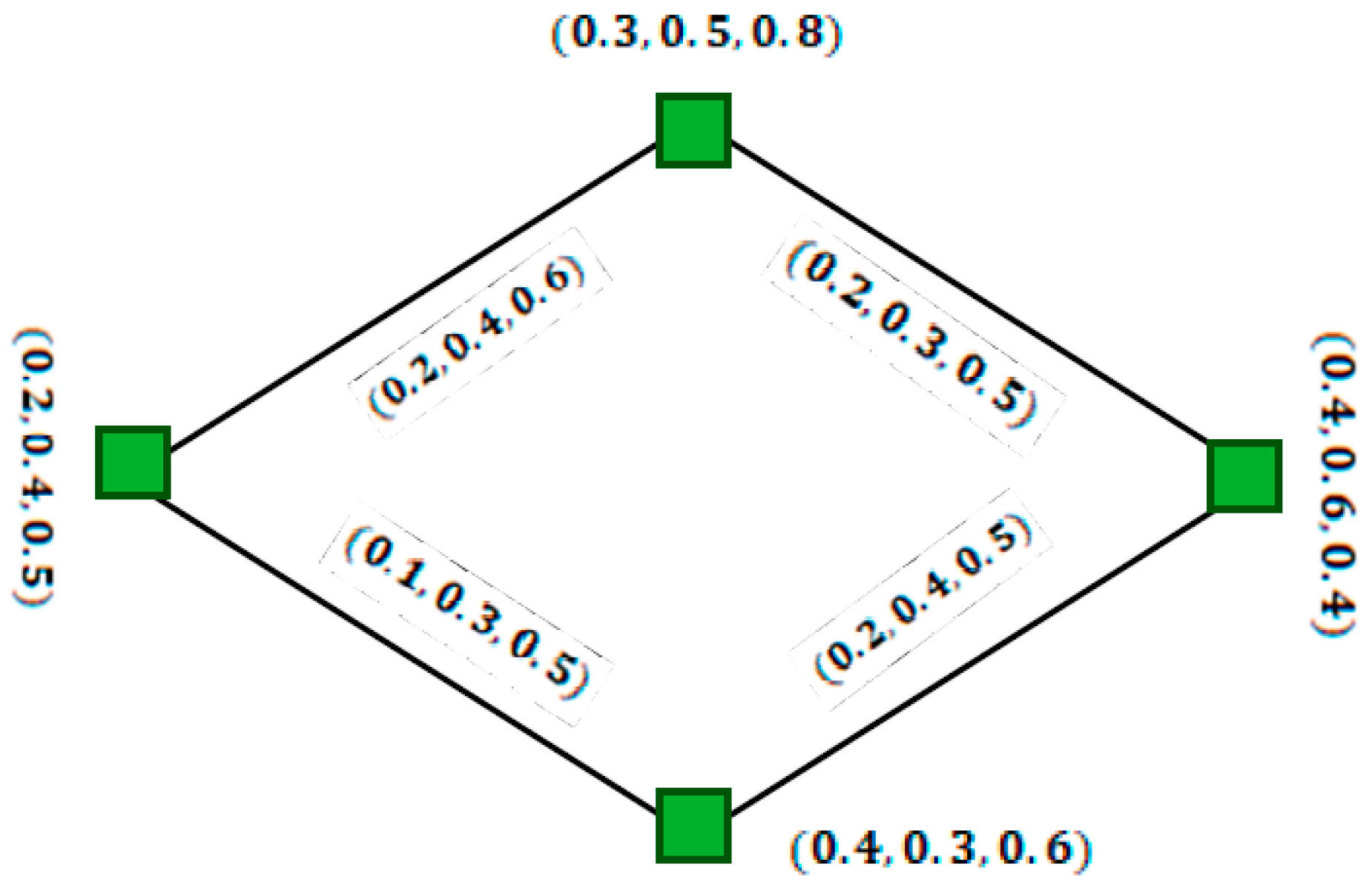
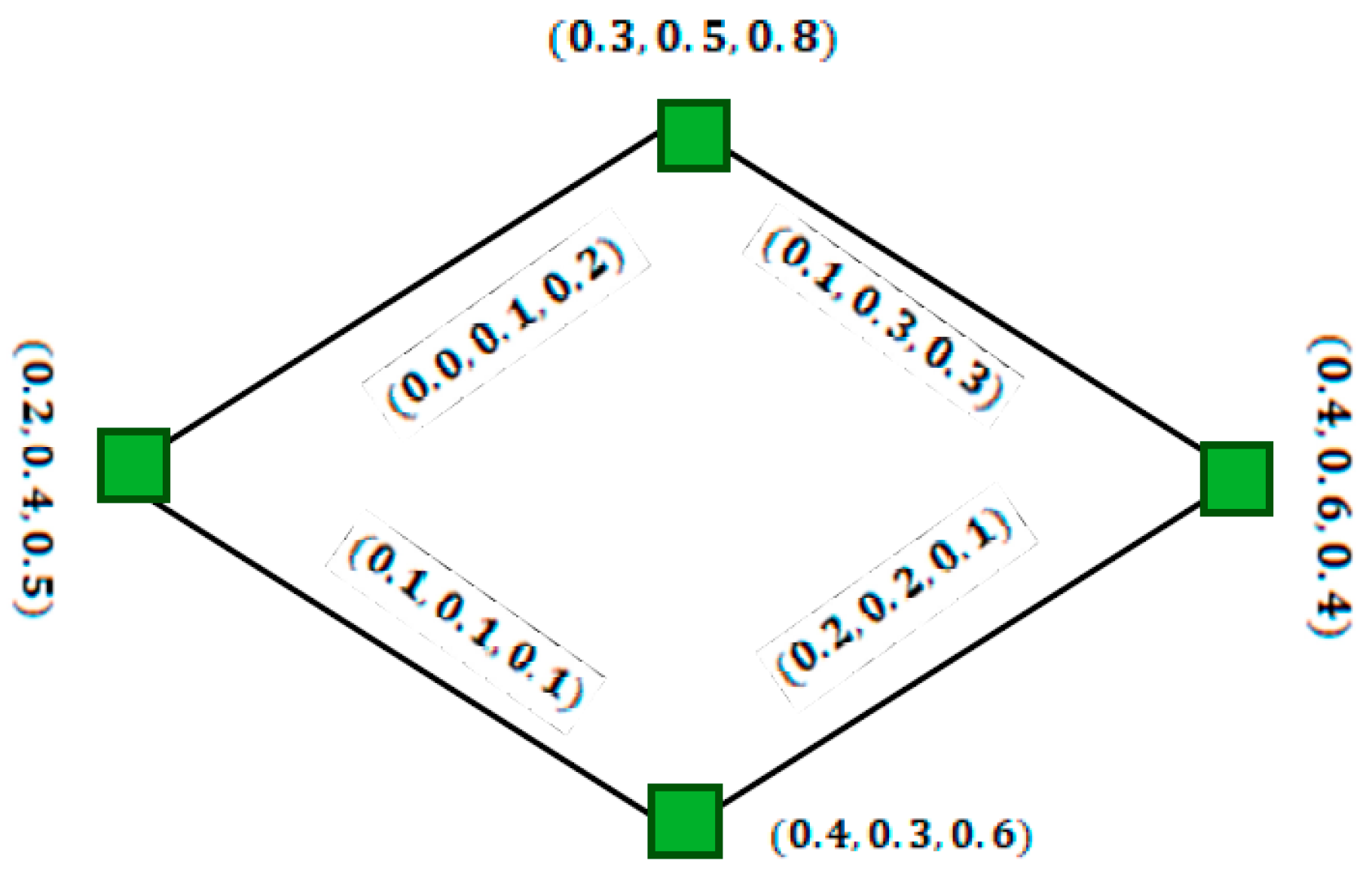
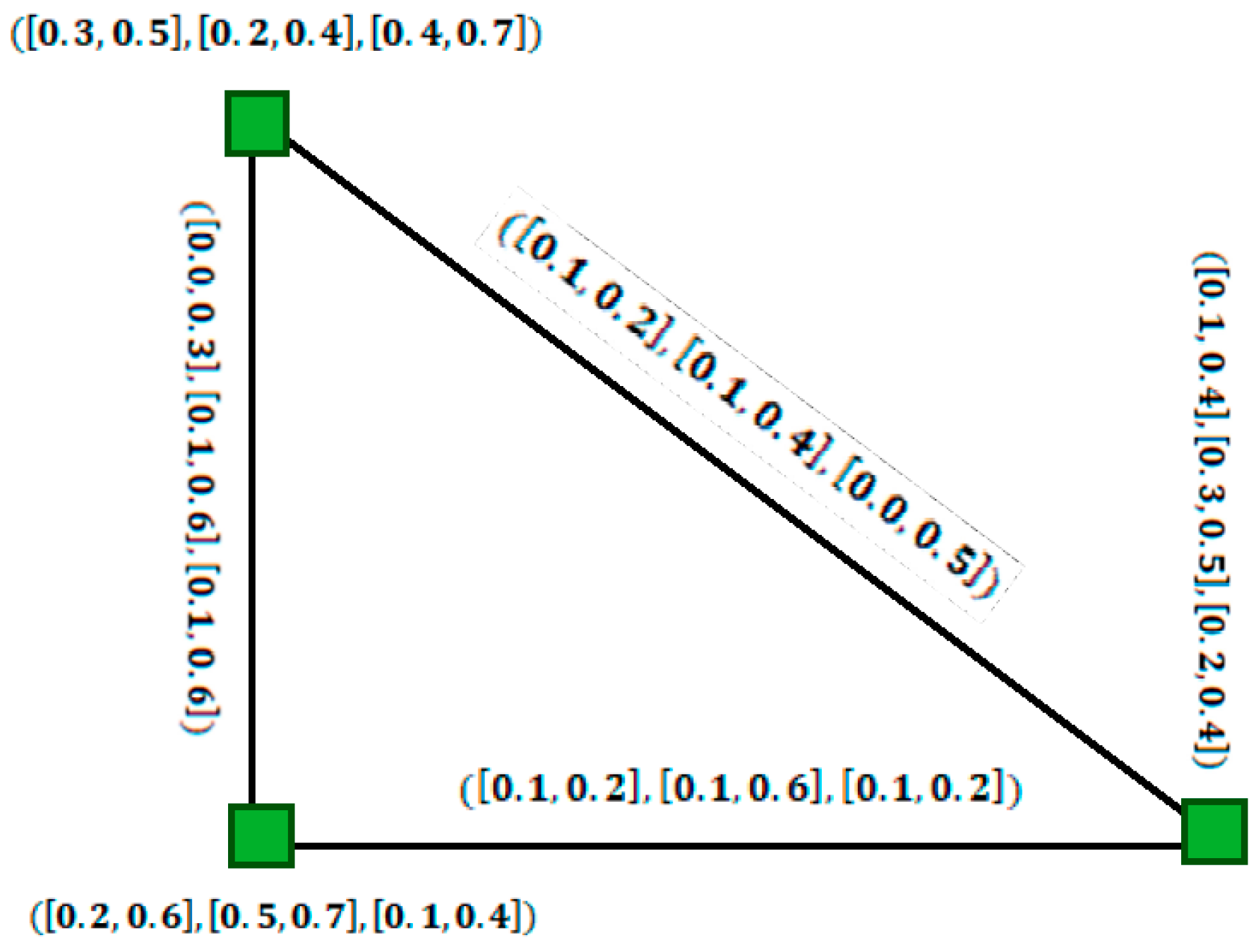
5. Improvements in Single-Valued Neutrosophic Graphs and Interval-Valued Neutrosophic Graphs
- (1)
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades ofwhich satisfy;
- (2)
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades ofsatisfieswhich satisfy the inequality.
- 1.
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades ofwhich satisfy the inequality.;
- 2.
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades ofsatisfyingprovided that.
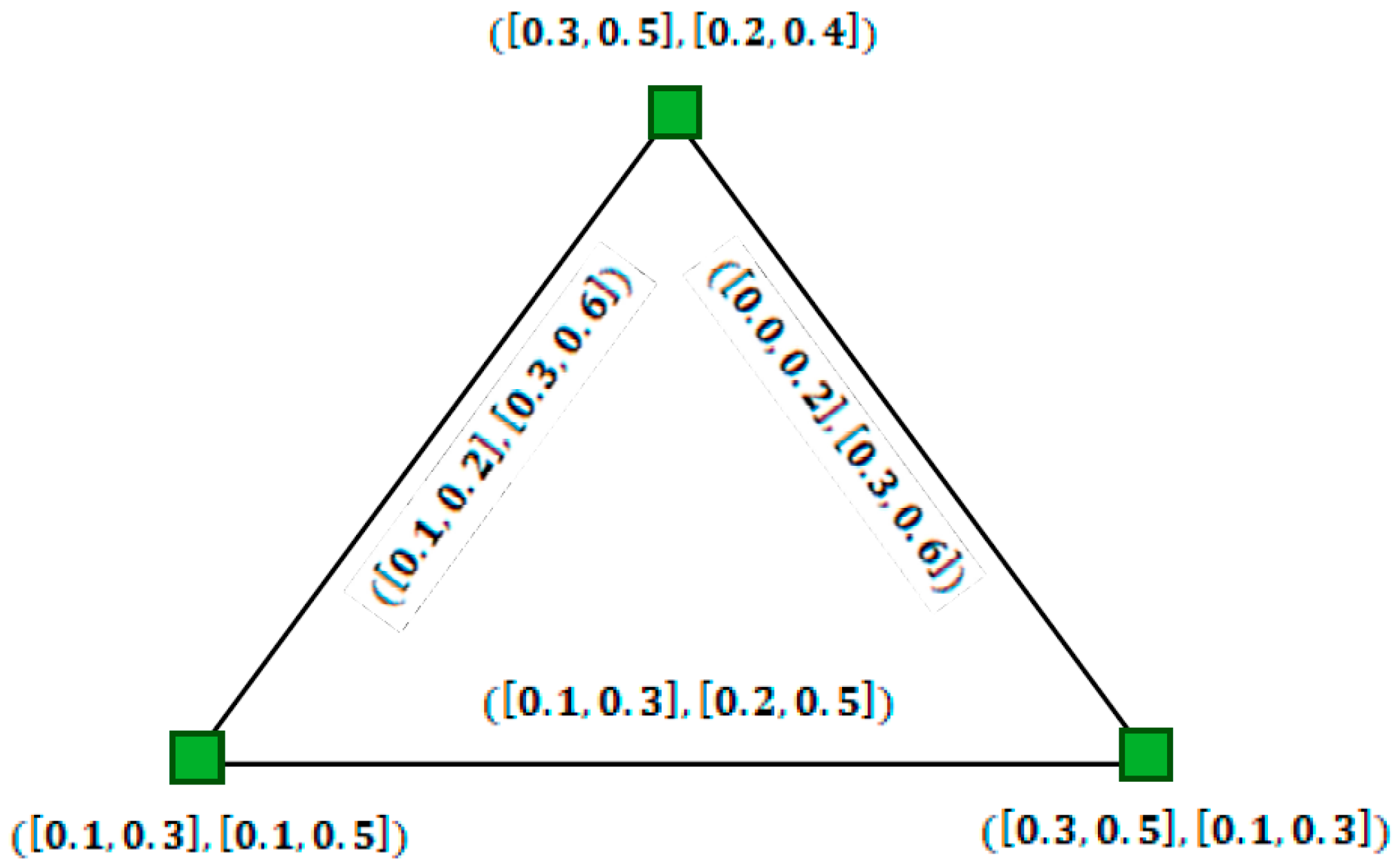
- 1.
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades of. Basically,andare closed subintervals of the unit interval [0, 1] which satisfy the inequality.;
- 2.
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades of. Basically,andare such that:which satisfy the inequality.
- (1)
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades of. Basically,andare closed subintervals of the unit interval [0, 1] with a condition that.;
- (2)
- Everyis characterized by three functionsanddenoting the membership, neutral and non-membership grades of. Basicallyandare such thatprovided that,,and.
6. Illustrative Example
- Step 1:
- Establishing SVNPRs: This step involves the evaluation of objects by decision-makers in the form of SVNGs;
- Step 2:
- The SVNPRs form a relational matrix known as the single-valued neutrosophic relational matrix (SVNRM) denoted by where such that and ;
- Step 3:
- Aggregating the different preferences by using the weighted averaging aggregation operator named as single-valued neutrosophic weighted averaging (SVNWA) operators [8] as follows:where is the weight vector for each preference such that and ;
- Step 4:
- Computing the score value of the aggregated number by using the score function
- Step 5:
- Ranking all the alternatives based on the descending order of the score values.
- Step 1:
- The information from QEC of HEC Pakistan related to each university is taken in the form of SVNGs and summarized in Figure 25.
- Step 2:
- From the SVNPRs provided in Figure 25, we have the following relational matrix.
- Step 3:
- Using single-valued neutrosophic weighted averaging operators on the relational matrix to aggregate the data,and the aggregated values are obtained as
- Step 4:
- The score values of the aggregated data are obtained as
- Step 5:
- Since , we obtained the ranking order of the given universities as , where refers to “preferred to’’. Thus, the ranking results indicate that International Islamic University Islamabad performs best in research productivity among the four universities of federal capital of Islamabad in the evaluation of the quality assurance cell of HEC.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Gorzalczany, M.B. A method of inference in approximate reasoning based on interval—Valued fuzzy sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic, ProQuest Information & Learning; American Research Press Rehoboth: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multisp. Multistruct. 2010, 4, 410–413. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Smarandache, R. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing; Hexis: Phoenix, AZ, USA, 2005. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, Z.H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Garg, H. New exponential operational laws and their aggregation operators for interval-valued Pythagorean fuzzy multicriteria decision—Making. Int. J. Intell. Syst. 2018, 33, 653–683. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Zhang, H.Y.; Chen, X.H. An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets. Appl. Soft Comput. 2014, 25, 336–346. [Google Scholar] [CrossRef]
- Garg, H. Some robust improved geometric aggregation operators under interval-valued intuitionistic fuzzy environment for multi-criteria decision-making process. J. Ind. Manag. Optim. 2018, 14, 283–308. [Google Scholar] [CrossRef]
- Garg, H. Novel intuitionistic fuzzy decision making method based on an improved operation laws and its application. Eng. Appl. Artif. Intell. 2017, 60, 164–174. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Algorithms for interval neutrosophic multiple attribute decision-making based on MABAC, similarity measure, and EDAS. Int. J. Uncertain. Quantif. 2017, 7, 395–421. [Google Scholar] [CrossRef]
- Peng, X.D.; Dai, J.G. Approaches to single-valued neutrosophic madm based on mabac, topsis and new similarity measure with score function. Neural Comput. Appl. 2018, 29, 939–954. [Google Scholar] [CrossRef]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. A novel exponential distance and its based TOPSIS method for interval-valued intuitionistic fuzzy sets using connection number of SPA theory. Artif. Intell. Rev. 2018, 1–30. [Google Scholar] [CrossRef]
- Smarandache, F. Subtraction and division of neutrosophic numbers. Crit. Rev. 2016, 13, 103–110. [Google Scholar]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Garg, H.; Arora, R. Generalized intuitionistic fuzzy soft power aggregation operator based on t-norm and their application in multi criteria decision-making. Int. J. Intell. Syst. 2019, 34, 215–246. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. Distance measures for connection number sets based on set pair analysis and its applications to decision making process. Appl. Intell. 2018, 48, 3346–3359. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. Non-linear programming method for multi-criteria decision making problems under interval neutrosophic set environment. Appl. Intell. 2018, 48, 2199–2213. [Google Scholar] [CrossRef]
- Wei, G.; Zhao, X. An approach to multiple attribute decision making with combined weight information in interval-valued intuitionistic fuzzy environmental. Control Cybern. 2012, 41, 97–112. [Google Scholar]
- Wei, G.W. Picture 2-tuple linguistic bonferroni mean operators and their application to multiple attribute decision making. Int. J. Fuzzy Syst. 2017, 19, 997–1010. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. Some hybrid weighted aggregation operators under neutrosophic set environment and their applications to multicriteria decision-making. Appl. Intell. 2018, 48, 4871–4888. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. New logarithmic operational laws and their applications to multiattribute decision making for single-valued neutrosophic numbers. Cogn. Syst. Res. 2018, 52, 931–946. [Google Scholar] [CrossRef]
- Kaufmann, A. Introduction to Fuzzy Subsets; Academic Press: New York, NY, USA, 1975; Volume 1. [Google Scholar]
- Zadeh, L.A., Fu, K.S., Tanaka, K., Eds.; Fuzzy sets and their applications to cognitive and decision processes. In Proceedings of the US–Japan Seminar on Fuzzy Sets and Their Applications, Berkeley, CA, USA, 1–4 July 1974. [Google Scholar]
- Akram, M.; Dudek, W.A. Interval-valued fuzzy graphs. Comput. Math. Appl. 2011, 61, 289–299. [Google Scholar] [CrossRef]
- Bhattacharya, P. Some remarks on fuzzy graphs. Pattern Recognit. Lett. 1987, 6, 297–302. [Google Scholar] [CrossRef]
- Bhutani, K.R. On automorphisms of fuzzy graphs. Pattern Recognit. Lett. 1989, 9, 159–162. [Google Scholar] [CrossRef]
- Bhutani, K.R.; Rosenfeld, A. Strong arcs in fuzzy graphs. Inf. Sci. 2003, 152, 319–322. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Chang-Shyh, P. Operations on fuzzy graphs. Inf. Sci. 1994, 79, 159–170. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Jun, Y.B. Complete interval-valued fuzzy graphs. Ann. Fuzzy Math. Inform. 2013, 6, 677–687. [Google Scholar]
- Pal, M.; Rashmanlou, H. Irregular interval valued fuzzy graphs. arXiv, 2014; arXiv:1407.6190. [Google Scholar]
- Akram, M. Interval-valued fuzzy line graphs. Neural Comput. Appl. 2012, 21, 145–150. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Pal, M. Balanced interval-valued fuzzy graphs. J. Phys. Sci. 2013, 17, 43–57. [Google Scholar]
- Pramanik, T.; Samanta, S.; Pal, M. Interval-valued fuzzy planar graphs. Int. J. Mach. Learn. Cybern. 2016, 7, 653–664. [Google Scholar] [CrossRef]
- Talebi, A.; Rashmanlou, H. Isomorphism on interval-valued fuzzy graphs. Ann. Fuzzy Math. Inform. 2013, 6, 47–58. [Google Scholar]
- Parvathi, R.; Karunambigai, M. Intuitionistic fuzzy graphs. In Computational Intelligence, Theory and Applications; Springer: New York, NY, USA, 2006; pp. 139–150. [Google Scholar]
- Mishra, S.; Pal, A. Product of interval valued intuitionistic fuzzy graph. Ann. Pure Appl. Math. 2013, 5, 37–46. [Google Scholar]
- Mishra, S.; Pal, A. Regular interval-valued intuitionistic fuzzy graphs. J. Inform. Math. Sci. 2017, 9, 609–621. [Google Scholar]
- Ismayil, A.M.; Ali, A.M. On strong interval-valued intuitionistic fuzzy graph. Int. J. Fuzzy Math. Syst. 2014, 4, 161–168. [Google Scholar]
- Broumi, S.; Talea, M.; Bakali, A.; Smarandache, F. Single valued neutrosophic graphs. Florentin Smarandache Surapati Pramanik 2015, 187. [Google Scholar]
- Broumi, S.; Talea, M.; Bakali, A.; Smarandache, F.; Kumar, P.K. Shortest path problem on single valued neutrosophic graphs. In Proceedings of the 2017 International Symposium on Networks, Computers and Communications (ISNCC), Marrakech, Morocco, 16–18 May 2017; pp. 1–6. [Google Scholar]
- Broumi, S.; Bakal, A.; Talea, M.; Smarandache, F.; Vladareanu, L. Applying dijkstra algorithm for solving neutrosophic shortest path problem. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems (ICAMechS), Melbourne, VIC, Australia, 30 November–3 December 2016; pp. 412–416. [Google Scholar]
- Broumi, S.; Ullah, K.; Bakali, A.; Talea, M.; Singh, P.K.; Mahmood, T.; Smarandache, F.; Bahnasse, A.; Patro, S.K.; Oliveira, A. Novel System and Method for Telephone Network Planing Based on Neutrosophic Graph. Glob. J. Comput. Sci. Technol. 2018, 18, 1–10. [Google Scholar]
- Akram, M.; Shahzadi, S. Neutrosophic soft graphs with application. J. Intell. Fuzzy Syst. 2017, 32, 841–858. [Google Scholar] [CrossRef]
- Broumi, S.; Talea, M.; Bakali, A.; Smarandache, F. Interval valued neutrosophic graphs. Crit. Rev. XII 2016, 2016, 5–33. [Google Scholar]
- Akram, M.; Nasir, M. Concepts of Interval-Valued Neutrosophic Graphs. Infin. Study 2017, 6, 22–41. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F.; Talea, M.; Bakali, A. Operations on Interval Valued Neutrosophic Graphs; Florentin Smarandache Surapati Pramanik. Infin. Study 2016. [Google Scholar]
- Broumi, S.; Talea, M.; Bakali, A.; Smarandache, F. On strong interval valued neutrosophic graphs. Crit. Rev. 2016, 12, 49–71. [Google Scholar]
- Garg, H.; Arora, R. Dual hesitant fuzzy soft aggregation operators and their application in decision making. Cogn. Comput. 2018, 10, 769–789. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arab. J. Sci. Eng. 2018, 10, 769–789. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Complex intuitionistic fuzzy power aggregation operators and their applications in multi-criteria decision-making. Expert Syst. 2018, 35, e12325. [Google Scholar] [CrossRef]
- Kaur, G.; Garg, H. Multi—Attribute decision—Making based on bonferroni mean operators under cubic intuitionistic fuzzy set environment. Entropy 2018, 20, 65. [Google Scholar] [CrossRef]
- Garg, H.; Nancy. Multi-criteria decision-making method based on prioritized muirhead mean aggregation operator under neutrosophic set environment. Symmetry 2018, 10, 280. [Google Scholar] [CrossRef]
- Wei, G.; Garg, H.; Gao, H.; Wei, C. Interval-Valued Pythagorean Fuzzy Maclaurin Symmetric Mean Operators in Multiple Attribute Decision Making. IEEE Access 2018, 6, 67866–67884. [Google Scholar] [CrossRef]
- Garg, H. Hesitant Pythagorean fuzzy Maclaurin symmetric mean operators and its applications to multiattribute decision making process. Int. J. Intell. Syst. 2018. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jan, N.; Ullah, K.; Mahmood, T.; Garg, H.; Davvaz, B.; Saeid, A.B.; Broumi, S. Some Root Level Modifications in Interval Valued Fuzzy Graphs and Their Generalizations Including Neutrosophic Graphs. Mathematics 2019, 7, 72. https://doi.org/10.3390/math7010072
Jan N, Ullah K, Mahmood T, Garg H, Davvaz B, Saeid AB, Broumi S. Some Root Level Modifications in Interval Valued Fuzzy Graphs and Their Generalizations Including Neutrosophic Graphs. Mathematics. 2019; 7(1):72. https://doi.org/10.3390/math7010072
Chicago/Turabian StyleJan, Naeem, Kifayat Ullah, Tahir Mahmood, Harish Garg, Bijan Davvaz, Arsham Borumand Saeid, and Said Broumi. 2019. "Some Root Level Modifications in Interval Valued Fuzzy Graphs and Their Generalizations Including Neutrosophic Graphs" Mathematics 7, no. 1: 72. https://doi.org/10.3390/math7010072
APA StyleJan, N., Ullah, K., Mahmood, T., Garg, H., Davvaz, B., Saeid, A. B., & Broumi, S. (2019). Some Root Level Modifications in Interval Valued Fuzzy Graphs and Their Generalizations Including Neutrosophic Graphs. Mathematics, 7(1), 72. https://doi.org/10.3390/math7010072








