Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function
Abstract
:1. Introduction
2. Proposed Explicit Approximations and Comparative Analysis
2.1. Transformation and Formulation
2.2. Accuracy
2.3. Complexity and Computational Burden
2.4. Simplifications
3. Software Description
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Constants: | |
| any | |
| Variables: | |
| variable that depends on and (dimensionless) | |
| variable that depends on (dimensionless) | |
| variable that depends on variables and (dimensionless) | |
| Darcy (Moody) flow friction factor (dimensionless) | |
| Reynolds number (dimensionless) | |
| variable that depends on R (dimensionless) | |
| variable in function on R and (dimensionless) | |
| Relative roughness of inner pipe surface (dimensionless) | |
| variables defined in Appendix A of this paper | |
| Functions: | |
| exponential function | |
| log10 | logarithm with base 10 |
| natural logarithm | |
| Padé approximant | |
| Lambert -function | |
| ω | Wright ω-function |
Appendix A
- -
- Here, developed Equations (3), (5), and (6); Equations (A1)–(A3):where , , .
- -
- Here, developed Equation (4); Equations (A4)–(A6):where , and .As parameter is larger, the approximation is more accurate. The value, , gives the sufficiently accurate approximation for gas hydraulic modelling, as the corresponding maximal relative error is less than 0.007% for the analysed Colebrook model.
- -
- Here, developed Equation (11); Equation (A7):Parameter from the Equations (A1)–(A3) and Equations (A4)–(A6) should be calculated using Equation (A7).
- -
- Buzzelli [39]; (A8):
- -
- Zigrang and Sylvester [42]; (A9):
- -
- Serghides [43]; (A10):
- -
- Romeo et al. [41]; (A11):
- -
- Vatankhah and Kouchakzadeh [40]; (A12):
- -
- Barr [44]; (A13):
- -
- Serghides-simple [43]; (A14):
- -
- Chen [45]; (A15):
- -
- Fang et al. [46]; (A16):
- -
- Papaevangelou et al. [47]; (A17):
- -
- Vatankhah [14]; (A18):
- -
- Offor and Alabi [38]; (A19):
References
- Colebrook, C.F.; White, C.M. Experiments with fluid friction in roughened pipes. Proc. R. Soc. A Math. Phys. Eng. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. (Lond.) 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Keady, G. Colebrook-White formula for pipe flows. J. Hydraul. Eng. 1998, 124, 96–97. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. 2017, 139, 031401. [Google Scholar] [CrossRef]
- Barry, D.A.; Parlange, J.Y.; Li, L.; Prommer, H.; Cunningham, C.J.; Stagnitti, F. Analytical approximations for real values of the Lambert W-function. Math. Comput. Simul. 2000, 53, 95–103. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Constraints for using Lambert W function-based explicit Colebrook–White equation. J. Hydraul. Eng. 2004, 130, 929–931. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Rollmann, P.; Spindler, K. Explicit representation of the implicit Colebrook–White equation. Case Stud. Therm. Eng. 2015, 5, 41–47. [Google Scholar] [CrossRef]
- Belkić, D. All the trinomial roots, their powers and logarithms from the Lambert series, Bell polynomials and Fox–Wright function: Illustration for genome multiplicity in survival of irradiated cells. J. Math. Chem. 2018. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Evolutionary optimization of Colebrook’s turbulent flow friction approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Improved method of determining friction factor in pipes. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 941–949. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. One-log call iterative solution of the Colebrook equation for flow friction based on Padé polynomials. Energies 2018, 11, 1825. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Symbolic regression based genetic approximations of the Colebrook equation for flow friction. Water 2018, 10, 1175. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evolvable Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef]
- Baker, G.A.; Graves-Morris, P. Padé approximants. In Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Roy, D. Global approximation for some functions. Comput. Phys. Commun. 2009, 180, 1315–1337. [Google Scholar] [CrossRef]
- Lawrence, P.W.; Corless, R.M.; Jeffrey, D.J. Algorithm 917: Complex double-precision evaluation of the Wright ω function. ACM Trans. Math. Softw. (TOMS) 2012, 38, 1–17. [Google Scholar] [CrossRef]
- Wright, E.M. Solution of the equation z · ez = a. Bull. Am. Math Soc. 1959, 65, 89–93. [Google Scholar] [CrossRef]
- Corless, R.M.; Jeffrey, D.J. The Wright ω Function. In Artificial Intelligence, Automated Reasoning, and Symbolic Computation; AISC 2002, Calculemus 2002. Lecture Notes in Computer Science; Calmet, J., Benhamou, B., Caprotti, O., Henocque, L., Sorge, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2385. [Google Scholar] [CrossRef]
- Goudar, C.T.; Sonnad, J.R. Explicit friction factor correlation for turbulent flow in smooth pipes. Ind. Eng. Chem. Res. 2003, 42, 2878–2880. [Google Scholar] [CrossRef]
- Goudar, C.T.; Sonnad, J.R. Comparison of the iterative approximations of the Colebrook-White equation. Hydrocarb. Process. 2008, 87, 79–83. [Google Scholar]
- Brkić, D. W solutions of the CW equation for flow friction. Appl. Math. Lett. 2011, 24, 1379–1383. [Google Scholar] [CrossRef]
- Brkić, D. New explicit correlations for turbulent flow friction factor. Nucl. Eng. Des. 2011, 241, 4055–4059. [Google Scholar] [CrossRef]
- Brkić, D. An explicit approximation of Colebrook’s equation for fluid flow friction factor. Pet. Sci. Technol. 2011, 29, 1596–1602. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Exact analytical solutions of the Colebrook-White equation” by Yozo Mikata and Walter S. Walczak. J. Hydraul. Eng. 2017, 143, 07017007. [Google Scholar] [CrossRef]
- Brkić, D. Lambert W function in hydraulic problems. Mathematica Balkanica 2012, 26, 285–292. Available online: http://www.math.bas.bg/infres/MathBalk/MB-26/MB-26-285-292.pdf (accessed on 26 December 2018).
- More, A.A. Analytical solutions for the Colebrook and White equation and for pressure drop in ideal gas flow in pipes. Chem. Eng. Sci. 2006, 61, 5515–5519. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng. 2006, 132, 863–867. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Explicit reformulation of the Colebrook−White equation for turbulent flow friction factor calculation. Ind. Eng. Chem. Res. 2007, 46, 2593–2600. [Google Scholar] [CrossRef]
- Mikata, Y.; Walczak, W.S. Exact analytical solutions of the Colebrook-White equation. J. Hydraul. Eng. 2016, 142, 04015050. [Google Scholar] [CrossRef]
- Kwon, T.J.; Draper, J. Floating-point division and square root using a Taylor-series expansion algorithm. Microelectron. J. 2009, 40, 1601–1605. [Google Scholar] [CrossRef]
- Offor, U.H.; Alabi, S.B. An accurate and computationally efficient friction factor model. Adv. Chem. Eng. Sci. 2016, 6, 237–245. [Google Scholar] [CrossRef]
- Buzzelli, D. Calculating friction in one step. Mach. Des. 2008, 80, 54–55. Available online: https://www.machinedesign.com/archive/calculating-friction-one-step (accessed on 29 October 2018).
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion of “Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation” by Jagadeesh R. Sonnad and Chetan T. Goudar. J. Hydraul. Eng. 2008, 134, 1187. [Google Scholar] [CrossRef]
- Romeo, E.; Royo, C.; Monzón, A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J. 2002, 86, 369–374. [Google Scholar] [CrossRef]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. (N. Y.) 1984, 91, 63–64. [Google Scholar]
- Barr, D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. Proc. Inst. Civ. Eng. 1981, 71, 529–535. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y.; Zhou, Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des. 2011, 241, 897–902. [Google Scholar] [CrossRef]
- Papaevangelou, G.; Evangelides, C.; Tzimopoulos, C. A new explicit relation for friction coefficient f in the Darcy-Weisbach equation. In Proceedings of the Tenth Conference on Protection and Restoration of the Environment, Corfu, Greece, 5–9 July 2010; Volume 166, pp. 1–7. Available online: http://blogs.sch.gr/geopapaevan/files/2010/07/full-paper_pre1128act.pdf (accessed on 29 October 2018).
- Zigrang, D.J.; Sylvester, N.D. A review of explicit friction factor equations. J. Energy Resour. Technol. 1985, 107, 280–283. [Google Scholar] [CrossRef]
- Gregory, G.A.; Fogarasi, M. Alternate to standard friction factor equation. Oil Gas J. 1985, 83, 120–127. [Google Scholar]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Brkić, D. Determining friction factors in turbulent pipe flow. Chem. Eng. (N. Y.) 2012, 119, 34–39. Available online: https://www.chemengonline.com/determining-friction-factors-in-turbulent-pipe-flow/?printmode=1 (accessed on 29 October 2018).
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Pimenta, B.D.; Robaina, A.D.; Peiter, M.X.; Mezzomo, W.; Kirchner, J.H.; Ben, L.H.B. Performance of explicit approximations of the coefficient of head loss for pressurized conduits. Rev. Bras. Eng. Agríc. Ambient. 2018, 22, 301–307. [Google Scholar] [CrossRef]
- Taherdangkoo, M.; Taherdangkoo, R. Modified BNMR algorithm applied to Loney’s solenoid benchmark problem. Int. J. Appl. Electromagn. Mech. 2014, 46, 683–692. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Taherdangkoo, M. Modified stem cells algorithm-based neural network applied to bottom hole circulating pressure in underbalanced drilling. Int. J. Pet. Eng. 2015, 1, 178. [Google Scholar] [CrossRef]
- Sobol’, I.M.; Turchaninov, V.I.; Levitan, Y.L.; Shukhman, B.V. Quasi-Random Sequence Generators; Distributed by OECD/NEA Data Bank; Keldysh Institute of Applied Mathematics, Russian Academy of Sciences: Moscow, Russia, 1991; Available online: http://www.oecd-nea.org/tools/abstract (accessed on 29 October 2018).
- Bratley, P.; Fox, B.L. Algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. (TOMS) 1988, 14, 88–100. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Syst. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Brkić, D. An improvement of Hardy Cross method applied on looped spatial natural gas distribution networks. Appl. Energy 2009, 86, 1290–1300. [Google Scholar] [CrossRef]
- Pambour, K.A.; Cakir Erdener, B.; Bolado-Lavin, R.; Dijkema, G.P. Development of a simulation framework for analyzing security of supply in integrated gas and electric power systems. Appl. Sci. 2017, 7, 47. [Google Scholar] [CrossRef]
- Biagi, M.; Carnevali, L.; Tarani, F.; Vicario, E. Model-Based Quantitative Evaluation of Repair Procedures in Gas Distribution Networks. ACM Trans. Cyber-Phys. Syst. 2018, 3. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation” by Saeed Samadianfard [J. Pet. Sci. Eng. 92–93 (2012) 48–55]. J. Pet. Sci. Eng. 2014, 124, 399–401. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. (EJSiE) 2017, 10, 2. Available online: https://sie.scholasticahq.com/article/4663-solution-of-the-implicit-colebrook-equation-for-flow-friction-using-excel (accessed on 29 December 2018).
- Brkić, D. Spreadsheet-based pipe networks analysis for teaching and learning purpose. Spreadsheets Educ. (EJSiE) 2016, 9, 4. Available online: https://sie.scholasticahq.com/article/4646-spreadsheet-based-pipe-networks-analysis-for-teaching-and-learning-purpose (accessed on 29 December 2018).
- Brkić, D. Discussion of “Economics and Statistical Evaluations of Using Microsoft Excel Solver in Pipe Network Analysis” by Oke, I.A., Ismail, A., Lukman, S., Ojo, S.O., Adeosun, O.O., Nwude, M.O. J. Pipeline Syst. Eng. Pract. 2018, 9, 07018002. [Google Scholar] [CrossRef]
- Nikolić, B.; Jovanović, M.; Milošević, M.; Milanović, S. Function k-as a link between fuel flow velocity and fuel pressure, depending on the type of fuel. Facta Univ. Ser. Mech. Eng. 2017, 15, 119–132. [Google Scholar] [CrossRef]
- Brkić, D. Iterative methods for looped network pipeline calculation. Water Resour. Manag. 2011, 25, 2951–2987. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Unified friction formulation from laminar to fully rough turbulent flow. Appl. Sci. 2018, 8, 2036. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Brkić, D. A note on explicit approximations to Colebrook’s friction factor in rough pipes under highly turbulent cases. Int. J. Heat Mass Transf. 2016, 93, 513–515. [Google Scholar] [CrossRef]
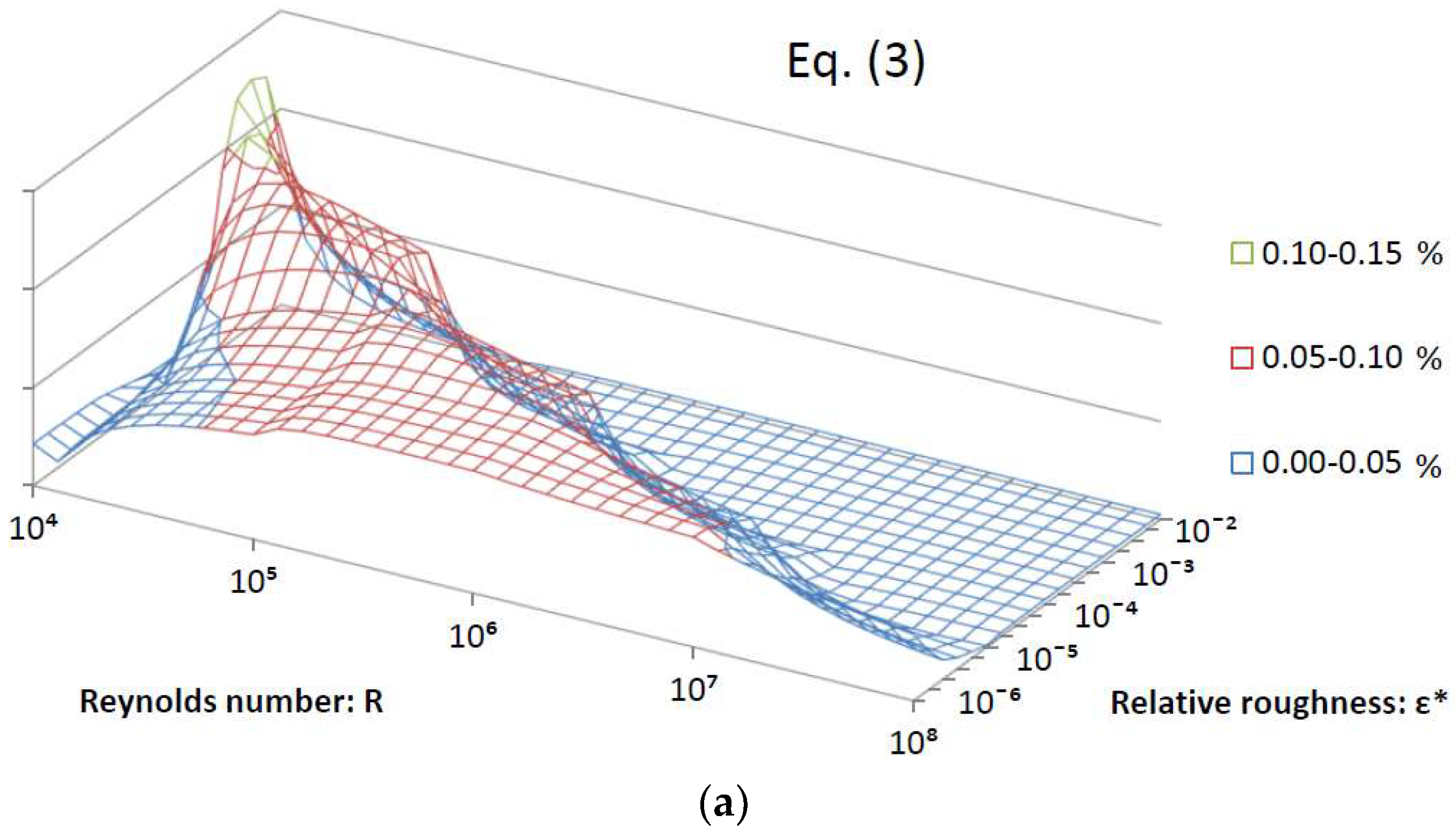
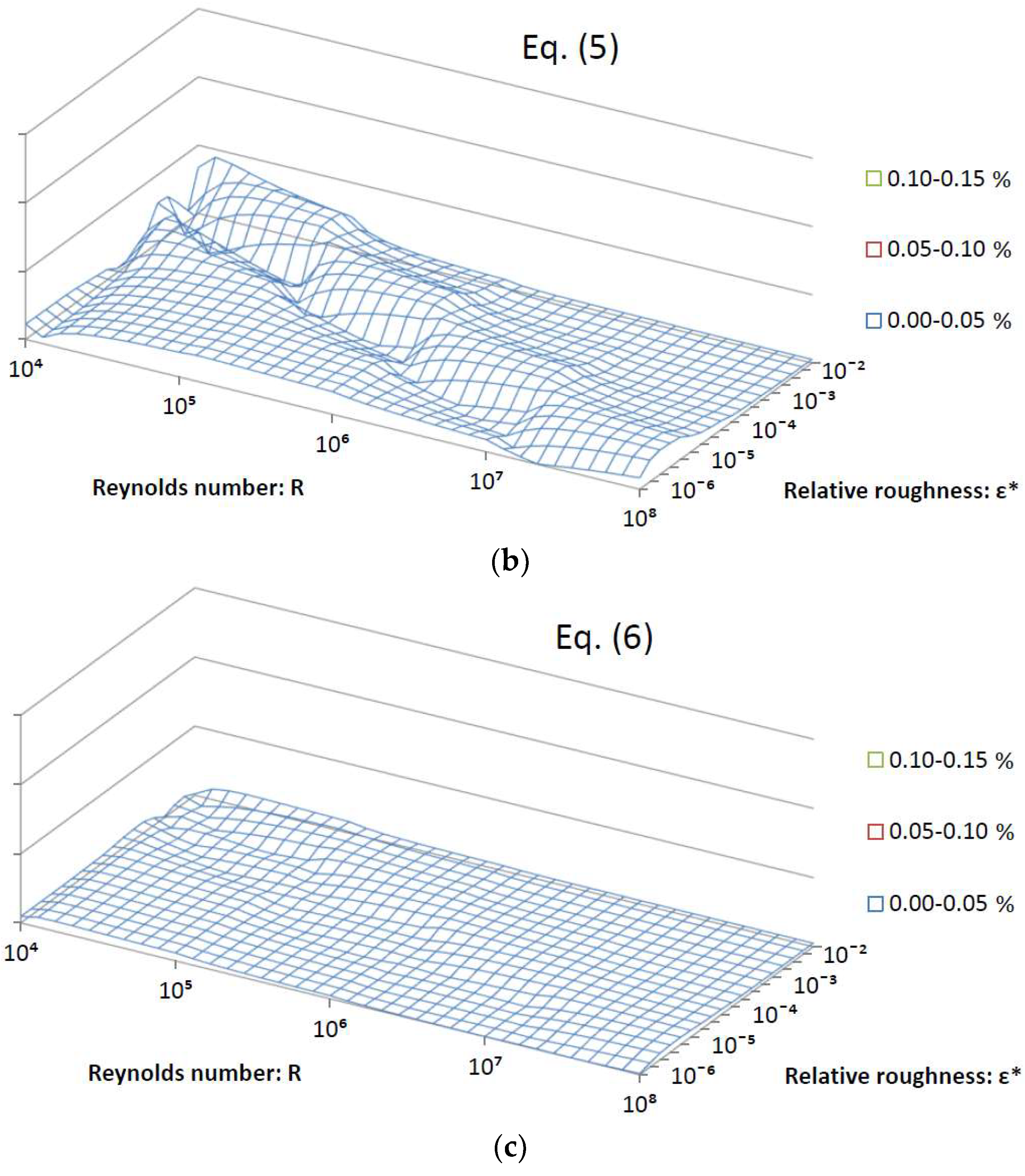
| R = 4000 | R = 104 | R = 105 | R = 106 | R = 107 | R = 108 | |
| 10−6 | 5.763586714 | 6.552354737 | 8.594740889 | 10.78188015 | 13.94025768 | 26.71930109 |
| 10−5 | 5.767379666 | 6.562009418 | 8.694474328 | 11.80401384 | 24.50329461 | 125.7849498 |
| 10−3 | 5.805329409 | 6.658658836 | 9.697953496 | 22.29514802 | 124.0554132 | #VALUE! |
| 10−2 | 6.186774452 | 7.63459358 | 20.09639172 | 122.325789 | #VALUE! | #VALUE! |
| 0.05 | 10.14320931 | 17.90904123 | 120.5960672 | #VALUE! | #VALUE! | #VALUE! |
| R = 4000 | R = 104 | R = 105 | R = 106 | R = 107 | R = 108 | |
| 10−6 | 5.766606874 | 6.552971455 | 8.592338256 | 10.7784212 | 13.93654591 | 26.71669441 |
| 10−5 | 5.770385511 | 6.562602762 | 8.691991603 | 11.80037821 | 24.50049484 | 136.3596559 |
| 10−3 | 5.808193728 | 6.659024862 | 9.694862641 | 22.29214094 | 134.073966 | 1246.853296 |
| 10−2 | 6.188374207 | 7.633218988 | 20.093168 | 131.7885643 | 1244.552558 | 12,371.62215 |
| 0.05 | 10.13993873 | 17.90560354 | 129.5034606 | 1242.251823 | 12,369.31975 | 123,639.9564 |
| 1 Approximation | Maximal Relative Error % | Function | ||
|---|---|---|---|---|
| Logarithms | Non-Integer Powers | 2 TOTAL | ||
| Vatankhah [14] | 0.0028% | 1 | 2 | 3(5) |
| Here developed; Equation (6) | 0.0096% | 2 | 0 | 2 |
| Here developed; Equation (5) | 0.045%, | 2 | 0 | 2 |
| Offor and Alabi [38] | 0.0602% | 2 | 1 | 3(4) |
| Here developed; Equation (3) | 0.13% | 2 | 0 | 2 |
| Here developed; Equation (4) | 0.13% | 0 | 2 | 2(4) |
| 3 Buzzelli [39] | 0.14% | 2 | 0 | 2 |
| Zigrang and Sylvester [42] | 0.14% | 3 | 0 | 3 |
| Serghides [43] | 0.14% | 3 | 0 | 3 |
| Romeo et al. [41] | 0.14% | 3 | 2 | 5(7) |
| Vatankhah and Kouchakzadeh [40] | 0.15% | 2 | 1 | 3(4) |
| Barr [44] | 0.27% | 2 | 2 | 4(6) |
| Serghides-simple [43] | 0.35% | 2 | 0 | 2 |
| Chen [45] | 0.36% | 2 | 2 | 4(6) |
| Here developed; Equation (11) | Up to 0.4% | 1 | 0 | 1 |
| Fang et al. [46] | 0.62% | 1 | 3 | 4(7) |
| Papaevangelou et al. [47] | 0.82% | 2 | 1 | 3(4) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brkić, D.; Praks, P. Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function. Mathematics 2019, 7, 34. https://doi.org/10.3390/math7010034
Brkić D, Praks P. Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function. Mathematics. 2019; 7(1):34. https://doi.org/10.3390/math7010034
Chicago/Turabian StyleBrkić, Dejan, and Pavel Praks. 2019. "Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function" Mathematics 7, no. 1: 34. https://doi.org/10.3390/math7010034
APA StyleBrkić, D., & Praks, P. (2019). Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function. Mathematics, 7(1), 34. https://doi.org/10.3390/math7010034






