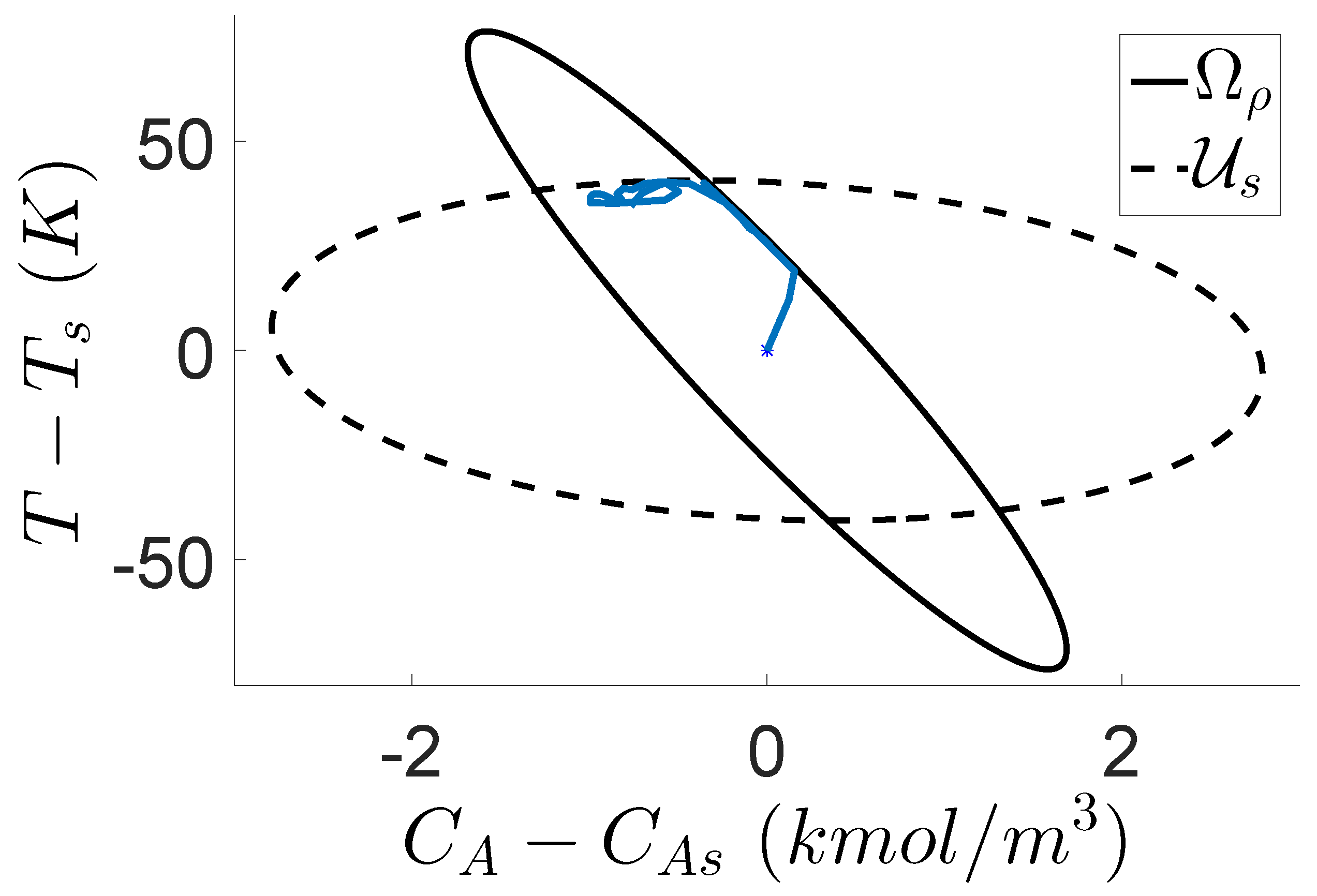1. Introduction
Process operational safety has become crucially important in the chemical industry since the failure of process safety devices/human error often leads to disastrous incidents causing human and capital loss [
1]. Motivated by this, recently, a new class of economic model predictive control systems (EMPC), in which the cost function penalizes process economics instead of the distances from the steady-state in a general quadratic form, was utilized to account for process operational safety and economic optimality based on a function called the Safeness Index [
2,
3]. These new EMPC methods complement previous efforts on economic model predictive control (e.g., [
4,
5,
6,
7]), which were not concerned explicitly with process operational safety. Specifically, in [
2], a Safeness Index function that indicates the level of safety of a given state was utilized to characterize a safe operating region and used as a constraint in the EMPC design such that the closed-loop state of a nonlinear process is guaranteed to be driven into the safe operating region in finite time in the presence of sufficiently small bounded disturbances and, if the Safeness Index takes a special form related to a Lyapunov function used in the EMPC design, to never again exit that safe operating region while maximizing the economics of the process. However, in general, the Safeness Index does not have to take this special form and may therefore leave the safe operating region for finite periods of time (this may be acceptable depending on how the notion of a “safe” region of operation is selected; e.g., perhaps a “safe” region of operation means it is safe to operate in for all times, but that if the state is not in that region for short periods of time, there is not an immediate concern). Therefore, with a general form of the Safeness Index, the hard constraint on this function in the EMPC design of [
2] with a Safeness Index-based constraint may not be feasible. Due to the potential infeasibility issue caused by the hard constraint, the potential for the state to leave the safe operating region unless the Safeness Index has a specific form and the fact that disturbances may not be sufficiently small to guarantee that the closed-loop state re-enters this safe operating region, the EMPC design with a Safeness Index-based constraint may be limited in terms of its applicability to stochastic nonlinear systems.
On the other hand, MPC and EMPC of stochastic nonlinear systems have received a lot of attention recently (e.g., [
8,
9]). Uncertainty in the process model may be considered to have a worst-case upper and lower bound, or it may be considered to have unbounded variation and therefore be treated in a probabilistic manner. Since the variation of disturbances is not bounded in a stochastic nonlinear system, the Lyapunov-based economic model predictive control (LEMPC) framework [
4] developed for nonlinear systems with small bounded disturbances is unable to guarantee closed-loop stability (i.e., the state of the closed-loop system stays within a well-characterized region of the state-space); instead, probabilistic closed-loop stability results are expected in this case. To that end, in [
10], the Markov-chain Monte Carlo technique was used to derive the probabilistic convergence to a near-optimal solution for a constrained stochastic optimization problem. In [
9], a Lyapunov-based model predictive control (LMPC) method was proposed for stochastic nonlinear systems to drive the state to a steady-state within an explicitly characterized region of attraction in probability. Recently, the work [
11] developed a Lyapunov-based EMPC method for stochastic nonlinear systems by utilizing the probability distribution of the disturbance term to derive closed-loop stability and recursive feasibility results in probability.
In the same direction, this work focuses on the design of Safeness Index-based economic model predictive control systems for a broad class of stochastic nonlinear systems with input constraints. Specifically, under the assumption of the stabilizability of the origin of the stochastic nonlinear system via a stochastic Lyapunov-based control law, a process Safeness Index function and the level sets of multiple Lyapunov functions are first utilized to characterize a safe operating region in state-space, starting from which recursive feasibility and process operational safety are derived in probability for the stochastic nonlinear system under an economic model predictive controller. This economic model predictive control method is then designed that utilizes stochastic Lyapunov-based constraints to achieve economic optimality, as well as feasibility and process operational safety in probability in the well-characterized safe operating region.
The rest of the manuscript is organized as follows: in the Preliminaries, the notation, the class of systems and the stabilizability assumptions are given. In the Main Results, the process Safeness Index and the Safeness Index-based LEMPC are introduced. Subsequently, the Safeness Index-based LEMPC using multiple level sets of Lyapunov functions (to broaden the state-space set for which it is recursively feasible) is developed for the nominal system. Based on this, the corresponding stochastic Safeness Index-based LEMPC and its probabilistic process operational safety and feasibility properties are developed for the nonlinear stochastic system. Finally, a nonlinear chemical process example is used to demonstrate the application of the proposed stochastic Safeness Index-based LEMPC.
4. Application to a Chemical Process Example
A chemical process example is used to illustrate the application of the stochastic Safeness Index-based LEMPC of Equation (7) to maintain the closed-loop state within a safe operating region in state-space in probability. Specifically, a well-mixed, non-isothermal continuous stirred tank reactor (CSTR) where an irreversible second-order exothermic reaction takes place is considered. The reaction transforms a reactant
A to a product
B (
). The inlet concentration of
A, the inlet temperature and the feed volumetric flow rate of the reactor are
,
and
F, respectively. The CSTR is equipped with a heating jacket that supplies/removes heat at a rate
Q. The CSTR dynamic model is described by the following material and energy balance equations:
where
is the concentration of reactant
A in the reactor,
is the volume of the reacting liquid in the reactor,
T is the temperature of the reactor and
Q denotes the heat input rate. The concentration of reactant
A in the feed is
. The feed temperature and the volumetric flow rate are
and
F, respectively. The reacting liquid has a constant density of
and a heat capacity of
.
,
,
E and
R represent the enthalpy of reaction, pre-exponential constant, activation energy and ideal gas constant, respectively. Process parameter values are given in
Table 1. The disturbance terms
and
in Equation (25) are independent standard Gaussian white noise with the standard deviations
and
, respectively. It is noted that the disturbance terms of Equation (25) vanish at the steady state.
The initial steady-state of the CSTR is at , and . The manipulated inputs are the inlet concentration of species A and the heat input rate, which are represented by the deviation variables and , respectively. The manipulated inputs are bounded as follows: and . Therefore, the states and the inputs of the closed-loop system are represented by and , respectively.
The control objective of the stochastic Safeness Index-based LEMPC of Equation (7) is to maximize the production rate of
B, while maintaining the closed-loop state trajectories in the safe operating region
in probability. The objective function of Equation (7a) is the production rate of
B:
. The Lyapunov functions are designed using the standard quadratic form
, where the positive definite matrices
and
are chosen to characterize the set
for the stochastic system of Equation (25). The nonlinear feedback controllers in [
13,
18] are utilized as
and
, respectively. The level sets of the Lyapunov functions
and
are chosen as
and
to create a safe operating region
. The explicit Euler method with an integration time step of
h is applied to numerically simulate the dynamic model of Equation (25). The nonlinear optimization problem of the stochastic Safeness Index-based LEMPC of Equation (7) is solved using the IPOPT software package [
19] with the sampling period
h. With the fixed sampling period
h,
and
, we focus on the impact of
and
on probabilistic process operational safety in the following simulations.
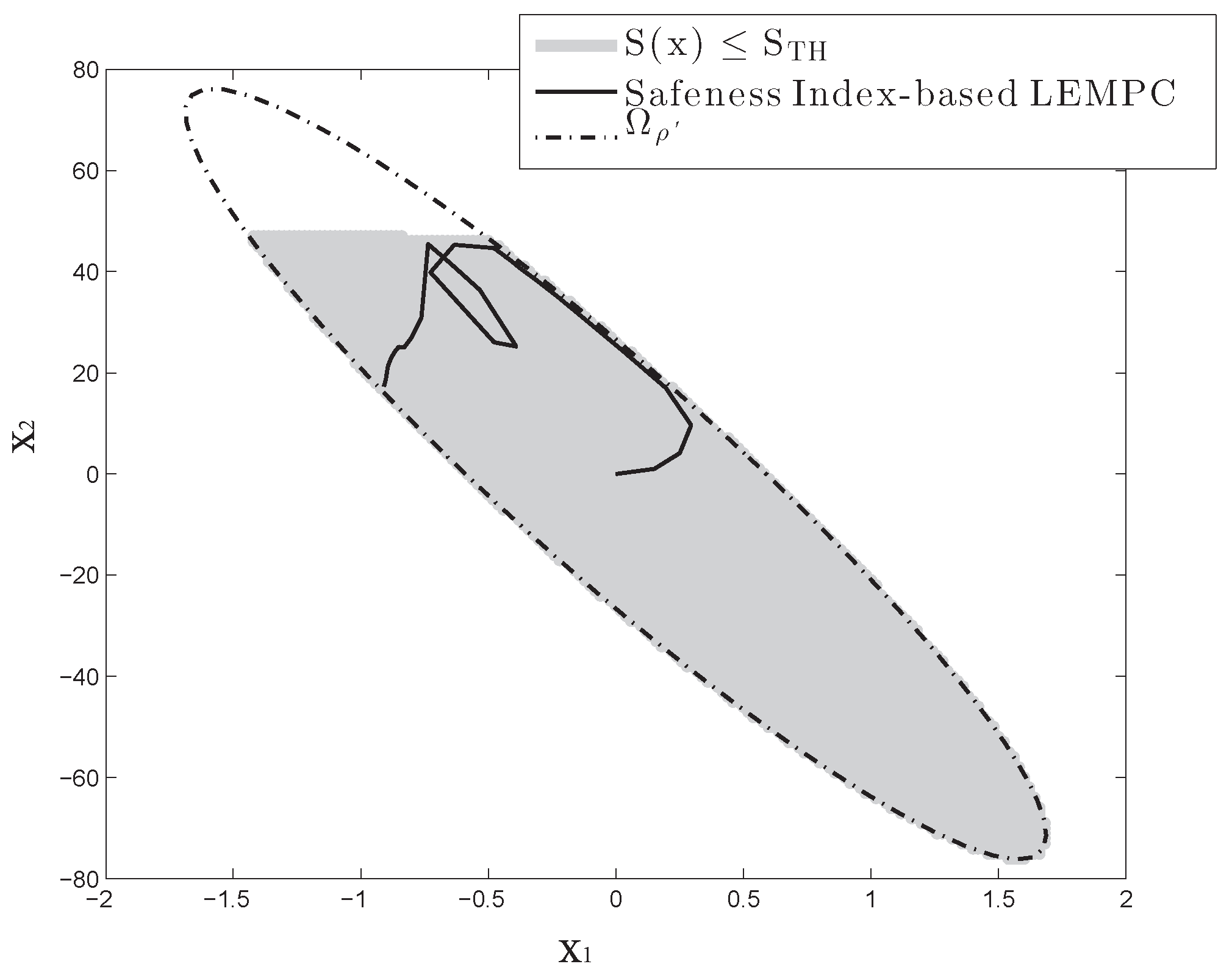
It is first shown in
Figure 4 that under the Safeness Index-based LEMPC of Equation (6) designed for the nominal system of Equation (25), the closed-loop state of the nominal system of Equation (25) stays in the safe operating region
within the entire operation period
h. Additionally, the Safeness Index-based LEMPC of Equation (6) is solved successfully in each iteration to obtain a feasible control action
that is applied in the next sampling period.
It follows that under the stochastic Safeness Index-based LEMPC of Equation (7), the state of the closed-loop system of Equation (25) stays in
with different probabilities for different
and
. To better understand the relationship between probabilistic process operational safety and the choices of
and
, we derived the experimental probabilities via 500 simulation runs for the same initial condition
and different choices of
and
(without the material constraint applied for the nominal system). Let
denote the event that the closed-loop state stays in
over the operation period
h. The results are reported in
Table 2.
From
Table 2, it is observed that with fixed
,
becomes larger as
decreases. Likewise, with fixed
,
increases as
decreases. It is demonstrated that a higher probability of closed-loop process operational safety of the system of Equation (25) is achieved when
and
are more conservative. Let
and
. It is obtained that the probability of the states of the closed-loop system of Equation (25) remaining in the safe operating region
reaches
. Additionally, the averaged total economic benefit (i.e., the time integral of the stage cost
over the operation period
h) is
under the Safeness Index-based LEMPC of Equation (7), which has an improvement of
compared to
under steady-state operation. Therefore, in this example, the closed-loop system of Equation (25) under the Safeness Index-based LEMPC achieves a relatively high probability of process safety and a satisfactory process economic performance simultaneously with
and
. For an actual process, additional work should likely be performed, which can use techniques like those demonstrated here, to increase the probability of the states of the closed-loop system remaining within the safe operating region to higher values considered acceptable for the process at hand given its design, hazards and the backup measures (alarms/operators, safety systems, relief systems) in place.
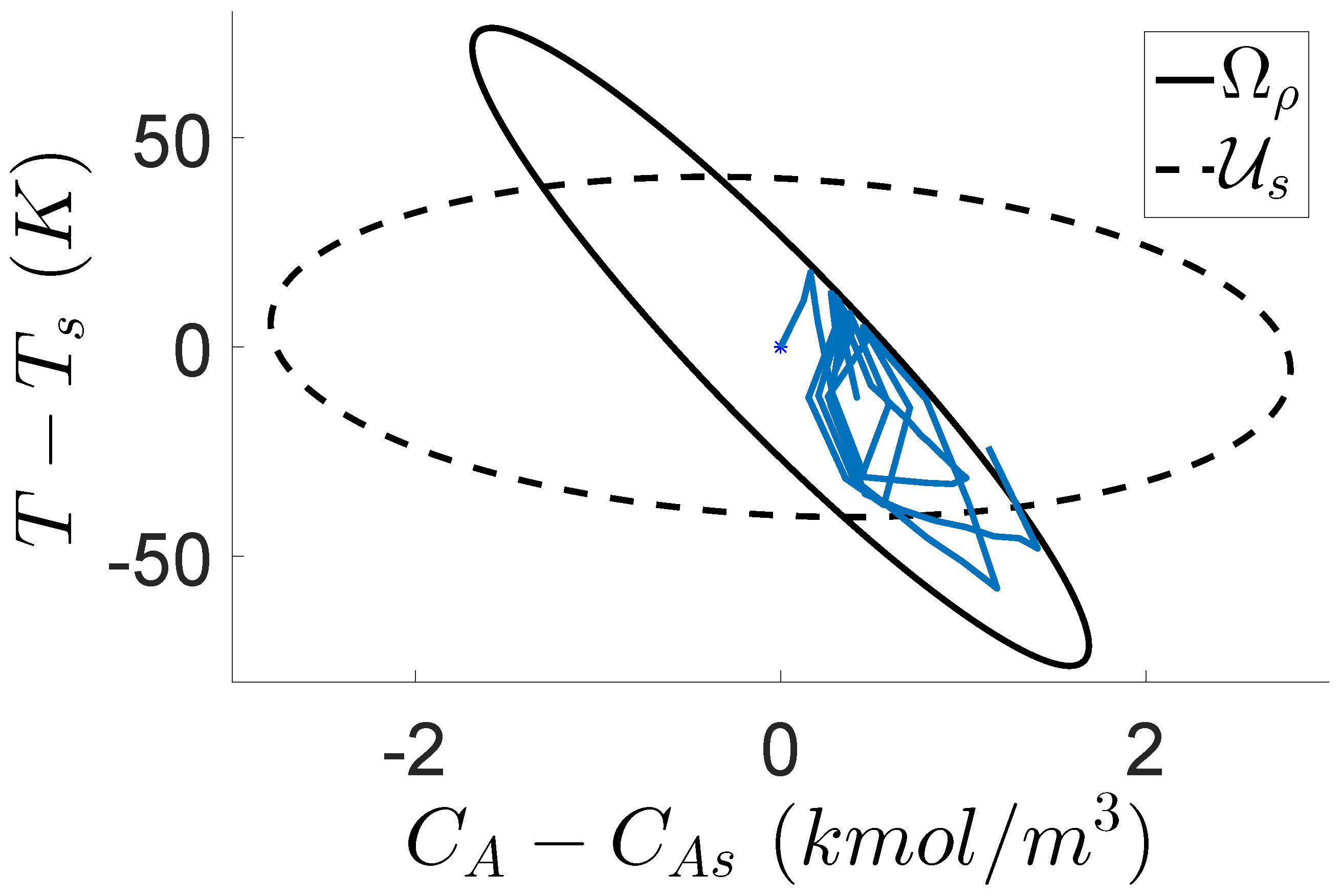
On the other hand, it is observed from
Table 2 that decreasing
increases the probability
. By looking at unsafe closed-loop trajectories (i.e., trajectories that leave the safe operating region
under the Safeness Index-based LEMPC of Equation (7) during the operation period
) in 500 simulation runs (one of them is shown in
Figure 5), it is observed that almost all of the unsafe trajectories leave
through the boundary of
(i.e., the right edge of
in
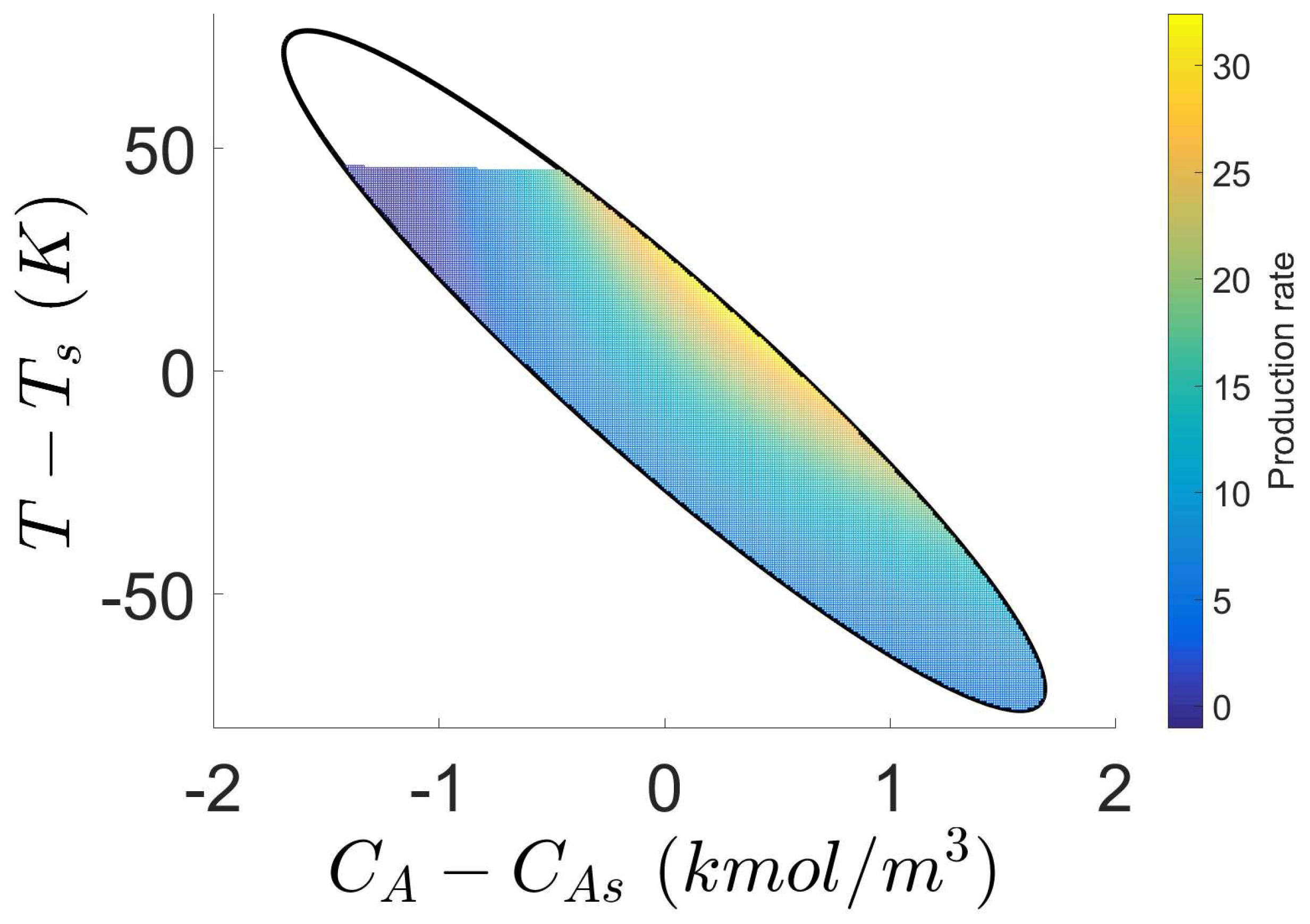
Figure 5). The reason for this behavior is that the local optimum value of
is calculated to be at the right edge of
, which is shown as the yellow region in
Figure 6. Therefore, under the Safeness Index-based LEMPC of Equation (7), the closed-loop trajectory is optimized to approach this high production rate region and begin circling back due to the disturbances, which leads to a higher probability of leaving the safe operating region
from
. Additionally, it is observed in
Figure 6 that the production rate decreases as the safe operating region shrinks (i.e., the color becomes darker), which is consistent with the fact that smaller
and
lead to safer process operation, at the cost of lower economic performance.