Global Dynamics of an SIQR Model with Vaccination and Elimination Hybrid Strategies
Abstract
1. Introduction
2. Model Formulation
3. Equilibrium and Basic Reproductive Number
4. Global Stability of Equilibriums
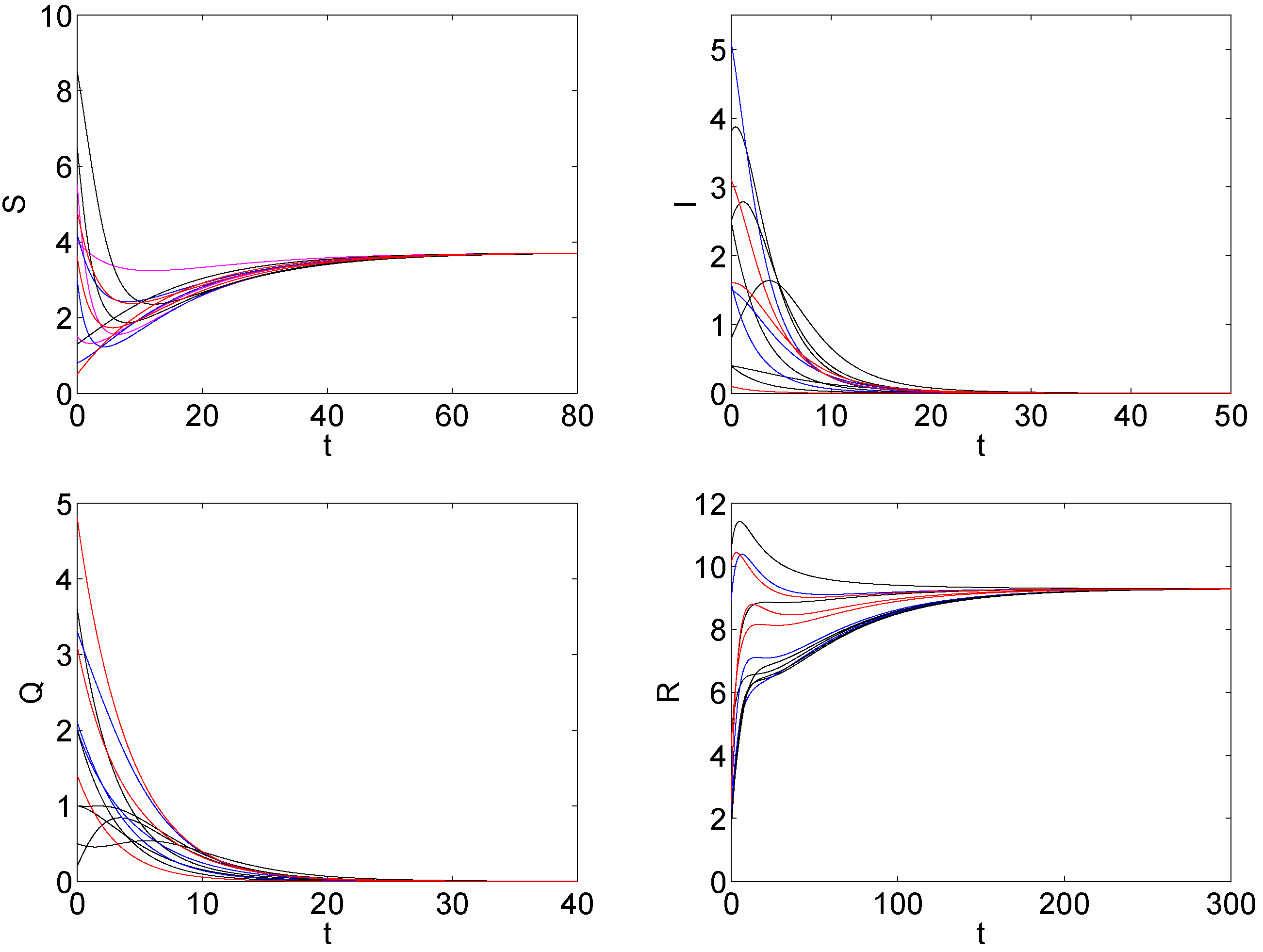
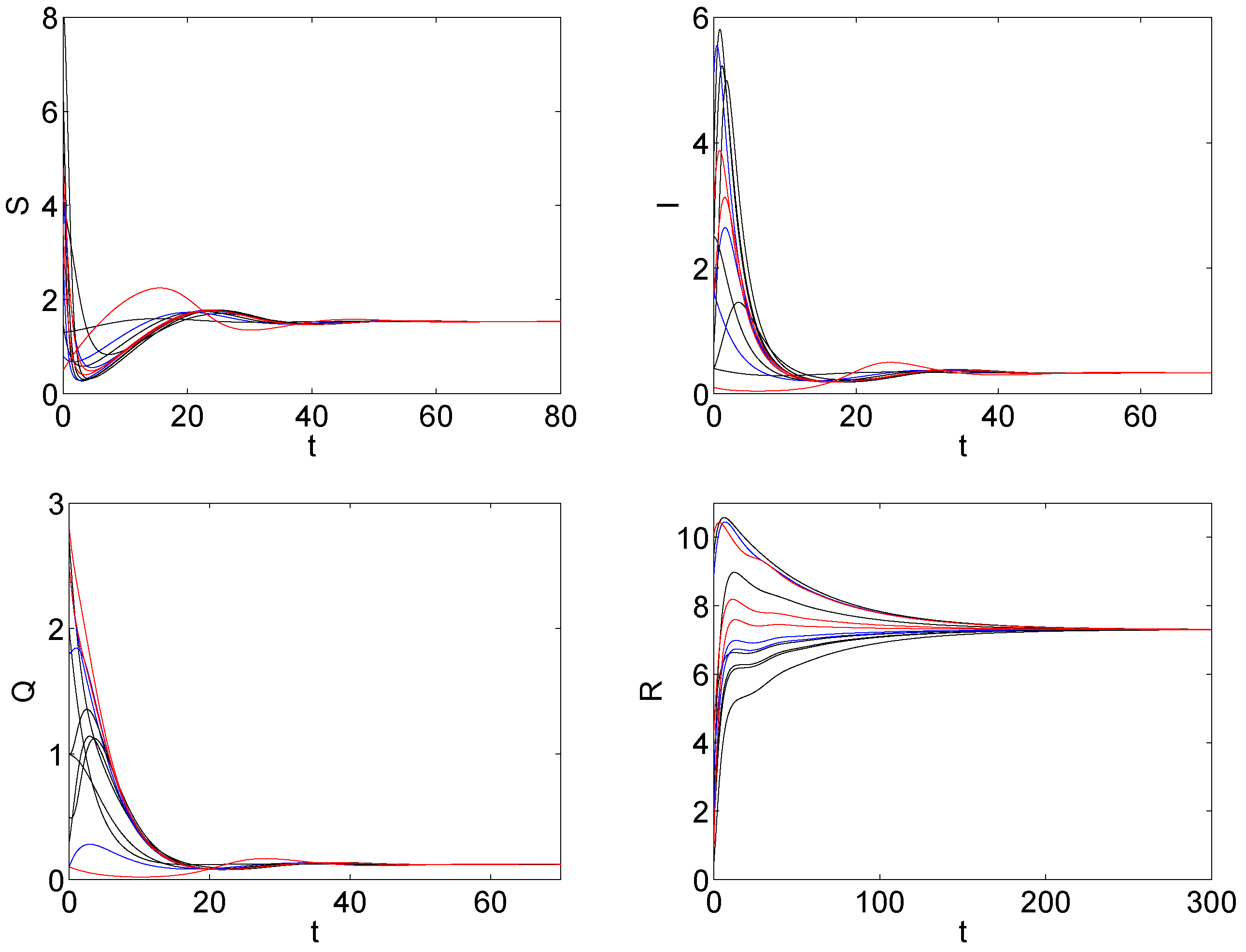
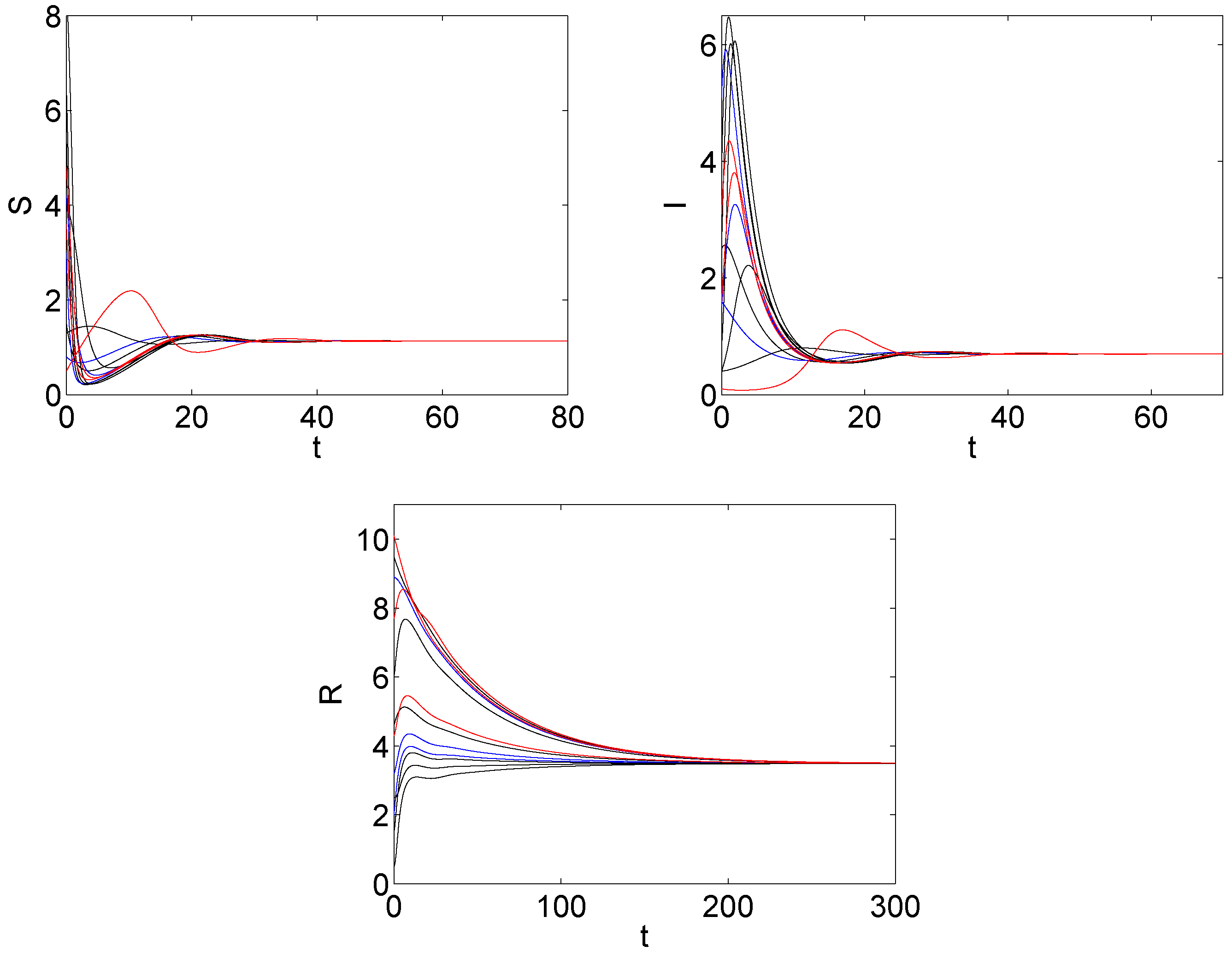
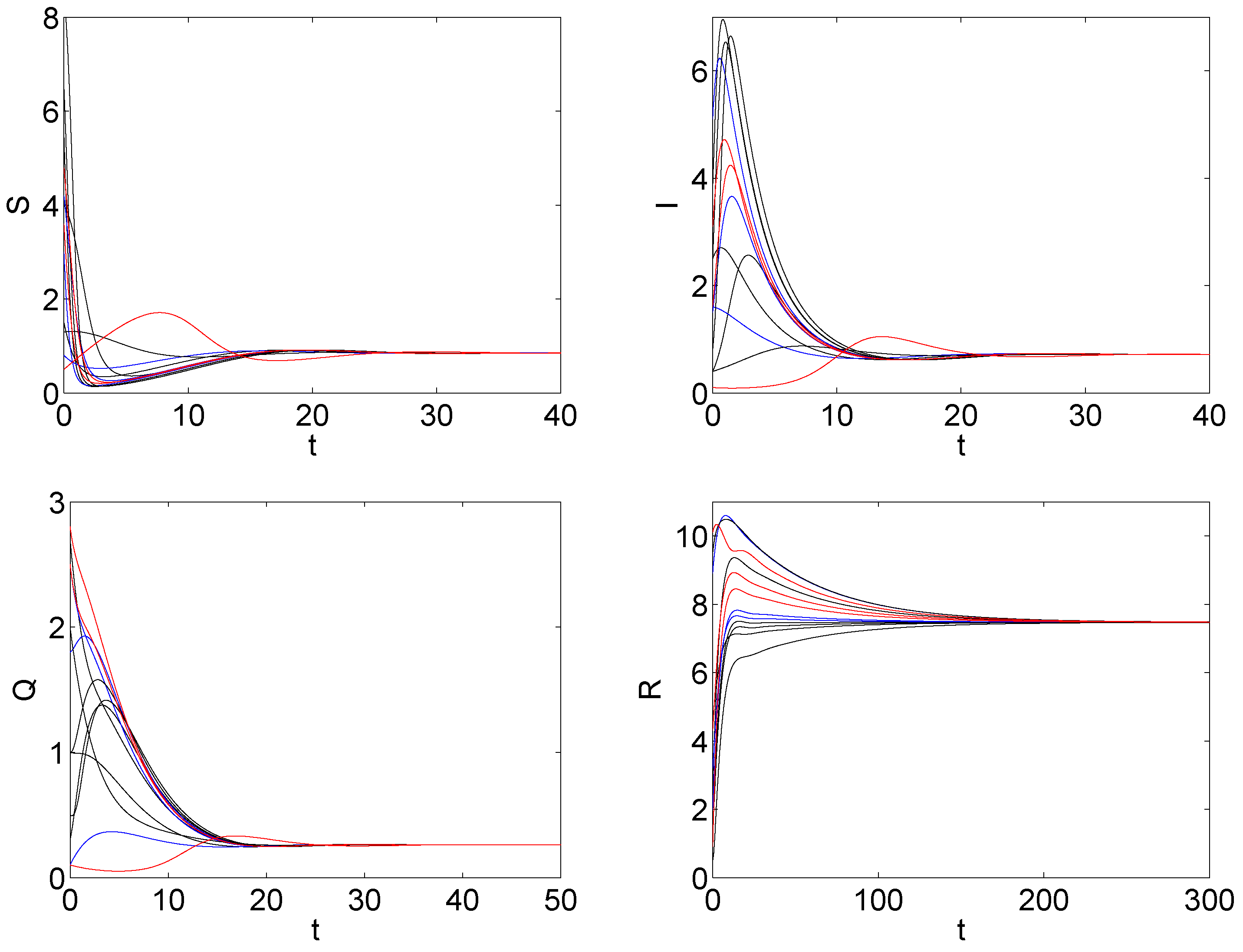
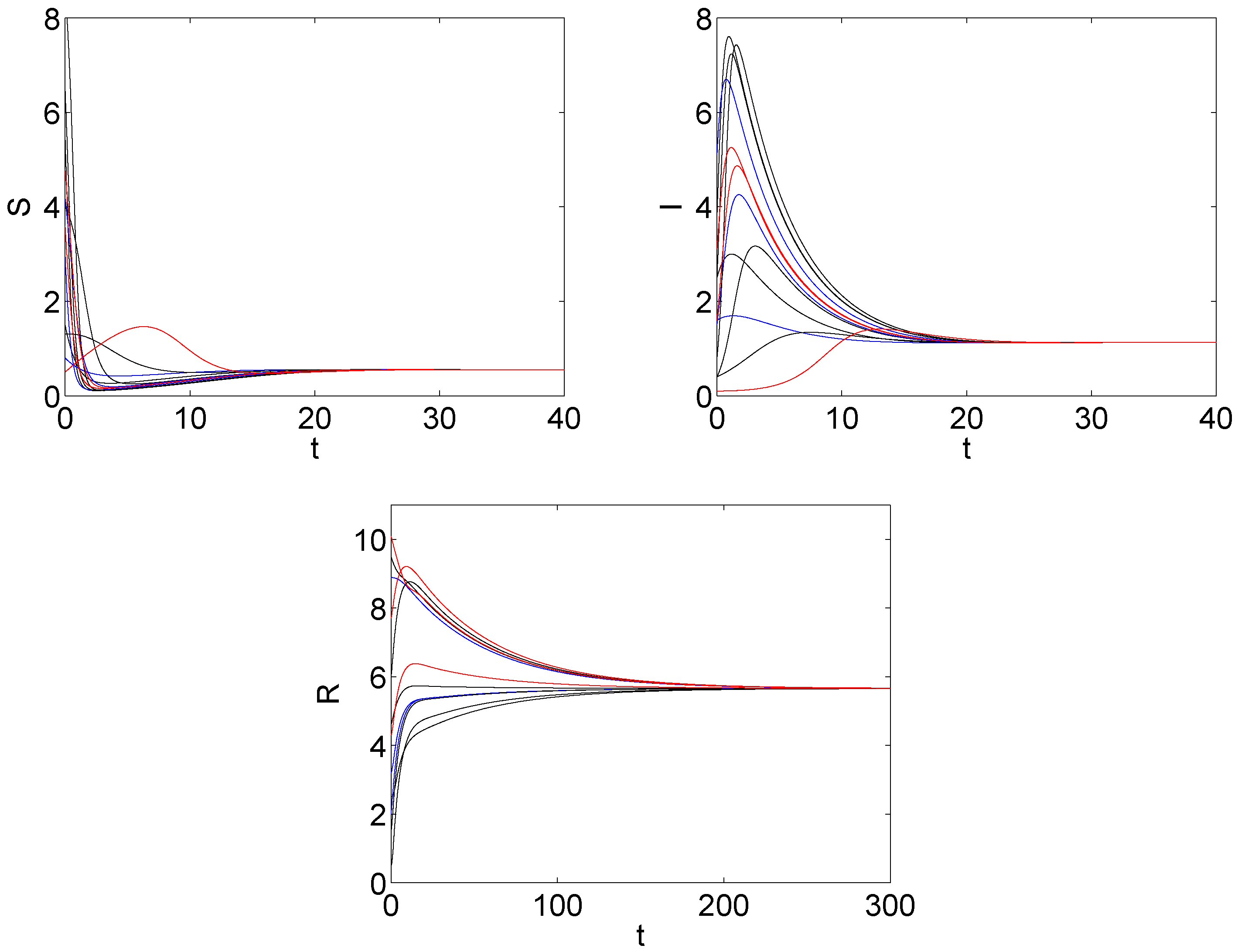
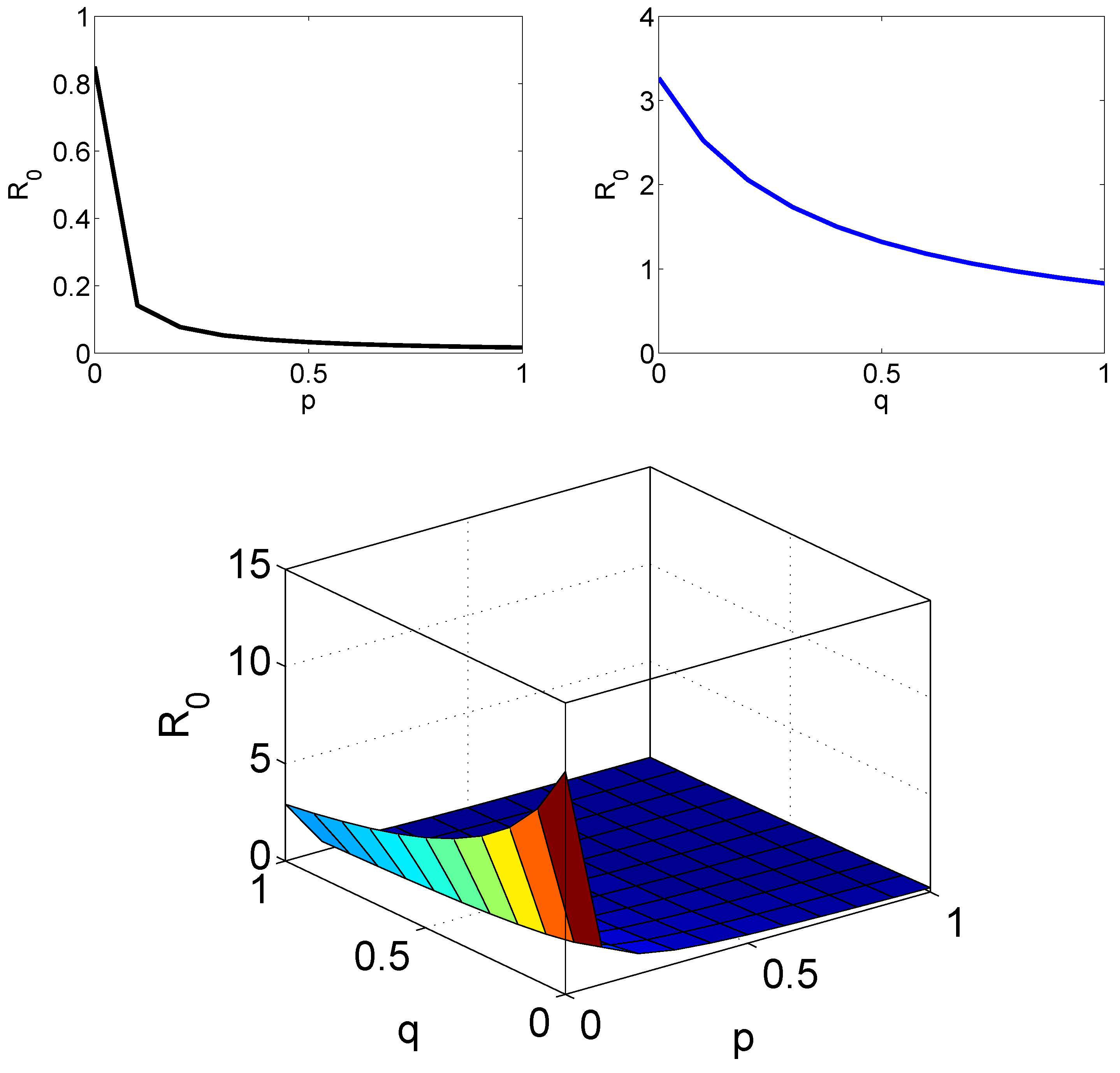
5. The Numerical Simulation
6. Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kermark, M.; Mckendrick, A. Contributions to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Misra, A.; Sharma, A.; Shukla, J. Stability analysis and optimal control of an epidemic model with awareness programs by media. Biosystems 2015, 138, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.; Jiang, D.; Shi, N. The behavior of an SIR epidemic model with stochastic perturbation. Stoch. Anal. Appl. 2012, 30, 755–773. [Google Scholar] [CrossRef]
- Yang, Q.; Jiang, D.; Shi, N.; Ji, C. The ergodicity and extinction of stochastically perturbed SIR and SEIR epidemic models with saturated incidence. J. Math. Anal. Appl. 2012, 388, 248–271. [Google Scholar] [CrossRef]
- Muroya, Y.; Enatsu, Y.; Nakata, Y. Global stability of a delayed SIRS epidemic model with a non-monotonic incidence rate. J. Math. Anal. Appl. 2011, 377, 1–14. [Google Scholar] [CrossRef]
- Toshikazu, K.; Yoshiaki, M. Global stability of a multi-group SIS epidemic model with varying total population size. Appl. Math. Comput. 2015, 265, 785–798. [Google Scholar]
- Muroya, Y.; Kuniya, T.; Wang, J. Stability analysis of a delayed multi-group SIS epidemic model with nonlinear incidence rates and patch structure. J. Math. Anal. Appl. 2015, 425, 415–439. [Google Scholar] [CrossRef]
- Muroya, Y.; Li, H.; Kuniya, T. Complete global analysis of an SIRS epidemic model with graded cure and incomplete recovery rates. J. Math. Anal. Appl. 2014, 410, 719–732. [Google Scholar] [CrossRef]
- Wang, W.J.; Xiao, Y.; Cheke, R.A. Modelling the effects of contaminated environments on HFMD infections in mainland China. Biosystems 2016, 140, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Elaiw, A.M.; Alade, S.M.; Alsulami, T.O. Global Stability of within-host Virus Dynamics Models with Multitarget Cells. Mathematics 2018, 6, 118. [Google Scholar] [CrossRef]
- Tennenbaum, S.; Freitag, C.; Roudenko, S. Modeling the Influence of Environment and Intervention on Cholera in Haiti. Mathematics 2014, 2, 136–171. [Google Scholar] [CrossRef]
- Erhardt, A.H. Bifurcation Analysis of a Certain Hodgkin-Huxley Model Depending on Multiple Bifurcation Parameters. Mathematics 2018, 6, 103. [Google Scholar] [CrossRef]
- Kuniya, T. Stability Analysis of an Age-Structured SIR Epidemic Model with a Reduction Method to ODEs. Mathematics 2018, 6, 147. [Google Scholar] [CrossRef]
- Hategekimana, F.; Saha, S.; Chaturvedi, A. Dynamics of Amoebiasis Transmission: Stability and Sensitivity Analysis. Mathematics 2017, 5, 58. [Google Scholar] [CrossRef]
- Mishra, B.K.; Jha, N. SEIQRS model for the transmission of malicious objects in computer network. Appl. Math. Model. 2010, 34, 710–715. [Google Scholar] [CrossRef]
- Cesar, M.S. A nonautonomous epidemic model with general incidence and isolation. Math. Methods Appl. Sci. 2014, 37, 1974–1991. [Google Scholar]
- Yan, X.; Zou, Y. Optimal and sub-optimal quarantine and isolation control in SARS epidemics. Math. Comput. Model. 2008, 47, 235–245. [Google Scholar] [CrossRef]
- Tan, X.X.; Li, S.J.; Dai, Q.W.; Gang, J.T. An epidemic model with isolated intervention based on cellular automata. Adv. Mater. Res. 2014, 926, 1065–1068. [Google Scholar] [CrossRef]
- Li, J.; Ma, Z.; Zhou, Y. Global analysis of SIS epidemic model with a simple vaccination and multiple endemic equilibria. Acta Math. Sci. 2006, 26, 83–93. [Google Scholar] [CrossRef]
- Liu, X.; Takeuchi, Y.; Iwami, S. SVIR epidemic models with vaccination strategies. J. Theor. Biol. 2008, 253, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Trawicki, M.B. Deterministic Seirs Epidemic Model for Modeling Vital Dynamics, Vaccinations, and Temporary Immunity. Mathematics 2017, 5, 7. [Google Scholar] [CrossRef]
- Chauhan, S.; Misra, O.P.; Dhar, J. Stability Analysis of SIR Model with Vaccination. Am. J. Comput. Appl. Math. 2014, 4, 17–23. [Google Scholar]
- Kar, T.; Batabyal, A. Stability analysis and optimal control of an SIR epidemic model with vaccination. Biosystems 2011, 104, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Wang, B.; Guo, S. Stability analysis of a novel epidemics model with vaccination and nonlinear infectious rate. Appl. Math. Comput. 2013, 221, 786–801. [Google Scholar] [CrossRef]
- Lahrouz, A.; Omari, L.; Kiouach, D.; Belmaati, A. Complete global stability for an SIRS epidemic model with generalized non-linear incidence and vaccination. Appl. Math. Comput. 2012, 218, 6519–6525. [Google Scholar] [CrossRef]
- Sun, C.; Yang, W. Global results for an SIRS model with vaccination and isolation. Nonlinear Anal. Real World Appl. 2010, 11, 4223–4237. [Google Scholar] [CrossRef]
- Eckalbar, J.C.; Eckalbar, W.L. Dynamics of an SIR model with vaccination dependent on past prevalence with high-order distributed delay. Biosystems 2015, 129, 50–65. [Google Scholar] [CrossRef]
- LaSalle, J.P. Stability theory of ordinary differential equations. J. Differ. Equ. 1968, 4, 57–65. [Google Scholar] [CrossRef]
- LaSalle, J.P. The Stability of Dynamical Systems; SIAM: Philadephia, PE, USA, 1976; p. 457. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Liu, J.-B.; Li, H. Global Dynamics of an SIQR Model with Vaccination and Elimination Hybrid Strategies. Mathematics 2018, 6, 328. https://doi.org/10.3390/math6120328
Ma Y, Liu J-B, Li H. Global Dynamics of an SIQR Model with Vaccination and Elimination Hybrid Strategies. Mathematics. 2018; 6(12):328. https://doi.org/10.3390/math6120328
Chicago/Turabian StyleMa, Yanli, Jia-Bao Liu, and Haixia Li. 2018. "Global Dynamics of an SIQR Model with Vaccination and Elimination Hybrid Strategies" Mathematics 6, no. 12: 328. https://doi.org/10.3390/math6120328
APA StyleMa, Y., Liu, J.-B., & Li, H. (2018). Global Dynamics of an SIQR Model with Vaccination and Elimination Hybrid Strategies. Mathematics, 6(12), 328. https://doi.org/10.3390/math6120328





