Symmetric Radial Basis Function Method for Simulation of Elliptic Partial Differential Equations
Abstract
1. Introduction
2. Governing Equations
3. Numerical Scheme
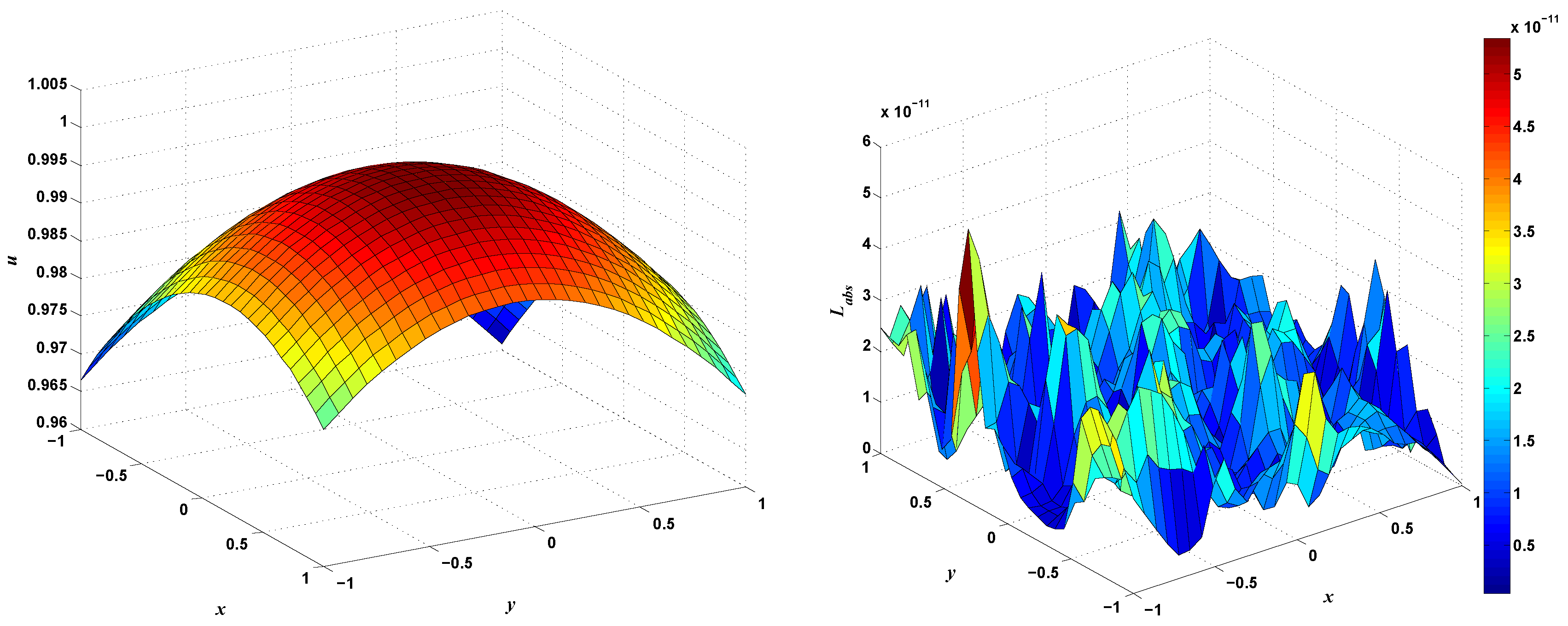
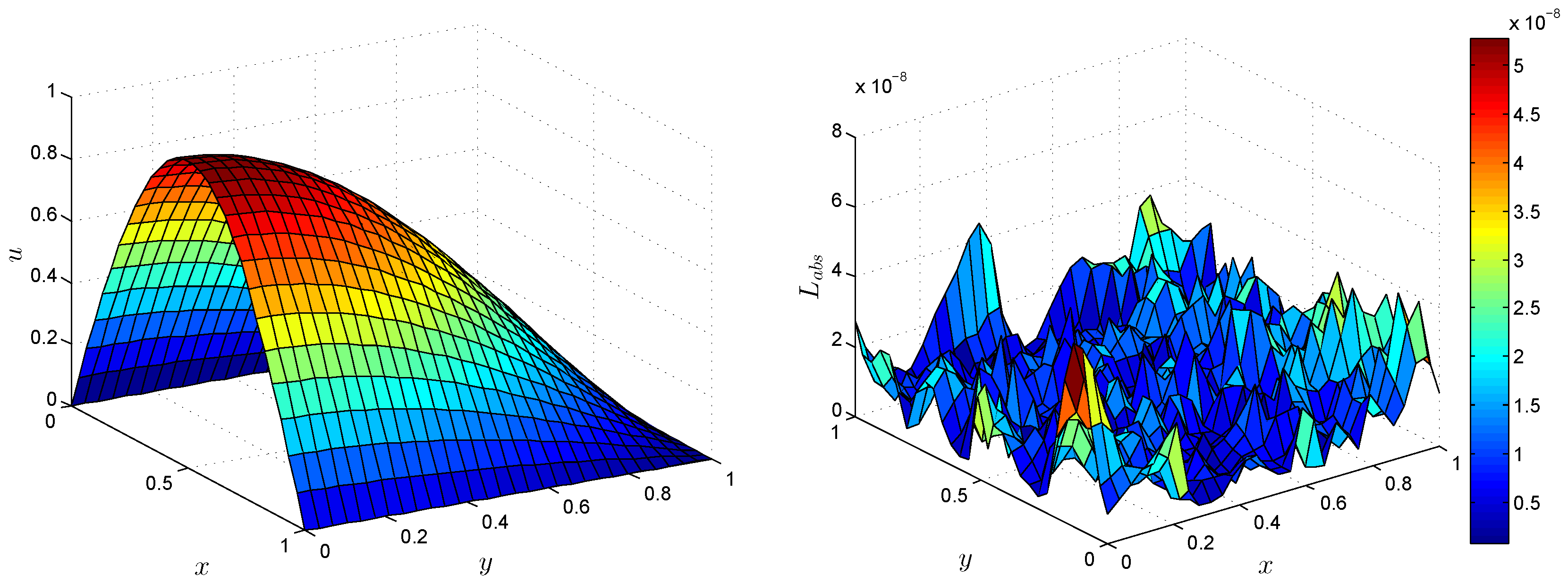
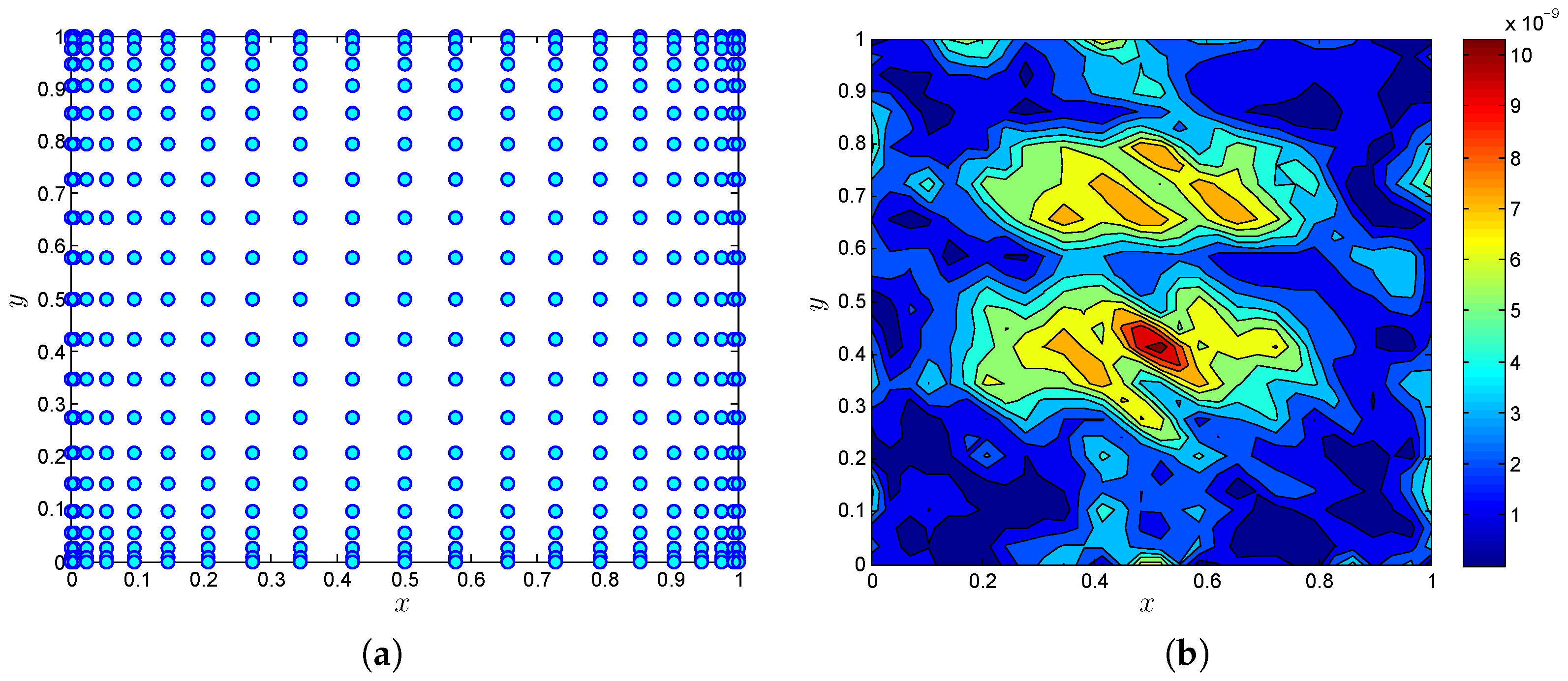
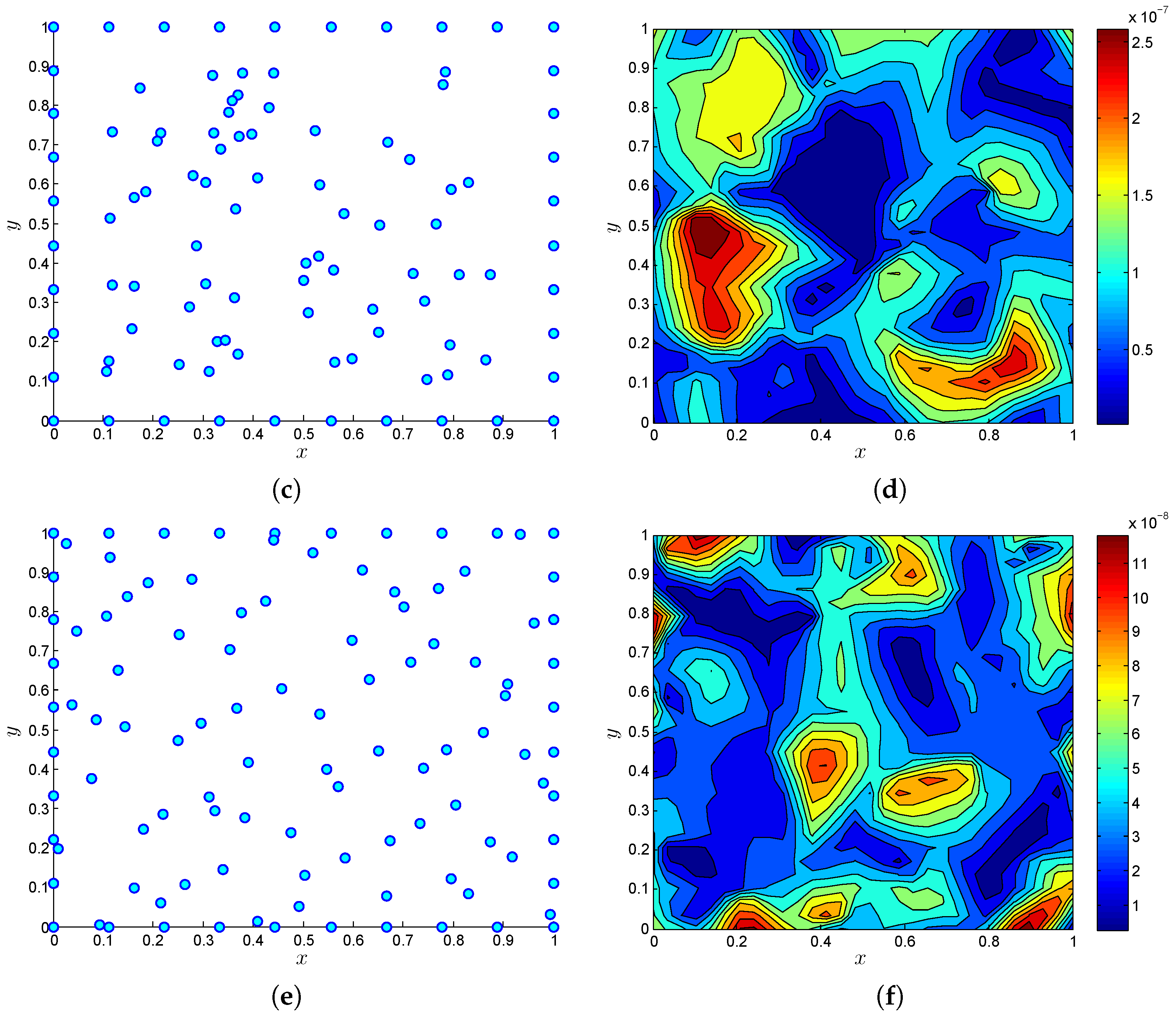
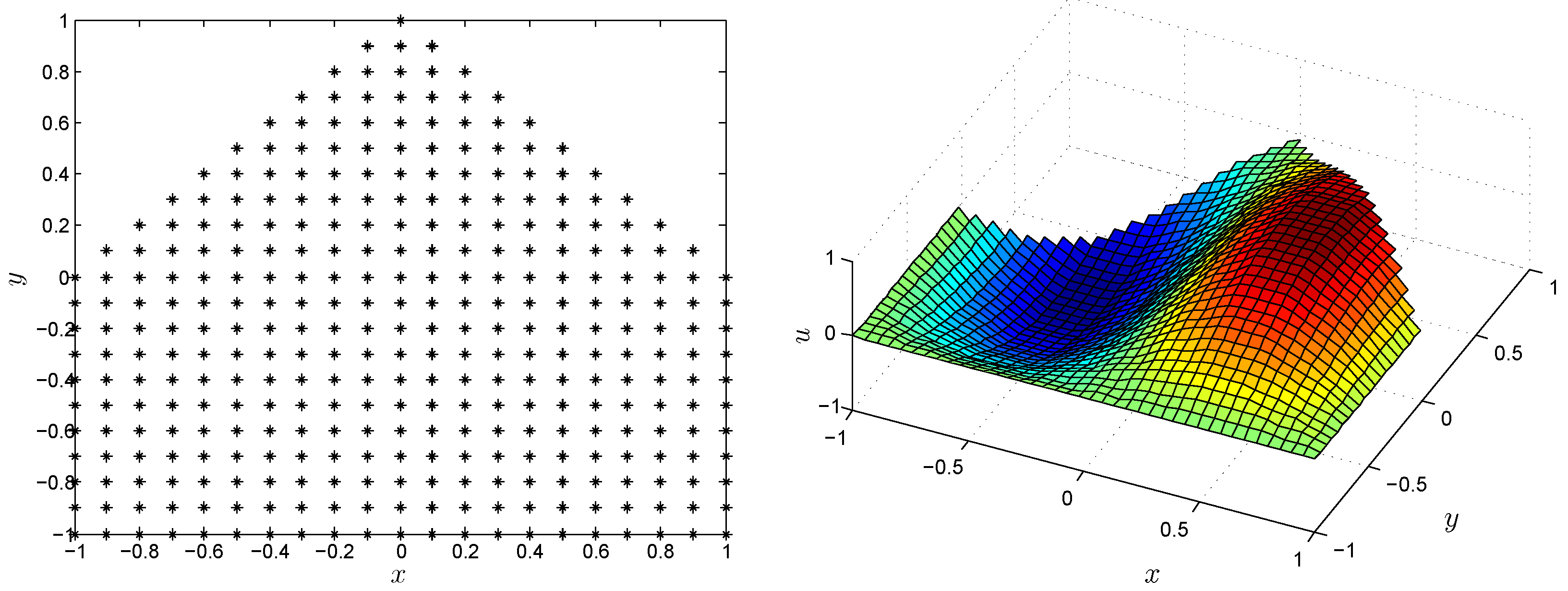
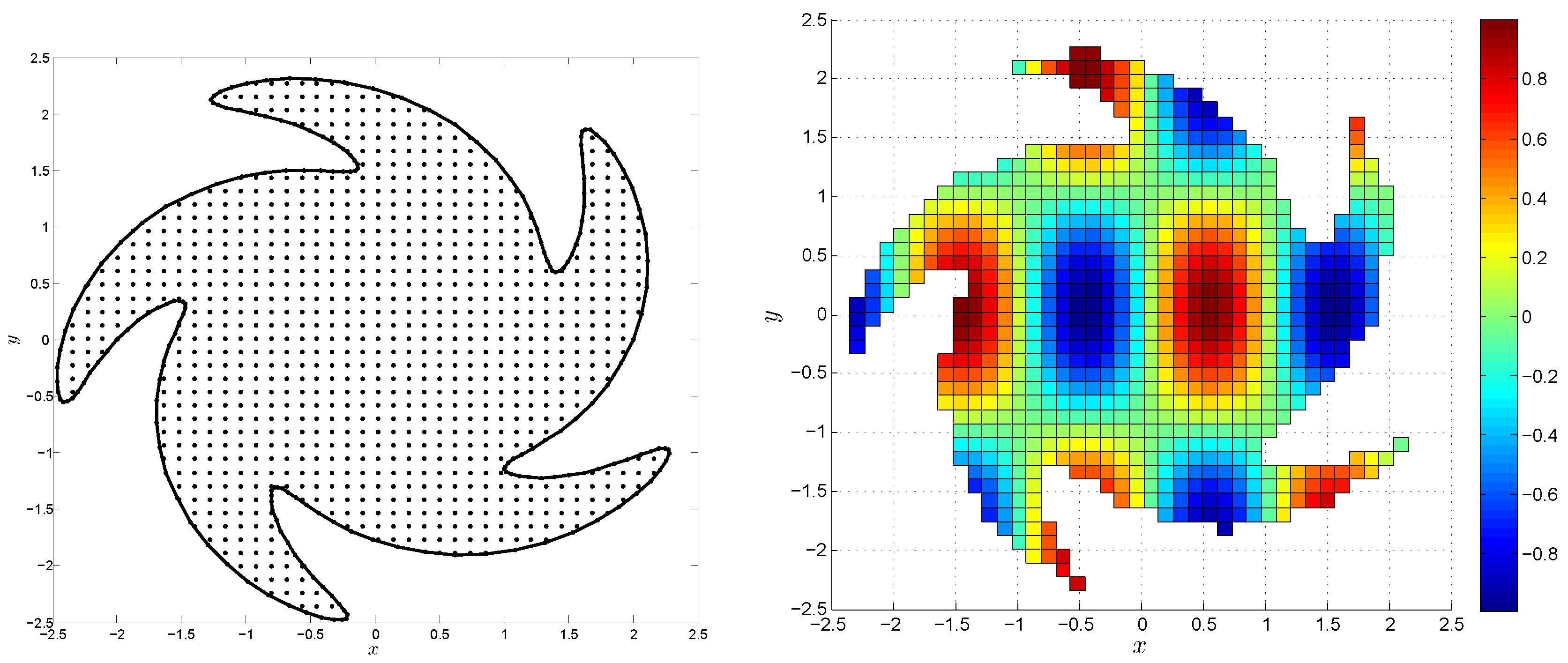
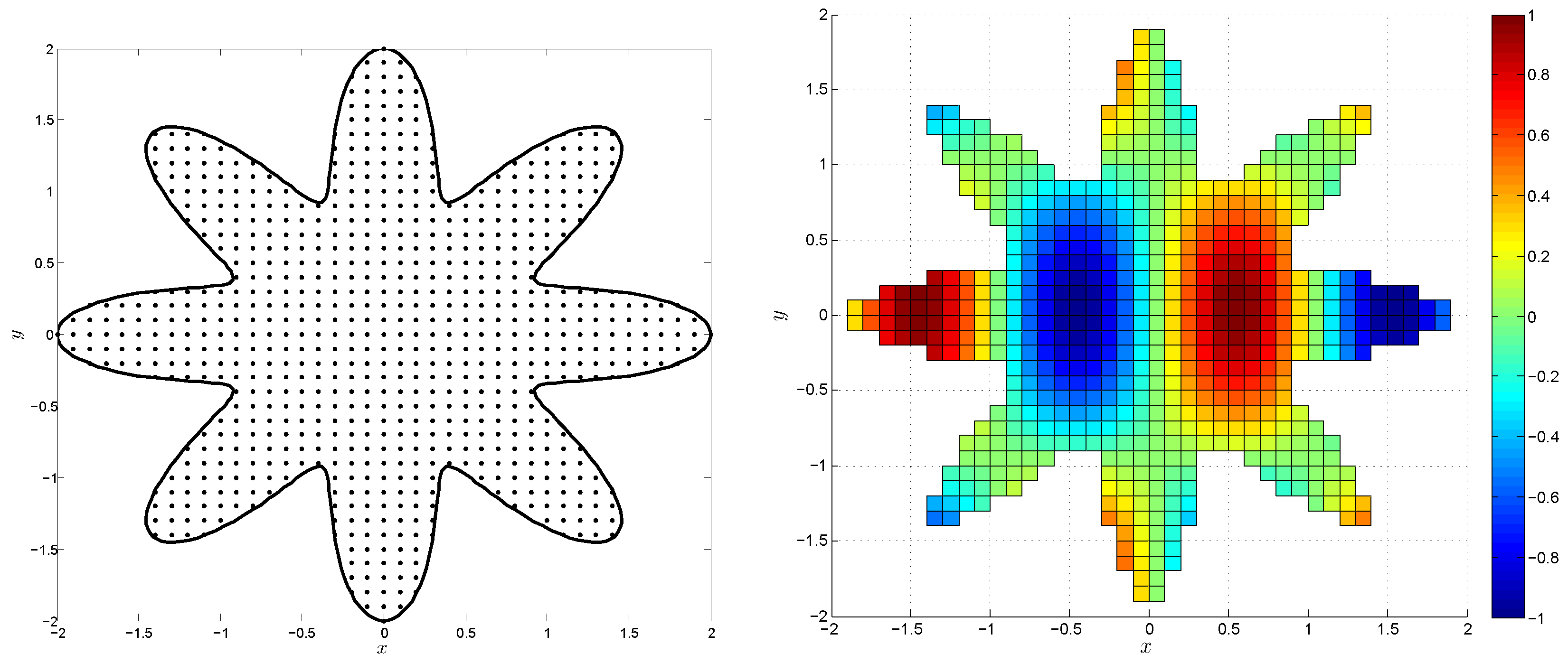
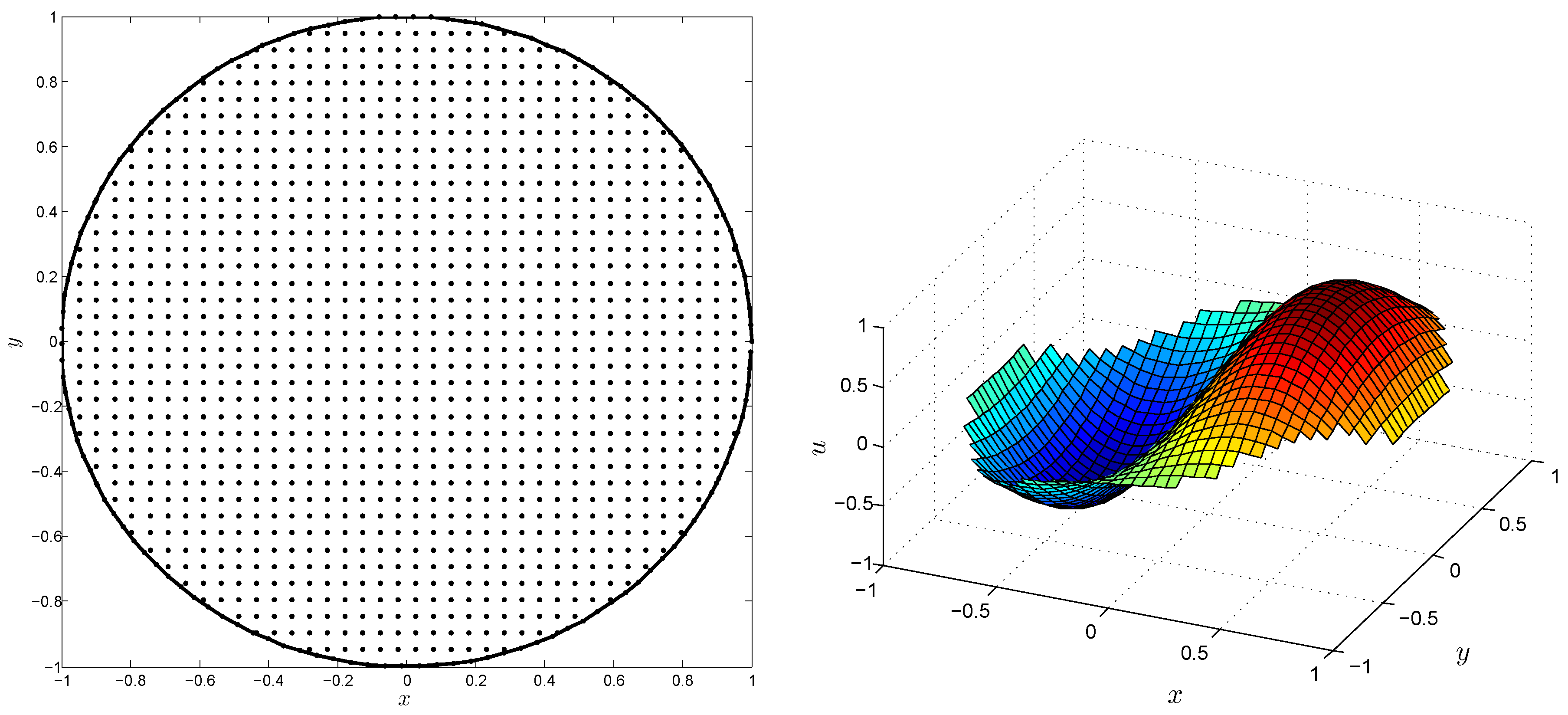
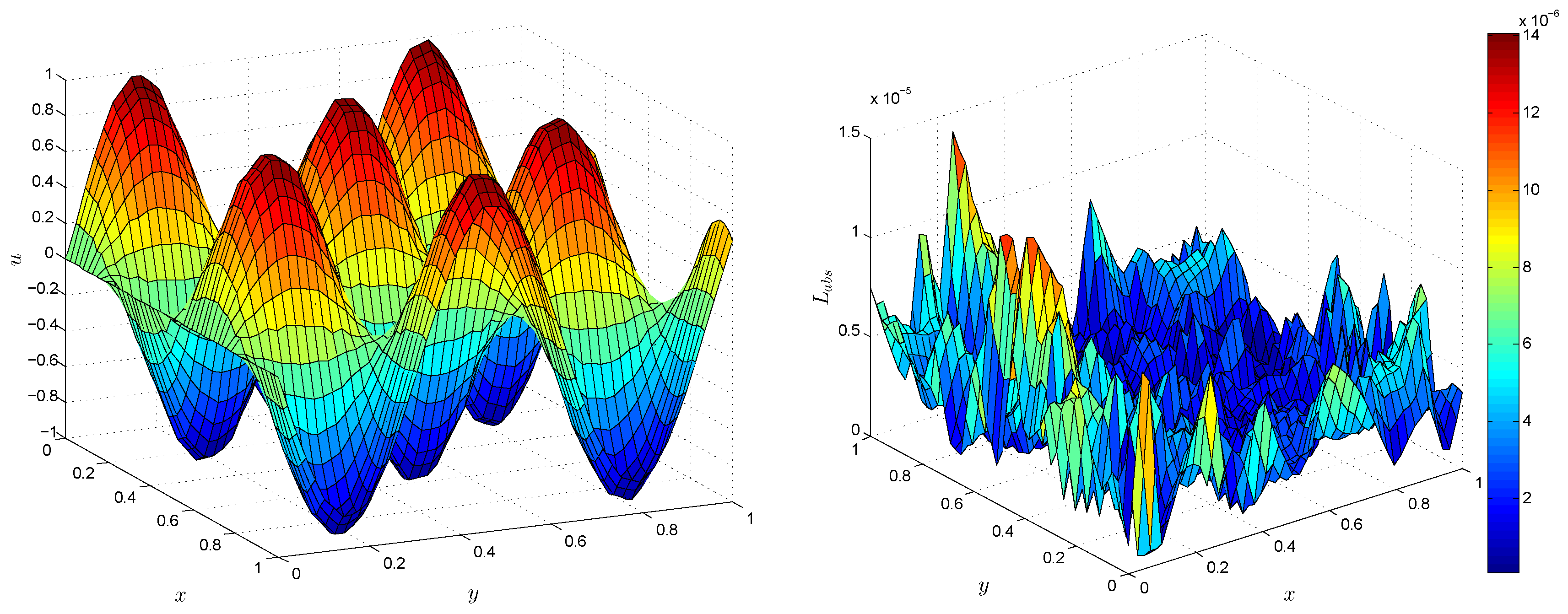
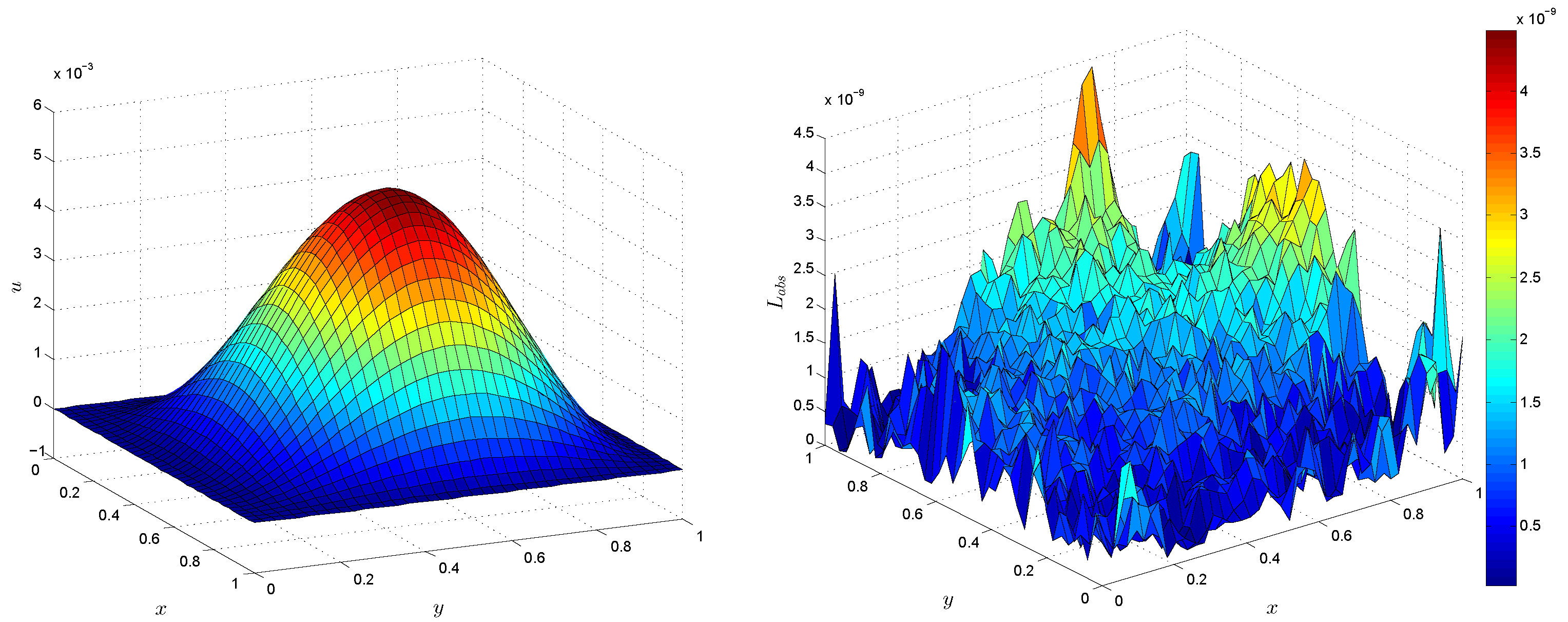
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Graeme, F.; Andreas, K.; Jon, M. Compact optimal quadratic spline collocation methods for the Helmholtz equation. J. Comput. Phys. 2011, 230, 2880–2895. [Google Scholar]
- Ali, A.A.; Bernard, B. Modified nodal cubic spline collocation for Poisson’s equation. SIAM J. Numer. Anal. 2008, 46, 397–418. [Google Scholar]
- Philippe, C. The Finite Element Method for Elliptic Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Britt, S.; Semyon, T.; Eli, T. A compact fourth order scheme for the Helmholtz equation in polar coordinates. J. Sci. Comput. 2010, 45, 26–47. [Google Scholar] [CrossRef]
- Ronald, B. Families of high order accurate discretizations of some elliptic problems. SIAM J. Sci. Stat. Comput. 1981, 2, 268–284. [Google Scholar]
- Romina, G.; Renato, S. Comparing Shannon to autocorrelation-based wavelets for solving singularly perturbed elliptic BV problems. BIT Numer. Math. 2012, 52, 21–43. [Google Scholar]
- Fasshauer, G.E. Meshfree Approximation Methods with MATLAB; World Scientific: Singapore, 2007; Volume 6. [Google Scholar]
- Nam, M.; Thanh, T. An integrated-RBF technique based on Galerkin formulation for elliptic differential equations. Eng. Anal. Bound. Elem. 2009, 33, 191–199. [Google Scholar]
- Khan, W.; Ullah, B. Analysis of meshless weak and strong formulations for boundary value problems. Eng. Anal. Bound. Elem. 2017, 80, 1–17. [Google Scholar] [CrossRef]
- Siraj-ul-Islam; Ahmad, I. A comparative analysis of local meshless formulation for multi-asset option models. Eng. Anal. Bound. Elem. 2016, 65, 159–176. [Google Scholar] [CrossRef]
- Ahmad, I. Local meshless method for PDEs arising from models of wound healing. Appl. Math. Model. 2017, 48, 688–710. [Google Scholar]
- Aziz, I.; Ahmad, M. Numerical solution of two-dimensional elliptic PDEs with nonlocal boundary conditions. Comput. Math. Appl. 2015, 69, 180–205. [Google Scholar]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—I surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Leevan, L.; Roland, O.; Robert, S. Results on meshless collocation techniques. Eng. Anal. Bound. Elem. 2006, 30, 247–253. [Google Scholar]
- Damian, B.; Leevan, L.; Kansa, E.; Jermy, L. On approximate cardinal preconditioning methods for solving PDEs with radial basis functions. Eng. Anal. Bound. Elem. 2005, 29, 343–353. [Google Scholar]
- Fasshauer, G.E. Solving partial differential equations by collocation with radial basis functions. In Surface Fitting and Multiresolution Methods, 1st ed.; Vanderbilt University Press: Nashville, TN, USA, 1997; pp. 1–8. [Google Scholar]
- Wu, Z. Hermite-Birkhoff interpolation of scattered data by radial basis functions. Approx. Theory Its Appl. 1992, 8, 1–10. [Google Scholar]
- Robert, S. Multivariate interpolation and approximation by translates of a basis function. Ser. Approx. Decompos. 1995, 6, 491–514. [Google Scholar]
- Bartur, J.; Sia, A.; Ke, C. The Hermite collocation method using radial basis functions. Eng. Anal. Bound. Elem. 2000, 24, 607–611. [Google Scholar]
- Rocca, L.; Hernandez, R.A.; Power, H. Radial basis function Hermite collocation approach for the solution of time dependent convection–diffusion problems. Eng. Anal. Bound. Elem. 2005, 29, 359–370. [Google Scholar] [CrossRef]
- David, S.; Power, H.; Michael, L.; Herve, M. A meshless solution technique for the solution of 3D unsaturated zone problems, based on local Hermitian interpolation with radial basis functions. Transp. Porous Media 2009, 79, 149–169. [Google Scholar]
- David, S.; Power, H.; Herve, M. An order-N complexity meshless algorithm for transport-type PDEs, based on local Hermitian interpolation. Eng. Anal. Bound. Elem. 2009, 33, 425–441. [Google Scholar]
- Scott, S.; Kansa, E.J. Multiquadric radial basis function approximation methods for the numerical solution of partial differential equations. Adv. Comput. Mech. 2009, 2, 1–206. [Google Scholar]
- Aziz, I.; Šarler, B. Wavelets collocation methods for the numerical solution of elliptic Boundary Value problems. Appl. Math. Model. 2013, 37, 676–694. [Google Scholar] [CrossRef]
- Alemayehu, S.; Chand, M.R. An efficient direct method to solve the three dimensional Poisson’s equation. Am. J. Comput. Math. 2011, 1, 285. [Google Scholar]
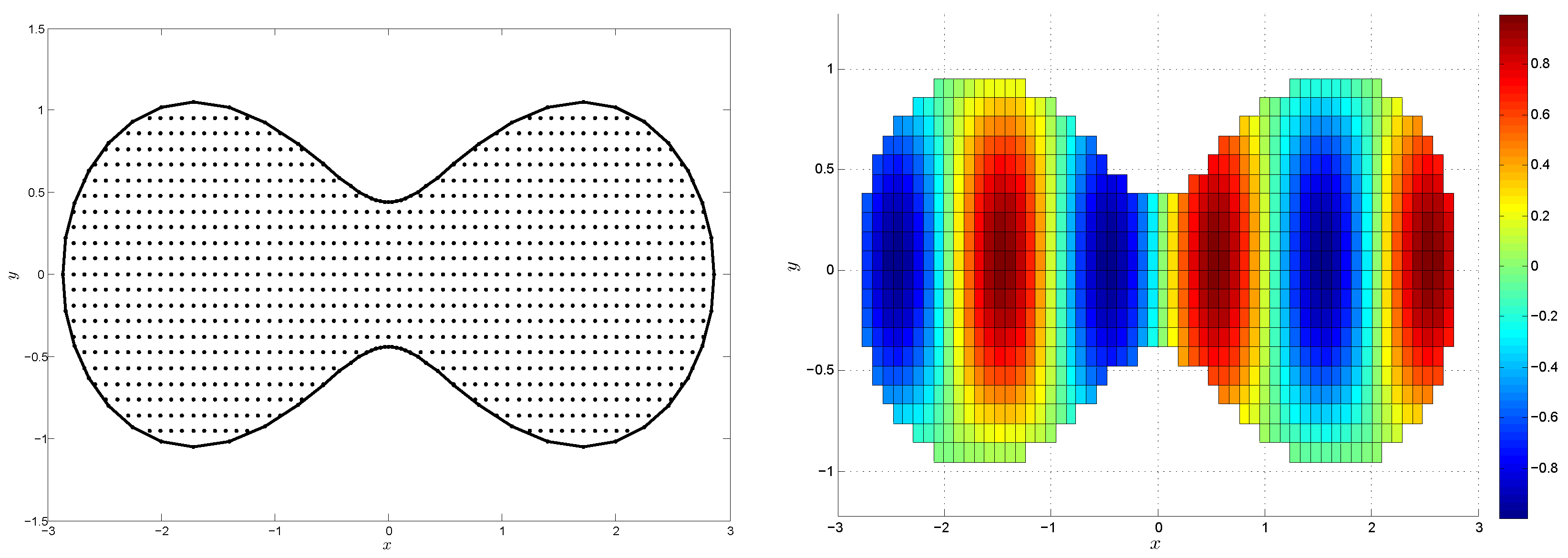
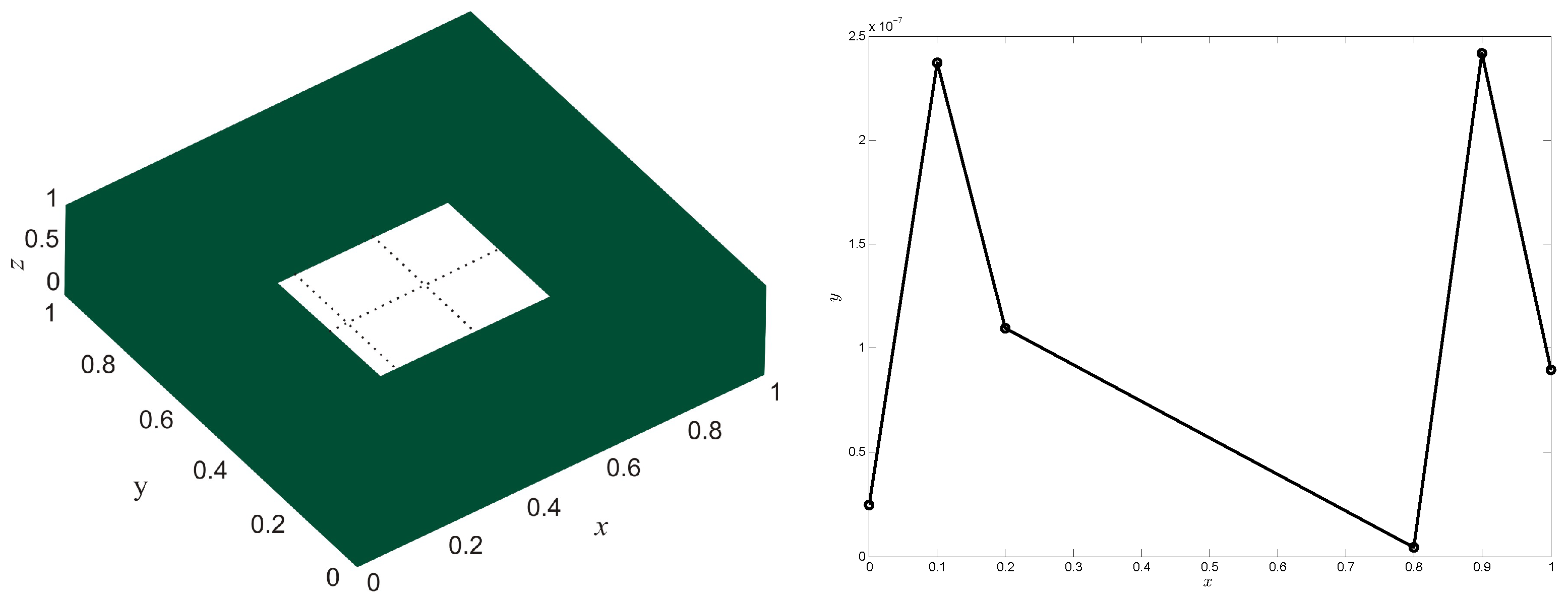
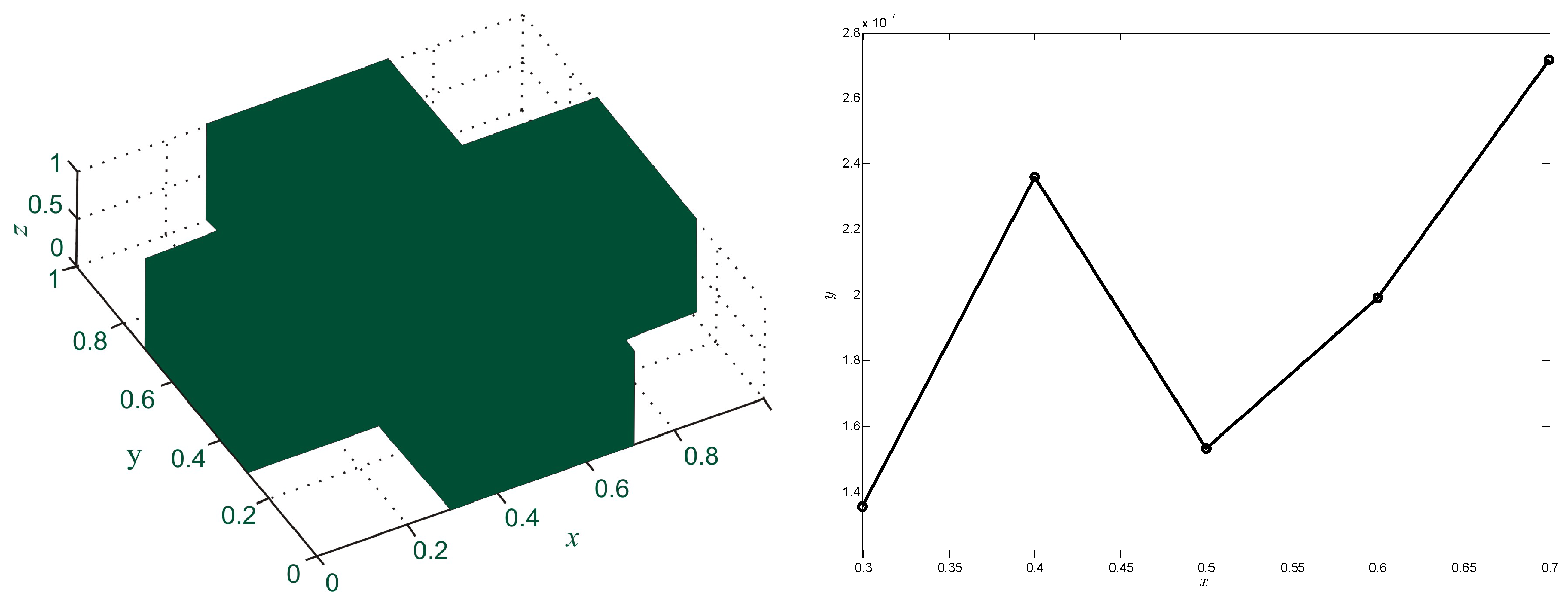
| N | c | RMS | |
|---|---|---|---|
| 81 | 0.124 | ||
| 256 | 0.125 | ||
| 400 | 0.125 | ||
| 900 | 0.129 | ||
| 1600 | 0.126 | ||
| 2500 | 0.126 |
| N | c | RMS | |
|---|---|---|---|
| 81 | 0.406 | ||
| 256 | 0.52 | ||
| 400 | 0.96 | ||
| 900 | 1.67 | ||
| 1600 | 2.15 | ||
| 2500 | 2.52 |
| t | N | c | RMS | |
|---|---|---|---|---|
| 1 | 81 | 0.3 | ||
| 400 | 0.8 | |||
| 900 | 1.59 | |||
| 5 | 81 | 0.43 | ||
| 400 | 1.1 | |||
| 900 | 1.69 | |||
| 10 | 81 | 1.15 | ||
| 400 | 1.22 | |||
| 900 | 1.93 | |||
| 20 | 81 | 4.13 | ||
| 400 | 1.97 | |||
| 900 | 2.22 |
| N | c | RMS | |
|---|---|---|---|
| 81 | 0.73 | ||
| 256 | 0.9 | ||
| 400 | 1.31 | ||
| 900 | 2.02 | ||
| 1600 | 2.42 | ||
| 2500 | 2.92 |
| N | c | RMS | |
|---|---|---|---|
| 343 | 0.06 | ||
| 1331 | 0.06 | ||
| 3375 | 0.06 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thounthong, P.; Khan, M.N.; Hussain, I.; Ahmad, I.; Kumam, P. Symmetric Radial Basis Function Method for Simulation of Elliptic Partial Differential Equations. Mathematics 2018, 6, 327. https://doi.org/10.3390/math6120327
Thounthong P, Khan MN, Hussain I, Ahmad I, Kumam P. Symmetric Radial Basis Function Method for Simulation of Elliptic Partial Differential Equations. Mathematics. 2018; 6(12):327. https://doi.org/10.3390/math6120327
Chicago/Turabian StyleThounthong, Phatiphat, Muhammad Nawaz Khan, Iltaf Hussain, Imtiaz Ahmad, and Poom Kumam. 2018. "Symmetric Radial Basis Function Method for Simulation of Elliptic Partial Differential Equations" Mathematics 6, no. 12: 327. https://doi.org/10.3390/math6120327
APA StyleThounthong, P., Khan, M. N., Hussain, I., Ahmad, I., & Kumam, P. (2018). Symmetric Radial Basis Function Method for Simulation of Elliptic Partial Differential Equations. Mathematics, 6(12), 327. https://doi.org/10.3390/math6120327







