A Meshless Method for Burgers’ Equation Using Multiquadric Radial Basis Functions With a Lie-Group Integrator
Abstract
:1. Introduction
2. Numerical Scheme
2.1. The Multiquadric Radial Basis Approximation
2.2. Lie-Group Method
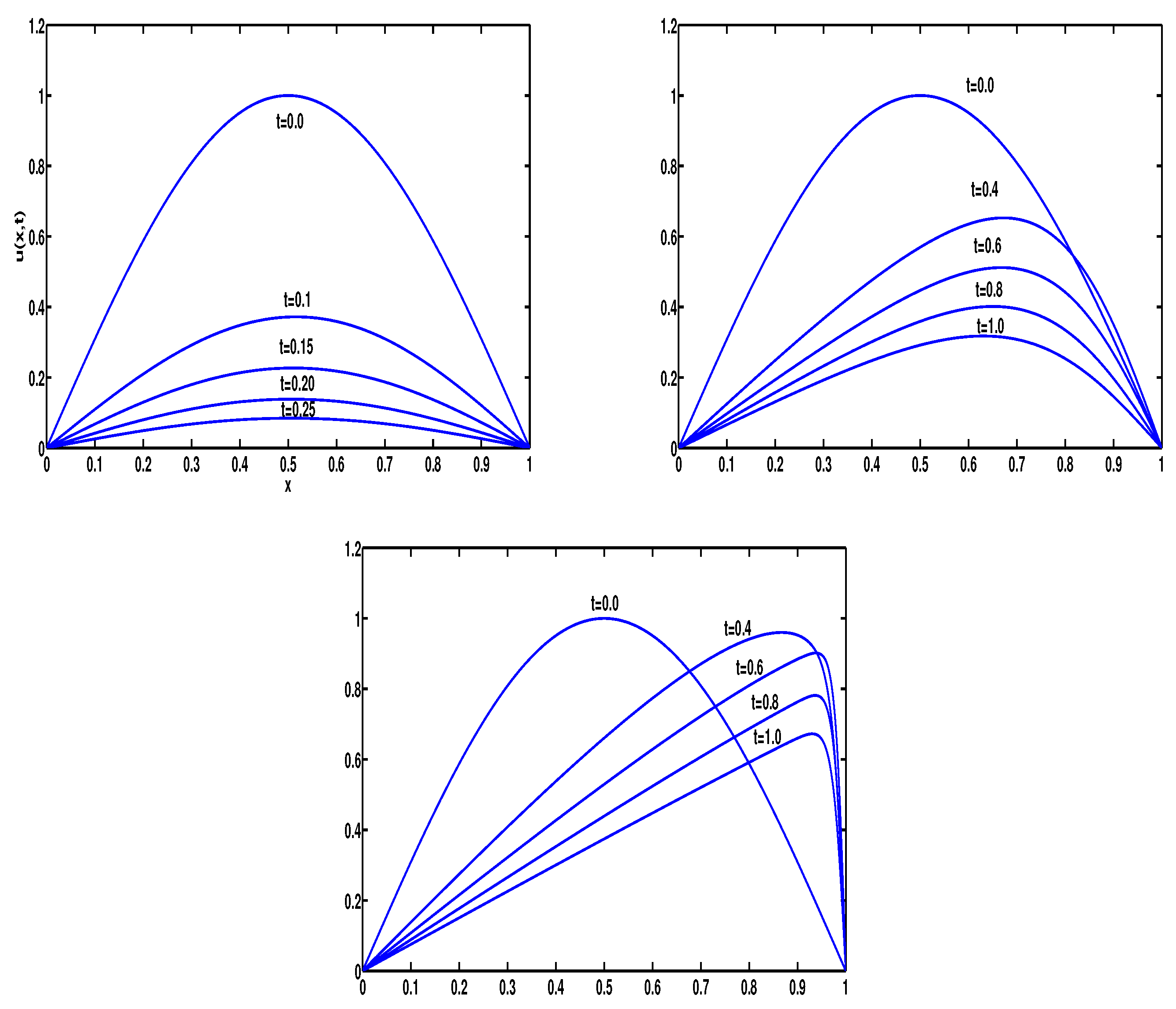
3. Numerical Results
4. Conclusions
Funding
Conflicts of Interest
References
- Bateman, H. Some recent researches on the motion of fluids. Mon. Weather Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Burger, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Math. 1948, 1, 171–199. [Google Scholar] [CrossRef]
- Cole, J.D. On a quasi-linear parabolic equation in aerodynamics. Q. Appl. Math. 1948, 9, 225–236. [Google Scholar] [CrossRef]
- Hopf, E. The partial differential equation ut + uux = μuxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Bonkile, M.P.; Awasthi, A.; Lakshmi, C.; Mukundan, V.; Aswin, V.S. A systematic literature review of Burgers’ equation with recent advances. Pramana 2018, 90, 69. [Google Scholar] [CrossRef]
- Caldwell, J.; Smith, P. Solution of Burgers’ equation with a large Reynolds numbe. Appl. Math. Model. 1982, 6, 381–385. [Google Scholar] [CrossRef]
- Kutluay, S.; Bahadir, A.R.; Ozdes, A. Numerical solution of one-dimensional Burgers’ equation: Explicit and exact-explicit finite difference methods. J. Comput. Appl. Math. 1999, 103, 251–261. [Google Scholar] [CrossRef]
- Acedo, L. On the gravitational instability of a set of random walkers. Europhys. Lett. 2006, 73, 698–704. [Google Scholar] [CrossRef]
- Jiwari, R.; Mittal, R.C.; Sharma, K.K. A umerical scheme based on weighted average differential quadrature method for the numerical solution of Burgers’ equation. Appl. Math. Comput. 2013, 219, 6680–6691. [Google Scholar] [CrossRef]
- Cordero, A.; Franques, A.; Torregrosa, J.R. Numerical solution of turbulence problems by solving Burgers’ equation. Algorithms 2015, 8, 224–233. [Google Scholar] [CrossRef]
- Jiwari, R. A hybrid numerical scheme for the numerical solution of the Burgers’ equation. Comput. Phys. Commun. 2015, 188, 59–67. [Google Scholar] [CrossRef]
- Chen, R.; Wu, Z. Applying multiquadric quasi-interpolation to solve Burgers’ equation. Appl. Math. Comput. 2006, 172, 472–484. [Google Scholar] [CrossRef]
- Haq, S.; Hussain, A.; Uddin, M. On the numerical solution of nonlinear Burgers’-type equations using meshless method of lines. Appl. Math. Comput. 2012, 218, 6280–6290. [Google Scholar] [CrossRef]
- Xie, H.; Li, D.; Li, F. A new Numerical Method of Particular Solutions for Inhomogeneous Burgers’ equation. Math. Prob. Eng. 2013. [Google Scholar] [CrossRef]
- Sarboland, M.; Aminataei, A. On the Numerical Solution of One-Dimensional Nonlinear Nonhomogeneous Burgers’ Equation. J. Appl. Math. 2014. [Google Scholar] [CrossRef]
- Fan, C.M.; Yang, C.H.; Gu, M.H. Applications of the local RBF collocation method and the fictitious time integration method for Burgers’ equations. Procedia Eng. 2014, 79, 569–574. [Google Scholar] [CrossRef]
- Bouhamidi, A.; Hached, M.; Jbilou, K. A meshless RBF method for computing a numerical solution of unsteady Burgers’-type equations. Comput. Math. Appl. 2014, 68, 238–256. [Google Scholar] [CrossRef]
- Xie, H.; Zhou, J.; Jiang, Z.; Guo, X. Approximations for Burgers’ equations with C-N scheme and RBF collocation methods. J. Nonlinear Sci. Appl. 2016, 9, 3727–3734. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer: Berlin, Germany, 2006. [Google Scholar]
- Blanes, S.; Casas, F. A Concise Introduction to Geometric Numerical Integration; CRC Press: New York, NY, USA, 2016. [Google Scholar]
- Iserles, A.; Munthe-Kaas, H.Z.; Norsett, S.P.; Zanna, A. Lie-group methods. Acta Numer. 2000, 9, 215–365. [Google Scholar] [CrossRef]
- Liu, C.S. A Group Preserving Scheme for Burgers Equation with Very Large Reynolds Number. CMES 2006, 12, 197–211. [Google Scholar]
- Liu, C.S. An Efficient Backward Group Preserving Scheme for the Backward in Time Burgers’ Equation. CMES 2006, 12, 5565. [Google Scholar]
- Hajiketabi, M.; Abbasbandy, S. The combination of meshless method based on radial basis functions with a geometric numerical integration method for solving partial differential equations: Application to the heat equation. Eng. Anal. Bound. Elem. 2018, 87, 36–46. [Google Scholar] [CrossRef]
- Hajiketabi, M.; Abbasbandy, S.; Casas, F. The Lie-group method based on radial basis functions for solving nonlinear high dimensional generalized Benjamin-Bona-Mahony-Burgers equation in arbitrary domains. Appl. Math. Comput. 2018, 321, 223–243. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid dynamics—I surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Liu, C.S. Cone of non-linear dynamical system and group preserving schemes. Int. J. Nonlinear Mech. 2001, 36, 1047–1068. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Bau, D., III. Numerical Linear Algebra; Siam: Philadelphia, PA, USA, 1997. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; Siam: Philadelphia, PA, USA, 2000. [Google Scholar]
- Öziş, T.; Aksan, E.N.; Özdeş, A. A finite element approach for solution of Burgers’ equation. Appl. Math. Comput. 2003, 139, 417–428. [Google Scholar] [CrossRef]
- Mukundan, V.; Awasthi, A. Efficient numerical techniques for Burgers’ equation. Appl. Math. Comput. 2015, 262, 282–297. [Google Scholar] [CrossRef]
| x | t | Galerkin [22] | GPS [22] | LG-RBFs | Exact |
|---|---|---|---|---|---|
| 0.25 | 0.10 | 0.25469 | 0.25376 | 0.25364 | 0.25364 |
| 0.15 | 0.15672 | 0.15672 | 0.15660 | 0.15660 | |
| 0.20 | 0.09619 | 0.09654 | 0.09644 | 0.09644 | |
| 0.25 | 0.05924 | 0.05929 | 0.05922 | 0.05922 | |
| 0.50 | 0.10 | 0.37134 | 0.37177 | 0.37157 | 0.37158 |
| 0.15 | 0.22674 | 0.22700 | 0.22682 | 0.22682 | |
| 0.20 | 0.13829 | 0.13862 | 0.13847 | 0.13847 | |
| 0.25 | 0.08457 | 0.08464 | 0.08454 | 0.08454 | |
| 0.75 | 0.10 | 0.27102 | 0.27273 | 0.27258 | 0.27258 |
| 0.15 | 0.16411 | 0.16450 | 0.16437 | 0.16437 | |
| 0.20 | 0.09929 | 0.09954 | 0.09943 | 0.09944 | |
| 0.25 | 0.06036 | 0.06042 | 0.06035 | 0.06035 |
| x | t | Galerkin [22] | GPS [22] | LG-RBFs | Exact |
|---|---|---|---|---|---|
| 0.25 | 0.4 | 0.31429 | 0.30889 | 0.30864 | 0.30889 |
| 0.6 | 0.24373 | 0.24077 | 0.24061 | 0.24074 | |
| 0.8 | 0.19758 | 0.19573 | 0.19559 | 0.19568 | |
| 1.0 | 0.16391 | 0.16264 | 0.16251 | 0.16256 | |
| 3.0 | 0.02743 | 0.02725 | 0.02720 | 0.02720 | |
| 0.50 | 0.4 | 0.57636 | 0.56988 | 0.56944 | 0.56963 |
| 0.6 | 0.45169 | 0.44745 | 0.44707 | 0.44721 | |
| 0.8 | 0.36245 | 0.35948 | 0.35914 | 0.35924 | |
| 1.0 | 0.29437 | 0.29215 | 0.29184 | 0.29192 | |
| 3.0 | 0.04057 | 0.04028 | 0.04020 | 0.04020 | |
| 0.75 | 0.4 | 0.62952 | 0.62605 | 0.62564 | 0.62544 |
| 0.6 | 0.49034 | 0.48778 | 0.48727 | 0.48721 | |
| 0.8 | 0.37713 | 0.37438 | 0.37389 | 0.37392 | |
| 1.0 | 0.29016 | 0.28784 | 0.28741 | 0.28747 | |
| 3.0 | 0.01334 | 0.02983 | 0.02977 | 0.02977 |
| x | t | Exact-Explicit [7] | RK4 [22] | GPS [22] | LG-RBFs | Exact |
|---|---|---|---|---|---|---|
| 0.25 | 0.4 | 0.34164 | 0.34197 | 0.34193 | 0.34189 | 0.34191 |
| 0.6 | 0.26890 | 0.26900 | 0.26897 | 0.26890 | 0.26896 | |
| 0.8 | 0.22150 | 0.22151 | 0.22149 | 0.22140 | 0.22148 | |
| 1.0 | 0.18825 | 0.18821 | 0.18820 | 0.18816 | 0.18819 | |
| 3.0 | 0.07515 | 0.07512 | 0.07511 | 0.07512 | 0.07511 | |
| 0.50 | 0.4 | 0.65606 | 0.66083 | 0.66079 | 0.66068 | 0.66071 |
| 0.6 | 0.52658 | 0.52950 | 0.52946 | 0.52938 | 0.52942 | |
| 0.8 | 0.43743 | 0.43919 | 0.43916 | 0.43910 | 0.43914 | |
| 1.0 | 0.37336 | 0.37446 | 0.37443 | 0.37439 | 0.37442 | |
| 3.0 | 0.15015 | 0.15019 | 0.15018 | 0.15018 | 0.15018 | |
| 0.75 | 0.4 | 0.90111 | 0.91053 | 0.91058 | 0.91031 | 0.91026 |
| 0.6 | 0.75862 | 0.76741 | 0.76739 | 0.76723 | 0.76724 | |
| 0.8 | 0.64129 | 0.64750 | 0.64747 | 0.64737 | 0.64740 | |
| 1.0 | 0.55187 | 0.55620 | 0.55609 | 0.55603 | 0.55605 | |
| 3.0 | 0.22454 | 0.22484 | 0.22483 | 0.22481 | 0.22481 |
| BDF-1, [32] | 1.8457 × 10 | 2.6102 × 10 | 1.9600 × 10 | 2.7713 × 10 |
| LG-RBFs | 1.1727 × 10 | 1.5587 × 10 | 4.8120 × 10 | 6.7895× 10 |
| BDF-1 [32] | 4.2130 × 10 | 5.9753 × 10 | 3.0024 × 10 | 4.2509 × 10 |
| LG-RBFs | 5.0581 × 10 | 7.1572 × 10 | 3.0291 × 10 | 4.3053 × 10 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seydaoğlu, M. A Meshless Method for Burgers’ Equation Using Multiquadric Radial Basis Functions With a Lie-Group Integrator. Mathematics 2019, 7, 113. https://doi.org/10.3390/math7020113
Seydaoğlu M. A Meshless Method for Burgers’ Equation Using Multiquadric Radial Basis Functions With a Lie-Group Integrator. Mathematics. 2019; 7(2):113. https://doi.org/10.3390/math7020113
Chicago/Turabian StyleSeydaoğlu, Muaz. 2019. "A Meshless Method for Burgers’ Equation Using Multiquadric Radial Basis Functions With a Lie-Group Integrator" Mathematics 7, no. 2: 113. https://doi.org/10.3390/math7020113
APA StyleSeydaoğlu, M. (2019). A Meshless Method for Burgers’ Equation Using Multiquadric Radial Basis Functions With a Lie-Group Integrator. Mathematics, 7(2), 113. https://doi.org/10.3390/math7020113





