Abstract
It is well known that major error occur in the time integration instead of the spatial approximation. In this work, anisotropic kernels are used for temporal as well as spatial approximation to construct a numerical scheme for solving nonlinear Burgers’ equations. The time-dependent PDEs are collocated in both space and time first, contrary to spatial discretization, and time stepping procedures for time integration are then applied. Physically one cannot in general expect that the spatial and temporal features of the solution behaves on the same order. Hence, one should have to incorporate anisotropic kernels. The nonlinear Burgers’ equations are converted by nonlinear transformation to linear equations. The spatial discretizations are carried out to construct differentiation matrices. Comparisons with most available numerical methods are made to solve the Burgers’ equations.
MSC:
65M12; 65M22; 65M70
1. Introduction
Nonlinear partial differential equations can be approximated by various numerical methods such as finite volume methods, finite element methods, meshless methods, boundary element methods, wavelets methods, methods of fundamental solutions, and spectral methods (see [1,2,3,4,5,6,7,8,9] and references therein). In all these approaches, the time derivative is discretized using Runge–Kutta methods, Lie splitting methods, and various explicit and implicit methods. Some work is available in the literature to approximate space derivatives as well as time derivatives. For example, a space–time formulation was developed by Netuzhylov (see [10]); the author used the inverse moving least squares (IMLS) method to solve the problem of moving boundaries. Li and Mao [11] used RBFs on the space–time domain and developed a space–time global RBF method to solve inverse problems. Their resultant system was not square, so they used the least square method to overcome the ill-posedness of the problem. Li’s and Mao’s techniques were further used in the work [12] to solve other inverse problems. Furthermore, in [13], the authors developed a method to estimate river pollution using global space–time RBFs. Various types of space–time formulations can be found in [14,15,16,17,18]. Recently, the authors in the work [19,20] developed efficient space–time methods for solving time-dependent PDEs. In this work, a space–time numerical scheme is constructed using anisotropic kernels to solve nonlinear Burgers’ equations. The time-dependent PDEs are collocated using space–time kernels in both space and time dimensions. We tested our approach to solve 1-D and 2-D Burgers’ equations.
2. Space–Time Kernel-Based Approximation
The time-dependent PDE in the spatial domain , where and for time interval satisfies the equation
along with some well defined initial and boundary conditions. Here, is some spatial operator. The time-dependent problem is seen as the problem in -dimensions. The summarized form of Equation (1) along with the boundary and the initial condition is given by the following:
These give rise to a well-posed problem (since the resulting system is square) that is used to approximate the solution to of our problem. The space–time formulation combines space and time variables so that the functional space on contains the unknown function . The following functional space is incorporated in our work.
where is radial kernel, and is any norm. We have used the Euclidean norm, and points in are centers. The solution at the point is then defined by
The space–time kernel-based method requires the approximated unknown to satisfy equations as well as initial and boundary conditions at all nodes in domain . For simplicity, we take internal nodes, boundary nodes, and initial time nodes. The unknown is used to satisfy the equation by putting Equations (2) and (3). We then have
3. Stability of the Numerical Scheme
To discuss the stability of our numerical scheme expressed in Equation (11), which is given by
where M is differentiation matrix, the stability constant of Equation (12) is defined by
The value is bounded for every discrete norms on . Hence, we have
Similarly, in the case of pseudoinverse of , we obtain
and we thus write
4. Numerical Experiments
To validate the accuracy and robustness of our numerical scheme, we solve a nonlinear Burgers’ equation. The Hopf–Cole transformation [21] is used to transform a nonlinear Burgers’ equation into a heat equation. The solution accuracy greatly depends on the scale factor in the kernel function (for example, see [22,23] and references therein) The space–time method is applied with anisotropic radial kernels, namely anisotropic Matern. To achieve a desirable accuracy, we used two scale factors: one for the time variable and one for the space variable, as involved in the anisotropic kernels.
The anisotropic kernel Matern and its derivative, which has enough smoothness, are defined by
where is the space shape parameter, is the temporal shape parameter, and is a Matlab function. The accuracy of the space–time method is tested in terms of the maximum absolute error (MAE) defined by
where u and are the exact and the approximate solutions, respectively.
4.1. Example 1
We consider a Burgers’ equation defined by
with the following boundary conditions:
and the initial condition
Using the Hopf–Cole transformation [21,24],
The nonlinear Equation (18) is converted into a linear heat equation
with the boundary and initial conditions given by
Hence, the solution u of the heat equation expressed in Equation (22) with conditions expressed in Equations (23) and (24) can be obtained using the space–time method discussed above. The solution to the Burgers’ equation can then be recovered from the transformation expressed in Equation (21). The exact solution to the linearized problem is defined by Equations (22)–(24) [25]:
where the coefficients are defined by
and
Hence, using the Hopf–Cole transformation given by Equation (21), the (exact) Fourier solution to the problem given by Equations (18)–(20) is obtained as
where and are defined by Equations (26) and (27), respectively.
All results are obtained by the space–time meshless method using the anisotropic kernel with two scale factors: one in a time variable and one in a space variable. The results are displayed in Figure 1 and Figure 2 and Table 1, respectively. The results obtained by the space–time kernel-based method are comparable to the exact solution and the results in [25]. The main advantage of the current method is the avoidance of a time stepping procedure that requires a small time step for higher accuracy and stability. On the contrary, here the dimensions of our problem is increased by 1, yet it faces no difficulty, as these kernel-based methods are designed for multi-dimensional domains. The second advantage is that we can apply the method for irregular domains as well.
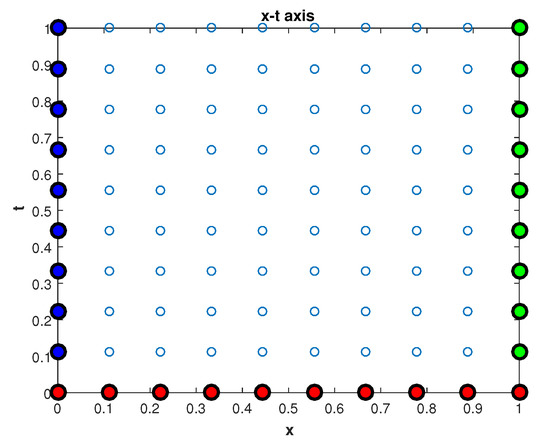
Figure 1.
Distribution of centers in the space–time domain: Initial time centers (red) at ; boundaries centers at (blue) and at (green). Others are internal centers.
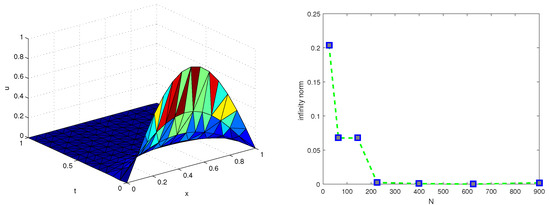
Figure 2.
The first plot shows the approximate solution in the space–time domain, while the second plot shows the error norm versus the nodes in the space–time domain, respectively, corresponding to Example 1.

Table 1.
The space–time method results and the results in [25] at , in the space–time domain , where N denotes the number of collocation points, corresponding to Example 1.
4.2. Example 2
As a second test problem, we considered the Burgers’ Equation in Equation (18) with the exact solution
The initial and boundary conditions can be extracted from the exact solution. The Hopf–Cole transformation converts the Burgers’ equation to the heat equation
with initial condition
The solution to the heat equation for the specified initial condition is given by
where to ensure that for all time. The solution to the Burgers equation can now be easily obtained using the Hopf–Cole transformation
The space–time meshless method is used to solve the test problem given in Equation (2) incorporating anisotropic kernel with two scale factors: one in the time variable and one in the space variable, as shown in Figure 3 and Figure 4 and Table 2, respectively. It is observed that the space–time kernel-based method results are comparable to exact solutions.
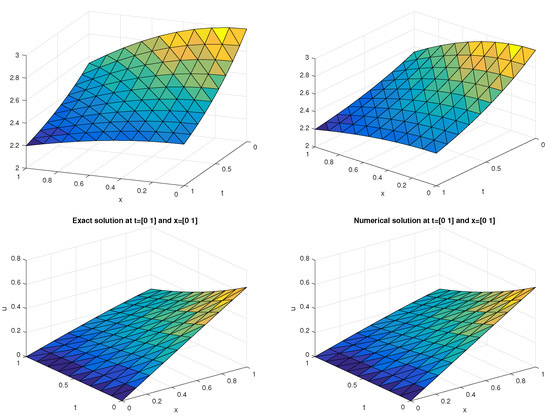
Figure 3.
The first two plots show the solution to heat equations, while the second two plots show the solution to Burgers equation in the space–time domain corresponding to Example 2.
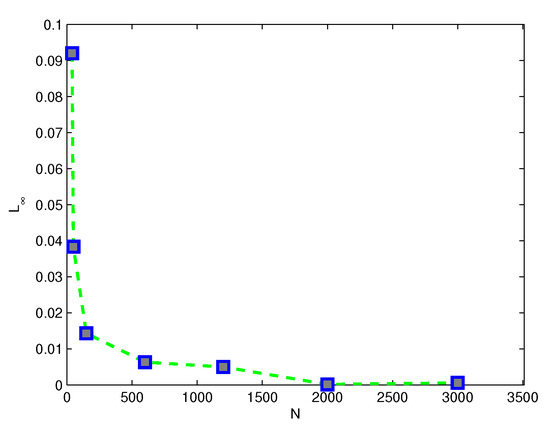
Figure 4.
Error norm versus collocation nodes in the space–time domain corresponding to Example 2.

Table 2.
Numerical results when , , and in the space–time domain , where points in the direction and in the direction denotes the number of collocation points in the space–time domain, corresponding to Example 2.
4.3. Example 3
In the last test example, we consider a 2D Burgers’ equation that can be transformed into the 2D heat equation using Hopf–Cole transformation [26]. We consider the transformed 2D heat equation to validate the space–time kernel-based method for anisotropic kernels:
with initial and boundary conditions defined by
with an exact solution given by
We applied the space–time method to solve a 2D heat equation in the space–time domain . The results are displayed in Figure 5 and Figure 6 and Table 3. Once again we obtained very accurate results with ease and stability. The present method can work in multi-dimensions in irregular domains as well.
Figure 5.
Centers distribution in the space–time domain: initial time centers (red), boundary centers and (yellow), and centers (blue), and interior points (green) corresponding to Example 3.
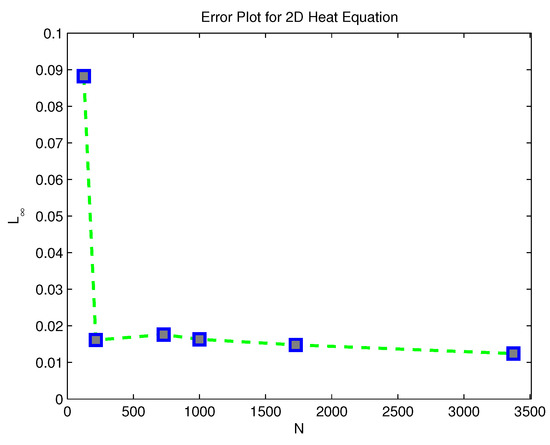
Figure 6.
L error norm versus collocations points N, corresponding to Example 3.

Table 3.
Numerical results corresponding to Example 3, when domain .
4.4. Concluding Remarks
In the present work, we constructed a numerical scheme for Burgers equations. The scheme is based on space–time anisotropic kernels. The time variable is also considered as a space variable, and this increases the space dimension by 1. This space–time method avoids time-integration methods such as -weighted schemes and implicit and explicit numerical schemes. Such methods require a very small time step for stability and higher accuracy. The present numerical scheme reduces the cost of computation by avoiding the need to recompute the matrix for each time level, as contrary to methods such as the RK4 method for evolutionary PDEs.
Author Contributions
Investigation, M.U.; Methodology, H.A.
Funding
This research was funded by Higher Education Commission of Pakistan, grant number 112-25237-2PSI-127, and University of Engineering and Technology Peshawar Pakistan.
Acknowledgments
This work is supported by HEC Pakistan under grant: 112-25237-2PSI-127. We also appreciate the valuable comments and suggestions raised by the reviewers to improve the manuscript.
Conflicts of Interest
The authors declared no conflict of interest.
References
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and Matlab; Springer: Berline Germany, 2016; pp. 3–8. [Google Scholar]
- Sauter, S.A.; Schwab, C. Boundary Element Methods; Springer: Berlin, Germany, 2010; pp. 183–287. [Google Scholar]
- Fasshauer, G.E. Meshfree Approximation Methods with MATLAB; World Scientific: Singapore, 2007; Volume 6. [Google Scholar]
- Cohen, A. Numerical Analysis of Wavelet Methods; Elsevier: Amsterdam, The Netherlands, 2003; Volume 32. [Google Scholar]
- Chen, C.-S.; Karageorghis, A.; Smyrlis, Y.S. The Method of Fundamental Solutions: A Meshless Method; Dynamic Publishers Atlanta: Atlanta, Georgia, 2008. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods; Springer: Berlin, Germany, 2006. [Google Scholar]
- Turchetti, C.; Conti, M.; Crippa, P.; Orcioni, S. On the approximation of stochastic processes by approximate identity neural networks. IEEE Trans. Neural Netw. 1998, 9, 1069–1085. [Google Scholar] [CrossRef] [PubMed]
- Turchetti, C.; Crippa, P.; Pirani, M.; Biagetti, G. Representation of nonlinear random transformations by non-Gaussian stochastic neural networks. IEEE Trans. Neural Netw. 2008, 19, 1033–1060. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.; Kamran, K.; Usman, M.; Ali, A. On the Laplace-transformed-based local meshless method for fractional-order diffusion equation. Int. J. Comput. Methods Eng. Sci. Mech. 2018, 19, 1–5. [Google Scholar] [CrossRef]
- Netuzhylov, H. A Space-Time Meshfree Collocation Method for Coupled Problems on Irregularly-Shaped Domains. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 2008. [Google Scholar]
- Li, Z.; Mao, X. Global multiquadric collocation method for groundwater contaminant source identification. Environ. Model. Softw. 2011, 26, 1611–1621. [Google Scholar] [CrossRef]
- Li, Z.; Mao, X. Global space–time multiquadric method for inverse heat conduction problem. Int. J. Numer. Methods Eng. 2011, 85, 355–379. [Google Scholar] [CrossRef]
- Li, M.; Chen, W.; Chen, C.S. The localized RBFs collocation methods for solving high dimensional PDEs. Eng. Anal. Bound. Elements 2013, 37, 1300–1304. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Sathe, S.; Keedy, R.; Stein, K. Space–time finite element techniques for computation of fluid–structure interactions. Comput. Methods Appl. Mech. Eng. 2006, 195, 2002–2027. [Google Scholar] [CrossRef]
- Klaij, C.M.; van der Vegt, J.J.W.; van der Ven, H. Space–time discontinuous Galerkin method for the compressible Navier–Stokes equations. J. Comput. Phys. 2006, 217, 589–611. [Google Scholar] [CrossRef]
- Sudirham, J.J.; van der Vegt, J.J.W.; van Damme, R.M.J. Space–time discontinuous Galerkin method for advection–diffusion problems on time-dependent domains. Appl. Numer. Math. 2006, 56, 1491–1518. [Google Scholar] [CrossRef]
- Ambati, V.R.; Bokhove, O. Space–time discontinuous Galerkin finite element method for shallow water flows. J. Comput. Appl. Math. 2007, 204, 452–462. [Google Scholar] [CrossRef]
- Young, D.L.; Tsai, C.C.; Murugesan, K.; Fan, C.M.; Chen, C.W. Time-dependent fundamental solutions for homogeneous diffusion problems. Eng. Anal. Bound. Elements 2004, 28, 1463–1473. [Google Scholar] [CrossRef]
- Fasshauer, G.; McCourt, M. Kernel-Based Approximation Methods Using Matlab; World Scientific Publishing Company: Singapore, 2015; Volume 19. [Google Scholar]
- Hamaidi, M.; Naji, A.; Charafi, A. Space–time localized radial basis function collocation method for solving parabolic and hyperbolic equations. Eng. Anal. Bound. Elements 2016, 67, 152–163. [Google Scholar] [CrossRef]
- Hopf, E. The partial differential equation ut + uux = μxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Uddin, M. On the selection of a good value of shape parameter in solving time-dependent partial differential equations using RBF approximation method. Appl. Math. Model. 2014, 38, 135–144. [Google Scholar] [CrossRef]
- Cole, J.D. On a quasi-linear parabolic equation occurring in aerodynamics. Q. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- Kutluay, S.; Bahadir, A.R.; Özdeş, A. Numerical solution of one-dimensional Burgers equation: Explicit and exact-explicit finite difference methods. J. Comput. Appl. Math. 1999, 103, 251–261. [Google Scholar] [CrossRef]
- Vaganan, B.M.; Priya, E.E. Generalized Cole–Hopf transformations for generalized Burgers equations. Pramana 2015, 85, 861–867. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).