Abstract
We develop a Lax–Wendroff scheme on time discretization procedure for finite volume weighted essentially non-oscillatory schemes, which is used to simulate hyperbolic conservation law. We put more focus on the implementation of one-dimensional and two-dimensional nonlinear systems of Euler functions. The scheme can keep avoiding the local characteristic decompositions for higher derivative terms in Taylor expansion, even omit partly procedure of the nonlinear weights. Extensive simulations are performed, which show that the fifth order finite volume WENO (Weighted Essentially Non-oscillatory) schemes based on Lax–Wendroff-type time discretization provide a higher accuracy order, non-oscillatory properties and more cost efficiency than WENO scheme based on Runge–Kutta time discretization for certain problems. Those conclusions almost agree with that of finite difference WENO schemes based on Lax–Wendroff time discretization for Euler system, while finite volume scheme has more flexible mesh structure, especially for unstructured meshes.
1. Introduction
1.1. Background
In this paper, a new scheme is proposed using Lax–Wendroff scheme to discretize the time derivative and finite volume WENO (Weighted Essentially Non-oscillatory) scheme to discretize the spatial derivative of PDEs (partial differential equations). The scheme is adopted to simulate one-dimensional and two-dimensional nonlinear Euler systems of compressible gas dynamics; in fact, the scheme and results can be generalized to other hyperbolic conservation laws easily.
1.2. Formulation of the Problem of Interest for This Investigation
It has been an important work to study nonlinear PDE [1] due to their rich mathematical structures and features [2,3,4,5] as well as important applications in fluid dynamics and plasma physics [6,7,8,9,10,11,12]. Although many theories and methods were proposed to discuss the PDE [13,14,15,16,17,18,19,20], however, most nonlinear PDE have no analytic solutions; numerical methods are necessary to study hydrodynamic characteristics of PDEs [21,22,23,24]. For the discretization of time derivative in time-dependent PDEs for numerical methods, the well-known ways is the ODE solver, such as multi-step method and Runge–Kutta method. These approaches are popular for their simplicity in concept and in coding, and better stability properties. Mostly, a total variation diminishing (TVD) time discretization is preferred. Of course, there also exist disadvantages, the main disadvantage being that total variation diminishing (TVD) Runge–Kutta methods with positive coefficients cannot reach fifth order accuracy or a higher order. In many practical schemes, a third TVD Runge–Kutta method has also been used, even for a very high order in spatial. This combination gives satisfactory results as spatial accuracy is more crucial than temporal accuracy for many problems.
For the discretization of spatial derivative in PDEs for numerical methods, especially for hyperbolic conservation law, traditional finite difference methods and finite volume methods are not fit to simulate Riemann solutions. In recent years, even many numerical methods have been developed and applied in recent years, many studies have more interest on WENO scheme. WENO is one of the very important high accuracy numerical methods, as WENO provides a procedure of spatial discretization for PDE. WENO schemes are shown to be very robust, especially at those regions where solutions are discontinuities, or have sharp gradient and other complicated solution structures. The WENO schemes have been developed as a class of high order finite difference or finite volume methods for hyperbolic conservation laws [25,26] in recent years. Finite difference methods are easily programmed and are convenient for high dimensional cases, while weakness is only fit for structured mesh with regular computational domain. In fact, the areas of inshore coastal waters and rivers have irregularly shaped areas.
1.3. Literature Survey
WENO [27,28] is a numerical method [29] used to approximate the spatial derivative terms to solve PDEs. WENO schemes have been very important high accuracy numerical methods, since the first WENO scheme was constructed for the third order finite volume version based on ENO (Essentially Non-oscillatory) scheme [30]. The main idea of WENO schemes is a non-linear-weighted combination of several local reconstructions based on different stencils and the usage of it as a final WENO reconstruction. Now, many improved WENO scheme are developed, such as Hermite-WENO [31], hybrid-WENO [32], positivity-preserving WENO [33], ADER-WENO [34], CWENO [35] and so on. The finite difference and the finite volume WENO schemes are widely used in many areas [36,37,38,39,40,41]. Lu and Qiu [42] investigated the performance of finite volume WENO methods for shallow water equations on unstructured meshes and simulated the tidal bore on Qiantang River.
Another way to approximate the time derivative is Lax–Wendroff-type time discretization procedure [43]. The method is based on traditional Lax–Wendroff method [44], which is an alternative method for time discretization, referring to a Taylor expansion in time, also called Taylor type. Qiu and Shu [43] developed Lax–Wendroff time discretization procedure with finite difference WENO scheme to solve Euler system of compressible gas dynamics, which obtained an interesting conclusion of exploring a balance between reducing the cost and maintaining the non-oscillatory properties. Lu and Qiu [45] also developed Lax–Wendroff with finite difference WENO scheme for shallow water equations, and similar results were obtained.
1.4. Scope and Contribution of This Study
The Lax–Wendroff time discretization method is via the classical Lax–Wendroff procedure, which relies on the conversion that makes all the time derivatives into spatial derivatives in a temporal Taylor expansion, and by using the PDE, discrete spatial derivatives. When the two ways obtain the same high order accuracy, the Lax–Wendroff time discretization needs a smaller effective stencil than the ODE solver, and it makes full use of the original PDE. However, the formulation and coding of this method can be quite complex to understand. The Lax–Wendroff time discretization formula based on finite volume is easier than that of the finite difference, but the computation is little more complex than that of finite difference method, as cell averages have to be calculated for finite volume method, while finite difference method only needs to calculate the point value.
Thus, in this paper, we mainly discuss finite volume WENO scheme in space as it is more flexible than finite difference scheme. We follow the same ideas of the previous papers [46,47] about finite volume WENO schemes.
1.5. Organization of the Paper
We develop the fifth order WENO finite volume schemes based on the third order Lax–Wendroff-type time discretization in this paper, which is used to solve the one-dimensional and two-dimensional nonlinear systems of Euler equations to see if similar conclusions still hold. The main work of this paper is organized as follows, in Section 2, we describe details of the discretization for Euler system with finite volume WENO schemes and Lax–Wendroff-type time discretization. Numerical examples are given in Section 3. The results demonstrate the accuracy, resolution and efficiency of the constructed schemes. Concluding remarks are included in Section 4.
2. Description of Numerical Model
2.1. The Nonlinear Euler System
We introduce the nonlinear Euler system in two dimensions; it has the following form
with
where stands for the density, E is the total energy, are the velocity in directions, p is the pressure, and p is related to , with related to specific heat ratio, for ideal gas . Euler system is important and typical hyperbolic conservation laws. In the Euler system (Equation (1)), is the conserved vector, are the flux terms. We rewrite the Euler system in a quasi-linear form as follows
where are Jacobian matrices,
and
The eigenvalues of Jacobian matrices and are
respectively, where is the sound speed of the polytropic gas. The corresponding right and left eigenvectors of Jacobian matrices and as follows:
where and , . and hold for hyperbolic conservation law, where I is unit matrix.
Neglecting all the variables in y direction of the above formula, we can easily get the characteristic of one-dimensional Euler system (Equation (6)), thus the following procedure is done:
with
2.2. Overview of the Fifth Order Finite Volume WENO Schemes
We use the finite volume WENO scheme to solve the spatial derivative of Euler equations. We take a brief look at WENO scheme [28] for the typical scalar one-dimensional hyperbolic conservation law Equation (8)
Denote the ith cell; the center is . We assume that the meshes are uniform and . For a finite volume scheme, we define the approximate average value of at mesh cell in time. We construct the discrete finite volume scheme of Equation (8) as
where is approximated by numerical flux ; here, the simplest and monotone Lax–Friedrich flux is employed, which has the form
where and are the high order point approximations to of left side and right side at interface , which are obtained from the cell averages by a WENO reconstruction procedure.
For a th WENO scheme, the point values of are computed through k neighboring mean values , based on stencil with r cells to the left on the order of accuracy k. Thus, there exist constants and , such that
The constants are obtained by the unique degree polynomial , which is
so the approximate point value is , .
For example, for the fifth order WENO scheme (), the approximated point values of are given by
The following part describes the computation of the smoothness indicators and the nonlinear weights . The th order WENO reconstruction is a convex combination based on all these k point values
The nonlinear weights have the following new definitions:
where is a small positive constant to avoid zero denominator; usually, we take it as . are linear weights which yield th order accuracy on area of smooth solution, are the so-called “smoothness indicators", which are usually used to measure the smoothness of the polynomials and they have the form:
For the fifth order WENO scheme on uniform mesh, the linear weights have the form:
and the smoothness indicators are given by
On uniform meshes, we do not have to calculate . The reconstruction of is mirror symmetry to that of . For the Euler system, the reconstruction is performed in eigenspace, so local characteristic decompositions should be used. The reconstruction in eigenspace is more robust than a component by component method. We need to calculate the right eigenvectors and the left eigenvectors of the Jacobian matrices and Roe’s average in the local characteristic decomposition.
For two-dimensional finite volume case, we cannot simply procede in a dimension-by-dimension fashion as in finite difference method. The spatial surface integration on rectangular cell can be converted to line integration by Gauss theorem. To obtain the fifth order, we can use three-point Gaussian quadrature for line integration of every rectangular cell as in Figure 1. For example, to calculate numerical flux in x direction, three Gaussian point values on every vertical lines should be reconstructed from cell average values in y direction first; then left and right Gaussian point values should be reconstructed by the WENO scheme; next is the numerical flux; and finally the cell average value can be approximate on next time level. When dissipation does not exist, we first suppose
where c is a constant and denote the phase speed of the wave. Equation (8) implies that
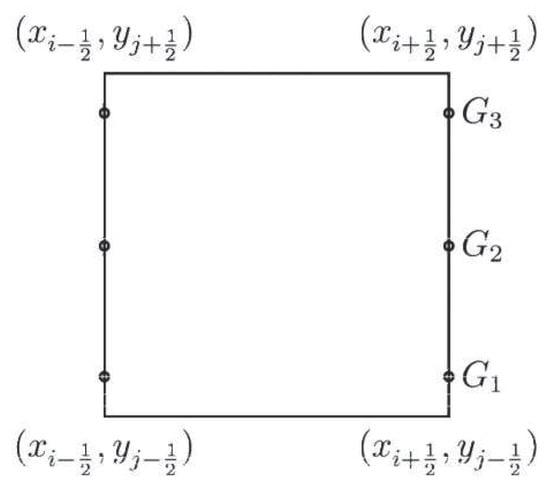
Figure 1.
A sketch of WENO reconstruction on a rectangular cell.
When
we can easy infer that the relative vorticity is a function of stream function u only. Thus, we get
2.3. The Lax–Wendroff-Type Time Discretization Procedure for Euler Equations
The details of Lax–Wendroff-type time discretization are described based on finite volume WENO schemes for two-dimensional Euler system (Equation (1)) [43,45] in this section.
Define as the time step; then time level . We introduce as the approximate average values of on rectangular cell at the nth time level. For simplicity, we denote the rth order time derivative of as rather than , and , and stand for the first, the second and the third time derivatives of , respectively. The idea of Lax–Wendroff-type time discretization procedure is to replace time derivative by spatial derivatives using the original PDE (Equation (1)) [43]. By a temporal Taylor’s expansion for conservative vector , we obtain
The sliding average is
where means mean value of in space. If we need to obtain kth degree of accuracy in time, we should approximate those terms until the kth time derivatives on the right hand side in Equation (17). Here, we calculate the third order in time and the fifth order in space, which means that we should approximate until the third order time derivatives on the right hand side in Equation (17), and for every time derivative the fifth order spatial approximation method should be used; actually, the fifth order WENO reconstruction is used.
Using Euler system (Equation (1)), by Lax–Wendroff type dime discretization, we replace the time derivatives in Equation (16) by the spatial derivatives as follows
where brief notes are used, such as , the details are given below. Thus, Equation (16) can be written as
Then, the sliding average (Equation (17)) with third order in time on a rectangular cell is approximated as
with
where and are approximated by numerical flux and , such as .
For example, the first term in and are for the approximation of the first time derivative , where . In the fifth order finite volume WENO scheme, on rectangle control volume ,
three point Gaussian quadrature formulae are used for the above line integration. The integrand, that is numerical flux vector and , at every Gaussian point , , is obtained by the regular fifth order WENO finite volume reconstruction and the Lax–Friedrich numerical flux, as described in Section 2.2, where are the three Gaussian points. Meanwhile, the reconstruction of , and , in the second and third term (Equation (21)) on Gaussian points of cell interface are calculated in this procession of WENO reconstruction. That is, in this procession, we calculate , , , in subroutine of WENO reconstruction. Notice that the extra factor multiplying by in Equation (21) leads to a one order lower flux approximation than that of the first time derivative . In x-direction, the linear polynomial and constant are the approximations to and . According to polynomial (Equation (9)), on small stencil, we have
The same linear weights of are used for . According to the definition of smooth, Equation (11) indicates constant and zero are used for and , as
Similar formulae can be written for and in y-direction in WENO reconstruction.
In Equation (21), the Jacobian matrices are , which have been mentioned above. are vectors. If we denote
where are matrices,
which is also a vector and have been calculated in a previous step, in which we known is a vector, with
If we denote
where are matrices, and
If a higher accuracy order in time is required, the procedure needs to be continued until the corresponding derivatives in a similar fashion. For convenience, in the following parts, WENO5-LW3 denotes a scheme coupling the fifth order finite volume WENO scheme in space and the third order Lax–Wendroff-type method in time and WENO5-RK3 denotes a scheme coupling the fifth order finite volume WENO schemes and the third order Runge–Kutta methods.
3. Numerical Results
In this section, extensive numerical examples are used for performance testing for the new finite volume WENO5-LW3 schemes. We compare the results of WENO5-LW3 for one- and two-dimensional Euler equations and that of the WENO5-RK3 schemes, focusing on the important issue of CPU time cost, non-oscillatory and efficiency. For comparison of CPU time cost, all computations are performed on a personal computer, Core (TM) i5-3470 CPU @ 3.20 GHz with 4 GB RAM. In these numerical simulations, we use CFL number 0.4 and 0.6 for WENO5-LW3 and WENO-RK3 schemes, respectively. The small positive constant is used to avoid denominator zero in the nonlinear weight formula. All of these simulations are based on uniform meshes.
Example 1 (One-Dimensional Accuracy Test).
To check the order accuracy of the finite volume WENO5-LW3 schemes based on one-dimensional Euler system with a smooth solution (Equation (6)), for comparison, we use the same test as in [43]. In the computational domain , the initial condition is given below:
Two-periodic boundary conditions are used; we simulate until the ending time , when the solutions are continuous and there are no shocks. The exact solution is
The numerical errors and orders of accuracy based on and norm metric for density by WENO5-LW3 are shown in Table 1. N stands for the number of mesh grids; adjusted adaptive time step size should be used to get the fifth order as mesh refining. For comparison, the and numerical errors and accuracy orders by WENO5-RK3 schemes are displayed in Table 1. In Table 1, we can find that the designed accuracy order are attained for both WENO5-LW3 and WENO5-RK3, and they generate similar numerical errors.

Table 1.
and errors and numerical orders of accuracy for density of one-dimensional order test, WENO5-LW3 and WENO5-RK3 using N space mesh points.
In Figure 2, we give the numerical errors and CPU time cost for density based on and norm metric with cell numbers are , and Log scale is used for numerical errors in y axis. In this figure, the line of WENO5-LW3 always underneath the line of WENO5-RK3, which implies that, with the same CPU time cost, WENO5-LW3 obtains a higher accuracy than WENO5-RK3. From the trend of the line, it seems that the phenomenon will be more serious when the test has more mesh points.
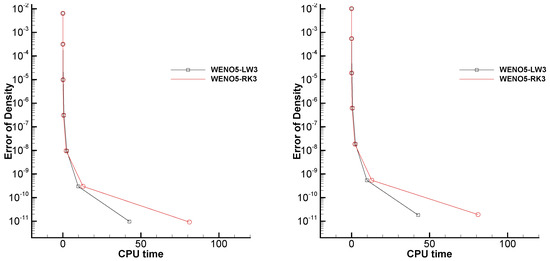
Figure 2.
Numerical errors of density and CPU time for the one-dimensional order test in Example 1: (Left) error; and (Right) error.
Example 2 (One-Dimensional Test with Shocks).
This problem is commonly applied to test the ability of shock capturing for schemes in one-dimensional Euler system [43]. In this case, we considertwo different initial conditions in the domain , with continuation boundary condition for two boundary; the first test is Lax Problem,
and the second test is Sod Problem,
Both problems have Riemann initial condition. The simulation is performed up to final time for the Lax Problem and ending time for the Sod Problem, when shocks have appeared in the solutions.
In this case, we put more concern on the resolution of numerical shocks. The computed density based on the WENO5-LW3 and WENO5-RK3 schemes with on uniform mesh are plotted in Figure 3 and compared with the exact solution. The numerical results and the exact solution fit very well, no spurious oscillations occur, and the results are comparable with that in [43]. In this test, we take the CPU time based on 2000 uniform mesh grids and tested for 10 times; the CPU time for WENO5-LW3 and WENO5-RK3 schemes are 23.41 s and 26.52 s, respectively. From the data, we find that the CPU time cost of WENO5-LW3 scheme is about 10% less than that of WENO5-RK3 scheme.
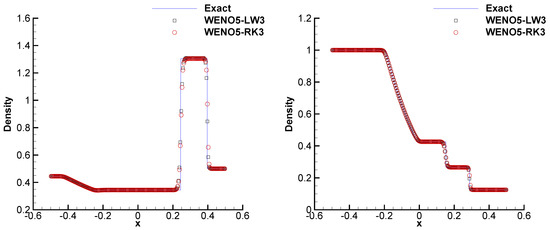
Figure 3.
One-dimensional test with shocks problem at for the Lax Problem (Left) and (Right) for the Sod Problem by WENO5-LW3 and WENO5-RK3 against exact solution.
Example 3 (One-Dimensional Test of Shocks Interaction with Entropy Waves).
This problem is a typical one-dimensional test for higher order method to evaluate the non-oscillatory properties [43], as this case contains not only shocks but also complex smooth region structure; more specifically, it is a problem about the interaction with entropy waves of shocks. The given initial condition is:
where is used. Actually, this is a problem about a moving shock interacting with sine waves. The simulation is performed until the ending time with continuation boundary condition on the domain .
The computed density based on the WENO5-LW3 schemes and WENO5-RK3 schemes with the mesh points and and zoomed in pictures are plotted in Figure 4 against a reference exact solution by 2000 mesh points, which show that the computed solution converges to the reference exact solution, and no spurious oscillations occur. The WENO5-LF3 scheme could get much better resolution than that of WENO5-RK3 scheme. The results are better confirmed with reference solution on than that on , which also shows a converged solution computed by WENO5-LW3. All results agree with that in [43]. The time cost to run 10 times based on uniform mesh with is taken as the CPU time for every problem. The CPU time is 59.94 s for WENO5-LW3 and 66.24 s for WENO5-RK3, respectively, so the CPU time cost of WENO5-RK3 is around 8.5% more than that of WENO5-LW3.
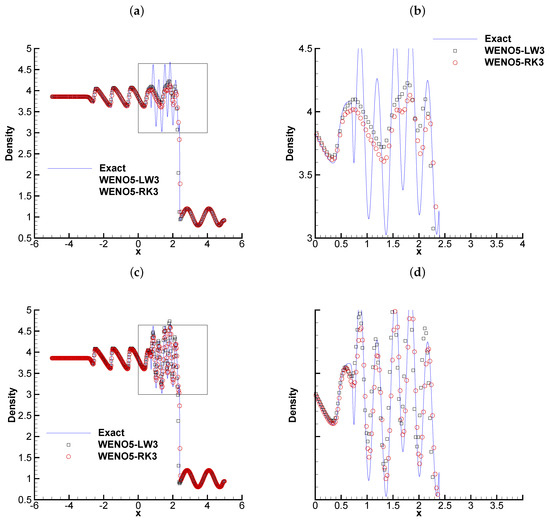
Figure 4.
The shock density wave interaction problem at by WENO5-LW3 and WENO5-RK3 with and . (a) N = 200 for density; (b) N = 200 density zoomed in; (c) N = 400 for density; (d) N = 400 density zoomed in.
Example 4 (Two-Dimensional Accuracy Order Test).
To check the order accuracy of the schemes for two-dimensional Euler system with a smooth solution, for comparison, we use the test in [43]. In the computational domain , we take the following initial conditions:
Four-periodic boundary conditions are used; the final time is when no shocks appear in the solution. The exact solution for the problem is
In Table 2, the numerical errors and accuracy orders for by WENO5-LW3 based on and norm metric are shown, while N is the number of mesh cells. The rectangle cell is used to avoid cancelations of some special error due to the symmetry axis being in the diagonals of cells. and numerical errors and accuracy orders by WENO5-RK3 schemes are also displayed in Table 2 to compare with the results of WENO5-LW3. The two schemes have achieved the fifth order accuracy at the final time and generate similar numerical errors.

Table 2.
and errors and numerical orders of accuracy for density of two-dimensional accuracy test, WENO5-LW3 and WENO5-RK3 with N cells.
On mesh , the corresponding CPU time costs for WENO5-LW3 and WENO5-RK3 are 986.73 s and 1103.93 s. We can see that WENO5-RK3 cost about 10% more CPU time than WENO5-LW3.
Example 5 (Two-Dimensional Double Mach Reflection).
This problem is a two-dimensional double mach reflection test; complex boundary conditions are implemented. For the example, multiple shocks with complex self-similar structure are emergent, and the initial geometry is very simple [43].
In this test, the wedge of the oblique shock is set as a partially reflecting horizontal lower boundary. The computational domain is , the x axis is 4.0 units long. At the first units, the outflow is free and the remaining units reflect the rest of the boundary. At the upper boundary, the flow values are used to describe the exact motion of a shock at Mach = 10. The left boundary is constant with the post oblique shock values, and there is no limit for the right boundary. In the whole calculation, the final time is .
At the ending time, we plot the computed density contours by the WENO5-LW3 scheme with meshes in Figure 5, which is almost the same as the results by WENO5-RK3, and comparable with previous results in [43]. When the CPU time is considered, we can find that WENO5-RK3 also costs a little more time than WENO5-LW3.
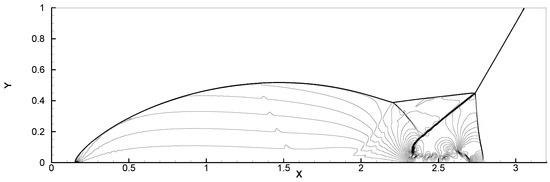
Figure 5.
The two-dimensional double mach reflection problem at by WENO5-LW3.
4. Concluding Remarks
In this paper, we take advantage of Lax–Wendroff-type time discretizations and high resolution finite volume WENO schemes to simulate one-dimensional and two-dimensional Euler equations. By comparing the addressing on CPU time, non-oscillatory, resolution and relevant efficiency of finite volume WENO schemes using time discetizations, the numerical results show that the WENO5-LW3 schemes takes smaller CPU costs than WENO5-RK3 schemes, while WENO5-LW3 schemes got the same order of accuracy with Runge–Kutta time discretization on the same mesh grids number. These conclusions agree with the theory of the finite difference WENO with Lax–Wendroff-type and Runge–Kutta time discretizations for Euler system of compressible gas dynamics.
Author Contributions
These authors contributed equally to this work.
Acknowledgments
The work was partially supported by the China Postdoctoral Science Foundation funded project (2017M610436); Nature Science Foundation of Shandong Province of China (No.ZR2018MA017); Natural Science Foundation of China (11801280); Natural Science Foundation of Jiangsu Province (BK20180780); and Natural Science Foundation of the Jiangsu Higher Education Institutions (18KJB110020).
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Guo, M.; Zhang, Y.; Wang, M.; Chen, Y.D.; Yang, H.W. A new ZK-ILW equation for algebraic gravity solitary waves in finite depth stratified atmosphere and the research of squall lines formation mechanism. Comput. Math. Appl. 2018, 75, 3589–3603. [Google Scholar] [CrossRef]
- Lu, C.N.; Fu, C.; Yang, H.W. Time-fractional generalized Boussinesq Equation for Rossby solitary waves with dissipation effect in stratified fluid and conservation laws as well as exact solutions. Appl. Math. Comput. 2018, 327, 104–116. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, H.H.; Zhang, X.E.; Yang, H.W. Rational solutions and lump solutions to the generalized (3 + 1)-dimensional Shallow Water-like equation. Comput. Math. Appl. 2017, 73, 246–252. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhao, Q.L.; Li, Y.X. Binary Bargmann symmetry constraint associated with 3 × 3 discrete matrix spectral problem. J. Nonlinear Sci. Appl. 2015, 8, 496–506. [Google Scholar] [CrossRef]
- Barnett, M.P.; Capitani, J.F.; Joachim, V.Z. Symbolic calculation in chemistry: Selected examples. Int. J. Quantum Chem. 2004, 100, 80–104. [Google Scholar] [CrossRef]
- Yang, H.W.; Chen, X.; Guo, M.; Chen, Y.D. A new ZK-BO equation for three-dimensional algebraic Rossby solitary waves and its solution as well as fission property. Nonlinear Dyn. 2018, 91, 2019–2032. [Google Scholar] [CrossRef]
- Yang, H.W.; Xu, Z.H.; Yang, D.Z. ZK-Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect. Adv. Differ. Equ. 2016, 2016, 167. [Google Scholar] [CrossRef]
- Saleh, M.F.; Chang, W.; Travers, J.C. Plasma-induced asymmetric self-phase modulation and modulational instability in gas-filled hollow-core photonic crystal fibers. Phys. Rev. Lett. 2012, 109, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Gorza, S.P.; Deconinck, B.; Emplit, P. Experimental demonstration of the oscillatory snake instability of the bright soliton of the (2 + 1)D hyperbolic nonlinear Schrödinger equation. Phys. Rev. Lett. 2011, 106, 094101. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Yin, B.; Yang, H. Dissipative nonlinear Schrödinger equation for envelope solitary Rossby waves with dissipation effect in stratified fluids and its solution. Abstr. Appl. Anal. 2014, 2014, 643652. [Google Scholar] [CrossRef]
- Guo, M.; Fu, C.; Zhang, Y.; Liu, J.X.; Yang, H.W. Study of ion-acoustic solitary waves in a magnetized plasma using the three-dimensional time-space fractional Schamel-KdV equation. Complexity 2018, 2018, 6852548. [Google Scholar] [CrossRef]
- Yang, H.W.; Yin, B.; Wang, Q. Forced ILW-Burgers Equation As A Model For Rossby Solitary Waves Generated By Topography In Finite Depth Fluids. J. Appl. Math. 2012, 2012, 491343. [Google Scholar] [CrossRef]
- Bekir, A. Painlevé test for some (2 + 1)-dimensional nonlinear equations. Chaos Solitons Fractals 2007, 32, 449–455. [Google Scholar] [CrossRef]
- Xu, X.X.; Sun, Y.P. An integrable coupling hierarchy of Dirac integrable hierarchy, its Liouville integrability and Darboux transformation. J. Nonlinear Sci. Appl. 2017, 10, 3328–3343. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhang, Y.Q.; Zhao, Q.L. Positive and negative integrable hierarchies, associated conservation laws and darboux transformation. J. Comput. Appl. Math. 2009, 233, 1096–1107. [Google Scholar] [CrossRef]
- Guo, X.R. On bilinear representations and infinite conservation laws of a nonlinear variable-coefficient equation. Appl. Math. Comput. 2014, 248, 531–535. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, Y. Lump solutions to nonlinear partial differential equations via hirota bilinear forms. J. Differ. Equ. 2018, 264, 2639–2659. [Google Scholar] [CrossRef]
- Dong, H.H.; Chen, T.; Chen, L.; Zhang, Y. A new integrable symplectic map and the lie point symmetry associated with nonlinear lattice equations. J. Nonlinear Sci. Appl. 2016, 9, 5107–5118. [Google Scholar] [CrossRef]
- Fu, C.; Lu, C.N.; Yang, H.W. Time-space fractional (2 + 1) dimensional nonlinear Schrédinger equation for envelope gravity waves in baroclinic atmosphere and conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 2018, 56. [Google Scholar] [CrossRef]
- Tang, J.; He, G.P.; Fang, L. A new non-interior continuation method for second-order cone programming. J. Numer. Math. 2013, 21, 301–323. [Google Scholar] [CrossRef]
- Wang, Z. A numerical method for delayed fractional-order differential equations. J. Appl. Math. 2013, 2013, 256071. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Meng, X.Z.; Zhang, T.H. Dynamics analysis and numerical simulations of a stochastic non-autonomous predator-prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 2017, 26, 19–37. [Google Scholar] [CrossRef]
- Liu, X.K.; Li, Y.; Zhang, W.H. Stochastic linear quadratic optimal control with constraint for discrete-time systems. Appl. Math. Comput. 2014, 228, 264–270. [Google Scholar] [CrossRef]
- Zhou, S.W.; Zhang, W.H. Discrete-time indefinite stochastic Lq control via sdp and Lmi methods. J. Appl. Math. 2012, 2012, 638762. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Effecient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Balsara, D.S.; Shu, C.W. Monotonicity preserving weithted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comput. Phys. 2000, 160, 405–452. [Google Scholar] [CrossRef]
- Shu, C.W. Essential non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Springer: Berlin, Gemany, 1998; pp. 325–432. [Google Scholar]
- Wang, Z.; Huang, X.; Zhou, J.P. A numerical method for delayed fractional-order differential equations: Based on G-L definition. Appl. Math. Inf. Sci. 2013, 7, 525–529. [Google Scholar] [CrossRef]
- Harten, A.; Engguist, B.; Osher, S.; Chakravarthy, S. Uniformly high order essentially non-oscillatory schemes. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J.X. Finite volume Hermite WENO schemes for solving the Hamilton-Jacobi equations II: Unstructured meshes. Comput. Math. Appl. 2014, 68, 1137–1150. [Google Scholar] [CrossRef]
- Li, G.; Qiu, J.X. Hybrid weighted essentially non-oscillatory schemes with different indicators. J. Comput. Phys. 2010, 229, 8105–8129. [Google Scholar] [CrossRef]
- Christlieb, A.J.; Liu, Y.; Tang, Q.; Xu, Z.F. High order parametrized maximum-principle-preserving and positivity-preserving WENO schemes on unstructured meshes. J. Comput. Phys. 2015, 281, 334–351. [Google Scholar] [CrossRef]
- Dumbser, M. Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume schemes with time-accurate local time stepping for hyperbolic conservation laws. Comput. Methods Appl. Mech. Eng. 2014, 280, 57–83. [Google Scholar] [CrossRef]
- Huang, C.S.; Arbogast, T.; Hung, C.H. A re-averaged WENO reconstruction and a third order CWENO scheme for hyperbolic conservation laws. J. Comput. Phys. 2014, 262, 291–312. [Google Scholar] [CrossRef]
- Arándiga, F.; Belda, A.M.; Mulet, P. Point-Value WENO Multiresolution Applications to Stable Image Compression. J. Sci. Comput. 2009, 43, 158–182. [Google Scholar] [CrossRef]
- Balsara, D.S. Divergence-free reconstruction of magnetic fields and WENO schemes for magnetohydrodynamics. J. Comput. Phys. 2009, 228, 5040–5054. [Google Scholar] [CrossRef]
- Vukovic, S.; Sopta, L. ENO and WENO schemes with the exact conservation property for one-dimensional shallow water equations. J. Comput. Phys. 2002, 179, 593–621. [Google Scholar] [CrossRef]
- Zhao, S.; Lardjane, N.; Fedioun, I. Comparison of improved finite-difference WENO schemes for the implicit large eddy simulation of turbulent non-reacting and reacting high-speed shear flows. Comput. Fluid 2014, 99, 74–87. [Google Scholar] [CrossRef]
- Vecil, F.; Mestre, P.M.; Labrunie, S. WENO schemes applied to the quasi-relativistic Vlasov-Maxwell model for laser-plasma interaction. C. R. Mecanique 2014, 342, 583–594. [Google Scholar] [CrossRef]
- Zhu, H.; Qiu, J.; Qiu, J.M. An h-adaptive RKDG method for the two-dimensional incompressible Euler equations and the guiding center vlasov model. J. Sci. Comput. 2017, 73, 1316–1337. [Google Scholar] [CrossRef]
- Lu, C.N.; Qiu, J.X.; Wang, R.Y. Weighted Essential Non-oscillatory Schemes for Tidal Bore on Unstructured Meshes. Int. J. Numer. Method Fluid 2009, 59, 611–630. [Google Scholar] [CrossRef]
- Qiu, J.X.; Shu, C.W. Finite difference WENO schemes with Lax-wendroff-type time discretizations. SIAM J. Sci. Comput. 2003, 24, 2185–2198. [Google Scholar] [CrossRef]
- Lax, P.D.; Wendroff, B. Systems of conservation law. Commun. Pure Appl. Math. 1960, 13, 217–237. [Google Scholar] [CrossRef]
- Lu, C.N.; Qiu, J.X. Simulation of shallow water equations with finite difference Lax–Wendroff weighted essential non-oscillatory schemes. J. Sci. Comput. 2011, 47, 281–302. [Google Scholar] [CrossRef]
- Lu, C.N.; Qiu, J.X.; Wang, R.Y. A numerical study for the performance of the WENO schemes based on different numerical fluxes for the shallow water equations. J. Comput. Math. 2010, 28, 807–825. [Google Scholar] [CrossRef]
- Lu, C.N.; Xie, L.Y.; Yang, H.W. The Simple Finite Volume Lax-Wendroff Weighted Essentially Nonoscillatory Schemes for Shallow Water Equations with Bottom Topography. Math. Probl. Eng. 2018, 2018, 2652367. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).