An Adaptive WENO Collocation Method for Differential Equations with Random Coefficients
Abstract
:1. Introduction
2. Formulation
2.1. Multi-Element Stochastic Collocation Method (ME-SCM)
2.2. High-Order WENO Interpolation in Random Space
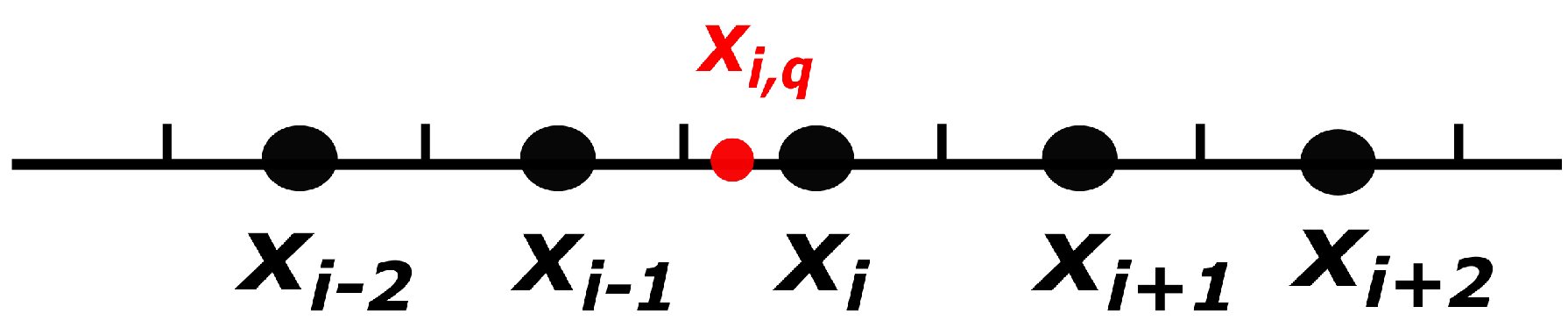
2.2.1. One-Dimensional Case
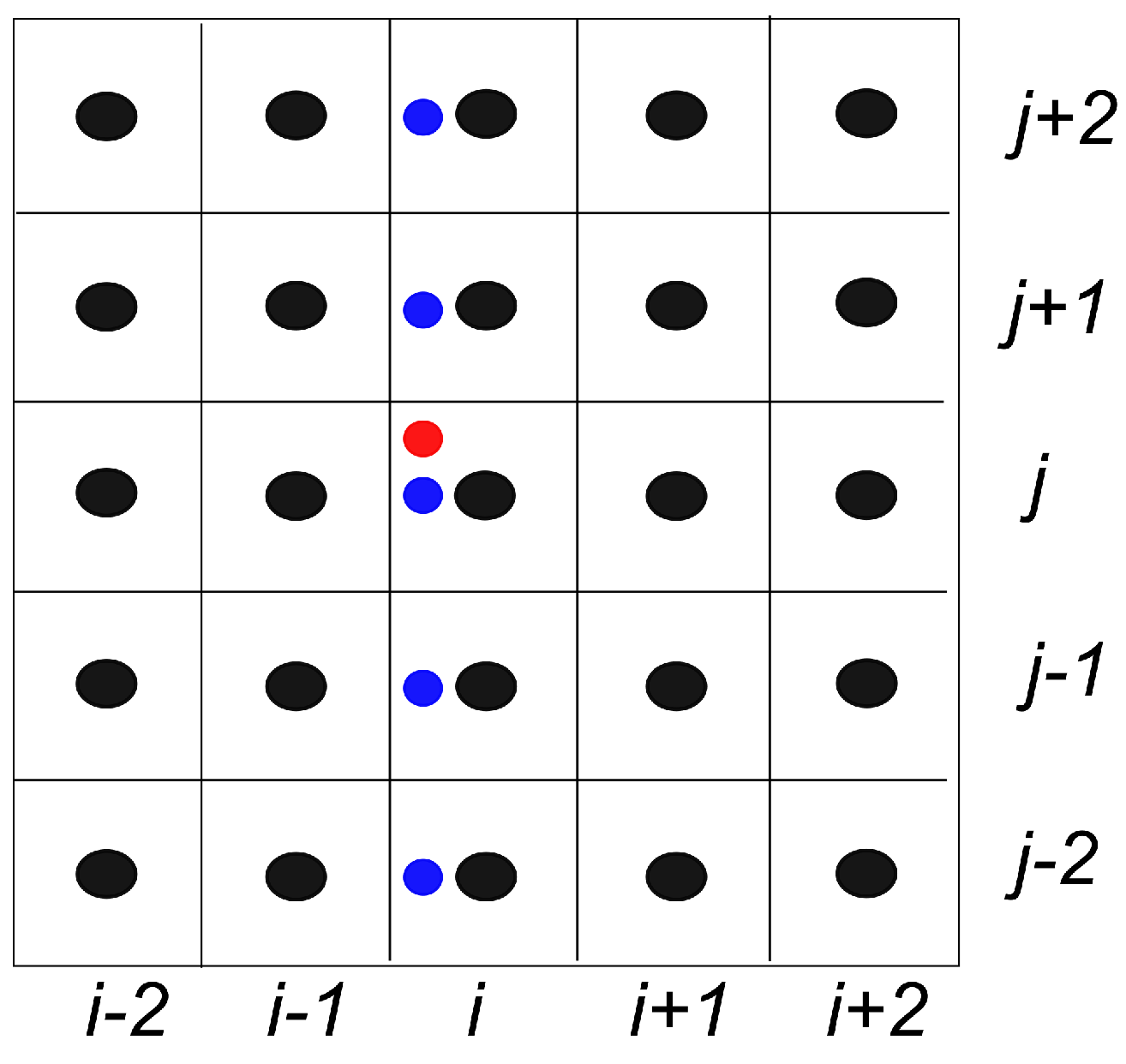
2.2.2. Two-Dimensional Extension
2.3. AMR Methodology in Random Space
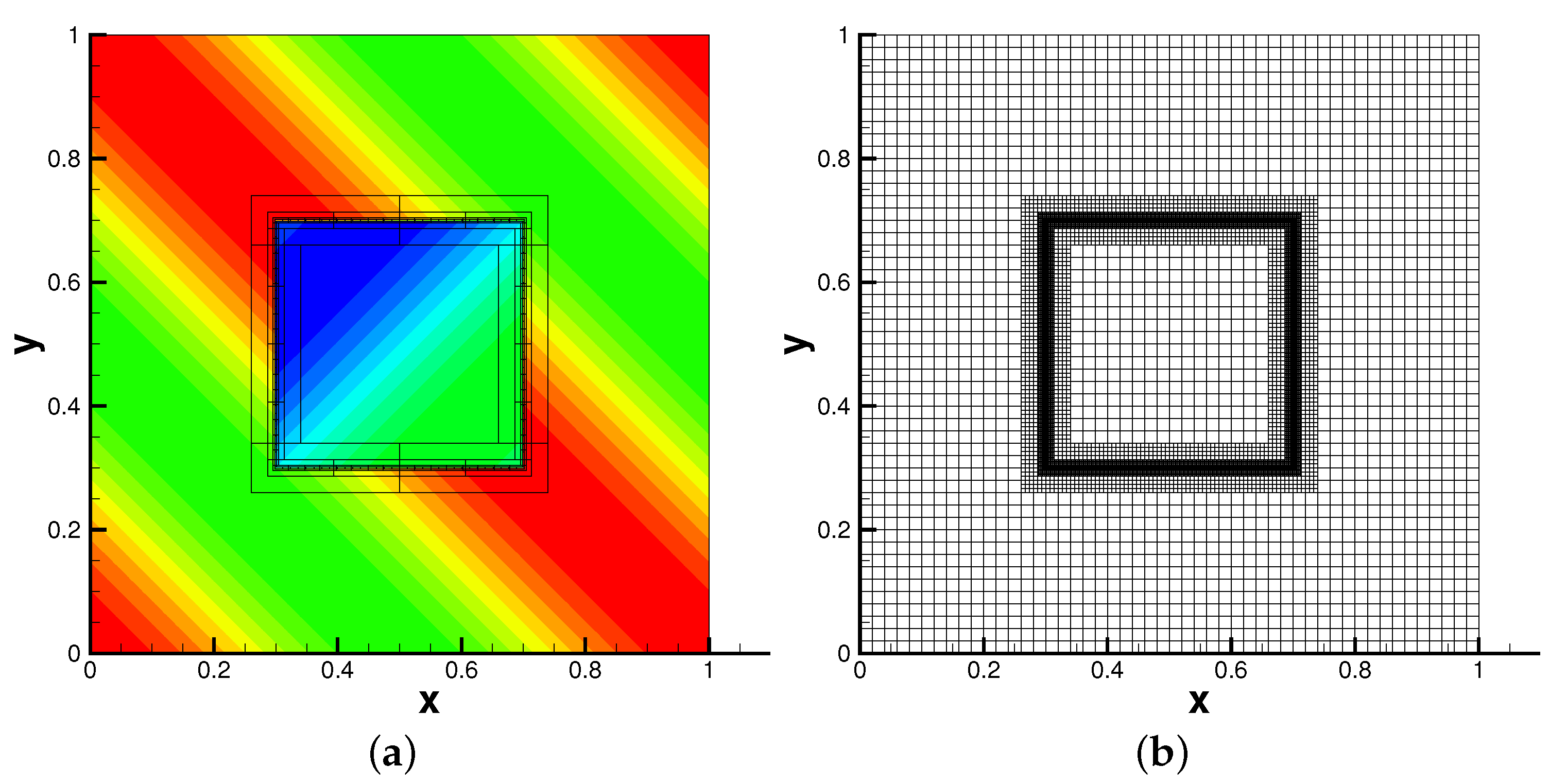
- Use a multi-resolution analysis to flag the regions of refinement interest (RRI): We compute the difference between the solution and the average of its four neighbors . If , where ϵ is a user specified constant, then the point and its eight neighbors are marked as regions of refinement interest (RRI).
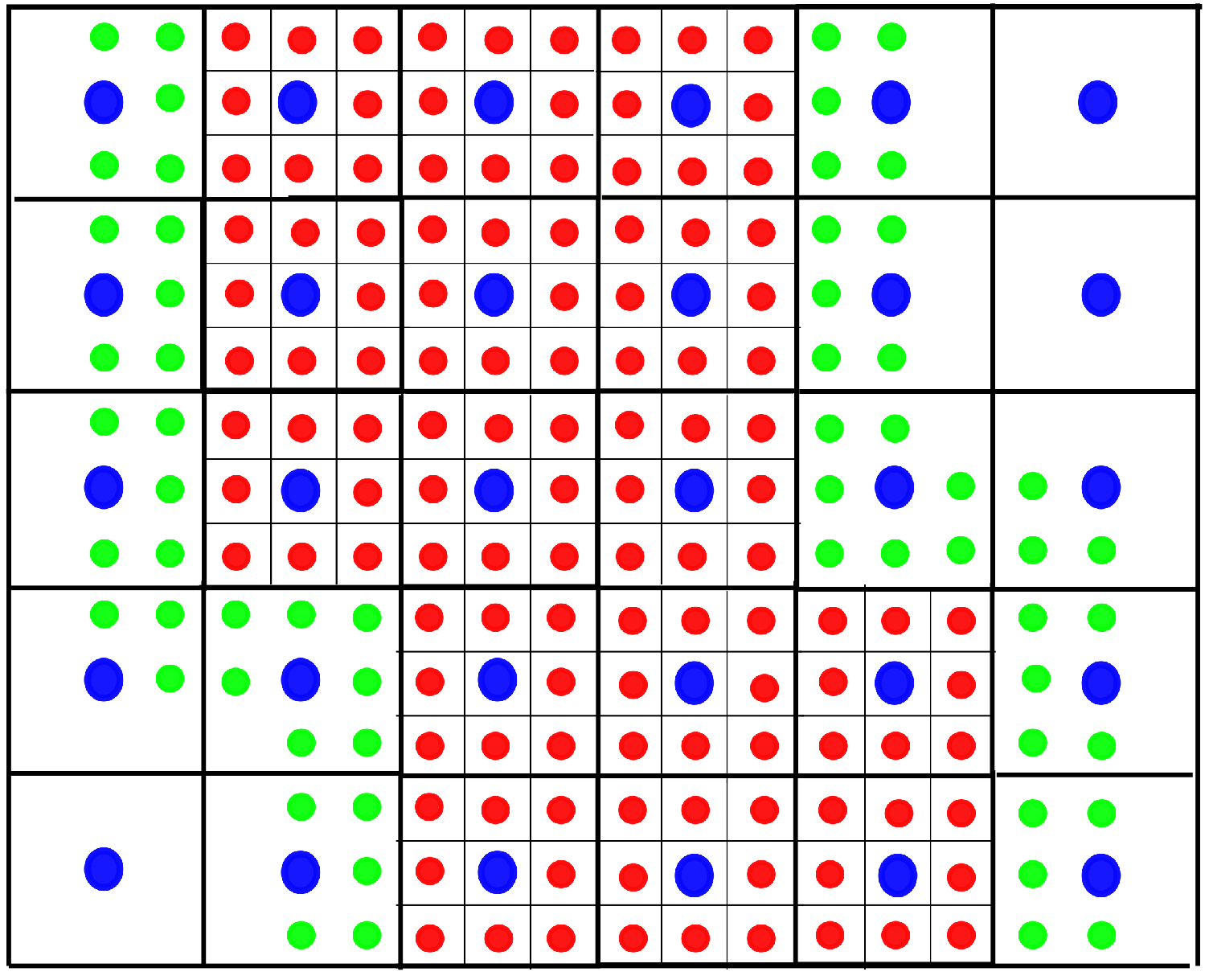
- Generate finer grids using the algorithm proposed in [33]: We generate some non-overlapping rectangular clusters that cover the RRI. In each cluster, the grid is refined with a ratio of three, i.e., , where denotes the mesh size on the mesh level l (see Figure 3; two non-overlapping clusters are generated, and red circles denote point values on the fine grid).
- Repeat steps 1 and 2 until the maximal mesh level is attained.
- Generate the WENO interpolating polynomial by applying the algorithm reviewed in Section 2.2. We start from the clusters with the finest mesh level. The needed boundary values in the WENO interpolation procedure can be either obtained from the neighboring cluster with same mesh level or interpolated from coarser clusters. Again, the WENO interpolation should be used in order to avoid the oscillations (see Figure 3; the green circles are interpolated from the blue circles on a coarser cluster).
3. Numerical Results
3.1. Approximation Investigation for Non-Smooth Functions
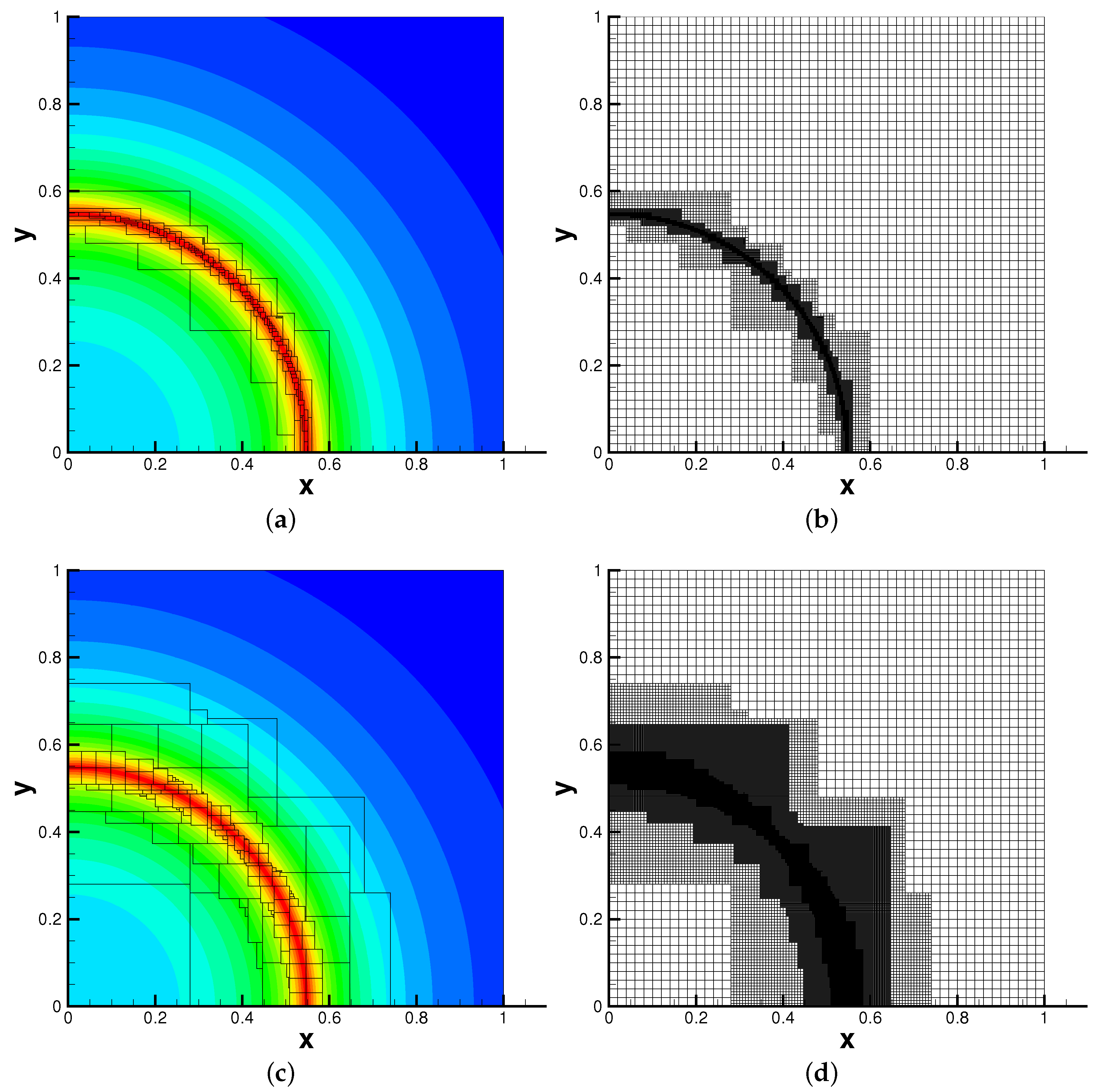
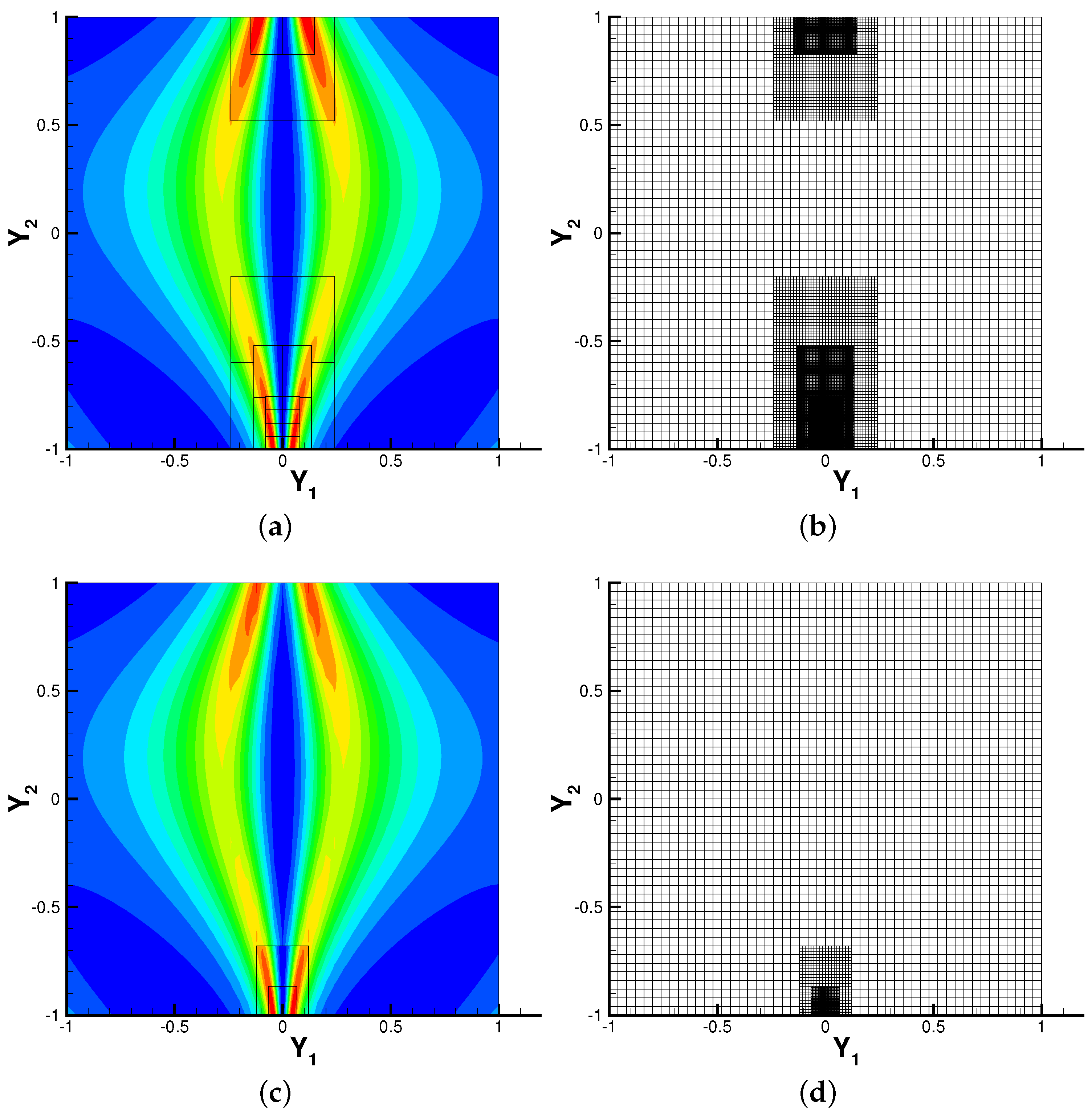
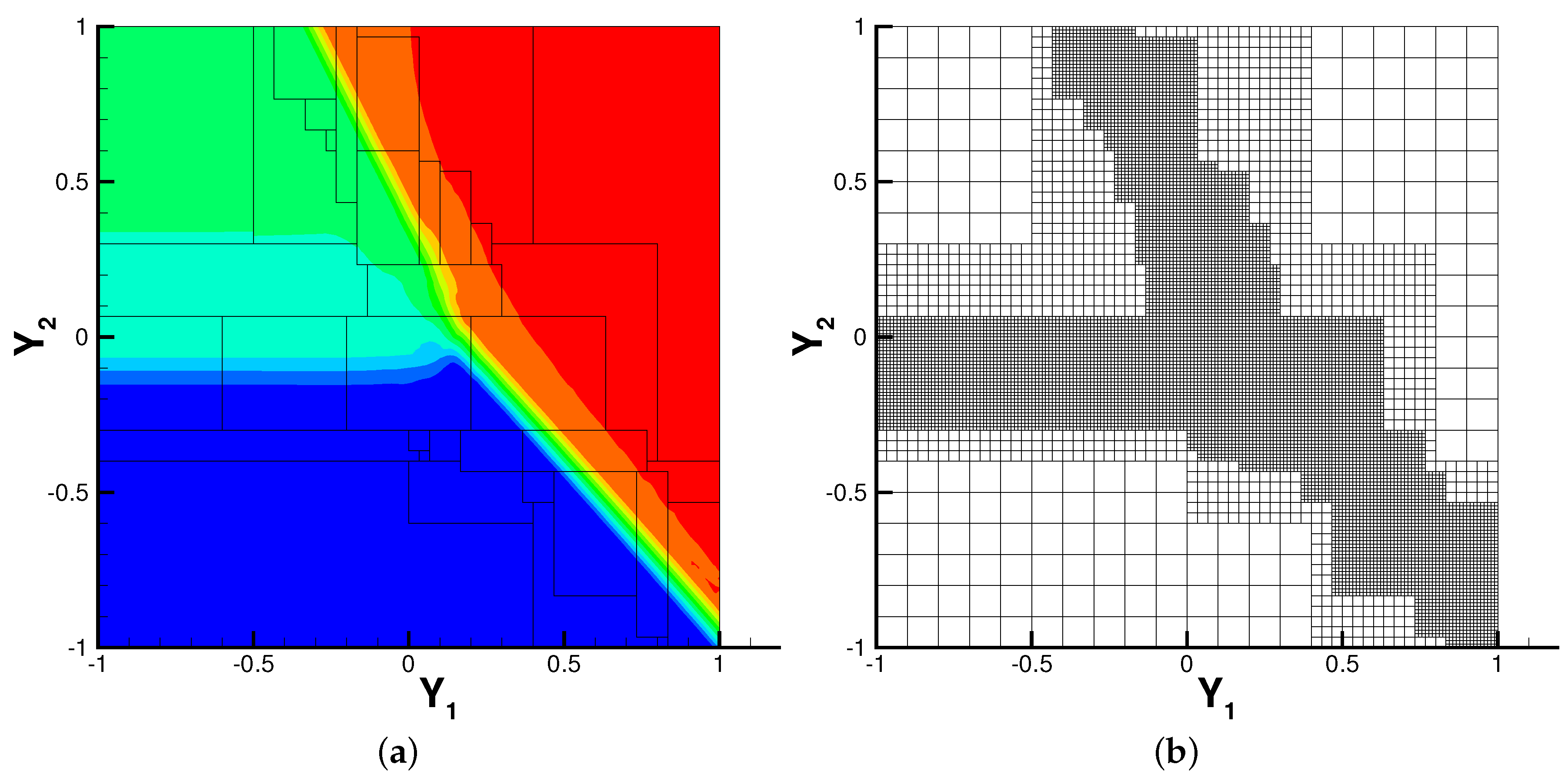
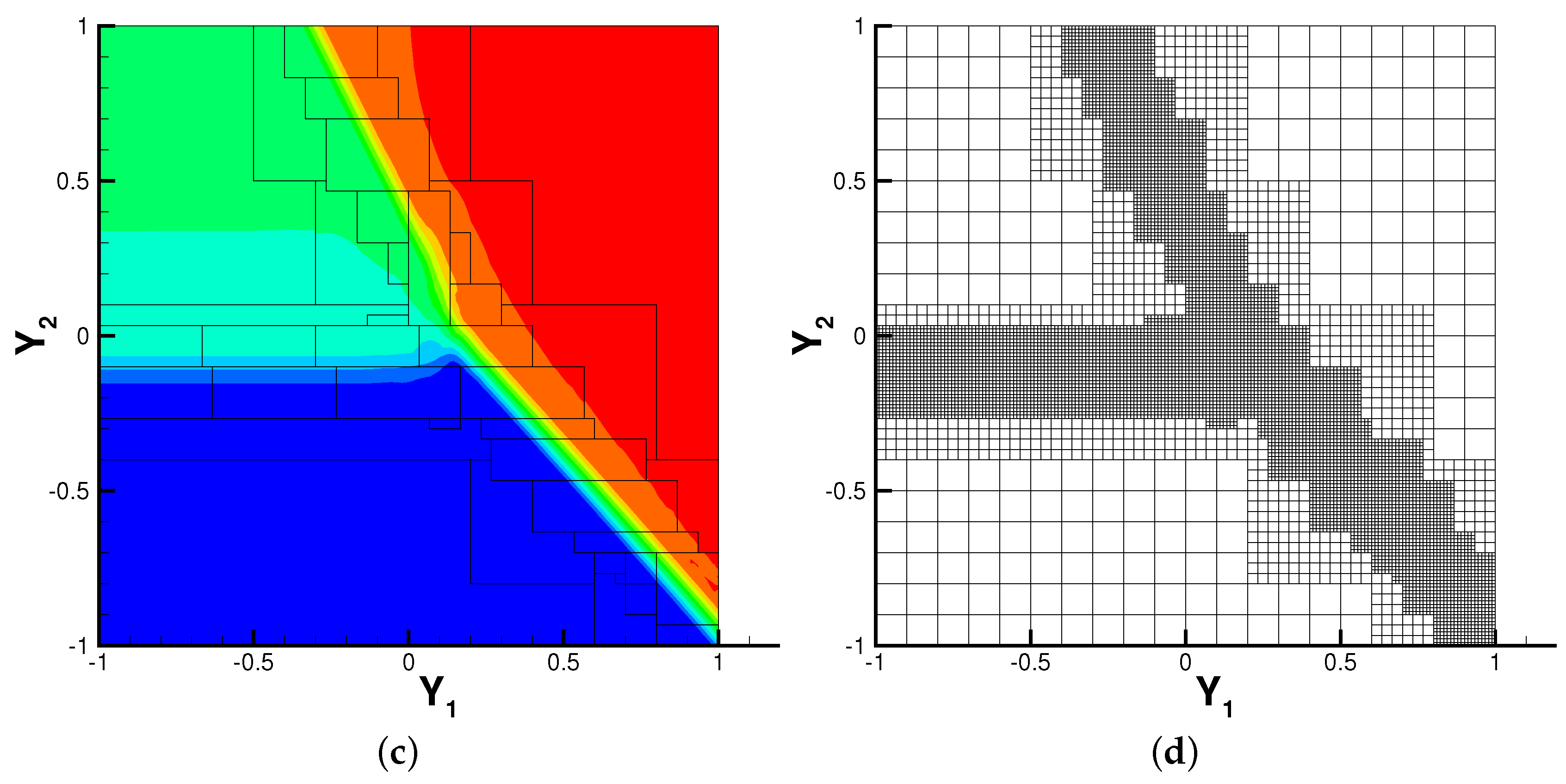
3.2. Two-Dimensional Kraichnan-Orszag (K-O) Problem
3.3. Burgers’ Equation with Random Initial Conditions
4. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lin, G.; Su, C.-H.; Karniadakis, G.E. Random roughness enhances lift in supersonic flow. Phys. Rev. Lett. 2007, 99, 104501. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.; Su, C.-H.; Karniadakis, G.E. Stochastic modeling of random roughness in shock scattering problems: Theory and simulations. Comput. Methods Appl. Mech. Eng. 2008, 197, 3420–3434. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer-Verlag: New York, NY, USA, 1991. [Google Scholar]
- Babuška, I.; Nobile, F.; Tempone, R. A stochastic collocation method for elliptic partial differential equations with random input data. SIAM Rev. 2010, 52, 317–355. [Google Scholar] [CrossRef]
- Ganapathysubramanian, B.; Zabaras, N. Sparse grid collocation schemes for stochastic natural convection problems. J. Comput. Phys. 2007, 225, 652–685. [Google Scholar] [CrossRef]
- Hampton, J.; Doostan, A. Compressive sampling of polynomial chaos expansions: Convergence analysis and sampling strategies. J. Comput. Phys. 2015, 280, 363–386. [Google Scholar] [CrossRef]
- Jakeman, J.D.; Eldred, M.S.; Sargsyan, K. Enhancing ℓ1-minimization estimates of polynomial chaos expansions using basis selection. J. Comput. Phys. 2015, 289, 18–34. [Google Scholar] [CrossRef]
- Karagiannis, G.; Konomi, B.A.; Lin, G. A bayesian mixed shrinkage prior procedure for spatial-stochastic basis selection and evaluation of gpc expansions: Applications to elliptic SPDEs. J. Comput. Phys. 2015, 284, 528–546. [Google Scholar] [CrossRef]
- Lei, H.; Yang, X.; Zheng, B.; Lin, G.; Baker, N. Constructing surrogate models of complex systems with enhanced sparsity: Quantifying the influence of conformational uncertainty in biomolecular solvation. Multiscale Model. Simul. 2015, 13, 1327–1353. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Zabaras, N. An adaptive high-dimensional stochastic model representation technique for the solution of stochastic partial differential equations. J. Comput. Phys. 2010, 229, 3884–3915. [Google Scholar] [CrossRef]
- Peng, J.; Hampton, J.; Doostan, A. A weighted ℓ1-minimization approach for sparse polynomial chaos expansions. J. Comput. Phys. 2014, 267, 92–111. [Google Scholar] [CrossRef]
- Sargsyan, K.; Safta, C.; Najm, H.N.; Debusschere, B.J.; Ricciuto, D.; Thornton, P. Dimensionality reduction for complex models via bayesian compressive sensing. Int. J. Uncertain. Quantif. 2014, 4, 63–93. [Google Scholar] [CrossRef]
- Tang, G.; Iaccarino, G. Subsampled gauss quadrature nodes for estimating polynomial chaos expansions. SIAM J. Uncertain. Quantif. 2014, 2, 423–443. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, T. On sparse interpolation and the design of deterministic interpolation points. SIAM J. Sci. Comput. 2014, 36, A1752–A1769. [Google Scholar] [CrossRef]
- Wan, X.; Karniadakis, G.E. An adaptive multi-element generalized polynomial chaos method for stochastic differential equations. J. Comput. Phys. 2005, 209, 617–642. [Google Scholar] [CrossRef]
- Wan, X.; Karniadakis, G.E. Multi-element generalized polynomial chaos for arbitrary probability measures. SIAM J. Sci. Comput. 2006, 28, 901–928. [Google Scholar] [CrossRef]
- Foo, J.; Karniadakis, G.E. Multi-element probabilistic collocation method in high dimensions. J. Comput. Phys. 2010, 229, 1536–1557. [Google Scholar] [CrossRef]
- Foo, J.; Wan, X.; Karniadakis, G.E. The multi-element probabilistic collocation method (ME-PCM): Error analysis and applications. J. Comput. Phys. 2008, 227, 9572–9595. [Google Scholar] [CrossRef]
- Archibald, R.; Gelb, A.; Saxena, R.; Xiu, D. Discontinuity detection in multivariate space for stochastic simulations. J. Comput. Phys. 2009, 228, 2676–2689. [Google Scholar] [CrossRef]
- Bilionis, I.; Zabaras, N.; Konomi, B.; Lin, G. Multi-output separable gaussian process: Towards an efficient, fully bayesian paradigm for uncertainty quantification. J. Comput. Phys. 2013, 241, 212–239. [Google Scholar] [CrossRef]
- Chantrasmi, T.; Doostan, A.; Iaccarino, G. Pade-legendre approximants for uncertainty analysis with discontinuous response surface. J. Comput. Phys. 2009, 228, 7159–7180. [Google Scholar] [CrossRef]
- Jakeman, J.; Archibald, R.; Xiu, D. Characterization of discontinuities in high-dimensional stochastic problmes on adaptive sparse grids. J. Comput. Phys. 2011, 230, 3977–3997. [Google Scholar] [CrossRef]
- Jakeman, J.; Narayan, A.; Xiu, D. Minimal multi-element stochastic collocation for uncertainty quantification of discontinuous functions. J. Comput. Phys. 2013, 242, 790–808. [Google Scholar] [CrossRef]
- Konomi, B.; Karagiannis, G.; Sarkar, A.; Lin, G. Bayesian treed multivariate gaussian process with adaptive design: Application to a carbon capture unit. Technometrics 2014, 56, 145–158. [Google Scholar] [CrossRef]
- Ma, X.; Zabaras, N. An adaptive hierarchical sparse grid collocation algorithm for the solution of stochastic differential equations. J. Comput. Phys. 2009, 228, 3084–3113. [Google Scholar] [CrossRef]
- Shen, C.; Qiu, J.-M.; Christlieb, A. Adaptive mesh refinement based on high order finite difference WENO scheme for multi-scale simulations. J. Comput. Phys. 2011, 230, 3780–3802. [Google Scholar] [CrossRef]
- Shu, C.-W. High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 2009, 51, 82–126. [Google Scholar] [CrossRef]
- Qiu, J.; Shu, C.-W. Runge-Kutta discontinuous Galerkin method using WENO limiters. SIAM J. Sci. Comput. 2005, 26, 907–929. [Google Scholar] [CrossRef]
- Tan, S.; Shu, C.-W. Inverse Lax-Wendroff procedure for numerical boundary conditions of conservation laws. J. Comput. Phys. 2010, 229, 8144–8166. [Google Scholar] [CrossRef]
- Berger, M.; Colella, P. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 1989, 82, 64–84. [Google Scholar] [CrossRef]
- Berger, M.; Oliger, J. Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
- Berger, M.; Rigoutsos, I. An algorithm for point clustering and grid generation. IEEE Trans. Syst. Man Cybern. 1991, 21, 1278–1286. [Google Scholar] [CrossRef]

| Mesh Level | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| points | var. err. | max. err. | points | var. err. | max. err. | points | var. err. | max err. | |
| 2 | 4812 | 2.21 × 10 | 1.48 × 10 | 9964 | 2.20 × 10 | 1.18 × 10 | 22,500 | 2.19 × 10 | 8.62 × 10 |
| 3 | 11,028 | 5.22 × 10 | 1.65 × 10 | 47,140 | 2.25 × 10 | 8.94 × 10 | 135,308 | 1.65 × 10 | 6.85 × 10 |
| 4 | 22,332 | 4.05 × 10 | 6.08 × 10 | 144,468 | 1.13 × 10 | 7.64 × 10 | 676,324 | 3.75 × 10 | 6.51 × 10 |
| Mesh Level | |||
|---|---|---|---|
| Points | Linear Reconstruction | WENO Reconstruction | |
| 1 | 2500 | 6.01 × 10 | 3.15 × 10 |
| 2 | 5060 | 1.99 × 10 | 1.04 × 10 |
| 3 | 12,740 | 6.51 × 10 | 3.43 × 10 |
| 4 | 35,780 | 2.16 × 10 | 1.13 × 10 |
| 5 | 104,900 | 7.08 × 10 | 3.66 × 10 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Lin, G.; Christlieb, A.J.; Qiu, J. An Adaptive WENO Collocation Method for Differential Equations with Random Coefficients. Mathematics 2016, 4, 29. https://doi.org/10.3390/math4020029
Guo W, Lin G, Christlieb AJ, Qiu J. An Adaptive WENO Collocation Method for Differential Equations with Random Coefficients. Mathematics. 2016; 4(2):29. https://doi.org/10.3390/math4020029
Chicago/Turabian StyleGuo, Wei, Guang Lin, Andrew J. Christlieb, and Jingmei Qiu. 2016. "An Adaptive WENO Collocation Method for Differential Equations with Random Coefficients" Mathematics 4, no. 2: 29. https://doi.org/10.3390/math4020029
APA StyleGuo, W., Lin, G., Christlieb, A. J., & Qiu, J. (2016). An Adaptive WENO Collocation Method for Differential Equations with Random Coefficients. Mathematics, 4(2), 29. https://doi.org/10.3390/math4020029






