Stagnation-Point Flow towards a Stretching Vertical Sheet with Slip Effects

Abstract

The effects of partial slip on stagnation-point flow and heat transfer due to a stretching vertical sheet is investigated. Using a similarity transformation, the governing partial differential equations are reduced into a system of nonlinear ordinary differential equations. The resulting equations are solved numerically using a shooting method. The effect of slip and buoyancy parameters on the velocity, temperature, skin friction coefficient and the local Nusselt number are graphically presented and discussed. It is found that dual solutions exist in a certain range of slip and buoyancy parameters. The skin friction coefficient decreases while the Nusselt number increases as the slip parameter increases.

1. Introduction

The investigation of flow and heat transfer of a viscous and incompressible fluid over a stretching/shrinking sheet has received great interest among researchers. This growing attention is because of its massive applications in engineering and industrial processes include manufacturing processes of polymer, paper production, glass fiber production, etc. The heat transfer and flow field is very important for determining the quality of the final products of such processes. In this case, the quality of the final products depends on heat and mass transfer between the fluid and the stretching/shrinking sheet [1]. Crane [2] is the first who analyzed the steady two dimensional flow over a linearly stretching sheet and found the similarity solution in closed analytical form. In extension to that, various aspect of this problem was investigated by researchers. On the other hand, Chiam [3] reported the analytical and numerical solutions of the stagnation-point flow over a flat stretching sheet with variable thermal conductivity. Since then, many researchers, such as Mahapatra and Gupta [4,5], Ishak et al. [6,7], Layek et al. [8], Nadeem et al. [9], Bachok et al. [10], Bhattacharyya and Layek [11], and Lok et al. [12] have investigated the behavior of stagnation-point flow with different aspects and conditions such as considering magnetic field effect, homogeneous-heterogeneous reactions effect, thermal radiation effect, suction/blowing, and micropolar fluid.

In the above-mentioned papers, the investigations did not consider the partial slip boundary condition. In certain circumstances, the no-slip condition is not consistent with all physical characteristics, i.e., it is essential to replace the no-slip boundary condition by the partial slip boundary condition [13]. In addition to this, partial slips over a moving surface also occur for fluids with particulates, such as emulsions, suspensions, foams, and polymer solutions [14]. Over the years, the study of slip effects for different types of flow and surfaces has been done by Andersson [15], Wang [16,17], Ariel et al. [18], Abbas et al. [19], and Fang et al. [20,21].

The aim of the present study is to investigate the slip effects on the stagnation point flow towards a stretching vertical sheet. In this study, we tend to continue the work by Ishak et al. [6] and Bhattacharyya et al. [13], by taking into account the slip effect and mixed convection/buoyancy parameter for stretching sheet case. To our best knowledge, the present study has not been considered before.

2. Mathematical Formulation

Consider a steady, two dimensional stagnation point flow of a viscous and incompressible fluid towards a stretching vertical sheet placed in the plane y = 0. The flow being confined to y > 0. Under the Boussinesq and the usual boundary layer approximations, the basic equations are (see [6,13])

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=U\frac{dU}{dx}+\mathsf{\nu }\frac{{\partial }^{2}u}{\partial y^2}+g\mathsf{\beta }(T-T_{\infty })$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\mathsf{\alpha }\frac{{\partial }^{2}T}{\partial y^2}$$

(3)

subject to boundary conditions

$$\begin{array}{l}u=cx+L\left(\partial u/\partial y\right),v=0,T=T_w\mathrm{at}y=0\\ u\to U(x)=ax,T\to T_{\infty }\mathrm{as}y\to \infty \end{array}$$

(4)

where u and v are the velocity components in the x and y directions, respectively, T is the temperature of the fluid, g is the gravity acceleration, ν is the kinematic viscosity, β is the thermal expansion coefficient, α is the thermal diffusivity, c is the stretching rate, U(x) is the straining velocity of the stagnation point flow, a is the straining rate parameter, T_w(x) = T_∞ + bx is the surface temperature, T_∞ is the ambient temperature, and L denotes the slip length/coefficient. The slip model introduced by Navier in 1823 (Mehmood and Ali [22]) assumed that the velocity of the fluid on the surface of the solid body is proportional to the shear rate on the surface $\partial u/\partial y$, which is written as $u=L\left(\partial u/\partial y\right)$. For the case L = 0, the no-slip condition is obtained. If the finite slip length L is considered, the slip condition occurs on the surface of the fluid-solid (Mehmood and Ali [22]).

We look for similarity solutions of the Equations (1)–(3) of the following form:

$$\mathsf{\eta }={\left(\frac{U}{\mathsf{\nu }x}\right)}^{1/2}y,\mathsf{\psi }={\left(\mathsf{\nu }xU\right)}^{1/2}f\left(\mathsf{\eta }\right),\mathsf{\theta }\left(\mathsf{\eta }\right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}$$

(5)

where η is the independent similarity variable, f(η) is the dimensionless stream function, θ(η) is the dimensionless temperature and Ψ is the stream function defined as $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$, which identically satisfies Equation (1). Using Equation (5) we obtain:

$$u=ax{f}^{\prime }(\eta )\mathrm{and}v=-{(\nu a)}^{1/2}f(\eta )$$

(6)

where primes denote differentiation with respect to η.

Substituting variables in Equations (5) and (6) into Equations (2) and (3), we obtain the following nonlinear ordinary differential equations:

$$f^{‴}+f{f}^{″}+1-{f^{\prime }}^2+\lambda \theta =0$$

(7)

$${\theta }^{″}+\mathrm{Pr}(f{\theta }^{\prime }-f^{\prime }\theta )=0$$

(8)

where $\lambda =g\beta b/a^2$ is the buoyancy parameter, with λ > 0 for assisting flow and λ < 0 for opposing flow, and $\mathrm{Pr}=\nu /\alpha$ is the Prandtl number. The boundary conditions in Equation (4) now become:

$$\begin{array}{l}f(0)=0,f^{\prime }(0)=\epsilon +\delta f^{″}(0),\theta (0)=1\\ f^{\prime }(\eta )\to 1,\theta (\eta )\to 0\mathrm{as}\eta \to \infty \end{array}$$

(9)

where $\epsilon =c/a$ is the stretching parameter and $\delta =L{(a/\nu )}^{1/2}$ is the velocity slip parameter. The slip parameter is a measure of the drag force acting on the surface at the boundary (Murthy and Kumar [23]).

The physical quantities of interest are the skin friction coefficient C_f and the local Nusselt number Nu_x, which are defined as (see [13,24]):

$$C_f=\frac{{\tau }_w}{\rho U^2},{\text{Nu}}_x=\frac{x{q}_w}{k\left(T_w-T_{\infty }\right)},$$

(10)

where the surface shear stress τ_w and the surface heat flux q_w are given by:

$${\tau }_w=\mu {\left(\frac{\partial u}{\partial y}\right)}_{y=0},q_w=-k{\left(\frac{\partial T}{\partial y}\right)}_{y=0},$$

(11)

with μ and k being the dynamic viscosity and the thermal conductivity, respectively. Using the similarity variables of Equation (5), we obtain:

$$C_f{Re}_x^{1/2}=f^{″}\left(0\right),{\text{Nu}}_x/{Re}_x^{1/2}=-{\theta }^{\prime }\left(0\right)$$

(12)

where ${\mathrm{Re}}_x=Ux/\nu$ is the local Reynolds number.

3. Results and Discussion

The nonlinear ordinary differential Equations (7) and (8) subjected to the boundary conditions in Equations (9) were solved numerically using a shooting method. We study the slip effect on the velocity and temperature profiles, as well as the skin friction coefficient and the local Nusselt number. The equations were solved for some values of the governing parameters namely buoyancy parameter λ and velocity slip parameter δ with fixed values of the stretching parameter ε and Prandtl number Pr. In the present study, dual solutions are obtained using different initial guesses of f″(0) and −θ′(0), where all velocity and temperature profiles satisfy the far field boundary conditions of Equation (9) asymptotically but with two different shapes.

Table 1. Comparison of the values of ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Nu}}_x{\mathrm{Re}}_x^{-1/2}$ with those of Ishak et al. [6], by setting $a/c=1$ and λ = 1 in Equations (6) and (8) of Ishak et al. [6].

Pr	Buoyancy Assisting Flow				Buoyancy Opposing Flow
	Rex1/2Cf		NuxRex−1/2		Rex1/2Cf		NuxRex−1/2
	Ishak et al. [6]	Present	Ishak et al. [6]	Present	Ishak et al. [6]	Present	Ishak et al. [6]	Present
0.72	0.3645	0.36449	1.0931	1.09310	−0.3852	−0.38518	1.0293	1.02925
6.8	0.1804	0.18041	3.2902	3.28957	−0.1832	−0.18323	3.2466	3.24608
10		0.15563		3.98240		−0.15747		3.94370
20	0.1175	0.11750	5.6230	5.62013	−0.1183	−0.11831	5.5923	5.58959
30		0.09889		6.87771		−0.09938		6.85149
40	0.0873	0.08724	7.9463	7.93830	−0.0876	−0.08758	7.9227	7.91489
50		0.07903		8.87292		−0.07929		8.85153
60	0.0729	0.07284	9.7327	9.71801	−0.0731	−0.07304	9.7126	9.69818
70		0.06794		10.49524		−0.06810		10.47665
80	0.0640	0.06394	11.2413	11.21874	−0.0642	−0.06407	11.2235	11.20117
90		0.06059		11.89831		−0.06070		11.88161
100	0.0578	0.05772	12.5726	12.54109	−0.0579	−0.05782	12.5564	12.52515

shows the comparison values of ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Nu}}_x{\mathrm{Re}}_x^{-1/2}$ with those of Ishak et al. [6] with no-slip condition for both cases of assisting and opposing flows by setting $a/c=1$ and λ = 1 in Equations (6) and (8) of the paper by Ishak et al. [6]. To obtain the similar form of similarity equations by Ishak et al. [6], we take ε = 1 and δ = 0 (no-slip boundary condition) in boundary conditions of Equation (9). We let λ = 1 and λ = −1 in Equation (7) to get particular case of buoyancy assisting and opposing flows, which considered by Ishak et al. [6]. The comparisons are in a favorable agreement, thus provide confidence to the present results.

Figure 1 and Figure 2 present the skin friction coefficient $C_f{\mathrm{Re}}_x^{1/2}$ and the local Nusselt number ${\mathrm{Nu}}_x{\mathrm{Re}}_x^{-1/2}$ as a function of the buoyancy parameter λ for some values of the slip parameter δ when ε = 1 and Pr = 1. In both Figure 1 and Figure 2, it is found that dual solutions exist for system of Equations (7)–(9) for opposing flow (λ < 0). A unique solution is found to exist for the assisting flow (λ > 0) not limited to the result reported in Figure 1 and Figure 2. Both Figure 1 and Figure 2 indicate that the magnitude of critical values $\left|{\lambda }_c\right|$ for which the solution exist increase as δ increases. This finding suggests that slip effect widens the region of dual solutions to the similarity Equations (7)–(9). These values are presented in

Table 2. Values of critical values λ_c for some values of δ when ε = 1 and Pr = 1.

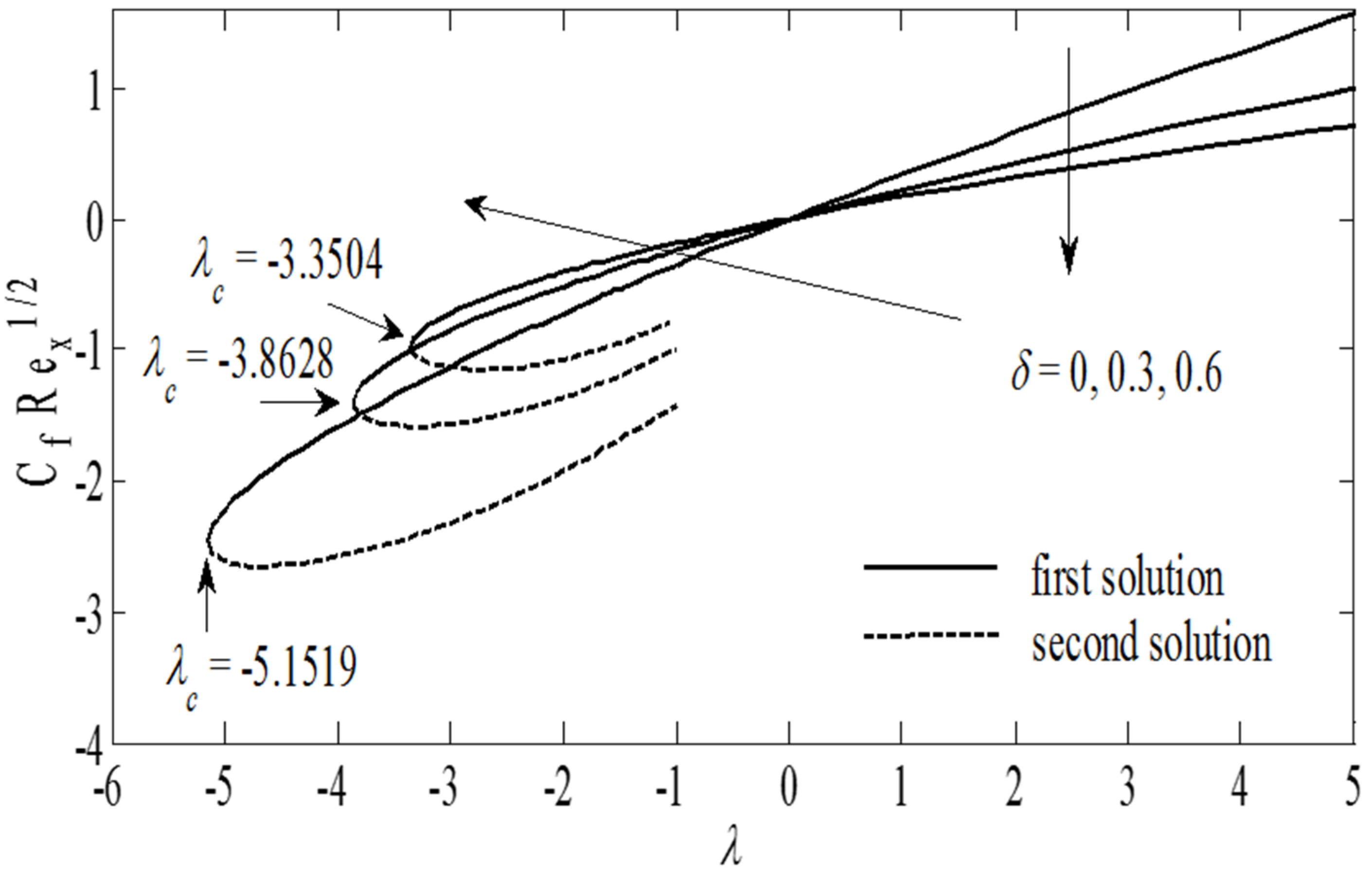
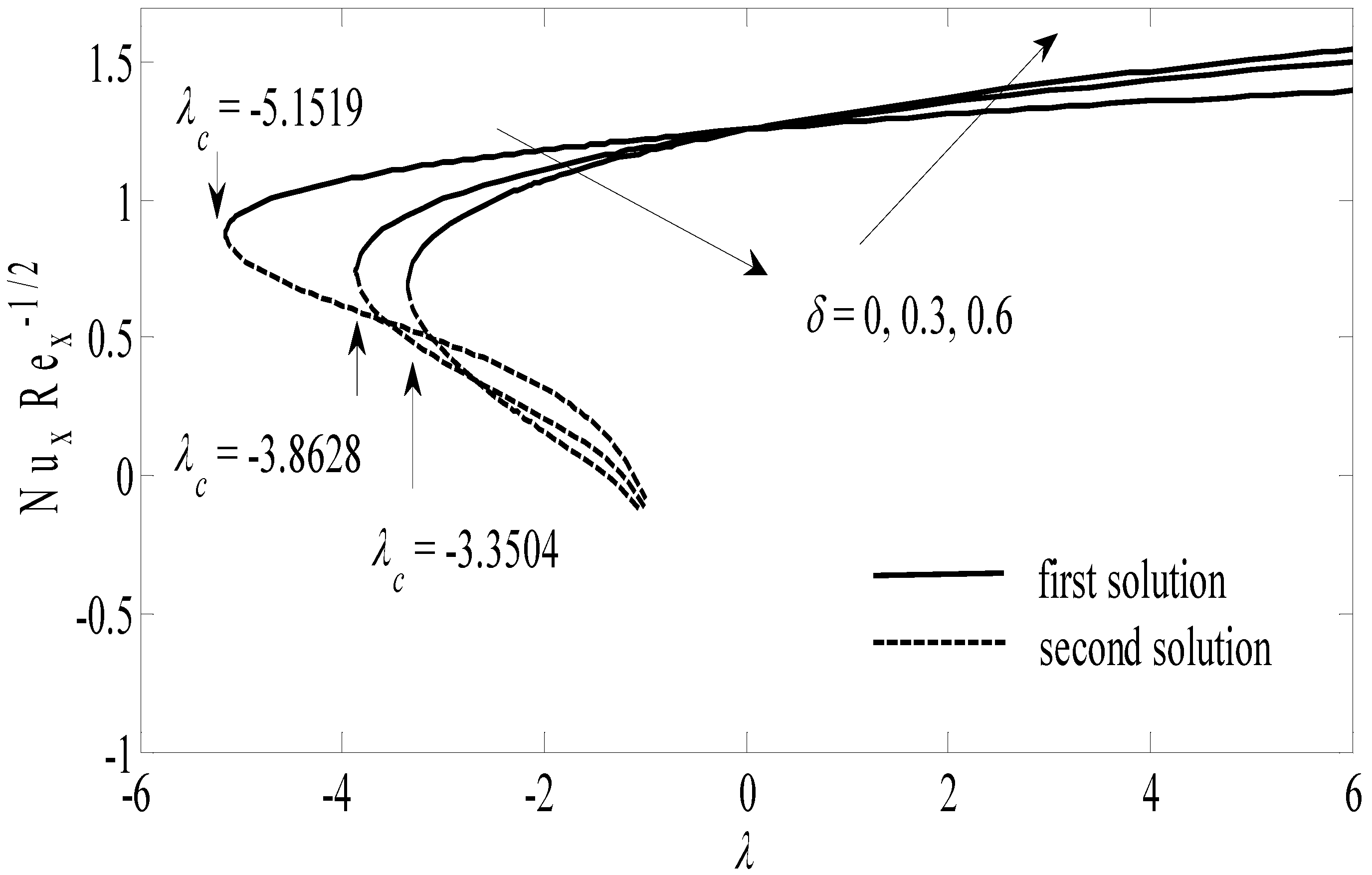
δ	λc
0	−3.3504
0.3	−3.8628
0.6	−5.1519

. The first solutions are expected to be stable and physically realizable, whilst those of second solutions are not. The temporal stability analysis for the multiple solutions has been done by several researchers such as Merkin [25], Weidman et al. [26], Paullet and Weidman [27], Harris et al. [28], and Postelnicu and Pop [29]. However, the stability analysis is not in the scope of this study and, thus, we expect that finding hold for the present study.

In Figure 1, it is observed that the magnitude of the skin friction coefficient $\left|C_f{\mathrm{Re}}_x^{1/2}\right|$ decreases as δ increases for both first and second solutions. This is because of slip effect which decreases the velocity gradient at the surface f″(0) and in turn decreases the surface shear stress. Consequently, the skin friction coefficient decreases with the increasing of velocity slip parameter as supported by the skin friction coefficient values presented in

Table 3. The values of $C_f{\mathrm{Re}}_x^{1/2}$ and ${\mathrm{Nu}}_x/{\mathrm{Re}}_x^{1/2}$ for different values of δ when ε = 1 and Pr = 1.

δ	λ = 1 (Assisting Flow)		λ = −2 (Opposing Flow)
	CfRex1/2	Nux/Rex1/2	CfRex1/2	Nux/Rex1/2
0	0.3349	1.2826	−0.7244 (−1.9285)	1.1814 (0.3191)
0.3	0.2223	1.3064	−0.5180 (−1.3669)	1.1130 (0.2101)
0.6	0.1659	1.3180	−0.4086 (−1.0775)	1.0713 (0.1596)

( ): second solution.

. From Figure 1, a positive value for $C_f{\mathrm{Re}}_x^{1/2}$ for assisting flow means the fluid impose a drag on the sheet, while the opposite trends occurs for negative value of $C_f{\mathrm{Re}}_x^{1/2}$. It is also important to mention that all the curve intersects at $C_f{\mathrm{Re}}_x^{1/2}=0$ when λ = 0 i.e., for the forced convection. This is due to the fact that the surface shear stress is zero when the both stretching sheet and fluid move in the same velocity at λ = 0 and ε = 1.

From Figure 2, the local Nusselt number increases with δ for the assisting flow, while the opposite behaviors are shown for the opposing flow. Physically, it is shown that the heat transfer rate at the surface increases in the presence of the slip effect at the boundary. This is because the temperature gradient at the surface increases as δ increases, which implies an increase in the heat transfer rate at the surface. It is also noticed that all the values of $\mathrm{N}{\mathrm{u}}_x/{\mathrm{Re}}_x^{1/2}$ are positive for the first solution as depicted in Figure 2 and shown in Table 3, which indicate that the heat is transferred from heated surface to the cooler fluid. Similar to Figure 1, all the curve in Figure 2 intersects at λ = 0 (forced convection) with $\mathrm{N}{\mathrm{u}}_x/{\mathrm{Re}}_x^{1/2}=1.2533$. It seems that, even though the skin friction coefficient is zero at λ = 0, as shown in Figure 1, the non-zero value obtained for $\mathrm{N}{\mathrm{u}}_x/{\mathrm{Re}}_x^{1/2}$, which indicates that heat transfer process remain occur between the surface and fluid since both are in different temperatures.

Figure 3 and Figure 4 exhibit the effect of slip on the velocity and temperature profiles for opposing flow λ = −2 when Pr = 1 and ε = 1. From Figure 3, the slip parameter increases the velocity boundary layer thickness and in turn decreases the velocity gradient at the surface. As consequence, the surface shear stress decreases. This result is consistent with the result presented in Figure 1. It is also noted that the negative velocity gradient is obtained near the surface and then the positive velocity gradient is shown for both first and second solutions, which consistent with the variation of the skin friction coefficient presented in Figure 1.

Figure 4 shows the influences of slip effect on the temperature profiles for the opposing flow when the values of ε and Pr are fixed. From Figure 4, it is seen that the temperature increases with increasing δ for the first solution while for the second solution it acts oppositely. This observation occurs because of increasing of thermal boundary layer thicknesses which imply a decrease in the temperature gradient at the surface. As a consequence, the local Nusselt number decreases as shown in Figure 2 for the opposing flow when λ = −2. For the second solution, it is noticed that the thermal boundary layer thickness decreases as slip parameter increase and in consequence increases the temperature gradient at the surface. As a results, heat transfer rate at the surface increases for the second solution. This result is consistent with the result presented in Figure 2. As illustrated in Figure 3 and Figure 4, both the velocity and temperature profiles satisfy the infinity boundary conditions of Equation (9) asymptotically which support the numerical results obtained besides supporting the duality nature of the solutions displayed in Figure 1 and Figure 2.

4. Conclusions

In this paper, we have numerically investigated the steady stagnation point flow towards a stretching vertical sheet with partial slip effect at the boundary. The similarity transformation was employed to transform the governing partial differential equations into a system of nonlinear ordinary differential equations. The effect of slip and buoyancy parameters on the fluid flow and heat transfer characteristics was thoroughly examined. It was found that the skin friction coefficient decreased as the slip parameter increased for both assisting and opposing flows. The local Nusselt number increased with the increasing of the slip parameter for the assisting flow, while the opposite trend was observed for the opposing flow. An increment in the value of the slip parameter widened the range of the buoyancy parameter for which the solution exists. The present problem showed the existence of dual solutions for the opposing flow.