POD-Based Constrained Sensor Placement and Field Reconstruction from Noisy Wind Measurements: A Perturbation Study
Abstract
:1. Introduction
2. A POD-Based Sensor Placement Strategy
2.1. A Review of Gappy-POD
2.2. Constrained Sensor Placement
3. Uncertainty in Measurements
3.1. Results for Uniform Measurement Errors
3.2. Results for Non-Uniform Measurement Errors
4. Detecting the Malfunctioning Sensor
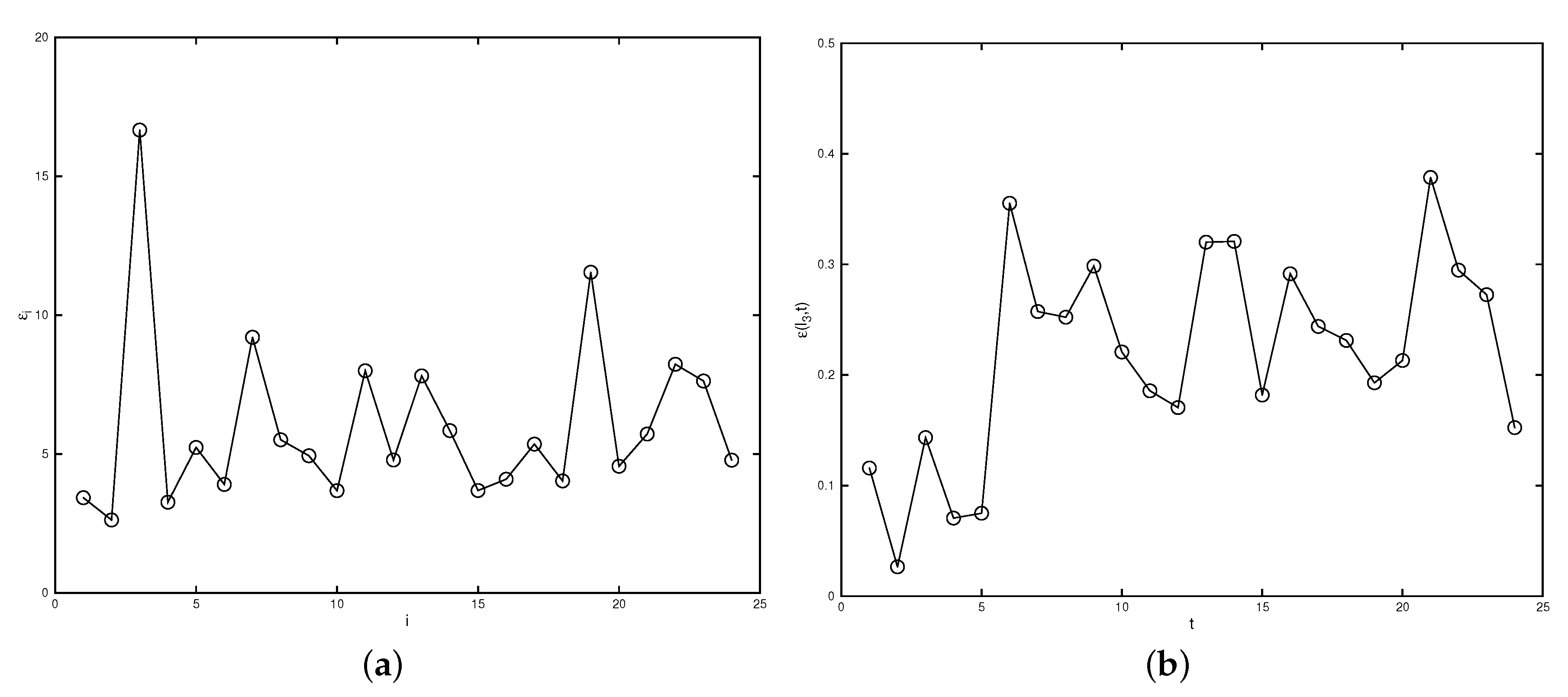
- For each sensor location , we use the data from , , …, , , …, to reconstruct the field and denote the reconstructed valued at this point as . Here, we take as we consider only the first 24 snapshot from our data.
- Compute the difference between the reconstructed value and the observed value at each : , .
- Compare the sum of over all snapshots at each . When is large, we claim that the i-th sensor is not functioning well.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Venturi, D. On Proper Orthogonal Decomposition of Randomly Perturbed Fields with Applications to Flow past a Cylinder and Natural Convection over a Horizontal Plate. J. Fluid Mech 2006, 559, 215–254. [Google Scholar] [CrossRef]
- Rempfer, D. Low-dimensional modeling and numerical simulation of transition in simple shear flow. Ann. Rev. Fluid Mech. 2003, 35, 229–265. [Google Scholar] [CrossRef]
- Bekooz, G.; Holmes, P.; Lumley, J. The proper orthogonal decomposition in the analysis of turbulent flows. Ann. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Aubry, N.; Guyonnet, R.; Stone, E. Spatio-temporal analysis of complex signals: Theory and applications. J. Stat. Phys. 1991, 64, 683–739. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures, Parts I, II and III. Quart. Appl. Math. 1987, XLV, 561–590. [Google Scholar]
- Zhang, Y.; Bellingham, J. An efficient method of selecting ocean observing locations for capturing the leading modes and reconstructing the full field. J. Geophys. Res. 2008, 113, C04005. [Google Scholar] [CrossRef]
- Venturi, D.; Karniadakis, G. Gappy Data and Reconstruction Procedures for Flow Past a Cylinder. J. Fluid Mech. 2004, 519, 315–336. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Rixen, M.; Beckers, J.M. Reconstruction of incomplete oceanographic data sets using empirical orthogonal functions: Application to the Adriatic Sea surface temperature. Ocean Modelling 2005, 9, 325–346. [Google Scholar] [CrossRef]
- Beckers, J.; Rixen, M. EOF Calculations and Data Filling from Incomplete Oceanographic datasets. J. Atmos. Ocean Tech. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- D’Andrea, F.; Vautard, R. Extratropical low-frequency variability as a low dimensional problem. Part I: A simplified model. Quart. J. Roy. Meteor. Soc. 2001, 127, 1357–1375. [Google Scholar] [CrossRef]
- Hendricks, J.; Leben, R.; Born, G.; Koblinsky, C. Empirical orthogonal function analysis of global TOPEX/POSEIDON altimeter data and implications for detection of global sea rise. J. Geophys. Res. 1996, 101, 14131–14145. [Google Scholar] [CrossRef]
- Everson, R.; Cornillon, P.; Sirovich, L.; Webber, A. An empirical eigenfunction analysis of sea surface temperatures in the North Atlantic. J. Phys. Ocean. 1995, 27, 468–479. [Google Scholar] [CrossRef]
- Wilkin, J.; Zhang, W. Modes of mesoscale sea surface height and temperature variability in the East Australian Current. J. Geophys. Res. 2006, 112, C01013. [Google Scholar] [CrossRef]
- Pedder, M.; Gomis, D. Application of EOF Analysis to the spatial estimation of circulation features in the ocean sampled by high-resolution CTD samplings. J. Atmos. Ocean Tech. 1998, 15, 959–978. [Google Scholar] [CrossRef]
- Houseago-Stokes, R. Using optimal interpolation and EOF analysis on North Atlantic satellite data. International WOCE Newsletter 2000, 28, 26–28. [Google Scholar]
- Preisendorfer, W.; Mobley, C.D. Principal component analysis in meteorology and oceanography; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Dickey, T. Emerging ocean observations for interdisciplinary data assimilation systems. J. Mar. Syst. 2003, 40–41, 5–48. [Google Scholar] [CrossRef]
- Yildirim, B.; Chryssostomidis, C.; Karniadakis, G.E. Efficient sensor placement for ocean measurement using low-dimensional concepts. Ocean Modelling 2009, 27, 160–173. [Google Scholar] [CrossRef]
- Yang, X.; Venturi, D.; Chen, C.; Chryssostomidis, C.; Karniadakis, G.E. EOF-based constrained sensor placement and field reconstruction from noisy ocean measurements: Application to Nantucket Sound. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Xue, P.; Chen, C.; Beardsley, R.C.; Limeburner, R. Observing system simulation experiments with ensemble Kalman filters in Nantucket Sound, Massachusetts. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Li, W.; Sun, S.; Jia, Y.; Du, J. Robust unscented Kalman filter with adaptation of process and measurement noise covariances. Digit. Signal Process. 2016, 48, 93–103. [Google Scholar] [CrossRef]
- Barrault, M.; Maday, Y.; Nguyen, N.C.; Patera, A.T. An ’empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathematique 2004, 339, 667–672. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.; Cueto, E.; González, D.; Alfaro, I.; Ammar, A.; Huerta, A. PGD-based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20, 31–59. [Google Scholar] [CrossRef]
- Nadal, E.; Chinesta, F.; Díez, P.; Fuenmayor, F.; Denia, F. Real time parameter identification and solution reconstruction from experimental data using the Proper Generalized Decomposition. Comput. Methods in Appl. Mech. Eng. 2015, 296, 113–128. [Google Scholar] [CrossRef]
- Everson, R.; Sirovich, L. The Karhunen-Loève procedure for gappy data. J. Opt. Soc. Am., A 1995, 12, 1657–1664. [Google Scholar] [CrossRef]
- Willcox, K. Unsteady flow sensing and estimation via the gappy proper orthogonal decomposition. Comput. Fluids 2006, 35, 208–226. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K.E. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition. AIAA J. 2004, 42, 1505–1516. [Google Scholar] [CrossRef]
- Mokhasi, P.; Rempferm, D. Optimized sensor placement for urban flow measurement. Phys. Fluids 2004, 16, 1758–1764. [Google Scholar] [CrossRef]
- Cohen, K.; Siegel, S.; McLaughlin, T. Sensor placement based on proper orthogonal decomposition modeling of a cylinder wake. AIAA Paper 2003-4259. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-located Conferences, Orlando, FL, USA, 23–26 June 2003.
- Mathelin, L.; Maître, O.L. Robust control of uncertain cylinder wake flows based on robust reduced order models. Comput. Fluids 2009, 38, 1168–1182. [Google Scholar] [CrossRef]
- Venturi, D.; Wan, X.; Karniadakis, G.E. Stochastic low-dimensional modelling of a random laminar wake past a circular cylinder. J. Fluid Mech. 2008, 606, 339–367. [Google Scholar] [CrossRef]




| Four Modes | Six Modes | Eight Modes |
|---|---|---|
| 6s-6s-6s-6s | 4s-4s-4s-4s-4s-4s | 3s-3s-3s-3s-3s-3s-3s-3s |
| R Value | ||||
|---|---|---|---|---|
| Cond(M) |
| R Value | ||||
|---|---|---|---|---|
| maximum of | ||||
| average of |
| R Value | ||||
|---|---|---|---|---|
| maximum of | ||||
| average of |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Yang, X.; Lin, G. POD-Based Constrained Sensor Placement and Field Reconstruction from Noisy Wind Measurements: A Perturbation Study. Mathematics 2016, 4, 26. https://doi.org/10.3390/math4020026
Zhang Z, Yang X, Lin G. POD-Based Constrained Sensor Placement and Field Reconstruction from Noisy Wind Measurements: A Perturbation Study. Mathematics. 2016; 4(2):26. https://doi.org/10.3390/math4020026
Chicago/Turabian StyleZhang, Zhongqiang, Xiu Yang, and Guang Lin. 2016. "POD-Based Constrained Sensor Placement and Field Reconstruction from Noisy Wind Measurements: A Perturbation Study" Mathematics 4, no. 2: 26. https://doi.org/10.3390/math4020026
APA StyleZhang, Z., Yang, X., & Lin, G. (2016). POD-Based Constrained Sensor Placement and Field Reconstruction from Noisy Wind Measurements: A Perturbation Study. Mathematics, 4(2), 26. https://doi.org/10.3390/math4020026






