1. Introduction
We study the asymptotic expansion of the Riemann–Liouville fractional integral (fI) and fractional derivative (fD) of a function f(z), by using their relations with the corresponding Liouville fI and fD, respectively. We then present a method of deriving the asymptotic expansion of a function, when this is expressed by the Riemann–Liouville fI or fD of a function, which is analytic in a domain in the complex plane. As an example, we take up the confluent hypergeometric function.
We adopt the following definition of the Riemann–Liouville fI [
1,
2] (Section 2.3.2).
Definition 1. Let c ∈ ℂ,
z ∈ ℂ,
f(
ζ) ∈
1(
P(
c, z))
and f(
ζ)
be continuous in a neighborhood of ζ =
z. Then, the Riemann–Liouville fI of order λ ∈
+ℂ
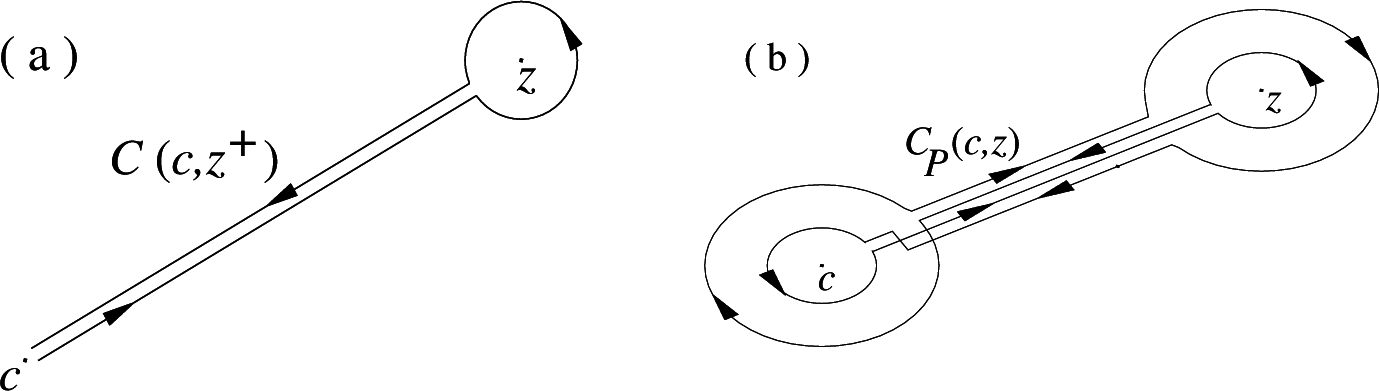
is defined by: Here, P(c, z) is the path of integration from c to z,
denotes that the function f(ζ) is integrable on P(c, z) and ℂ, ℝ and ℤ represent the sets of all complex numbers, of all real numbers and of all integers, respectively. We also use notations +ℂ := {z ∈ ℂ|Re z > 0}, ℤ>a := {n ∈ ℤ|n > a}, ℤ<b := {n ∈ ℤ|n < b}, ℤ[a,b] := {n ∈ ℤ|a ≤ n ≤ b} for a ∈ ℤ and b ∈ ℤ and ℝ>0 := {x ∈ ℝ|x > 0}.
In [
1], the
ϕ-dependent (ϕ-dept) Liouville fI :
D−λ L ϕ
f(
z) of order
λ ∈
+ ℂ is defined for ϕ ∈ ℝ. It was mentioned that it is equal to
(1) if
c is chosen to be
z +
∞ · eiϕ, in [
3]. We now consider the paths of integration
Pϕ(
z) and
Pϕ(
c), which are from
z to
z + ∞ · eiϕ and from
c to
c+
∞ · eiϕ, respectively, as shown in
Figure 1. Here, we consider the cases in which
f(
z) satisfies one of the following conditions.
Condition A. (a) f(ζ) is analytic on neighborhoods of the paths P(c, z], Pϕ[z] and Pϕ(c), and (b) it is analytic also in the region enclosed by them.
Condition B. f(ζ) is expressed as f(ζ) = fγ(ζ) := (ζ − c)γ · f0(ζ), where γ ∈ ℂ\ℤ and f0(ζ) satisfies Condition A with P(c, z] replaced by P[c, z].
Here, notations P(c, z], Pϕ[z] and Pϕ(c) are used to denote that f(ζ) is analytic at the point ζ = z, but not so at ζ = c, and P[c, z] and Pϕ[c] are used when f(ζ) is analytic also at the point ζ = c.
If the ϕ-dept Liouville fI exists, the difference of the Riemann–Liouville and ϕ-dept Liouville fIs is expressed by the path integral along the path Pϕ(c). When the asymptotic expansions of the ϕ-dept Liouville fI and the last path integral are given, the asymptotic expansion of the Riemann–Liouville fI is obtained.
In [
1], the fD corresponding to an fI is defined in the form of a contour integral, for a function
f(
z), which is analytic on a neighborhood of the path of integration. They are analytic continuations of the corresponding fI. As a consequence, the relation between the Riemann–Liouville fI and the corresponding ϕ-dept Liouville fI is analytically continued to the relation between the corresponding fDs. It follows that the same recipe is useful in obtaining the asymptotic expansion of the Riemann–Liouville fD.
In Section 2, we first recall the expressions of the Riemann–Liouville fD, which are expressed by a contour integral. As examples of functions that are expressed by the Riemann–Liouville fD, we consider the incomplete gamma function γ(λ, z) and the confluent hypergeometric function 1F1(a; b; z), in Sections 2.3 and 3, respectively.
In Section 4, we recall the expressions of the ϕ-dept Liouville fD, which are expressed by a contour integral. We then present the ϕ-dept Liouville fD of the functions of which the Riemann–Liouville fD is studied, in Sections 4.4 and 5.
We show the list of fI and fD, which we use in the present paper, with the places where they are defined.
In Section 6, we deform the path or contour of integration, which appears in the Riemann–Liouville fD, and show that the Riemann–Liouville fD of a function f(z) is expressed as a sum of the ϕ-dept Liouville fD of f(z) and a path or contour integral of f(z). By writing the asymptotic expansions of the ϕ-dept Liouville fD, as well as of the path or contour integral that appears, we obtain the asymptotic expansions of the Riemann–Liouville fD under consideration. We confirm that we can obtain the asymptotic expansions of γ(λ, z) and 1F1(a; b; z), by this procedure in Sections 6.1~7.
The function
1F1(
a;
b;
z) treated in Sections 3 and 7 is a solution of Kummer’s differential equation (DE), and is expressed by a Riemann–Liouville fD. In Sections 5 and 7, we treat Kummer’s function
U(
a,
b,
z), which is another solution of Kummer’s DE and is expressed by ϕ-dept Liouville fD. In Sections 3.1 and 5, we show that the expressions of these functions in the form of fD are obtained by the method, which Nishimoto [
4] (Chapter 5, Section 2) used in obtaining the solution of the hypergeometric DE, that is the hypergeometric function, in the form of ϕ-dept Liouville fI. Concluding remarks are given in Section 8.
4. The ϕ-dept Liouville fI and Its Analytic Continuations
4.1. Definitions of ϕ-dept Liouville fI
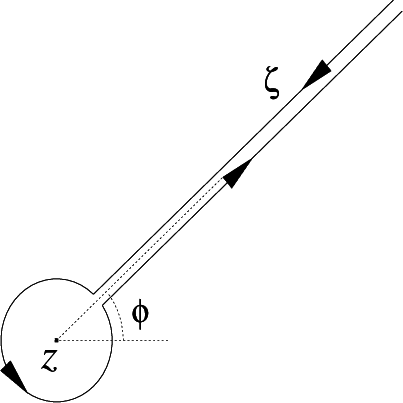
Let
z ∈ ℂ and ϕ ∈ ℝ. We denote the half line {
z +
teiϕ| 0
< t < ∞}, as shown in
Figure 1b, by
Pϕ(
z). When
f(
z +
teiϕ) is locally integrable as a function of
t in the interval (0,
∞), we denote this by
.
Definition 5. Let z ∈ ℂ, ϕ ∈ ℝ, s ∈ ℝ and. Let s1 be such that converges for s > s1 and diverges for s < s1. We then call s1 the abscissa of convergence, and denote it by s1[f] or s1[f(z)]. We then have s1 ∈ ℝ or s1 = −∞.
We note that there exists such a series {tl}l∈Z>0 of tl ∈ ℝ>0, such that
and tl → ∞ as l → ∞, if s > s1[f].
Definition 6. Let z ∈ ℂ, ϕ ∈ ℝ,
and f(
ζ)
be continuous in a neighborhood of ζ =
z. Let λ ∈
+ℂ,
s1[
f] < 0
and Re
λ < −s1[
f].
Then, we define two types of fI,
and,
by: We call
the ϕ-dept Liouville fI of f(z).
4.2. Definitions of ϕ-dept Liouville fD
Let z ∈ ℂ and ϕ ∈ ℝ. When f(z + teiϕ) is infinitely differentiable as a function of t in the interval (0, ∞), we denote this by
.
Definition 7. Let. We denote by m2[f], the supremum of n ∈ ℤ>−1 for which n > s1[f] and Dnf(z) exists on Pϕ(z). When, we put m2[f] = ∞.
We note that if n ∈ ℤ>0 satisfies s1[f] < n ≤ m2[f], then m2[f(n)] = m2[f] − n.
Definition 8. Let.
Let ν ∈ ℂ
satisfy Re
ν ≥ 0
and Re
ν > s1[
f],
and m = ⌊Re
ν⌋
+ 1.
We then define fD,
,
by:where for m ∈ ℤ
>−1.
Formula (28) applies when Re
ν − 1
> s1[
f]
and the rhs exists. When exists,
also exists and is given by: We call
the ϕ-dept Liouville fD of f(z).
4.3. Analytic Continuations of ϕ-dept Liouville fI
In [
1,
4,
12,
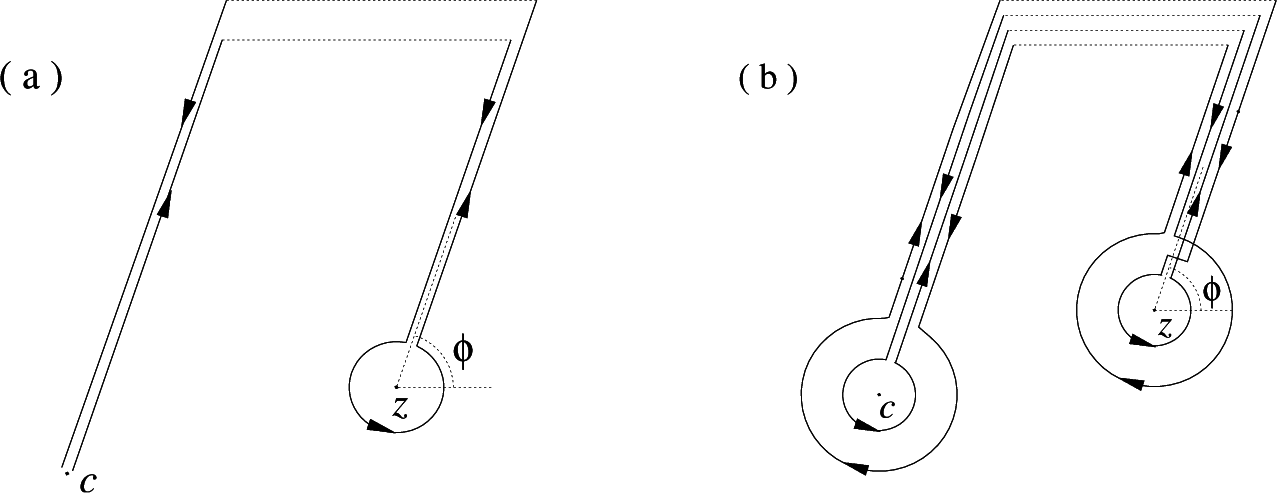
13], analytic continuations of ϕ-dept Liouville fI via contour integrals are discussed. The analytic continuation via Hankel’s contour
Cϕ(
z), which is shown in
Figure 3, is defined as follows.
Definition 9. Let f(
ζ)
be analytic on a neighborhood of Pϕ[
z],
and ν ∈ ℂ
satisfy Re
ν > s1[
f].
Then: Definition 10. Let fγ(ζ) = (ζ − c)γ · f0(ζ) where γ ∈ ℂ\ℤ and f0(ζ) is analytic on a neighborhood of Pϕ[z]. Then,
is defined by Definition 9.
The following lemmas follow from the arguments there.
Lemma 12. is an analytic function of ν on the domain Re ν > s1[f].
Lemma 13. is analytic with respect to γ ∈ ℂ, as well as to ν ∈ ℂ on the domain Re ν > s1[f].
Lemma 14. Let exist. Then,
exists, and holds.
Lemma 15. Let exist. Then,
exists, and holds.
We now present the index law and Leibniz’s rule corresponding to Lemmas 2 and 3.
Lemma 16. If Re
ν > s1[
f]
and Re (
µ + ν)
> s1[
f]
for µ ∈ ℂ,
ν ∈ ℂ
and ϕ ∈ ℝ,
then: This index law is Theorem 4.3 in [
1].
Lemma 17. Let ν ∈ ℂ,
ϕ ∈ ℝ
and f(
z)
satisfy −1 + Re
ν > s1[
f].
Then: Proof We see that both sides are equal to:
■
In the following sections, we use
for the Liouville fD.
4.4. The ϕ-dept Liouville fD of the Exponential Function
Lemma 18. Let z ∈ ℂ, a ∈ ℂ, ν ∈ ℂ, and ϕ ∈ ℝ satisfy Re (ae
iϕ) > 0. Then, the abscissa of convergence of e
−az is given by s
1[e
−az] = −∞, and:
Proof When
λ ∈
+ℂ, Re (
aeiϕ) > 0,
by using
(25). The proof of the second equation of
(34) is finished by using
(26) and Lemma 14. ■
We present the following lemma, but we will not use it later.
Lemma 19. Let b ∈ ℝ\{0},
f(
z) =
eibz. Then, s1[
f] = 0
and if ν ∈
+ℂ
and x ∈ ℝ
>0,
there exist:and: Proof We put ϕ = 0,
f(
z) =
e(−ϵ+ib)z in
(30) and take the limit
ϵ→ 0+. We then note that we can exchange the order of the limit and the integration, by Lebesgue’s theorem [
14] (p. 37), obtaining the first equation in
(37). By using
(34) in the rhs of that equation, we obtain the first equation in
(38). ■
6. Asymptotic Expansions of Riemann–Liouville fD
Comparing the third member of
(26) with
(1) and
Figure 1, we have the following lemma.
Lemma 23. Let Condition A in Section 1 be satisfied, f(
ζ) ∈
1(
P(
c, z)),
s1[
f] < 0
and s1[
f]
< −Re
λ < 0.
Then: Lemma 24. Let Condition A be satisfied, f(
ζ) ∈
1(
P(
c, z)),
and ν ∈ ℂ\ℤ
>−1 satisfy Re
ν > s1[
f].
Then: Remark 4. Let Condition A be satisfied, f(ζ) ∈ 1(P(c, z)), and n ∈ ℤ>−1 satisfy n > s1[f]. Then,
.
Lemma 25. Let fγ(
ζ)
satisfy Condition B, and ν ∈ ℂ\ℤ
>−1 satisfy Re
ν > s1[
fγ].
Then: Remark 5. Let fγ(ζ) satisfy Condition B, and n ∈ ℤ>−1 satisfy n > s1[fγ]. Then,
.
We express the integral on the rhs of
(49) as:
where
y =
z − c and
η =
ζ − c. We now obtain the asymptotic expansion of
(51) as a function of
y.
We use the Taylor series given in [
10] (Section 5.4):
for
a ∈ ℂ,
h ∈ ℂ,
µ ∈ ℂ and
n ∈ ℤ
>0, where:
Here, C is a contour, including a and a + h, but not zero.
We now choose
α ∈ ℝ
>0 and
β ∈ ℝ
>0 satisfying
α < 1 and
β < 1, and choose
C, such that
ξ ∈ ℂ on
C satisfies:
We then choose
r ∈ ℝ
>0, such that:
Remark 6. In using the Taylor series (52), we put a =
z − c, h being on Pϕ(0)
or Cϕ(0),
which are shown in Figures 1 and
3, respectively, and hence, a+
h is on Pϕ(
z −c)
or Cϕ(
z −c).
If we see Figure 4a with c and z replaced by zero and z − c, respectively, we can easily choose a contour C, as described above.
Remark 7. If |arg ξ| ≤ π, we may choose r = eπ|Im µ|.
Using
(52) with
(56), we obtain the following lemma.
Lemma 26. Let
, Re ν > s
1[g], δ = 1 or −1, and n ∈ ℤ
>0. Then:
where:for k ∈ ℤ
>−1 and ρ ∈ ℝ
>0.
Theorem 1. Let Condition A be satisfied, f(
ζ)
∈ 1(
P(
c, z)),
ν ∈ ℂ\ℤ
>−1 satisfy Re
ν > s1[
f]
and n ∈ ℤ
>0.
Then:where Δ
n(
z − c)
is estimated by (59) and (60), and Ak and are given by (61) with g(
η)
replaced by f(
c +
η).
Proof We express the integral on the rhs of
(49) as
(51). Putting
g(
η) =
f(
c +
η) and using
(58) in
(49), we obtain
(62). ■
Theorem 2. Let fγ(
ζ)
satisfy Condition B, ν ∈ ℂ\ℤ
>−1 satisfy Re
ν > s1[
fγ]
and n ∈ ℤ
>0.
Then:where: Remark 8. If n +
γ > −1, Δ
n(
z − c)
is estimated by (59) and (60) and if k +
γ > −1,
Bk is equal to Ak given by (61) with g(
η)
replaced by f(
c +
η).
Remark 9. When ϕ
satisfies z−c = |
z−c|·ei(ϕ+π),
Theorems 1 and 2 are valid even when the Condition (b) in Condition A is not satisfied. Formula (68) given below is a trivial example. 6.1. fD of the Exponential Function
We now apply Theorem 1 to the function
f(
z) =
e−az. By using
(34), we obtain the following results.
Corollary 1. Let a ∈ ℂ\{0},
ν ∈ ℂ\ℤ
>−1 and n ∈ ℤ
>0.
Then:where: Proof We choose ϕ, such that aeiϕ = |a|, and obtain
. ■
Remark 10. In the above derivation of the second term on the rhs of (65), we use (52) in the integral.
This derivation is the one given in [10] (Section 16.3), for Whittaker’s function Wk,m(
z).
When a = −ib, we have:
Corollary 2. Let b ∈ ℝ\{0}, x ∈ ℝ and ν ∈ ℂ\ℤ
>−1. Then, the asymptotic expansion of
is given by
(65) with −a and z replaced by ib and x, respectively.
Remark 11. Sakakibara [16] used the fact that the leading term of the asymptotic expansion of for γ ∈ ℝ and x ≫ 1 is
.
6.2. Incomplete Gamma Function
We now put
f(
z) =
ez and ϕ =
−π in
(49). Then, we obtain:
By multiplying this by Γ(
λ)
e−z and comparing it with
(8) and
(35), we obtain a well-known formula:
where
.
The asymptotic expansion of
(67) is obtained by putting
a = −1 and
ν =
−λ in
(65) with
(66). By multiplying Γ(
λ)
e−z to the result, we obtain the asymptotic expansion of
(68).