Analytical Solution of Generalized Space-Time Fractional Cable Equation
Abstract
:1. Introduction
2. Solution of the problem
3. Fractional Moments
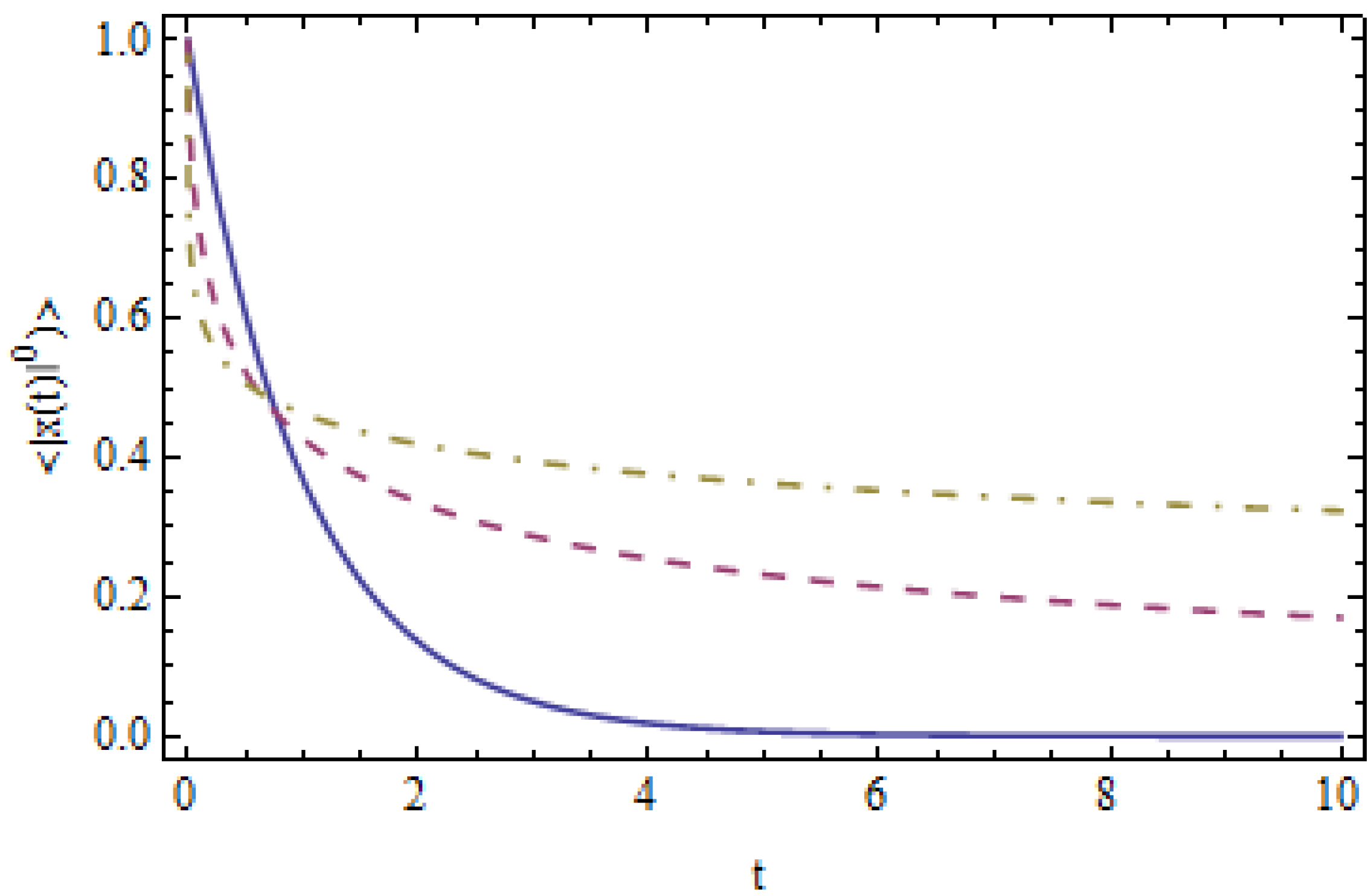

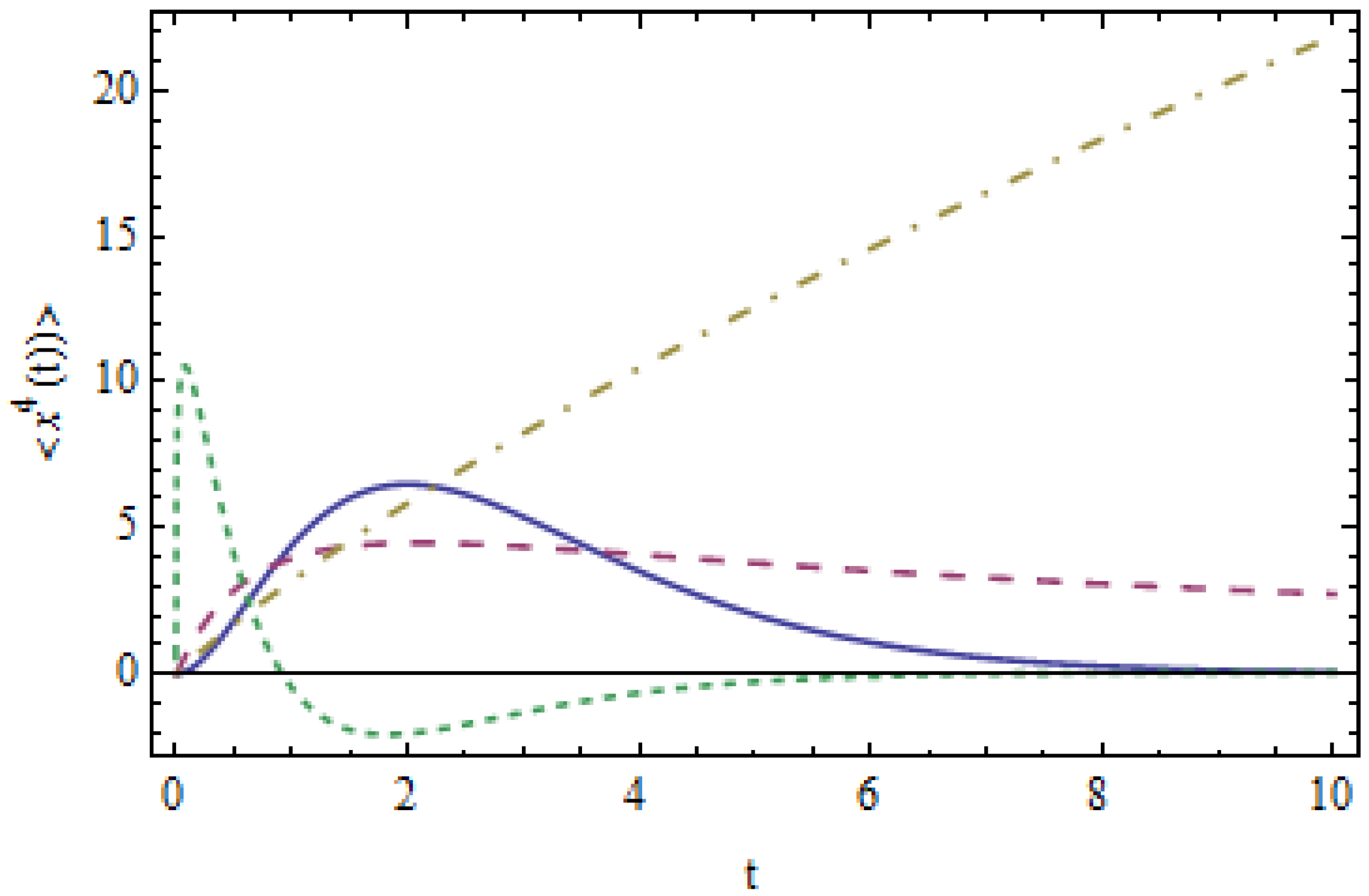
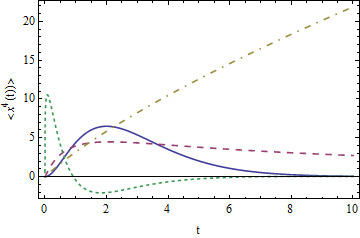
Positivity of the Even Moments
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Segev, I.; London, M. Untangling dendrites with quantitative models. Science 2000, 290, 744–750. [Google Scholar] [CrossRef] [PubMed]
- Baer, S.M.; Rinzel, J. Propagation of dendritic spikes mediated by excitable spines: A continuum theory. J. Neurophysiol. 1991, 65, 874–890. [Google Scholar] [PubMed]
- Qian, N.; Sejnowski, T.J. An electro-diffusion model for computing membrane potentials and ionic concentrations in branching dendrites, spines and axons. Biol. Cybern. 1989, 62, 1–15. [Google Scholar] [CrossRef]
- Henry, B.I.; Langlands, T.A.M.; Wearne, S.L. Fractional cable models for spiny neuronal dendrites. Phys. Rev. Lett. 2008, 100, 128103. [Google Scholar] [CrossRef] [PubMed]
- Henry, B.I.; Wearne, S.L. Fractional cable equation models for anomalous electrodiffusion in nerve cells: infinite domain solutions. J. Math. Biol. 2009, 59, 761–808. [Google Scholar]
- Langlands, T.A.M.; Henry, B.I.; Wearne, S.L. Fractional cable equation models for anomalous electrodiffusion in nerve cells: Finite domain solutions. SIAM J. Appl. Math. 2011, 71, 1168–1203. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Analytical solutions, moments, and their asymptotic behaviors for the time-space fractional cable equation. Commun. Theor. Phys. 2014, 62, 54–60. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academin Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, the Netherlands, 2006. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: London, UK, 1993. [Google Scholar]
- Bazhlekova, E.G.; Dimovski, I.H. Exact solution for the fractional cable equation with nonlocal boundary conditions. Cent. Eur. J. Phys. 2013, 11, 1304–1313. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Fractional diffusion equation with a generalized Riemann-Liouville time fractional derivative. J. Phys. A: Math. Theor. 2011, 44, 255203. [Google Scholar] [CrossRef]
- Tomovski, Z.; Sandev, T.; Metzler, R.; Dubbeldam, J. Generalized space-time fractional diffusion equation with composite fractional time derivative. Phys. A 2012, 391, 2527–2542. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Rossato, R.; Lenzi, M.K.; da Silva, L.R.; Goncalves, G. Fractional diffusion equation and external forces: solutions in a confined region. Z. Naturforschung Sect. A 2010, 65, 423–430. [Google Scholar]
- Huang, F.; Liu, F. The space-time fractional diffusion equation with Caputo derivatives. J. Appl. Math. Comput. 2005, 19, 179–190. [Google Scholar] [CrossRef]
- Huang, F.; Liu, F. The time fractional diffusion equation and advection-dispersion equation. ANZIAM J. 2005, 46, 317–330. [Google Scholar] [CrossRef]
- Huang, F.; Liu, F. The fundamental solution of the space-time fractional advection-dispersion equation. J. Appl. Math. Comput. 2005, 18, 339–350. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of the space fractional Fokker-Planck equation. J. Comput. Appl. Math. 2004, 166, 209–219. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and Convergence of the difference Methods for the space-time fractional advection-diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Q.; Turner, I. Two new implicit numerical methods for the fractional cable equation. J. Comput. Nonlinear Dyn. 2010, 6, 01109. [Google Scholar] [CrossRef]
- Chen, C.; Liu, F.; Burrage, K. Numerical analysis for a variable-order nonlinear cable equation. J. Comput. Appl. Math. 2011, 236, 209–224. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, F.; Turner, I.; Anh, V. A novel high order space-time spectral method for the time-fractional Fokker-Planck equation. SIAM J. Sci. Comput. 2015, 37, A701–A724. [Google Scholar] [CrossRef]
- Liu, F.; Chen, S.; Turner, I.; Burrage, K.; Anh, V. Numerical simulation for two-dimensional Riesz space fractional diffusion equations with a nonlinear reaction term. Cent. Eur. J. Phys. 2013, 11, 1221–1232. [Google Scholar] [CrossRef]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, Singapore, 2000. [Google Scholar]
- Atangana, A.; Secer, A. A note on fractional order derivative and table of fractional derivative of some special function. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef]
- Atangana, A. Drawdown in prolate spheroidal-spherical coordinates obtained via Green’s function and perturbation methods. Comun. Nonlin. Sci. Numer. Simul. 2014, 29, 1259–1269. [Google Scholar] [CrossRef]
- Hilfer, R. Experimental evidence for fractional time evolution in glass forming materials. Chem. Phys. 2002, 284, 399–408. [Google Scholar] [CrossRef]
- Hilfer, R. On fractional relaxation. Fractals 2003, 11, 251–257. [Google Scholar] [CrossRef]
- Hilfer, R. Exact solutions for a class of fractal time random walks. Fractals 1995, 3, 211–216. [Google Scholar] [CrossRef]
- Hilfer, R. An extension of the dynamical foundations for the statistical equilibrium concept. Phys. A 1995, 221, 89–96. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K. Distribution of a product and the structural set up of densities. Ann. Math. Statist. 1969, 40, 1439–1448. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Srivastava, H.M.; Gupta, K.C.; Goyal, S.P. The H-Functions of One and Two Variables with Applications; South Asian Publishers: New Delhi, Madras, India, 1982. [Google Scholar]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Sandev, T.; Tomovski, Z.; Dubbeldam, J.L.A. Generalized Langevin equation with a three parameter Mittag-Leffler noise. Phy. A 2011, 390, 3627–3636. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Tomovski, Z. Fractional calculus with an integral operator containing a generalized Mittag-Leffler function in the kernel. Appl. Math. Comput. 2009, 211, 198–210. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Solutions of fractional reaction-diffusion equations in terms of the H-function. Bull. Astr. Soc. India 2007, 35, 681–689. [Google Scholar]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Unified fractional kinetic equation and a fractional diffusion equation. Astrophys. Space Sci. Trans. 2004, 209, 299–310. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelesticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Seybold, H.; Hilfer, R. Numerical algorithm for calculating the generalized Mittag-Leffler function. SIAM J. Numer. Anal. 2008, 47, 69–88. [Google Scholar] [CrossRef]
- Hilfer, R. Classification theory for anequilibrium phase transitions. Phys. Rev. E 1993, 48, 2466. [Google Scholar] [CrossRef]
- Bisquert, J. Fractional diffusion in the multiple-trapping regime and revision of the equivalence with the continuous-time random walk. Phys. Rev. Let. 2003, 91, 010602. [Google Scholar] [CrossRef]
- Orenstein, J.; Kastner, M. Photocurrent transient spectroscopy: measurement of the density of localized states in a –As2Se3. Phys. Rev. Lett. 1981, 46, 1421. [Google Scholar] [CrossRef]
- Schilling, R.; Song, R.; Vondracek, Z. Bernstein Functions; De Gruyter: Berlin, Germany, 2010. [Google Scholar]
- Tomovski, Z.; Pogany, T.; Srivastava, H.M. Laplace type integral expressions for a certain three-parameter family of generalized Mittag-Leffler functions with applications involving complete monotonicity. J. Frankl. Inst. 2014, 351, 5437–5454. [Google Scholar] [CrossRef]
- Sandev, T.; Tomovski, Z. Langevin equation for a free particle driven by power law type noises. Phys. Lett. A 2014, 378, 1–9. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Correlation functions for the fractional generalized Langevin equation in the presence of internal and external noise. J. Math. Phys. 2014, 55, 023301. [Google Scholar]
- Spanner, M.; Hoefling, F.; Schroeder-Turk, G.; Mecke, K.; Franosch, T. Anomalous transport of a tracer on percolation clusters. J. Phys.: Condens. Matter 2011, 23, 234120. [Google Scholar]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and aging at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Z. Hilfer-Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Berg, C.; Forst, G. Potential Theory on Locally Compact Abelian Groups; Springer: Berlin, Germany, 1975. [Google Scholar]
- Fujita, Y. A generalization of the results of Pillai. Ann. Inst. Statist. Math. 1993, 45, 361–365. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saxena, R.K.; Tomovski, Z.; Sandev, T. Analytical Solution of Generalized Space-Time Fractional Cable Equation. Mathematics 2015, 3, 153-170. https://doi.org/10.3390/math3020153
Saxena RK, Tomovski Z, Sandev T. Analytical Solution of Generalized Space-Time Fractional Cable Equation. Mathematics. 2015; 3(2):153-170. https://doi.org/10.3390/math3020153
Chicago/Turabian StyleSaxena, Ram K., Zivorad Tomovski, and Trifce Sandev. 2015. "Analytical Solution of Generalized Space-Time Fractional Cable Equation" Mathematics 3, no. 2: 153-170. https://doi.org/10.3390/math3020153
APA StyleSaxena, R. K., Tomovski, Z., & Sandev, T. (2015). Analytical Solution of Generalized Space-Time Fractional Cable Equation. Mathematics, 3(2), 153-170. https://doi.org/10.3390/math3020153