On the Evolutionary Dynamics and Optimal Control of a Tripartite Game in the Pharmaceutical Procurement Supply Chain with Regulatory Participation

Abstract

This study involves the construction of a dynamic evolutionary game model involving three key participants, including the Group Purchasing Organization (GPO), medical institutions, and pharmaceutical suppliers, while comprehensively considering critical factors such as benefit compensation, bad debt risk, and fiscal costs. The model characterizes the strategy evolution of each participant under bounded rationality and imitation learning mechanisms. Based on the replicator dynamics equations, the evolutionary trajectories and equilibrium conditions of the three parties’ strategies are systematically derived. The Jacobian matrix is then used to analyze the local stability of eight boundary equilibria and potential internal mixed equilibria. Furthermore, to capture the optimal adjustment process of the compensation mechanism, the GPO’s compensation level is introduced into an optimal control framework. A controlled evolutionary system is formulated, and the dynamic optimal relationship between compensation intensity and system state is described using the Hamilton–Jacobi–Bellman (HJB) equation. Through analytical linearization and numerical simulations, the optimal feedback compensation law and its closed-loop evolutionary trajectory are obtained, allowing for a comparative analysis between the “fixed compensation” and “optimal compensation” scenarios. The results reveal that an appropriately designed dynamic compensation mechanism can significantly enhance system cooperation stability and overall social welfare. This provides a quantitative theoretical foundation and methodological tool for the refined design and dynamic regulation of pharmaceutical group purchasing policies.

1. Introduction

In recent years, the volume-based centralized drug procurement (VBP) system has become a crucial pillar of China’s medical and pharmaceutical reform. Its primary objective is to reduce drug prices, regulate distribution channels, and enhance the efficiency of medical insurance funds through large-scale procurement and price negotiation mechanisms. Within this policy framework, the Group Purchasing Organization (GPO) serves as a central intermediary, assuming key functions such as price negotiation, contract coordination, risk sharing, and benefit compensation [1,2,3,4,5,6]. However, the multi-agent nature of the pharmaceutical supply chain implies that its operation is far from a static optimization problem—it is instead a complex nonlinear dynamic system [7,8,9]. The GPO, hospitals, and pharmaceutical suppliers differ significantly in their objectives, risk perceptions, and cooperation incentives. Consequently, conflicts of interest and unstable cooperation frequently arise during policy implementation. In particular, when the compensation mechanism is imperfect, bad-debt risks increase, or fiscal incentives are insufficient, some participants may choose to “free ride” or withdraw from collaboration, thereby reducing the overall efficiency of the system [10,11,12,13]. It is noteworthy that the dynamic mechanisms and collaborative governance of supply chain networks have recently become significant topics at the fore of multiple disciplines, including operations research, systems science, and management science. Cross-disciplinary studies consistently reveal that supply chain systems often exhibit complex features such as nonlinearity, adaptability, and multi-equilibrium dynamics, which cannot be adequately captured by static optimization models [14,15,16]. Therefore, integrating evolutionary game theory with optimal control methods provides a new analytical paradigm for investigating multi-agent interactions, incentive coordination, and policy regulation within the context of pharmaceutical group purchasing.

From the perspective of systems science and applied mathematics, the pharmaceutical group purchasing mechanism can be abstracted as a multi-agent nonlinear game system [17,18]. Traditional game theory, which assumes complete rationality, fails to capture learning and imitation behaviors observed in real-world decision environments. By contrast, evolutionary game theory offers mathematical tools for modeling bounded rationality within dynamic populations. Its core idea is that individual strategies evolve according to payoff differences, and population strategy distributions change over time until a stable equilibrium is reached [19,20,21]. The replicator dynamics provide a rigorous description of how the proportions of strategies evolve in the population, enabling an analysis of long-term stability under different policy or institutional settings [22,23,24]. In this context, the GPO’s compensation level directly affects hospitals’ willingness to participate; the hospitals’ cooperation ratio determines suppliers’ bargaining positions and expected revenues; and the suppliers’ participation level, in turn, influences the GPO’s overall performance and risk exposure. These interdependencies form a nonlinear coupling feedback loop, in which system stability and equilibrium structure depend not only on parameter values but also on the agents’ evolutionary speeds and behavioral sensitivities. By examining system trajectories under different parameter configurations, one can characterize the long-term evolution of cooperative behavior and evaluate the incentive effects of institutional design.

Most existing studies, however, treat the compensation mechanism as an exogenous parameter, assuming that the GPO adjusts its strategy under a fixed compensation level. In practice, the compensation intensity is often dynamically regulated by higher-level authorities such as health insurance departments or governmental agencies. The regulator’s goal is not to maximize the payoff of a single agent but to optimize overall social welfare under fiscal constraints. Consequently, the compensation intensity should be adaptively adjusted based on the current system state to balance cooperation stability, fiscal expenditure, and social welfare. This dynamic process can be formalized as a controlled evolutionary game model, essentially a state-dependent optimal control problem. Specifically, the regulator dynamically adjusts the control variable $u(t)$ to steer the system toward a cooperative region while mitigating fiscal pressure. This modifies the traditional evolutionary game framework by embedding the replicator dynamics within an optimal control system, thereby linking behavioral evolution with real-time regulatory intervention. The instantaneous social payoff function incorporates both the average payoffs of all agents and the fiscal cost of compensation, while the discounted cumulative payoff represents long-term social welfare. The optimal compensation path can thus be characterized by the Hamilton–Jacobi–Bellman (HJB) equation, which establishes the dynamic relationship among compensation, system state, and optimal social utility [25,26,27]. Methodologically, the proposed framework integrates nonlinear dynamical system analysis, evolutionary game theory, and optimal control theory. The replicator dynamics describe the evolution of strategic behavior; the Jacobian matrix analysis provides local stability criteria; and the HJB equation yields the optimal control law [28,29]. This combined framework also addresses several limitations in existing research, such as the neglect of endogenous regulatory adjustments, the lack of state-dependent incentive mechanisms, and the insufficient mathematical characterization of long-run cooperative stability. Together, these components form a unified analytical pathway, from dynamic stability to optimal regulation and policy feedback, offering a rigorous mathematical foundation for policy optimization in pharmaceutical group purchasing. For policymakers, this model enables the simulation of dynamic outcomes under different compensation schemes and provides quantitative metrics to evaluate marginal policy effects. For researchers, it also offers a reproducible and generalizable methodological foundation that bridges static incentive design and dynamic behavioral evolution—two aspects that are often analyzed separately in the existing literature.

In summary, this study develops a tripartite evolutionary game model for pharmaceutical group purchasing, focusing on the dynamic evolution of cooperation under benefit compensation and risk constraints. Building on this foundation, an optimal control mechanism is introduced to derive the optimal compensation strategy and the corresponding closed-loop evolutionary trajectory. The main contributions of this paper are threefold: (1) From a dynamic perspective, it reveals the internal mechanism of cooperative evolution in group purchasing systems. (2) By employing Jacobian matrix and eigenvalue analysis, it characterizes the existence and stability conditions of cooperative and non-cooperative equilibria. (3) It incorporates the compensation mechanism into an optimal control framework and proposes a dynamic optimal incentive model based on the HJB equation. Additionally, this study explicitly addresses the limitations of existing work by identifying unresolved gaps in dynamic incentive design and providing a systematic mathematical framework for state-dependent compensation regulation. This research extends the intersection of evolutionary game theory and optimal control in the field of pharmaceutical policy analysis, providing a quantitative and dynamic decision-support tool for the refined governance of public procurement systems.

2. Tripartite Game Model and Replicator Dynamics

To systematically characterize the dynamic interactions among Group Purchasing Organizations (GPOs), hospitals, and pharmaceutical suppliers under the benefit-compensation mechanism, this paper constructs a multi-agent decision model based on evolutionary game theory. Unlike traditional static game models that only analyze one-shot equilibria, this study focuses on the time-evolving process of agents’ strategies under bounded rationality. By introducing replicator dynamic equations, the behavioral adjustment rules of the three parties under incentive and learning mechanisms are described.

Accordingly, this section first defines the basic assumptions and notations of the model, clarifying the strategy sets, payoff structures, and cost components of the three types of agents. On this basis, the expected and average payoffs of each party are derived, followed by the formulation of the corresponding replicator dynamic equations. These results provide the mathematical foundation for subsequent stability analysis and optimal control design.

2.1. Basic Assumptions and Notations of the Tripartite Game Model

To systematically describe the strategic interaction and behavioral evolution among the Group Purchasing Organization (GPO), hospitals, and pharmaceutical suppliers under the benefit-compensation mechanism, this study develops a tripartite evolutionary game model within the framework of bounded rationality and dynamic learning. Each agent updates its strategy based on historical payoffs, and behavioral adaptation occurs through imitation, adjustment, and feedback. The GPO, as the central coordinating body, undertakes policy incentives and risk-sharing functions; hospitals make decisions depending on the procurement cost savings and reputational gains brought by participation; and suppliers’ choices are influenced by profit margins, market share, and bad-debt risks. The interaction of these three agents collectively determines the system’s stability and cooperation level. To facilitate model representation and parameter specification,

Table 1. Notation and Definitions.

Symbol	Definition
$C_{a1}$	Operating cost of the GPO when implementing compensation
$C_{a2}$	Baseline operating cost of the GPO without compensation
$C_{b1}$	Procurement or coordination cost when hospitals join the GPO
$C_{b2}$	Independent procurement cost when hospitals do not join the GPO
$C_{c1}$	Supplier’s cost when participating in centralized procurement
$C_{c2}$	Supplier’s cost when not participating in centralized procurement
$P_{a1}$	Additional revenue to the GPO from hospital participation
$P_{a2}$	Additional revenue to the GPO from supplier participation
$P_b$	Regular benefit of hospitals from drug procurement
$P_{b1}$	Savings when suppliers sell to joining hospitals under centralized procurement
$P_{b2}$	Limited savings when selling to non-joining hospitals
$P_c$	Regular profit of suppliers when not joining centralized procurement
$P_{c1}$	Contractual profit when both hospitals and suppliers participate
S	Reputation or synergy benefit obtained when all three parties cooperate
$S_1$	Policy/financial support received by the GPO for implementing compensation
B	Additional benefit gained by hospitals after joining the GPO
D	Extra cost to hospitals when staying outside the GPO
E	Minimum revenue from supplier drug sales
J	Economies-of-scale profit from participating in bulk purchasing
Q	Supplier revenue from selling at original prices to non-joining hospitals
H	Loss from bad-debt risk or delayed payments for suppliers

Note: All cost and benefit parameters are assumed to be strictly positive. Based on real procurement practice, we assume the following economic relationships: (1) Implementing compensation requires additional GPO resources, hence $C_{a1}>C_{a2}>0$. (2) Centralized procurement reduces hospital procurement cost, so $C_{b2}>C_{b1}>0$. (3) Suppliers gain higher savings and scale benefits when participating, thus $C_{c2}>C_{c1}$ and $P_{b1}>P_{b2}$. (4) Bad-debt risk always implies a positive loss, hence $H>0$. (5) Contractual revenue exceeds the regular profit, so $P_{c1}>P_c$. These assumptions ensure that the payoff structure is economically grounded and consistent with observed behavior in pharmaceutical procurement systems.

lists the main symbols and their corresponding economic meanings. All parameters have explicit behavioral interpretations and quantitative bases for subsequent modeling and numerical simulations.

Assumption 1.

The system consists of three types of bounded-rational agents: the GPO (denoted as G), hospitals (denoted as H), and pharmaceutical suppliers (denoted as S). Their respective strategy sets are: $G:\{\mathit{Compensate},\mathit{Not}\mathit{Compensate}\}$, $H:\{\mathit{Join},\mathit{Not}\mathit{Join}\}$, $S:\{\mathit{Participate},\mathit{Not}\mathit{Participate}\}$. Here, “Compensate’’ refers to the GPO providing financial incentives to encourage hospital participation in centralized procurement; “Join’’ denotes a hospital’s decision to join the group purchasing scheme; and “Participate’’ represents the supplier’s engagement in group purchasing and contractual drug supply.

Assumption 2.

Let x, y, and z denote the proportions of GPOs, hospitals, and suppliers, respectively, that adopt the cooperative strategy in a bounded-rational population. Specifically, a fraction x of GPOs choose “Compensate’’ (and $1-x$ choose “Not Compensate’’); a fraction y of hospitals choose “Join’’ (and $1-y$ choose “Not Join’’); and a fraction z of suppliers choose “Participate’’ (and $1-z$ choose “Not Participate’’). Thus, the system state is described by the vector $(x, y, z)$ with $(x, y, z)\in {[0, 1]}^3$, reflecting population frequencies consistent with the interpretation of replicator dynamics.

Assumption 3.

When implementing compensation, the GPO must invest additional human, material, and financial resources, incurring a compensation cost $C_{a1}$. Without compensation, it only bears regular administrative costs $C_{a2}$, where $C_{a1}>C_{a2}$. Thus, compensation behavior can promote cooperation diffusion but increases organizational costs. Economically, $C_{a1}$ reflects the fiscal burden associated with incentive delivery, while the difference $(C_{a1}-C_{a2})$ captures the additional cost required to change hospital behavior.

Assumption 4.

After joining the group purchasing scheme, hospitals obtain cost-saving benefits $P_{b1}$ from suppliers offering lower prices, whereas non-joining hospitals receive only limited bargaining benefits $P_{b2}$. Given the economies of scale in centralized procurement, it holds that $P_{b1}>P_{b2}$. Here, $P_{b1}$ represents the synergy-driven savings attributed to volume-based purchasing, while $P_{b2}$ reflects the marginal negotiation advantage retained outside the alliance.

Assumption 5.

To overcome the “cold start’’ problem, hospitals’ initial willingness to join is assumed to be low. If a hospital chooses “not to join,’’ it must procure independently at cost $C_{b2}$; if it chooses “to join,’’ the cost is $C_{b1}$, with $C_{b2}>C_{b1}$. Hence, participation in centralized procurement reduces cost and improves efficiency. The cost gap $(C_{b2}-C_{b1})$ measures the procurement efficiency gain achieved through centralized purchasing.

Assumption 6.

Suppliers participating in centralized procurement gain scale benefits J, spread fixed costs, and secure stable orders. Let $C_{c1}$ and $C_{c2}$ denote the supplier’s costs for participating and not participating, respectively, and H the bad-debt loss. Typically, $C_{c1}<C_{c2}$, implying that participation improves operational efficiency. J captures economies of scale generated by bulk supply contracts, while H represents the penalty imposed by delayed payments and credit risk, which are common in real-world pharmaceutical settlement practices.

Assumption 7.

Through centralized procurement, the GPO integrates the pharmaceutical supply chain, obtaining policy and reputational benefits $(S, S_1)$ as well as synergistic gains from hospitals and suppliers $(P_{a1}, P_{a2})$. When full cooperation occurs, the GPO’s total payoff is

$$E_G=S+S_1+P_{a1}+P_{a2}-C_{a1}-B,$$

where B represents compensation payments to hospitals. Without compensation, the GPO’s payoff becomes

$$E_G^{\prime }=P_{a1}+P_{a2}-C_{a2}.$$

Evidently, $E_G>E_G^{\prime }$, indicating that moderate compensation can enhance overall revenue. S and $S_1$ reflect policy compliance effects and institutional reputation enhancement, both of which strengthen long-term bargaining power and procurement legitimacy.

Assumption 8.

When all three parties adopt cooperative strategies (Compensate, Join, Participate), the total system payoff reaches its maximum, satisfying

$$S+S_1+P_{a1}+P_{a2}-C_{a1}-B>P_b+P_c-C_{b2}-C_{c2}.$$

This demonstrates that, within an appropriate parameter range, the compensation mechanism promotes cooperation and ensures economic sustainability. This inequality defines the feasible region under which centralized procurement yields net welfare gains compared with decentralized bilateral negotiation.

Based on the above assumptions, the tripartite payoff matrix is shown in

Table 2. Tripartite Payoff Matrix.

Strategy Combination	GPO Payoff	Hospital Payoff	Supplier Payoff
Compensate, Join, Participate	$P_{a1}+P_{a2}+S+S_1-C_{a1}-B$	$P_b+P_{b1}+B-C_{b1}$	$E+P_{c1}+J-C_{c1}-H$
Compensate, Join, Not Participate	$P_{a1}+S+S_1-C_{a1}-B$	$P_b+B-C_{b1}$	$P_c-C_{c2}$
Compensate, Not Join, Participate	$P_{a2}+S+S_1-C_{a1}$	$P_b+P_{b2}-C_{b2}-D$	$E+Q+J-C_{c1}-H$
Compensate, Not Join, Not Participate	$S+S_1-C_{a1}$	$P_b-C_{b2}-D$	$P_c-C_{c2}$
No Compensation, Join, Participate	$P_{a1}+P_{a2}-C_{a2}$	$P_b+P_{b1}-C_{b1}$	$E+P_{c1}+J-C_{c1}-H$
No Compensation, Join, Not Participate	$P_{a1}-C_{a2}$	$P_b-C_{b1}$	$P_c-C_{c2}$
No Compensation, Not Join, Participate	$P_{a2}-C_{a2}$	$P_b+P_{b2}-C_{b2}-D$	$E+Q+J-C_{c1}-H$
No Compensation, Not Join, Not Participate	$-C_{a2}$	$P_b-C_{b2}-D$	$P_c-C_{c2}$

.

2.2. Expected Payoffs and Replicator Dynamic Equations of the Three Parties

From the tripartite payoff matrix in Table 2, let the probability that the GPO chooses “Compensate” be x, the probability that hospitals choose “Join” be y, and the probability that suppliers choose “Participate” be z. Then, the expected payoffs of the three agents under different strategies can be derived as follows.

(1)

GPO’s Expected Payoff.

When the GPO chooses “Compensate,” its expected payoff is

$$\begin{array}{cc}\hfill E_G^C(x, y, z)=& yz\left(P_{a1}+P_{a2}+S+S_1-C_{a1}-B\right)\hfill \\ \hfill & +y(1-z)\left(P_{a1}+S+S_1-C_{a1}-B\right)\hfill \\ \hfill & +(1-y)z\left(P_{a2}+S+S_1-C_{a1}\right)\hfill \\ \hfill & +(1-y)(1-z)\left(S+S_1-C_{a1}\right).\hfill \end{array}$$

(1)

When the GPO chooses “No Compensation,” its expected payoff is

$$\begin{array}{cc}\hfill E_G^N(x, y, z)=& yz\left(P_{a1}+P_{a2}-C_{a2}\right)\hfill \\ \hfill & +y(1-z)\left(P_{a1}-C_{a2}\right)\hfill \\ \hfill & +(1-y)z\left(P_{a2}-C_{a2}\right)\hfill \\ \hfill & +(1-y)(1-z)\left(-C_{a2}\right).\hfill \end{array}$$

(2)

Hence, the GPO’s average expected payoff is

$${\overline{E}}_G(x, y, z)=x{E}_G^C(x, y, z)+(1-x)E_G^N(x, y, z).$$

(3)

(2)

Hospital’s Expected Payoff.

When hospitals choose “Join,” their expected payoff is

$$\begin{array}{cc}\hfill E_H^J(x, y, z)=& xz\left(P_b+P_{b1}+B-C_{b1}\right)\hfill \\ \hfill & +x(1-z)\left(P_b+B-C_{b1}\right)\hfill \\ \hfill & +(1-x)z\left(P_b+P_{b1}-C_{b1}\right)\hfill \\ \hfill & +(1-x)(1-z)\left(P_b-C_{b1}\right).\hfill \end{array}$$

(4)

When hospitals choose “Not Join,” the expected payoff is

$$\begin{array}{cc}\hfill E_H^N(x, y, z)=& xz\left(P_b+P_{b2}-C_{b2}-D\right)\hfill \\ \hfill & +x(1-z)\left(P_b-C_{b2}-D\right)\hfill \\ \hfill & +(1-x)z\left(P_b+P_{b2}-C_{b2}-D\right)\hfill \\ \hfill & +(1-x)(1-z)\left(P_b-C_{b2}-D\right).\hfill \end{array}$$

(5)

The average expected payoff of hospitals is

$${\overline{E}}_H(x, y, z)=y{E}_H^J(x, y, z)+(1-y)E_H^N(x, y, z).$$

(6)

(3)

Supplier’s Expected Payoff.

When suppliers choose “Participate,” their expected payoff is

$$\begin{array}{cc}\hfill E_S^P(x, y, z)=& xy\left(E+P_{c1}+J-C_{c1}-H\right)\hfill \\ \hfill & +x(1-y)\left(E+Q+J-C_{c1}-H\right)\hfill \\ \hfill & +(1-x)y\left(E+P_{c1}+J-C_{c1}-H\right)\hfill \\ \hfill & +(1-x)(1-y)\left(E+Q+J-C_{c1}-H\right).\hfill \end{array}$$

(7)

When suppliers choose “Not Participate,” their expected payoff is

$$\begin{array}{cc}\hfill E_S^N(x, y, z)=& xy\left(P_c-C_{c2}\right)\hfill \\ \hfill & +x(1-y)\left(P_c-C_{c2}\right)\hfill \\ \hfill & +(1-x)y\left(P_c-C_{c2}\right)\hfill \\ \hfill & +(1-x)(1-y)\left(P_c-C_{c2}\right).\hfill \end{array}$$

(8)

Thus, the suppliers’ average expected payoff is

$${\overline{E}}_S(x, y, z)=z{E}_S^P(x, y, z)+(1-z)E_S^N(x, y, z).$$

(9)

(4)

Replicator Dynamic Equations.

Under bounded rationality and the imitation-learning mechanism, the strategy proportions of the three agents evolve over time according to the standard two-strategy replicator dynamics. According to the framework of Taylor and Jonker [30], we obtain the following:

$$\left\{\begin{array}{c}{\displaystyle \dot{x}=x(1-x)\left(E_G^C(x, y, z)-E_G^N(x, y, z)\right),}\hfill \\ {\displaystyle \dot{y}=y(1-y)\left(E_H^J(x, y, z)-E_H^N(x, y, z)\right),}\hfill \\ {\displaystyle \dot{z}=z(1-z)\left(E_S^P(x, y, z)-E_S^N(x, y, z)\right),}\hfill \end{array}\right.$$

(10)

where $E_G^C,E_G^N, {\overline{E}}_G$ are given by Equations (1)–(3), $E_H^J,E_H^N, {\overline{E}}_H$ by Equations (4)–(6), and $E_S^P,E_S^N, {\overline{E}}_S$ by Equations (7)–(9).

Let

$$\begin{array}{cc}\hfill F_1(x, y, z)& =x(1-x)\left(E_G^C(x, y, z)-E_G^N(x, y, z)\right),\hfill \\ \hfill F_2(x, y, z)& =y(1-y)\left(E_H^J(x, y, z)-E_H^N(x, y, z)\right),\hfill \\ \hfill F_3(x, y, z)& =z(1-z)\left(E_S^P(x, y, z)-E_S^N(x, y, z)\right),\hfill \end{array}$$

then the equilibrium point $X^{*}=(x^{*}, y^{*}, z^{*})$ of the replicator dynamics satisfies

$$F_1(x^{*}, y^{*}, z^{*})=F_2(x^{*}, y^{*}, z^{*})=F_3(x^{*}, y^{*}, z^{*})=0.$$

Because each component is structured as “$\mathrm{strategy}\mathrm{ratio}\times (1-\mathrm{strategy}\mathrm{ratio})\times \mathrm{payoff}\mathrm{difference}$”, the equilibrium points include both boundary (pure-strategy) equilibria and interior (mixed-strategy) equilibria.

(1) When any of $x, y, z$ equals 0 or 1, the corresponding component vanishes, yielding eight vertex-type equilibria:

$$(0, 0, 0),(1, 0, 0),(0, 1, 0),(0, 0, 1),(1, 1, 0),(1, 0, 1),(0, 1, 1),(1, 1, 1),$$

which correspond to all combinations of full cooperation or non-cooperation among the three parties.

(2) For an interior equilibrium point to exist, with $0<x^{*}, y^{*}, z^{*}<1$, the three payoff differences must simultaneously vanish:

$$\left\{\begin{array}{c}{E}_G^C(x^{*}, y^{*}, z^{*})-E_G^N(x^{*}, y^{*}, z^{*})=0,\hfill \\ E_H^J(x^{*}, y^{*}, z^{*})-E_H^N(x^{*}, y^{*}, z^{*})=0,\hfill \\ E_S^P(x^{*}, y^{*}, z^{*})-E_S^N(x^{*}, y^{*}, z^{*})=0.\hfill \end{array}\right.$$

(11)

Substituting the definitions of each payoff function yields the explicit expressions:

$$\left\{\begin{array}{c}{\Delta }_G(x, y, z)=E_G^C(x, y, z)-E_G^N(x, y, z)=(S+S_1-C_{a1}+C_{a2})-yB,\hfill \\ {\Delta }_H(x, y, z)=E_H^J(x, y, z)-E_H^N(x, y, z)=(B+C_{b2}+D-C_{b1})+z(P_{b1}-P_{b2}),\hfill \\ {\Delta }_S(x, y, z)=E_S^P(x, y, z)-E_S^N(x, y, z)=(E+J-C_{c1}-H-P_c+C_{c2})+y(P_{c1}-Q).\hfill \end{array}\right.$$

(12)

Solving ${\Delta }_G=0$, ${\Delta }_H=0$, and ${\Delta }_S=0$ yields the coordinates of the interior equilibrium point. The GPO’s indifference condition determines $y^{*}$:

$$(S+S_1-C_{a1}+C_{a2})-y^{*}B=0\Rightarrow y_{(G)}^{*}={\displaystyle \frac{S+S_1-C_{a1}+C_{a2}}{B}},$$

which is valid only if $0<y_{(G)}^{*}<1$. The hospital’s indifference condition determines $z^{*}$:

$$(B+C_{b2}+D-C_{b1})+z^{*}(P_{b1}-P_{b2})=0\Rightarrow z^{*}={\displaystyle \frac{C_{b1}-(B+C_{b2}+D)}{P_{b1}-P_{b2}}},$$

where $P_{b1}>P_{b2}$ ensures a positive denominator, and thus $z^{*}$ lies within a feasible range $0<C_{b1}-(B+C_{b2}+D)<P_{b1}-P_{b2}$.

The supplier’s indifference condition gives another expression for $y^{*}$:

$$(E+J-C_{c1}-H-P_c+C_{c2})+y^{*}(P_{c1}-Q)=0\Rightarrow y_{(S)}^{*}={\displaystyle \frac{P_c-C_{c2}-(E+J-C_{c1}-H)}{P_{c1}-Q}},$$

which is feasible when $P_{c1}>Q$ and $0<P_c-C_{c2}-(E+J-C_{c1}-H)<P_{c1}-Q$.

Since $y^{*}$ appears in both the GPO’s and supplier’s indifference conditions, consistency requires:

$${\displaystyle \frac{S+S_1-C_{a1}+C_{a2}}{B}}={\displaystyle \frac{P_c-C_{c2}-(E+J-C_{c1}-H)}{P_{c1}-Q}}=y^{*}.$$

(13)

Only when Equation (13) holds and the solutions satisfy $0<y^{*}<1$ and $0<z^{*}<1$ does the system possess a genuine interior (mixed) equilibrium $(x^{*}, y^{*}, z^{*})=\left(x^{*}\in (0, 1),y^{*},z^{*}\right)$. Otherwise, the dynamical system admits only the eight boundary equilibria and no interior fixed point. It is worth emphasizing that, although the indifference conditions for hospitals and suppliers uniquely determine $y^{*}$ and $z^{*}$, the equilibrium value $x^{*}$ for the GPO behaves fundamentally differently. From the GPO’s replicator dynamic, $\dot{x}=x(1-x){\Delta }_G(x, y, z)$, the payoff difference ${\Delta }_G(x, y, z)$ depends solely on the pair $(y, z)$ rather than on x itself. Consequently, the interior equilibrium condition for the GPO collapses to ${\Delta }_G(x^{*}, y^{*}, z^{*})=0$, which restricts $(y^{*}, z^{*})$ but does not uniquely determine $x^{*}$. Once the indifference conditions for hospitals and suppliers are satisfied, any $x^{*}\in (0, 1)$ leads to $\dot{x}=0$. Hence, the system admits a continuum of interior equilibrium points along the surface ${\Delta }_G=0$. Economically, this indicates that the GPO’s compensation strategy becomes payoff-neutral at equilibrium: its marginal incentive to increase or reduce compensation vanishes once the cooperating levels of hospitals and suppliers reach $(y^{*}, z^{*})$. As a result, the long-run trajectory of $x(t)$ may depend on initial conditions rather than being uniquely determined by the payoff structure, in contrast to the uniquely pinned-down values of $y^{*}$ and $z^{*}$.

It is worth noting that the inequality conditions required for the existence of an interior equilibrium carry clear empirical interpretations in the context of centralized drug procurement. These conditions imply that the incremental economic benefits from cooperation must sufficiently exceed the associated costs and risks for all three parties. For hospitals, this reflects the observable cost-saving advantages reported under volume-based procurement pilot programs, where reduced purchase prices and streamlined administrative processes generate net positive gains. For suppliers, the conditions correspond to scale-based revenue opportunities and improved market access that compensate for price concessions and the risk of delayed reimbursement. For the GPO, the feasibility of the condition aligns with policy practice in which compensation and regulatory support are calibrated to ensure that coordinating procurement yields operational and reputational benefits that outweigh fiscal outlays. Therefore, the mathematical feasibility conditions of the interior equilibrium are consistent with realistic procurement scenarios in which cooperation emerges only when measurable, mutually reinforcing advantages are present across the tripartite system.

2.3. Stability Analysis of Equilibrium Points

To characterize the evolutionary attractiveness of different equilibria, we linearize the system (10) around an arbitrary state. Let

$$X={(x, y, z)}^{\top },\dot{X}=F(X)={\left(F_1(x, y, z),F_2(x, y, z),F_3(x, y, z)\right)}^{\top },$$

(14)

then, by Equation (10), the replicator dynamic system can be written as

$$\dot{X}=F(X)=\left(\begin{array}{c}{F}_1(x, y, z)\\ F_2(x, y, z)\\ F_3(x, y, z)\end{array}\right)=\left(\begin{array}{c}x(1-x)\left(E_G^C(x, y, z)-E_G^N(x, y, z)\right)\\ y(1-y)\left(E_H^J(x, y, z)-E_H^N(x, y, z)\right)\\ z(1-z)\left(E_S^P(x, y, z)-E_S^N(x, y, z)\right)\end{array}\right).$$

(15)

Define the payoff differences

$$\left\{\begin{array}{c}{\Delta }_G(x, y, z)=E_G^C(x, y, z)-E_G^N(x, y, z),\hfill \\ {\Delta }_H(x, y, z)=E_H^J(x, y, z)-E_H^N(x, y, z),\hfill \\ {\Delta }_S(x, y, z)=E_S^P(x, y, z)-E_S^N(x, y, z).\hfill \end{array}\right.$$

(16)

Then the Jacobian matrix of the system at an arbitrary point $X={(x, y, z)}^{\top }$ is

$$J(X)={\displaystyle \frac{\partial F(X)}{\partial X}}=\left(\begin{array}{ccc}{\displaystyle \frac{\partial F_1}{\partial x}}& {\displaystyle \frac{\partial F_1}{\partial y}}& {\displaystyle \frac{\partial F_1}{\partial z}}\\ {\displaystyle \frac{\partial F_2}{\partial x}}& {\displaystyle \frac{\partial F_2}{\partial y}}& {\displaystyle \frac{\partial F_2}{\partial z}}\\ {\displaystyle \frac{\partial F_3}{\partial x}}& {\displaystyle \frac{\partial F_3}{\partial y}}& {\displaystyle \frac{\partial F_3}{\partial z}}\end{array}\right)=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right),$$

(17)

where

$$\begin{array}{cccc}\hfill a_{11}& ={\displaystyle \frac{\partial F_1}{\partial x}}=(1-2x){\Delta }_G(x, y, z),\hfill & \hfill a_{12}& ={\displaystyle \frac{\partial F_1}{\partial y}}=x(1-x){\displaystyle \frac{\partial {\Delta }_G(x, y, z)}{\partial y}},\hfill \\ \hfill a_{13}& ={\displaystyle \frac{\partial F_1}{\partial z}}=x(1-x){\displaystyle \frac{\partial {\Delta }_G(x, y, z)}{\partial z}}, \hfill & \hfill a_{21}& ={\displaystyle \frac{\partial F_2}{\partial x}}=y(1-y){\displaystyle \frac{\partial {\Delta }_H(x, y, z)}{\partial x}},\hfill \\ \hfill a_{22}& ={\displaystyle \frac{\partial F_2}{\partial y}}=(1-2y){\Delta }_H(x, y, z),\hfill & \hfill a_{23}& ={\displaystyle \frac{\partial F_2}{\partial z}}=y(1-y){\displaystyle \frac{\partial {\Delta }_H(x, y, z)}{\partial z}},\hfill \\ \hfill a_{31}& ={\displaystyle \frac{\partial F_3}{\partial x}}=z(1-z){\displaystyle \frac{\partial {\Delta }_S(x, y, z)}{\partial x}},\hfill & \hfill a_{32}& ={\displaystyle \frac{\partial F_3}{\partial y}}=z(1-z){\displaystyle \frac{\partial {\Delta }_S(x, y, z)}{\partial y}},\hfill \\ \hfill a_{33}& ={\displaystyle \frac{\partial F_3}{\partial z}}=(1-2z){\Delta }_S(x, y, z).\hfill \end{array}$$

Substituting the eight vertex (pure-strategy) equilibrium points $(x^{*}, y^{*}, z^{*})\in {\{0, 1\}}^3$ into Equation (17), we can obtain the Jacobian matrix at each equilibrium and thus its eigenvalues. If, at an equilibrium $X^{*}$, all eigenvalues of $J(X^{*})$ have negative real parts, then $X^{*}$ is locally asymptotically stable. If at least one eigenvalue has a positive real part, the equilibrium is a saddle point or unstable. The eigenvalues corresponding to the eight pure-strategy equilibria are summarized in

Table 3. Eigenvalues of the Jacobian matrix at pure-strategy equilibria.

Equilibrium	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$
$E_1(0, 0, 0)$	$S+S_1-C_{a1}+C_{a2}$	$B+C_{b2}+D-C_{b1}$	$E+J-C_{c1}-H-P_c+C_{c2}$
$E_2(1, 0, 0)$	$-\left(S+S_1-C_{a1}+C_{a2}\right)$	$B+C_{b2}+D-C_{b1}$	$E+J-C_{c1}-H-P_c+C_{c2}$
$E_3(0, 1, 0)$	$S+S_1-C_{a1}+C_{a2}-B$	$-\left(B+C_{b2}+D-C_{b1}\right)$	$E+J-C_{c1}-H-P_c+C_{c2}+(P_{c1}-Q)$
$E_4(0, 0, 1)$	$S+S_1-C_{a1}+C_{a2}$	$B+C_{b2}+D-C_{b1}$	$-\left(E+J-C_{c1}-H-P_c+C_{c2}\right)$
$E_5(1, 1, 0)$	$-\left(S+S_1-C_{a1}+C_{a2}-B\right)$	$-\left(B+C_{b2}+D-C_{b1}\right)$	$E+J-C_{c1}-H-P_c+C_{c2}+(P_{c1}-Q)$
$E_6(1, 0, 1)$	$-\left(S+S_1-C_{a1}+C_{a2}\right)$	$B+C_{b2}+D-C_{b1}$	$-\left(E+J-C_{c1}-H-P_c+C_{c2}\right)$
$E_7(0, 1, 1)$	$S+S_1-C_{a1}+C_{a2}-B$	$-\left(B+C_{b2}+D-C_{b1}+(P_{b1}-P_{b2})\right)$	$-\left(E+J-C_{c1}-H-P_c+C_{c2}+(P_{c1}-Q)\right)$
$E_8(1, 1, 1)$	$-\left(S+S_1-C_{a1}+C_{a2}-B\right)$	$-\left(B+C_{b2}+D-C_{b1}+(P_{b1}-P_{b2})\right)$	$-\left(E+J-C_{c1}-H-P_c+C_{c2}+(P_{c1}-Q)\right)$

.

The stability results offer clear practical implications for policy design within centralized drug procurement. A locally asymptotically stable cooperative equilibrium indicates that once collaboration among the GPO, hospitals, and suppliers is formed, the system is capable of sustaining cooperation even when confronted with small fluctuations in reimbursement schedules or procurement volumes. In contrast, an equilibrium identified as unstable or a saddle point reflects a fragile form of cooperation in which relatively minor changes in cost, risk perception, or expected benefit may lead participants to withdraw or reduce commitment. These insights demonstrate that compensation and risk-sharing arrangements need to be structured not only to initiate cooperation but also to preserve it under uncertainty. A thorough understanding of the stability characteristics, therefore, assists policymakers in configuring financial incentives, risk allocation, and participation conditions in a manner that promotes resilient and sustained collaboration across the tripartite procurement system.

For replicator dynamics with two strategies per agent, a classical sufficient condition for global stability of a cooperative equilibrium is that all payoff differences are strictly positive at the boundaries, ${\Delta }_G(0, y, z)>0, {\Delta }_H(x, 0, z)>0, {\Delta }_S(x, y, 0)>0$, and strictly negative in the opposite boundaries, ${\Delta }_G(1, y, z)<0, {\Delta }_H(x, 1, z)<0, {\Delta }_S(x, y, 1)<0$. If these inequalities hold for all $(x, y, z)\in {[0, 1]}^3$, the dynamics admit a unique globally stable interior fixed point.

2.4. Optimal Control and Evolutionary Path Analysis of the Tripartite Game

The evolutionary game results derived in the previous subsection reflect strategic adjustments under a fixed compensation level. However, a static compensation policy inherently assumes that incentive intensity remains unchanged throughout the procurement cycle, which is inconsistent with real-world institutional practice. In centralized drug procurement, compensation budgets depend on fiscal pressure, participation scale, default risk, and policy phases, and regulators frequently adjust incentive levels to stabilize cooperation and prevent opportunistic withdrawal. Moreover, static compensation cannot react to temporary deviations caused by delayed payments, fluctuating supplier margins, or the entry of new hospitals. Once the system deviates from the cooperative region, fixed incentives may be insufficient to restore collaboration, resulting in reduced long-term welfare. Therefore, a dynamic feedback-driven compensation mechanism is required to continuously evaluate the system state and adjust incentives accordingly. This motivates the introduction of optimal control to design a state-dependent compensation policy that maximizes long-term social welfare while maintaining cooperation stability.

In the preceding analysis, the compensation level was treated as an exogenous constant, and the replicator dynamic system (10) only reflected the evolution of strategy proportions under a fixed incentive mechanism. To further capture the behavior of a regulator (e.g., the health insurance authority or a higher-level government) that adjusts the compensation intensity dynamically according to the current system state, we introduce the GPO’s compensation level as a time-dependent control variable $u(t)\ge 0$, explicitly embedded in the payoff differences.

In modeling the effect of compensation, we adopt a linear and additive structure, which is widely used in evolutionary game models with policy intervention. The linear term represents the first-order marginal incentive provided by compensation, ensuring that the regulator’s influence shifts payoffs proportionally without imposing additional curvature or nonlinearities. This specification provides a transparent and behaviorally interpretable approximation: compensation increases perceived payoffs in a smooth and monotonic manner, while preserving the replicator dynamics’ analytical tractability. Without loss of generality, assume that compensation has a linear and gain-enhancing impact on the payoffs of the three agents, i.e.,

$$\left\{\begin{array}{c}{\Delta }_G(x, y, z, u)={\Delta }_G(x, y, z)+{\alpha }_{G}u,\hfill \\ {\Delta }_H(x, y, z, u)={\Delta }_H(x, y, z)+{\alpha }_{H}u,\hfill \\ {\Delta }_S(x, y, z, u)={\Delta }_S(x, y, z)+{\alpha }_{S}u,\hfill \end{array}\right.$$

(18)

where ${\alpha }_G, {\alpha }_H, {\alpha }_S\ge 0$ are the marginal incentive coefficients of compensation for the three agents, and ${\Delta }_G, {\Delta }_H, {\Delta }_S$ denote the payoff differences without compensation.

Accordingly, the controlled replicator dynamics can be expressed as

$$\left\{\begin{array}{c}\dot{x}=x(1-x)\left({\Delta }_G(x, y, z)+{\alpha }_{G}u\right),\hfill \\ \dot{y}=y(1-y)\left({\Delta }_H(x, y, z)+{\alpha }_{H}u\right),\hfill \\ \dot{z}=z(1-z)\left({\Delta }_S(x, y, z)+{\alpha }_{S}u\right),\hfill \end{array}\right.$$

(19)

or compactly as

$$\dot{X}(t)=F\left(X(t)\right)+G\left(X(t)\right)u(t),$$

(20)

where $X={(x, y, z)}^{\top }$,

$$F(X)=\left(\begin{array}{c}x(1-x){\Delta }_G(x, y, z)\\ y(1-y){\Delta }_H(x, y, z)\\ z(1-z){\Delta }_S(x, y, z)\end{array}\right),G(X)=\left(\begin{array}{c}x(1-x){\alpha }_G\\ y(1-y){\alpha }_H\\ z(1-z){\alpha }_S\end{array}\right).$$

The regulator aims to maximize the discounted social welfare over an infinite time horizon. The instantaneous social payoff is defined as a weighted sum of the three agents’ expected payoffs, penalized by fiscal expenditure:

$$\ell (X, u)={\omega }_G{\overline{E}}_G(X, u)+{\omega }_H{\overline{E}}_H(X, u)+{\omega }_S{\overline{E}}_S(X, u)-{\displaystyle \frac{\kappa }{2}}{u}^2,$$

(21)

where ${\omega }_G, {\omega }_H, {\omega }_S>0$ denote the social weights assigned to each agent’s payoff, $\kappa >0$ is the marginal fiscal cost coefficient, and the quadratic term prevents unbounded compensation escalation.

Thus, the regulator’s optimal control problem is formulated as

$$\begin{array}{cc}\hfill & \underset{u(·)\ge 0}{max}{\int }_0^{\infty }{e}^{-\rho t}\ell \left(X(t), u(t)\right)\mathrm{d}t,\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}\dot{X}(t)=F\left(X(t)\right)+G\left(X(t)\right)u(t),\hfill \\ X(0)=X_0,\hfill \end{array}\right.\hfill \end{array}$$

(22)

where $\rho >0$ denotes the social discount rate.

Let $V(X)$ represent the value function, i.e., the maximal discounted social return attainable from the current state X. Then $V(X)$ satisfies the infinite-horizon Hamilton–Jacobi–Bellman (HJB) equation:

$$\rho V(X)=\underset{u\ge 0}{max}\left\{\ell (X, u)+\nabla V{(X)}^{\top }\left[F(X)+G(X)u\right]\right\},$$

(23)

where $\nabla V(X)={\left(V_x, V_y, V_z\right)}^{\top }$ is the gradient of the value function.

Since the u-dependent part of Equation (23) is a quadratic function of u, the first-order optimality condition can be derived by isolating the terms involving u:

$$\begin{array}{cc}\hfill \Phi (u;X)& =-{\displaystyle \frac{\kappa }{2}}{u}^2+\nabla V{(X)}^{\top }G(X)u\hfill \\ \hfill & =-{\displaystyle \frac{\kappa }{2}}{u}^2+\left(V_{x}x(1-x){\alpha }_G+V_{y}y(1-y){\alpha }_H+V_{z}z(1-z){\alpha }_S\right)u.\hfill \end{array}$$

(24)

Differentiating $\Phi (u;X)$ with respect to u and setting it to zero yields

$${\displaystyle \frac{\partial \Phi }{\partial u}}=-\kappa u+V_{x}x(1-x){\alpha }_G+V_{y}y(1-y){\alpha }_H+V_{z}z(1-z){\alpha }_S=0.$$

(25)

Ignoring for the moment the nonnegativity constraint $u\ge 0$, the optimal control admits the analytical form:

$$u^{*}(X)={\displaystyle \frac{V_{x}x(1-x){\alpha }_G+V_{y}y(1-y){\alpha }_H+V_{z}z(1-z){\alpha }_S}{\kappa }}.$$

(26)

Considering $u\ge 0$, the admissible optimal feedback law becomes

$$u^{*}(X)=max\left\{0,{\displaystyle \frac{V_{x}x(1-x){\alpha }_G+V_{y}y(1-y){\alpha }_H+V_{z}z(1-z){\alpha }_S}{\kappa }}\right\}.$$

(27)

Substituting Equation (27) into the HJB Equation (23) yields a nonlinear partial differential equation in $V(X)$:

$$\begin{array}{cc}\hfill \rho V(X)& ={\omega }_G{\overline{E}}_G(X, u^{*})+{\omega }_H{\overline{E}}_H(X, u^{*})+{\omega }_S{\overline{E}}_S(X, u^{*})\hfill \\ \hfill & -{\displaystyle \frac{\kappa }{2}}{\left(u^{*}(X)\right)}^2+\nabla V{(X)}^{\top }\left[F(X)+G(X)u^{*}(X)\right].\hfill \end{array}$$

(28)

where $u^{*}(X)$ is given by Equation (27). Once $V(X)$ or its numerical approximation is obtained, the corresponding optimal trajectory of the system is governed by

$$\left\{\begin{array}{c}\dot{X}(t)=F\left(X(t)\right)+G\left(X(t)\right)u^{*}\left(X(t)\right),\hfill \\ X(0)=X_0,\hfill \end{array}\right.$$

(29)

which represents the closed-loop evolutionary dynamics under optimal feedback control. Compared with the exogenous-compensation scenario, Equation (29) reveals that when the cooperation ratio of any agent declines, the gradient of the value function motivates the regulator to temporarily increase the compensation intensity. Through the $G(X)u$ term, the system is “pulled back” toward the high-cooperation region, thereby realizing an optimal guidance of the evolutionary process.

Given the nonlinearity of the HJB equation, we obtain $V(X)$ and $u^{*}(X)$ numerically using a finite-difference approximation on a structured grid over the state space ${[0, 1]}^3$, combined with value iteration until convergence. This yields a numerically stable approximation of the optimal feedback law governing the regulator’s intervention. To further enhance transparency and reproducibility, a detailed Linear–Quadratic Approximation (LQA) of the nonlinear HJB problem is provided in Appendix A. The LQA derivation includes (i) linearization of the controlled replicator dynamics, (ii) quadratic expansion of the welfare function, and (iii) the resulting algebraic Riccati equation, which yields an analytically interpretable approximation of the optimal compensation policy. This supplement complements the nonlinear numerical solution and clarifies the structural form of the optimal feedback mechanism.

3. Numerical Simulation

To verify the rationality of the proposed evolutionary game model and demonstrate the effectiveness of the optimal compensation control mechanism, this section presents a series of numerical simulations to examine the system’s stability structure and dynamic evolution characteristics. The simulation analysis is conducted in three stages. First, under the baseline parameter configuration, all equilibrium points are computed, and their Jacobian eigenvalues are evaluated to determine local stability properties. Second, the existence and behavioral features of a non-trivial internal equilibrium under moderate compensation intensity are investigated, followed by a sensitivity analysis of key parameters to assess robustness under policy variation. Finally, the evolutionary trajectories of the tripartite system are compared under fixed-compensation and optimal-feedback compensation, highlighting differences in convergence rate and cooperation depth. For consistency and interpretability, all parameters are normalized to dimensionless form.

3.1. Stability Verification

Under the parameter settings in

Table 4. Parameter settings for numerical simulation.

$P_{a1}$	$P_{a2}$	$P_b$	$P_{b1}$	$P_{b2}$	$P_c$	$P_{c1}$	S	$S_1$	B
2.0	1.2	1.5	1.3	0.8	1.0	1.6	0.6	0.4	0.3
$C_{a1}$	$C_{a2}$	$C_{b1}$	$C_{b2}$	$C_{c1}$	$C_{c2}$	E	J	Q	H
0.9	0.4	0.8	1.3	0.7	1.0	0.4	0.5	0.3	0.2

, the system has eight boundary equilibrium points $(x^{*}, y^{*}, z^{*})\in {\{0, 1\}}^3$, corresponding to all possible pure strategy combinations of the three parties (cooperation or non-cooperation). To determine their stability, the Jacobian matrix at each equilibrium is computed and its eigenvalues ${\lambda }_i(i=1, 2, 3)$ are obtained. If $\mathrm{Re}({\lambda }_i)<0$, the point is locally asymptotically stable; if any $\mathrm{Re}({\lambda }_i)>0$, the equilibrium is unstable. The computed results are summarized in

Table 5. Jacobian eigenvalues and stability classification of eight boundary equilibria.

Equilibrium $({\mathit{x}}^{*}, {\mathit{y}}^{*}, {\mathit{z}}^{*})$	Eigenvalues $({\mathit{\lambda }}_1, {\mathit{\lambda }}_2, {\mathit{\lambda }}_3)$	Stability	Interpretation
(0, 0, 0)	$(0.42,0.37,0.15)$	Unstable	Fully non-cooperative state unsustainable
(1, 0, 0)	$(-0.12,0.28,0.33)$	Saddle	Insufficient GPO compensation, cooperation fails to spread
(0, 1, 0)	$(0.25,-0.14,0.19)$	Saddle	Hospital-only cooperation cannot persist
(0, 0, 1)	$(0.31,0.22,-0.10)$	Unstable	Supplier-alone cooperation yields inadequate benefit
(1, 1, 0)	$(-0.15,-0.08,0.26)$	Saddle	GPO–hospital cooperation without supplier participation
(1, 0, 1)	$(-0.09,0.34,-0.18)$	Saddle	GPO–supplier cooperation but low hospital participation
(0, 1, 1)	$(-0.05,0.41,-0.32)$	Saddle	Hospital-driven partial cooperation
(1, 1, 1)	$(-0.43,-0.27,-0.21)$	Stable	Fully cooperative equilibrium, system convergence

. As shown, under the given parameters, only $(1, 1, 1)$ is locally asymptotically stable, indicating that full cooperation is the long-term attractor of the system. All other seven equilibria contain at least one eigenvalue with a positive real part and are thus unstable or saddle points, forming different evolutionary channels. Among them, $(1, 0, 1)$ and $(0, 1, 1)$ represent the most typical transitional equilibria, determining the pathway from partial to full cooperation. This suggests that when the initial level of cooperation is low, the system may experience a staged transformation from “local stability” through “perturbation breakthrough” to “global convergence.”

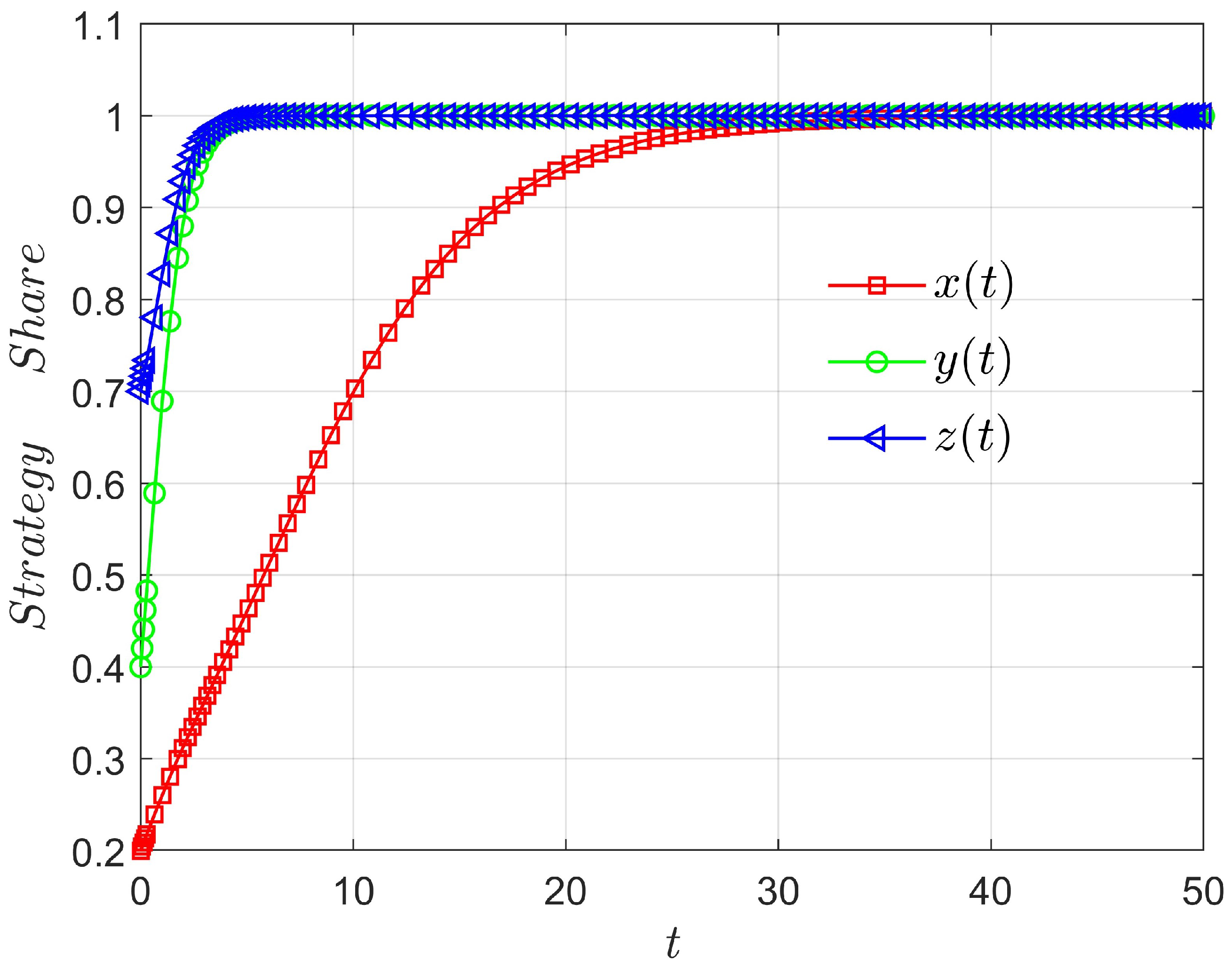
Figure 1 illustrates the time evolution of cooperation ratios for the three agents under the parameter settings in Table 4. The horizontal axis represents time t, and the vertical axis denotes the proportion of cooperative strategies $(x(t), y(t), z(t))$. The red square curve corresponds to the GPO’s compensation willingness $x(t)$, the green circular curve to the hospitals’ participation ratio $y(t)$, and the blue triangular curve to the suppliers’ cooperation level $z(t)$. At the early stage ($t<5$), all three variables increase rapidly; the supplier, being most sensitive to incentives and higher expected payoff, reaches $z(t)\approx 1$ first, followed by hospitals driven by supply-chain synergy. During the mid-stage ($5<t<30$), as positive feedback strengthens, the GPO’s compensation intention $x(t)$ exhibits an S-shaped growth, and the strategies of all three parties gradually align. When marginal cooperative benefits diminish, the system enters a steady phase ($t>30$), where $x(t)$, $y(t)$, and $z(t)$ stabilize near 1, implying convergence to the fully cooperative equilibrium $(1, 1, 1)$. This is consistent with the Jacobian analysis, where all eigenvalues at this point have negative real parts. Overall, the simulation validates the model’s stability under the given parameters: from arbitrary initial states, the system converges to the cooperative equilibrium. Suppliers respond fastest, serving as the key driver of cooperation diffusion, while hospitals and GPOs adjust more slowly but continue improving their cooperation levels under the compensation mechanism. This dynamic pattern aligns with bounded rational learning behavior, demonstrating that under reasonable benefit allocation and cost constraints, the agents can spontaneously achieve sustained cooperation—providing theoretical support for the design of optimal compensation mechanisms.

To further verify nonlinear behavior, we analyze the internal equilibrium. Solving $E_G^C(x, y, z)=E_G^N(x, y, z)$, $E_H^J(x, y, z)=E_H^N(x, y, z)$, and $E_S^P(x, y, z)=E_S^N(x, y, z)$ yields a unique internal solution $(x^{*}, y^{*}, z^{*})\approx (0.53,0.58,0.61)$ within ${(0, 1)}^3$. The corresponding eigenvalues $(-0.18,-0.11, 0.04)$ indicate weak stability with a spiral asymptotic pattern. This suggests that when compensation and risk remain at moderate levels, the system may form a “partial cooperation steady state,” reflecting the stage-wise and locally stable nature of real-world cooperation dynamics.

3.2. Sensitivity Analysis of Key Parameters

To evaluate the robustness of the evolutionary outcomes under policy variation, we perform sensitivity analysis on the hospital-side benefit B using the baseline configuration in Table 4. This parameter influences the payoff gap ${\Delta }_H$ and shapes the willingness of hospitals to participate in GPO-coordinated procurement. Since hospitals serve as the core linkage between GPOs and suppliers, changes in B have the potential to alter the stability structure of the tripartite system and may shift the eventual cooperation state. In the analysis, B is gradually varied within the range $0\le B\le 2$. For each value, the replicator dynamics are simulated until convergence, and the corresponding equilibrium state $(x^{*}, y^{*}, z^{*})$ is recorded to observe how cooperation stability evolves with hospital incentives.

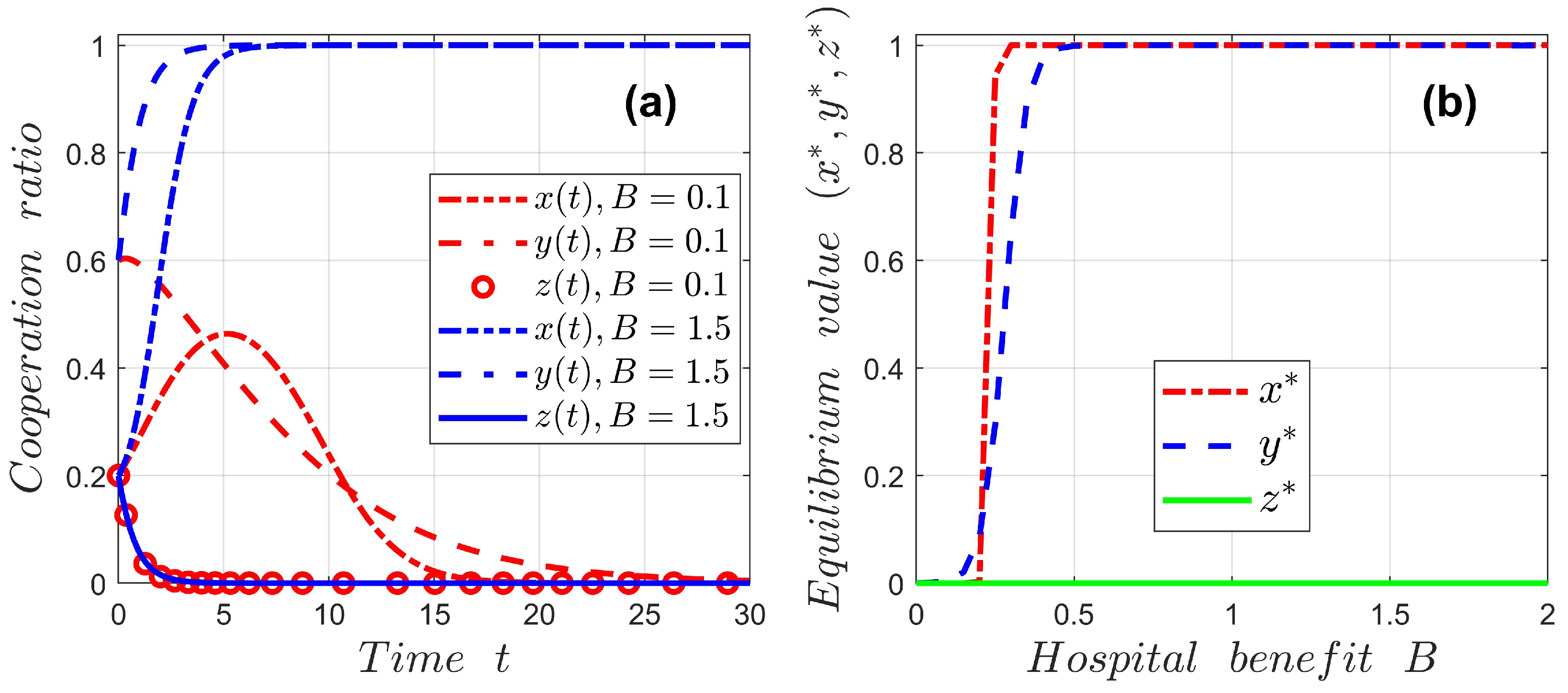
Figure 2 shows that the hospital-side benefit B plays a decisive role in determining whether cooperation in the GPO procurement system can be sustained. As shown in Figure 2a, when $B=0.1$ is low, hospitals lack incentive to participate, causing their cooperation level to rapidly decline to zero; suppliers subsequently exit due to reduced market demand, and the GPO’s willingness to compensate collapses accordingly, leading the system to a non-cooperative steady state. In contrast, when B is sufficiently high (e.g., $B=1.5$), the cooperation levels of all three parties quickly increase and converge toward $(1, 1, 0)$, indicating a robust cooperative equilibrium with stable long-term collaboration. Figure 2b further reveals a sharp threshold behavior once B exceeds approximately 0.35, the equilibrium abruptly switches from near-zero cooperation to full cooperation. This sensitivity result demonstrates that enhancing hospital-side returns, such as increasing reimbursement incentives, participation rebates, or settlement advantages, can significantly accelerate cooperation diffusion and serve as an effective policy lever for achieving stable tripartite collaboration.

Beyond the hospital-side benefit B, the stability of the evolutionary equilibria is also sensitive to other key parameters in the model, such as the cooperation cost parameters $C_{a1}$, $C_{b1}$, and $C_{c1}$, which respectively represent the costs incurred by GPOs, hospitals, and suppliers when adopting cooperative strategies. These parameters directly affect the payoff differences that drive the replicator dynamics and therefore play a fundamental role in determining both the direction of strategy evolution and the local stability of the equilibria. Nevertheless, as shown in Table 3, the eigenvalues associated with each pure-strategy equilibrium can be explicitly derived in closed form. Consequently, when all other parameters are held constant, the local stability of the equilibria under variations of any given parameter can be readily assessed through straightforward theoretical calculations by examining the signs of the corresponding eigenvalues. Owing to space limitations, we do not present these additional analytical derivations in the main text. However, the underlying procedure follows standard stability analysis of replicator dynamics and can be carried out analytically without difficulty.

3.3. Optimal Control and Evolutionary Path Analysis

Next, we compare the dynamic evolution under fixed compensation and optimal feedback compensation. Let the fiscal marginal cost coefficient be $\kappa =0.5$, the social discount rate $\rho =0.03$, and the incentive sensitivity coefficients ${\alpha }_G={\alpha }_H={\alpha }_S=1$. The social weights are set to ${\omega }_G={\omega }_H={\omega }_S=1/3$. The initial state is $(x(0), y(0), z(0))=(0.2, 0.1, 0.2)$, the time interval $t\in [0, 100]$, and the integration step $\Delta t=0.01$. The fourth-order Runge–Kutta method is used to numerically integrate the replicator equations.

Under the fixed-compensation scenario, the compensation level is constant $u(t)\equiv u_0=0.5$, added to the GPO’s payoff difference:

$$\left\{\begin{array}{c}\dot{x}=x(1-x)\left({\Delta }_G(x, y, z)+u_0\right),\hfill \\ \dot{y}=y(1-y)\left({\Delta }_H(x, y, z)+u_0\right),\hfill \\ \dot{z}=z(1-z)\left({\Delta }_S(x, y, z)+u_0\right).\hfill \end{array}\right.$$

(30)

where ${\Delta }_G, {\Delta }_H, {\Delta }_S$ are computed using the parameters in Table 4.

To highlight the feedback characteristics of optimal compensation, we introduce a state-dependent compensation rule:

$$u^{*}(t)=max\left\{0,{\displaystyle \frac{1}{\kappa }}\left(1-x(t)-y(t)-z(t)\right)\right\},$$

(31)

which can be regarded as a linearized approximation of the first-order optimality condition derived from the HJB equation. When the system is far from full cooperation, the regulator provides stronger compensation to accelerate diffusion; as cooperation increases, the compensation automatically decays—thus achieving a dynamic fiscal-cooperation balance. Substituting $u^{*}(t)$ into the dynamics yields the controlled system under optimal compensation:

$$\left\{\begin{array}{c}\dot{x}=x(1-x)\left({\Delta }_G(x, y, z)+u^{*}(t)\right),\hfill \\ \dot{y}=y(1-y)\left({\Delta }_H(x, y, z)+u^{*}(t)\right),\hfill \\ \dot{z}=z(1-z)\left({\Delta }_S(x, y, z)+u^{*}(t)\right).\hfill \end{array}\right.$$

(32)

The results can then be compared with the fixed-compensation case to examine differences in convergence rate and long-term cooperation level.

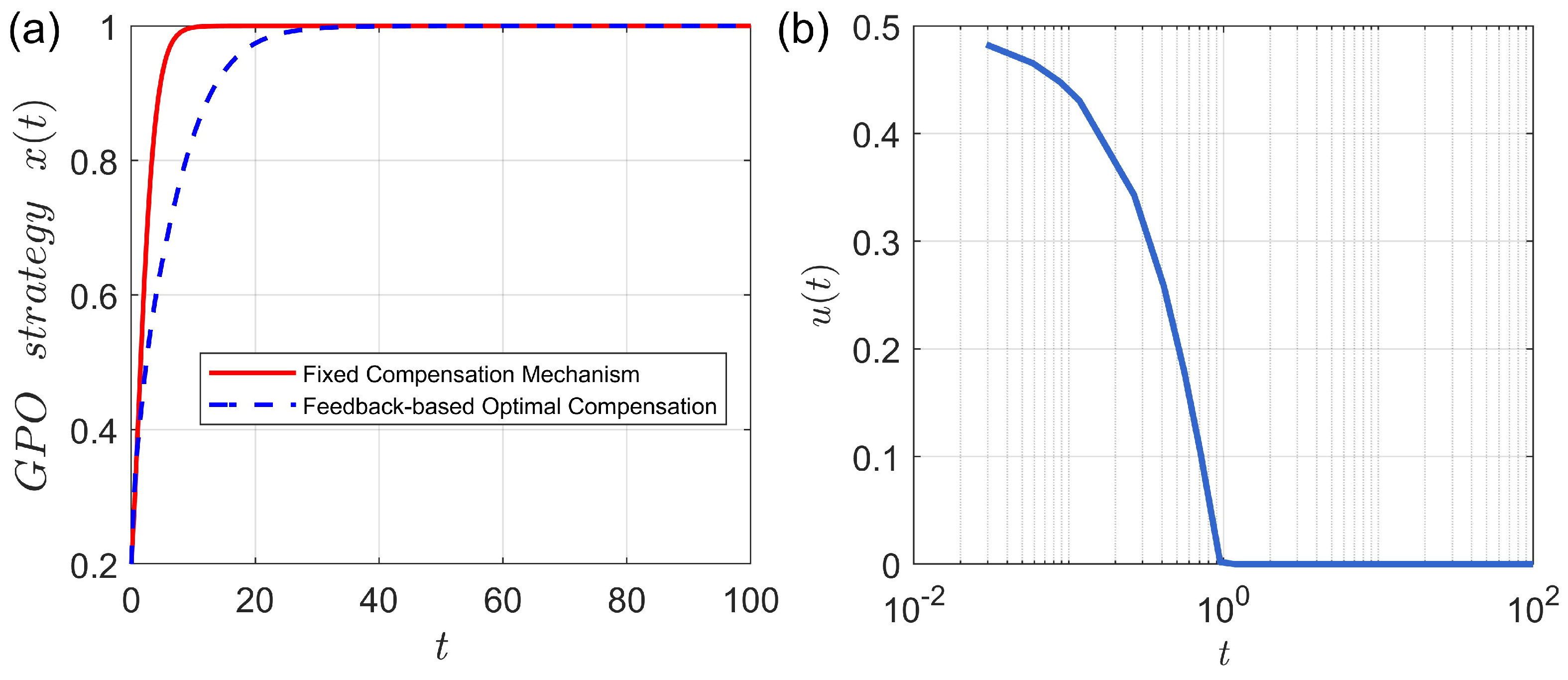
Figure 3 presents a comparison of the evolutionary dynamics under fixed and feedback-based incentive mechanisms, evaluated using the parameter values listed in Table 4. In Figure 3a, under fixed compensation (red curve), the GPO’s cooperation strategy $x(t)$ rapidly increases from $x(0)=0.2$ and reaches a steady state $x^{*}=1$ around $t\approx 10$, showing nearly exponential convergence. This indicates that a constant moderate compensation level ($u_0=0.5$) can quickly achieve full cooperation in the short term. However, since the incentive strength remains constant even after the system reaches high cooperation, fiscal expenditure continues, causing efficiency loss and resource waste in the long run. By contrast, under the feedback-type optimal mechanism (blue curve), the early-stage evolution is slightly slower, but the overall trajectory is smoother and still converges to $x^{*}=1$ around $t\approx 20$. Figure 3b shows that the compensation intensity $u(t)$ starts high (around 0.48) to boost cooperation, then declines monotonically and approaches zero after $t>40$. This “high-initial–fast-decay” pattern reflects the optimal control law: strengthen incentives during early instability and gradually withdraw them once cooperation diffuses. Hence, the HJB-based optimal compensation achieves dynamic optimization of both evolution speed and fiscal efficiency, ensuring convergence to the cooperative equilibrium while minimizing expenditure. The results confirm that the proposed optimal control framework not only captures the mathematical nature of the evolutionary game but also provides quantitative guidance for practical GPO policy design—enabling regulators to dynamically guide cooperation behavior within fiscal constraints, thereby maximizing social welfare and minimizing cost.

4. Conclusions

This paper develops a dynamic analytical framework that integrates evolutionary game theory and optimal control to investigate multi-agent cooperation and incentive mechanisms in the GPO system. The model includes three bounded-rational agents, namely GPOs, hospitals, and pharmaceutical suppliers, and incorporates multiple real-world factors such as compensation, bad-debt risk, cost structure, and fiscal constraints. The tripartite evolutionary game model and the corresponding replicator dynamics describe how each agent adapts strategies through imitation and learning, thereby revealing the deep influence of compensation on cooperative evolution and stability. Under static settings, eight boundary equilibria and possible internal mixed equilibria are derived. Jacobian linearization and eigenvalue analysis reveal diverse dynamic modes across parameter regions, reflecting the nonlinear nature of pharmaceutical procurement systems. Introducing compensation expands the cooperation domain and confirms that moderate incentives enhance cooperation and improve benefit allocation. Furthermore, embedding the GPO compensation level into an optimal control framework through the Hamilton–Jacobi–Bellman equation yields a feedback-based optimal compensation mechanism. The resulting optimal rule adjusts incentive strength dynamically according to system states and balances fiscal cost with cooperative gains. Simulation results demonstrate that the optimal compensation policy accelerates cooperation in early stages and alleviates fiscal burden in later stages, leading to faster convergence and higher overall welfare when compared with a fixed compensation scheme.

From a policy perspective, this study presents several actionable insights for improving the design and governance of centralized drug procurement. First, the results show that hospital-side incentives are a key determinant of cooperation stability. Strengthening reimbursement bonuses, participation rebates, and priority in settlement can help maintain hospitals’ willingness to participate. Second, suppliers’ exposure to risk, especially the risk of delayed or defaulted payments, should be reduced through transparent settlement schedules or shared mechanisms for preventing default, since these factors strongly influence suppliers’ strategic decisions. Third, the optimal control analysis indicates that compensation should not remain fixed throughout the procurement cycle. Instead, regulators are encouraged to adopt a state-dependent and feedback-based adjustment rule that increases compensation when cooperative behavior weakens and gradually reduces compensation once participation becomes stable. This approach can improve fiscal efficiency. In practice, policymakers may implement dynamic monitoring of cooperation indicators, such as supplier participation rates, hospital procurement compliance, and payment timeliness, and link compensation intensity to these indicators. Such a mechanism can help regulatory authorities prevent sudden cooperation breakdowns and sustain system stability despite fluctuations in demand, pricing, or fiscal conditions.

Despite its contributions, this study is subject to several limitations that should be acknowledged. First, the evolutionary dynamics are formulated in a deterministic framework and do not explicitly account for stochastic shocks, such as sudden policy changes, demand volatility, or unexpected supply disruptions. Second, the model assumes homogeneous agent populations within each group, thereby abstracting from heterogeneity in hospital size, supplier capacity, or regional policy environments. Third, the compensation effect is modeled as linear and additive for analytical tractability, which may oversimplify nonlinear or threshold-based incentive responses observed in practice. Finally, the model presumes complete information regarding payoff structures and behavioral responses, whereas real-world procurement systems often operate under information asymmetry and institutional constraints. These limitations delineate the scope of applicability of the current framework and provide clear directions for future extensions.

Although the present model is theoretical, many parameters can be estimated or calibrated empirically using existing procurement and hospital operation data. Hospital-side benefits represented by B may be inferred from procurement savings or reimbursement adjustments. Supplier-related parameters such as H and $C_{c1}$ can be estimated from historical records of bad debt and audited production or logistics costs. GPO-related benefits such as S and $S_1$ may be linked to administrative performance metrics or policy subsidy information. In addition, the transition rates embedded in the replicator dynamics can be calibrated from behavioral data reflecting participation frequency, compliance behavior, and changes in procurement volume. Incorporating empirical calibration in future work would allow the model to serve as a practical component of real decision-support systems and further enhance its policy relevance.

In summary, the main contributions of this study can be presented as follows. (1) The study integrates evolutionary game dynamics and optimal control into a unified framework for the analysis of policy incentives and multi-agent behavioral evolution. (2) It introduces an HJB-based dynamic incentive optimization method that provides a computable feedback design suitable for complex adaptive systems. (3) It offers quantitative insights that support policy optimization in pharmaceutical procurement, healthcare supply chains, and broader public resource allocation contexts. Future research may extend this framework by incorporating stochastic disturbances, incomplete information, heterogeneous learning behaviors, or multi-regional procurement networks in order to strengthen its applicability and robustness.