Isotonic and Convex Regression: A Review of Theory, Algorithms, and Applications

Abstract

Shape-restricted regression provides a flexible framework for estimating an unknown relationship between input variables and a response when little is known about the functional form, but qualitative structural information is available. In many practical settings, it is natural to assume that the response changes in a systematic way as inputs increase, such as increasing, decreasing, or exhibiting diminishing returns. Isotonic regression incorporates monotonicity constraints, requiring the estimated function to be nondecreasing with respect to its inputs, while convex regression imposes convexity constraints, capturing relationships with increasing or decreasing marginal effects. These shape constraints arise naturally in a wide range of applications, including economics, operations research, and modern data-driven decision systems, where they improve interpretability, stability, and robustness without relying on parametric model assumptions or tuning parameters. This review focuses on isotonic and convex regression as two fundamental examples of shape-restricted regression. We survey their theoretical properties, computational formulations based on optimization, efficient algorithms, and practical applications, and we discuss key challenges such as non-smoothness, boundary overfitting, and scalability. Finally, we outline open problems and directions for future research.

1. Introduction

In many statistical and data-driven problems, the goal is to understand how a response variable changes as one or more input variables vary. In practice, the exact functional relationship is often unknown and difficult to specify parametrically. Nevertheless, domain knowledge frequently provides qualitative information about the structure of the relationship. For example, demand typically decreases as price increases, waiting times in queueing systems decrease as service capacity increases, and costs often exhibit diminishing returns as resources grow.

Shape-restricted regression is a class of nonparametric methods that incorporate qualitative prior knowledge by constraining the shape of the estimated function, rather than specifying a parametric form. Common shape constraints include monotonicity and convexity, which arise naturally in many applications.

Imposing such constraints fundamentally changes the fitted function. Isotonic regression enforces monotonicity and typically yields a piecewise constant estimator, while convex regression produces a piecewise linear fit with monotone slopes. These estimators can be viewed as projections of the data onto a space of functions satisfying the prescribed shape constraints.

By preventing local fluctuations and enforcing global structural properties, shape-restricted regression often improves stability, interpretability, and robustness relative to unconstrained nonparametric methods. When qualitative relationships are known a priori, such as increasing risk with exposure or diminishing returns, these methods provide flexible, data-driven models that remain aligned with domain knowledge. Isotonic and convex regression are two fundamental and widely studied examples of this broader framework; Figure 1 and Figure 2 later in the paper provide visual illustrations of how monotonicity and convexity constraints shape the fitted functions in practice.

With this motivation in mind, we consider the problem of estimating an unknown regression function from noisy observations. Let ${\mathit{X}}_1,\dots ,{\mathit{X}}_n$ denote input variables and $Y_1,\dots ,Y_n$ the corresponding responses, where each observation is subject to random noise.

Mathematically, we want to estimate an unknown function $f_0:\Omega \subset {\mathbb{R}}^d\to \mathbb{R}$ from observations $({\mathit{X}}_1,Y_1),\dots ,({\mathit{X}}_n,Y_n)$, where we assume

$$Y_i=f_0\left({\mathit{X}}_i\right)+{\epsilon }_i,$$

for $i=1,\dots ,n$, $\Omega$ is a closed convex subset of ${\mathbb{R}}^d$, and the ${\epsilon }_i$’s are independent and identically distributed (iid) mean zero random variables with finite variance ${\sigma }^2$. This type of problem arises in many settings. For instance, $\mathit{x}$ may represent a parameter in a stochastic system, such as the service rate of a single-server queue, and $f_0\left(\mathit{x}\right)$ a performance metric, such as the steady-state mean waiting time in that single server queue when the service rate equals $\mathit{x}$.

In many applications, there is no-closed form formula for $f_0\left(\mathit{x}\right)$. In such a case, a practical approach is to simulate the system at selected design points $\mathit{x}={\mathit{X}}_1,\dots ,{\mathit{X}}_n$, obtain simulated outputs $Y_1,\dots ,Y_n$ as estimates of $f_0\left({\mathit{X}}_1\right),\dots ,f_0\left({\mathit{X}}_n\right)$, respectively, and use the data $({\mathit{X}}_1,Y_1),\dots ,$$({\mathit{X}}_n,Y_n)$ to approximate $f_0$: This is a typical regression problem. The problem becomes challenging when it is impossible to place the relationship into a simple parametric form. However, when $f_0$ is known to satisfy certain structural properties such as monotonicity or convexity, shape-restricted regression offers powerful estimators.

Given such prior shape information, a natural estimator of $f_0$ fits a function f with such a shape characterization to the data set and solves

$$\begin{array}{cccc}\hfill & \underset{f\in \mathcal{F}}{\mathrm{minimize}}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(Y_i-f\left({\mathit{X}}_i\right)\right)}^2,\hfill \end{array}$$

(1)

where $\mathcal{F}$ is the class of functions satisfying the assumed shape constraint. For example, if $f_0$ is known to be nondecreasing, we can set $\mathcal{F}={\mathcal{F}}_m$, where

$$\begin{array}{c}{\mathcal{F}}_m=\{f:\Omega \to \mathbb{R}\mid f\left(\mathit{v}\right)\le f\left(\mathit{w}\right) \mathrm{if} v_i\le w_i \mathrm{for} i=1,\dots ,d, \hfill \\ \hfill \mathit{v}=(v_1,\dots ,v_d),\mathit{w}=(w_1,\dots ,w_d)\}.\end{array}$$

On the other hand, if $f_0$ is known to be convex, then we can set $\mathcal{F}={\mathcal{F}}_c$, where

$$\begin{array}{cc}\hfill {\mathcal{F}}_c=\{f:\Omega \to & \mathbb{R}\mid f \mathrm{is} \mathrm{convex}, i.e.,\hfill \\ & f(\alpha \mathit{v}+(1-\alpha \left)\mathit{w}\right)\le \alpha f\left(\mathit{v}\right)+(1-\alpha )f\left(\mathit{w}\right) \mathrm{for} \alpha \in [0,1] \mathrm{and} \mathit{v},\mathit{w}\in \Omega \}.\hfill \end{array}$$

Throughout this paper, we will focus on these two types of problems, the one with $\mathcal{F}={\mathcal{F}}_m$ which leads to isotonic regression and the other with $\mathcal{F}={\mathcal{F}}_c$ which leads to convex regression.

One of the first questions that arises is how to compute the solution to (1) numerically when $\mathcal{F}={\mathcal{F}}_m$ or $\mathcal{F}={\mathcal{F}}_c$. Below, we describe how the solution to (1) can be obtained by solving quadratic programming (QP) problems.

1.1. QP Formulation for Isotonic Regression When $d=1$

We begin with the one-dimensional case to provide a simple and intuitive introduction to isotonic regression. In this setting, the monotonicity constraint reduces to a set of ordered inequalities on the fitted values, which clearly illustrates the basic structure of the estimator and its connection to quadratic programming. This case serves as a conceptual foundation for the more general multivariate formulation discussed later.

When $f_0$ is nondecreasing in $\mathit{x}$, as when price increases with demand, we estimate $f_0$ by fitting a nondecreasing function f that minimizes squared errors ${\sum }_{i=1}^n{(Y_i-f\left({\mathit{X}}_i\right))}^2$. Writing $f_i\triangleq f\left({\mathit{X}}_i\right)$ and assuming the design is ordered so ${\mathit{X}}_1<\cdots <{\mathit{X}}_n$, the existence of a nondecreasing fit through $({\mathit{X}}_i,f_i)$ is equivalent to $f_1\le \cdots \le f_n$. Thus, the estimator solves the following quadratic programming (QP) problem:

$$\begin{array}{cccc}\hfill & \underset{f_1,\dots ,f_n\in \mathbb{R}}{\mathrm{minimize}}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f_i)}^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & f_1\le f_2\le \cdots \le f_n.\hfill \end{array}$$

(2)

Let ${\widehat{f}}_1^m,\dots ,{\widehat{f}}_n^m$ be a solution to (2). Any nondecreasing function interpolating $(({\mathit{X}}_i,{\widehat{f}}_i^m)$: $1\le i\le n)$ defines the isotonic regression estimator and we will denote it by ${\widehat{f}}_n^m(·)$; see, for example, Brunk [1].

1.2. QP Formulation for Convex Regression When $d=1$

As with isotonic regression, we first consider convex regression in the one-dimensional setting to highlight its essential structure in the simplest possible form. When the covariate is scalar, convexity translates into monotonicity of successive slopes, leading to transparent linear inequality constraints. This formulation provides intuition for how convexity is enforced and motivates the multivariate extension presented in subsequent sections.

Suppose instead $f_0$ is convex. Writing $f_i\triangleq f\left({\mathit{X}}_i\right)$ and assuming the design is ordered so ${\mathit{X}}_1<\cdots <{\mathit{X}}_n$, a convex fit through $({\mathit{X}}_i,f_i)$ exists if and only if

$${\displaystyle \frac{f_2-f_1}{{\mathit{X}}_2-{\mathit{X}}_1}}\le \cdots \le {\displaystyle \frac{f_n-f_{n-1}}{{\mathit{X}}_n-{\mathit{X}}_{n-1}}}.$$

Hence, the least-squares convex fit solves

$$\begin{array}{cccc}\hfill & \underset{f_1,\dots ,f_n\in \mathbb{R}}{\mathrm{minimize}}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f_i)}^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & {\displaystyle \frac{f_2-f_1}{{\mathit{X}}_2-{\mathit{X}}_1}}\le \cdots \le {\displaystyle \frac{f_n-f_{n-1}}{{\mathit{X}}_n-{\mathit{X}}_{n-1}}}.\hfill \end{array}$$

(3)

Let ${\widehat{f}}_1^c,\dots ,{\widehat{f}}_n^c$ be a solution to (3). Any convex function interpolating $(({\mathit{X}}_i,{\widehat{f}}_i^c):1\le i\le n)$ is a convex regression estimator and we will denote it by ${\widehat{f}}_n^c(·)$; see, for example, Hildreth [2].

1.3. Scope, Motivation, and Organization of the Review

Over the past several decades, isotonic and convex regression have attracted sustained interest due to their ability to incorporate qualitative structural information into nonparametric estimation; see [3,4] for recent survey papers. Despite extensive theoretical and methodological development, the literature remains fragmented across statistical theory, optimization-based computation, and applied practice.

One central issue concerns computation. Although isotonic and convex regression estimators can be formulated as solutions to constrained least-squares problems, their practical implementation depends critically on efficient algorithms capable of handling large and possibly high-dimensional data sets. Understanding how these estimators can be computed numerically, and what algorithmic trade-offs arise in practice, is therefore a key focus of this review.

A second major theme involves statistical properties. A substantial body of work has established consistency, convergence rates, and limiting distributions under various assumptions, yet these results differ markedly between isotonic and convex regression and between univariate and multivariate settings. Clarifying these similarities and differences is essential for understanding when and how shape-restricted regression methods can be effectively applied.

Beyond theory and computation, isotonic and convex regression play an important role in applications across economics, operations research, and modern data-driven decision systems. At the same time, practical use of these methods reveals recurring challenges, including non-smoothness of the estimators, boundary overfitting, and scalability limitations. Addressing these issues has motivated a range of extensions and regularization strategies, many of which introduce new theoretical and computational questions.

The objective of this paper is to provide an integrated review of isotonic and convex regression that connects these methodological, theoretical, and practical perspectives. We emphasize a unified optimization-based viewpoint, highlight common challenges, and identify open problems that remain insufficiently explored.

The remainder of the paper is organized as follows: Section 2 reviews quadratic programming formulations of isotonic and convex regression. Section 3 focuses on isotonic regression, covering statistical properties, algorithms, applications, and challenges. Section 4 examines convex regression in greater detail. Section 5 presents concluding remarks, and Section 6 discusses open challenges and directions for future research.

1.4. Notation and Definitions

Throughout this paper, we view vectors as columns and write ${\mathit{x}}^{\mathsf{T}}$ to denote the transpose of a vector $\mathit{x}\in {\mathbb{R}}^d$. For $\mathit{x}\in {\mathbb{R}}^d$, we write its ith component as $x_i$, so $\mathit{x}={(x_1,\cdots ,x_d)}^{\mathsf{T}}$. We define $\parallel \mathit{x}\parallel ={(x_1^2+\cdots +x_d^2)}^{1/2}$ and ${\parallel \mathit{x}\parallel }_{\infty }={max}_{1\le i\le d}\left|x_i\right|$.

For any convex set $S\subset {\mathbb{R}}^d$ and a convex function $g:S\to \mathbb{R}$, a vector $\mathit{\beta }\in {\mathbb{R}}^d$ is said to be a subgradient of g at $\mathit{x}\in S$ if $g\left(\mathit{y}\right)\ge g\left(\mathit{x}\right)+{\mathit{\beta }}^{\mathsf{T}}(\mathit{y}-\mathit{x})$ for all $\mathit{y}\in S$. We denote a subgradient of f at $\mathit{x}\in S$ by $\mathrm{subgrad} g\left(\mathit{x}\right)$. The set of all subgradients of g at $\mathit{x}$ is called the subdifferential of g at $\mathit{x}$, denoted by $\partial g\left(\mathit{x}\right)$. When a function $g:S\to \mathbb{R}$ is differentiable at $\mathit{x}\in {[a,b]}^d$, we denote its gradient at $\mathit{x}$ by $\nabla g\left(\mathit{x}\right)$. When $g:\mathbb{R}\to \mathbb{R}$ is differentiable, we denote its gradient at $\mathit{x}$ by $g^{\prime }\left(\mathit{x}\right)$.

For a sequence of random variables $(Z_n:n\ge 1)$ and a sequence of positive real numbers $({\alpha }_n:n\ge 1)$, we say $Z_n={\mathcal{O}}_p\left({\alpha }_n\right)$ as $n\to \infty$ if, for any $ϵ>0$, there exist constants c and $n_0$ such that $\mathbb{P}\left(\right|Z_n/{\alpha }_n|>c)<ϵ$ for all $n\ge n_0$.

For any sequences of real numbers $(a_n:n\ge 1)$ and $(b_n:n\ge 1)$, $a_n=O\left(b\left(n\right)\right)$ if there exists a positive real number M and a real number $n_0$ such that $|a_n|\le Mb\left(n\right)$ for all $n\ge n_0$.

For any sequence of random variables $(A_n:n\ge 1)$ and any random variable B, $A_n\Rightarrow B$ means $A_n$ converges in distribution to B, or $A_n$ converges weakly to B as $n\to \infty$.

2. The Basic QP Formulation

In this section, we describe how the isotonic and convex regression estimators can be found by solving QP problems. Since there are many efficient algorithms for solving QP problems, expressing the isotonic and convex regression estimators as solutions to QP problems offers a basic way to compute them numerically. In $d=1$, (2) and (3) already provide QP formulations for the isotonic and convex regression estimators, respectively. We now present multivariate analogues.

2.1. Isotonic Regression When $d>1$

The main challenge in finding the QP formulation for the multivariate isotonic regression estimator is how to express the monotonicity of a multivariate function in linear inequalities as in the constraints of (2). We will define a non-decreasing function g as follows:

$$g\left(\mathit{v}\right)\le g\left(\mathit{w}\right)\mathrm{whenever}\mathit{v}⪯\mathit{w}$$

for $\mathit{v}=(v_1,\dots ,v_d)$ and $\mathit{w}=(w_1,\dots ,w_d)$ in ${\mathbb{R}}^d$, where $\mathit{v}⪯\mathit{w}$ indicates $v_i\le w_i$ for $1\le i\le d$.

Using this definition, the nondecreasing function with the minimum sum of squared errors can be found by solving the following QP problem in decision variables $f_1,\dots ,f_n\in \mathbb{R}$:

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f_i)}^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & f_i\le f_j\mathrm{if} {\mathit{X}}_i⪯{\mathit{X}}_j \mathrm{for} 1\le i,j\le n.\hfill \end{array}$$

(4)

Let ${\widehat{f}}_1^m,\dots ,{\widehat{f}}_n^m$ be a solution to (4).

To clarify the form of the resulting estimator, solving the quadratic program (4) yields fitted values ${\widehat{f}}_1^m,\dots ,{\widehat{f}}_n^m$ at the observed design points ${\mathit{X}}_1,\dots ,{\mathit{X}}_n$. The multivariate isotonic regression estimator is then defined as any nondecreasing function that interpolates these fitted values. In practice, the estimator is typically taken to be a piecewise constant function over regions of the covariate space determined by the order constraints.

As a result, the estimator can be readily evaluated at any point $\mathit{x}\in \Omega$ by assigning it the fitted value corresponding to the maximal design point ${\mathit{X}}_i⪯\mathit{x}$ under the partial order; i.e.,

$${\widehat{f}}_n^m\left(\mathit{x}\right)=\left\{\begin{array}{cc}\underset{1\le i\le n}{min}\left\{{\widehat{f}}_i^m\right\}\hfill & \mathrm{if} \mathit{x}⪯{\mathit{X}}_i \mathrm{for} \mathrm{all} 1\le i\le n\hfill \\ \underset{1\le i\le n}{max}\{{\widehat{f}}_i^m\mid {\mathit{X}}_i⪯\mathit{x}\}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

This representation highlights both the interpretability and the practical usability of the multivariate isotonic regression estimator once the underlying optimization problem has been solved.

2.2. Convex Regression When $d>1$

Again, the key question is how to express the existence of a convex function going through $({\mathit{X}}_1,f_1),\dots ,({\mathit{X}}_n,f_n)$ as a set of linear constraints. One should notice that there exists a convex function passing through $({\mathit{X}}_1,f_1),\dots ,({\mathit{X}}_n,f_n)$ if and only if there exist ${\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_n\in {\mathbb{R}}^d$ satisfying

$$f_i\ge f_j+{\mathit{\beta }}_j^{\mathsf{T}}({\mathit{X}}_i-{\mathit{X}}_j)\mathrm{for} 1\le i,j\le n;$$

see page 338 of Boyd and Vandenberghe [5]. Here, ${\mathit{\beta }}_i$ serves as a subgradient of the convex function f at ${\mathit{X}}_i$. Hence, a convex function with the least squares can be found by solving the following QP problem in decision variables $f_1,\dots ,f_n\in \mathbb{R}$ and ${\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_n\in {\mathbb{R}}^d$:

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f_i)}^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & f_i\ge f_j+{\mathit{\beta }}_j^{\mathsf{T}}({\mathit{X}}_i-{\mathit{X}}_j)\mathrm{for} 1\le i,j\le n.\hfill \end{array}$$

(5)

Let ${\widehat{f}}_1^c,\dots ,{\widehat{f}}_n^c,{\widehat{\mathit{\beta }}}_1,\dots ,{\widehat{\mathit{\beta }}}_n$ be a solution to (5). Any convex function going through $({\mathit{X}}_1,{\widehat{f}}_1^c),\dots ,$$({\mathit{X}}_n,{\widehat{f}}_n^c)$ can serve as the convex regression estimator in the multidimensional case. However, to remove any ambiguity, we will define the convex regression estimator ${\widehat{f}}_n^c(·)$ as follows:

$${\widehat{f}}_n^c\left(\mathit{x}\right)=\underset{1\le i\le n}{max}\{{\widehat{f}}_i^c+{\mathit{\beta }}_i^{\mathsf{T}}(\mathit{x}-{\mathit{X}}_i)\}$$

for $\mathit{x}\in \Omega$.

In (2)–(5), we established the isotonic and convex regression estimators as solutions to QP problems. Since there are many efficient numerical algorithms to solve QP problems, these QP formulations enable us to compute the isotonic and convex regression estimators numerically.

3. Isotonic Regression

In this section, we review statistical properties, interesting applications, and some challenges of isotonic regression estimator. We also review some algorithms for computing the isotonic regression estimator numerically.

3.1. Statistical Properties

3.1.1. Univariate Case

The isotonic regression estimator in one and multiple dimensions was first introduced by Brunk [1]. In one dimension, Brunk [6] established its strong consistency. More specifically, Brunk [6] proved that if $\Omega =(a,b)\subset \mathbb{R}$, for any $c>a$ and $d<b$,

$$\underset{c\le \mathit{x}\le d}{max}|{\widehat{f}}_n^m\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)|\to 0$$

as $n\to \infty$ with probability one.

Brunk [7] established the asymptotic distribution theory for the isotonic regression estimator when $d=1$. Brunk [7] proved that when $f_0^{\prime }\left(\mathit{x}\right)\ne 0$,

$$n^{1/3}\left({\widehat{f}}_n^m\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)\right)\Rightarrow {\left[4{\sigma }^2{f}_0^{\prime }\left(\mathit{x}\right)\right]}^{1/3}{\mathrm{argmin}}_{t\in \mathbb{R}}\{W\left(t\right)+t^2\}$$

as $n\to \infty$, where $W(·)$ is the two-sided Brownian motion starting from 0.

The $l_2$-risk of the isotonic regression estimator, defined by

$$R(f_0,{\widehat{f}}_n^m)\triangleq \mathbb{E}\left[{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left({\widehat{f}}_n^m\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right)\right)}^2\right],$$

(6)

is proven to have the following bound

$$R(f_0,{\widehat{f}}_n^m)\le C{\sigma }^{4/3}V{\left(f_0\right)}^{2/3}{n}^{-2/3},$$

where $V\left(f_0\right)$ is the total variation of $f_0$ and $C>0$ is a universal constant. Meyer and Woodroofe [8] proved (6) under the assumption that the ${\epsilon }_i$’s are normally distributed, and Zhang [9] proved (6) under a more general assumption that the ${\epsilon }_i$’s are iid with mean zero and variance ${\sigma }^2$.

3.1.2. Multivariate Case

In multiple dimensions, Lim [10] established the strong consistency. Corollary 3.1 of Lim [10] proved that when $\Omega ={(0,1)}^d$, for any $ϵ>0$

$$\underset{\mathit{x}\in {[ϵ,1-ϵ]}^d}{sup}|{\widehat{f}}_n^m\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)|\to 0$$

as $n\to \infty$ with probability one.

Lim [10] also established the rate of convergence and proved that

$$\mathbb{E}\left[{\left({\tilde{f}}_n^m\left(\mathit{X}\right)-f_0\left(\mathit{X}\right)\right)}^2\right]=\left\{\begin{array}{cc}{\mathcal{O}}_p\left(n^{-2/3}\right),\hfill & \mathrm{if} d=1\hfill \\ {\mathcal{O}}_p\left(n^{-1/2}{(logn)}^2\right),\hfill & \mathrm{if} d=2\hfill \\ {\mathcal{O}}_p\left(n^{-{\displaystyle \frac{1}{2(d-1)}}}\right),\hfill & \mathrm{if} d>2,\hfill \end{array}\right.$$

where the expectation is taken with respect to $\mathit{X}$, $\mathit{X}$ has the same distribution as the ${\mathit{X}}_i$’s, and ${\tilde{f}}_n^m(·)$, a variant of the isotonic regression estimator, minimizes the sum of squared errors ${\sum }_{i=1}^n{(Y_i-f\left({\mathit{X}}_i\right))}^2$ over all nondecreasing functions f satisfying $\left|f\right(\mathit{x}\left)\right|\le C$ for some pre-set constant C for all $\mathit{x}\in \Omega$.

Bagchi and Dhar [11] derived the pointwise limit distribution of the isotonic regression estimator in multiple dimensions. In particular, Bagchi and Dhar [11] proved

$$n^{-1/(d+2)}({\widehat{f}}_n^m\left(\mathit{x}\right)-f_0\left(\mathit{x}\right))\Rightarrow H$$

as $n\to \infty$ for some non-degenerate limit distribution H.

Han et al. [12] showed that the $l_2$-risk of a multivariate isotonic regression estimator is bounded by a constant multiple of $n^{-1/d}{(logn)}^4$ for all $d\ge 1$.

These results reveal a pronounced dependence of the convergence behavior on the dimension d. In particular, the rapid deterioration of rates as d increases highlights the intrinsic difficulty of multivariate isotonic regression, even under strong shape constraints. This dimensional effect partially explains the limited practical adoption of multivariate isotonic regression and underscores the need for improved algorithms and regularization strategies.

3.2. Computational Algorithms

Formulations (2) and (3) are QPs with linear constraints, and hence, can be solved by off-the-shelf solvers such as CVX (a package for disciplined convex programming), CPLEX (IBM ILOG CPLEX Optimization Studio), or MOSEK (a commercial optimization solver for large-scale convex problems).

However, there exist algorithms tailored to the specific setting of the isotonic regression estimator. In $d=1$, Barlow et al. [13] discussed a graphical procedure to compute the isotonic regression estimator by identifying it as the greatest common minorant for a cumulative sum diagram, and proposed a tabular procedure called the pool-adjacent-violators (PAV) algorithm. The PAV algorithm computes the isotonic regression estimator in $O\left(n\right)$ steps. Various modifications of the PAV algorithm have been proposed in the literature; see Brunk [1], Mukerjee [14], Mammen [15], Friedman and Tibshirani [16], Ramsay [17], or Hall and Huang [18], among many others.

However, for regression functions of more than one variable, the problem of computing isotonic regression estimators is substantially more difficult, and good algorithms are not available except for special cases. Most of the literature deals with algorithms for multivariate isotonic regression on a grid (see Gebhardt [19], Dykstra and Robertson [20], Lee [21], or Qian and Eddy [22], among others), but little work has been done for the case of random design.

Table 1. Comparison of computational algorithms for isotonic regression.

Method	Dimension	Design	Complexity
PAV algorithm [13]	$d=1$	Ordered	$O\left(n\right)$
Graphical/cumulative sum	$d=1$	Ordered	$O\left(n\right)$
General QP solvers	Any d	Any	Polynomial
Grid-based methods	$d>1$	Grid	–

summarizes the main computational approaches discussed above.

From a methodological standpoint, existing algorithms for isotonic regression reveal a clear tension between computational efficiency and general applicability. While the pool-adjacent-violators algorithm is exact and optimal in the univariate setting, its reliance on an ordered design severely limits its extension to higher dimensions. Multivariate formulations, on the other hand, are conceptually straightforward but quickly become computationally prohibitive due to the explosion of monotonicity constraints. As a result, many practical implementations either restrict attention to structured designs or sacrifice exactness for scalability, highlighting a gap between theoretical formulations and real-world deployment.

3.3. Applications

In many applications of economics, operations research, biology, and medical sciences, monotonicity is often assumed to be hold or is mathematically proven to hold. For example, in economics, economists often assume the downward slope of the demand as a function of the price. Also, monotonicity applies to indirect utility, expenditure production, profit, and cost functions; see Gallant and Golub [23], Matzkin [24], or Aït-Sahalia and Duarte [25], among many others. In operations research, the steady-state mean waiting time of a customer in a single-server queue is proven to be nonincreasing as a function of the service rate; see Weber [26]. In biology, the weight or height of growing objects over time are known to be nondecreasing over time. In medical sciences, the blood pressure is believed to be a monotone function of the use of tobacco and the body weight (see Moolchan et al. [27]) and the probability of contracting a cancer depends monotonically on certain factors such as smoking frequency, drinking frequency, and weight.

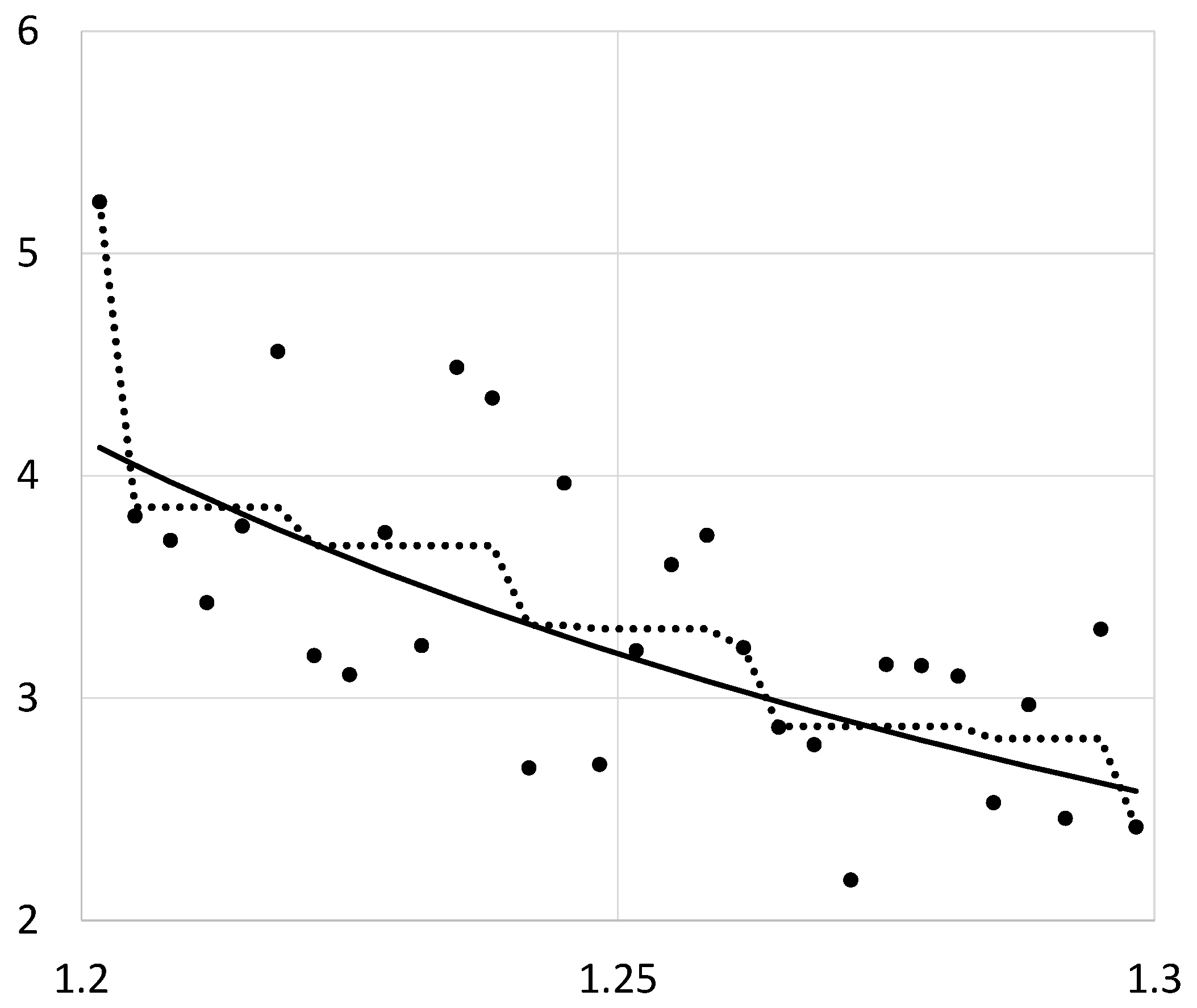
Illustration of Isotonic Regression

To illustrate how isotonic regression operates in practice, we consider a simple univariate example. We consider the case where $f_0$ represents the expected average waiting time of the first 5000 customers in an M/M/1 queue with a first in/first out discipline, unit arrival rate, and a service rate $x\in [1.2,1.3]$, initialized as empty and idle. The service rate is set as ${\mathit{X}}_i=1.2+0.1(i-1)/n+0.1/\left(2n\right)$ for $1\le i\le n$. For each ${\mathit{X}}_i$, the corresponding $Y_i$ is the average waiting time of the first 5000 customers in this M/M/1 queue with a unit arrival rate and a service rate of ${\mathit{X}}_i$. Once the pairs $({\mathit{X}}_i,Y_i)$ for $1\le i\le n$ are generated, we computed the isotonic regression estimator by solving (2) using CVX.

Figure 1 displays the observed data along with the isotonic regression estimator. Its mean square error of the isotonic regression estimator, ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{({\widehat{f}}_n^m\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right))}^2$, is 0.0596 while the mean square error of the $Y_i$’s, ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(Y_i-f_0\left({\mathit{X}}_i\right))}^2$, is 0.2743. This shows improved performance of the isotonic regression estimator compared to the $Y_i$’s.

The estimator enforces monotonicity while fitting the data in a least-squares sense, resulting in a piecewise constant function. This example highlights two key features of isotonic regression: (i) the automatic enforcement of shape constraints without tuning parameters, and (ii) the tendency toward non-smoothness and boundary effects, which motivate the extensions discussed later in this paper.

3.4. Challenges

Two common issues in the isotonic regression estimator are (i) non-smoothness (piecewise constant fits) and (ii) boundary overfitting (“spiking”). Figure 1 displays an instance of the true regression function $f_0$, the $({\mathit{X}}_i,Y_i)$’s, and the isotonic regression estimator. The isotonic regression estimator in Figure 1 is piecewise constant, and hence, non-smooth. Also, it overfits near the boundary of its domain.

3.4.1. Non-Smoothness of Isotonic Regression

To overcome the non-smoothness of the isotonic regression estimator, several researchers proposed variants of the isotonic regression estimator. Ramsay [17] considered the univariate case and proposed estimating $f_0$ as a nonnegative linear combination of the I-splines given the knot sequence ${\mathit{X}}_1,\dots ,{\mathit{X}}_n$ in $\mathbb{R}$. The I-splines are monotone by definition, so the corresponding estimator is guaranteed to be monotone. This method, however, can be sensitive to the number and placement of knots and the order of the I-splines. Mammen [15] also considered the univariate case and proposed computing the isotonic regression estimator and then making it smooth by applying kernel regression. He and Shi [28] considered the univariate case and proposed fitting normalized B-splines to the data set given the knot sequence ${\mathit{X}}_1,\dots ,{\mathit{X}}_n$ in $\mathbb{R}$. This method is also sensitive to the number and placement of the knots. See Mammen and Thomas-Agnan [29] and Meyer [30] for other approaches in the univariate case.

In multiple dimensions, Dette and Scheder [31] proposed a procedure that smooths the data points using a kernel-type method and then applies an isotonization step to each coordinate so that the resulting estimate maintains the monotonicity in each coordinate.

3.4.2. Overfitting of Isotonic Regression

The isotonic regression estimator is known to be inconsistent at boundaries; this is called the “spiking” problem. See Figure 1 for an illustration of this phenomenon. Proposition 1 of Lim [32] proved that when $\Omega =[a,b]$, ${\widehat{f}}_n^m\left(a\right)$ does not converge to $f_0\left(a\right)$ in probability as $n\to \infty$. One popular remedy for this is using a penalized isotonic regression estimator, which minimizes the sum of squared errors plus a penalty term over all monotone functions. A penalized isotonic regression estimator can be expressed as the solution to the following problem:

$$\begin{array}{cccc}\hfill & \underset{f\in {\mathcal{F}}_m}{\mathrm{minimize}}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f\left({\mathit{X}}_i\right))}^2+{\lambda }_n{P}_n\left(f\right),\hfill \end{array}$$

(7)

where ${\lambda }_n\ge 0$ is a smoothing parameter and $P_n(·)$ is a penalty term. Wu et al. [33] considered the case where $P_n\left(f\right)$ equals the range of f divided by n. They proved that when $d=1$, the solution to (7) (which is often referred to as the “bounded isotonic regression”) evaluated at $\mathit{x}\in \Omega$ converges to $f_0\left(\mathit{x}\right)$ in probability as $n\to \infty$. This proves that the bounded isotonic regression estimator is consistent at the boundary unlike the traditional isotonic regression estimator. Wu et al. [33] also proved similar results for the $d=2$ case when the covariates are on a grid. Luss and Rosset [34] proposed an algorithm for solving the bounded isotonic regression for the multivariate case. On the other hand, Lim [32] considered the case where $P_n\left(f\right)={max}_{\mathit{x}\in \Omega }\left|f^{\prime }\left(\mathit{x}\right)\right|$ for the $d=1$ case and established the strong consistency of the corresponding estimator at $\mathit{x}\in \Omega$, thereby proving that the estimator is consistent at the boundary of $\Omega$. Lim [32] also computed the convergence rate of $n^{-1/3}$ for the proposed estimator.

Even though several approaches are proposed for the $d=1$ case, limited work is available for the multivariate case. Isotonic regression estimator’s overfitting problem in the $d>1$ case is a good research topic for future.

4. Convex Regression

In this section, we review statistical properties, interesting applications, and some challenges of convex regression estimator. We also review some algorithms for computing the convex regression estimator numerically.

4.1. Statistical Properties

4.1.1. Univariate Case

The convex regression estimator, along with its QP formulation in (3), was first introduced by Hildreth [2] for the $d=1$ case. Hanson and Pledger [35] established strong consistency on compact subsets of $\Omega$. They proved that, if $\Omega =(a,b)$, for any $c>a$ and $d<b$,

$$\underset{c\le \mathit{x}\le d}{max}|{\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)|\to 0$$

as $n\to \infty$ with probability one.

Results on rates of convergence were obtained by Mammen [36] and Groeneboom et al. [37]. In particular, Mammen [36] showed that at any interior point $\mathit{x}\in \Omega$,

$${\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)={\mathcal{O}}_p\left(n^{-2/5}\right)$$

as $n\to \infty$, provided that the second derivative of $f_0$ at $\mathit{x}$ does not vanish.

Groeneboom et al. [37] identified the limiting distribution of $n^{2/5}({\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right))$ at a fixed point $\mathit{x}\in \Omega$. Groeneboom et al. [37] proved that if the errors are iid sub-Gaussian with mean zero and $f_0^{\prime }\left(\mathit{x}\right)\ne 0$,

$$n^{2/5}\left({\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)\right)\Rightarrow {\mathbb{H}}^{\prime \prime }\left(0\right),$$

where $\mathbb{H}$ denotes the greatest convex minorant (i.e., envelope) of integrated Brownian motion with quartic drift $h^4$, and ${\mathbb{H}}^{\prime \prime }\left(0\right)$ is its second derivative at 0. The envelope can be viewed as a cubic curve lying above and touching the integrated Brownian motion $+h^4$.

More recently, Chatterjee [38] derived an upper bound on the $l_2$-risk of the convex regression estimator. Under the assumption of iid Gaussian errors with mean zero, they showed that

$$R(f_0,{\widehat{f}}_n^c)\triangleq \mathbb{E}\left[{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left({\widehat{f}}_n^c\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right)\right)}^2\right]\le C{n}^{-4/5}$$

for all $n\ge 1$, where C is a constant.

4.1.2. Multivariate Case

The multivariate convex regression estimator and its QP formulation in (5) were first introduced by Allon et al. [39]. Strong consistency over any compact subset of the interior of $\Omega$ was established by Seijo and Sen [40] and Lim and Glynn [41]. Seijo and Sen [40] proved that for any compact subset A of the interior of $\Omega$,

$$\underset{\mathit{x}\in A}{max}|{\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)|\to 0$$

as $n\to \infty$ with probability one under some modest assumptions.

Rates of convergence were obtained by Lim [42]. In particular, Lim [42] considered a variant of the convex regression estimator, say ${\tilde{f}}_n^c(·)$, which minimizes the sum of squared errors ${\sum }_{i=1}^n{(Y_i-f\left(X_i\right))}^2$ over the set of convex functions f with subgradients bounded uniformly by a constant. Lim [42] showed that

$${\displaystyle \frac{1}{n}}\sum _{i=1}^n{({\tilde{f}}_n^c\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right))}^2=\left\{\begin{array}{cc}{\mathcal{O}}_p\left(n^{-4/(4+d)}\right),\hfill & \mathrm{if} d<4\hfill \\ {\mathcal{O}}_p\left((logn)n^{-1/2}\right),\hfill & \mathrm{if} d=4\hfill \\ {\mathcal{O}}_p\left(n^{-2/d}\right),\hfill & \mathrm{if} d>4\hfill \end{array}\right.$$

as $n\to \infty$.

A bound on the global risk has been established by Han and Wellner [43] as follows:

$$\mathbb{E}\left[{\int }_{\Omega }{({\overline{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right))}^2\lambda \left(\mathit{x}\right)d\mathit{x}\right]=\left\{\begin{array}{cc}O\left(n^{-4/(4+d)}\right),\hfill & \mathrm{if} d<4\hfill \\ O\left((logn)n^{-1/2}\right),\hfill & \mathrm{if} d=4\hfill \\ O\left(n^{-2/d}\right),\hfill & \mathrm{if} d>4\hfill \end{array}\right.$$

as $n\to \infty$, where $\lambda (·)$ is the density function of ${\mathit{X}}_1$ and ${\overline{f}}_n^c(·)$ minimizes the sum of squared errors ${\sum }_{i=1}^n{(Y_i-f\left(X_i\right))}^2$ over the set of convex functions f bounded uniformly by a constant.

The limiting distribution of $r_n^{-1}({\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right))$ for an appropriate rate of convergence $r_n$ has not be established so far and this is still an open problem.

4.2. Computational Algorithms

In the univariate case, Dent [44] introduced a QP formulation of the convex regression estimator as in (3). Dykstra [45] developed an iterative algorithm to compute the convex regression estimator numerically. The procedure proposed by Dykstra [45] is guaranteed to converge to the convex regression estimator as the number of iterations approaches infinity. For other algorithms for solving the QP in (3), see Wu [46] and Fraser and Massam [47].

For the multivariate setting, Allon et al. [39] first presented the QP formulation given in (5). However, this formulation requires $O\left(n^2\right)$ linear constraints, which limits its applicability to data sets of only a few hundred observations under current computational capabilities. To address this, Mazumder et al. [48] proposed an algorithm based on the augmented Lagrangian method. Their approach was able to solve (5) for $n=1000$ and $d=10$ within a few seconds.

To mitigate the computational burden, several authors (Magnani and Boyd [49]; Aguilera et al. [50]; Hannah and Dunson [51]) proposed approximating the convex regression estimator by the maximum of a small set of hyperplanes. Specifically, they solved the optimization problem

$$({\alpha }^{\ast },{\mathit{\beta }}^{\ast },K^{\ast })={\mathrm{argmin}}_{\alpha \in \mathbb{R},\mathit{\beta }\in {\mathbb{R}}^d,K\in \mathbb{N}}\sum _{i=1}^n{\left[Y_i-\underset{k=1,\cdots ,K}{max}\left({\alpha }_k+{\mathit{\beta }}_k^{\mathsf{T}}{\mathit{x}}_i\right)\right]}^2,$$

where $(\alpha ,\mathit{\beta })\in \mathbb{R}\times {\mathbb{R}}^d$ defines a hyperplane and $\mathbb{N}$ is the set of positive integers. Their estimator ${\widehat{f}}_n(·)$ is then given by the maximum over these hyperplanes:

$${\widehat{f}}_n\left(\mathit{x}\right)=\underset{k=1,\cdots ,K^{\ast }}{max}\left({\alpha }_k^{\ast }+{\mathit{\beta }}_k^{\ast \mathsf{T}}\mathit{x}\right).$$

More recently, to handle larger data sets, Bertsimas and Mundru [52] introduced a penalized convex regression estimator defined as the solution to the following QP problem in decision variables $f_1,\dots ,f_n\in \mathbb{R}$ and ${\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_n\in {\mathbb{R}}^d$:

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f_i)}^2+{\displaystyle \frac{{\lambda }_n}{n}}\sum _{i=1}^n{\parallel {\mathit{\beta }}_i\parallel }^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & f_i\ge f_j+{\mathit{\beta }}_j^{\mathsf{T}}({\mathit{X}}_i-{\mathit{X}}_j),1\le i,j\le n,\hfill \end{array}$$

(8)

where ${\lambda }_n>0$ is a smoothing parameter. They proposed a cutting-plane algorithm for solving (8) and reported that it can handle data sets with n = 10,000 and $d=10$ within minutes.

Another strategy to alleviate the computational burden of the convex regression estimator is to reformulate the problem as a linear programming (LP) problem rather than a quadratic program. Luo and Lim [53] proposed estimating the convex function that minimizes the sum of absolute deviations (instead of the sum of squared errors). The resulting estimator can be obtained by solving the following LP problem in decision variables $f_1,\dots ,f_n\in \mathbb{R}$ and ${\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_n\in {\mathbb{R}}^d$:

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n|Y_i-f_i|\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & f_i\ge f_j+{\mathit{\beta }}_j^{\mathsf{T}}({\mathit{X}}_i-{\mathit{X}}_j)\mathrm{for} 1\le i,j\le n.\hfill \end{array}$$

(9)

Luo and Lim [53] further showed that the corresponding estimator converges a.s. to the true function as $n\to \infty$ over any compact subset of the interior of $\Omega$.

Table 2. Comparison of computational algorithms for convex regression.

Method	Dimension	Remarks
QP formulation [2]	$d=1$	Exact solution
Iterative projection [45]	$d=1$	Guaranteed convergence
Standard multivariate QP [39]	$d>1$	Severe computational burden
Augmented Lagrangian [48]	$d>1$	Scales to $n\approx {10}^3$
Cutting-plane methods [52]	$d>1$	Handles $n\approx {10}^4$
Hyperplane approximation	$d>1$	Approximate estimator

summarizes the main computational approaches discussed above.

Taken together, these algorithmic developments highlight a fundamental trade-off between statistical exactness and computational scalability. While the exact QP formulation provides a principled estimator with strong theoretical guarantees, its quadratic growth in constraints severely limits its applicability in large-scale settings. Approximate and penalized methods alleviate this burden, but at the cost of introducing additional tuning parameters or approximation error. Understanding this trade-off remains central to the practical deployment of convex regression.

4.3. Applications

Convexity and concavity play an important role across various fields, including economics and operations research. In economics, for instance, it is common to assume diminishing marginal productivity with respect to input resources, which implies that the production function is concave in its inputs (Allon et al. [39]). Also, demand (Varian [54]) and utility (Varian [55]) functions are often assumed to be convex/concave. In operations research, the steady-state waiting time in a single-server queue has been shown to be convex in the service rate; see, for example, Weber [26]. An additional example is provided in Demetriou and Tzitziris [56], where infant mortality rates are modeled as exhibiting increasing returns with respect to the gross domestic product (GDP) per capita, leading to the assumption that the infant mortality function is convex in GDP per capita. For further applications of convex regression, see Johnson and Jiang [4].

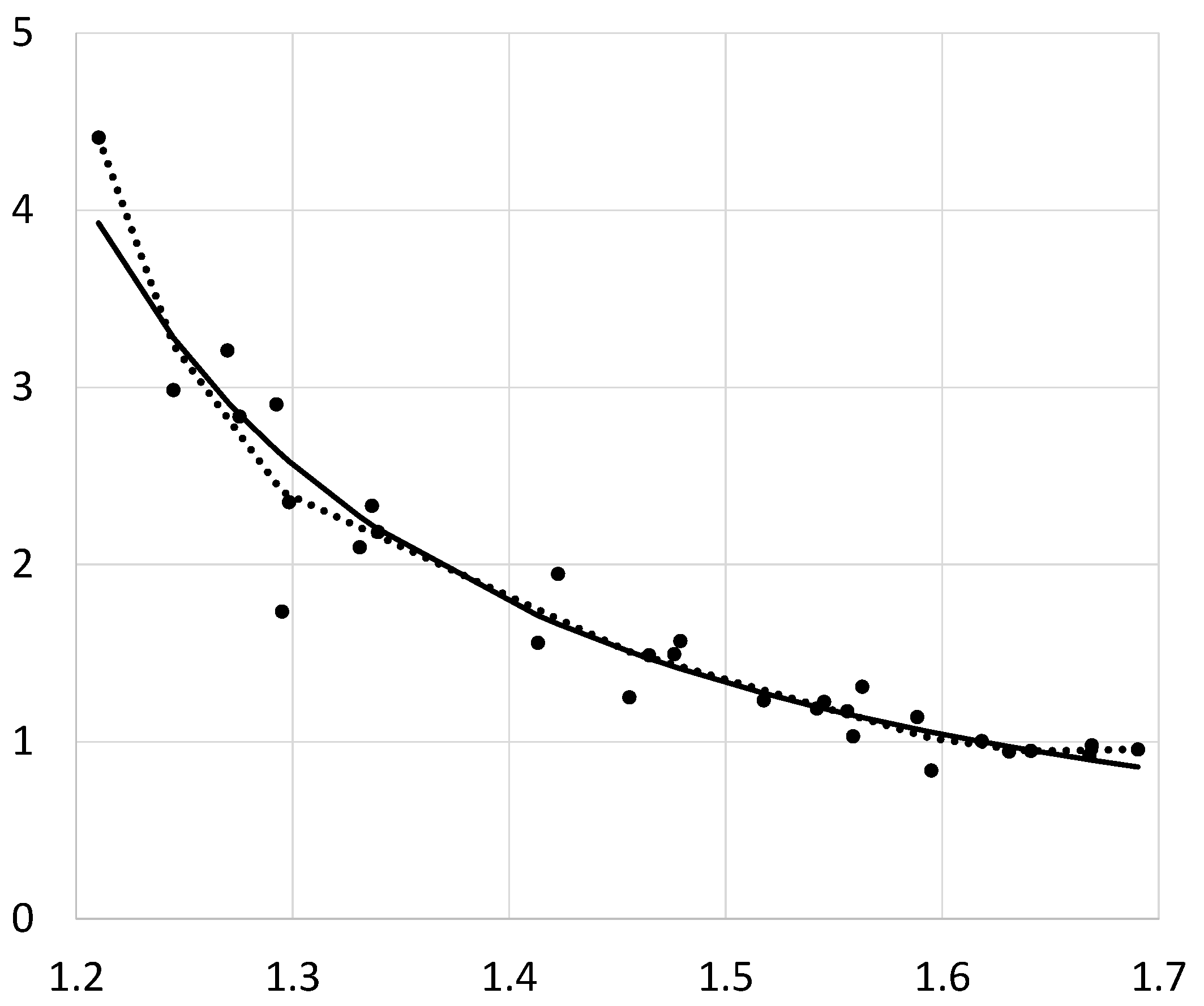
Illustration of Convex Regression

To illustrate how convex regression operates in practice, we consider a simple univariate example. We consider the case where $f_0\left(x\right)$ is the steady–state mean waiting time of a customer in a single server queue with the first-in/first-out discipline, where the service times are iid exponential random variables with a mean of $1/\mathit{x}$ for $\mathit{x}\in (1.2,1.7)$, and the interarrival times are iid exponential random variables with a mean of 1.

The ${\mathit{X}}_i$’s are drawn uniformly from $(1.2,1.7)$. For each ${\mathit{X}}_i$, $Y_i$ is generated by averaging the waiting times of the first 5000 customers in the single server queue, initialized empty and idle, with the service rate of ${\mathit{X}}_i$. Once the $({\mathit{X}}_i,Y_i)$’s are obtained, we computed the convex regression estimator by solving (3) using CVX.

Figure 2 displays the observed data along with the convex regression estimator. Its mean square error of the convex regression estimator, ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{({\widehat{f}}_n^c\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right))}^2$, is 0.0132 while the mean square error of the $Y_i$’s, ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(Y_i-f_0\left({\mathit{X}}_i\right))}^2$, is 0.0554. This shows improved performance of the convex regression estimator compared to the $Y_i$’s.

The estimator enforces convexity while fitting the data in a least-squares sense, resulting in a piecewise linear function. This example highlights two key features of convex regression: (i) the automatic enforcement of shape constraints without tuning parameters, and (ii) the tendency toward non-smoothness and boundary effects, which motivate the extensions discussed later in the next subsection.

4.4. Challenges

The convex regression estimator faces two primary limitations: (i) non-smoothness (piecewise linear fits) and (ii) overfitting near the boundary of its domain (“spiking”). Figure 2 illustrates these issues by displaying the true regression function $f_0$, the observed data $({\mathit{X}}_i,Y_i)$, and the convex regression estimator. As shown in Figure 2, the convex regression estimator is piecewise linear and therefore non-smooth. It also exhibits boundary overfitting.

4.4.1. Non-Smoothness of Convex Regression

In the univariate setting, several approaches have been proposed to address the lack of smoothness. Mammen and Thomas-Agnan [29] developed a two-step procedure in which the data are first smoothed using nonparametric smoothing methods, followed by convex regression applied to the smoothed values. Alternatively, Aït-Sahalia and Duarte [25] suggested first estimating the convex regression estimator and then applying local polynomial smoothing to the estimator. Birke and Dette [57] proposed a different strategy: smoothing the data with a nonparametric method such as the kernel, local polynomial, series, or spline methods, computing its derivative, applying isotonic regression to the derivative, and integrating to obtain a convex estimator. Other methods for the univariate case are discussed in Du et al. [58].

In the multivariate case, Mazumder et al. [48] constructed a smooth approximation to the convex regression estimator that remains uniformly close to the original estimator.

4.4.2. Overfitting of Convex Regression

As with isotonic regression, convex regression tends to overfit near domain boundaries, often producing extremely large subgradients and inconsistent estimates of $f_0$ near the boundary. For $d=1$, Ghosal and Sen [59] showed that the convex regression estimator fails to converge in probability to the true value at boundary points and that its subgradients at the boundary are unbounded in probability as $n\to \infty$.

A common strategy to mitigate overfitting is to constrain the subgradients. Lim [42] proposed bounding the ${\parallel ·\parallel }_{\infty }$ norm of the subgradients, imposing $\parallel {\mathit{\beta }}_i{\parallel }_{\infty }\le C$ for all i for some fixed $C>0$ to the constraints of (5). Instead, Mazumder et al. [48] added $\parallel {\mathit{\beta }}_i\parallel \le C$ to the constraints of (5).

Another widely used approach is penalization, which adds a penalty term to the objective function of (1). Chen et al. [60] and Bertsimas and Mundru [52] studied a penalized multivariate convex regression estimator defined as the solution to the following QP problem in decision variables $f_1,\dots ,f_n\in \mathbb{R},{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_n\in {\mathbb{R}}^d$:

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f_i)}^2+{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\parallel {\mathit{\beta }}_i\parallel }^2\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & f_i\ge f_j+{\mathit{\beta }}_j^{\mathsf{T}}({\mathit{X}}_i-{\mathit{X}}_j)\mathrm{for} 1\le i,j\le n.\hfill \end{array}$$

(10)

Lim [61] generalized this idea and proposed the following three alternative approaches:

$$\begin{array}{cccc}\left(\mathrm{A}\right)\hfill & {\widehat{f}}_n^A={\mathrm{argmin}}_{f\in {\mathcal{F}}_c}\hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f\left({\mathit{X}}_i\right))}^2+{\lambda }_{n}J\left(f\right)\hfill & \\ \left(\mathrm{B}\right)\hfill & {\widehat{f}}_n^B={\mathrm{argmin}}_{f\in {\mathcal{F}}_c}\hfill & {\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f\left({\mathit{X}}_i\right))}^2\hfill & \mathrm{subject} \mathrm{to}J\left(f\right)\le u_n\hfill \\ \left(\mathrm{C}\right)\hfill & {\widehat{f}}_n^C={\mathrm{argmin}}_{f\in {\mathcal{F}}_c}\hfill & J\left(f\right)\hfill & \mathrm{subject} \mathrm{to}{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Y_i-f\left({\mathit{X}}_i\right))}^2\le s_n\hfill \end{array}$$

for some smoothing parameter ${\lambda }_n\ge 0$ and constants $u_n,s_n\ge 0$, where $J\left(f\right)$ is a penalty term measuring the overall magnitude of the subgradient of f.

In particular, Lim [61] considered the case where

$$J\left(f\right)=\underset{1\le i\le d}{max}\underset{\mathit{x}\in \Omega }{sup}\left|{\displaystyle \frac{\partial f}{\partial x_i}}\left(\mathit{x}\right)\right|$$

and $\partial f/\partial x_i\left(\mathit{x}\right)$ represents the partial derivative of f with respect to the ith component of $\mathit{x}$. Lim [61] established the uniform strong consistency of ${\widehat{f}}_n^A$ and ${\widehat{f}}_n^C$ and their derivatives. Specifically, she showed that

$$\underset{\mathit{x}\in \Omega }{sup}|{\widehat{f}}_n^A\left(\mathit{x}\right)-f_0\left(\mathit{x}\right)|\to 0$$

(11)

and

$$\underset{\mathit{x}\in \Omega }{sup}\underset{\mathit{\beta }\in \partial {\widehat{f}}_n^A\left(\mathit{x}\right)}{sup}{\parallel \mathit{\beta }-\nabla f_0\left(\mathit{x}\right)\parallel }_{\infty }\to 0$$

(12)

as $n\to \infty$ with probability one. Analogous results were shown for ${\widehat{f}}_n^C$. These results confirm that penalization successfully eliminates boundary overfitting.

Finally, Lim [61] derived convergence rates for ${\widehat{f}}_n^A$ and ${\widehat{f}}_n^C$. For ${\widehat{f}}_n^A$, she proved

$${\displaystyle \frac{1}{n}}\sum _{i=1}^n{({\widehat{f}}_n^A\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right))}^2=\left\{\begin{array}{cc}{\mathcal{O}}_p(n^{-\frac{4}{4+d}}),\hfill & \mathrm{if} d<4\hfill \\ {\mathcal{O}}_p(n^{-1/2}logn),\hfill & \mathrm{if} d=4\hfill \\ {\mathcal{O}}_p\left(n^{-2/d}\right),\hfill & \mathrm{if} d>4\hfill \end{array}\right.$$

as $n\to \infty$, and for ${\widehat{f}}_n^C$, she established

$${\displaystyle \frac{1}{n}}\sum _{i=1}^n{({\widehat{f}}_n^C\left({\mathit{X}}_i\right)-f_0\left({\mathit{X}}_i\right))}^2=\left\{\begin{array}{cc}{\mathcal{O}}_p(n^{-1/2}\sqrt{logn}),\hfill & \mathrm{if} d<4\hfill \\ {\mathcal{O}}_p(n^{-1/2}logn),\hfill & \mathrm{if} d=4\hfill \\ {\mathcal{O}}_p\left(n^{-2/d}\right),\hfill & \mathrm{if} d>4\hfill \end{array}\right.$$

as $n\to \infty$.

5. Connections to Contemporary Machine Learning

Beyond their traditional applications in economics and operations research, isotonic and convex regression have found increasing use in contemporary machine learning, where structural constraints are often imposed to improve interpretability, stability, and compliance with domain knowledge.

A prominent example is probability calibration in classification and ranking systems. In large-scale recommender systems and online advertising platforms, raw model outputs (e.g., click-through rate (CTR) scores) are often poorly calibrated as probabilities. Isotonic regression is widely used as a post-hoc calibration method in CTR prediction and recommendation systems, enforcing monotonicity between model scores and observed click frequencies while preserving predictive ordering.

Shape constraints also arise naturally in learning-to-rank and monotone prediction problems, where certain features are known a priori to have a monotone effect on the response. Such constraints are increasingly emphasized in interpretable and trustworthy machine learning, particularly in high-stakes applications such as credit scoring, hiring, and healthcare, where monotonicity is often required for regulatory or ethical reasons.

From an optimization perspective, convex regression connects directly to learning convex functions and convex potentials, which appear in areas such as structured prediction, energy-based modeling, and optimal transport. In these settings, convex regression provides a principled way to estimate convex functions from data while preserving global shape properties. Related ideas also appear in modern machine learning through neural network architectures designed to learn convex functions. A notable example is Input Convex Neural Networks (ICNNs) [62], which impose architectural constraints to guarantee convexity with respect to the inputs. While ICNNs are not direct implementations of the nonparametric convex regression methods reviewed here, they are conceptually motivated by the same need to learn convex cost or loss functions from data. This parallel highlights the continued relevance of convexity constraints across both classical statistical estimation and contemporary machine learning.

Finally, the computational challenges discussed in this paper—scalability, overfitting, and the need for efficient algorithms—are closely aligned with current concerns in large-scale machine learning. Recent developments such as augmented Lagrangian methods, cutting-plane algorithms, and penalized formulations mirror optimization techniques widely used in modern ML, highlighting shape-restricted regression as a natural and increasingly relevant component of the contemporary machine learning toolkit.

6. Future Directions

This section outlines several open problems that, in our view, remain both important and insufficiently explored. The goal of this section is not only to list unresolved questions, but also to provide readers with a research roadmap highlighting where significant theoretical, computational, and applied advances can be made. Each problem below is motivated by practical limitations of existing methods and points to concrete opportunities for future research.

6.1. Problem 1—Scalable Algorithms for Large-Scale Data

Modern applications increasingly involve data sets with millions or even billions of observations. For example, in large-scale hiring platforms or online advertising systems, isotonic regression is routinely used for score calibration, yet existing algorithms are unable to scale to such data sizes.

Despite decades of progress in computational optimization, no algorithm is currently capable of computing isotonic or convex regression estimators efficiently at this scale under general designs. Developing scalable algorithms—possibly through distributed optimization, streaming methods, or approximation schemes—remains a critical challenge. This problem is particularly relevant to researchers working at the intersection of optimization, machine learning, and large-scale data analysis.

6.2. Problem 2—Algorithms for Multivariate Isotonic Regression

While univariate isotonic regression enjoys highly efficient algorithms such as the pool-adjacent-violators method, the multivariate case remains far less understood. In particular, for isotonic regression under random designs in higher dimensions, efficient and practically implementable algorithms are largely unavailable.

Most existing work focuses on grid-based designs or highly structured settings, leaving a substantial gap between theory and practice. Closing this gap would significantly expand the applicability of isotonic regression in modern data-driven problems involving multiple covariates.

6.3. Problem 3—Pointwise Limit Distribution of Multivariate Convex Regression

Although many global theoretical properties of convex regression estimators have been established, a central question remains unresolved: the pointwise limiting distribution of the multivariate convex regression estimator.

Specifically, it is unknown whether

$$r_n^{-1}({\widehat{f}}_n^c\left(\mathit{x}\right)-f_0\left(\mathit{x}\right))$$

converges weakly to a non-degenerate limit for an appropriate normalization $r_n$, and if so, what the form of this limit might be. Resolving this problem would place multivariate convex regression on a theoretical footing comparable to its univariate counterpart and would substantially deepen our understanding of the local behavior of shape-restricted estimators.

6.4. Problem 4—Incorporating Smoothness into Shape-Restricted Regression in Multiple Dimensions

A well-known limitation of isotonic and convex regression is their inherent lack of smoothness, resulting in piecewise constant or piecewise linear estimators. While several smoothing and regularization techniques have been proposed, most are either heuristic or limited to low-dimensional settings.

Developing principled methods that simultaneously enforce shape constraints and smoothness in multiple dimensions remains an open challenge. Progress in this direction would be particularly valuable for applications requiring stable derivatives, such as sensitivity analysis, optimization, and decision-making systems.

6.5. Problem 5—Overfitting in Isotonic and Convex Regression

Both isotonic and convex regression are known to suffer from overfitting near the boundaries of the design space. Existing remedies typically rely on penalization or hard constraints on the estimator or its subgradients, which introduce tuning parameters that are often selected in an ad-hoc or problem-specific manner.

This raises several fundamental questions: How should such tuning parameters be chosen in a principled way? Are there alternative approaches to controlling overfitting that avoid explicit penalization altogether? Addressing these questions would improve both the theoretical robustness and practical usability of shape-restricted regression methods.

6.6. Problem 6—Theory for Penalized Isotonic and Convex Regression

While penalization has proven effective in mitigating non-smoothness and boundary overfitting, the theoretical understanding of penalized shape-restricted estimators remains incomplete. For isotonic regression, most existing results are confined to the univariate setting, and extensions to higher dimensions are largely unexplored.

For convex regression, many foundational questions remain open, including optimal convergence rates, adaptive behavior, and the interaction between penalization and dimensionality. Advancing the theory of penalized isotonic and convex regression would provide essential guidance for both methodological development and practical implementation.