Revocable Attribute-Based Encryption with Efficient and Secure Verification in Smart Health Systems
Abstract
1. Introduction
1.1. Motivations and Contributions
- First, to achieve integrity verification, we introduce an auxiliary random message . Through ingenious computations, we ensure that the entire encryption process only requires executing the secret sharing operation once, which reduces computational overhead on IoT medical devices and makes the verification mechanism more efficient. Furthermore, in the access structure, we utilize the linear integer secret sharing (LISS) that operates over integers and achieves lower secret sharing overhead, which we experimentally demonstrate in Appendix A.
- Second, during the revocation process, both the verification tag and the access policy are updated, which ensures that ciphertexts are fully updated and prevents revoked users from accessing any useful information from previous ciphertexts.
- Third, the decryption key is split into a user’s key and a corresponding cloud server’s key, which allows partial decryption task to be outsourced to the cloud server. In addition, by outsourcing revocation and partial encryption procedures to the cloud server, we minimize the local computational load on IoT medical devices.
1.2. Related Work
2. Preliminaries
2.1. Bilinear Mapping
- For all and , the equality holds.
- There exists such that , where denotes the identity element in .
- The value can be efficiently computed for any in polynomial time.
2.2. Target Collision-Resistant Hash Function
2.3. Complex Assumptions
2.4. Linear Integer Secret Sharing (LISS)
2.5. Integer Span Program (ISP)
- If , there exists a vector such that , where is called the spanning vector of A.
- If , there exists a vector such that , where , and is defined as the elimination vector of A.
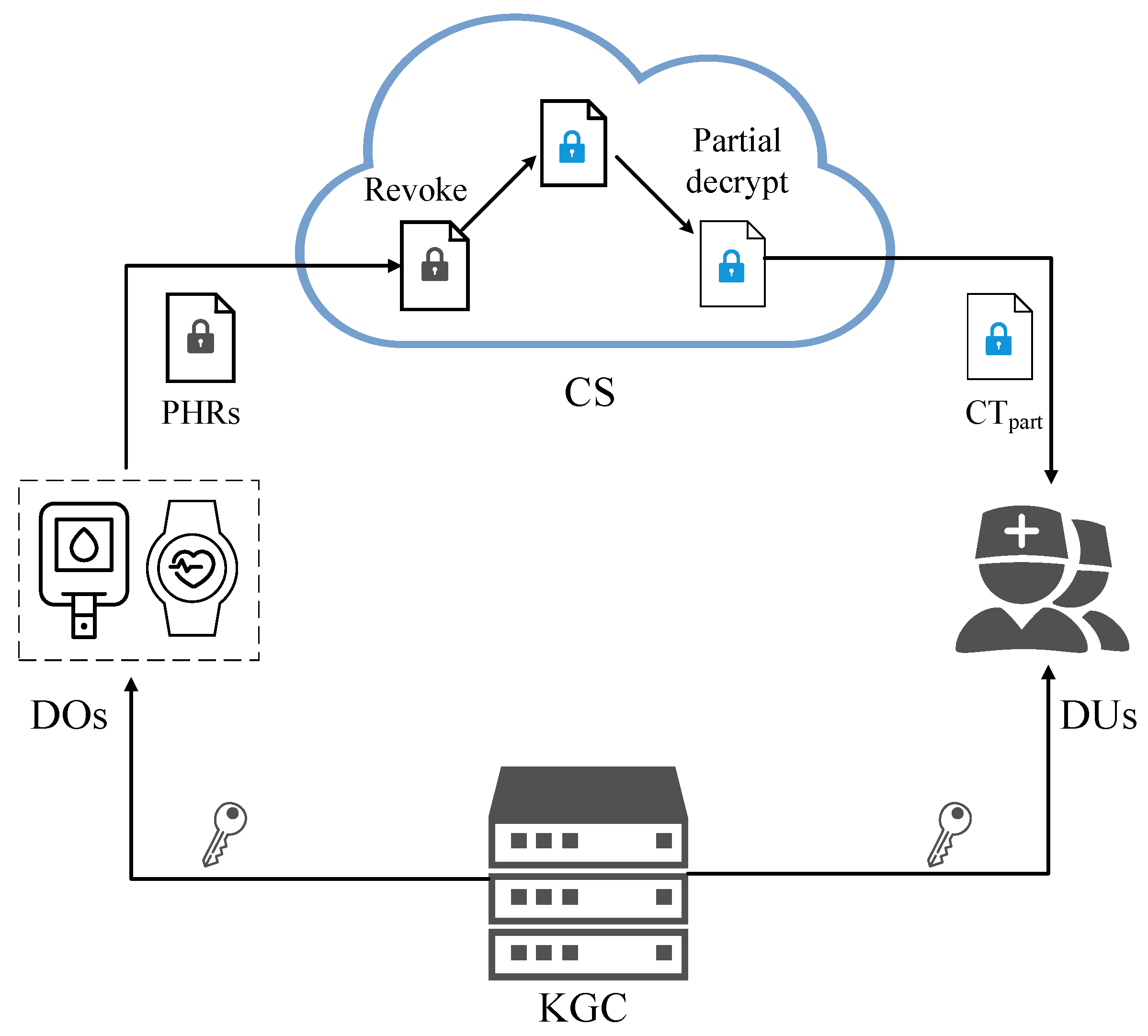
3. System Architecture and Definitions
3.1. System Architecture
- Key Generation Center (KGC): In smart health systems, the KGC generates and distributes keys for all participants, including IoT medical devices, cloud servers, and doctors.
- Cloud Server (CS): The CS is tasked with storing ciphertexts and assisting in complex revocation operations and partial encryption/decryption operations.
- Data Owner (DO): DOs are IoT medical devices that collect PHRs, perform local encryption operations, and upload ciphertexts to the CS. Additionally, when the access policy of the data changes, the DO sends a revocation delegation to the CS.
- Data User (DU): Doctors act as DUs. They submit decryption requests to the CS based on their attributes, decrypt intermediate ciphertexts from the CS using their private keys and perform the treatment procedures according to the data content.
3.2. Threat Model
- Confidentiality Adversary: This category represents any malicious entity that aims to compromise data confidentiality. Without valid decryption keys, this adversary attempts to decrypt ciphertexts and access sensitive messages.
- Integrity Adversary: This adversary is typically a semi-honest cloud server that aims to violate data integrity by generating incorrect computational results during outsourced operations.
3.3. Scheme Definition
- (1)
- : Inputting the security parameter λ and attribute universe U, the KGC generates public parameters and master secret key .
- (2)
- : Given the master secret key and a user’s attribute set , the KGC produces the user’s private key and the corresponding CS’s private key . These keys are distributed to the user and cloud server, respectively.
- (3)
- : This algorithm contains two steps. First, the DO performs local encryption () by processing message with access policy to create initial ciphertext . The CS then executes outsourced encryption () to generate final ciphertext .
- (4)
- : This takes as input the access policy to be revoked. The DO generates a revocation delegation using the message m and parameters from , and sends to the CS.
- (5)
- : Given the initial and revocation delegation , the CS constructs the revoked access policy and outputs the revoked ciphertext based on this policy.
- (6)
- : The decryption process comprises two sequential phases. First, the cloud server performs partial decryption () by verifying if the attribute set satisfies using inputs , , and . If the verification succeeds, it generates the partial decryption result and sends it to the DU. The DU then executes final decryption () with , , and , verifying the equivalence between the tag in and . If the tags match, the user computes m and validates . If valid, output m; otherwise, ⊥ is returned.
3.4. Security Definitions
- (1)
- Init. The adversary submits a challenge access policy , where .
- (2)
- Setup. The challenger executes the algorithm to produce as public parameters and as the master secret key, then sends to .
- (3)
- Phase I. adaptively issues private key queries for attribute sets that do not satisfy . generates and returns the corresponding private keys.
- (4)
- Challenge. provides two messages of equal length. randomly selects , encrypts under to generate the challenge ciphertext , and delivers to .
- (5)
- Phase II. proceeds to issue key queries under the same restrictions as in Phase I.
- (6)
- Guess. outputs . The advantage of the adversary is quantified as
- (1)
- Setup: The challenger performs the algorithm to create the public parameters and the master secret key , then sends to .
- (2)
- Phase I: adaptively issues private key queries for any attribute set . generates and returns the corresponding private keys.
- (3)
- Challenge: selects an access policy and a message m. generates an initial ciphertext and returns it. In revocation scenarios, additionally generates and sends a revocation delegation .
- (4)
- Phase II: proceeds to issue queries as in Phase I.
- (5)
- Output: outputs a partial decryption result and corresponding verification tags or . The adversary wins if either of the following apply:
- Case 1 (no revocation).
- but the decrypted message ;
- Case 2 (with revocation).
- but the decrypted message .
The advantage of the adversary is defined as
4. Construction
- (1)
- : The algorithm generates a bilinear pairing tuple and selects random elements , where along with a hash function . Then, KGC computes and outputs the public parameters as well as the master secret key as follows:
- (2)
- : When a user u registers with the system, KGC picks a random element and calculatesThen, KGC transmits to the CS and sends to the user u.
- (3)
- : The encryption algorithm is structured in two steps, as detailed in Algorithm 1. Initially, the DO performs the core initial encryption to convert the message m into an initial ciphertext . Subsequently, the CS executes computationally intensive operations to expand into the final ciphertext . Notably, the entire encryption process requires only a single secret sharing operation, which reduces the computational overhead. The sub-algorithms are detailed below:
- (i)
- : Given a private message and an access policy , where M is a matrix, the DO randomly selects and for to construct a vector . Here, k is the security parameter and is a predefined constant. The DO then computes for all , where denotes the i-th row of M. Subsequently, DO randomly selects and calculatesFinally, the DO transmits the initial ciphertexts , to the CS.
- (ii)
- : Upon receiving , CS randomly chooses for all and computes:Then, CS stores the final ciphertext ,
- (4)
- : When the access policy is updated, to prevent the verification tag from leaking any information about the message m, the DO updates the verification tag and issues a revocation delegation to the CS. Specifically, DO randomly selects and computesthen sends to the CS.
| Algorithm 1: Encryption Algorithm () |
 |
- (5)
- : The revocation process is described in Algorithm 2. On receiving the delegation , CS first defines the revoked access policy as follows:Note that refers to the first column of M, and is a matrix, where . For each , the CS setsNext, the CS selects a vector , where and for , computes for all , and randomly chooses (). The CS then calculatesFinally, the CS outputs the revoked ciphertext: , .
| Algorithm 2: Revoke Algorithm () |
 |
- (6)
- : The decryption algorithm involves two phases, as outlined in Algorithm 3. Firstly, the DU submits a decryption request to the CS. Upon confirming that the DU is authorized for data decryption, the CS executes the partial decryption algorithm with to generate and forwards it to the DU. Secondly, the DU decrypts with and checks the message validity via the tag. The sub-algorithms are defined as follows:
- (i)
- : Given a ciphertext and a user’s attribute set , the CS first verifies if satisfies . If not, the process terminates and outputs ⊥. Otherwise, the CS defines and finds constant elements such that . Then, the CS computesThe CS sends the partially decrypted ciphertext , to the DU.
- (ii)
- : Taking as input an intermediate ciphertext and the verification tag from , the DU first verifies whether the verification tag in is equal to . If not, the algorithm outputs ⊥ and aborts. Otherwise, it computesThe DU verifies whether . If valid, it outputs m; otherwise, ⊥ is returned.
| Algorithm 3: Decryption Algorithm () |
 |
5. Security Analysis
- (1)
- Init. submits a challenge access policy , where .
- (2)
- Setup. The simulator first randomly selects and a hash function with . Then, it implicitly defines , and , such that . For each attribute , computes , where , and is randomly selected from . Note that if . The public key is published as
- (3)
- Phase I. For each private key query on a set that does not satisfy , first constructs a vector with and for all i, where . Then, it randomly selects , implicitly defines , and computesNote that if , . Finally, sends to .
- (4)
- Challenge. submits . flips a coin and chooses random element to generate the vector . Then, it randomly selects , defines the set for all , and computessends the challenge ciphertext to .
- (5)
- Phase II. continues private key queries for unauthorized sets as in Phase I.
- (6)
- Guess. output a guess of b. If , outputs 0 to guess that ; otherwise, outputs 1.
- (1)
- Setup. Simulator sets a bilinear pairing and selects , as well as a hash function . Then, sets and outputs the public parameters , to .
- (2)
- Phase I. When issues a private key query for an attribute set S, since possesses the master secret key, is able to generate the corresponding private keys and return them to .
- (3)
- Challenge. chooses a message m as well as the access policy , and sends them to the challenger . executes the algorithm to obtain the ciphertext , where .Case 1 (no revocation). returns to .Case 2 (with revocation). executes to obtain , where . Then, sends to .
- (4)
- Phase II. continues to issue queries as in Phase I, and responds the queries as in Phase I.
- (5)
- Output. outputs a partially decrypted ciphertext . When there is no revocation, the ciphertext contains the verification tag ; when revocation occurs, the ciphertext contains the verification tag (we set the updated access policy as ).
6. Performance Analysis
6.1. Theoretical Analysis
6.2. Experimental Tests
7. Future Work
- Decentralized KGC Architectures: The current scheme relies on a single KGC, which introduces risks such as single points of failure and centralized trust. To address these limitations, the framework can be extended to multi-authority KGC architectures or threshold-based KGC architectures. The former distributes trust among independent authorities, which eliminates centralized control and improves compatibility with decentralized healthcare ecosystems. The latter employs -threshold cryptography to ensure that key generation requires collaboration from at least t out of n authorities. This design prevents compromises even if some authorities are corrupted.
- Security Model Strengthening: While the current scheme achieves selective security under static adversarial assumptions, it cannot fully resist attacks from adversaries who adaptively select attack targets during security games. To overcome this limitation, the scheme must be upgraded to achieve full adaptive security, which would significantly enhance its resilience in dynamic real-world environments.
- For decentralized KGC architectures, secure and efficient distributed key generation protocols must be designed to balance cryptographic robustness with computational overhead. This requires establishing reliable communication channels among multiple KGC nodes to prevent eavesdropping and tampering. Furthermore, dynamic scenarios such as nodes join/exit demand adaptable protocols to maintain stability without sacrificing security.
- For achieving full adaptive security, we must redesign the scheme to include a hash function that maps bit strings to points in group . Due to the computational overhead of this function, it is critical to rigorously define where and how it should be applied. Furthermore, the security proof must be reformulated under a stronger adversarial model where attackers adaptively query secrets and issue challenges. Finally, even with the increased complexity of addressing adaptive attacks, the scheme must maintain computational efficiency to ensure practical deployment in real-world scenarios.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Linear Secret Sharing Scheme (LSSS)
- Secret Distribution: Consider the vector , where is the shared secret and are random numbers used to conceal s. Each secret share is computed as , where denotes the i-th row of matrix A. The share corresponds to the i-th portion of the secret s, which is mapped to an authorized attribute index by the injective function .
- Secret Reconstruction: For any authorized attribute set in the access structure, define . There exists a polynomial-time algorithm that generates coefficients based on the generation matrix A, which satisfy . Consequently, the secret value s can be reconstructed through . For unauthorized sets, no valid coefficients exist, and thus, the secret cannot be recovered.
Appendix A.2. Performance Comparison Between LISS and LSSS
- (1)
- Theoretical Analysis. The LSSS scheme is based on the finite field , which requires modular arithmetic operations. When p is large, these modular operations can significantly increase the computational overhead. In contrast, LISS operates over the integer domain without requiring any modular arithmetic. Furthermore, the parameters of LISS (such as the range of random numbers) can be flexibly adjusted according to security requirements, which avoids excessive redundancy.
- (2)
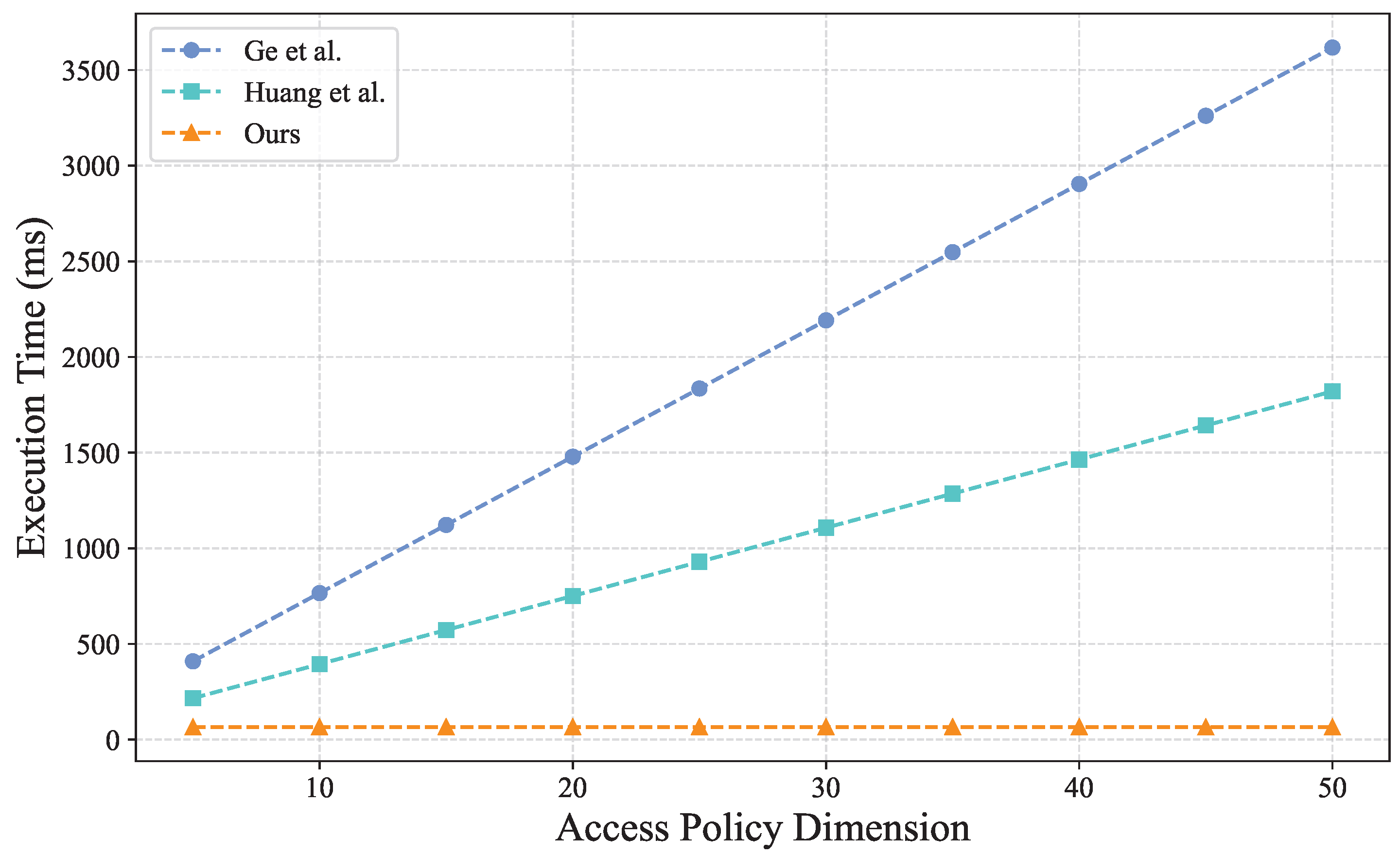
- Experimental Evaluation. To further evaluate the efficiency of LISS and LSSS in secret distribution and reconstruction, we conducted an experiment on a Windows 11 system with an Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz. The parameters were set as follows: , prime , and . For secret distribution, the number of shareholders ranged from 5 to 20 in increments of 5. For reconstruction, authorized attribute sets of sizes 2 to 8 (in steps of 2) were tested. The results are shown in Figure A1 and Figure A2. Figure A1 compares the execution time of LISS and LSSS during secret distribution, while Figure A2 highlights their performance in reconstruction. Both figures clearly demonstrate that LISS outperforms LSSS in terms of efficiency, which aligns with our theoretical analysis.


References
- Sallabi, F.M.; Khater, H.M.; Tariq, A.; Hayajneh, M.; Shuaib, K.; Barka, E.S. Smart Healthcare Network Management: A Comprehensive Review. Mathematics 2025, 13, 988. [Google Scholar] [CrossRef]
- Zhang, L.; You, W.; Mu, Y. Secure outsourced attribute-based sharing framework for lightweight devices in smart health systems. IEEE Trans. Serv. Comput. 2021, 15, 3019–3030. [Google Scholar] [CrossRef]
- Wu, T.Y.; Wang, L.; Chen, C.M. Enhancing the security: A lightweight authentication and key agreement protocol for smart medical services in the ioht. Mathematics 2023, 11, 3701. [Google Scholar] [CrossRef]
- Xu, F.; Luo, J.; Ziaur, R. Cryptanalysis of Two Privacy-Preserving Authentication Schemes for Smart Healthcare Applications. Mathematics 2023, 11, 3314. [Google Scholar] [CrossRef]
- Chinnasamy, P.; Deepalakshmi, P.; Dutta, A.K.; You, J.; Joshi, G.P. Ciphertext-policy attribute-based encryption for cloud storage: Toward data privacy and authentication in AI-enabled IoT system. Mathematics 2021, 10, 68. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.; Wang, Z.; Zhu, Y. Revocable-Attribute-Based Encryption with En-DKER from Lattices. Mathematics 2023, 11, 4986. [Google Scholar] [CrossRef]
- Ge, C.; Susilo, W.; Baek, J.; Liu, Z.; Xia, J.; Fang, L. Revocable attribute-based encryption with data integrity in clouds. IEEE Trans. Dependable Secur. Comput. 2021, 19, 2864–2872. [Google Scholar] [CrossRef]
- Sahai, A.; Waters, B. Fuzzy identity-based encryption. In Advances in Cryptology–EUROCRYPT 2005, Proceedings of the 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005, Proceedings 24; Springer: Berlin/Heidelberg, Germany, 2005; pp. 457–473. [Google Scholar]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 89–98. [Google Scholar]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. In Proceedings of the 2007 IEEE Symposium on Security and Privacy (SP’07), Berkeley, CA, USA, 20–23 May 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 321–334. [Google Scholar]
- Lewko, A.; Waters, B. New proof methods for attribute-based encryption: Achieving full security through selective techniques. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 180–198. [Google Scholar]
- Waters, B. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization. In Proceedings of the International Workshop on Public Key Cryptography, Taormina, Italy, 6–9 March 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 53–70. [Google Scholar]
- Chen, J.; Wee, H. Semi-adaptive attribute-based encryption and improved delegation for boolean formula. In Proceedings of the International Conference on Security and Cryptography for Networks, Amalfi, Italy, 3–5 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 277–297. [Google Scholar]
- Lewko, A.; Okamoto, T.; Sahai, A.; Takashima, K.; Waters, B. Fully secure functional encryption: Attribute-based encryption and (hierarchical) inner product encryption. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 62–91. [Google Scholar]
- Emura, K.; Miyaji, A.; Nomura, A.; Omote, K.; Soshi, M. A ciphertext-policy attribute-based encryption scheme with constant ciphertext length. In Information Security Practice and Experience, Proceedings of the 5th International Conference, ISPEC 2009 Xi’an, China, 13–15 April 2009, Proceedings 5; Springer: Berlin/Heidelberg, Germany, 2009; pp. 13–23. [Google Scholar]
- Hohenberger, S.; Waters, B. Attribute-based encryption with fast decryption. In Public-Key Cryptography–PKC 2013, Proceedings of the 16th International Conference on Practice and Theory in Public-Key Cryptography, Nara, Japan, 26 February–1 March 2013, Proceedings 16; Springer: Berlin/Heidelberg, Germany, 2013; pp. 162–179. [Google Scholar]
- Attrapadung, N.; Libert, B.; De Panafieu, E. Expressive key-policy attribute-based encryption with constant-size ciphertexts. In Public Key Cryptography–PKC 2011, Proceedings of the 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, 6–9 March 2011, Proceedings 14; Springer: Berlin/Heidelberg, Germany, 2011; pp. 90–108. [Google Scholar]
- Herranz, J.; Laguillaumie, F.; Ràfols, C. Constant size ciphertexts in threshold attribute-based encryption. In Proceedings of the International Workshop on Public Key Cryptography, Paris, France, 26–28 May 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 19–34. [Google Scholar]
- Attrapadung, N.; Herranz, J.; Laguillaumie, F.; Libert, B.; De Panafieu, E.; Ràfols, C. Attribute-based encryption schemes with constant-size ciphertexts. Theor. Comput. Sci. 2012, 422, 15–38. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Z.; Feng, D. Efficient ciphertext policy attribute-based encryption with constant-size ciphertext and constant computation-cost. In Provable Security, Proceedings of the 5th International Conference, ProvSec 2011, Xi’an, China, 16–18 October 2011, Proceedings 5; Springer: Berlin/Heidelberg, Germany, 2011; pp. 84–101. [Google Scholar]
- Balu, A.; Kuppusamy, K. An expressive and provably secure ciphertext-policy attribute-based encryption. Inf. Sci. 2014, 276, 354–362. [Google Scholar] [CrossRef]
- Wan, Z.; Liu, J.E.; Deng, R.H. HASBE: A hierarchical attribute-based solution for flexible and scalable access control in cloud computing. IEEE Trans. Inf. Forensics Secur. 2011, 7, 743–754. [Google Scholar] [CrossRef]
- Chase, M. Multi-authority attribute based encryption. In Theory of Cryptography, Proceedings of the 4th Theory of Cryptography Conference, TCC 2007, Amsterdam, The Netherlands, 21–24 February 2007, Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2007; pp. 515–534. [Google Scholar]
- Chase, M.; Chow, S.S. Improving privacy and security in multi-authority attribute-based encryption. In Proceedings of the 16th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 9–13 November 2009; pp. 121–130. [Google Scholar]
- Damgård, I.; Thorbek, R. Linear integer secret sharing and distributed exponentiation. In Proceedings of the International Workshop on Public Key Cryptography, New York, NY, USA, 24–26 April 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–90. [Google Scholar]
- Devevey, J.; Libert, B.; Nguyen, K.; Peters, T.; Yung, M. Non-interactive CCA2-secure threshold cryptosystems: Achieving adaptive security in the standard model without pairings. In Proceedings of the IACR International Conference on Public-Key Cryptography, Edinburgh, UK, 5–13 May 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 659–690. [Google Scholar]
- Zhao, X.; Wang, S.; Zhang, Y.; Wang, Y. Attribute-based access control scheme for data sharing on hyperledger fabric. J. Inf. Secur. Appl. 2022, 67, 103182. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, L.; Ruan, Y.; Feng, S.; Wang, T.; Wang, B. Certificateless Broadcast Encryption with Authorization Suitable for Storing Personal Health Records. Comput. J. 2023, 67, 617–631. [Google Scholar] [CrossRef]
- Cui, H.; Deng, R.H.; Li, Y.; Qin, B. Server-aided revocable attribute-based encryption. In Computer Security–ESORICS 2016, Proceedings of the 21st European Symposium on Research in Computer Security, Heraklion, Greece, 26–30 September 2016, Proceedings, Part II 21; Springer: Berlin/Heidelberg, Germany, 2016; pp. 570–587. [Google Scholar]
- Boldyreva, A.; Goyal, V.; Kumar, V. Identity-based encryption with efficient revocation. In Proceedings of the 15th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 27–31 October 2008; pp. 417–426. [Google Scholar]
- Liang, K.; Liu, J.K.; Wong, D.S.; Susilo, W. An efficient cloud-based revocable identity-based proxy re-encryption scheme for public clouds data sharing. In Computer Security-ESORICS 2014, Proceedings of the 19th European Symposium on Research in Computer Security, Wroclaw, Poland, 7–11 September 2014, Proceedings, Part I 19; Springer: Berlin/Heidelberg, Germany, 2014; pp. 257–272. [Google Scholar]
- Sun, Y.; Chatterjee, P.; Chen, Y.; Zhang, Y. Efficient identity-based encryption with revocation for data privacy in internet of things. IEEE Internet Things J. 2021, 9, 2734–2743. [Google Scholar] [CrossRef]
- Susilo, W.; Chen, R.; Guo, F.; Yang, G.; Mu, Y.; Chow, Y.W. Recipient revocable identity-based broadcast encryption: How to revoke some recipients in IBBE without knowledge of the plaintext. In Proceedings of the 11th ACM on Asia Conference on Computer and Communications Security, Xi’an, China, 30 May–3 June 2016; pp. 201–210. [Google Scholar]
- Datta, P.; Dutta, R.; Mukhopadhyay, S. Adaptively secure unrestricted attribute-based encryption with subset difference revocation in bilinear groups of prime order. In Proceedings of the International Conference on Cryptology in Africa, Fes, Morocco, 13–15 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 325–345. [Google Scholar]
- Ge, C.; Liu, Z.; Xia, J.; Fang, L. Revocable identity-based broadcast proxy re-encryption for data sharing in clouds. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1214–1226. [Google Scholar] [CrossRef]
- Liu, J.K.; Yuen, T.H.; Zhang, P.; Liang, K. Time-based direct revocable ciphertext-policy attribute-based encryption with short revocation list. In Applied Cryptography and Network Security, Proceedings of the 16th International Conference, ACNS 2018, Leuven, Belgium, 2–4 July 2018, Proceedings 16; Springer: Berlin/Heidelberg, Germany, 2018; pp. 516–534. [Google Scholar]
- Jiang, Y.; Susilo, W.; Mu, Y.; Guo, F. Ciphertext-policy attribute-based encryption supporting access policy update and its extension with preserved attributes. Int. J. Inf. Secur. 2018, 17, 533–548. [Google Scholar] [CrossRef]
- Chen, S.; Li, J.; Zhang, Y.; Han, J. Efficient revocable attribute-based encryption with verifiable data integrity. IEEE Internet Things J. 2023, 11, 10441–10451. [Google Scholar] [CrossRef]
- Huang, M.; Liu, Y.; Yang, B.; Zhao, Y.; Zhang, M. Efficient revocable attribute-based encryption with data integrity and key escrow-free. Information 2024, 15, 32. [Google Scholar] [CrossRef]
- Miao, Y.; Li, F.; Li, X.; Ning, J.; Li, H.; Choo, K.K.R.; Deng, R.H. Verifiable outsourced attribute-based encryption scheme for cloud-assisted mobile e-health system. IEEE Trans. Dependable Secur. Comput. 2023, 21, 1845. [Google Scholar] [CrossRef]
- Lynn, B. Standard Pairing-Based Cryptography Library. Available online: https://crypto.stanford.edu/pbc/ (accessed on 20 January 2025).
- Xiong, H.; Choo, K.K.R.; Vasilakos, A.V. Revocable identity-based access control for big data with verifiable outsourced computing. IEEE Trans. Big Data 2017, 8, 1–13. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Han, L.; Hu, B. Revocable Attribute-Based Encryption with Efficient and Secure Verification in Smart Health Systems. Mathematics 2025, 13, 1541. https://doi.org/10.3390/math13091541
Chen Z, Han L, Hu B. Revocable Attribute-Based Encryption with Efficient and Secure Verification in Smart Health Systems. Mathematics. 2025; 13(9):1541. https://doi.org/10.3390/math13091541
Chicago/Turabian StyleChen, Zhou, Lidong Han, and Baokun Hu. 2025. "Revocable Attribute-Based Encryption with Efficient and Secure Verification in Smart Health Systems" Mathematics 13, no. 9: 1541. https://doi.org/10.3390/math13091541
APA StyleChen, Z., Han, L., & Hu, B. (2025). Revocable Attribute-Based Encryption with Efficient and Secure Verification in Smart Health Systems. Mathematics, 13(9), 1541. https://doi.org/10.3390/math13091541