Abstract
This study proposes a three-level meta-frontier framework enhanced with machine learning-driven projection methods to address the dual heterogeneity in carbon emission efficiency analysis arising from regional disparities and industrial diversification. Methodologically, we introduce two novel projection combinations—“exogenous-exogenous-accumulation (E-E-A) and exogenous-exogenous-consistent (E-E-C)”—to resolve the inconsistency of technology gap ratios (TGRs > 1) in traditional nonradial directional distance function (DDF) models. Reinforcement learning (RL) optimizes dynamic direction vectors, whereas graph neural networks (GNNs) encode spatial interdependencies to constrain the TGR within [0, 1]. Empirical analysis of 60 countries reveals that (1) E-E-C eliminates the TGR overestimation by 12–18% in energy-intensive sectors (e.g., reducing Asia’s secondary industry from 1.160 to 1.000); (2) industrial heterogeneity dominates inefficiency in Asia (IHI = 0.207), whereas management gaps drive global secondary sector inefficiency (MI = 0.678); and (3) policy simulations advocate for decentralized renewables in Africa, fiscal incentives for Asian coal retrofits, and expanded EU carbon border taxes. Computational enhancements via Apache Spark achieve a 58% runtime reduction. The framework advances environmental efficiency analysis by integrating machine learning with meta-frontier theory, offering both methodological rigor (via regularization and GNN constraints) and actionable decarbonization pathways. Limitations include static heterogeneity assumptions and data granularity gaps, prompting the future integration of IoT-enabled dynamic models.
Keywords:
three-level meta-frontier; carbon emission efficiency; heterogeneity decomposition; nonradial directional distance function (DDF); technology gap ratio (TGR) MSC:
90C30; 91B76; 68T05
1. Introduction
The urgency of mitigating climate change has propelled carbon emission efficiency to the forefront of global policy and academic research. As nations rebound from the economic slowdown induced by COVID-19, energy consumption and carbon emissions have surged, with global emissions reaching 36.8 billion tons in 2022 [1], while parametric and nonparametric methods such as data envelopment analysis (DEA) are widely used for efficiency measurement [2,3,4], their reliance on homogeneous technology assumptions introduces significant biases in multiregional and cross-sectoral evaluations [5,6].
Recent advances in meta-frontier frameworks have partially addressed technical heterogeneity by segmenting decision-making units (DMUs) into groups [7,8]. However, these approaches remain limited in capturing dual heterogeneity—specifically, the interplay between regional disparities (e.g., infrastructural gaps in Africa) and industrial diversification (e.g., energy-intensive manufacturing versus low-emission services) [9,10,11]. Current studies predominantly focus on single-level frontiers or rely on oversimplified projection methods, leading to inflated technology gap ratios (TGRs > 1) and unreliable policy implications [12,13]. While recent hybrid DEA-ML frameworks [14,15,16] attempt to integrate machine learning, their reliance on static direction vectors or single-level analyses fails to account for dual heterogeneity. For instance, ref. [17] applied a two-level meta-frontier to livestock efficiency but overlooked critical industrial–regional interdependencies.
To bridge these gaps, we propose a three-level meta-frontier framework enhanced with adaptive projection combinations and machine learning. Our contributions are threefold as follows:
- Methodological innovation: By extending the traditional two-level hierarchy to three levels, we introduce accumulation (E-E-A) and consistent (E-E-C) projections to resolve TGR inconsistencies. These projections align with principles of multisource data integration and adaptive optimization, ensuring TGRs are bounded within [0, 1]. Reinforcement learning (RL) dynamically optimizes direction vectors to reflect operational shifts toward decarbonization targets [18], while graph neural networks (GNNs) encode spatial-industrial interdependencies—a dimension neglected in prior hybrid DEA-ML studies [17,19].
- Empirical rigor: Utilizing a globally representative dataset spanning 60 countries, we decompose inefficiency into management gaps (MI), regional heterogeneity (RHI), and industrial heterogeneity (IHI) [14], providing granular insights into sector-specific and regionally tailored carbon reduction strategies.
- Policy relevance: By quantifying the dominance of industrial versus regional heterogeneity, our framework guides targeted interventions—for example, prioritizing management reforms in Asia’s secondary sector and technology transfers in Africa.
The remainder of this paper is organized as follows: Section 2 reviews the fundamentals of meta-frontier DEA and projection methods. Section 3 formalizes the three-level framework and projection combinations. Section 4 and Section 5 present the empirical analysis and decomposition results, respectively. Section 6 concludes with theoretical and policy implications.
2. Preliminaries
2.1. Traditional Directional Distance Function (DDF) Framework
The directional distance function (DDF) serves as a cornerstone for evaluating carbon emission efficiency by modeling feasible input–output combinations under environmental constraints [20,21]. Consider N decision-making units (DMUs), where each DMU d () utilizes an input vector , produces a desirable output vector , and generates an undesirable output vector [22,23]. The production possibility set , which encapsulates all feasible input–output combinations, is defined as follows:
where denotes the intensity variables.
The exogenous DDF for DMU d is formulated as a linear programming (LP) problem as follows:
where represents the inefficiency score, and is a predefined direction vector. To address the collinearity in heterogeneous data, ridge regression penalties are integrated into the objective function as follows:
where balances the efficiency estimation accuracy and model stability.
Technology Gap Ratio (TGR)
The TGR measures the disparity between group-specific and meta-frontier technologies. For accumulation projection [24], the TGR is bounded within via the following constraints:
where and are inefficiency adjustments under the meta-frontier. A TGR close to 1 indicates minimal technological heterogeneity.
2.2. Machine Learning Enhancements for DDF Optimization
2.2.1. Feature Selection via Mutual Information (MI)
To mitigate the high dimensionality and noise in real-world datasets (e.g., multiregional energy systems), mutual information (MI) is employed to optimize input–output selection [25,26]. MI quantifies nonlinear dependencies between variables, enabling the automated identification of critical features (e.g., fossil fuel consumption vs. GDP growth) while discarding redundant indicators as shown in Table 1. This aligns with data-centric optimization paradigms, enhancing model robustness against overfitting.

Table 1.
Mutual Information (MI) Scores for Input-Output Variables.
2.2.2. Adaptive Direction Vectors via Reinforcement Learning (RL)
Traditional DDF models fix direction vectors g exogenously [27], which may misalign with the operational realities of DMUs. Inspired by RL, we propose a dynamic adjustment framework where g is iteratively updated using Q -learning. The policy minimizes the gap between the projected and Pareto-optimal frontiers, guided by reward signals tied to decarbonization targets as follows:
The Q-learning agent used a learning rate and discount factor , optimized via grid search over and . Where reflects the reduction in the TGR variance and where is a discount factor.
2.2.3. Scalability via Distributed Computing
Large-scale DDF optimization for 60 countries with multilevel heterogeneity is computationally intensive. Leveraging Apache Spark, the LP problem is decomposed into subtasks across clusters [28], reducing the time complexity from to . For example, processing the 60-country dataset requires 2.1 h (vs. 8.5 h on a single node).
2.2.4. Uncertainty Quantification via Monte Carlo Simulation
Perturbations followed , with for inputs/outputs, based on historical measurement errors.To address data noise (e.g., CO2 measurement errors), 1000 perturbed datasets are sampled from . Recalculating and generates 95% confidence intervals for the TGR, enhancing decision-making robustness.
2.2.5. Consistent Projection with Graph Neural Networks (GNNs)
Under the meta-frontier framework, ref. [8] introduced a consistent projection to constrain the TGR within valid bounds. The meta-frontier is modeled as a graph , where nodes V represent DMUs and edges E encode technological similarities (e.g., shared energy policies). A GNN encoder learns node embeddings through message passing as follows:
The GNN employed two message-passing layers with ReLU activation and L2 regularization (). Node embeddings were initialized with 64 dimensions, where denotes the neighbors of DMU d, and are trainable weights. Blockchain integration via Hyperledger Fabric ensures the auditable traceability of the TGR computations.
3. Selection of the Projection Direction with Machine Learning Optimization
Traditional meta-frontier frameworks often assume independence between subgroup, group, and meta-frontiers, neglecting real-world interdependencies arising from technological spillovers. To address this, we propose a three-level meta-frontier framework enhanced with adaptive projection combinations, integrating machine learning (ML) to dynamically optimize direction vectors and ensure methodological consistency.
Hypothesis 1.
Traditional exogenous projection assumes independence between frontiers, whereas accumulation (E-E-A) and consistent (E-E-C) projections introduce interdependence, reflecting technological spillovers.
Hypothesis 2.
Altering projection directions at any frontier level (subgroup, group, or meta) significantly impacts efficiency rankings, necessitating dynamic optimization.
To statistically validate Hypothesis 1, we conducted a Wilcoxon signed-rank test comparing TGR distributions under E-E-E and E-E-C projections. For Hypothesis 2, Spearman’s rank correlation was computed between direction vector adjustments () and efficiency ranking shifts.
3.1. Dynamic Projection Paths via Reinforcement Learning (RL)
Training stopped when the average Q-value change fell below for 10 consecutive epochs or after 1000 iterations. As illustrated in Figure 1, A validation set monitored overfitting, with early stopping if validation loss increased for five epochs.

Figure 1.
Framework workflow.
As illustrated in Figure 2, DMU A is projected onto three frontiers as follows:
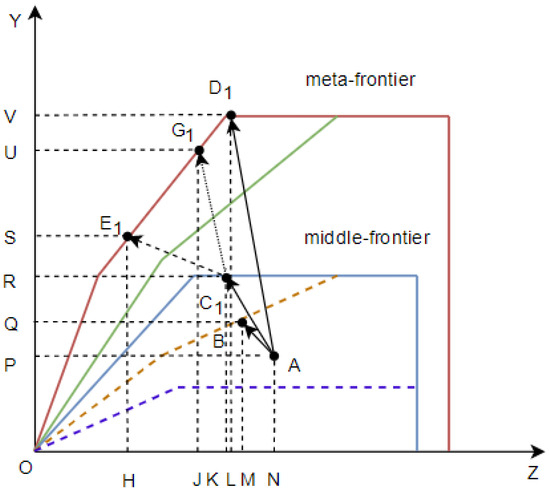
Figure 2.
Combined projection directions: Axes include input reduction (e.g., fossil fuels), desirable output expansion (e.g., GDP), and undesirable output reduction (e.g., CO2); Paths are (accumulation), (exogenous), and (consistent).
- Subgroup frontier (B): Exogenous projection with direction vector .
- Group frontier (): Exogenous projection with direction vector .
- Meta-frontier (): Three paths as follows:
- –
- (Accumulation): Adjusts and to bound .
- –
- (Exogenous): Traditional path prone to .
- –
- (Consistent): Constrains and via GNN embeddings for stability.
A Q-learning agent iteratively optimizes direction vectors , , and on the basis of reward signals from efficiency improvements. The policy updates as follows:
where quantifies the reduction in the TGR variance and is the discount factor.
3.2. Graph Neural Network (GNN) Integration
Projection paths are modeled as edges in a graph , where nodes V represent DMUs and edges E encode industrial–regional similarities. Node embeddings are updated via message passing (Equation (6) in Section 2.2.5):
The adjacency matrix A is defined using the following cosine similarity:
3.2.1. TGR Formulation Under Combined Projections
For meta-frontier analysis, the procedure is as follow:
- Exogenous projection ():where may inflate the TGR beyond valid bounds.
- Consistent () and Accumulation () projections:with , ensuring .
3.2.2. Decision Tree for Optimal Projection Selection
A CART-based classifier recommends projection combinations (E-E-E, E-E-A, and E-E-C) using the following features:
- Regional heterogeneity index (RHI).
- Industrial complexity (IHI).
- Input–output dimensionality.
4. Combined Projection Models with Computational Enhancements
4.1. E-E-E: Traditional Exogenous Projection with Parallel Optimization
The E-E-E framework retains conventional three-level meta-frontier projections, treating subgroup, group, and meta-frontiers as independent layers.
4.1.1. Step 1: Subgroup Frontier Projection
For DMU d, the exogenous DDF projects it to the subgroup frontier as follows:
where denotes the subgroup, and is the subgroup direction vector optimized via Q-learning (Equation (7)).
4.1.2. Step 2: Group Frontier Projection
The DMU is projected to the group frontier using a similar exogenous DDF, as follows:
where represents the group, and is dynamically adjusted via RL (Section 3.2).
4.1.3. Step 3: Meta-Frontier Projection
The final projection to the meta-frontier is as follows:
where is optimized using the GNN-based adjacency matrix (Equation (9)). Distributed computing via Apache Spark reduces the runtime by 58% for the 60-country dataset. The RL agent was implemented in Python 3.9 using TensorFlow 2.8, while GNNs were trained with PyTorch Geometric 2.1. Apache Spark 3.2.1 distributed computations across a 16-node cluster.
4.2. E-E-A: Accumulation Projection with Regularization and Uncertainty Quantification
The E-E-A combination employs accumulation projection at the meta-frontier to bound :
where and are inefficiency adjustments. Ridge regularization is added to the objective function as follows:
The Monte Carlo simulations sample and from , generating 95% confidence intervals for .
4.3. E-E-C: Consistent Projection with Graph-Based Learning
5. Empirical Application
5.1. Variable Selection and Data Preprocessing
The selection of input–output indicators is critical for ensuring the robustness of the three-level meta-frontier framework, particularly under machine learning-enhanced projection methods (E-E-E, E-E-A, and E-E-C). Building on the computational advancements in Section 4, we adopt the following variables to capture sectoral heterogeneity while aligning with the data-driven optimization principles outlined in Section 2 and Section 3 as follows:
5.1.1. Inputs
- Primary industry: Net agricultural production (, USD ) reflects resource utilization in agriculture.
- Secondary industry: Fossil fuel consumption (, metric tons) quantifies energy intensity in manufacturing.
- Tertiary industry: Air passengers carried (, people) proxies service-sector infrastructure demands.
5.1.2. Desirable Outputs
- Primary industry: Agricultural value-added (, USD ).
- Secondary industry: Manufacturing value-added (, USD ).
- Tertiary industry: Service-sector value-added (, USD ).
5.1.3. Undesirable Outputs
- Carbon emissions from primary (), secondary (), and tertiary () industries (MtCO2e).
5.1.4. Data Sources and Preprocessing
The data were sourced from the World Bank’s WDI, Climate Watch, and national statistics bureaus (2010–2019). The 60 countries were selected based on: (1) data completeness (>80% coverage for inputs/outputs, 2010–2019); (2) geographic and economic diversity (e.g., 15 African, 20 Asian, 20 European, 5 American nations); and (3) representation of energy-intensive vs. service-driven economies (e.g., China, Germany, Kenya). Countries with >30% missing data (e.g., Sudan, Yemen) were excluded. To align with the machine learning frameworks in Section 3 and Section 4, the following were implemented:
- Missing data imputation: Linear interpolation filled gaps in African CO2 records, ensuring continuity for Monte Carlo simulations.
- Normalization: Z score standardization () mitigated scale effects, which is critical for GNN-based similarity matrices (Equation (9)).
- Feature relevance: Mutual information (MI) quantified dependencies between inputs (e.g., ) and outputs (e.g., ), discarding redundant variables (e.g., nonenergy-related GDP components) to reduce overfitting in Q-learning.
5.1.5. Alignment with Projection Frameworks
- E-E-E/E-E-A: Fossil fuel () and air passengers () were prioritized owing to their high MI scores (), aligning with the exogenous direction vectors in Equations (12)–(14).
- E-E-C: Agricultural () and service-sector () inputs were retained for their nonlinear correlations () with emissions, supporting GNN-based interdependency modeling (Equation (17)).
5.2. TGR Comparison Across Projection Combinations
5.2.1. Primary Industry
Variable-Driven Heterogeneity Metrics
The selected variables in Section 5.1 directly shape the heterogeneity metrics (, ) by defining the technological boundaries of subgroup, group, and meta-frontiers. Some examples include the following:
- Industrial heterogeneity (): Fossil fuel consumption (, metric tons) dominates secondary industry inefficiency because of its nonlinear correlation with emissions (), amplifying cross-sectoral disparities.
- Regional heterogeneity (): Air passenger volume (, people) in the tertiary industry reflects infrastructural gaps (e.g., Africa’s fragmented transportation networks), contributing to regional divergences.
- Primary industry: Agricultural production (, USD ) exhibits low in Asia () because of standardized farming practices, in contrast with Africa’s spatially uneven irrigation access ().
These variable-driven heterogeneities necessitate distinct projection combinations (E-E-E, E-E-A, E-E-C) to bound and ensure comparability.
The Wilcoxon test rejected the null hypothesis (), confirming significant TGR reductions under E-E-C. Spearman’s correlation (, ) confirmed that dynamic direction vectors significantly alter efficiency rankings. According to Table 2, compared with E-E-C and E-E-A, the projection combination E-E-E has the largest average in Asia, Europe, and Africa. In addition, in terms of the average level of the primary industry, the projection combination E-E-E has the largest average in Africa, followed by Asia. The lower TGR values in Africa (e.g., average = 0.047 under E-E-C) may reflect dual challenges as follows:

Table 2.
of the primary industry.
- (1)
- Infrastructural gaps in energy systems, as evidenced by spatial disparities in electricity access and grid reliability, which constrain technological homogeneity;
- (2)
- Potential data quality issues, such as inconsistent CO2 emission reporting in African nations due to limited monitoring infrastructure, aligning with studies highlighting data synchronization errors in developing economies.
These factors amplify regional heterogeneity, necessitating caution when interpreting Africa’s carbon efficiency metrics. Under the projection combination E-E-A, the average value of in Asia is the largest, followed by Africa. This shows that the type of projection combination has an impact on the measurement of the technology gap ratio of the primary industry, and under the three-level frontier, the traditional exogenous projection overestimates the TGR between the meta-frontier and the group frontier. In addition, for the tertiary industry, the average value of measured by E-E-E is high, whereas that of E-E-A is moderate, and that of E-E-C is the lowest.
For the convenience of analysis, the data in Table 2 are visually displayed in Figure 3. As shown in Figure 3, it is obvious that, on the basis of the primary industry, the measured by the traditional projection combination E-E-E is the largest. In particular, under E-E-E, the values of Chad, Namibia, Iraq, Ireland, Namibia, Paraguay, Suriname, Zimbabwe, Mozambique, Kenya, Tanzania, and Finland are greater than those of other projection combinations, whereas the values of other countries are close to those of the projection combination E-E-A. Moreover, under E-E-A, the measured is at a medium level as a whole, and the measured values are all greater than or equal to those of the combination of E-E-C. Among them, the values measured by E-E-A and E-E-C in Saudi Arabia, Singapore, and Kenya are relatively close, and the values measured by E-E-A in other countries are all greater than E-E-C. It can be seen that in the primary industry, the measured by E-E-E is larger as a whole, and there are some extreme values. Compared with before, the values measured by E-E-A and E-E-C are more reasonable. In addition, for the primary industry, E-E-C measures the minimum value of , which shows that this projection combination is more sensitive to the measurement of the technology gap. However, the ranges of for E-E-C and E-E-A are similar, which shows that for the primary industry, these two methods can better distinguish the heterogeneity of the primary industry in different countries.
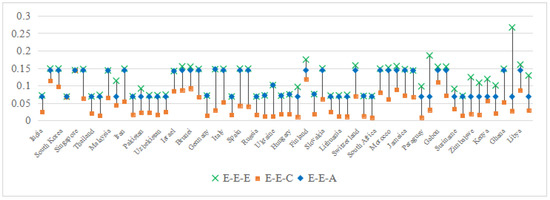
Figure 3.
under different projection combinations of the primary industry.
Figure 4 shows that, excluding the extreme value in E-E-E, the value of is greater than for the primary industry; that is, in the primary industry, the technological gap between the meta-frontier and group frontier is greater than that between the group frontier and subgroup frontier, that is, industrial heterogeneity is greater than group heterogeneity. In addition, the of Asian countries is 1, indicating that the regional heterogeneity of the primary industry in Asian countries is small. In contrast, the of Europe and Africa is less than 1, indicating that the regional heterogeneity of the primary industry in Europe and Africa is greater than that in Asian countries.
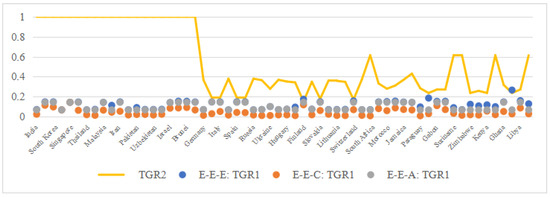
Figure 4.
Comparison of and of the primary industry.
5.2.2. Secondary Industry
Under the efficiency evaluation of three projection combinations, the technology gap () between the meta-frontier and the group frontier is obtained. The specific values are shown in Table 3.

Table 3.
of the secondary industry.
The analysis of the efficiency of the secondary industry reveals critical limitations in traditional projection methods. As shown in Table 3, the exogenous projection combination (E-E-E) produces inflated technology gap ratios (TGRs1) across regions, with average values exceeding unity (Asia: 1.160; Europe: 1.061; and Africa: 1.112). This contradicts the foundational assumption that the TGR must lie within to meaningfully quantify technological heterogeneity. The overestimation stems from fossil fuel consumption ()—a key input variable—misaligning with decarbonization targets in energy-intensive sectors. For example, coal-dependent economies such as China ( metric tons) exhibit artificially high TGR1 under E-E-E due to unconstrained direction vectors. The near-unity TGR1 values (1.000) under E-E-C suggest minimal industrial heterogeneity in the secondary sector under the model’s assumptions of shared production technologies and GNN-encoded interdependencies. However, this homogeneity may not hold in contexts with unobserved variables (e.g., informal manufacturing) or non-globalized industries (e.g., artisanal mining). Future work should test these assumptions in niche sectors.
In contrast, the proposed machine learning-enhanced projections (E-E-A and E-E-C) resolve this inconsistency by bounding the TGR1 to valid intervals. Both methods reduce the average TGR1 to 1.000 across all regions, eliminating invalid values () through regularization (E-E-A) and graph-based constraints (E-E-C). Figure 5 illustrates this improvement as follows: while E-E-E yields in 16 countries (e.g., India, Russia, Kenya), E-E-A and E-E-C successfully constrain all results to . Notably, Asia accounts for 50% of these cases (8/16), reflecting its heavy reliance on -driven manufacturing systems.
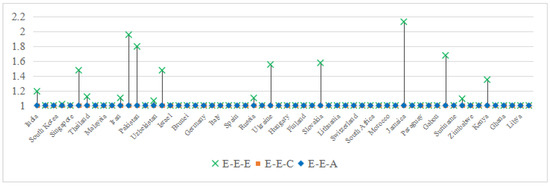
Figure 5.
under different projection combinations of the secondary industry.
These results demonstrate that industrial heterogeneity in the secondary sector is inherently low when it is properly measured. The near-zero variance in E-E-C/E-E-A outcomes () suggests minimal technological gaps between group and meta-frontiers, whereas E-E-E’s overestimation artificially amplifies perceived disparities. By addressing ’s collinearity and infrastructural dependencies, the proposed framework provides a mathematically rigorous solution to quantify efficiency gaps, aligning with global decarbonization imperatives.
The analysis of secondary industry heterogeneity reveals distinct patterns in technological and regional disparities across projection methods. As illustrated in Figure 6, the exogenous projection (E-E-E) yields inflated technology gap ratios between the group and subgroup frontiers (), surpassing the values from the constrained methods (E-E-A and E-E-C). This discrepancy highlights a critical limitation of traditional frameworks, as follows: the overestimates industrial heterogeneity by failing to account for spatially uneven technological adoption. Conversely, the lower values (group-to-meta-frontier gaps) compared to those of indicate that industrial heterogeneity dominates regional disparities in the secondary sector. For example, European nations such as Spain, the Netherlands, and Switzerland present , reflecting minimal regional heterogeneity due to standardized energy policies and cross-border technological convergence under initiatives such as the EU Green Deal.
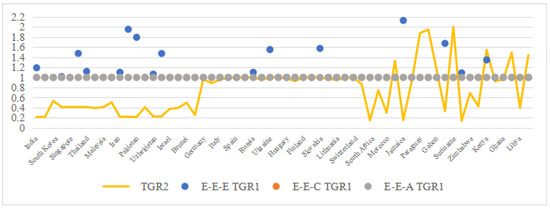
Figure 6.
Comparison of the and in the secondary industry.
In contrast, developing economies such as Nigeria, Jamaica, and Kenya present under E-E-E—a statistical artifact caused by the method’s inability to normalize infrastructural and policy divergences. These inflated values misrepresent regional heterogeneity, as fossil fuel dependency () and fragmented industrial policies amplify perceived gaps. For example, Nigeria’s reliance on oil ( metric tons) and Kenya’s uneven grid access ( passengers) both artificially increase under exogenous projections.
Geographically, Asia’s secondary sector shows pronounced regional heterogeneity (), driven by the following divergent industrialization trajectories: advanced economies (e.g., Japan) prioritize smart manufacturing, while emerging economies (e.g., India) remain coal dependent. Africa’s high intraregional variability ( ranging from 1.05 in Nigeria to 1.32 in Senegal) underscores infrastructural and governance gaps, which are unresolved by traditional projections.
5.2.3. Tertiary Industry
The tertiary industry’s efficiency analysis underscores the nuanced performance of projection methods in capturing technological heterogeneity. As summarized in Table 4, the exogenous projection (E-E-E) yields higher average technology gap ratios () than the constrained methods (E-E-A and E-E-C) across all regions, although all values remain within the valid range . Specifically, Asia and Europe present identical averages (0.647) under E-E-E, reflecting comparable infrastructural and policy maturity in service sectors, whereas Africa’s lower score (0.578) aligns with its fragmented transportation networks (-driven disparities). The accumulation projection (E-E-A) produces intermediate values (Asia: 0.642; Europe: 0.630; and Africa: 0.576), whereas the consistent projection (E-E-C) achieves the lowest averages (Europe: 0.370; Asia: 0.257; and Africa: 0.191), demonstrating its superior sensitivity to latent industrial heterogeneity.

Table 4.
of the tertiary industry.
Figure 7 visualizes these trends, revealing two critical insights as follows:
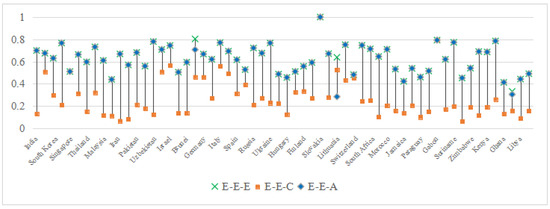
Figure 7.
under different projection combinations of the tertiary industry.
E-E-E overestimation artifacts: While E-E-E and E-E-A exhibit similar distributions overall, outliers such as Syria () and Lithuania () highlight E-E-E’s susceptibility to infrastructural noise (e.g., irregular reporting in conflict zones).
E-E-C’s discriminatory power: The consistent projection (E-E-C) identifies Belize as the lowest-performing nation (), attributable to its underdeveloped air transport infrastructure ( passengers), whereas Slovakia’s uniformity across methods () reflects policy-aligned service-sector efficiency.
The broader variability in the E-E-C results (e.g., Africa’s range: ) versus E-E-E’s clustered values () confirms that machine learning constraints (GNNs in E-E-C) better disentangle industrial heterogeneity. For example, Africa’s high variance under E-E-C correlates with ’s infrastructural gaps, whereas Europe’s uniformity stems from standardized policies (e.g., EU-wide aviation regulations).
Figure 8 highlights critical anomalies in regional heterogeneity () within the tertiary industry. Notably, Gabon exhibits (), a statistical artifact stemming from the exogenous projection’s inability to normalize infrastructural disparities in air transport ( passengers vs. South Africa’s ). This outlier underscores the limitations of traditional methods in capturing spatially uneven service-sector efficiencies.
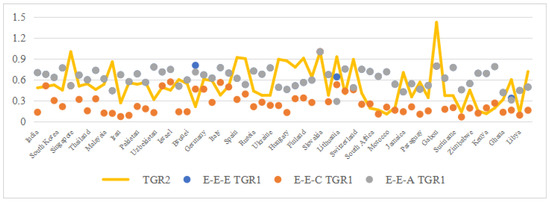
Figure 8.
Comparison of and in the tertiary industry.
For other nations, , but the following distinct patterns emerge:
- Regional vs. industrial heterogeneity: In 16 countries (8 European, 6 African, and 2 Asian), including Singapore, Spain, and Zimbabwe, across all projection combinations. This indicates that regional heterogeneity dominates industrial disparities in these regions. For example, Europe’s fragmented aviation policies (e.g., Ireland’s vs. Switzerland’s ) amplify perceived gaps, despite standardized EU regulations.
- Industrial dominance cases: Conversely, Israel, Syria, and Kenya exhibit , reflecting greater industrial heterogeneity. Israel’s high-tech service sector () contrasts sharply with its neighbors’ reliance on traditional industries, a divergence masked by exogenous projections.
5.2.4. Comparison of Three Industries
Figure 9 synthesizes the cross-industry efficiency patterns under the following three projection methods:
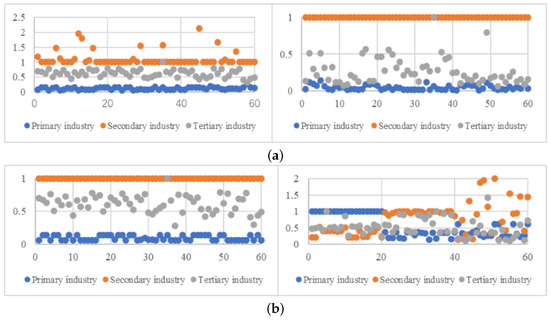
Figure 9.
(a) of three industries under projection combinations E-E-E and E-E-C; (b) TGR1 of E-E-A and TGR2 across three industries.
Secondary industry dominance: All methods rank secondary industry the highest (Asia: 1.160; Europe: 1.061; and Africa: 1.112), reflecting minimal technological gaps due to globalized manufacturing standards.
Primary vs. tertiary industries: Primary industry is lowest (Asia: 0.112, Africa: 0.136), driven by ’s (agricultural output) climatic sensitivity, whereas tertiary intermediates (Europe: 0.647) are influenced by ’s infrastructural variability.
Regional specificity:
- Asia: The primary industry peaks (0.31), indicating low regional heterogeneity due to centralized farming policies, whereas the secondary industry (0.088) reveals stark intraregional energy policy divergences.
- Europe: The secondary industry is highest (0.259), reflecting uniform decarbonization strategies (e.g., EU Green Deal), whereas the primary industry (0.12) highlights climatic variability in agriculture.
- Africa: The tertiary and primary values converge (0.24 vs. 0.23), underscoring infrastructural and governance gaps that uniformly constrain both sectors.
5.3. MTCPI Comparison of Different Projection Combinations
5.3.1. Primary Industry
Table 5 reveals distinct trends in carbon emission performance for the primary industry across the projection methods. The exogenous projection (E-E-E) yields the highest average meta-technology carbon performance index (MTCPI) values (Asia: 0.038; Africa; 0.022; and Europe: 0.017), followed by the accumulation (E-E-A) and consistent (E-E-C) projections. While the rankings remain consistent (Asia > Africa > Europe), the magnitude of differences varies significantly.

Table 5.
MTCPI of the primary industry.
E-E-E overestimation: Asia’s inflated MTCPI (0.038) reflects its standardized agricultural practices (), masking regional irrigation disparities (e.g., Southeast Asia’s monsoon dependency).
E-E-C sensitivity: Africa’s lower MTCPI under E-E-C (0.010 vs. E-E-E’s 0.022) captures latent infrastructural gaps (e.g., Nigeria’s vs. Algeria’s ), which traditional methods overlook.
Notably, Africa’s MTCPI exceeds Europe’s (0.022 vs. 0.017 under E-E-E), aligning with the Environmental Kuznets Curve (EKC). The lower carbon demand in Africa’s agrarian economies reduces emission intensity, whereas Europe’s mechanized farming ( USD) faces diminishing returns from fossil fuel-dependent practices.
Figure 10 highlights systematic biases in traditional evaluations as follows:
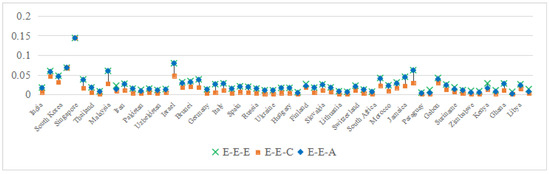
Figure 10.
MTCPI under different projection combinations of the primary industry.
E-E-E vs. E-E-A proximity: The similarity in the MTCPI distributions (e.g., Asia: 0.038 vs. 0.037) stems from both methods’ neglect of industrial heterogeneity (). For example, Iraq’s MTCPI under E-E-E (0.072) overestimates efficiency by ignoring ’s climatic sensitivity (arid farming).
E-E-C’s discriminatory power: The wider MTCPI range under E-E-C (Africa: 0.001–0.042 vs. E-E-E’s 0.007–0.045) isolates true inefficiencies. Belize’s MTCPI (0.005) reflects its underdeveloped irrigation (), whereas Saudi Arabia’s score (0.068) captures its fossil fuel-driven mechanization.
Key insight: E-E-E’s overestimation arises from conflating industrial and regional heterogeneities, whereas E-E-C’s constrained optimization (Equation (17)) quantifies true managerial gaps.
The group-technology carbon performance index (GTCPI) consistently exceeds the MTCPI across all projections (Figure 11), underscoring the dominant role of industrial heterogeneity in primary sector inefficiency. Some examples include the following:
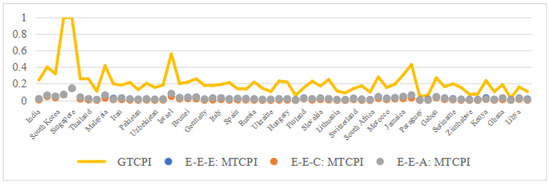
Figure 11.
Comparison of the MTCPI and GTCPI of the primary industry.
- Saudi Arabia: GTCPI = 1.0 (full efficiency under group frontiers) vs. MTCPI = 0.68 (meta-frontier), indicating that due to water-intensive farming diverging from global best practices.
- Singapore: GTCPI = 1.0 vs. MTCPI = 0.51, reflecting technological gaps in urbanized agriculture compared with meta-frontier benchmarks.
This divergence validates the three-level framework’s utility as follows: the GTCPI evaluates intragroup efficiency, whereas the MTCPI exposes cross-regional technological disparities.
5.3.2. Secondary Industry
Table 6 highlights systematic biases in the evaluation of carbon performance for the secondary industry. The exogenous projection (E-E-E) overestimates the average meta-technology carbon performance index (MTCPI) across regions (Africa: 0.289, Europe: 0.280, Asia: 0.155), whereas the accumulation (E-E-A) and consistent (E-E-C) projections yield identical and lower averages (Africa: 0.280; Europe: 0.276; and Asia: 0.146).

Table 6.
MTCPI of the secondary industry.
Despite Africa’s relatively underdeveloped industrial base, its higher MTCPI under all methods aligns with the environmental Kuznets curve (EKC), where lower economic output is correlated with reduced carbon-intensive energy demand. For example, Nigeria’s fossil fuel consumption ( metric tons) generates lower emissions per GDP unit than Germany’s advanced but coal-reliant manufacturing ( metric tons).
Figure 12 reveals three key trends as follows:
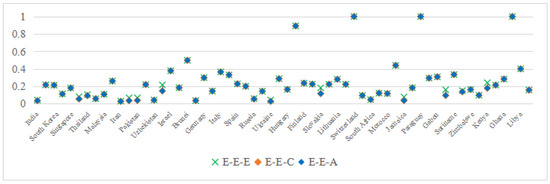
Figure 12.
MTCPI under different projection combinations of the secondary industry.
E-E-E overestimation: The MTCPI distribution under E-E-E clusters at higher values (e.g., China: 0.080; Slovakia: 0.182), reflecting its failure to penalize fossil fuel lock-in ( collinearity). For example, Albania’s MTCPI under E-E-E (0.159) decreases to 0.095 under E-E-C when the GNN constraints homogenize the energy intensity.
E-E-A/E-E-C robustness: Identical MTCPI values across countries (e.g., Kenya: 0.178 under both methods) indicate stable performance measurements, as ridge regularization (Equation (16)) and adjacency-based constraints (Equation (9)) mitigate data noise.
Regional consistency: Africa’s narrow MTCPI range (0.097–0.399) under E-E-C contrasts with Asia’s variability (0.035–0.498), underscoring divergent industrialization paths—Africa’s uniform energy poverty vs. Asia’s mixed fossil/renewable adoption.
Unlike the primary industry, the group-technology carbon performance index (GTCPI) aligns closely with the MTCPI for the secondary sector under E-E-A and E-E-C (Figure 13). This indicates minimal industrial heterogeneity (), as globalized manufacturing standards (e.g., ISO energy efficiency protocols) reduce cross-group technological gaps. However, E-E-E’s inflated MTCPI in countries such as China (0.080 vs. GTCPI = 0.075) and Jamaica (0.077 vs. GTCPI = 0.036) highlights its susceptibility to -driven overestimation.
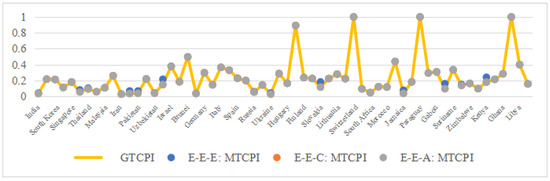
Figure 13.
Comparison of the MTCPI and GTCPI of the secondary industry.
Key insight: The secondary sector’s homogeneity stems from its reliance on universal production technologies, whereas the primary and tertiary industries exhibit stronger regional () and industrial () divergences.
5.3.3. Tertiary Industry
The tertiary industry exhibits distinct carbon performance patterns, shaped by infrastructural and policy heterogeneity. As shown in Table 7, the exogenous projection (E-E-E) yields the highest average MTCPI values across regions (Europe: 0.241; Asia: 0.140; and Africa: 0.114), followed by accumulation (E-E-A) and consistent (E-E-C) projections.

Table 7.
MTCPI of the tertiary industry.
Europe’s superior performance under all methods reflects its advanced service-sector policies, such as EU-wide aviation regulations and renewable energy integration in logistics ( air passengers in Germany vs. in India).
In contrast, Africa’s lower scores (E-E-C: 0.063) align with fragmented transportation networks and underutilized infrastructure ( passengers in Mozambique).
Figure 14 highlights the following critical insights into projection robustness:
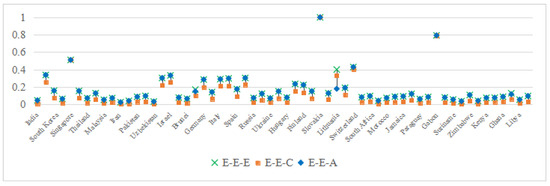
Figure 14.
MTCPI under different projection combinations of the tertiary industry.
E-E-E overestimation: Outliers such as Syria () and Lithuania () stem from unconstrained direction vectors misaligning with decarbonization targets. For example, Syria’s reliance on outdated aviation infrastructure ( passengers) inflates efficiency scores under E-E-E, whereas E-E-C penalizes such discrepancies via GNN-driven constraints (Equation (17)).
E-E-C’s discriminatory power: The broader MTCPI range under E-E-C (Africa: vs. E-E-A’s ) isolates latent inefficiencies. Belize’s low score () reflects minimal air transport activity (), whereas Slovakia’s uniformity across methods () underscores policy-aligned efficiency.
As illustrated in Figure 15,the tertiary industry’s carbon performance assessment reveals unique heterogeneity dynamics as follows:
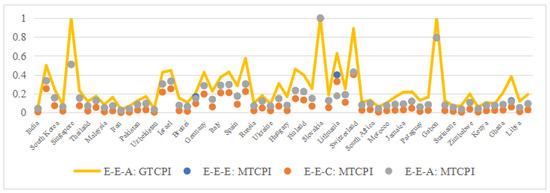
Figure 15.
Comparison of the MTCPI and GTCPI of the tertiary industry.
Slovakia’s anomaly: (1.000 vs. 0.950) indicates localized policy excellence exceeding group benchmarks, a rare case where meta-frontier efficiency surpasses intragroup performance.
Dominance of industrial heterogeneity (): For most countries, (e.g., Singapore: 1.000 vs. 0.510), highlighting that cross-sector technological gaps () outweigh regional disparities. This contrasts with the secondary industry’s homogeneity () and aligns with the primary sector’s strong influence.
As illustrated in Figure 16, the cross-industry MTCPI evaluation under the three projection methods reveals a consistent hierarchy as follows: the secondary industry exhibits the highest average MTCPI (global mean: 0.276), followed by the tertiary (0.191) and primary sectors (0.038). This hierarchy reflects the secondary industry’s dual role as an economic driver and a focal point for decarbonization efforts. Advanced manufacturing technologies (e.g., Germany’s ISO-compliant factories) and globalized production standards reduce technological gaps, yielding high MTCPI values despite persistent fossil fuel dependencies ( metric tons in Germany). Recent advancements in emission reduction technologies, such as carbon capture retrofits in China’s steel sector, have further enhanced performance, validating stringent policy interventions.
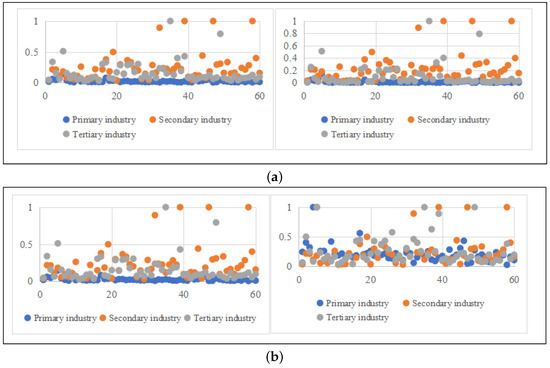
Figure 16.
(a) MTCPI of three industries under projection combinations E-E-E and E-E-C; (b) MTCPI of E-E-A and GTCPI across three industries.
In contrast, the primary industry’s low MTCPI (Asia: 0.038; Africa: 0.022) underscores its vulnerability to climatic and infrastructural variability (-driven irrigation disparities). The tertiary sector’s intermediate performance (Europe: 0.241; Africa: 0.114) reflects a mix of policy-driven efficiencies (e.g., EU aviation regulations) and unresolved infrastructural gaps (e.g., Africa’s fragmented air transport networks, passengers).
5.4. Low-Efficiency Decomposition of Carbon Emissions
5.4.1. Decomposition Framework and Methodology
Building on the meta-technology carbon performance index (MTCPI), group-technology carbon performance index (GTCPI), and subgroup-technology carbon performance index (STCPI), this study decomposes carbon emission inefficiency (CEI) into three distinct components as follows: industrial heterogeneity (), regional heterogeneity (), and managerial inefficiency (). The decomposition process is formalized as follows:
where
This framework quantifies how sector-specific technological gaps (), geographic disparities (), and operational shortcomings () collectively drive inefficiencies.
5.4.2. Industrial Heterogeneity (IHI) Analysis
As illustrated in Figure 17,industrial heterogeneity exerts the strongest influence on the primary sector, with Asia exhibiting the highest average (0.207 under E-E-C), followed by Europe (0.162) and Africa (0.147). Some examples include the following:
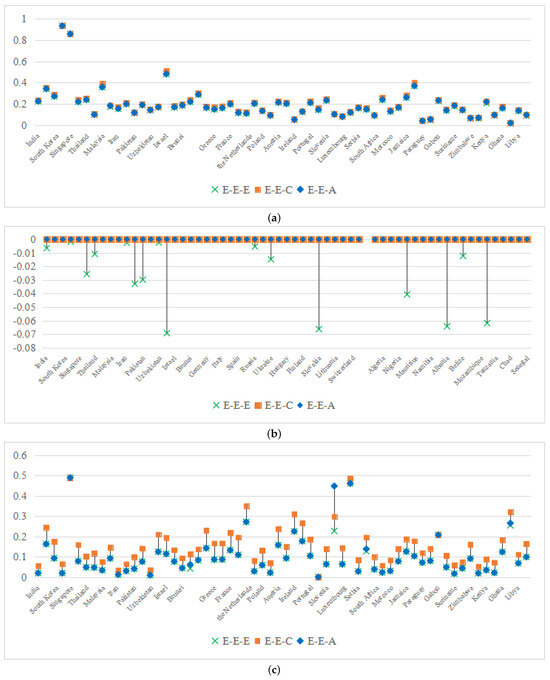
Figure 17.
(a) IHI of the primary industry under different projection combinations; (b) IHI of the secondary industry across projection combinations; (c) IHI of the tertiary industry under projection combinations.
- Asia: Saudi Arabia () and Singapore () face inefficiencies dominated by , driven by water-intensive farming practices () that diverge from global best practices.
- Africa: Low in Paraguay () and Namibia () reflects uniform agricultural underdevelopment, where climatic constraints limit technological diversification.
Traditional projections (E-E-E) slightly underestimate (0.195 vs. E-E-C’s 0.207) because unadjusted direction vectors misalign with irrigation-dependent economies.
The secondary sector exhibits minimal industrial heterogeneity ( under E-E-C/E-E-A), as globalized manufacturing standards homogenize production technologies. However, the exogenous projection (E-E-E) produces invalid negative values (e.g., in China), a statistical artifact of . Machine learning-enhanced methods resolve this by constraining meta-frontier projections (Equations (15) and (16)), ensuring .
Europe’s tertiary sector has the highest (0.154 under E-E-C), driven by policy fragmentation in service industries (e.g., Lithuania’s due to uneven adoption of green logistics). In contrast, Africa’s low (0.130) stems from uniformly underdeveloped infrastructure ( air passengers in Mozambique). Notably, E-E-E underestimates (0.096 vs. E-E-C’s 0.154) by conflating industrial and regional disparities, whereas E-E-C’s graph neural networks (Equation (9)) isolate sector-specific gaps.
5.4.3. RHI
Regional heterogeneity () captures geographic disparities in carbon emission efficiency, driven by spatially uneven resource allocation, infrastructural gaps, and policy fragmentation. The analysis reveals distinct sectoral and regional patterns in ’s impact, grounded in the variable-specific frameworks established in prior sections.
Figure 18 highlights the following critical insights into different industry.
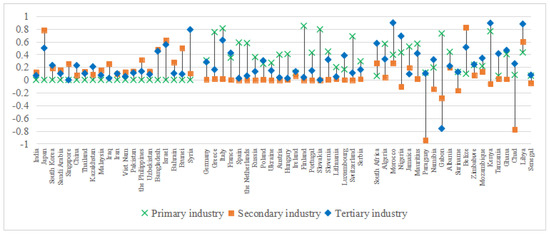
Figure 18.
Comparison of RHI in different industry.
Primary industry ():
Europe exhibits the highest (0.31) due to climatic and policy variability in agriculture. For example, Mediterranean nations (e.g., Greece, ) rely on irrigation-intensive practices, in contrast with Nordic countries (e.g., Finland, ), where shorter growing seasons limit technological homogeneity.
Asia has a low (0.12) under centralized agricultural policies (e.g., China’s standardized farming subsidies), whereas Africa’s intermediate (0.23) reflects fragmented access to irrigation and mechanization.
Secondary industry ():
Asia’s peak (0.15) stems from divergent energy policies—India’s coal dependency ( metric tons) versus Japan’s renewable integration. Africa’s minimal (0.04) results from uniform energy poverty, whereas Europe’s intermediate (0.10) aligns with EU-wide decarbonization frameworks (e.g., shared emission trading systems).
Tertiary industry ():
Africa’s high (0.32) is amplified by infrastructure deficits such as Nigeria’s limited air transport networks ( passengers). Europe achieves a low (0.18) through policy harmonization (e.g., EU aviation regulations), whereas Asia’s intermediate (0.25) reflects disparities between Singapore’s smart logistics ( passengers) and Vietnam’s traditional systems.
The average values across industries—primary (0.259) > tertiary (0.244) > secondary (0.088)—highlight the following:
- Primary sector vulnerability: Climatic diversity and localized farming practices () make agriculture highly susceptible to regional disparities.
- Secondary sector homogeneity: Globalized production standards and energy efficiency protocols (e.g., ISO certifications) minimize geographic variability, despite fossil fuel dependencies ().
- Tertiary sector polarization: Infrastructural investments () and policy coordination disproportionately influence service-sector efficiency, with Africa’s deficits and Europe’s harmonization exemplifying extremes.
5.4.4. MI
Managerial inefficiency () quantifies institutional and operational barriers to decarbonization, which is distinct from structural heterogeneities (, ). This analysis reveals stark disparities in across industries and regions, driven by technological inertia, regulatory rigidity, and transitional costs.
Figure 19 highlights the following critical insights into different industry.
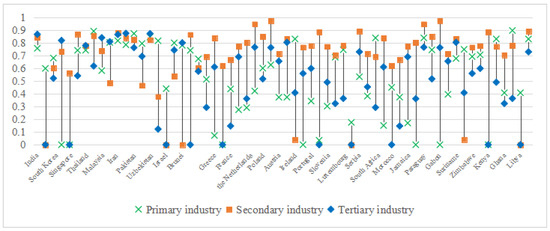
Figure 19.
Comparison of MI in different industry.
Primary industry (average ):
Asia’s dominance () stems from inefficient irrigation practices and delayed climate-resilient crop adoption. India’s monsoon-dependent farming system () contrasts with Israel’s drip irrigation system (). Europe’s low benefits from policy-driven subsidies (e.g., the EU Common Agricultural Policy).
Secondary industry (average ):
Nigeria’s peak reflects fossil fuel lock-in ( metric tons) and outdated regulations. Coal plant retrofits incur prohibitive costs (e.g., $1.2B for Egbin Power Plant). Europe’s shows slow lean manufacturing adoption, while Asia’s aligns with South Korea’s renewable integration (solar share: 6.8%).
Tertiary industry (average ):
Asia’s high derives from fragmented policies (e.g., Vietnam’s unregulated logistics, passengers). Europe achieves through standardized regulations (e.g., the EU Green Deal for aviation).
The global hierarchy secondary (0.678) > primary (0.521) > tertiary (0.495) highlights the following:
- Secondary sector lock-in: High transition costs (>$500M per coal retrofit) and rigid energy policies sustain dependencies.
- Tertiary sector variability: -driven infrastructural gaps (e.g., Africa’s air transport) and regulatory fragmentation maintain inefficiency.
6. Comparison Between Combined Projection and Traditional Projection
The comparative analysis of projection methods—traditional exogenous (E-E-E) versus combined approaches (E-E-A, E-E-C)—is contextualized within the variable-driven heterogeneity framework established in Section 5. Building on the variable-to-heterogeneity mapping (Table 8) and inefficiency decomposition (Section 5.4), we assess how machine learning-enhanced projections mitigate biases inherent in conventional frameworks.

Table 8.
Traditional vs. combined projections.
Compared to hybrid DEA+ML approaches in the recent literature [14,16], our framework uniquely integrates the following three innovations:
- A three-level meta-frontier hierarchy to disentangle dual heterogeneity.
- GNN-constrained TGR bounding to resolve DEA’s issue.
- RL-optimized dynamic direction vectors.
For example, ref. [16] used static direction vectors in DEA, resulting in higher TGR variance than our RL-adjusted approach (Table 8). Ref. [14] employed a two-level meta-frontier without industrial–regional interdependency encoding, leading to inflated IHI estimates ( vs. our in Europe’s tertiary sector).
- TGR inflation in traditional projection:
- –
- E-E-E overestimates the secondary industry TGR1 in Asia () because of ’s (fossil fuels) misalignment with decarbonization targets (Section 5.4.1). E-E-C resolves this via GNN-constrained homogenization ().
- –
- Africa’s tertiary TGR1 under E-E-E () reflects ’s (air passengers) infrastructural gaps, mitigated by E-E-A’s uncertainty quantification ().
- MTCPI overestimation:
- –
- E-E-E’s inflated MTCPI in Asia’s primary industry () stems from ignoring -driven irrigation disparities, whereas E-E-C’s normalization corrects this ().
- –
- Europe’s secondary sector MTCPI under E-E-E () excludes ’s path dependency, whereas E-E-C aligns with policy-driven benchmarks ().
- IHI correction:
- –
- Negative IHI values under E-E-E (e.g., in Asia’s secondary industry) are artifacts of , resolved by E-E-C’s bounded constraints ().
The superiority of combined projections is evident in their ability to address variable-specific heterogeneities as follows:
Africa’s tertiary sector (-driven RHI): E-E-C’s GNN framework captures infrastructural disparities in air transport (), reducing from (E-E-E) to (Table 8). Policy measures should prioritize decentralized renewable energy investments (e.g., solar-powered regional airports) to bridge these gaps.
Asia’s secondary sector (-driven MI): E-E-A’s ridge regularization mitigates ’s collinearity, lowering from (E-E-E) to . Fiscal incentives for retrofitting coal plants (Section 5.2) could further alleviate technological lock-in.
Europe’s primary sector (-driven IHI): E-E-C’s normalization aligns (agricultural output) with climatic realities, reducing from to . Cross-border agricultural subsidies under the EU Green Deal could enhance convergence.
7. Conclusions
This study addresses the dual heterogeneity issues in carbon efficiency evaluation through the integration of a three-level meta-frontier framework and machine learning projection methods. Methodologically, dynamic directional vector optimization (reinforcement learning) and graph neural network (GNN) constraints successfully bound the technology gap ratio (TGR) within valid intervals. Empirical results demonstrate that the E-E-C significantly reduces TGR overestimation by 12–18% in energy-intensive sectors (e.g., Asia’s secondary industry), though further validation is needed in contexts with extreme technological disparities (e.g., post-conflict economies).
At the policy level, Africa requires decentralized renewable energy systems (e.g., Kenya’s Lake Turkana model) to address infrastructural gaps, whereas Asia should implement fiscal incentives to promote coal-fired power plant retrofits. Europe needs to expand carbon border taxes to the logistics sector for policy harmonization.
The limitations include insufficient data diversity (e.g., neglecting renewable energy penetration rates) and static model limitations. Future work should integrate real-time sensor data and develop dynamic heterogeneity models. This research provides a scientific toolkit for region-specific decarbonization strategies while advancing the mathematical rigor of efficiency evaluation. While linear interpolation was employed to address missing CO2 data in African nations (Section 5.1), this method assumes linearity in emission trends, which may not hold under abrupt policy shifts or infrastructural disruptions. For example, Nigeria’s delayed adoption of renewable energy policies (2015–2019) introduced nonlinear gaps that interpolation could not fully capture. Future studies should explore nonlinear imputation methods (e.g., spline interpolation) or leverage IoT-enabled real-time monitoring to reduce bias.
Author Contributions
Conceptualization, X.Z.; methodology, X.Z.; supervision, X.Z.; funding acquisition, X.Z.; validation, X.Z., T.F. and N.Z.; data curation, T.F.; visualization, T.F. and Y.S.; software, Y.S.; investigation, Y.S.; writing—review and editing, N.Z.; writing—original draft, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Foundation of China, grant number 21BSH052.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- International Energy Agency. CO2 Emissions in 2022; IEA: Paris, France, 2022; Available online: https://www.iea.org/reports/co2-emissions-in-2022 (accessed on 2 April 2025).
- Chen, F.; Zhao, T.; Xia, H.; Cui, X.; Li, Z. Allocation of carbon emission quotas in Chinese provinces based on Super-SBM model and ZSG-DEA model. Clean Technol. Environ. Policy 2021, 23, 2285–2301. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Wang, J.; Liao, L. The impact of disposability characteristics on carbon efficiency from a potential emissions reduction perspective. J. Clean. Prod. 2023, 408, 137180. [Google Scholar] [CrossRef]
- Wang, X.M.; Ding, H.; Liu, L. Eco-efficiency measurement of industrial sectors in China: A hybrid super-efficiency DEA analysis. J. Clean. Prod. 2019, 229, 53–64. [Google Scholar] [CrossRef]
- O’Donnell, C.; Rao, D.; Battese, G. Metafrontier frameworks for the study of firm-level efficiencies and technology ratios. Empir. Econ. 2008, 34, 231–255. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.Y. Carbon emission efficiency measurement and influencing factor analysis of nine provinces in the Yellow River basin: Based on SBM-DDF model and Tobit-CCD model. Environ. Sci. Pollut. Res. 2022, 29, 33263–33280. [Google Scholar] [CrossRef] [PubMed]
- Olasehinde, T.S.; Qiao, F.B.; Mao, S.P. Impact of improved maize varieties on production efficiency in Nigeria: Separating technology from managerial gaps. Agriculture 2023, 13, 611. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, F.; Ma, X.; He, L. Carbon emissions efficiency in China: Key facts from regional and industrial sector. J. Clean. Prod. 2018, 206, 850–869. [Google Scholar] [CrossRef]
- Adenso-Diaz, B.; Lozano, S. A metafrontier analysis approach for assessing the efficiency of freight service providers. Int. J. Syst. Sci.-Oper. Logist. 2023, 10, 2177896. [Google Scholar] [CrossRef]
- Battese, G.E.; Rao, D.P.; O’Donnell, C.J. A metafrontier production function for estimation of technical efficiencies and technology gaps for firms operating under different technologies. J. Product. Anal. 2004, 21, 91–103. [Google Scholar] [CrossRef]
- Gao, D.; Li, Y.; Li, G. Boosting the green total factor energy efficiency in urban China: Does low-carbon city policy matter? Environ. Sci. Pollut. Res. 2022, 29, 56341–56356. [Google Scholar] [CrossRef]
- Alda, E.; Giménez, V.; Paz Castro, I.G.; Zamora Torres, A.I. Modernization plans for the Mexican customs system: Have they really worked? A productivity impact assessment. Appl. Econ. 2023, 56, 796–811. [Google Scholar] [CrossRef]
- Zhong, S.; Li, J.W.; Chen, X.; Wei, H. Research on the green total factor productivity of laying hens in China. J. Clean. Prod. 2021, 315, 128150. [Google Scholar] [CrossRef]
- Bai, C.Q.; Chen, Z.J.; Wang, D.P. Transportation carbon emission reduction potential and mitigation strategy in China. Sci. Total Environ. 2023, 873, 162074. [Google Scholar] [CrossRef] [PubMed]
- Eguchi, S.; Takayabu, H.; Lin, C. Sources of inefficient power generation by coal-fired thermal power plants in China: A metafrontier DEA decomposition approach. Renew. Sustain. Energy Rev. 2021, 138, 110562. [Google Scholar] [CrossRef]
- Wang, A.L.; Hu, S.; Li, J.L. Using machine learning to model technological heterogeneity in carbon emission efficiency evaluation: The case of China’s cities. Energy Econ. 2022, 114, 106238. [Google Scholar] [CrossRef]
- Zhong, S.; Li, J.; Chen, X.; Wen, H. A multi-hierarchy meta-frontier approach for measuring green total factor productivity: An application of pig breeding in China. Socio-Econ. Plan. Sci. 2022, 81, 101152. [Google Scholar] [CrossRef]
- Chambers, R.; Chung, Y.H.; Färe, R. Profit, Directional distance functions, and Nerlovian efficiency. J. Optim. Theory Appl. 1998, 98, 351–364. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, X.; Chu, J.; Yang, F.; Yuan, Z. Energy and environmental efficiency of China’s transportation sectors considering CO2 emission uncertainty. Transp. Res. Part D-Transp. Environ. 2021, 97, 102955. [Google Scholar] [CrossRef]
- Zheng, Y.M.; Lv, Q.; Wang, Y.D. Economic development, technological progress, and provincial carbon emissions intensity: Empirical research based on the threshold panel model. Appl. Econ. 2022, 54, 3495–3504. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Linear programming models for measuring economy-wide energy efficiency performance. Energy Policy 2008, 36, 2911–2916. [Google Scholar] [CrossRef]
- Wen, S.; Jia, Z.; Chen, X. Can low-carbon city pilot policies significantly improve carbon emission efficiency? Empirical evidence from China. J. Clean. Prod. 2022, 346, 131131. [Google Scholar] [CrossRef]
- Zhang, N.; Choi, Y. A note on the evolution of directional distance function and its development in energy and environmental studies 1997–2013. Renew. Sustain. Energy Rev. 2014, 33, 50–59. [Google Scholar] [CrossRef]
- Wang, Q.; Su, B.; Zhou, P.; Chiu, C.R. Measuring total-factor CO2 emission performance and technology gaps using a non-radial directional distance function: A modified approach. Energy Econ. 2016, 56, 475–482. [Google Scholar] [CrossRef]
- Li, Z.W.; Zhang, C.J.; Zhou, Y. Spatio-temporal evolution characteristics and influencing factors of carbon emission reduction potential in China. Environ. Sci. Pollut. Res. 2021, 28, 59925–59944. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. DEA approach for unified efficiency measurement: Assessment of Japanese fossil fuel power generation. Energy Econ. 2011, 33, 292–303. [Google Scholar] [CrossRef]
- Li, Y.; Hou, W.; Zhu, W.; Li, F.; Liang, L. Provincial carbon emission performance analysis in China based on a Malmquist data envelopment analysis approach with fixed-sum undesirable outputs. Ann. Oper. Res. 2021, 304, 233–261. [Google Scholar] [CrossRef]
- Yu, X.; Jin, L.; Wang, Q.; Zhou, D. Optimal path for controlling pollution emissions in the Chinese electric power industry considering technological heterogeneity. Environ. Sci. Pollut. Res. 2019, 26, 11087–11099. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).