Expressions for the First Two Moments of the Range of Normal Random Variables with Applications to the Range Control Chart †
Abstract
1. Introduction
2. The Distribution and First Two Moments of the Range
2.1. Approximations to d2 and d3 for Samples Sizes of at Least 6
Approximation Method
3. Results
3.1. Analytical Results for n = 2, 3, 4 and 5
3.2. Approximation Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Derivation of the Expected Value of the Range for n = 4 and 5
Appendix A.1.1. n = 4 Case
Appendix A.1.2. n = 5 Case
Appendix A.2. Derivation of the Variance of the Range for n = 4 and 5
Appendix B. Complete Tables for the Rational Function Approximations
| a. m + k = 9. | ||||||||
| (m, k) | (7, 2) | |||||||
| Maximum Error | 4.37 × 10−6 | |||||||
| a0 | −4.68 × 10−5 | |||||||
| a1 | 4.1601706 | |||||||
| a2 | −1.072159 | |||||||
| a3 | 0.2862847 | |||||||
| a4 | −0.0791025 | |||||||
| a5 | 0.0128782 | |||||||
| a6 | −0.0011768 | |||||||
| a7 | 4.36 × 10−5 | |||||||
| b1 | 0.1108409 | |||||||
| b2 | −0.036305 | |||||||
| b. m + k = 8. | ||||||||
| (m, k) | (2, 6) | (8, 0) | (6, 2) | (5, 3) | (4, 4) | (7, 1) | (3, 5) | (1, 7) |
| Maximum Error | 4.39 × 10−6 | 4.40 × 10−6 | 4.45 × 10−6 | 4.50 × 10−6 | 4.82 × 10−6 | 5.69 × 10−6 | 6.68 × 10−6 | 1.23 × 10−5 |
| a0 | 0.0002117 | 0.0001602 | −0.0003999 | 0.0003858 | 0.0005454 | 0.0003989 | 0.0017505 | −0.0022132 |
| a1 | 4.157714 | 4.1582259 | 4.1627898 | 4.1561616 | 4.1545675 | 4.1561546 | 4.1424508 | 4.1789954 |
| a2 | 0.3491476 | −1.5259333 | −0.950065 | 1.4537905 | 0.7921954 | −1.5117788 | 4.4979643 | |
| a3 | 0.5924688 | 0.2092784 | 0.2428315 | −0.2792372 | 0.5775411 | −1.3731118 | ||
| a4 | −0.1840047 | −0.0564231 | −0.0142767 | −0.1098239 | −0.1706958 | |||
| a5 | 0.0429772 | 0.0076955 | 0.0007023 | 0.0354162 | ||||
| a6 | −0.0070858 | −0.000464 | −0.0045255 | |||||
| a7 | 0.0007349 | 0.0002648 | ||||||
| a8 | −3.60 × 10−5 | |||||||
| b1 | 0.4502653 | 0.1420291 | 0.71454 | 0.5539226 | 0.0017124 | 1.4332245 | 0.3843422 | |
| b2 | 0.0245085 | −0.0462027 | 0.1823815 | 0.0012477 | 0.0864897 | −0.0338921 | ||
| b3 | −0.0137816 | 0.0005872 | −0.0705542 | −0.1716855 | 0.0137563 | |||
| b4 | 0.004125 | −0.0034663 | 0.0147776 | −0.0105444 | ||||
| b5 | −0.0006383 | −0.0008095 | 0.0043436 | |||||
| b6 | 4.18 × 10−5 | −0.0008831 | ||||||
| b7 | 7.16 × 10−5 | |||||||
| c. m + k = 7. | ||||||||
| (m, k) | (5, 2) | (7, 0) | (3, 4) | (2, 5) | (1, 6) | (6, 1) | (4, 3) | |
| Maximum Error | 4.52 × 10−6 | 5.76 × 10−6 | 1.20 × 10−5 | 1.83 × 10−5 | 2.47 × 10−5 | 3.36 × 10−5 | 8.85 × 10−5 | |
| a0 | 0.0003945 | 0.0004069 | −0.0013429 | 0.0674587 | −0.0023136 | 0.0019498 | −0.0049402 | |
| a1 | 4.1560808 | 4.1560877 | 4.1706731 | 3.5533193 | 4.1779037 | 4.144603 | 4.1994308 | |
| a2 | 1.4690251 | −1.5186854 | −0.6775001 | 133.74141 | −1.4869875 | −3.479488 | ||
| a3 | 0.2391045 | 0.5798019 | 0.3559161 | 0.5353291 | 0.697147 | |||
| a4 | −0.0147213 | −0.1713809 | −0.137747 | 0.0833977 | ||||
| a5 | 0.0007021 | 0.0355484 | 0.0215142 | |||||
| a6 | −0.0045384 | −0.0015042 | ||||||
| a7 | 0.0002651 | |||||||
| b1 | 0.7181305 | 0.2137831 | 32.001851 | 0.3814535 | −0.0001152 | −0.4379041 | ||
| b2 | 0.1829496 | 0.0046636 | 12.604867 | −0.0254915 | −0.1903784 | |||
| b3 | 0.0331532 | −1.0269053 | 0.0018241 | 0.1142485 | ||||
| b4 | −0.0013196 | 0.0535564 | −0.0014589 | |||||
| b5 | 0.0010865 | 0.0005456 | ||||||
| b6 | −6.26 × 10−5 | |||||||
| d. m + k = 6. | ||||||||
| (m, k) | (2, 4) | (6, 0) | (1, 5) | (3, 3) | (4, 2) | (5, 1) | ||
| Maximum Error | 2.18 × 10−5 | 4.01 × 10−5 | 4.13 × 10−5 | 5.93 × 10−5 | 7.91 × 10−5 | 8.66 × 10−5 | ||
| a0 | 0.0740863 | 0.0021644 | −0.0024841 | 0.1112902 | −0.0039991 | −0.004793 | ||
| a1 | 3.5003552 | 4.1431818 | 4.1779643 | 3.2300901 | 4.1888288 | 4.1941431 | ||
| a2 | 133.77185 | −1.4831307 | 112.82908 | −0.5261395 | 0.4951024 | |||
| a3 | 0.5314118 | 13.842787 | −0.0412288 | −0.0515586 | ||||
| a4 | −0.1356001 | −0.0023828 | 0.0141002 | |||||
| a5 | 0.0209355 | −0.0016136 | ||||||
| a6 | −0.0014438 | |||||||
| b1 | 31.970664 | 0.3803881 | 26.769961 | 0.2610645 | 0.5094877 | |||
| b2 | 12.65184 | −0.0223003 | 14.24345 | −0.0863658 | ||||
| b3 | −1.0557861 | −0.0019663 | 0.2333121 | |||||
| b4 | 0.0625968 | 0.0007101 | ||||||
| b5 | −4.89 × 10−5 | |||||||
| e. m + k = 5. | ||||||||
| (m, k) | (1, 4) | (2, 3) | (3, 2) | (4, 1) | (5, 0) | |||
| Maximum Error | 7.04 × 10−5 | 1.93 × 10−4 | 1.98 × 10−4 | 2.34 × 10−4 | 2.81 × 10−4 | |||
| a0 | −0.0021528 | −0.0068195 | −0.0069689 | −0.0079574 | 0.0087059 | |||
| a1 | 4.1778096 | 4.2048559 | 4.2056463 | 4.2118095 | 4.1014476 | |||
| a2 | 0.3389855 | 0.4231483 | 0.4123636 | −1.3881892 | ||||
| a3 | 0.0040529 | −0.0093844 | 0.4305764 | |||||
| a4 | 0.0008702 | −0.0815235 | ||||||
| a5 | 0.0067557 | |||||||
| b1 | 0.3812861 | 0.4760923 | 0.496602 | 0.4973312 | ||||
| b2 | −0.0240701 | −0.0019042 | 0.0066181 | |||||
| b3 | −0.0006661 | 0.0001546 | ||||||
| b4 | 0.0002934 | |||||||
| f. m + k = 4. | ||||||||
| (m, k) | (1, 3) | (2, 2) | (3, 1) | (4, 0) | ||||
| Maximum Error | 1.61 × 10−4 | 2.53 × 10−4 | 5.07 × 10−4 | 2.61 × 10−3 | ||||
| a0 | −0.0058338 | −0.0046286 | −0.0123297 | 0.0390467 | ||||
| a1 | 4.1990741 | 4.1962377 | 4.2343323 | 3.9449081 | ||||
| a2 | 0.3417114 | 0.4466871 | −1.1263646 | |||||
| a3 | −0.0082 | 0.2442248 | ||||||
| a4 | −0.0227788 | |||||||
| b1 | 0.3919365 | 0.4738405 | 0.5145802 | |||||
| b2 | −0.0310113 | −0.0006776 | ||||||
| b3 | 0.0016884 | |||||||
| g. m + k = 3 and m + k = 2. | ||||||||
| m + k | 3 | 3 | 3 | 2 | 2 | |||
| (m, k) | (2, 1) | (1, 2) | (3, 0) | (1, 1) | (2, 0) | |||
| Maximum Error | 5.61 × 10−4 | 2.35 × 10−3 | 1.09 × 10−2 | 2.19 × 10−2 | 5.80 × 10−2 | |||
| a0 | −0.0023213 | 0.0172151 | 0.1008629 | 0.1295186 | 0.2907984 | |||
| a1 | 4.1871142 | 4.0937756 | 3.6822471 | 3.6681333 | 3.0786409 | |||
| a2 | 0.3449063 | −0.8018105 | −0.3446446 | |||||
| a3 | 0.0949052 | |||||||
| b1 | 0.4720972 | 0.3546785 | 0.2410842 | |||||
| b2 | −0.0184772 | |||||||
| a. m + k = 10. | ||||||||
| (m, k) | (9, 1) | |||||||
| Maximum Error | 1.04 × 10−6 | |||||||
| a0 | 0.315104 | |||||||
| a1 | 5.547612 | |||||||
| a2 | −2.84442 | |||||||
| a3 | −0.78335 | |||||||
| a4 | 2.852878 | |||||||
| a5 | −2.51086 | |||||||
| a6 | 1.234777 | |||||||
| a7 | −0.36344 | |||||||
| a8 | 0.059829 | |||||||
| a9 | −0.00424 | |||||||
| b1 | 3.396075 | |||||||
| b. m + k = 9. | ||||||||
| (m, k) | (2, 7) | (7, 2) | (8, 1) | (6, 3) | (9, 0) | (4, 5) | (3, 6) | (5, 4) |
| Maximum Error | 1.49 × 10−5 | 1.67 × 10−5 | 1.83 × 10−5 | 2.13 × 10−5 | 2.85 × 10−5 | 3.40 × 10−5 | 3.46 × 10−5 | 3.48 × 10−5 |
| a0 | 0.222874 | 0.296684 | 0.288269 | 0.282365 | 0.425844 | −0.84597 | 0.415148 | 0.416896 |
| a1 | 7.435075 | 5.72538 | 5.824849 | 5.81292 | 2.891117 | 156.1599 | 4.140362 | 3.804773 |
| a2 | −1.74755 | −2.7717 | −3.84618 | −5.82438 | −7.15265 | 1102.012 | 2.558952 | −0.02747 |
| a3 | 0.802064 | 1.369529 | 3.523224 | 9.656155 | −308.826 | −1.32839 | −0.29831 | |
| a4 | 0.200033 | 0.068175 | −1.19533 | −8.5306 | −24.3344 | −0.03858 | ||
| a5 | −0.2218 | −0.26892 | 0.230026 | 5.088273 | −0.00149 | |||
| a6 | 0.063196 | 0.104807 | −0.01879 | −2.024 | ||||
| a7 | −0.00636 | −0.0174 | 0.512864 | |||||
| a8 | 0.00106 | −0.07467 | ||||||
| a9 | 0.004743 | |||||||
| b1 | 5.437382 | 3.460118 | 3.421473 | 3.145292 | 330.4889 | 2.79654 | 2.043444 | |
| b2 | 0.138415 | 0.668103 | −0.99902 | 514.4913 | 3.534685 | 2.385689 | ||
| b3 | 2.584673 | 0.379228 | 605.6943 | 0.912601 | −0.35895 | |||
| b4 | −2.56493 | −303.519 | −1.08252 | −0.23241 | ||||
| b5 | 1.00801 | 11.36619 | 0.102501 | |||||
| b6 | −0.20567 | −0.0042 | ||||||
| b7 | 0.017412 | |||||||
| c. m + k = 8. | ||||||||
| (m, k) | (1, 7) | (6, 2) | (4, 4) | (3, 5) | (5, 3) | (7, 1) | (2, 6) | (8, 0) |
| Maximum Error | 2.63 × 10−5 | 3.29 × 10−5 | 3.49 × 10−5 | 3.65 × 10−5 | 4.85 × 10−5 | 5.25 × 10−5 | 6.56 × 10−5 | 1.06 × 10−4 |
| a0 | −0.22202 | 0.361297 | 0.417448 | 0.419877 | 0.437844 | 0.19618 | 0.464882 | 0.457687 |
| a1 | 16.809 | 4.604874 | 3.713019 | 3.598293 | 3.391173 | 7.40356 | 2.936455 | 2.580339 |
| a2 | −3.34365 | −0.73609 | −1.34281 | −0.28428 | −3.57152 | 0.112444 | −5.92177 | |
| a3 | 2.01313 | −0.12318 | 0.036971 | −0.2868 | 0.096022 | 7.037428 | ||
| a4 | −0.72414 | −0.0197 | 0.043483 | 1.070521 | −5.20663 | |||
| a5 | 0.145333 | −0.00508 | −0.62695 | 2.458343 | ||||
| a6 | −0.01238 | 0.153482 | −0.71801 | |||||
| a7 | −0.01431 | 0.117911 | ||||||
| a8 | −0.00831 | |||||||
| b1 | 15.37598 | 2.36091 | 1.839365 | 1.629358 | 1.60254 | 4.905237 | 1.221915 | |
| b2 | −2.99882 | 0.458887 | 2.04778 | 1.768778 | 2.332491 | 2.699692 | ||
| b3 | 14.3693 | −0.74976 | −1.10774 | −0.79915 | −0.76911 | |||
| b4 | −10.1252 | −0.05782 | 0.117442 | 0.336715 | ||||
| b5 | 3.946838 | −0.00475 | −0.09027 | |||||
| b6 | −0.83038 | 0.009819 | ||||||
| b7 | 0.072844 | |||||||
| d. m + k = 7. | ||||||||
| (m, k) | (4, 3) | (1, 6) | (5, 2) | (6, 1) | (2, 5) | (3, 4) | (7, 0) | |
| Maximum Error | 3.90 × 10−5 | 6.68 × 10−5 | 7.97 × 10−5 | 8.37 × 10−5 | 8.73 × 10−5 | 9.96 × 10−5 | 4.00 × 10−4 | |
| a0 | 0.414579 | 0.448364 | 0.514699 | 0.267489 | 0.354628 | 0.347222 | 0.506673 | |
| a1 | 3.718122 | 3.171776 | 2.357509 | 5.998534 | 4.667852 | 4.701032 | 2.154437 | |
| a2 | −0.92875 | 3.387868 | −4.38089 | −0.57936 | −1.3774 | −4.46778 | ||
| a3 | −0.07681 | −1.25034 | 2.220661 | 0.284086 | 4.464941 | |||
| a4 | −0.00913 | 0.32038 | −0.68974 | −2.59734 | ||||
| a5 | −0.033 | 0.120869 | 0.887721 | |||||
| a6 | −0.00918 | −0.1648 | ||||||
| a7 | 0.012798 | |||||||
| b1 | 1.802498 | 1.407458 | 1.17619 | 3.425601 | 2.675402 | 2.570444 | ||
| b2 | 1.976001 | 2.652334 | 4.470245 | 2.285831 | 1.913318 | |||
| b3 | −0.86642 | −0.74001 | −0.33457 | −0.66506 | ||||
| b4 | 0.292182 | −0.06511 | 0.143048 | |||||
| b5 | −0.07846 | 0.012773 | ||||||
| b6 | 0.008683 | |||||||
| e. m + k = 6. | ||||||||
| (m, k) | (4, 2) | (1, 5) | (2, 4) | (3, 3) | (5, 1) | (6, 0) | ||
| Maximum Error | 1.10 × 10−4 | 1.28 × 10−4 | 1.36 × 10−4 | 1.91 × 10−4 | 2.26 × 10−4 | 1.34 × 10−3 | ||
| a0 | 0.342748 | 0.427834 | 0.444321 | 0.475274 | 0.217224 | 0.569274 | ||
| a1 | 4.964747 | 3.719638 | 3.378007 | 2.995876 | 6.915992 | 1.677416 | ||
| a2 | −0.67509 | −0.51529 | 0.213881 | −4.33346 | −3.09547 | |||
| a3 | 0.305956 | −0.05469 | 1.749774 | 2.508293 | ||||
| a4 | −0.03384 | −0.37293 | −1.08081 | |||||
| a5 | 0.032428 | 0.239276 | ||||||
| a6 | −0.02135 | |||||||
| b1 | 2.973567 | 2.011761 | 1.613263 | 1.41501 | 4.279257 | |||
| b2 | 2.179108 | 2.353528 | 2.087442 | 2.394381 | ||||
| b3 | −0.12915 | −0.59247 | −0.25408 | |||||
| b4 | −0.04059 | 0.040986 | ||||||
| b5 | 0.007675 | |||||||
| f. m + k = 5. | ||||||||
| (m, k) | (2, 3) | (1, 4) | (3, 2) | (4, 1) | (5, 0) | |||
| Maximum Error | 2.03 × 10−4 | 5.27 × 10−4 | 6.82 × 10−4 | 7.5 × 10−4 | 3.88 × 10−4 | |||
| a0 | 0.457381 | 0.523099 | 0.576235 | −0.05848 | 0.650202 | |||
| a1 | 3.232791 | 2.395738 | 1.709512 | 11.17565 | 1.145273 | |||
| a2 | 0.559042 | 0.826375 | −5.5501 | −1.84151 | ||||
| a3 | −0.05561 | 1.594977 | 1.130005 | |||||
| a4 | −0.17954 | −0.31863 | ||||||
| a5 | 0.034104 | |||||||
| b1 | 1.648605 | 0.940191 | 0.51129 | 7.753653 | ||||
| b2 | 2.65881 | 2.042514 | 2.324483 | |||||
| b3 | 0.024817 | −0.35739 | ||||||
| b4 | 0.036746 | |||||||
| g. m + k = 4. | ||||||||
| (m, k) | (2, 2) | (1, 3) | (3, 1) | (4, 0) | ||||
| Maximum Error | 2.13 × 10−4 | 8.98 × 10−4 | 5.25 × 10−3 | 1.08 × 10−2 | ||||
| a0 | 0.452862 | 0.476886 | −1.42047 | 0.762477 | ||||
| a1 | 3.338977 | 3.230196 | 36.39687 | 0.533722 | ||||
| a2 | 0.491674 | −12.4903 | −0.74534 | |||||
| a3 | 1.832343 | 0.295284 | ||||||
| a4 | −0.03852 | |||||||
| b1 | 1.737353 | 1.694324 | 29.41969 | |||||
| b2 | 2.63829 | 2.130666 | ||||||
| b3 | −0.17919 | |||||||
References
- Snee, R.D. Statistical Thinking and Its Contribution to Total Quality. Am. Stat. 1990, 44, 116–121. [Google Scholar] [CrossRef]
- Hoerl, R.W.; Snee, R.D.; De Veaux, R.D. Applying Statistical Thinking to ‘Big Data’ Problems. WIREs Comput. Stat. 2014, 6, 222–232. [Google Scholar] [CrossRef]
- Hoerl, R.W.; Snee, R.D. Statistical Thinking: Improving Business Performance; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Khoo, M.B.; Lim, E.G. An Improved R (Range) Control Chart for Monitoring the Process Variance. Qual. Reliab. Eng. Int. 2005, 21, 43–50. [Google Scholar] [CrossRef]
- Chen, W.H.; Tirupati, D. On-line Quality Management: Integration of Product Inspection and Process Control. Prod. Oper. Manag. 1995, 4, 242–262. [Google Scholar] [CrossRef]
- Wardell, D.G. Algebraic Expressions for Range Control Chart Constants. In Proceedings of the Fiftieth Annual Meeting of the Western Decision Sciences Institute, Waikoloa, HI, USA, 5–8 April 2022. [Google Scholar]
- Burr, I.W. The Effect of Non-normality on Constants for and R charts. Ind. Qual. Control 1967, 23, 563–569. [Google Scholar]
- Qiu, P.; Zhang, J. On Phase II SPC in Cases When Normality is Invalid. Qual. Reliab. Eng. Int. 2015, 31, 27–35. [Google Scholar] [CrossRef]
- Khakifirooz, M.; Tercero-Gómeza, V.G.; Woodall, W.H. The Role of the Normal Distribution in Statistical Process Monitoring. Qual. Eng. 2021, 3, 497–510. [Google Scholar] [CrossRef]
- Mood, A.M.; Graybill, F.A.; Boes, D.C. Introduction to the Theory of Statistics; McGraw Hill: New York, NY, USA, 1974. [Google Scholar]
- David, H.A. Order Statistics; John Wiley & Sons, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Arnold, B.C.; Balakrishnan, N. Relations, Bounds and Approximations for Order Statistic; Lecture Notes in Statistics No. 53; Springer: New York, NY, USA, 1989. [Google Scholar]
- Royston, J.P. Algorithm AS 177: Expected Normal Order Statistics (Exact and Approximate). Appl. Stat. 1982, 31, 161–165. [Google Scholar] [CrossRef]
- Pearson, E.S.; Hartley, H.O. (Eds.) Biometrika Tables for Statisticians; Biometrika Trust: London, UK, 1976; Volume 1. [Google Scholar]
- Harter, H.L.; Balakrishnan, N. Tables for the Use of Range and Studentized Range in Tests of Hypotheses; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Petrushev, P.P.; Popov, V.A. Rational Approximation of Real Functions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ralston, A.; Rabinowitz, P. A First Course in Numerical Analysis; Dover Publications, Inc.: New York, NY, USA, 2001. [Google Scholar]
- McKay, A.T.; Pearson, E.S. A Note on the Distribution of Range in Samples of n. Biometrika 1933, 25, 415–420. [Google Scholar] [CrossRef]
- Bose, R.C.; Gupta, S.S. Moments of Order Statistics from a Normal Population. Biometrika 1959, 46, 433–440. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Cohen, A.C. Order Statistics and Inference: Estimation Methods; Academic Press, Inc.: London, UK, 2014. [Google Scholar]
- Ryan, T.P. Statistical Methods for Quality Improvement; John Wiley and Sons: Weinheim, Germany, 2011. [Google Scholar]
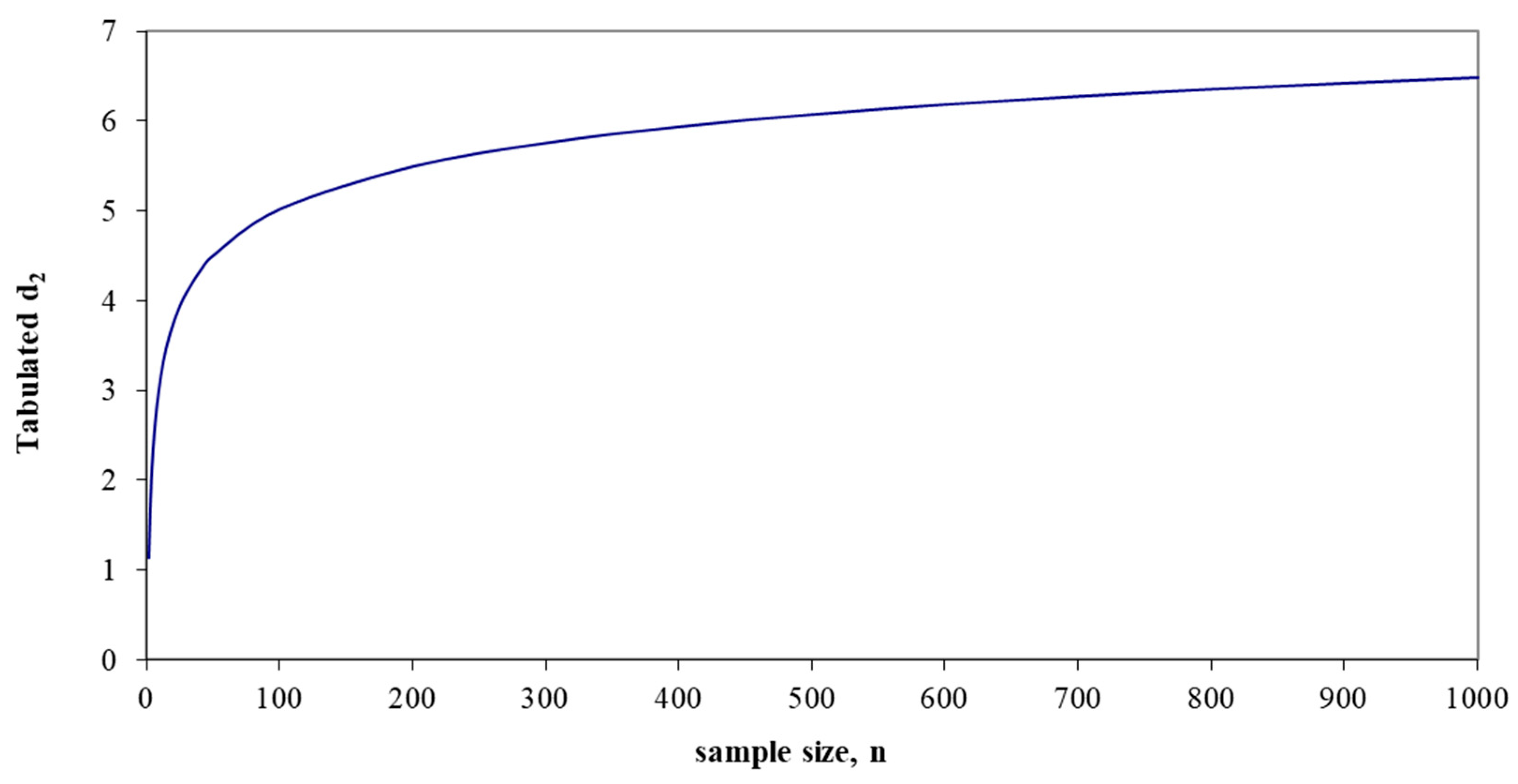
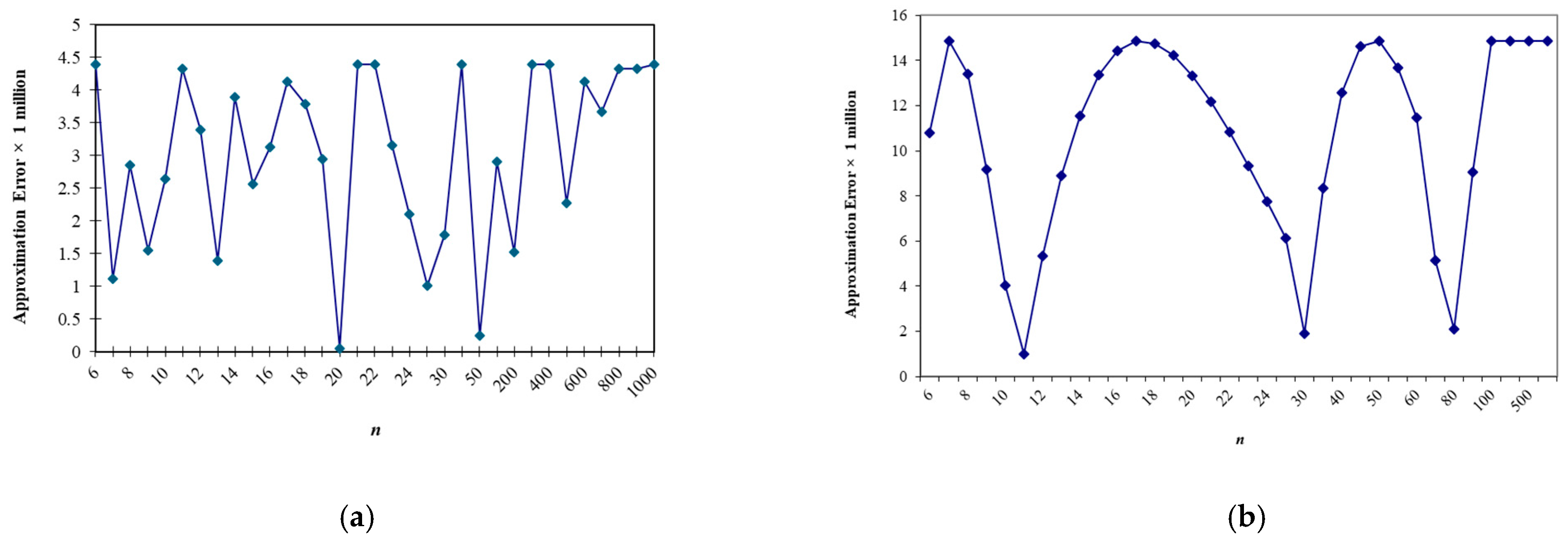
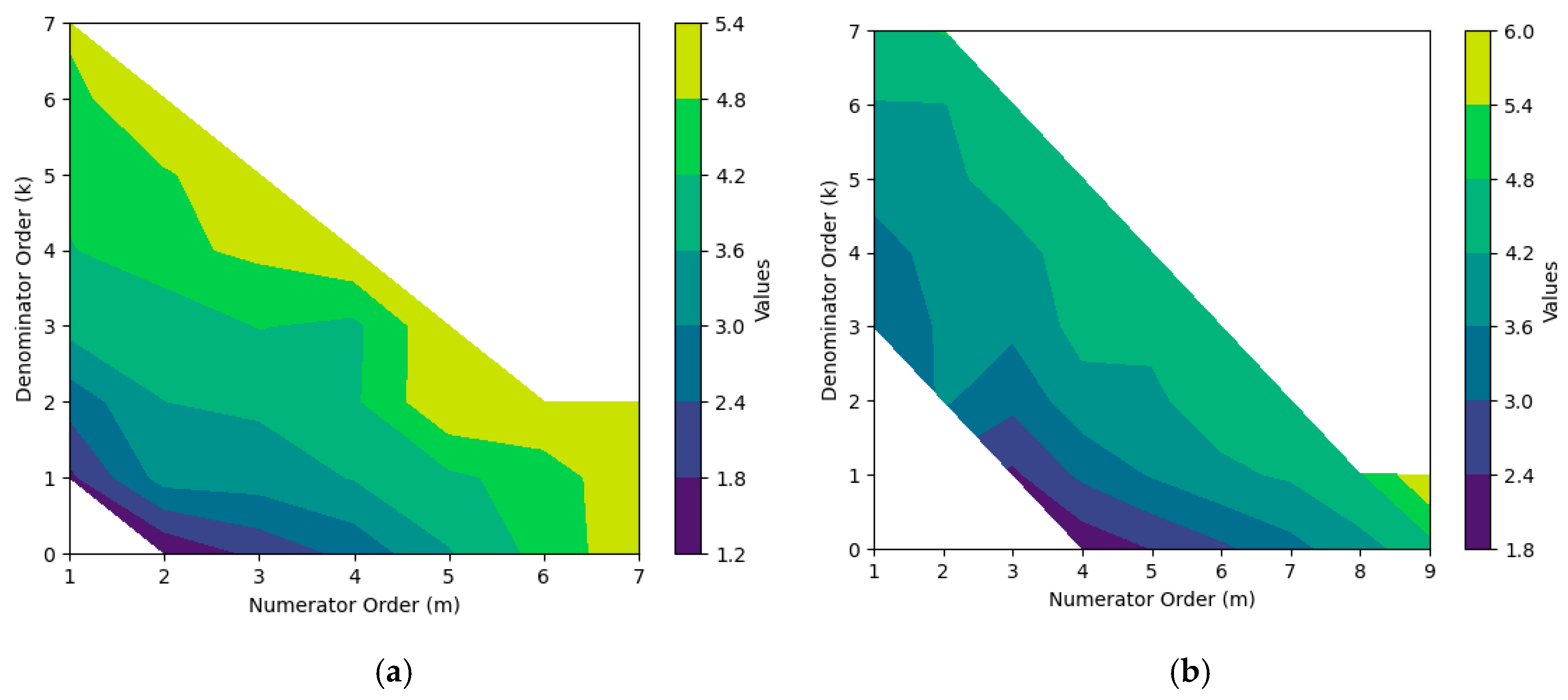
| Sample Size n | d2 | d3 |
|---|---|---|
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
| m + k | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
|---|---|---|---|---|---|---|---|---|
| (m, k) | (7, 2) | (2, 6) | (5, 2) | (2, 4) | (1, 4) | (1, 3) | (2, 1) | (1, 1) |
| Maximum Error | 4.3685 × 10−6 | 4.3907 × 10−6 | 4.5173 × 10−6 | 2.1767 × 10−5 | 7.0438 × 10−5 | 1.6052 × 10−4 | 5.6083 × 10−4 | 2.1880 × 10−2 |
| a0 | −4.6830 × 10−5 | 0.00021168 | 0.00039446 | 0.0740863 | −0.0021528 | −0.0058338 | −0.0023213 | 0.12951861 |
| a1 | 4.16017058 | 4.15771399 | 4.15608081 | 3.50035523 | 4.17780958 | 4.19907408 | 4.18711419 | 3.66813329 |
| a2 | −1.072159 | 0.34914757 | 1.4690251 | 133.771848 | 0.34490634 | |||
| a3 | 0.28628465 | 0.23910449 | ||||||
| a4 | −0.0791025 | −0.0147213 | ||||||
| a5 | 0.01287818 | 0.00070213 | ||||||
| a6 | −0.0011768 | |||||||
| a7 | 4.36 × 10−5 | |||||||
| b1 | 0.11084091 | 0.45026527 | 0.71813046 | 31.970664 | 0.38128612 | 0.3919365 | 0.47209716 | 0.24108419 |
| b2 | −0.036305 | 0.02450851 | 0.18294963 | 12.6518404 | −0.0240701 | −0.0310113 | ||
| b3 | −0.0137816 | −1.0557861 | −0.0006661 | 0.00168837 | ||||
| b4 | 0.00412501 | 0.06259679 | 0.00029336 | |||||
| b5 | −0.0006383 | |||||||
| b6 | 4.1793 × 10−5 |
| m + k | 10 | 9 | 8 | 7 | 6 | 5 | 4 |
|---|---|---|---|---|---|---|---|
| (m, k) | (9, 1) | (2, 7) | (1, 7) | (4, 3) | (4, 2) | (2, 3) | (2, 2) |
| Maximum Error | 1.0426 × 10−6 | 1.4861 × 10−5 | 2.6339 × 10−5 | 3.9049 × 10−5 | 1.1010 × 10−4 | 2.0261 × 10−4 | 2.1340 × 10−4 |
| a0 | 0.315104 | 0.222874 | −0.22202 | 0.414579 | 0.342748 | 0.457381 | 0.452862 |
| a1 | 5.547612 | 7.435075 | 16.809 | 3.718122 | 4.964747 | 3.232791 | 3.338977 |
| a2 | −2.84442 | −1.74755 | −0.92875 | −0.67509 | 0.559042 | 0.491674 | |
| a3 | −0.78335 | −0.07681 | 0.305956 | ||||
| a4 | 2.852878 | −0.00913 | −0.03384 | ||||
| a5 | −2.51086 | ||||||
| a6 | 1.234777 | ||||||
| a7 | −0.36344 | ||||||
| a8 | 0.059829 | ||||||
| a9 | −0.00424 | ||||||
| b1 | 3.396075 | 5.437382 | 15.37598 | 1.802498 | 2.973567 | 1.648605 | 1.737353 |
| b2 | 0.138415 | −2.99882 | 1.976001 | 2.179108 | 2.65881 | 2.63829 | |
| b3 | 2.584673 | 14.3693 | −0.86642 | 0.024817 | |||
| b4 | −2.56493 | −10.1252 | |||||
| b5 | 1.00801 | 3.946838 | |||||
| b6 | −0.20567 | −0.83038 | |||||
| b7 | 0.017412 | 0.072844 |
| a. Expressions for d2 | ||
| Sample Size n | Expression for d2 | Maximum Error |
| 2 | 0 | |
| 3 | 0 | |
| 4 | 0 | |
| 5 | 0 | |
| n = 6 to 1000 | 4.3907 × 10−6 | |
| b. Expressions for d3 | ||
| Sample Size n | Expression for d3 | Maximum Error |
| 2 | 0 | |
| 3 | 0 | |
| 4 | 0 | |
| 5 | 0 | |
| n = 6 to 1000 | 1.4861 × 10−5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wardell, D.G. Expressions for the First Two Moments of the Range of Normal Random Variables with Applications to the Range Control Chart. Mathematics 2025, 13, 1537. https://doi.org/10.3390/math13091537
Wardell DG. Expressions for the First Two Moments of the Range of Normal Random Variables with Applications to the Range Control Chart. Mathematics. 2025; 13(9):1537. https://doi.org/10.3390/math13091537
Chicago/Turabian StyleWardell, Don G. 2025. "Expressions for the First Two Moments of the Range of Normal Random Variables with Applications to the Range Control Chart" Mathematics 13, no. 9: 1537. https://doi.org/10.3390/math13091537
APA StyleWardell, D. G. (2025). Expressions for the First Two Moments of the Range of Normal Random Variables with Applications to the Range Control Chart. Mathematics, 13(9), 1537. https://doi.org/10.3390/math13091537






