Expressions for the First Two Moments of the Range of Normal Random Variables with Applications to the Range Control Chart ^†

Abstract

A common and simple estimate of variability is the sample range, which is the difference between the maximum and minimum values in the sample. While other measures of variability are preferred in most instances, process owners and operators regularly use range (R) control charts to monitor process variability. The center line and limits of the R charts use constants that are based on the first two moments (mean and variance) of the distribution of the range of normal random variables. Historically, the computation of moments requires the use of tabulated constants approximated using numerical integration. We provide exact results for the moments for sample sizes 2 through 5. For sample sizes from 6 to 1000, we used the differential correction method to find Chebyshev minimax rational-function approximations of the moments. The rational function we recommend for the mean (R-chart constant d₂) has a polynomial of order two in the numerator and six in the denominator and achieves a maximum error of 4.4 × 10⁻⁶. The function for the standard deviation (R-chart constant d₃) has a polynomial of order two in the numerator and seven in the denominator and achieves a maximum error of 1.5 × 10⁻⁵. The exact and approximate expressions eliminate the need for table lookup in the control chart design phase.

1. Introduction

Variation is central to both statistical methods and statistical thinking [1,2,3]. There are multiple measures of variation that differ in their ease of computation and usefulness. Perhaps the simplest to compute, but inferior in some of its statistical properties (e.g., consistency), is the sample range. In most applications, statistical performance outweighs computational ease; however, there are important exceptions. One of these applications is the use of control charts to monitor (and ultimately improve) processes.

Control charts are one of the central tools used in Six Sigma and quality management. When the variable of interest is measured (as opposed to counted), the most common control charts are $\overline{X}$ and R charts. The former is used to monitor the central tendency of the process, while the latter monitors process variation. To implement the charts, “rational” samples (often referred to as subgroups) are collected at regular intervals. The sample mean of each subgroup is plotted on the $\overline{X}$ chart, while the range of each is plotted on the R chart. The charts are time-series plots with superimposed limits. Plotted points falling within the limits indicate a stable (“in-control”) process, whereas points falling outside the limits point to a process change. The limits are typically set at three standard deviations from the mean of the statistic being plotted to reduce the chance of a false out-of-control signal while still providing sufficient power to identify out-of-control conditions when they occur.

While substitutes for the R chart have been proposed (see [4], for example), the original R chart is widely used in practice because of its computational simplicity and ease of interpretation. Process operators can easily compute the range and plot it on a control chart. By doing so, they can quickly identify potential changes and increase their involvement in process improvement initiatives.

While the use of R charts is simple, the mathematics behind the design of the chart is not as straightforward. The computation of R chart limits requires the use of tabulated constants. These constants were derived from the moments of the distribution of the range and are denoted d₂ (the expected value of the range of standard normal random variables) and d₃ (the standard deviation of the range of standard normal random variables). In almost all cases, the tabulated values of d₂ and d₃ have been approximated by numerical integration because analytical solutions have not been found. While the design procedure is not difficult, it is somewhat of a black box, and typically requires table lookup procedures for implementation. Moreover, the tabulated values are usually of limited precision (three decimal places) and scope, typically providing values only to a subgroup size of 20 or 25, which may be insufficient for some applications (We also note that having a computationally efficient way to estimate the moments could be of use in other statistical methods such as estimation or hypothesis testing. As explained at the beginning of the introduction, however, the range is rarely chosen as a measure of variability in such applications due to its poor statistical properties and hence we limit our attention to the application to control charts where the range is used regularly).

A preferred approach might be one in which data collection and processing are integrated into an online process control system. Ref. [5] described how an online system can be used to improve both control and inspection to reduce quality costs. While a lookup procedure could be used in such online systems, the preferred approach would be to automate the control chart computations and data collection.

In this paper (which extends our own work in [6]), we provide simple expressions that eliminate the need for table lookups. For sample sizes of 2 through 5, the provided expressions are exact and are obtained from a review of the previous literature. For larger sample sizes (up to 1000), the expressions are rational function (of the sample size) approximations. These expressions are simple to implement on a computer and are highly accurate.

In Section 2, we review the general expressions for the distribution, mean, and standard deviation of the range. We also discuss the approximation procedure for larger sample sizes. In Section 3, we review previously reported results for sample sizes of 2 through 5 and then present several possible rational functions that can be used to approximate d₂ and d₃ for sample sizes larger than 5. In Section 4, we compare the errors of various rational functions and provide recommended functions for general sample sizes. In Section 5, we provide concluding remarks.

2. The Distribution and First Two Moments of the Range

The constants used to design the range control chart are all derived from the distribution of the range of standard normal random variables. The usual assumption in control charting is that the process generates a random output that follows a normal distribution. It is not our purpose to explore violations of this assumption (see [7,8,9] for example discussions of potential problems when normality is not observed). All control chart constants associated with the range chart can be found if the mean and variance of the range are known. The mean of the range of normal random variables is denoted by d₂σ_x, where σ_x is the standard deviation of the process, and the standard deviation of the range is represented by d₃σ_x. In the remainder of the paper, we assume, without loss of generality, that the normal random output variable has a mean of 0 and a standard deviation of 1. Hence the design of the range control chart (and associated $\overline{X}$ chart) is equivalent to finding the constants d₂ and d₃.

To find the first two moments of the range, we begin with an expression for the probability density function (pdf) of R, f_R(r). The pdf of the range can be obtained by integrating the midrange T from the joint distribution of R and T [10] as follows:

$$f_R\left(r\right)=n\left(n-1\right){{\displaystyle \int }}_{-\infty }^{\infty }{\left[\Phi \left(t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)-\Phi \left(t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right]}^{n-2}\varphi \left(t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\varphi \left(t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)dt$$

(1)

where n is the sample size, and $\Phi$ and $\varphi$ are the distribution function and pdf of a standard normal random variable. From (1) we can find the control chart constants d₂ and d₃ as

$$d_2={{\displaystyle \int }}_0^{\infty }r{f}_R\left(r\right)dr$$

(2)

and

$$d_3=\sqrt{{{\displaystyle \int }}_0^{\infty }{r}^2{f}_R\left(r\right)dr-d_2^2}.$$

(3)

For general n, expressions (1)–(3) are difficult to solve analytically. Hence, the control chart constants d₂ and d₃, which are tabulated in many quality control handbooks and textbooks, were determined using numerical integration. However, it is possible to obtain analytical solutions for sample sizes 2–5. The simplified expressions and results are presented in the Results section.

2.1. Approximations to d₂ and d₃ for Samples Sizes of at Least 6

As mentioned above, we are not familiar with analytical solutions to expressions (1)–(3) when the sample size exceeds 5. However, numerical values of the control chart constants d₂ and d₃ are widely available. In this section, we describe how the numerical values were used to develop rational function approximations. Other authors have developed approximations for the moments of order statistics of normal random variables (see [11,12] for summaries of some of these methods; see [13] as well). We believe that these earlier approximations have at least three limitations. First, some approximations are less accurate, especially for extreme order statistics (those used to compute the range). Second, the methods are more complicated than those presented in this study. Third, some methods require the use of tabulated moments of neighboring order statistics, which defeats the purpose of having approximations that do not require table lookup procedures.

Approximation Method

We focus on the method for approximating d₂. The method was essentially the same for finding d₃. We began by plotting the tabulated values of d₂ as a function of the sample size n for values ranging from 2 to 1000, as given in [14] (We also used the values from [15] for d₃. We note that the tabulated values of [14] were presented to 5 decimal places and those of [15] were to 15 places). Figure 1 shows a plot that suggests that d₂ is a function of the logarithm of n. Hence, we sought an approximation relating the control chart constant values to the logarithm of n.

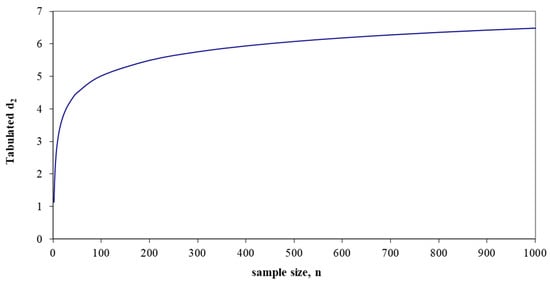
Figure 1. Plot of the tabulated values of d₂ as a function of sample size n. The plot suggests that the relationship between d₂ and n is logarithmic.

While numerous methods exist for estimating discrete values, we determined that a rational-function approximation would work well for this application. First, rational functions include polynomials (when the order of the polynomial in the denominator is of order 0). Second, other options such as splines, can result in more complex functions, and we wanted relatively simple expressions. Third, the rational functions have desirable asymptotic characteristics. For these and other advantages, see [16].

Instead of using a global measure of approximation error, such as the mean square error (MSE), we used the minimization of the maximum error between the approximations and the tabulated values of the control chart constants as our objective (As a final reason for using rational-function approximations rather than splines, we did look briefly at spline estimates and found that our rational function approximations resulted in smaller maximum errors). While MSE or mean absolute error (MAE) may be more appropriate if the overall accuracy of the approximation is important, we desired to ensure that the estimate of the control chart constants at every value of n was as close as possible to the tabulated values. Using MSE or MAE may result in an aggregate lower error, but it may do so at the expense of a few estimates having larger errors than desired. In other words, minimizing the maximum error is useful for guaranteeing worst-case (lack of) accuracy.

Because d₂ is defined on a discrete point set rather than on an interval, we used the differential correction method to determine the Chebyshev minimax approximations [17]. The algorithm is an iterative one that seeks to minimize the maximum difference between the rational function, R_mk(n) and the tabulated values of d₂, where

$$R_{mk}\left(n\right)={\displaystyle \frac{{{\displaystyle \sum }}_{j=0}^m{a}_j{\left[\log \left(n\right)\right]}^j}{{{\displaystyle \sum }}_{j=0}^k{b}_j{\left[\log \left(n\right)\right]}^j}}, \mathrm{with} b_0=1.$$

(4)

In (4), m is the order of the polynomial in the numerator of the rational function, k is the order of the denominator, and a_j and b_j are the coefficients of the numerator and denominator polynomials.

An initial rational function estimate is required to begin the procedure. We used multiple (polynomial) regression to find an initial polynomial solution and then used the minimax algorithm to convert the polynomial expression into a rational expression. The regression solutions were quite accurate, but in all cases, the estimates were improved by using the differential correction method.

The two parameters, m and k, can be adjusted to obtain better approximations. Generally, increasing m + k improves the accuracy of the estimates. Hence, we tried different combinations of parameters to find accurate and parsimonious approximations. For d_2, we tried m + k values from 2 to 9, and for d_3, we used values from 4 to 10. Combinations with sums greater than 9 (or 10 for d₃) did not yield significant improvements in accuracy and were discarded in the interest of parsimony. Combinations with sums less than 2 (4 for d₃) yielded unacceptable maximum errors.

We note that not all tabulated values were used for the computations. For d₂ we used tabulated values for n = 2 (1) 25, 30 (10) 50, 100 (100) 1000. For d₃, we used tabulated values for n = 2 (1) 25, 30 (5) 60, 70 (10) 100, 200, 500, and 1000 (the last three tabulated values were taken from [14] and were presented to only three decimal places). Removing some of the intermediate values where the curve in Figure 1 is relatively flat results in a more manageable optimization problem. As a post-hoc check, we evaluated the preferred rational function expressions at sample sizes 2 (1) 500 and 510 (10) 1000 for d₂ and 2 (1) 100 for d₃ and found only a few cases where the error only slightly exceeded the maximum error calculated during the estimation procedure (See Table 4 in the Results section for the preferred functions and the associated errors).

3. Results

We begin by presenting the analytical results for the first two moments of the range distribution for sample sizes 2 through 5. We then provide the results for the rational function approximations for larger sample sizes.

3.1. Analytical Results for n = 2, 3, 4 and 5

When n = 2, (1) simplifies substantially, and the solutions to (1)–(3) are straightforward. When n = 3, 4, and 5, the analytical solutions are not as simple. Ref. [18] showed that the pdf for the range when the sample size is 3 can be expressed as

$$f_R\left(r\right)={\displaystyle \frac{6}{\pi \sqrt{2}}}\exp \left({\displaystyle \frac{-r^2}{4}}\right){{\displaystyle \int }}_0^{r/\sqrt{6}}\exp \left({\displaystyle \frac{-u^2}{2}}\right)du={\displaystyle \frac{6}{\sqrt{\pi }}}\exp \left({\displaystyle \frac{-r^2}{4}}\right)\left[\Phi \left({\displaystyle \frac{r}{\sqrt{6}}}\right)-{\displaystyle \frac{1}{2}}\right].$$

(5)

They also showed that the ith moment μ_i of the distribution about the origin is

$${\mu }_i={\displaystyle \frac{3}{\pi }}{2}^{i+1}\Gamma \left({\displaystyle \frac{i}{2}}+1\right){{\displaystyle \int }}_0^{\pi /6}{\cos }^i\theta d\theta .$$

(6)

Other researchers have found moments of order statistics for samples of sizes 4 and 5. For a listing of these researchers and a description of the derivation by [19], see [20]. The author’s alternative derivations are provided in Appendix A. Table 1 summarizes the analytical results.

Table 1. Analytical results for d₂ and d₃ for samples of sizes 2 through 5.

Sample Size n	d2	d3
2	$2/\sqrt{\pi }$	$\sqrt{2-{\displaystyle \frac{4}{\pi }}}$
3	$3/\sqrt{\pi }$	$\sqrt{{\displaystyle \frac{2\pi +3\sqrt{3}-9}{\pi }}}$
4	${\displaystyle \frac{12}{\pi \sqrt{\pi }}}{\tan }^{-1}\left(\sqrt{2}\right)$	$\sqrt{{\displaystyle \frac{2\pi +2\sqrt{3}+6}{\pi }}-d_2^2}$
5	${\displaystyle \frac{30}{{\left(\pi \right)}^{3/2}}}{\tan }^{-1}\left(\sqrt{2}\right)-{\displaystyle \frac{5}{\sqrt{\pi }}}$	$\sqrt{{\displaystyle \frac{2{\pi }^2+10\sqrt{3}\left[{\tan }^{-1}\left(\sqrt{\frac{5}{3}}\right)+2\sqrt{3}{\tan }^{-1}\left(\sqrt{\frac{1}{5}}\right)\right]}{{\pi }^2}}-d_2^2}$

The analytical results reveal some common elements. For example, the arc tangent function and the term π^3/2 appear in most of the d₂ results. Despite these commonalities, we were unable to induce expressions for general sample sizes. Instead, in the next sections, we present accurate rational function approximations.

3.2. Approximation Results

Table 2 summarizes the results for the d₂ approximations, and Table 3 summarizes the results for the d₃ approximations. The tables show the values of m and k, the maximum error for the given rational function, and the coefficient values defined in (4). The tables are sorted first by the number of parameters (i.e., by m + k) and then by the maximum error. For the sake of brevity, the tables only show the case for a given m + k for which the maximum error is the smallest (More complete tables are given in Appendix B). For example, the first entry in Table 2 is for a rational function with m = 7 and k = 2. The maximum error for such a case was 4.3685 × 10⁻⁶, and the rational function approximation was

$$R_{72}\left(x\right)={\displaystyle \frac{-4.683\times {10}^{-5}+4.1602x-1.0722x^2+0.2863x^3-0.0791x^4+0.0129x^5-0.0012x^6+4.363\times {10}^{-5}{x}^7}{1+0.1108x-0.0363x^2}},$$

where x = log(n).

Table 2. Rational function values for approximating the control chart constant d₂. These results are for the functions with the lowest errors for each combination of m + k. More complete tables are found in Appendix B. See (4) for definitions of the terms used in the table.

m + k	9	8	7	6	5	4	3	2
(m, k)	(7, 2)	(2, 6)	(5, 2)	(2, 4)	(1, 4)	(1, 3)	(2, 1)	(1, 1)
Maximum Error	4.3685 × 10−6	4.3907 × 10−6	4.5173 × 10−6	2.1767 × 10−5	7.0438 × 10−5	1.6052 × 10−4	5.6083 × 10−4	2.1880 × 10−2
a0	−4.6830 × 10−5	0.00021168	0.00039446	0.0740863	−0.0021528	−0.0058338	−0.0023213	0.12951861
a1	4.16017058	4.15771399	4.15608081	3.50035523	4.17780958	4.19907408	4.18711419	3.66813329
a2	−1.072159	0.34914757	1.4690251	133.771848			0.34490634
a3	0.28628465		0.23910449
a4	−0.0791025		−0.0147213
a5	0.01287818		0.00070213
a6	−0.0011768
a7	4.36 × 10−5
b1	0.11084091	0.45026527	0.71813046	31.970664	0.38128612	0.3919365	0.47209716	0.24108419
b2	−0.036305	0.02450851	0.18294963	12.6518404	−0.0240701	−0.0310113
b3		−0.0137816		−1.0557861	−0.0006661	0.00168837
b4		0.00412501		0.06259679	0.00029336
b5		−0.0006383
b6		4.1793 × 10−5

Table 3. Rational function values for approximating the control chart constant d₃. These results are for the functions with the lowest error for each combination of m + k. More complete tables are found in Appendix B. See (4) for definitions of the terms used in the table.

m + k	10	9	8	7	6	5	4
(m, k)	(9, 1)	(2, 7)	(1, 7)	(4, 3)	(4, 2)	(2, 3)	(2, 2)
Maximum Error	1.0426 × 10−6	1.4861 × 10−5	2.6339 × 10−5	3.9049 × 10−5	1.1010 × 10−4	2.0261 × 10−4	2.1340 × 10−4
a0	0.315104	0.222874	−0.22202	0.414579	0.342748	0.457381	0.452862
a1	5.547612	7.435075	16.809	3.718122	4.964747	3.232791	3.338977
a2	−2.84442	−1.74755		−0.92875	−0.67509	0.559042	0.491674
a3	−0.78335			−0.07681	0.305956
a4	2.852878			−0.00913	−0.03384
a5	−2.51086
a6	1.234777
a7	−0.36344
a8	0.059829
a9	−0.00424
b1	3.396075	5.437382	15.37598	1.802498	2.973567	1.648605	1.737353
b2		0.138415	−2.99882	1.976001	2.179108	2.65881	2.63829
b3		2.584673	14.3693	−0.86642		0.024817
b4		−2.56493	−10.1252
b5		1.00801	3.946838
b6		−0.20567	−0.83038
b7		0.017412	0.072844

4. Discussion

Table 2 shows that the smallest maximum error was reported for the m + k = 9 case. We have only reported this case to show that a few of the m + k = 8 cases were very comparable in terms of their maximum error. The table also shows that there was no one systematically preferred form of the rational function approximations. For example, when m + k = 8, the best rational function approximation had more terms in the denominator (m = 2 and k = 6) than in the numerator; however, when m + k = 7, the lowest error was obtained from a rational function with more terms in the numerator (m = 5 and k = 2). Finally, the table shows that the d₂ terms can be accurately estimated to at least three decimal places (maximum errors on the order of 10⁻⁴) with rational functions having as few as five total terms (m + k = 4). The approximations are very good with only eight total terms, having maximum errors on the order of 10⁻⁶. Such accuracy is remarkable given that the tabulated values used for the estimation were only given to five decimal places. Hence, very accurate estimates of d₂ can be made for sample sizes from 2 to 1000 using simple algebraic expressions.

Similar results were obtained for d₃, although the approximations were not as good. To achieve maximum errors on the order of 10⁻⁶, m + k must be as high as 10. With a total of eight terms (m + k = 7), some maximum errors were just over 10⁻⁵, which is still very good. We believe that greater accuracy is worth sacrificing a small degree of parsimony in the expression. We suggest using the rational functions shown in the second rows of Table 2 and Table 3, as they provide excellent accuracy with reasonably sized rational functions. Table 4 summarizes our suggestions for determining when finding the values of d₂ and d₃ for sample sizes of 2 to 1000. Moreover, Figure 2 shows plots of the difference between the actual and estimated values of the control chart constants for the suggested expressions for sample sizes greater than 5. As can be seen in the figure, the error oscillates, and in some cases, it is much smaller than the maximum error.

Table 4. Suggested algebraic expressions for control chart constants d₂ and d₃ for sample sizes 2 to 1000. In the table, x = log(n).

a. Expressions for d2
Sample Size n	Expression for d2	Maximum Error
2	$2/\sqrt{\pi }$	0
3	$3/\sqrt{\pi }$	0
4	${\displaystyle \frac{12}{\pi \sqrt{\pi }}}{\tan }^{-1}\left(\sqrt{2}\right)$	0
5	${\displaystyle \frac{30}{{\left(\pi \right)}^{3/2}}}{\tan }^{-1}\left(\sqrt{2}\right)-{\displaystyle \frac{5}{\sqrt{\pi }}}$	0
n = 6 to 1000	${\displaystyle \frac{2.1168\times {10}^{-4}+4.1577x+0.3491x^2}{1+0.4503x+0.0245x^2-0.0138x^3+0.4125\times {10}^{-3}{x}^4-6.383\times {10}^{-4}{x}^5+4.1793\times {10}^{-5}{x}^6}}$	4.3907 × 10−6
b. Expressions for d3
Sample Size n	Expression for d3	Maximum Error
2	$\sqrt{2-{\displaystyle \frac{4}{\pi }}}$	0
3	$\sqrt{{\displaystyle \frac{2\pi +3\sqrt{3}-9}{\pi }}}$	0
4	$\sqrt{{\displaystyle \frac{2\pi +2\sqrt{3}+6}{\pi }}-d_2^2}$	0
5	$\sqrt{{\displaystyle \frac{2{\pi }^2+10\sqrt{3}\left[{\tan }^{-1}\left(\sqrt{\frac{5}{3}}\right)+2\sqrt{3}{\tan }^{-1}\left(\sqrt{\frac{1}{5}}\right)\right]}{{\pi }^2}}-d_2^2}$	0
n = 6 to 1000	${\displaystyle \frac{0.2229+7.4351\mathrm{x}-{1.7476\mathrm{x}}^2 }{1+5.4374\mathrm{x}+{0.1384\mathrm{x}}^2+{2.5847\mathrm{x}}^3-{2.5649\mathrm{x}}^4+{1.0080\mathrm{x}}^5-{0.2057\mathrm{x}}^6+{0.0174\mathrm{x}}^7}}$	1.4861 × 10−5

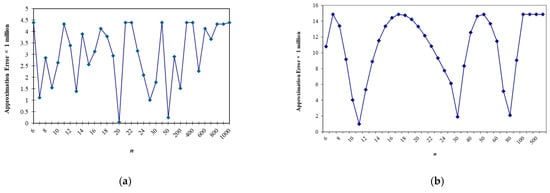
Figure 2. Plots of the approximation errors for (a) d₂ and (b) d₃ for the rational functions listed in Table 4. The plots show the sample sizes for which the estimation error is the largest.

While we recommend the expressions in Table 4, others may prefer a different combination of parsimony and accuracy. Appendix B shows more complete tables of the estimated expressions and their maximum errors, which can be used to determine the preferred combination. Similarly, Figure 3 shows the contour plots of the negative logarithm of the maximum error for different combinations of the orders of the polynomials in the rational functions. Higher values in the plot indicate lower errors. For example, a value of 5 in the plot is associated with a maximum error of 1 × 10⁻⁵.

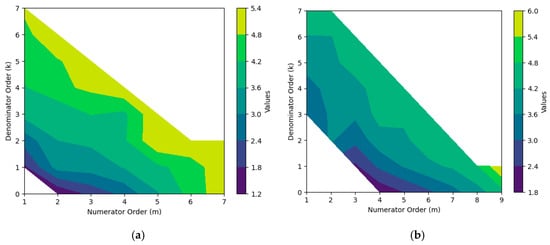
Figure 3. Contour plots of the negative logarithm of the maximum error for (a) d₂ and (b) d₃ for different combinations of the orders of the polynomials in (4). Larger values are associated with smaller errors.

5. Conclusions

We have provided algebraic expressions that can be used to easily compute the control chart constants d₂ and d₃ for sample sizes from 2 to 1000. For the cases of n = 2 through 5 we have reviewed the exact solutions, whereas for cases of n > 5, we have provided rational function approximations that are very accurate. Other constants that are based on range control charts (e.g., A₂, D₃, and D₄) can easily be computed from the two constants d₂ and d₃ (see [21] for example). Such expressions allow control chart designers and users, including control chart software producers, to compute the control chart constants without using lookup routines, which generally find control chart constants for a limited number of possible sample sizes with limited precision. Hence, the expressions simplify the process of automating the range control chart construction.

Appendix A.1. Derivation of the Expected Value of the Range for n = 4 and 5

We first note that from the definition of the standard normal pdf, we can rewrite the latter part of the integrand of (1) as

$$\varphi \left(t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\varphi \left(t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)={\displaystyle \frac{1}{2\pi }}\exp (-t^2)\exp \left(-{\displaystyle \frac{r^2}{4}}\right).$$

(A1)

For ease of exposition, we can use (A1) we can rewrite (1) as

$$f_R\left(r\right)={\displaystyle \frac{n\left(n-1\right)\exp \left(-\frac{r^2}{4}\right)}{2\pi }}{I}_n\left(r\right),$$

(A2)

where

$$I_n\left(r\right)={{\displaystyle \int }}_{-\infty }^{\infty }\left[{\left[\Phi \left(t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)-\Phi \left(t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right]}^{n-2}\right]\exp \left(-t^2\right)dt.$$

(A3)

From the definition of expected value we have

$$E\left(R\right)={\displaystyle \frac{n\left(n-1\right)}{2\pi }}{{\displaystyle \int }}_0^{\infty }r\exp \left({\displaystyle \frac{-r^2}{4}}\right)I_n\left(r\right)dr.$$

(A4)

We can integrate (A4) by parts to obtain

$$E\left(R\right)={\displaystyle \frac{n\left(n-1\right)}{\pi }}{{\displaystyle \int }}_0^{\infty }\exp \left({\displaystyle \frac{-r^2}{4}}\right){\displaystyle \frac{d{I}_n\left(r\right)}{dr}}dr$$

(A5)

where

$${\displaystyle \frac{d{I}_n\left(r\right)}{dr}}={\displaystyle \frac{n-2}{2\sqrt{2\pi }}}\exp \left({\displaystyle \frac{-r^2}{12}}\right)J_n\left(r\right)$$

(A6)

and

$$J_n\left(r\right)={{\displaystyle \int }}_{-\infty }^{\infty }{\left[\Phi \left(t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)-\Phi \left(t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right]}^{n-3}\left\{\exp \left[-{\displaystyle \frac{1}{2}}{\left(\sqrt{3}t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$\sqrt{12}$}\right.}\right)}^2\right]+\exp \left[-{\displaystyle \frac{1}{2}}{\left(\sqrt{3}t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$\sqrt{12}$}\right.}\right)}^2\right]\right\}dt$$

(A7)

Substituting z = $\sqrt{3}t+{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$\sqrt{12}$}\right.}$ in the first exponent and z = $\sqrt{3}t-{\displaystyle \raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$\sqrt{12}$}\right.}$ in the second, (A7) becomes

$$J_n\left(r\right)={\displaystyle \frac{1}{\sqrt{3}}}{{\displaystyle \int }}_{-\infty }^{\infty }{e}^{{\displaystyle \frac{-z^2}{2}}}\left\{{\left[\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{r}{3}}\right)-\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}-{\displaystyle \frac{2r}{3}}\right)\right]}^{n-3}+{\left[\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{2r}{3}}\right)-\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}-{\displaystyle \frac{r}{3}}\right)\right]}^{n-3}\right\}dz$$

(A8)

We can evaluate (A8) by taking the derivative of J_n with respect to r, evaluating the resulting integral with respect to z, and then integrating again with respect to r. The result is that

$$\begin{gathered} {\displaystyle \frac{d{J}_n\left(r\right)}{dr}}={\displaystyle \frac{n-3}{3\sqrt{3}}}\left\{{{\displaystyle \int }}_{-\infty }^{\infty }{e}^{-{\displaystyle \frac{z^2}{2}}}{\left[\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{r}{3}}\right)-\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}-{\displaystyle \frac{2r}{3}}\right)\right]}^{n-4}\left[\varphi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{r}{3}}\right)+2\varphi \left({\displaystyle \frac{z}{\sqrt{3}}}-{\displaystyle \frac{2r}{3}}\right)\right]dz\right. \\ +{{\displaystyle \int }}_{-\infty }^{\infty }\left.e^{-{\displaystyle \frac{z^2}{2}}}{\left[\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{2r}{3}}\right)-\Phi \left({\displaystyle \frac{z}{\sqrt{3}}}-{\displaystyle \frac{r}{3}}\right)\right]}^{n-4}\left[2\varphi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{2r}{3}}\right)+\varphi \left({\displaystyle \frac{z}{\sqrt{3}}}-{\displaystyle \frac{r}{3}}\right)\right]dz\right\}. \end{gathered}$$

(A9)

Expression (A9) has several products of the form $e^{{\displaystyle \frac{-z^2}{2}}}\varphi \left({\displaystyle \frac{z}{\sqrt{3}}}+{\displaystyle \frac{kr}{3}}\right)$, which can be recombined to obtain ${\displaystyle \frac{1}{\sqrt{2\pi }}}\exp \left({\displaystyle \frac{-k^2{r}^2}{24}}\right)\exp \left[-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{2z}{\sqrt{3}}}+{\displaystyle \frac{kr}{6}}\right)}^2\right]$. We can further substitute for z using $u={\displaystyle \frac{2z}{\sqrt{3}}}+{\displaystyle \frac{kr}{6}}$, which gives

$$\begin{gathered} {\displaystyle \frac{dJn\left(r\right)}{dr}}={\displaystyle \frac{n-3}{6\sqrt{2\pi }}}\left(e^{-{\displaystyle \frac{r^2}{24}}}{{\displaystyle \int }}_{-\infty }^{\infty }{e}^{-{\displaystyle \frac{u^2}{2}}}\left\{{\left[\Phi \left({\displaystyle \frac{u}{2}}+{\displaystyle \frac{r}{4}}\right)-\Phi \left({\displaystyle \frac{u}{2}}-{\displaystyle \frac{3r}{4}}\right)\right]}^{n-4}+{\left[\Phi \left({\displaystyle \frac{u}{2}}+{\displaystyle \frac{3r}{4}}\right)-\Phi \left({\displaystyle \frac{u}{2}}-{\displaystyle \frac{r}{4}}\right)\right]}^{n-4}\right\}du\right. \\ \left.+4e^{-{\displaystyle \frac{r^2}{6}}}{{\displaystyle \int }}_{-\infty }^{\infty }{e}^{-{\displaystyle \frac{u^2}{2}}}{\left[\Phi \left({\displaystyle \frac{u}{2}}+{\displaystyle \frac{r}{2}}\right)-\Phi \left({\displaystyle \frac{u}{2}}-{\displaystyle \frac{r}{2}}\right)\right]}^{n-4}du\right). \end{gathered}$$

(A10)

We now consider the special cases of n = 4 and n = 5.

Appendix A.1.1. n = 4 Case

In this case (A10) simplifies to

$${\displaystyle \frac{d{J}_4\left(r\right)}{dr}}={\displaystyle \frac{1}{3}}\left(e^{-{\displaystyle \raisebox{1ex}{$r^2$}\!\left/ \!\raisebox{-1ex}{$24$}\right.}}+2e^{-{\displaystyle \raisebox{1ex}{$r^2$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}\right)$$

(A11)

and so

$$J_4\left(r\right)={\displaystyle \frac{2\sqrt{6\pi }}{3}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{12}}}\right)+\Phi \left({\displaystyle \frac{r}{\sqrt{3}}}\right)-1\right].$$

(A12)

Using (A12) in (A6) and then (A5) for n = 4 gives

$$E\left(R\right)={\displaystyle \frac{8\sqrt{3}}{\pi }}\left[{{\displaystyle \int }}_0^{\infty }\exp \left({\displaystyle \frac{-r^2}{3}}\right)\left[\Phi \left({\displaystyle \frac{r}{\sqrt{12}}}\right)+\Phi \left({\displaystyle \frac{r}{\sqrt{3}}}\right)-1\right]dr\right].$$

(A13)

To find (A13) we evaluate the three terms separately, which we will call K₁, K₂ and K₃ (so that $E\left(R\right)={\displaystyle \frac{8\sqrt{3}}{\pi }}\left[K_1+K_2-K_3\right]$). The integral K₃ is straightforward and is $\sqrt{3\pi }/2$. The other two are of the same form K,

$$K={{\displaystyle \int }}_0^{\infty }\exp \left({\displaystyle \frac{-r^2}{3}}\right)\Phi \left({\displaystyle \frac{r}{\sqrt{b}}}\right)dr={\displaystyle \frac{1}{\sqrt{2\pi }}}{\displaystyle {\int }_0^{\infty }\exp \left(\frac{-r^2}{3}\right)dr}{\displaystyle \underset{-\infty }{\overset{r/\sqrt{b}}{\int }}\exp \left(\frac{-u^2}{2}\right)}du$$

(A14)

We will use the same technique as [18], which is to substitute v = ${\displaystyle \raisebox{1ex}{$u$}\!\left/ \!\raisebox{-1ex}{$r$}\right.}$ into (A14) and change the order of integration. The result is

$$K={\displaystyle \frac{1}{\sqrt{2\pi }}}{{\displaystyle \int }}_{-\infty }^{1/\sqrt{b}}{{\displaystyle \int }}_0^{\infty }r\exp \left(-{\displaystyle \frac{{(vr)}^2}{2}}\right)\exp \left({\displaystyle \frac{-r^2}{3}}\right)drdv={\displaystyle \frac{1}{\sqrt{2\pi }}}{{\displaystyle \int }}_{-\infty }^{1/\sqrt{b}}{{\displaystyle \int }}_0^{\infty }r\exp \left[-{\displaystyle \frac{r^2}{3}}\left(1+{\displaystyle \frac{v^2}{2/3}}\right)\right]drdv.$$

(A15)

We can now evaluate (A15) with respect to r, giving

$$K={\displaystyle \frac{3}{2\sqrt{2\pi }}}{{\displaystyle \int }}_{-\infty }^{1/\sqrt{b}}{\left(1+{\displaystyle \raisebox{1ex}{$3v^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}^{-1}dv$$

(A16)

We now let v = $\sqrt{{\displaystyle \raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}\tan \theta$ and obtain

$$K={\displaystyle \frac{\sqrt{3}}{2\sqrt{\pi }}}{{\displaystyle \int }}_{-\pi /2}^{{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{3}{2b}}}\right)}\theta d\theta ={\displaystyle \frac{\sqrt{3}}{2\sqrt{\pi }}}\left[{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{3}{2b}}}\right)+\pi /2\right].$$

(A17)

Comparing this result to the terms in (A13) shows that

$$K_1={\displaystyle \frac{\sqrt{3}}{2\sqrt{\pi }}}\left[{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{1}{8}}}\right)+\pi /2\right]$$

(A18)

and

$$K_2={\displaystyle \frac{\sqrt{3}}{2\sqrt{\pi }}}\left[{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{1}{2}}}\right)+\pi /2\right].$$

(A19)

Hence we have that

$$E\left(R\right)={\displaystyle \frac{8\sqrt{3}}{\pi }}\left[{\displaystyle \frac{\sqrt{3}}{2\sqrt{\pi }}}\left[{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{1}{8}}}\right)+{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{1}{2}}}\right)+\pi \right]-{\displaystyle \frac{\sqrt{3\pi }}{2}}\right],$$

(A20)

which simplifies to

$$E\left(R\right)=d_2={\displaystyle \frac{12}{\pi \sqrt{\pi }}}{\tan }^{-1}\left(\sqrt{2}\right).$$

(A21)

Appendix A.1.2. n = 5 Case

If we substitute n = 5 into (A10) we obtain

$$\begin{gathered} {\displaystyle \frac{d{J}_5\left(r\right)}{dr}}={\displaystyle \frac{1}{3\sqrt{2\pi }}}\left\{e^{-{\displaystyle \frac{r^2}{24}}}{{\displaystyle \int }}_{-\infty }^{\infty }{e}^{-{\displaystyle \frac{u^2}{2}}}\left[\Phi \left({\displaystyle \frac{u}{2}}+{\displaystyle \frac{r}{4}}\right)-\Phi \left({\displaystyle \frac{u}{2}}-{\displaystyle \frac{3r}{4}}\right)+\Phi \left({\displaystyle \frac{u}{2}}+{\displaystyle \frac{3r}{4}}\right)-\Phi \left({\displaystyle \frac{u}{2}}-{\displaystyle \frac{r}{4}}\right)\right]du\right.+ \\ \left.4e^{-{\displaystyle \frac{r^2}{6}}}{{\displaystyle \int }}_{-\infty }^{\infty }{e}^{-{\displaystyle \frac{u^2}{2}}}\left[\Phi \left({\displaystyle \frac{u}{2}}+{\displaystyle \frac{r}{2}}\right)-\Phi \left({\displaystyle \frac{u}{2}}-{\displaystyle \frac{r}{2}}\right)\right]du\right\}. \end{gathered}$$

(A22)

We can evaluate the integrals in (A22) by differentiating with respect to r first, then integrating with respect to u, and finally integrating again with respect to r. The first integral then is $2\sqrt{2\pi }\left[\Phi \left({\displaystyle \frac{r}{\sqrt{20}}}\right)+\Phi \left({\displaystyle \frac{3r}{\sqrt{20}}}\right)-1\right]$ and the second integral is $2\sqrt{2\pi }\left[\Phi \left({\displaystyle \frac{r}{\sqrt{5}}}\right)-{\displaystyle \frac{1}{2}}\right]$. Hence we have

$${\displaystyle \frac{d{J}_5\left(r\right)}{dr}}={\displaystyle \frac{2}{3}}{e}^{-{\displaystyle \frac{r^2}{24}}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{20}}}\right)+\Phi \left({\displaystyle \frac{3r}{\sqrt{20}}}\right)-1\right]+{\displaystyle \frac{8}{3}}{e}^{-{\displaystyle \frac{r^2}{6}}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{5}}}\right)-{\displaystyle \frac{1}{2}}\right].$$

(A23)

If we combine (A5) and (A6) for n = 5 we have

$$E\left(R\right)={\displaystyle \frac{30}{\pi \sqrt{2\pi }}}{{\displaystyle \int }}_0^{\infty }\exp \left({\displaystyle \frac{-r^2}{3}}\right)J_5\left(r\right)dr.$$

(A24)

We can integrate (A24) by parts again to obtain

$$\begin{gathered} E\left(R\right)={\displaystyle \frac{60}{\sqrt{\pi }}}-{\displaystyle \frac{30\sqrt{3}}{\pi \sqrt{2}}}{{\displaystyle \int }}_0^{\infty }\Phi \left(\sqrt{{\displaystyle \frac{2}{3}}}r\right){\displaystyle \frac{d{J}_5\left(r\right)}{dr}}dr \\ ={\displaystyle \frac{60}{\sqrt{\pi }}}-{\displaystyle \frac{20\sqrt{3}}{\pi \sqrt{2}}}{{\displaystyle \int }}_0^{\infty }\Phi \left(\sqrt{{\displaystyle \frac{2}{3}}}r\right)\left\{e^{-{\displaystyle \frac{r^2}{24}}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{20}}}\right)+\Phi \left({\displaystyle \frac{3r}{\sqrt{20}}}\right)-1\right]+4e^{-{\displaystyle \frac{r^2}{6}}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{5}}}\right)-{\displaystyle \frac{1}{2}}\right]\right\}dr. \end{gathered}$$

(A25)

To evaluate E(R) now, we must be able to evaluate integrals of the form L = ${{\displaystyle \int }}_0^{\infty }{e}^{-{\displaystyle \frac{r^2}{a}}}\Phi \left(\sqrt{{\displaystyle \frac{2}{3}}}r\right)\Phi \left({\displaystyle \frac{r}{\sqrt{b}}}\right)dr$. We will do so by integrating by parts, letting u = $\Phi \left(\sqrt{{\displaystyle \frac{2}{3}}}r\right)$ and dv = $e^{-{\displaystyle \frac{r^2}{a}}}\Phi \left({\displaystyle \frac{r}{\sqrt{b}}}\right)dr$. We can easily find du, but finding v is much more difficult. I will again use the method of [18]. First write v as $v={\displaystyle \frac{1}{\sqrt{2\pi }}}\int \exp \left(-{\displaystyle \frac{x^2}{a}}\right){{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}\exp \left(-{\displaystyle \frac{z^2}{2}}\right)dzdx$. Now let y = ${\displaystyle \raisebox{1ex}{$z$}\!\left/ \!\raisebox{-1ex}{$x$}\right.}$ in the second of these integrals, and then reverse the order of integration. The result is $v={\displaystyle \frac{1}{\sqrt{2\pi }}}{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}\int x\exp \left(-{\displaystyle \frac{x^2}{a}}-{\displaystyle \frac{x^2{y}^2}{2}}\right)dxdy$. We can now evaluate the inside integral to obtain

$$v={\displaystyle \frac{1}{2\sqrt{2\pi }}}{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}{\displaystyle \frac{-\exp \left(-\frac{r^2}{a}-\frac{r^2{y}^2}{2}\right)}{\frac{1}{a}+\frac{y^2}{2}}}dy={\displaystyle \frac{-1}{2\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{r^2}{a}}}\hspace{1em}{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}{\displaystyle \frac{e^{-\frac{r^2{y}^2}{2}}}{\frac{1}{a}+\frac{y^2}{2}}}dy.$$

(A26)

Now we have that L = ${{\displaystyle \int }}_0^{\infty }udv={\left.uv\right|}_0^{\infty }-{{\displaystyle \int }}_0^{\infty }vdu=$ ${\displaystyle \frac{1}{4\sqrt{2\pi }}}\left\{\sqrt{2a}{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{a}{2b}}}\right)+\pi \sqrt{{\displaystyle \frac{a}{2}}}\right\}+{\displaystyle \frac{1}{2\pi \sqrt{6}}}{{\displaystyle \int }}_0^{\infty }{e}^{-{\displaystyle \frac{r^2}{a}}}{e}^{-{\displaystyle \frac{r^2}{3}}}{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}{\displaystyle \frac{e^{-\frac{r^2{y}^2}{2}}}{\frac{1}{a}+\frac{y^2}{2}}}dydr$ or

$$L={\displaystyle \frac{1}{4\sqrt{2\pi }}}\left\{\sqrt{2a}{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{a}{2b}}}\right)+\pi \sqrt{{\displaystyle \frac{a}{2}}}\right\}+{\displaystyle \frac{a}{\pi \sqrt{6}}}{{\displaystyle \int }}_0^{\infty }{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}{\displaystyle \frac{\exp \left[-\frac{r^2}{2}\left(y^2+\frac{2}{a}+\frac{2}{3}\right)\right]}{2+a{y}^2}}dydr.$$

(A27)

For simplicity, let β = $y^2+{\displaystyle \frac{2}{a}}+{\displaystyle \frac{2}{3}}$ and reverse the order of integration to get

$$L={\displaystyle \frac{1}{4\sqrt{2\pi }}}\left\{\sqrt{2a}{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{a}{2b}}}\right)+\pi \sqrt{{\displaystyle \frac{a}{2}}}\right\}+{\displaystyle \frac{a}{\pi \sqrt{6}}}{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}{\displaystyle \frac{1}{2+a{y}^2}}{{\displaystyle \int }}_0^{\infty }\exp \left[-{\displaystyle \frac{\beta r^2}{2}}\right]drdy.$$

(A28)

The inner definite integral can now be evaluated, so that we have

$$L={\displaystyle \frac{1}{4\sqrt{2\pi }}}\left\{\sqrt{2a}{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{a}{2b}}}\right)+\pi \sqrt{{\displaystyle \frac{a}{2}}}\right\}+{\displaystyle \frac{a}{2}}\sqrt{{\displaystyle \frac{a}{\pi }}}{{\displaystyle \int }}_{-\infty }^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{b}$}\right.}}{\displaystyle \frac{dy}{\left(2+a{y}^2\right)\sqrt{3a{y}^2+2a+6}}}.$$

(A29)

The last integral can now be evaluated and gives

$$L={\displaystyle \frac{1}{4\sqrt{2\pi }}}\left\{\sqrt{2a}{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{a}{2b}}}\right)+\pi \sqrt{{\displaystyle \frac{a}{2}}}\right\}+{\displaystyle \frac{1}{4}}\sqrt{{\displaystyle \frac{a}{\pi }}}\left[{\sin }^{-1}\left({\displaystyle \frac{a\sqrt{2}}{\sqrt{\left(a+2b\right)\left(6+2a\right)}}}\right)+{\sin }^{-1}\left(\sqrt{{\displaystyle \frac{2a}{6+2a}}}\right)\right]$$

(A30)

The other terms in (A25) have the form K = ${{\displaystyle \int }}_0^{\infty }{e}^{-{\displaystyle \frac{r^2}{a}}}\Phi \left(\sqrt{{\displaystyle \frac{2}{3}}}r\right)dr$. From the n = 4 case we know that K = ${\displaystyle \frac{\sqrt{a}}{2\sqrt{\pi }}}\left[{\tan }^{-1}\left(\sqrt{{\displaystyle \frac{a}{3}}}\right)+{\displaystyle \frac{\pi }{2}}\right]$. Now we can combine this result with (A30) and substitute them for the appropriate terms in (A25). After (a large amount of) simplification, the result is that E(R) = ${\displaystyle \frac{30}{{\left(\pi \right)}^{3/2}}}{\tan }^{-1}\left(\sqrt{2}\right)-{\displaystyle \frac{5}{\sqrt{\pi }}}$.

Appendix A.2. Derivation of the Variance of the Range for n = 4 and 5

We again begin with the case for general n and use (A2) and (A3) as a base. To find the variance of the range, we first find E(R²),

$$E\left(R^2\right)={\displaystyle \frac{n\left(n-1\right)}{2\pi }}{{\displaystyle \int }}_0^{\infty }{r}^2\exp \left({\displaystyle \frac{-r^2}{4}}\right)I_n\left(r\right)dr.$$

(A31)

First, we can integrate this by parts to obtain

$$E\left(R^2\right)={\displaystyle \frac{n\left(n-1\right)}{\pi }}\left[{{\displaystyle \int }}_0^{\infty }r\exp \left({\displaystyle \frac{-r^2}{4}}\right){\displaystyle \frac{d{I}_n\left(r\right)}{dr}}dr+{{\displaystyle \int }}_0^{\infty }\exp \left({\displaystyle \frac{-r^2}{4}}\right)I_n\left(r\right)dr\right]$$

(A32)

where ${\displaystyle \frac{d{I}_n\left(r\right)}{dr}}$ is defined in (A6). By noting that the integrand of the second term in (A32) is essentially f_R(r), and by using (A6) and (A7) we can simplify (A32) to

$$E\left(R^2\right)=2+{\displaystyle \frac{n\left(n-1\right)\left(n-2\right)}{{\left(2\pi \right)}^{3/2}}}{{\displaystyle \int }}_0^{\infty }r\exp \left({\displaystyle \frac{-r^2}{3}}\right)J_n\left(r\right)dr.$$

(A33)

where J_n(r) is defined in (A8). Integrating by parts once again gives

$$E\left(R^2\right)=2+{\displaystyle \frac{3n\left(n-1\right)\left(n-2\right)}{2{\left(2\pi \right)}^{3/2}}}{{\displaystyle \int }}_0^{\infty }\exp \left({\displaystyle \frac{-r^2}{3}}\right){\displaystyle \frac{d{J}_n\left(r\right)}{dr}}dr$$

(A34)

where ${\displaystyle \frac{d{J}_n\left(r\right)}{dr}}$ is defined in (A12).

For the n = 4 case we can substitute (A11) into (A34) and integrate to find that E(R²) is ${\displaystyle \frac{2\pi +2\sqrt{3}+6}{\pi }}$.

For the case of n = 5, we can use (A23) in (A34) to obtain

$$E\left(R^2\right)=2+{\displaystyle \frac{60}{{\left(2\pi \right)}^{3/2}}}{{\displaystyle \int }}_0^{\infty }\left\{e^{-{\displaystyle \frac{3r^2}{8}}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{20}}}\right)+\Phi \left({\displaystyle \frac{3r}{\sqrt{20}}}\right)-1\right]+4e^{-{\displaystyle \frac{r^2}{2}}}\left[\Phi \left({\displaystyle \frac{r}{\sqrt{5}}}\right)-{\displaystyle \frac{1}{2}}\right]\right\}dr$$

(A35)

We have already seen in Appendix A.1 that integrals like most of those found in (A35) can be found using (A14)–(A17). Hence (A35) simplifies to E(R²) = ${\displaystyle \frac{2{\pi }^2+10\sqrt{3}\left[{\tan }^{-1}\left(\sqrt{\frac{5}{3}}\right)+2\sqrt{3}{\tan }^{-1}\left(\sqrt{\frac{1}{5}}\right)\right]}{{\pi }^2}}$.