On the Special Viviani’s Curve and Its Corresponding Smarandache Curves
Abstract
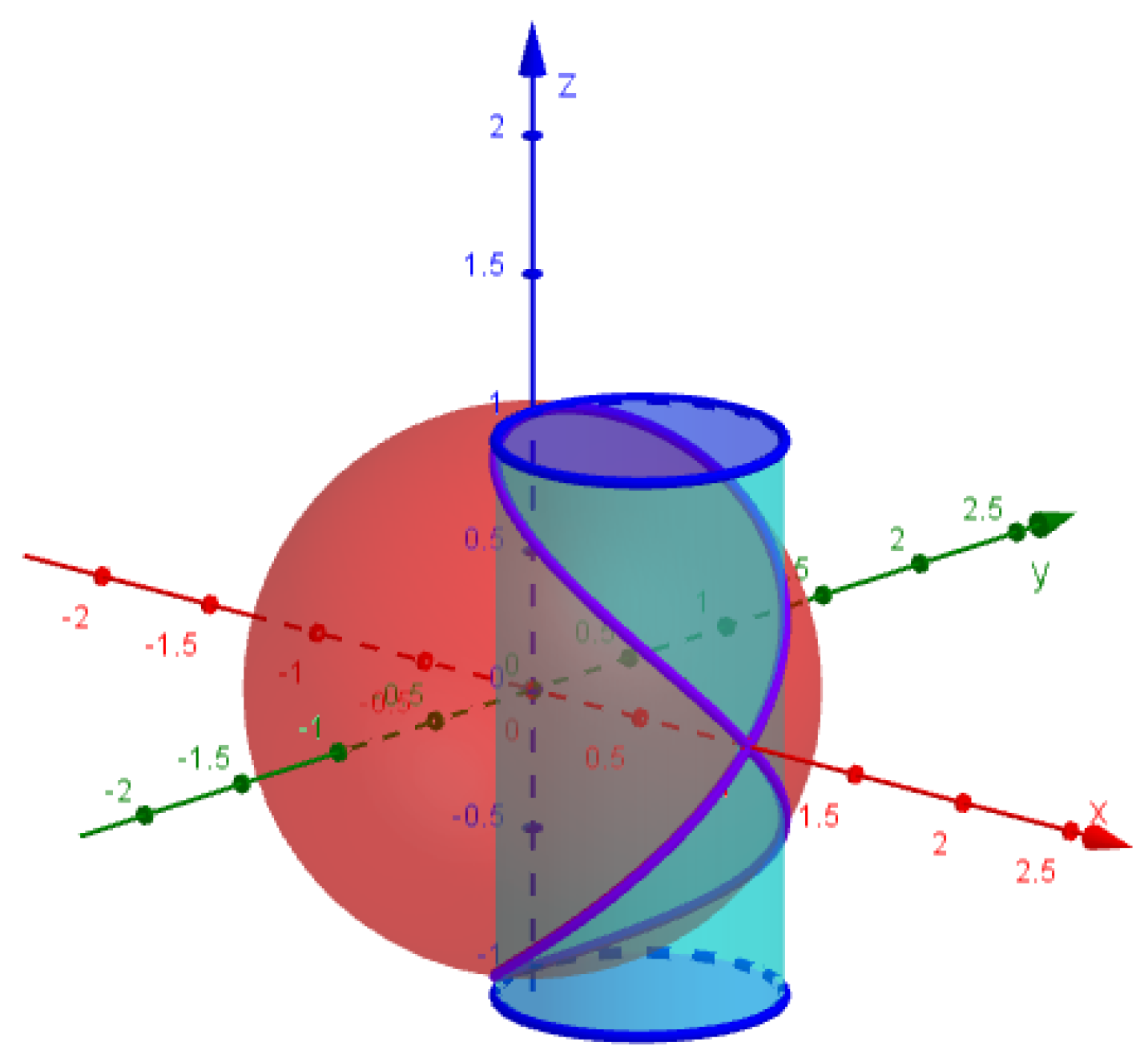
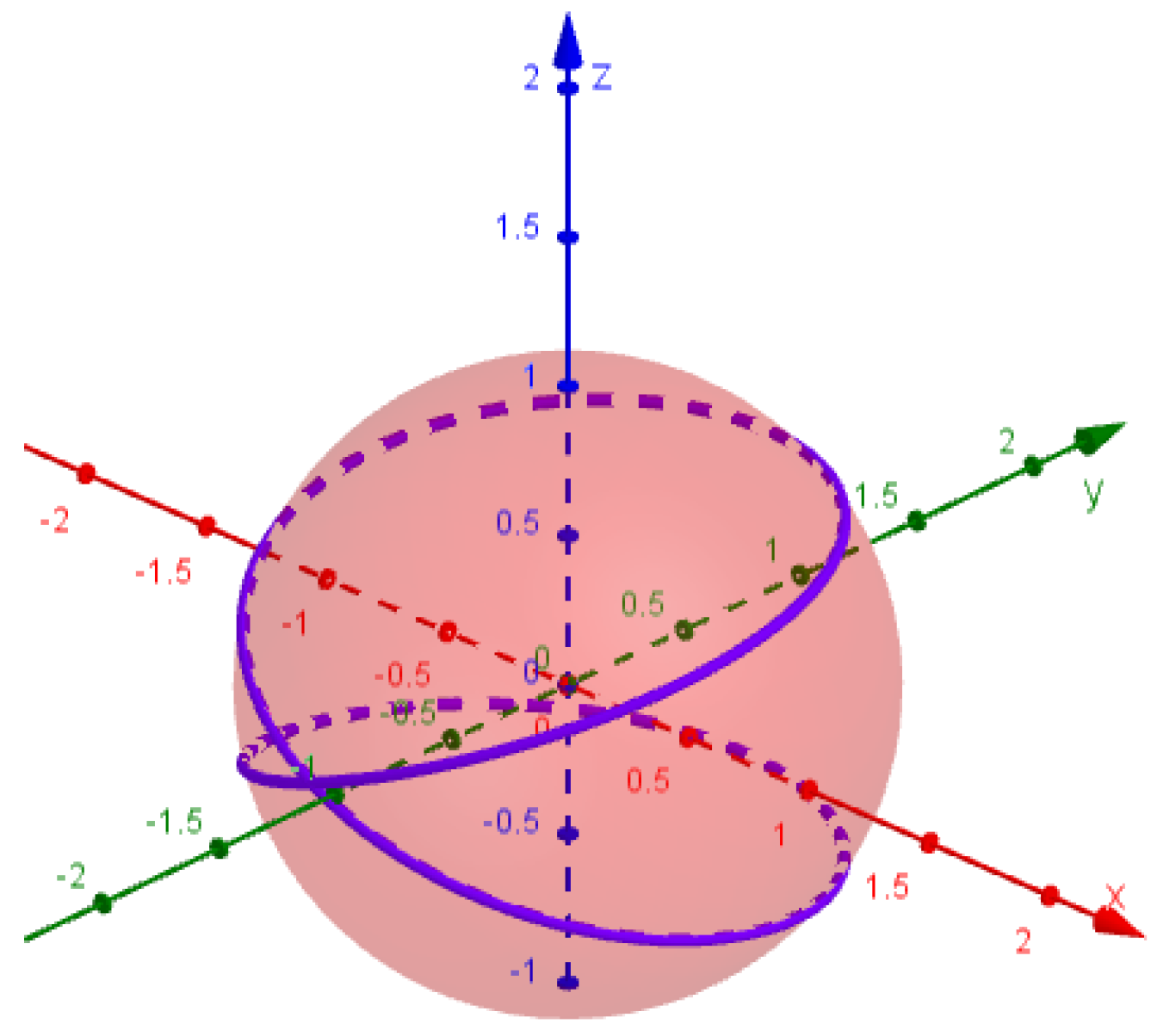
1. Introduction and Preliminaries
2. Special Smarandache Curves of Viviani’s Curve
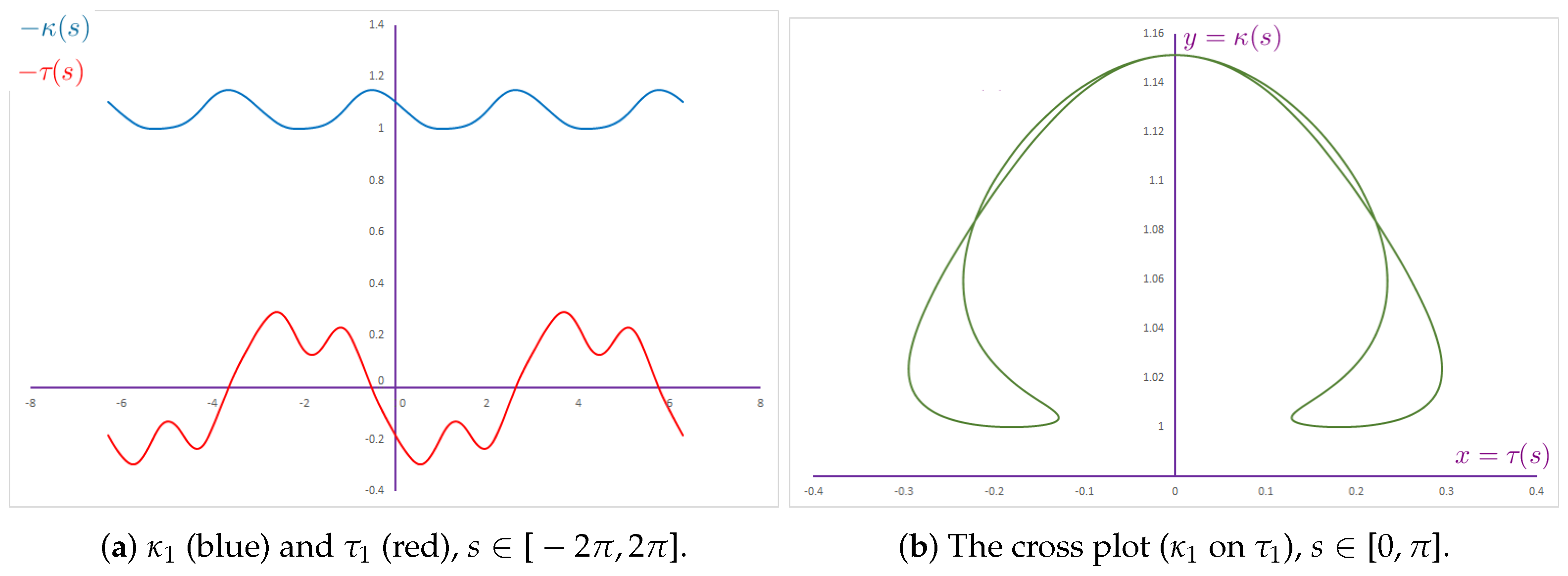
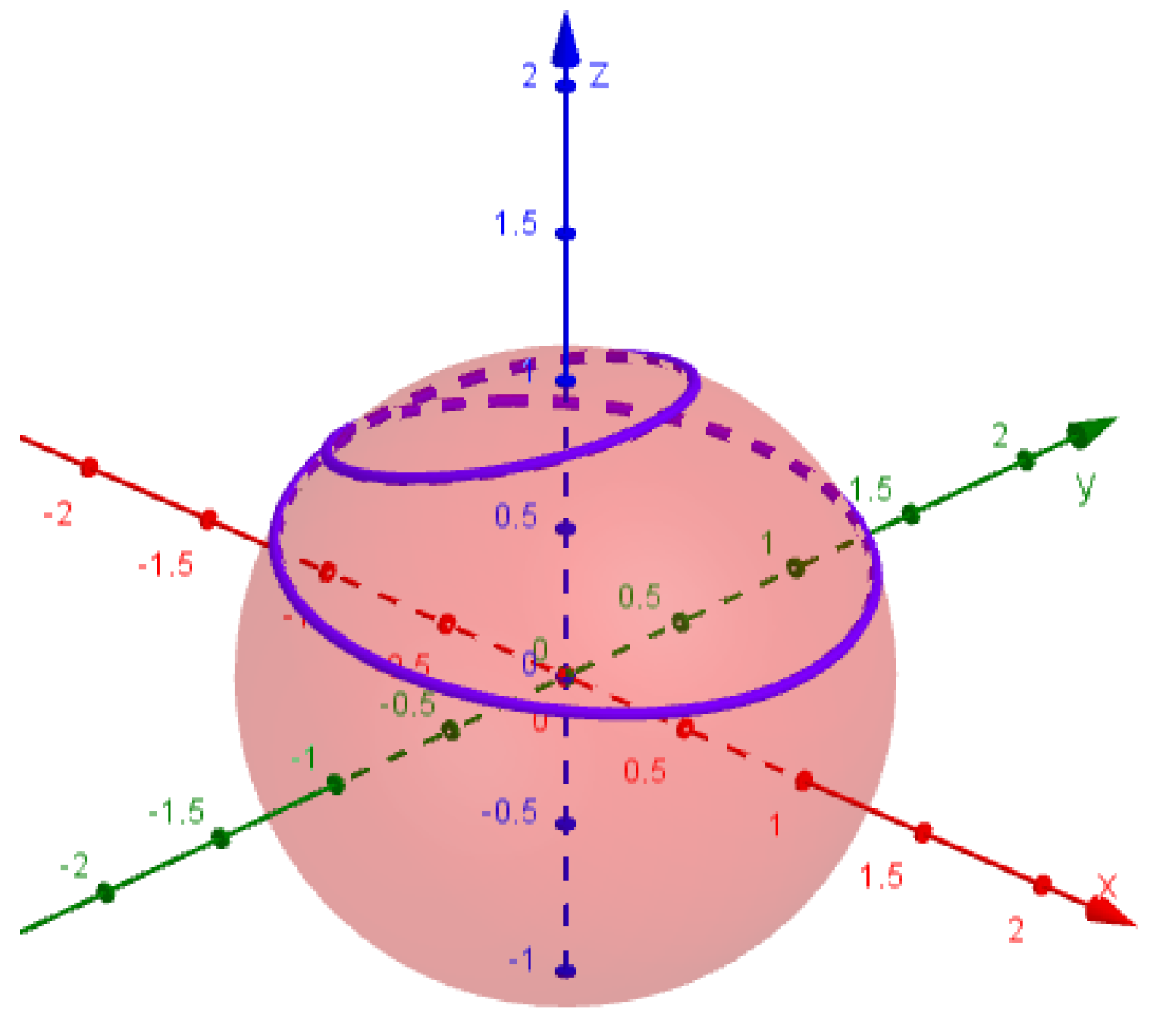
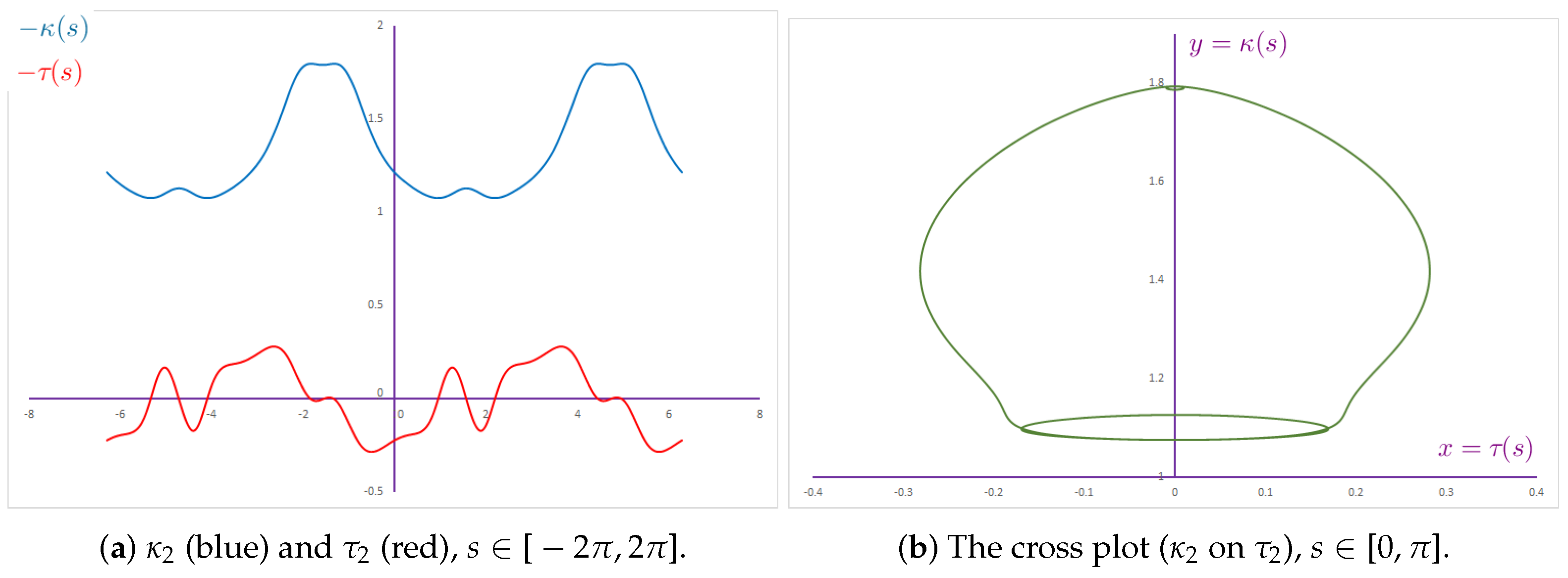
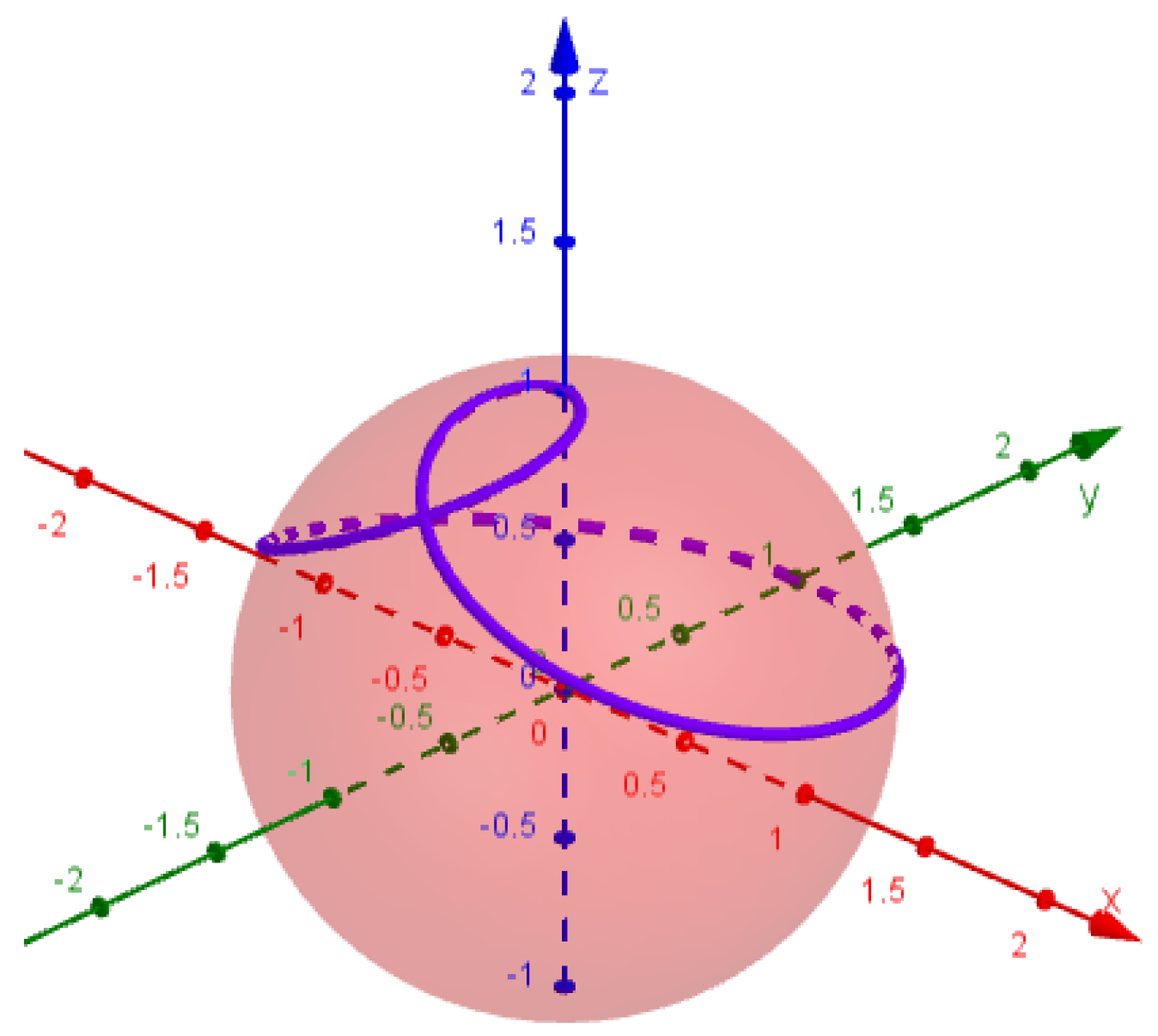
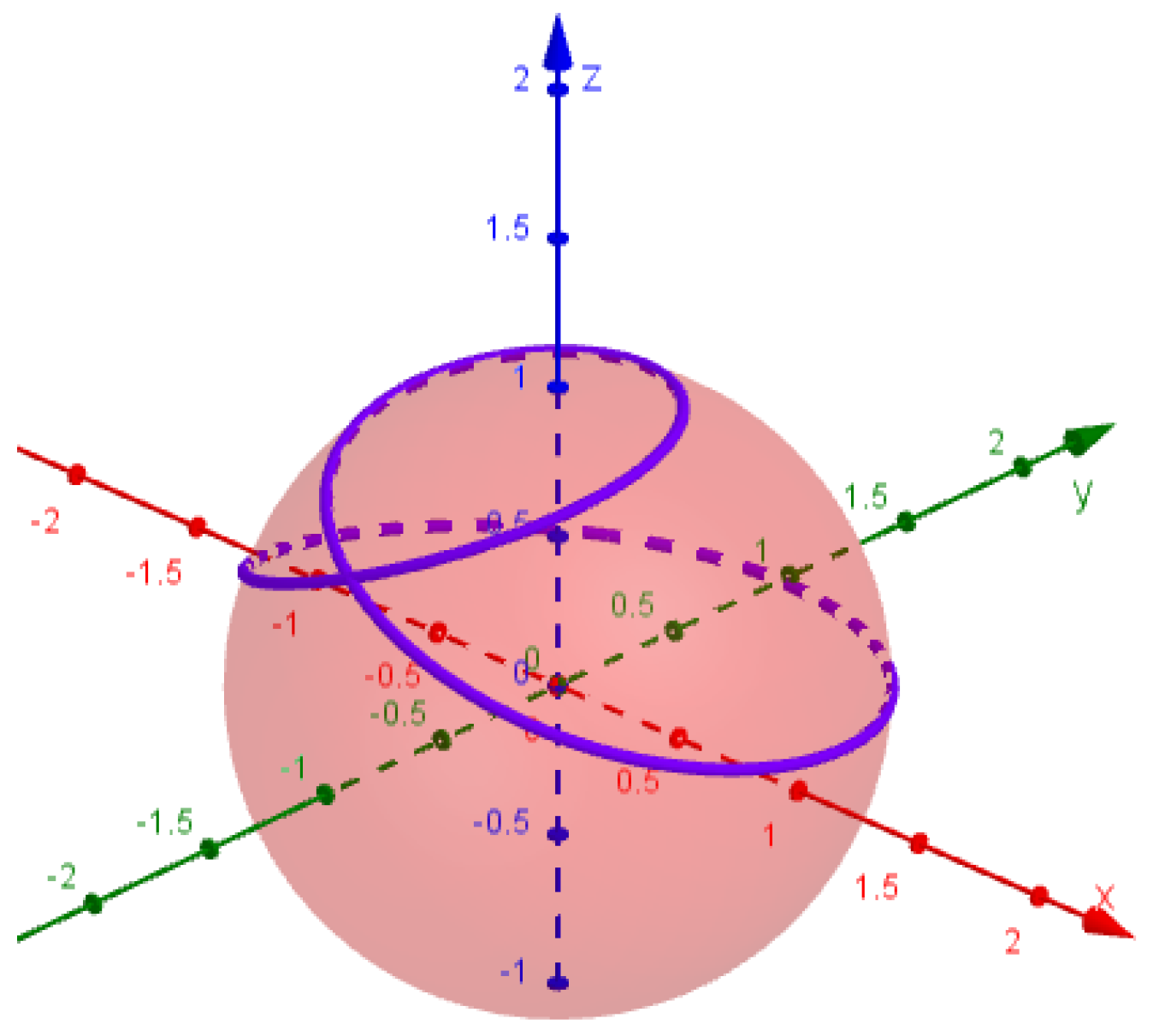
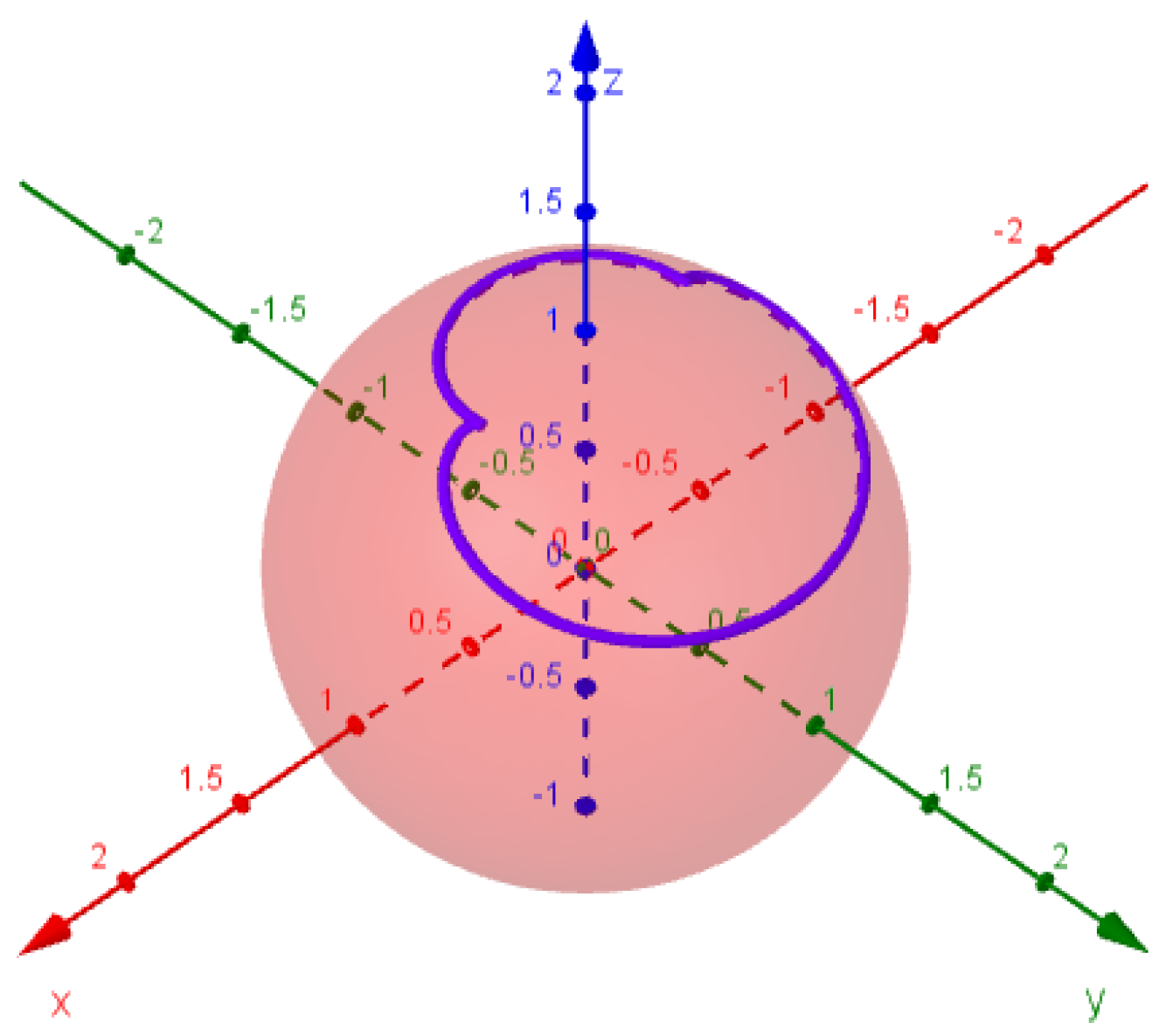
2.1. Smarandache Curve of Viviani’s Curve
2.2. Smarandache Curve of Viviani’s Curve
2.3. Smarandache Curve of Viviani’s Curve
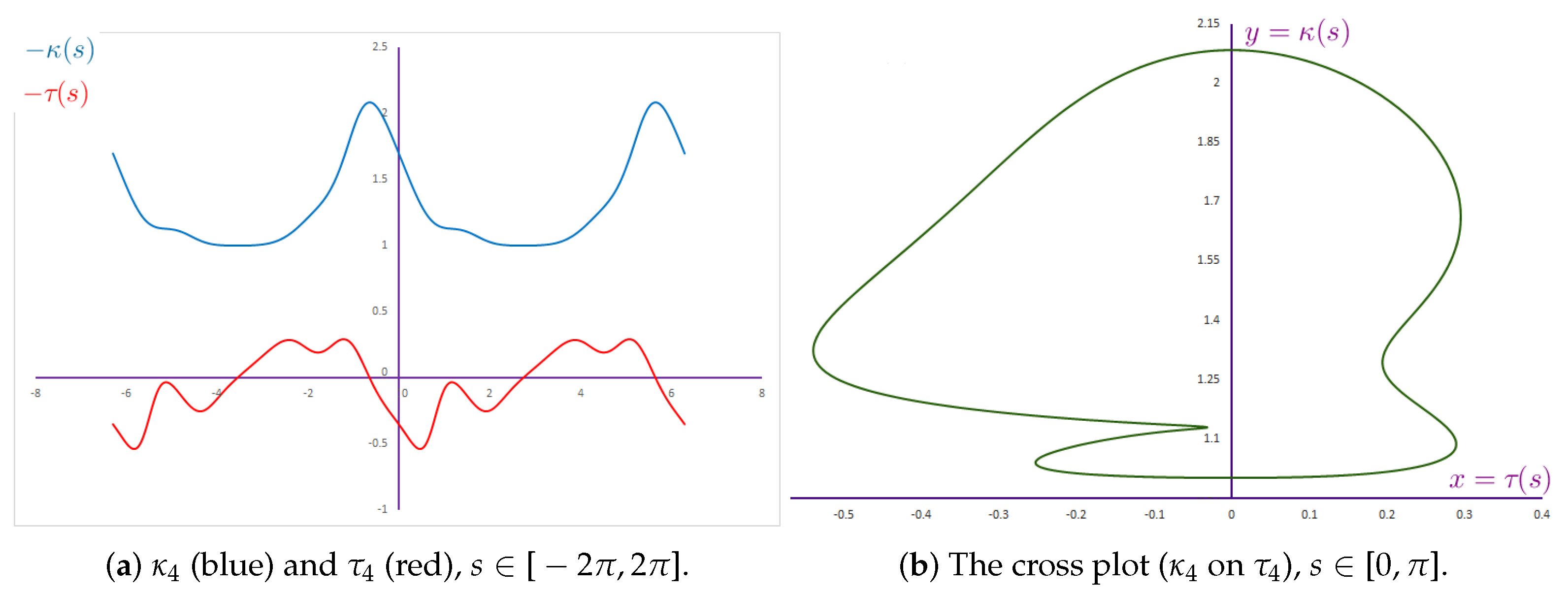
2.4. Smarandache Curve of Viviani’s Curve
2.5. Smarandache Curve of Viviani’s Curve
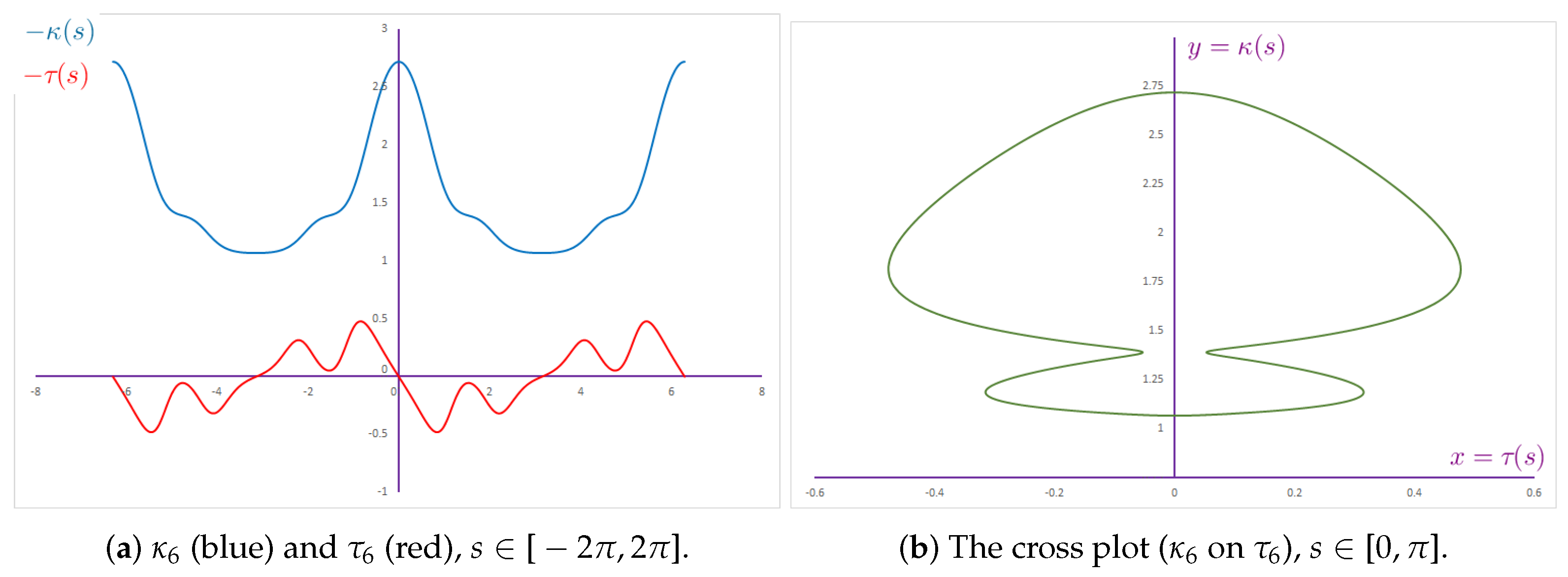
2.6. Smarandache Curve of Viviani’s Curve
2.7. Smarandache Curve of Viviani’s Curve
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
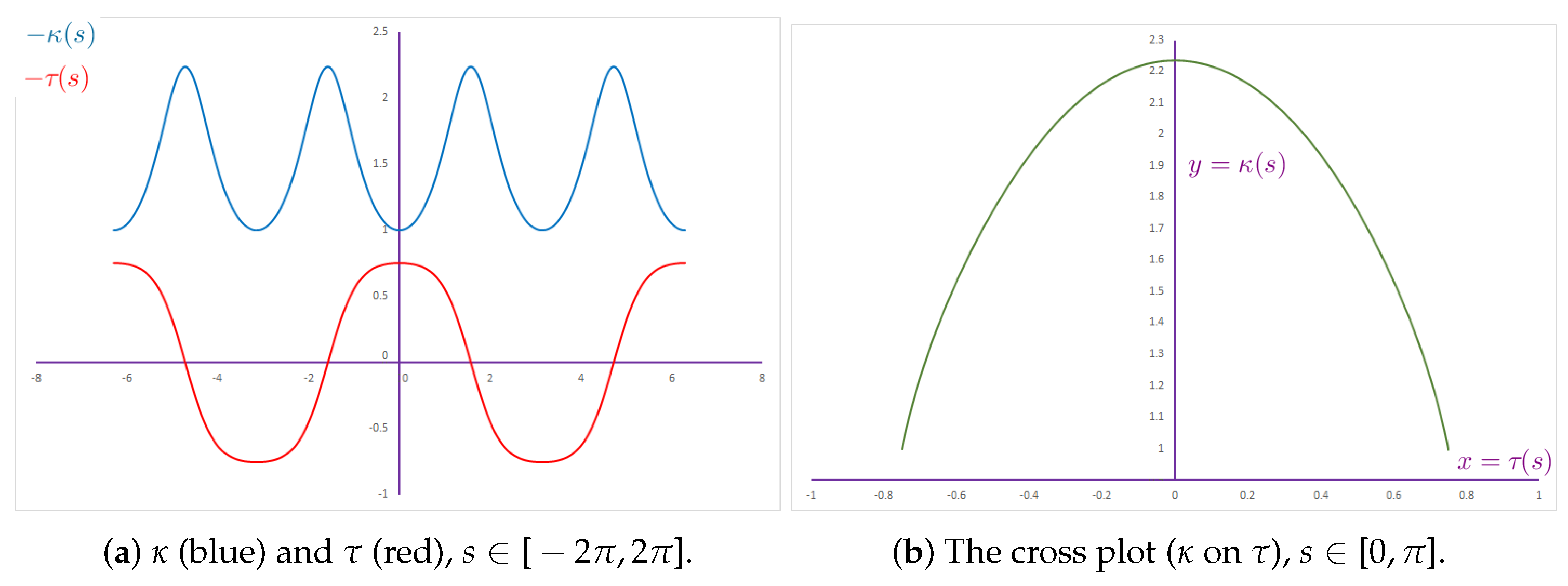
- Quadratic (parabolic curve) ;
- Exponential (normal (bell) curve ) ;
- Hyperbolic (Catenary’s chain curve) ;
- Rational (Gutschoven’s kappa curve)
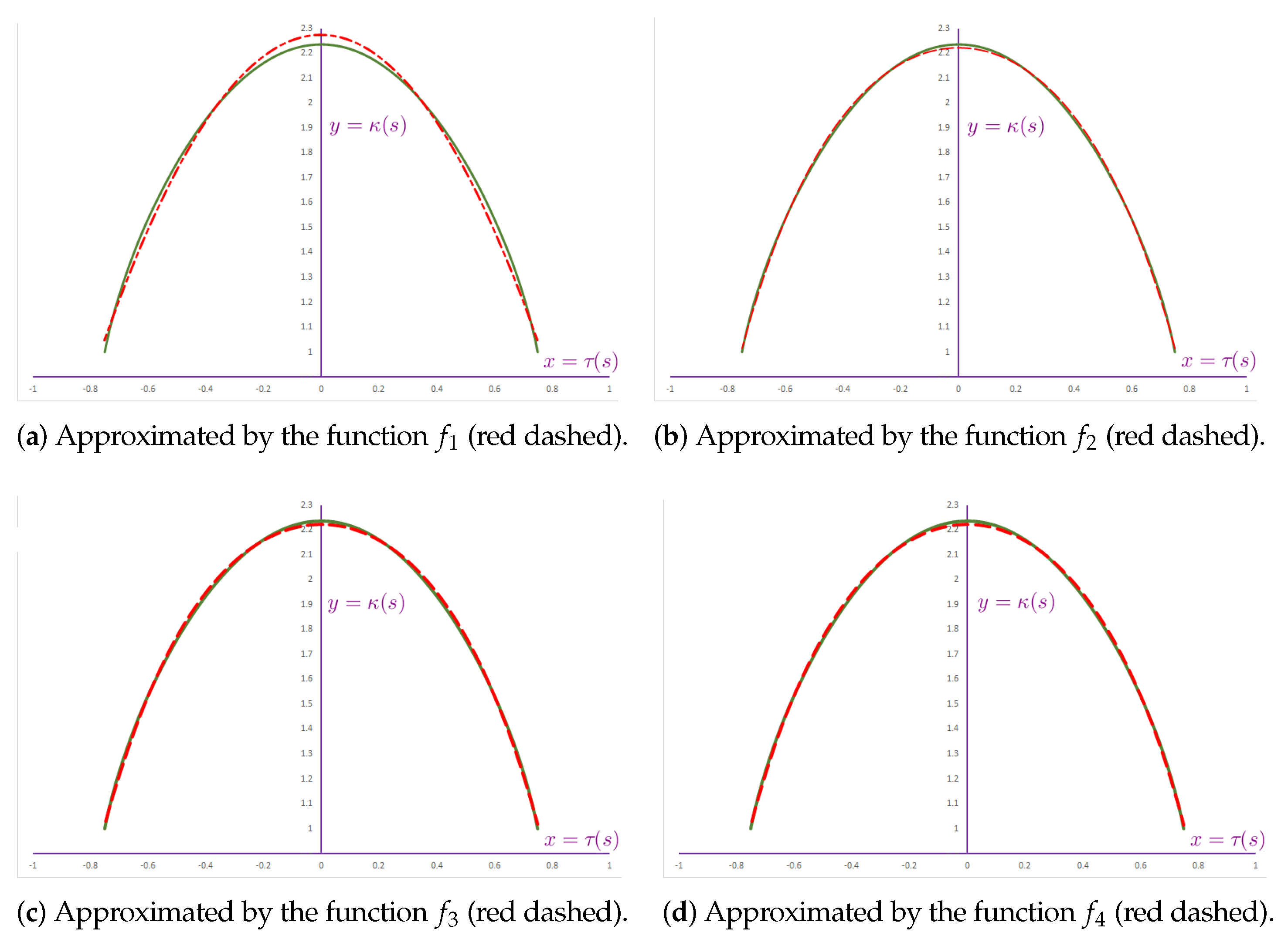
| Functional Form | Approximated Function with OLS Estimated Coefficients | SSE | RMSE | |
|---|---|---|---|---|
| Quadratic | 10.1 | 0.9945 | 0.032 | |
| Exponential | 1.112 | 0.9994 | 0.011 | |
| Hyperbolic | 1.217 | 0.9993 | 0.011 | |
| Rational (the best approx.) | 0.791 | 0.9996 | 0.009 |
References
- Lawrence, J.D. A Catalog of Special Plane Curves; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed.; CRC: Boca Raton, FL, USA, 1997. [Google Scholar]
- Havil, J. Curves for the Mathematically Curious; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Zhao, X.; Pei, D. Evolutoids of the Mixed-Type Curves. Adv. Math. Phy. 2021, 2021, 9330963. [Google Scholar] [CrossRef]
- Castro, I.; Castro-Infantes, I.; Castro-Infantes, J. New plane curves with curvature depending on distance from the origin. Mediterr. J. Math. 2017, 14, 1–19. [Google Scholar] [CrossRef]
- Izumiya, S.; Takeuchi, N. Evolutoids and pedaloids of plane curves. Note Mat. 2019, 39, 13–23. [Google Scholar]
- Struik, D.J. Lectures on Classical Differential Geometry; Courier Corporation: Chelmsford, MA, USA, 1961. [Google Scholar]
- Bertrand, J. Mémoire sur la théorie des courbes à double courbure. J. Math. Pures Appl. 1850, 15, 332–350. [Google Scholar]
- Mannheim, A. De l’emploi de la courbe représentative de la surface des normales principales d’une courbe gauche pour la démonstration de propriétés relatives à cette courbure. C. R. Comptes Rendus Séances l’Acad. Sci. 1878, 86, 1254–1256. [Google Scholar]
- Salkowski, E. Zur transformation von raumkurven. Math. Ann. 1909, 66, 517–557. [Google Scholar] [CrossRef]
- Monterde, J. Salkowski curves revisited: A family of curves with constant curvature and non-constant torsion. Comput. Aided Geom. Des. 2009, 26, 271–278. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, Y.H. Associated curves of a Frenet curve and their applications. Appl. Math. Comput. 2012, 218, 9116–9124. [Google Scholar] [CrossRef]
- Nurkan, S.K.; Güven, İ.A.; Karacan, M.K. Characterizations of adjoint curves in Euclidean 3-space. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2019, 89, 155–161. [Google Scholar] [CrossRef]
- Deshmukh, S.; Chen, B.Y.; Alghanemi, A. Natural mates of Frenet curves in Euclidean 3-space. Turk. J. Math. 2018, 42, 2826–2840. [Google Scholar] [CrossRef]
- Caddeo, R.; Montaldo, S.; Piu, P. The Mobius strip and Viviani’s windows. Math. Intell. 2001, 23, 36–40. [Google Scholar] [CrossRef]
- Ferreol, R. Viviani Curve. Available online: https://mathcurve.com/courbes3d.gb/viviani/viviani.shtml (accessed on 1 April 2023).
- Goemans, W.; de Woestyne, I.V. Clelia curves, twisted surfaces and Plücker’s conoid in Euclidean and Minkowski 3-space. In Recent Advances in the Geometry of Submanifolds: Dedicated to the Memory of Franki Dillen (1963–2013); American Mathematical Society: Providence, RI, USA, 2016; Volume 674, p. 59. [Google Scholar]
- Taner, T. Geometry of Spherical Viviani’s Curves in R 3 1 Lorentz-Minkowski 3-Space. Unpublished Doctoral Thesis, The Institute of Science, Manisa Celal Bayar University, Manisa, Türkiye, 2021. [Google Scholar]
- Graefe, E.M.; Korsch, H.J.; Strzys, M.P. Bose–Hubbard dimers, Viviani’s windows and pendulum dynamics. J. Phys. Math. Theor. 2014, 47, 085304. [Google Scholar] [CrossRef]
- Song, X.; Pei, D. Dual framed surfaces of traveling trajectories of geometrical particles. Mod. Phys. Lett. A 2025, 2025, 2550002. [Google Scholar] [CrossRef]
- Li, P.; Pei, D. Nullcone fronts of spacelike framed curves in Minkowski 3-space. Mathematics 2021, 9, 2939. [Google Scholar] [CrossRef]
- Zhu, M.; Yang, H.; Li, Y.; Abdel-Baky, R.A.; Al-Jedani, A.; Khalifa, M. Directional developable surfaces and their singularities in Euclidean 3-space. Filomat 2024, 38, 11333–11347. [Google Scholar]
- Li, Y.; Eren, K.; Ersoy, S.; Savic, A. Modified Sweeping Surfaces in Euclidean 3-Space. Axioms 2024, 13, 800. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Eren, K.; Ersoy, S. Sweeping Surfaces of Polynomial Curves in Euclidean 3-space. An. St. Univ. Ovidius Constanta 2025, 33, 293–311. [Google Scholar]
- Aldossary, M.T.; Abdel-Baky, R.A. Sweeping surface due to rotation minimizing Darboux frame in Euclidean 3-space E3. AIMS Math. 2022, 8, 447–462. [Google Scholar] [CrossRef]
- Li, Y.; Mallick, A.K.; Bhattacharyya, A.; Stankovic, M.S. A Conformal η-Ricci Soliton on a Four-Dimensional Lorentzian Para-Sasakian Manifold. Axioms 2024, 13, 753. [Google Scholar] [CrossRef]
- Li, Y.; Bouleryah, M.L.H.; Ali, A. On Convergence of Toeplitz Quantization of the Sphere. Mathematics 2024, 12, 3565. [Google Scholar] [CrossRef]
- Honda, S.; Takahashi, M. Framed curves in the Euclidean space. Adv. Geom. 2016, 16, 265–276. [Google Scholar] [CrossRef]
- Fukunaga, T.; Takahashi, M. Existence conditions of framed curves for smooth curves. J. Geom. 2017, 108, 763–774. [Google Scholar] [CrossRef]
- Huang, J.; Pei, D. Singularities of Non-Developable Surfaces in Three-Dimensional Euclidean Space. Mathematics 2019, 7, 1106. [Google Scholar] [CrossRef]
- Li, Y.; Siddesha, M.S.; Kumara, H.A.; Praveena, M.M. Characterization of Bach and Cotton Tensors on a Class of Lorentzian Manifolds. Mathematics 2024, 12, 3130. [Google Scholar] [CrossRef]
- Cao, L.; Xu, G.; Dai, Z. A New Characterization of totally umbilical hypersurfaces in de Sitter space. Adv. Pure Math. 2014, 4, 42–46. [Google Scholar] [CrossRef]
- Li, Y.; Bin-Asfour, M.; Albalawi, K.S.; Guediri, M. Spacelike Hypersurfaces in de Sitter Space. Axioms 2025, 14, 155. [Google Scholar] [CrossRef]
- Smarandache, F. Mixed noneuclidean geometries. arXiv 1991, arXiv:math/0010119. [Google Scholar]
- Mao, L.F. Smarandache Multi-Space Theory. In Partially Post-Doctoral Research for the Chinese Academy of Sciences; HEXIS: Phoenix, AZ, USA, 2006. [Google Scholar]
- Turgut, M.; Yılmaz, S. Smarandache Curves in Minkowski Spacetime. Int. J. Math. Comb. 2008, 3, 51–55. [Google Scholar]
- Ali, A.T. Special Smarandache curves in the Euclidean space. Int. J. Math. Comb. 2010, 2, 30–36. [Google Scholar]
- Do-Carmo, P. Differential Geometry of Curves and Surfaces; IMPA: London, UK; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Abdel-Aziz, H.S.; Saad, M.K. Computation of Smarandache curves according to Darboux frame in Minkowski 3-space. J. Egypt. Math. Soc. 2017, 25, 382–390. [Google Scholar] [CrossRef]
- Bektaş, Ö.; Yüce, S. Special Smarandache Curves According to Darboux Frame in E3. Rom. J. Math. Comput. Sci. 2013, 3, 48–59. [Google Scholar]
- Çalışkan, A.; Şenyurt, S. Smarandache curves in terms of Sabban frame of spherical indicatrix curves. Gen. Math. Notes 2015, 31, 1–15. [Google Scholar]
- Çetin, M.; Tuncer, Y.; Karacan, M.K. Smarandache curves according to Bishop frame in Euclidean 3-space. Gen. Math. Notes 2014, 20, 50–66. [Google Scholar]
- Çetin, M.; Kocayigit, H. On the quaternionic Smarandache curves in Euclidean 3-space. Int. J. Contemp. Math. Sci. 2013, 8, 139–150. [Google Scholar] [CrossRef]
- Elzawy, M.; Mosa, S. Smarandache curves in the Galilean 4-space G4. J. Egypt. Math. Soc. 2017, 25, 53–56. [Google Scholar] [CrossRef]
- Gürses, N.B.; Bektaş, O.; Yüce, S. Special Smarandache curves in R31. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2016, 65, 143–160. [Google Scholar] [CrossRef]
- Kahraman, T.; Uğurlu, H. Dual smarandache curves and smarandache ruled surfaces. Math. Sci. Appl. E-Notes 2014, 2, 83–98. [Google Scholar]
- Ozturk, E.B.K.; Ozturk, U.; İlarslan, K.; Nešović, E. On pseudohyperbolical Smarandache curves in Minkowski 3-space. Int. J. Math. Math. Sci. 2013, 2013, 658–670. [Google Scholar] [CrossRef]
- Saad, M.K. Spacelike and timelike admissible Smarandache curves in pseudo-Galilean space. J. Egypt. Math. Soc. 2016, 24, 416–423. [Google Scholar] [CrossRef]
- Taşköprü, K.; Tosun, M. Smarandache Curves on S2. Bol. Soc. Parana. Mat. 3 Srie 2014, 32, 51–59. [Google Scholar] [CrossRef]
- The University of New Mexico. Smarandache Geometries. Available online: https://fs.unm.edu/SG/ (accessed on 3 April 2025).





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Li, Y.; Şenyurt, S.; Canlı, D.; Gürler, İ. On the Special Viviani’s Curve and Its Corresponding Smarandache Curves. Mathematics 2025, 13, 1526. https://doi.org/10.3390/math13091526
Deng Y, Li Y, Şenyurt S, Canlı D, Gürler İ. On the Special Viviani’s Curve and Its Corresponding Smarandache Curves. Mathematics. 2025; 13(9):1526. https://doi.org/10.3390/math13091526
Chicago/Turabian StyleDeng, Yangke, Yanlin Li, Süleyman Şenyurt, Davut Canlı, and İremnur Gürler. 2025. "On the Special Viviani’s Curve and Its Corresponding Smarandache Curves" Mathematics 13, no. 9: 1526. https://doi.org/10.3390/math13091526
APA StyleDeng, Y., Li, Y., Şenyurt, S., Canlı, D., & Gürler, İ. (2025). On the Special Viviani’s Curve and Its Corresponding Smarandache Curves. Mathematics, 13(9), 1526. https://doi.org/10.3390/math13091526







