Optimizing Fuel Economy in Hybrid Electric Vehicles Using the Equivalent Consumption Minimization Strategy Based on the Arithmetic Optimization Algorithm
Abstract
1. Introduction
1.1. Research Background
1.2. Literature Review
- Disciplined optimum control refers to direct approaches.
1.3. Motivation and Novelty
- -
- To create a cutting-edge power management system (EMS) for FCEVs that optimizes power distribution, reduces fuel consumption, and maximizes electrical efficiency. The Arithmetic Optimization Algorithm (AOA) is incorporated into the proposed EMS to optimize the external energy maximization strategy (ECMS).
2. Architecture for FCEVs
2.1. Model for Vehicle Traction
2.2. Hydrogen Consumption Model for FCs
2.3. Estimation of Battery SOC
3. The Suggested Approach for Energy Management
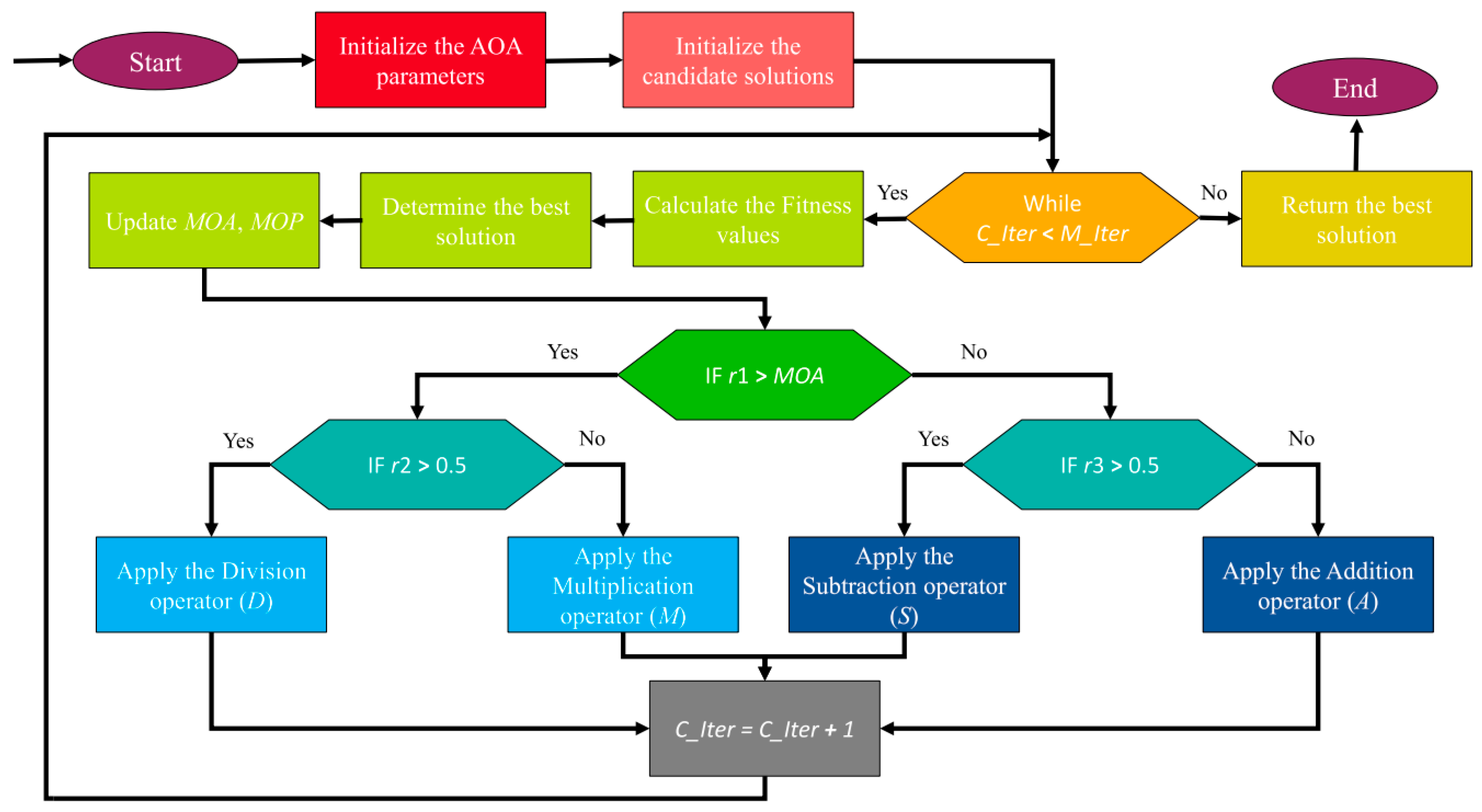
Arithmetic Optimization Algorithm
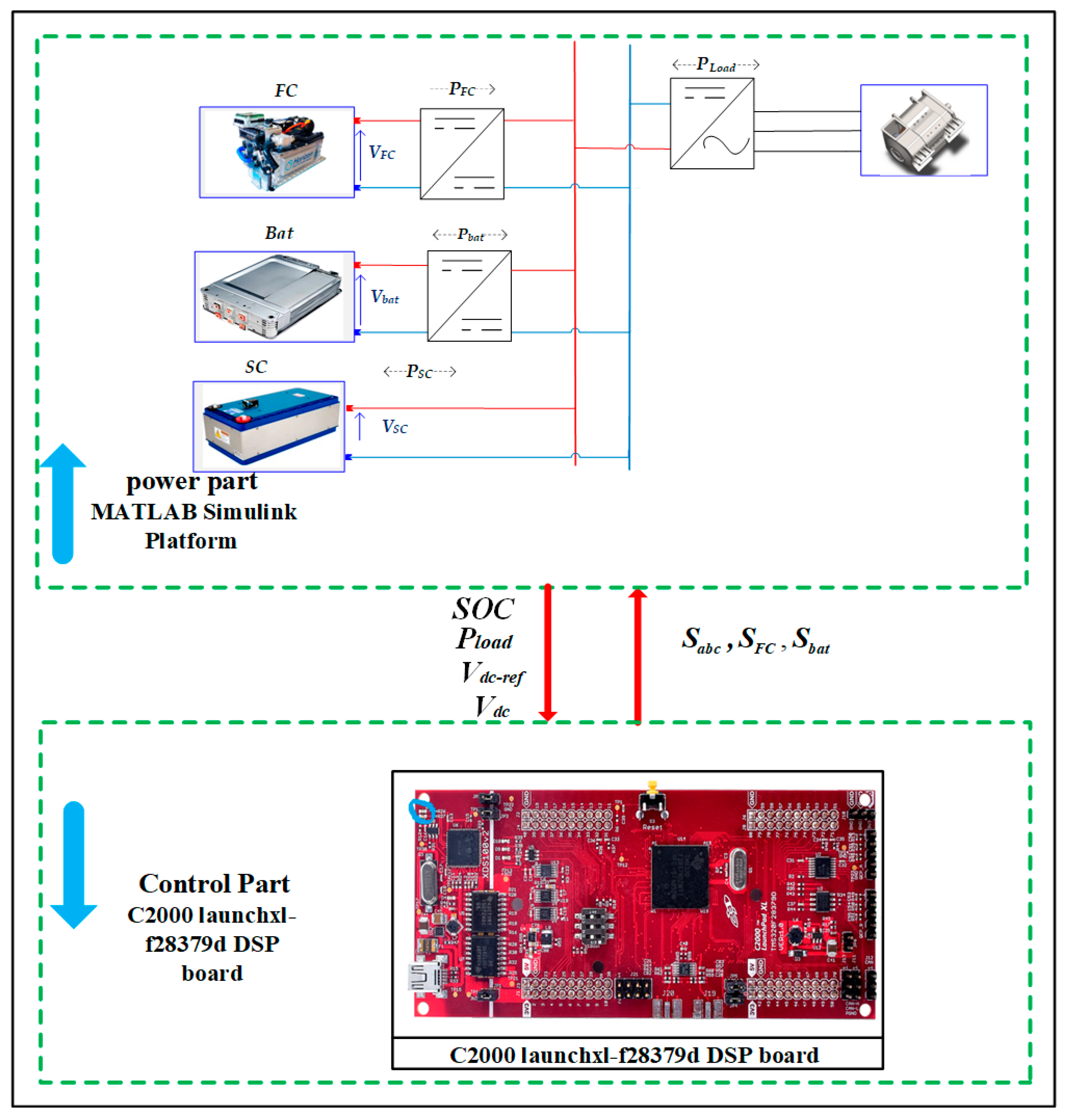
4. Implementation of Control Algorithms Using the PIL Technique
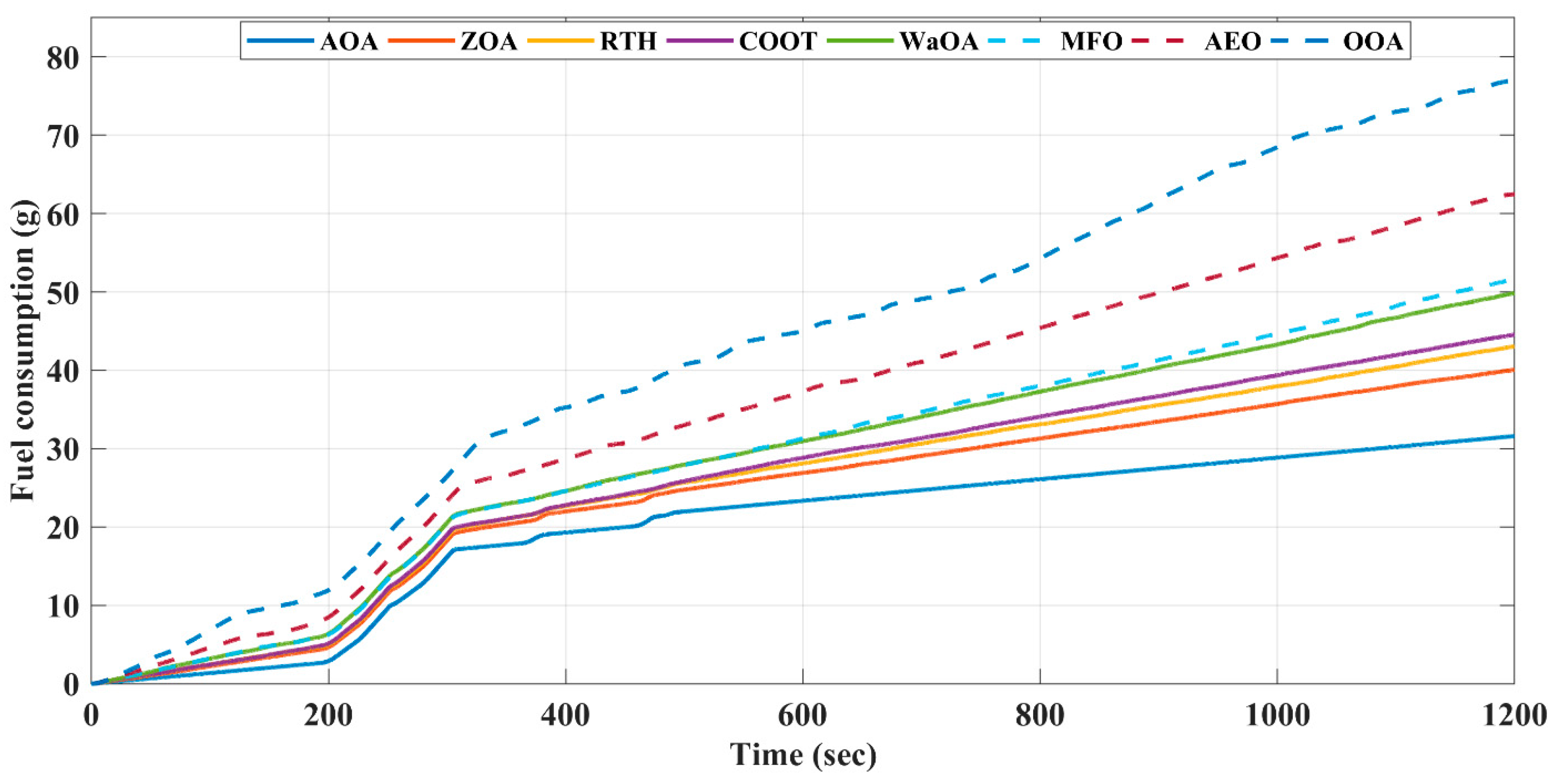
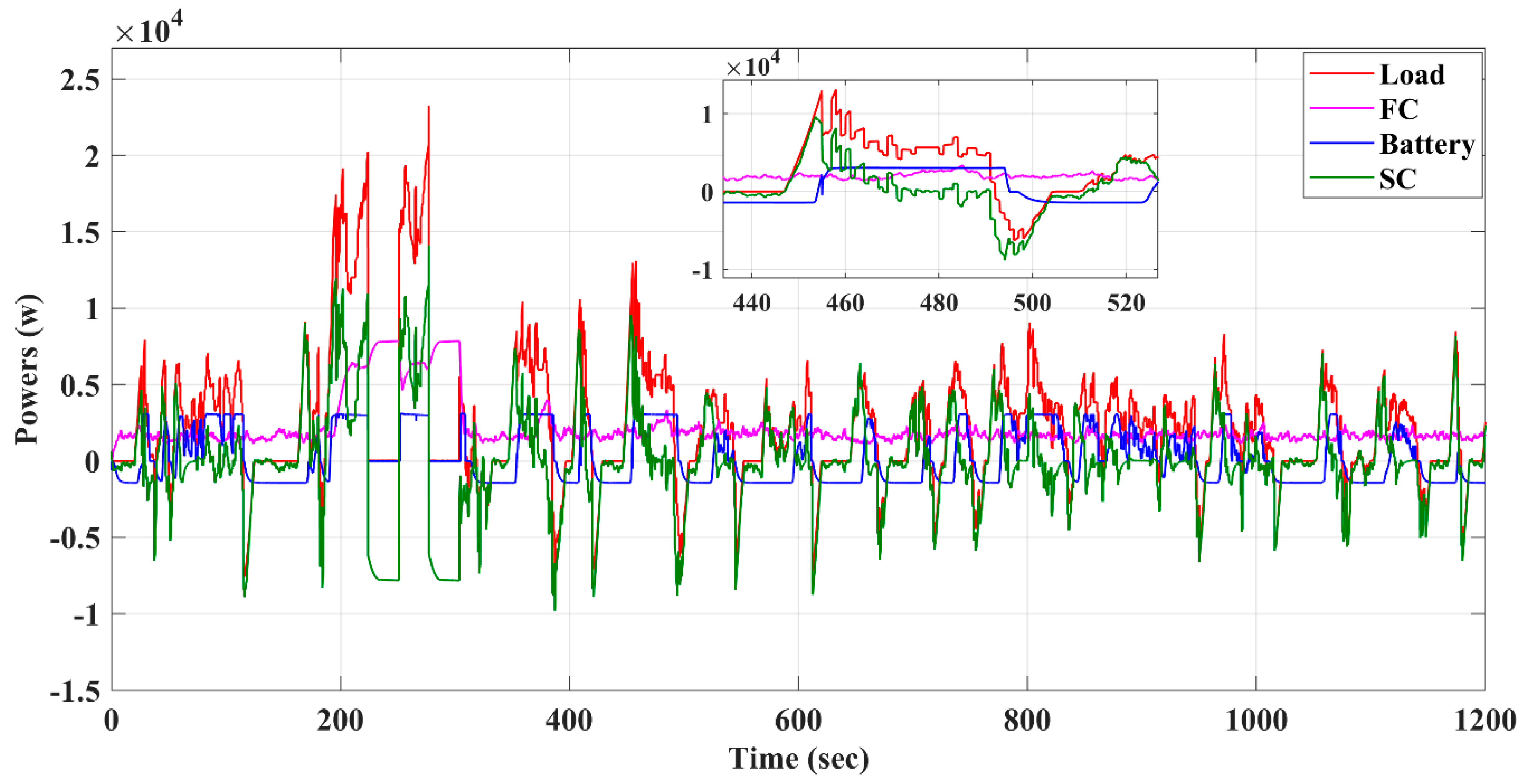
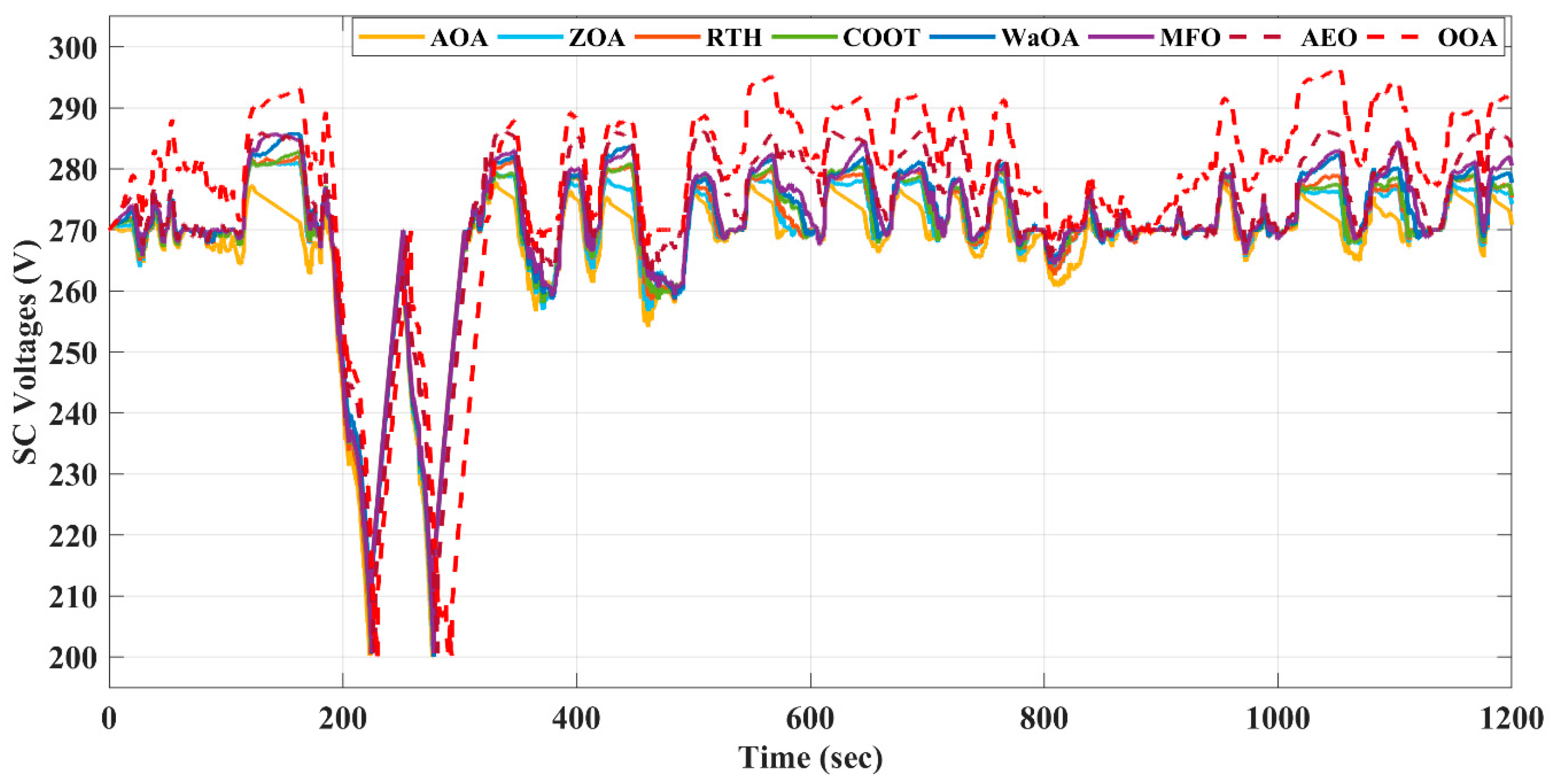
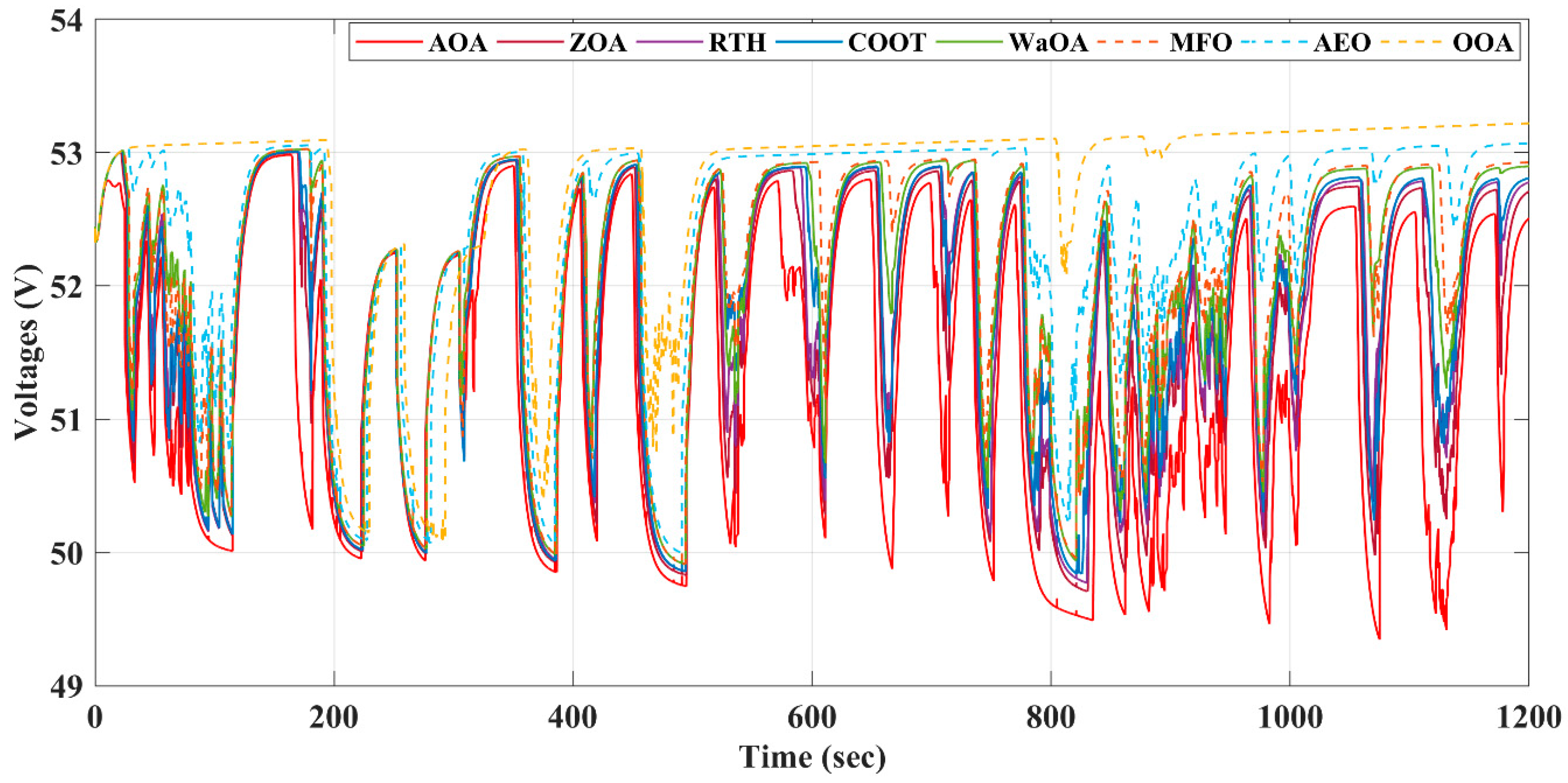
5. Findings and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Babangida, A.; Light Odazie, C.M.; Szemes, P.T. Optimal Control Design and Online Controller-Area-Network Bus Data Analysis for a Light Commercial Hybrid Electric Vehicle. Mathematics 2023, 11, 3436. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, N.; Fan, G.; Yang, D.; Rao, L.; Cheng, S.; Song, X. DLPformer: A Hybrid Mathematical Model for State of Charge Prediction in Electric Vehicles Using Machine Learning Approaches. Mathematics 2023, 11, 4635. [Google Scholar] [CrossRef]
- Roustai, M.; Rayati, M.; Sheikhi, A.; Ranjbar, A.M. A scenario-based optimization of Smart Energy Hub operation in a stochastic environment using conditional-value-at-risk. Sustain. Cities Soc. 2018, 39, 309–316. [Google Scholar] [CrossRef]
- Rimpas, D.; Kaminaris, S.D.; Piromalis, D.D.; Vokas, G. Real-Time Management for an EV Hybrid Storage System Based on Fuzzy Control. Mathematics 2023, 11, 4429. [Google Scholar] [CrossRef]
- Alshammari, N.F.; Samy, M.M.; Barakat, S. Comprehensive Analysis of Multi-Objective Optimization Algorithms for Sustainable Hybrid Electric Vehicle Charging Systems. Mathematics 2023, 11, 1741. [Google Scholar] [CrossRef]
- Mohammed, O.A.A.; Peng, L.; Hamid, G.H.A.; Ishag, A.M.; Abdalla, M.A.A. Effective Energy Management Strategy with Model-Free DC-Bus Voltage Control for Fuel Cell/Battery/Supercapacitor Hybrid Electric Vehicle System. Mathematics 2023, 11, 944. [Google Scholar] [CrossRef]
- Rudolf, T.; Schurmann, T.; Schwab, S.; Hohmann, S. Toward Holistic Energy Management Strategies for Fuel Cell Hybrid Electric Vehicles in Heavy-Duty Applications. Proc. IEEE 2021, 109, 1094–1114. [Google Scholar] [CrossRef]
- Aouzellag, H.; Amrouche, B.; Iffouzar, K.; Aouzellag, D. Proposed hysteresis energy management strategy based on storage system efficiency for hybrid electric vehicle. J. Energy Storage 2022, 54, 105259. [Google Scholar] [CrossRef]
- Fallah Ghavidel, H.; Mousavi-G, S.M. Modeling analysis, control, and type-2 fuzzy energy management strategy of hybrid fuel cell-battery-supercapacitor systems. J. Energy Storage 2022, 51, 104456. [Google Scholar] [CrossRef]
- Hu, H.; Yuan, W.W.; Su, M.; Ou, K. Optimizing fuel economy and durability of hybrid fuel cell electric vehicles using deep reinforcement learning-based energy management systems. Energy Convers. Manag. 2023, 291, 117288. [Google Scholar] [CrossRef]
- Hu, H.; Tan, J.; Chen, C.; Lu, C.; Xuan, D. Energy management strategy for fuel cell hybrid vehicles considering optimal performance of multiple energy sources combined with ant colony algorithm. Energy Storage 2022, 4, e381. [Google Scholar] [CrossRef]
- Payakkamas, P.; de Kraker, J.; Dijk, M. Transformation of the Urban Energy–Mobility Nexus: Implications for Sustainability and Equity. Sustainability 2023, 15, 1328. [Google Scholar] [CrossRef]
- Veziroglu, A.; MacArio, R. Fuel cell vehicles: State of the art with economic and environmental concerns. Int. J. Hydrog. Energy 2011, 36, 25–43. [Google Scholar] [CrossRef]
- Arat, H.T. Alternative fuelled hybrid electric vehicle (AF-HEV) with hydrogen enriched internal combustion engine. Int. J. Hydrog. Energy 2019, 44, 19005–19016. [Google Scholar] [CrossRef]
- Changizian, S.; Ahmadi, P.; Raeesi, M.; Javani, N. Performance optimization of hybrid hydrogen fuel cell-electric vehicles in real driving cycles. Int. J. Hydrog. Energy 2020, 45, 35180–35197. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Abapour, M.; Mohammadi-Ivatloo, B. An Updated Review and Outlook on Electric Vehicle Aggregators in Electric Energy Networks. Sustainability 2022, 14, 15747. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, W.; Xu, S.; Yan, Y.; Huang, L.; Wang, J.; Hao, W.; Yang, Z. Electric Vehicle Lithium-Ion Battery Fault Diagnosis Based on Multi-Method Fusion of Big Data. Sustainability 2023, 15, 1120. [Google Scholar] [CrossRef]
- Sorlei, I.S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel Cell Electric Vehicles—A Brief Review of Current Topologies and Energy Management Strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Djerioui, A.; Houari, A.; Zeghlache, S.; Wolf, G. ScienceDirect Energy management strategy of Supercapacitor / Fuel Cell energy storage devices for vehicle applications. Int. J. Hydrog. Energy 2019, 44, 23416–23428. [Google Scholar] [CrossRef]
- Guan, C.; Liu, Z. Real-Time Optimization Energy Management Strategy for Fuel Cell Hybrid Ships Considering Power Sources Degradation. IEEE Access 2020, 8, 87046–87059. [Google Scholar] [CrossRef]
- Eddine, G.H.; Said, B.; Houari, A.; Djeroui, A.; Mesbahi, T.; Abdelhak, H. Energy Management Strategy for Hybrid Power System Implemented with Processor in the Loop. In Proceedings of the 2022 IEEE International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 26–28 October 2022. [Google Scholar] [CrossRef]
- Ghadbane, H.E.; Barkat, S.; Houari, A.; Ferahtia, S.; Djerioui, A.; Mesbahi, T. A New Energy Management Strategy for Electric Vehicles Based on Optimal Adaptive State Machine Control. Smart Grids Sustain. Energy 2024, 9, 28. [Google Scholar] [CrossRef]
- Ghadbane, H.E.; Barkat, S.; Houari, A.; Ferahtia, S.; Djerioui, A.; Mesbahi, T. Load Following Energy Management Strategy for a Battery-Supercapacitor Hybrid Power System Implemented with a PIL Co-Simulation Approach. Smart Grids Sustain. Energy 2024, 9, 32. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Majlan, E.H.; Wan Daud, W.R. A review on energy management system for fuel cell hybrid electric vehicle: Issues and challenges. Renew. Sustain. Energy Rev. 2015, 52, 802–814. [Google Scholar] [CrossRef]
- Rahman, A.U.; Zehra, S.S.; Ahmad, I.; Armghan, H. Fuzzy supertwisting sliding mode-based energy management and control of hybrid energy storage system in electric vehicle considering fuel economy. J. Energy Storage 2021, 37, 102468. [Google Scholar] [CrossRef]
- Bauer, S.; Suchaneck, A.; Puente León, F. Thermal and energy battery management optimization in electric vehicles using Pontryagin’s maximum principle. J. Power Sources 2014, 246, 808–818. [Google Scholar] [CrossRef]
- Peng, H.; Li, J.; Löwenstein, L.; Hameyer, K. A scalable, causal, adaptive energy management strategy based on optimal control theory for a fuel cell hybrid railway vehicle. Appl. Energy 2020, 267, 114987. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K. Learning-based model predictive energy management for fuel cell hybrid electric bus with health-aware control. Appl. Energy 2024, 355, 122228. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K.; Shi, M. A novel energy management strategy for hybrid electric bus with fuel cell health and battery thermal- and health-constrained awareness. Energy 2023, 271, 127105. [Google Scholar] [CrossRef]
- Wang, K.; Xue, Y.; Shahidehpour, M.; Chang, X.; Li, Z.; Zhou, Y.; Sun, H. Resilience-Oriented Two-Stage Restoration Considering Coordinated Maintenance and Reconfiguration in Integrated Power Distribution and Heating Systems. IEEE Trans. Sustain. Energy 2024, 16, 124–137. [Google Scholar] [CrossRef]
- Zhai, X.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Wang, P.; Sun, H. Risk-averse energy management for integrated electricity and heat systems considering building heating vertical imbalance: An asynchronous decentralized approach. Appl. Energy 2025, 383, 125271. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Tona, T.L.F.V.P. Stochastic Dynamic Programming based Energy Management of HEV ’ s: An Experimental Validation. IFAC Proc. Vol. 2014, 47, 4813–4818. [Google Scholar]
- Lei, Z.; Qin, D.; Hou, L.; Peng, J.; Liu, Y.; Chen, Z. An adaptive equivalent consumption minimization strategy for plug-in hybrid electric vehicles based on traffic information. Energy 2020, 190, 116409. [Google Scholar] [CrossRef]
- Serrao, L.; Onori, S.; Rizzoni, G. ECMS as a realization of pontryagin’s minimum principle for HEV control. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3964–3969. [Google Scholar] [CrossRef]
- Zheng, C.H.; Xu, G.Q.; Cha, S.W.; Liang, Q. Numerical comparison of ECMS and PMP-based optimal control strategy in hybrid vehicles. Int. J. Automot. Technol. 2014, 15, 1189–1196. [Google Scholar] [CrossRef]
- Dhifli, M.; Lashab, A.; Guerrero, J.M.; Al-turki, Y.A. An Efficient External Energy Maximization-based Energy Management Strategy for a Battery/Supercapacitor of a Micro Grid System Enhanced Intelligent Energy Management System for a Renewable Energy-Based AC Microgrid. Energies 2020, 13, 3268. [Google Scholar] [CrossRef]
- Mohseni-Bonab, M.; Moeini, A.; Hajebrahimi, A.; Antarasee, P.; Premrudeepreechacharn, S.; Siritaratiwat, A.; Khunkitti, S. Optimal Design of Electric Vehicle Fast-Charging Station’s Structure Using Metaheuristic Algorithms. Sustainability 2022, 15, 771. [Google Scholar] [CrossRef]
- Rezk, H.; Nassef, A.M.; Abdelkareem, M.A.; Alami, A.H.; Fathy, A. Comparison among various energy management strategies for reducing hydrogen consumption in a hybrid fuel cell/supercapacitor/battery system. Int. J. Hydrog. Energy 2021, 46, 6110–6126. [Google Scholar] [CrossRef]
- Zhao, J.; Ramadan, H.S.; Becherif, M. Metaheuristic-based energy management strategies for fuel cell emergency power unit in electrical aircraft. Int. J. Hydrog. Energy 2019, 44, 2390–2406. [Google Scholar] [CrossRef]
- Li, F.; Zuo, W.; Zhou, K.; Li, Q.; Huang, Y. State of charge estimation of lithium-ion batteries based on PSO-TCN-Attention neural network. J. Energy Storage 2024, 84, 110806. [Google Scholar] [CrossRef]
- Li, F.; Zuo, W.; Zhou, K.; Li, Q.; Huang, Y.; Zhang, G. State-of-charge estimation of lithium-ion battery based on second order resistor-capacitance circuit-PSO-TCN model. Energy 2024, 289, 130025. [Google Scholar] [CrossRef]
- Ahmadi, S.; Bathaee, S.M.T.; Hosseinpour, A.H. Improving fuel economy and performance of a fuel-cell hybrid electric vehicle (fuel-cell, battery, and ultra-capacitor) using optimized energy management strategy. Energy Convers. Manag. 2018, 160, 74–84. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Ghadbane, H.E.; Barkat, S.; Houari, A.; Djerioui, A.; Rezk, H.; Louzazni, M. Optimal Adaptive Fractional Order Integral Sliding Mode Controller-Energy Management Strategy for Electric Vehicles Based on Bald Eagle Search Algorithm. Int. J. Energy Res. 2024, 2024, 7844084. [Google Scholar] [CrossRef]
- Ghadbane, H.E.; Barkat, S.; Djerioui, A.; Houari, A.; Oproescu, M.; Bizon, N. Energy management of electric vehicle using a new strategy based on slap swarm optimization and differential flatness control. Sci. Rep. 2024, 14, 3629. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Trojovska, E.; Dehghani, M.; Trojovsky, P. Zebra Optimization Algorithm: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Ferahtia, S.; Houari, A.; Rezk, H.; Djerioui, A.; Machmoum, M.; Motahhir, S.; Ait-Ahmed, M. Red-tailed hawk algorithm for numerical optimization and real-world problems. Sci. Rep. 2023, 13, 12950. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. A new optimization method based on COOT bird natural life model. Expert Syst. Appl. 2021, 183, 115352. [Google Scholar] [CrossRef]
- Han, M.; Du, Z.; Yuen, K.F.; Zhu, H.; Li, Y.; Yuan, Q. Walrus optimizer: A novel nature-inspired metaheuristic algorithm. Expert Syst. Appl. 2024, 239, 122413. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Artificial Ecosystem-Based Optimization: A Novel Nature-Inspired Meta-Heuristic Algorithm; Springer: London, UK, 2020; Volume 32, ISBN 0123456789. [Google Scholar]
- Dehghani, M.; Trojovský, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Eddine, G.H.; Said, B.; Houari, A.; Dieroui, A.; Mesbahi, T. Integral Sliding Mode Control of Synchronous Reluctance Machine based Electric Vehicle Powered by Battery/Supercapacitor Hybrid Source. In Proceedings of the 2022 19th IEEE Int. Multi-Conference Syst. Signals Devices, SSD, Sétif, Algeria, 6–10 May 2022; pp. 2133–2138. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. Online adaptive equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering power sources degradation. Energy Convers. Manag. 2019, 192, 133–149. [Google Scholar] [CrossRef]
- Ghadbane, H.E.; Rezk, H.; Ferahtia, S.; Barkat, S.; Al-Dhaifallah, M. Optimal parameter identification strategy applied to lithium-ion battery model for electric vehicles using drive cycle data. Energy Rep. 2024, 11, 2049–2058. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Viability study of a FC-battery-SC tramway controlled by equivalent consumption minimization strategy. Int. J. Hydrog. Energy 2012, 37, 9368–9382. [Google Scholar] [CrossRef]
- Motapon, S.N.; Dessaint, L.A.; Al-Haddad, K. A robust H2-consumption-minimization-based energy management strategy for a fuel cell hybrid emergency power system of more electric aircraft. IEEE Trans. Ind. Electron. 2014, 61, 6148–6156. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, X.; Yu, T.; Yao, W.; Shu, H.; Zeng, F. Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 2020, 208, 112595. [Google Scholar] [CrossRef]
- Rezk, H.; Abdelkareem, M.A.; Alshathri, S.I.; Sayed, E.T.; Ramadan, M.; Olabi, A.G. Fuel Economy Energy Management of Electric Vehicles Using Harris Hawks Optimization. Sustainability 2023, 15, 12424. [Google Scholar] [CrossRef]





| Parameter | Description | Unit |
|---|---|---|
| v | vehicle’s speed | m/s |
| vw | wind speed | m/s |
| slope angle | rad | |
| mv | vehicle’s mass | Kg |
| µ | tire’s rolling resistance coefficient | -- |
| Cd | aerodynamic coefficient | -- |
| Γ | air density | Kg/m3 |
| Af | vehicle’s frontal area | m2 |
| g | Earth’s gravitational | m/s2 |
| Fa | aerodynamic force | N |
| Fr | rolling resistance force | N |
| Facc | acceleration force | N |
| Fgr | resistance force | N |
| EMS | Consumed H2 (g) | Efficiency (%) | Final SOC | H2 Saving (%) | Efficiency Increase (%) | Decrease in SoC (%) | Performance Index (%) |
|---|---|---|---|---|---|---|---|
| AOA | 31.6 | 57.31 | 42.1 | 0 | 0 | 0 | 0 |
| ZOA | 40.1 | 55.75 | 49.85 | 21.2 | 1.56 | 7.75 | 15.01 |
| RTH | 43.01 | 55.49 | 52.52 | 26.53 | 1.82 | 10.42 | 17.93 |
| COOT | 44.56 | 54.92 | 53.74 | 29.08 | 3.57 | 11.64 | 21.01 |
| WaOA | 49.89 | 54.51 | 57.79 | 36.6 | 2.8 | 15.69 | 23.71 |
| MFO | 51.67 | 54.37 | 59.2 | 38.84 | 2.49 | 17.1 | 24.3 |
| AEO | 62.48 | 55.67 | 66.41 | 49.42 | 1.64 | 24.31 | 26.75 |
| OOA | 77.6 | 48.88 | 73.37 | 59.28 | 8.43 | 31.27 | 36.44 |
| EMS | Consumed H2 (g) | Efficiency (%) | Final SOC | H2 Saving (%) | Efficiency Increase (%) | Decrease in SoC (%) | Performance Index (%) |
|---|---|---|---|---|---|---|---|
| HHO | 44.78 | 55.04 | 58.21 | 29.43 | 2.72 | 16.11 | 16.05 |
| PSO | 59.1 | 48.7 | 62.93 | 46.53 | 8.61 | 20.83 | 34.31 |
| MRFO | 63.61 | 47.17 | 64.42 | 50.32 | 10.11 | 22.32 | 38.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghadbane, H.E.; Mohamed, A.F. Optimizing Fuel Economy in Hybrid Electric Vehicles Using the Equivalent Consumption Minimization Strategy Based on the Arithmetic Optimization Algorithm. Mathematics 2025, 13, 1504. https://doi.org/10.3390/math13091504
Ghadbane HE, Mohamed AF. Optimizing Fuel Economy in Hybrid Electric Vehicles Using the Equivalent Consumption Minimization Strategy Based on the Arithmetic Optimization Algorithm. Mathematics. 2025; 13(9):1504. https://doi.org/10.3390/math13091504
Chicago/Turabian StyleGhadbane, Houssam Eddine, and Ahmed F. Mohamed. 2025. "Optimizing Fuel Economy in Hybrid Electric Vehicles Using the Equivalent Consumption Minimization Strategy Based on the Arithmetic Optimization Algorithm" Mathematics 13, no. 9: 1504. https://doi.org/10.3390/math13091504
APA StyleGhadbane, H. E., & Mohamed, A. F. (2025). Optimizing Fuel Economy in Hybrid Electric Vehicles Using the Equivalent Consumption Minimization Strategy Based on the Arithmetic Optimization Algorithm. Mathematics, 13(9), 1504. https://doi.org/10.3390/math13091504






