Distributed Power Sharing Control Strategy for Interconnected AC and DC Microgrids Based on Event-Triggered Control Under Denial-of-Service Attack

Abstract

Although the problem of power sharing in interconnected AC and DC microgrids formed through interlinking converters (ICs) has been extensively studied, the problem of active power sharing under the extreme conditions of three-phase imbalance/nonlinear loads and Denial-of-Service (DoS) attack has not yet been resolved. Based on this, this paper proposes an event-triggered distributed consensus control method to achieve active power sharing under such extreme conditions. Firstly, aiming at the active power sharing problem in interconnected microgrids under DoS attack, this paper proposes a distributed power sharing control strategy based on event-triggered control under DoS attack. Each IC is defined as an agent, and its first-order agent dynamics are constructed. Secondly, a stability criterion and proof of asymptotic stability considering DoS attack are provided. Finally, simulation and experimental results verify the effectiveness of the proposed method.

1. Introduction

Currently, renewable energy sources (RESs) have been extensively integrated into microgrids to achieve zero fuel costs and zero pollution [1,2]. AC and DC microgrids are gaining increasing attention due to their high efficiency and reliability [3,4]. The primary objectives of interconnected microgrids are to achieve proportional sharing of active power and to reduce communication traffic, thereby enhancing system flexibility and reliability. However, as the microgrid environment composed of distributed energy resources becomes more complex, the number of network attacks during the communication process of interconnected microgrids is also increasing [5,6]. DoS is a typical type of network attack that blocks communication channels, rendering the data of the interconnected microgrid system unreliable. Therefore, this paper proposes a distributed power sharing control strategy based on event-triggered control under DoS attack to accomplish power sharing.

An important goal in microgrids is to achieve accurate power sharing among parallel distributed generations (DGs). In response to this goal, many scholars have carried out a significant amount of research. For example, many centralized and distributed control methods have been proposed in [7,8,9,10,11,12]. However, the above references mainly focus on AC or DC microgrids. Recently, many scholars have studied the power sharing problem of microgrid clusters formed by the IC interconnection of AC and DC microgrids. For example, in [13,14,15] scholars have studied the coordinated control of AC and DC microgrids, so that the interconnected microgrid can operate reliably and autonomously. In [13], a distributed normalized power coordination (NPC) control strategy was proposed, which can achieve accurate power sharing and frequency/voltage recovery among DGs at the same time, but the application of ICs was not considered. In [14], a distributed unified control strategy of parallel ICs was proposed to realize the power coordination among AC and DC microgrids. In [15], a distributed iterative observer and a resilient distributed secondary controller were proposed. Through this control method, active power sharing among ICs under false data injection attacks can be achieved. However, the communication link in [14,15] requires a large amount of data exchange, which is likely to reduce the reliability of the system. While improving the robustness of the system, distributed cooperative control inevitably faces a large number of cooperative communication requirements among agents. In the energy internet-oriented scenario, the real-time information interaction requirements among a large number of nodes will significantly increase the complexity of the system communication topology, which may cause problems such as channel congestion, information coupling risk, and lack of computing resources.

In terms of network attacks, the DoS attack blocks communication by attacking the communication equipment and occupying the channel’s communication messages. For interconnected microgrids that rely on distributed control to achieve power sharing, ICs need communication links to transmit data to one another. DoS is a typical network attack that blocks the communication channel and makes the data of the interconnected microgrid unreliable. Considering the need to establish communication links with adjacent ICs, it is important to enhance the flexibility of the interconnected microgrid to reduce the impact of DoS. In [16], an elastic control strategy for the microgrid was proposed to eliminate the effects of DoS attack. However, the above strategy does not consider the stability of the distributed secondary control system under DoS attack. Based on this, reference [17] considered DoS attacks, conducted time-domain stability research, and then proposed a network resilience control strategy with two control modes. However, this method did not consider the active power sharing problem of the DoS attack on interconnected microgrids. Based on this, reference [18] proposed a distributed control method to ensure the stable operation of the system under DoS attack. However, it also increased the amount of data sampling and calculation of the controller. Therefore, the above methods increase the complexity of the controller, which is a major challenge for the main control devices, such as the digital signal processor (DSP) with limited computing power commonly used in ICs.

Based on the above considerations, this paper mainly studies the power sharing of the interconnected microgrid and proposes a distributed power sharing control strategy based on event-triggered control under DoS attack to solve this problem. The main contributions of this article are as follows:

Firstly, a distributed power sharing control strategy based on event-triggered control under DoS attack is proposed to control the IC for achieving proportional active power sharing according to the capacity of AC and DC microgrids. Secondly, each IC is assigned to be an agent that needs only the information of its local and neighboring ICs. A stability proof considering DoS attack is also provided. Finally, the system performance of the control strategy under different DoS attack durations is verified by simulation and experiment.

The remainder of this paper is organized as follows. Section 2 establishes the system structure model of the interconnected microgrid and introduces the design of the DoS attack model. Section 3 proposes a distributed power sharing control strategy based on event-triggered control under DoS attack and provides proof of controller stability. Section 4 presents simulation results to verify the reliability of the proposed control strategy. Section 5 conducts experiments to validate the proposed approach. Section 6 summarizes the limitations of the control strategy in practical application. Section 7 concludes the paper.

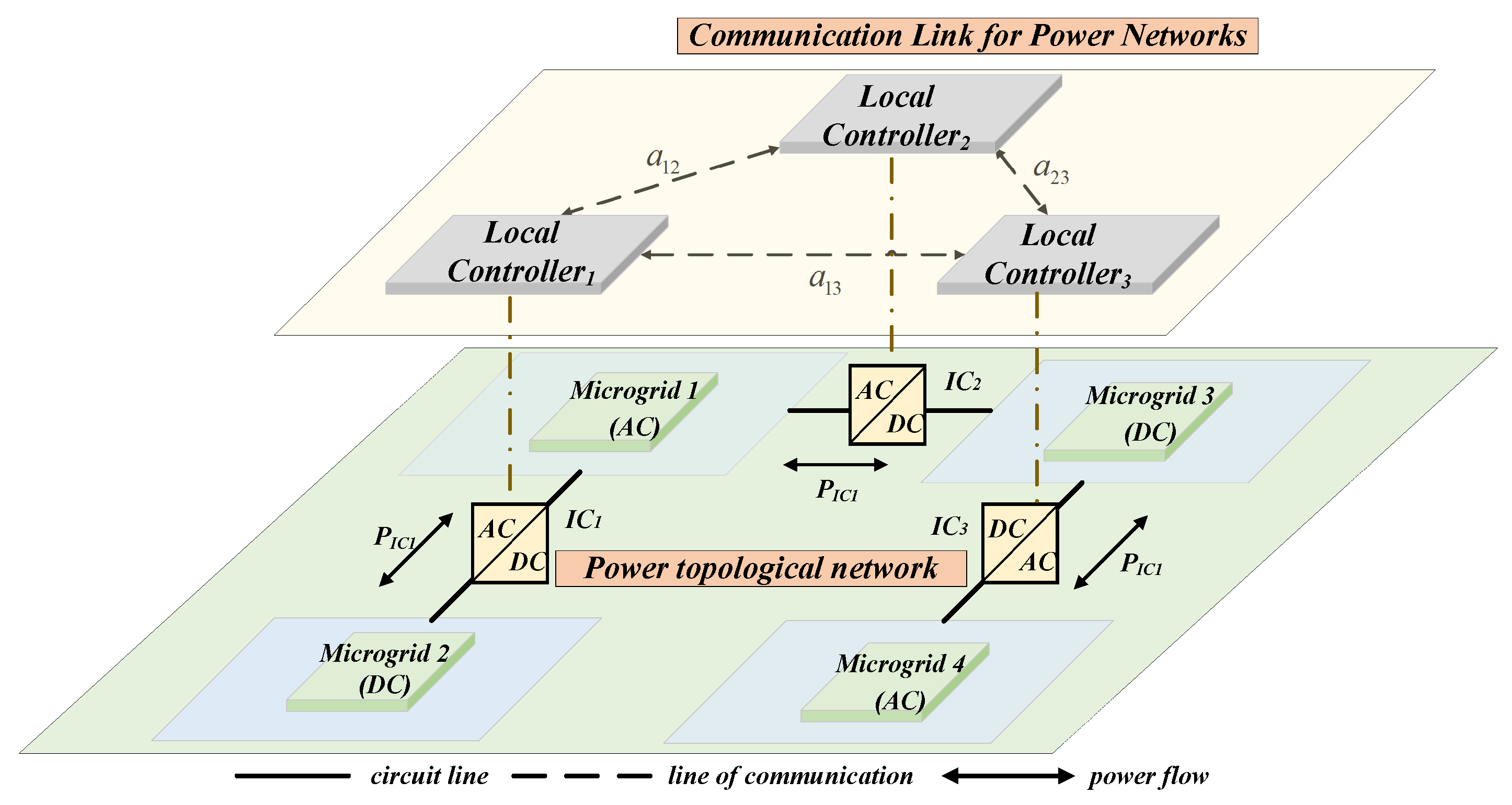
2. The Structure of the Interconnected Microgrid and DoS Attack Model

2.1. System Structure

In this section, the system structure model of the interconnected microgrid and the DoS attack model are presented. The structure of the interconnected microgrid is shown in Figure 1.

The interconnected microgrid is linked through ICs, and each microgrid has its own independent generation units, energy storage facilities, and local loads. The communication network of ICs is shown in Figure 2. The IC between microgrids enables bidirectional power flow. In this paper, the interconnected microgrid is not connected to the main grid. In this case, the key control objective of each IC is to decide and control the transmitted active power. The distributed control method proposed in this paper belongs to three-level control [19]. The interconnected microgrid consists of A units of ICs and B units of microgrids.

In the interconnected microgrid, the $\omega -P$ and $V_{dc}-P$ droop control equations are given as:

$${\omega }_{m,n,pu}^{*}=k_{ac,m,n}(P_{ac,m,n}-P_{ac,m,n}^{*})+{\omega }_{m,n,pu}$$

(1)

$$V_{dc,m,n,pu}^{*}=k_{dc,m,n}(P_{dc,m,n}-P_{dc,m,n}^{*})+V_{dc,m,n,pu}$$

(2)

where ${\omega }_{m,n,pu}^{*}$ and $V_{dc,m,n,pu}^{*}$ are the rated frequency and DC grid voltage of the system; $P_{ac,m,n}$ and $P_{dc,m,n}$, $P_{ac,m,n}^{*}$ and $P_{dc,m,n}^{*}$ are the output active power and rated active power of AC and DC microgrids, respectively; and $k_{ac,m,n}$ and $k_{dc,m,n}$ are the droop coefficients of $\omega -P$ and $V_{dc}-P$, respectively. Note that the subscript $pu$ in the formula represents the per-unit value [20]. This paper mainly considers the active power sharing problem of interconnected microgrids. According to the linear characteristics of (1), this paper can obtain the comprehensive droop control equation of the entire AC and DC microgrid. All DGs in each microgrid can be equivalent to one DG, as shown in (3) and (4):

$${\omega }_{m,pu}^{*}=k_{ac,m}(P_{ac,m}-P_{ac,m}^{*})+{\omega }_{m,pu}$$

(3)

$$V_{dc,m,pu}^{*}{k}_{dc,m}=(P_{dc,m}-P_{dc,k}^{*})+V_{dc,m,pu}$$

(4)

where ${\omega }_{m,pu}^{*}={\omega }_{m,n,pu}^{*}$, $V_{dc,m,pu}^{*}=V_{dc,m,n,pu}^{*}$, $P_{ac,m}={\displaystyle \sum _{r=1}^{\mathrm{n}}}{P}_{ac,m,n}$, $P_{dc,m}={\displaystyle \sum _{r=1}^{\mathrm{n}}}{P}_{dc,m,n}$, $P_{ac,m}^{*}={\displaystyle \sum _{r=1}}{P}_{ac,m,n}^{*}$, $P_{dc,m}^{*}={\displaystyle \sum _{r=1}}{P}_{dc,m,n}^{*}$, $k_{ac,m}=1/{\sum }_{r=1}^n(1/k_{ac,m,n})$, $k_{dc,m}=1/{\sum }_{r=1}^n(1/k_{dc,m,n})$, and ${\omega }_{m,pu}^{*}$ is the rated frequency. $V_{dc,m,pu}^{*}$ is the DC voltage, $P_{ac,m}$ is the output active power of the AC microgrid, $P_{dc,m}$ is the output active power of the DC microgrid, $P_{ac,m}^{*}$ and $P_{dc,m}^{*}$ are the corresponding rated output active power, respectively, and $k_{ac,m}$ and $k_{dc,m}$ are the droop coefficient. In addition, the line impedance mismatch in the DC microgrid does not affect the design of the controller, so it can be ignored here.

In this paper, $z_m$ denotes ${\omega }_{m,pu}$ and $V_{dc,m,pu}$, $P_m$ denotes $P_{ac,m}$ and $P_{dc,m}$, and $k_m$ denotes $k_{ac,m}$ and $k_{dc,m}$; then, (3) and (4) can be rewritten as:

$$z_m^{*}=k_m(P_m-P_m^{*})+z_m$$

(5)

The active power $P_m$ in (5) can be expressed as:

$$P_m=P_{Z_m}+\sum _{i\in {\mathcal{C}}_m}{P}_{IC,i}$$

(6)

where $P_{Z_m}$ is the active load of the mth microgrid, ${\mathcal{C}}_m$ is the set of ICs, and $P_{IC,i}$ is the power transmitted through the ith IC. Figure 2 shows the response curve of the integrated droop control (5) of each AC and DC microgrid.

In order to realize the active power dynamic equilibrium distribution of the interconnected microgrid, it is necessary to ensure that each microgrid satisfies $z_m=z_P$ (or $k_m{P}_m=k_P{P}_P$) ($k\ne p$) cooperative operation constraints. Although the traditional droop control mechanism has a mature application foundation in islanded AC/DC microgrids, its inherent control architecture is difficult to adapt to the interconnected microgrid. Because of this, this paper constructs a distributed power sharing control strategy based on event-triggered control. The energy transmission of different microgrids is dynamically optimized by ICs, so that the AC frequency and DC voltage per unit value of the interconnected microgrid are equal, and finally, the accurate proportional distribution of active power is realized.

2.2. DoS Attack Model

For the multi-agent system, the agent exchanges information with adjacent agents through communication links. In this paper, the ring communication link network shown in Figure 3 is provided for ICs to exchange information in order to achieve control objectives. In this microgrid, the communication lines are usually short, and the time delay can be ignored. The DoS attack mainly destroys the reliability of multi-agent systems by blocking communication links. During the DoS attack, the DoS attack in this paper is not cyclical. Although ICs have communication capabilities, the reliability of the data is still compromised in islanded mode [21].

At the same time, the following assumptions should be satisfied for the DoS attack:

(a) Each DoS attack can be detected.

(b) When the DoS attack occurs, communication between adjacent ICs is blocked, and the information of the droop controller is no longer updated.

(c) The DoS attack energy is constrained, and each attack has a maximum duration.

Since the DoS attack is extensively studied [22], it satisfies hypothesis (a). And DoS attacks generally require the supply of carrier equipment, which has the limitation of energy supply [23]. Therefore, hypothesis (c) is satisfied. In this paper, the local controllers of the multi-agent system are mainly responsible for information exchange. Therefore, when the availability of data is compromised, the performance of ICs under DoS network attack is as follows: (1) Local controller failure; (2) The state value is no longer updated; (3) The controller output is no longer updated. Therefore, it satisfies hypothesis (c).

Therefore, it is assumed that $\left\{{\tau }_s\right\}\left(s=1,2,\dots \right)$ represents the time when the DoS attack occurs, and ${\lambda }_s$ represents the duration of the DoS attack. Then, the time when the DoS attack occurs is $\{{\tau }_s,{\tau }_0\}$, and ${\tau }_{s+1}>{\tau }_s{+}_{\Delta }t,{\tau }_0={\tau }_s+{\lambda }_s$ is defined. During $\left(\begin{array}{c}0,t\end{array}\right)$, the time when the DG cannot communicate is $D_s\left(\begin{array}{cc}0,& t\end{array}\right)={\sum }_{s=1}^n{D}_S=\left(\begin{array}{cc}{\tau }_s,& {\tau }_0\end{array}\right)\bigcap \left[\begin{array}{cc}0,& t\end{array}\right]$. Among them, the communication time between ICs is $D\left(\begin{array}{cc}0,& t\end{array}\right)=\left[\begin{array}{cc}0,& t\end{array}\right]\setminus \left(\begin{array}{cc}{\tau }_s,& {\tau }_0\end{array}\right)$. In summary, we can get:

(1) Attack frequency: For any $t_2>t_1>t_0$, $N_a$($t_1$, $t_2$) is defined as the number of DoS attacks. The attack frequency is:

$$F_a(t_1,t_2)={\displaystyle \frac{N_a(t_1,t_2)}{t_2-t_1}}$$

(7)

(2) Attack duration: For any $t_2>t_1>t_0$, ($t_1$, $t_2$) is defined as the time interval of the DoS attack. The attack duration is:

$$T_a(t_1,t_2)\le {\displaystyle \frac{t_2-t_1}{{\tau }_a}}$$

(8)

where ${\tau }_a>0$ is the attack time ratio.

Note that condition (a) is satisfied because the DoS attack is extensively studied [24]. Therefore, we can set $\theta \left(t\right)$ as the detector of the DoS attack. When $\theta \left(t\right)=0$, this indicates the absence of any detected DoS attack. When $\theta \left(t\right)=1$, this implies the detection of a DoS attack.

3. Power Sharing Control Strategy Based on Event-Triggered Control Under DoS Attack

In this part, aiming at the active power sharing problem under DoS attack, each IC is defined as an agent, and its first-order agent dynamics are constructed. The stability judgment theorem and its asymptotic stability proof considering DoS attack are given, and a distributed power sharing control strategy based on event-triggered control is proposed.

3.1. Distributed Active Power Sharing Control Strategy

In this section, this paper solves how to achieve the goal of proportionally sharing active power, specifically how to meet:

$$k_1{P}_1=\cdots =k_m{P}_m=\cdots =k_p{P}_p=\cdots =k_B{P}_B$$

(9)

where $P_m=P_{Zm}+{\sum }_{i\in {\mathcal{C}}_m}{P}_{IC,i}$, $m=1\dots B,i=1\dots A$. It can be seen that, to achieve this goal, the controller can be designed to adaptively adjust the active power flow between m and p of the microgrid according to the load level $P_{Zm}$ control IC of each microgrid in different periods. Therefore, the key lies in the active power transmission of ICs. In this section, the multi-agent consensus theory is used to design a distributed controller to solve this problem. The power sharing deviation is defined as $E_i\left(t\right)=k_m{P}_m-k_p{P}_p$, where m and p denote the microgrid interconnected by the ith IC, and the dynamics of the multi-agent constructed are as follows:

$${\dot{E}}_i\left(t\right)=P_{IC,i}\left(t\right)i=1,\cdots ,A$$

(10)

where $E_i\left(t\right)$ is the power sharing deviation, which can be regarded as the system state variable, and $P_{IC,i}\left(t\right)$ is the control input. The goal of this paper is to design the controller $P_{IC,i}\left(t\right)$ to make the state variables $E_i\left(t\right)$ consistent, to achieve the purpose of sharing the active loads according to the proportion of the microgrid capacity. Thus, the power sharing problem of the microgrid is transformed into the consensus problem of the first-order linear multi-agent system. To make the system (10) achieve consistency, this section designs the following form of auxiliary control input:

$$P_{IC,i}\left(t\right)=-c{E}_{IC,ij}\left(t\right)=-c\sum _{j\in {\mathcal{B}}_i}{a}_{ij}\left(E_i\left(t\right)-E_j\left(t\right)\right)$$

(11)

where c represents the coupling gain and $E_{IC,ij}\left(t\right)$ is the sum of the state error of the local IC and the neighbor IC. According to [25], all first-order multi-agent dynamics are asymptotically stable under the action of consensus protocol (11), that is, $t\to \infty ,E_i\left(t\right)=E_j\left(t\right)=0,i\ne j$. Thus, the power is shared according to the proportion of AC/DC microgrid capacity, which satisfies (9). Then, the command active power that the ith IC needs to transmit can be obtained by the PI regulator $H_{IC,i}\left(s\right)$:

$$P_{PIC,i}=K_{IC,i}^P{P}_{IC,i}\left(t\right)+K_{IC,i}^I{\int }_0^t{P}_{IC,i}\left(\sigma \right)d\sigma$$

(12)

where $K_{IC,i}^P$ and $K_{IC,i}^I$ are PI controller parameters.

3.2. Distributed Power Sharing Control Strategy Based on Event-Triggered Communication

According to the theoretical derivation of (11), continuous communication is required among ICs. The continuous data interaction between traditional neighbor nodes will lead to a surge in the pressure of communication resource occupation, which is particularly significant for the energy internet. Aiming at this problem, this paper proposes a distributed power sharing control strategy based on event-triggered control, which replaces the periodic update strategy with dynamic threshold trigger conditions. This scheme significantly reduces the frequency of invalid information interaction between agents. Based on this, this section further applies the event-triggered control principle to design distributed control protocols to reduce communication within the interconnected microgrid. It is defined in the triggering interval $t_n^i\le t<t_{n+1}^i,{\widehat{E}}_i\left(t\right)=E_i\left(t_n^i\right)$, where $t_n^i$ represents the value of the active power sharing deviation between the AC and DC microgrids connected by the ith IC at the nth triggering moment. Based on this, when $\theta \left(t\right)=0$, that is, no DoS attack is detected, an event-triggered distributed consensus control protocol can be obtained:

$$P_{IC,i}\left(t\right)=-c\sum _{j\in {\mathcal{B}}_i}{a}_{ij}\left(E_i\left(t_{n\left(t\right)}^i\right)-E_j\left(t_{n\left(t\right)}^j\right)\right),t\in [t_n^i,t_{n+1}^i)$$

(13)

where $n\left(t\right)=argmax\{t_n^i\mid t_n^i\le t\}$ represents the nearest event-triggered time to the current time. To realize the effective deployment of the event-triggered communication control strategy, it is necessary to construct an appropriate event observer for each IC to update the controller control of the local and neighbor ICs. Here, this paper constructs the following event-triggered conditions:

$${∥{\partial }_i{\widehat{J}}_i\left(t\right)∥}_2^2\ge {∥E_{E_i}\left(t\right)∥}_2^2,t\in [t_{\mathrm{n}}^i,t_{n+1}^i)$$

(14)

where the error between the event-triggered time $t_n^i$ and the current time active power sharing deviation is expressed as $E_{E_i}\left(\begin{array}{c}t\end{array}\right)$. ${\partial }_i$ is a positive coefficient. ${\widehat{J}}_i\left(t\right)$ is the sum of the difference between the active power sharing deviation of the local IC and the neighbor IC at the event-triggered time, which is defined as:

$$E_{E_i}\left(t\right)=E_i\left(t_{n\left(t\right)}^i\right)-E_i\left(t\right)$$

(15)

$${\widehat{J}}_i\left(t\right)=\sum _{j\in {\mathcal{B}}_i}{a}_{ij}\left(E_i\left(t_{n\left(t\right)}^i\right)-E_j\left(t_{n\left(t\right)}^j\right)\right)$$

(16)

combined with the $E_{E_i}\left(\begin{array}{c}t\end{array}\right)$ definition, the closed-loop system of the ith agent can be dynamically written in the following compact form:

$$\dot{E}\left(t\right)=-c\Omega \widehat{E}\left(t\right)=-c\Omega \left(E\left(t\right)+E_E\left(t\right)\right),t\in [t_k^i,t_{k+1}^i)$$

(17)

where $E\left(t\right)={\left[E_1\left(t\right),\cdots ,E_A\left(t\right)\right]}^T$, $E_E\left(t\right)={[E_{E_1}\left(t\right),\cdots ,E_{E_A}\left(t\right)]}^T$, $\widehat{E}\left(t\right)={[{\widehat{E}}_1\left(t\right),\cdots ,{\widehat{E}}_A\left(t\right)]}^T$, and $\Omega$ is the Laplace matrix of the corresponding communication topology of the interconnected microgrid. The related parameters can be designed by using linear matrix inequality (LMI) theory.

Theorem 1. 

Multi-agent dynamics (10) for ICs that share active power proportionally according to the capacity of microgrids, and the communication graph $\mathbb{Z}$ is undirected. Under the action of the event-triggered distributed consensus control protocol (11) and event-triggered condition (20), the dynamic (10) of the IC used to achieve active power sharing is asymptotically stable, if $c>0,0<{\partial }_{max}<{\displaystyle \frac{1}{{\lambda }_n^2}}$.

Proof of Theorem 1. 

The following Lyapunov function is constructed:

$$V\left(E\left(t\right)\right)={\displaystyle \frac{1}{2}}{E}^T\left(t\right)E\left(t\right)$$

(18)

Then, in the trigger interval $t\in [t_n^i,t_{n+1}^i)$, we can obtain the differential of the Lyapunov function with respect to time:

$$\begin{array}{cc}& \dot{V}\left(t\right)=-c{E}^T\left(t\right)\Omega \widehat{E}\left(t\right)\hfill \\ & =-c{\widehat{E}}^T\left(t\right)\Omega \widehat{E}\left(t\right)+c{E}_E^T\left(t\right)\Omega \widehat{E}\left(t\right)\hfill \end{array}$$

(19)

Using the inequality:

$$E_E^T\left(t\right)\Omega \widehat{E}\left(t\right)\le {\displaystyle \frac{{\widehat{E}}^T\left(t\right)\Omega \widehat{E}\left(t\right)}{2}}+{\displaystyle \frac{1}{2}}{E}_E^T\left(t\right)\Omega E_E\left(t\right)$$

(20)

the following can be obtained:

$$\dot{V}\left(t\right)\le E_E^T\left(t\right)\Omega E_E\left(t\right))+{\displaystyle \frac{c}{2}}({\widehat{E}}^T\left(t\right)\Omega \widehat{E}\left(t\right)-c{E}^T\left(t\right)\Omega \widehat{E}\left(t\right)={\displaystyle \frac{c}{2}}{E}_E^T\left(t\right)\Omega E_E\left(t\right)-{\displaystyle \frac{c}{2}}{\widehat{E}}^T\left(t\right)\Omega \widehat{E}\left(t\right)$$

(21)

Combined with the event-triggered condition (14), there is:

$$\dot{V}\left(t\right)\le -{\displaystyle \frac{c}{2}}\left(1-{\lambda }_n^2{\partial }_{max}\right){\widehat{E}}^T\left(t\right)\Omega \widehat{E}\left(t\right)$$

(22)

where ${\partial }_{max}=max\{{\partial }_i,i=1,\cdots ,A\}$ and ${\lambda }_n$ is the largest eigenvalue of the Laplacian matrix. Therefore, for $t\in [t_n^i,t_{n+1}^i),c>0,0<{\partial }_{max}<{\displaystyle \frac{1}{{\lambda }_n^2}}$, there is $\dot{V}\left(t\right)\le 0$. According to LaSalle’s invariance principle, the state of the agent can be asymptotically stable to consensus, that is $t\to \infty ,E_i\left(t\right)=k_n{P}_n-k_p{P}_p={\displaystyle \frac{1}{A}}{\sum }_{i=1}^A{E}_i\left(\begin{array}{c}0\end{array}\right)=0$, that is $k_1{P}_1=k_2{P}_2=\cdots =k_B{P}_B$. Therefore, regardless of how the load is distributed in the microgrid and regardless of how the microgrid is connected through the IC, the active power can be shared proportionally. □

It is worth noting that the proof here only includes the consistent dynamics without considering the plant model. This is because the stability proof illustration methods can be divided into two methods: full-order stability proof and multi-control-bandwidth stability proof [26,27,28]. The stability proof can be simplified through multi-control-bandwidth theory. If the primary controller, consisting of the voltage–current double loop and droop loop, is designed so that the control bandwidth meets the design criteria, the stability proof of the secondary controller can be provided without considering the plant model consisting of the voltage–current double loop and droop loop [28].

Therefore, this paper gives the distributed event-triggered conditions of each agent:

$${∥E_{E_i}\left(t\right)∥}_2^2>{∥{\partial }_i\sum _{j\in {\mathcal{B}}_i}{\alpha }_{ij}\left(E_i\left(t_{n\left(t\right)}^i\right)-e_j\left(t_{n\left(t\right)}^j\right)\right)∥}_2^2,i=1,\cdots ,A$$

(23)

where $t\in \left[t_n^i,t_{n+1}^i\right),0<{\partial }_i\le {\partial }_{max}<{\displaystyle \frac{1}{{\lambda }_n^2}}$.

When the DoS attack is detected, according to [29], we can obtain the following: when the communication system of the micro-network is attacked by DoS, the data packet containing the IC state information cannot be transmitted in the communication line. To ensure the continuity of the control input, the controller will continue to use the information of the neighbor state stored in the memory to calculate the control input of the secondary control. When $\theta \left(t\right)=1$, the DoS attack is detected. According to the definition of formula (5) and $E_i\left(t\right)$, $E_i\left(t\right)=k_n{P}_n-k_p{P}_p=z_n-z_p$. If, $E_i\left(t\right)\to 0$, then $z_n\to z_p$. When the DoS attack occurs, the event-triggered controller (13) and the corresponding event-triggered condition (14) can be written as:

$$P_{IC,i}\left(t\right)=-c\sum _{j\in {\mathcal{B}}_i}{a}_{ij}\left({\widehat{E}}_i\left(t\right)-{\widehat{E}}_j\left({\tau }_s\right)\right)$$

(24)

$${∥E_{E_i}\left(t\right)∥}_2^2\le {\partial }_i{∥\sum _{j\in {\mathcal{B}}_i}{a}_{ij}\left({\widehat{E}}_i\left(t\right)-{\widehat{E}}_j\left({\tau }_s\right)\right)∥}_2^2$$

(25)

where $t\in [t_n^i,t_{n+1}^i),{\widehat{E}}_i\left(t\right)=E_i\left(t_{n\left(t\right)}^i\right),{\widehat{E}}_j\left({\tau }_s\right)=E_j\left({\tau }_{n\left(t\right)}^j\right),{\partial }_i={\left({\displaystyle \frac{{\ell }_i}{{\mathcal{B}}_i}}\right)}^2$, $E_{E_i}\left(t\right)={\widehat{E}}_i\left(t\right)-E_i\left({\tau }_s\right)$. When the communication system of the IC is attacked by DoS, for the power sharing deviation ${\widehat{E}}_i\left(t\right)$ of the ith IC, considering the information of the neighbor state stored in the memory at the previous time and the error of its own state quantity caused by the information transmission, the state deviation ${\delta }_i^{aj}$ of the neighbor j will be introduced. At this time:

$${\tilde{E}}_i\left(t\right)={\widehat{E}}_i\left(t\right)+{\delta }_i^{aj}$$

(26)

At the same time, under DoS attack, the $E_{E_i}\left(\begin{array}{c}t\end{array}\right)={\widehat{E}}_i\left(\begin{array}{c}t\end{array}\right)-E_i\left(\begin{array}{c}{\tau }_s\end{array}\right)$ of (22) in the multi-agent dynamic system will become ${\tilde{E}}_{E_i}\left(t\right)={\tilde{E}}_i\left(t\right)-E_i\left({\tau }_s\right)$. Because the DoS attack receives the limitation of supply resources, it can only last for a certain period, which causes the state deviation ${\delta }_i^{aj}$ of its neighbors to be bounded, and its derivative ${\dot{\delta }}_i^{aj}$ is bounded; then, ${\tilde{E}}_i\left(t\right)$ is bounded.

Theorem 2. 

The droop controller (5) and multi-agent dynamics (10) are used to realize active power sharing, assuming that the communication graph $\mathbb{Z}$ is undirected and connected. System dynamics (10) are asymptotically stable under the action of the event-triggered distributed controller (24) and triggering condition (25), which are used to realize the sharing of active power according to the capacity of the microgrid:

$${\tau }_0={\displaystyle \frac{\phi -\epsilon c_1{b}_1}{\epsilon (c_2+c_3{b}_1)}}>{\lambda }_s\ge 0$$

(27)

$${\left({\displaystyle \frac{{\beta }_0}{\tilde{B}}}\right)}^2>{\partial }_{max}>0$$

(28)

where $\epsilon \ge 1,\phi >0,\tilde{B}=min\left\{B_i\right\},\beta =max\left\{{\beta }_i\right\}$, $c_1=max\{c\Vert h\Vert ,c\Vert d_1\Vert \}$, $c_2=c^2{\parallel h\parallel }^2$, $c_3=c_{1}c\parallel h\parallel$, $c_3=c_{1}c∥h∥$, ${\beta }_0={\displaystyle \frac{\eta \sqrt{\tilde{B}}}{\epsilon c_1\sqrt{2A}(1+\sqrt{\tilde{B}})+\eta (\sqrt{A}+\sqrt{\tilde{B}})}}$, and $b_1={\displaystyle \frac{\sqrt{2A}\beta (1+\sqrt{\tilde{B}})}{\sqrt{\tilde{B}}-\beta \sqrt{\tilde{B}}-\beta \sqrt{A}}}$.

Proof of Theorem 2. 

It has been proven that the consensus of multi-agent system dynamics (8) is defined as:

$$\underset{t\to \infty }{lim}\Vert E_i-E_j\Vert =0,i,j=1,\dots ,A$$

(29)

Let ${\rho }_i\left(t\right)=E_i\left(t\right)-E_j\left(t\right)$, then (25) is equivalent to $t\to \infty ,\Vert {\rho }_i\left(t\right)\Vert \to 0,i=2,\dots ,A$. The multi-agent dynamic (8) is as follows:

$$\dot{\rho }\left(t\right)=-ch\rho (t-{\lambda }_s)-ch{\tilde{E}}_E\left(t\right)+c{d}_1{\tilde{E}}_{E_1}\left(t\right)$$

(30)

where $\rho \left(t\right)={({\rho }_2\left(t\right),\dots ,{\rho }_A\left(t\right))}^T$, $\rho (t-{\lambda }_s)={({\rho }_2(t-{\lambda }_s)...,{\rho }_A(t-{\lambda }_s))}^T$, ${\tilde{E}}_E\left(t\right)={({\tilde{E}}_{E_2}\left(t\right),\dots ,{\tilde{E}}_{E_A}\left(t\right))}^T$, ${\tilde{E}}_{E_1}\left(t\right)={({\tilde{E}}_{E_1}\left(t\right),\dots ,{\tilde{E}}_{E_1}\left(t\right))}^T$, $d_1=diag\{d_{d1}+a_{21},\dots ,d_{d1}+a_{A1}\}$, $h=l_{22}+1_{A-1}{a}_1^T,a_1={(a_{12},\dots ,a_{1A})}^T$, $l_{22}=\left[\begin{array}{cccc}{d}_{d2}& -a_{23}& \cdots & -a_{2A}\\ -a_{32}& d_{d3}& \cdots & -a_{3A}\\ ⋮& ⋮& \ddots & ⋮\\ -a_{A2}& -a_{A3}& \cdots & d_{dA}\end{array}\right]$. Then, (26) can be rewritten as:

$$\dot{\rho }\left(t\right)=ch\underset{t-\lambda s}{\overset{t}{\int }}\dot{\rho }\left(s\right)ds-ch\rho \left(t\right)-ch{\tilde{E}}_E\left(t\right)+c{d}_1{\tilde{E}}_{E_1}\left(t\right)$$

(31)

There is:

$$\begin{array}{cc}\hfill \rho \left(t\right)& =E^{-ch(t-t_0)}\rho \left(t_0\right)+c{\int }_{t_0}^t{E}^{-ch(t-\theta )}\hfill \\ & \times \{-h{\tilde{E}}_E\left(\theta \right)+d_1{\tilde{E}}_{E_1}\left(\theta \right)+h\underset{\theta -{\lambda }_s}{\overset{\theta }{\int }}\dot{\rho }\left(s\right)ds\}d\theta \hfill \end{array}$$

(32)

Further, the following can be obtained:

$$\begin{array}{cc}\hfill \Vert \rho \left(t\right)\Vert & \le \epsilon E^{-\phi (t-t_0)}\Vert \rho \left(t_0\right)\Vert +c\epsilon {\int }_{t_0}^t{E}^{-\phi (t-\theta )}\{\Vert h\Vert \Vert {\tilde{E}}_E\left(\theta \right)\Vert \hfill \\ & +\Vert d_1\Vert \Vert {\tilde{E}}_{E_1}\left(\theta \right)\Vert +\Vert h\Vert {\int }_0^{\theta }\Vert \dot{\rho }\left(s\right)\Vert ds\}d\theta \hfill \end{array}$$

(33)

where $\epsilon \ge 1$, $\phi >0$; combined with event triggering (25), this paper gets:

$$A^{{\displaystyle \frac{1}{2}}}\beta (1+{\tilde{B}}^{-{\displaystyle \frac{1}{2}}})\parallel \rho (t-{\lambda }_s)\parallel \ge (1-\beta -A^2\beta {\tilde{B}}^{-{\displaystyle \frac{1}{2}}})\parallel {\tilde{E}}_E(t)\parallel$$

(34)

There is:

$$b_1\Vert \rho (t-{\lambda }_s)\Vert \ge \sqrt{2}\Vert E_E\left(t\right)\Vert \ge \Vert {\overline{E}}_E\left(t\right)\Vert +\Vert {\overline{E}}_{E_1}\left(t\right)\Vert$$

(35)

where $\beta =max\left\{{\beta }_i\right\}$, $\tilde{N}=min\left\{N_i\right\}$, $b_1={\displaystyle \frac{\beta \sqrt{2A}(1+\sqrt{\tilde{B}})}{\sqrt{\tilde{B}}-\beta \sqrt{\tilde{B}}-\beta \sqrt{A}}}$. Then, combined with (30), (33) and (35), we can get:

$$\begin{array}{c}\Vert \rho \left(t\right)|\le c\epsilon {\int }_{t_0}^t{E}^{-\phi (t-\theta )}\{c_1{b}_1\Vert \rho (\theta -{\lambda }_s)\Vert +\epsilon E^{-\phi (t-t_0)}\Vert \rho \left(t_0\right)\Vert \\ +{\int }_{\theta -{\lambda }_s}^{\theta }(c_2+c_3{b}_1)\parallel \rho (s-{\lambda }_s)\parallel ds\}d\theta \\ <\epsilon \Vert \rho \left(t_0\right)\Vert \{E^{-\phi (t-t_0)}+(E^{-\lambda (t-t_0)}-E^{-\gamma (t-t_0)})\\ \times {\displaystyle \frac{\epsilon [(c_2+c_3{b}_1)(E^{\lambda {\lambda }_s}-1)E^{\lambda {\lambda }_s}+\lambda c_1{b}_1{E}^{\lambda {\lambda }_s}]}{\lambda (\phi -\lambda )}}\}\end{array}$$

(36)

where $\lambda \in (0,\phi )$. There must be $\lambda \in (0,\phi )$, such that, when ${\lambda }_s\in [0,{\lambda }_{s0})$, $\beta =(0,{\beta }_0)$, the inequality ${\displaystyle \frac{\epsilon [(c_2+c_3{b}_1)(E^{\lambda {\lambda }_s}-1)E^{\lambda {\lambda }_s}+\lambda c_1{b}_1{E}^{\lambda {\lambda }_s}]}{\lambda (\phi -\lambda )}}<1$ holds. Thus, formula (36) can be written as:

$$\Vert \rho \left(t\right)\Vert <\epsilon \Vert \rho \left(t_0\right)\Vert E^{-\lambda (t-t_0)}$$

(37)

This shows that, when the DoS attack is detected, the event-triggered controller (24), the event-triggered condition (25), and the multi-agent system dynamics (10) are asymptotically stable to consensus, namely, $t\to \infty ,\Vert {\rho }_i\left(t\right)\Vert \to 0$. Therefore, when a DoS attack occurs, the active power can still be shared proportionally among microgrids according to their capacity. □

The overall control structure of the power sharing control strategy is shown in Figure 4. At each sampling time, the IC will apply the local sampling information $E_i\left(t\right)$, the latest triggering time information ${\tilde{E}}_i\left(t\right)$, and the state information ${\tilde{E}}_j\left(t\right)$ from its latest event triggering time through the communication layer to determine whether or not the local converter event triggering condition is satisfied. If the trigger condition is satisfied, the IC will update the local control law $P_{IC,i}\left(t\right)$ and pass the sampling information at the trigger time to the neighbor IC when its control law $P_{IC,j}\left(t\right)$ updates. Then, according to the PI controller $H_{IC,i}\left(s\right)$, the active power transmission instruction $P_{IC,i}$ is adaptively obtained to adjust the bidirectional active power. The control law and event-triggered conditions of each agent are completely distributed, and the control law update and information transmission are only performed at the trigger time.

4. Simulation Result

Shown in Figure 5 is the AC and DC microgrid simulation test system diagram presented in this paper. To verify the effectiveness of the control strategy, the AC and DC interconnected microgrid shown in Figure 5 is simulated and analyzed in the MATLAB/Simulink (R2021a) environment. The distributed generation units and loads of each microgrid are simulated by inverters and Boost converters. A six-switch DC–AC inverter is used as an IC to connect the AC and DC microgrids.

4.1. The Performance of AC and DC Interconnected Microgrids Under DoS Attack

In this section, before $t=4.5$ s, the three-phase unbalanced/nonlinear loads of each microgrid are 3 kW, 8 kW, 10 kW, and 8 kW. According to Figure 6b,e,h, at this time, $k_{ac1}{P}_{ac1}\ne k_{dc2}{P}_{dc2}\ne k_{dc3}{P}_{dc3}\ne k_{ac4}{P}_{ac4}$. This shows that, before $t=4.5$ s, the active power of each microgrid cannot be shared by the IC in four microgrids according to the microgrid capacity. After $t=4.5$ s, the proportion of three-phase unbalanced and nonlinear loads of dc-MG2 and ac-MG4 increases, and the loads are 12 kW and 10 kW, respectively. Using the distributed active power sharing control strategy proposed in this paper, $k_{ac1}{P}_{ac1}=k_{dc2}{P}_{dc2}=k_{dc3}{P}_{dc3}=k_{ac4}{P}_{ac4}=0.97$, which can be seen in Figure 6b,e,h. The active power transmitted by each IC to each microgrid is shown in Figure 6a,d,g, and the power deviation between microgrids is shown in Figure 6c,f,i.

The active power deviation between microgrids approaches 0, which indicates that ICs can realize the proportional sharing of active power. Considering that the DoS attack occurs at $t=5.5$ s, according to the settings, the number of ICs is $A=3$ and ${\Omega }_n=3$. The main parameters are $c=3$, $\epsilon =1$, $d_1=\left[\begin{array}{ccc}3& 0;0& 3\end{array}\right]$. $c_1=15$, $c_2=c_3=225$, $\tilde{B}=2.95$, $b_1=0.08$ can be obtained, and ${\lambda }_s$ = 113.6 ms can be calculated by Theorem 2, so the attack duration is set to ${\lambda }_s$ = 100 ms, ${\lambda }_s$ = 150 ms, and ${\lambda }_s$ = 200 ms. After exceeding the maximum time limit of the DoS attack, the active power transmitted by ICs fluctuates greatly, and the active power deviation among each microgrid is large. At this time, due to the influence of the DoS attack, each microgrid cannot achieve the goal of proportional sharing of active power through ICs.

4.2. IC Realizes Proportional Sharing of Active Power Under DoS Attack

In this section, the simulation results after 5.5 s are shown in Figure 7. After the DoS attack, the active power transmitted by ICs fluctuates greatly, and the active power deviation between each microgrid is large. At this time, due to the influence of the DoS attack, each microgrid cannot achieve the goal of proportional sharing of active power through IC. Aiming at this problem, after adopting the power sharing control strategy based on event-triggered control under DoS attack proposed in this paper, the active power transmitted by ICs tends towards a stable value, and the active power deviation among each microgrid tends towards 0, and at this time $k_{ac1}{P}_{ac1}=k_{dc2}{P}_{dc2}=k_{dc3}{P}_{dc3}=k_{ac4}{P}_{ac4}=0.96$; it can be shown that, when a DoS attack occurs, ICs can realize the proportional sharing of active power.

5. Experimental Result

The hardware-in-the-loop (HIL) experimental platform of the interconnected microgrid test system is built according to Figure 5, as shown in Figure 8. The AC and DC microgrid replaces the DG units with an inverter. The star-connected three-phase linear load represents the unbalanced load (C-phase disconnection). The three-phase diode rectifier with capacitors and resistors on the DC side simulates the nonlinear load. The controller is implemented by the DSP. The main parameters of other power stage circuits and control systems are shown in

Table 1. Power stage parameters of the microgrid.

DG Capacity	Output Filter	Harmonic Loads
P	$L_f$/ $C_f$	$C_{HL}/R_{HL}$
20 kW	1.85 mH/55 µF	5 µF/2.5 $\Omega$
Unbalanced Loads	Rated Voltage and Frequency	Line Impedance
$P_{\mathrm{IL}}$/$Q_{\mathrm{IL}}$	E/f	$Z_{line}$
8 kW/10 kVAr	120 V/60 Hz	0.35 $\Omega$ + 0.55 mH

and

Table 2. Distributed controller parameters based on event-triggered control.

AC-MG Droop Controller	AC-MG PR Controller	DC-MG PI Controller	IC PI Controller
m(Hz/W)/V(V/VAr)	$k_{pV}/k_{pI}$	$k_{p1}/k_{i1}$	$k_{icp}/k_{ici}$
$2\times {10}^{-5}$/$1\times {10}^{-3}$	1/5	0.001/1.9	0.5/280

. It is worth noting that the experiment is based on TMS320F28335 (main frequency 150 MHz) and HIL. Limited by the development of HIL technology, the maximum switching frequency of the converter deployed in HIL can only reach 1.5 kHz. Although the switching frequency is lower than that of the converter in practical applications, the core verification goal of the proposed control strategy is the stability and anti-DoS performance of multi-objective cooperative control, rather than high-frequency dynamic response.

Figure 9 shows the experimental results of this paper. It is worth noting that the DoS attack in the experimental part is completely consistent with the parameters in the simulation part. It can be seen from the figure that the DoS attack is detected at 5.5 s. As shown in Figure 9a, the power transmitted by each IC without the control strategy of this paper has been unstable, which indicates that the IC cannot achieve power sharing between interconnected microgrids at this time. As shown in Figure 9d, the power transmitted by each IC under the control strategy of this paper remains stable after the DoS attack, which indicates that the IC can realize power sharing between interconnected microgrids at this time. The experimental conclusions are the same as the simulation.

6. Discussion

Firstly, the strategy can improve the system’s reliability under DoS attack. The strategy uses historical data to compensate for the loss of communication during the attack, which significantly improves the stability of the system under attack. For example, microgrids suitable for critical infrastructure such as hospitals and military bases ensure that basic power supply functions can still be maintained when subjected to DoS attack. Secondly, the strategy of this paper can be based on the multi-agent consensus theory. Each unit only needs local information to cooperate and support the ’plug-and-play’ extension. At the same time, the simulation and experimental parts of this paper also verify the performance of multiple ICs (three or more). So the control strategy in this paper is also scalable. For example, it is suitable for dynamic expansion scenarios of urban microgrids or community-level microgrids, which simplifies the access process of new distributed power sources. At the same time, there are some limitations in this paper. Firstly, the current strategy is designed for nonlinear and unbalanced loads, but the adaptability to high-frequency disturbances or abrupt loads is not fully verified. Secondly, the simulation and experiment in this paper only verify the small-scale microgrid (three ICs), and the scalability of the large-scale system needs to be further verified. Thirdly, the strategy of this paper only analyzes the performance of ICs under a single DoS attack with different attack durations. For the performance under high-frequency attacks, this method has not yet been verified.

7. Conclusions

In this paper, the issue of power sharing among the interconnected AC and DC microgrids formed through ICs has been studied. To realize the active power sharing among the interconnected microgrid under DoS attack., this paper has proposed a distributed power sharing control strategy based on event-triggered control under DoS attack. Each IC has been defined as an agent, its first-order agent dynamics have been constructed, and a consensus control protocol has been designed. The stability judgment theorem and its asymptotic stability proof considering the DoS attack have been given. Finally, the simulation results have been provided to verify the effectiveness of the method.