Macroelement Analysis in T-Patches Using Lagrange Polynomials
Abstract
1. Introduction
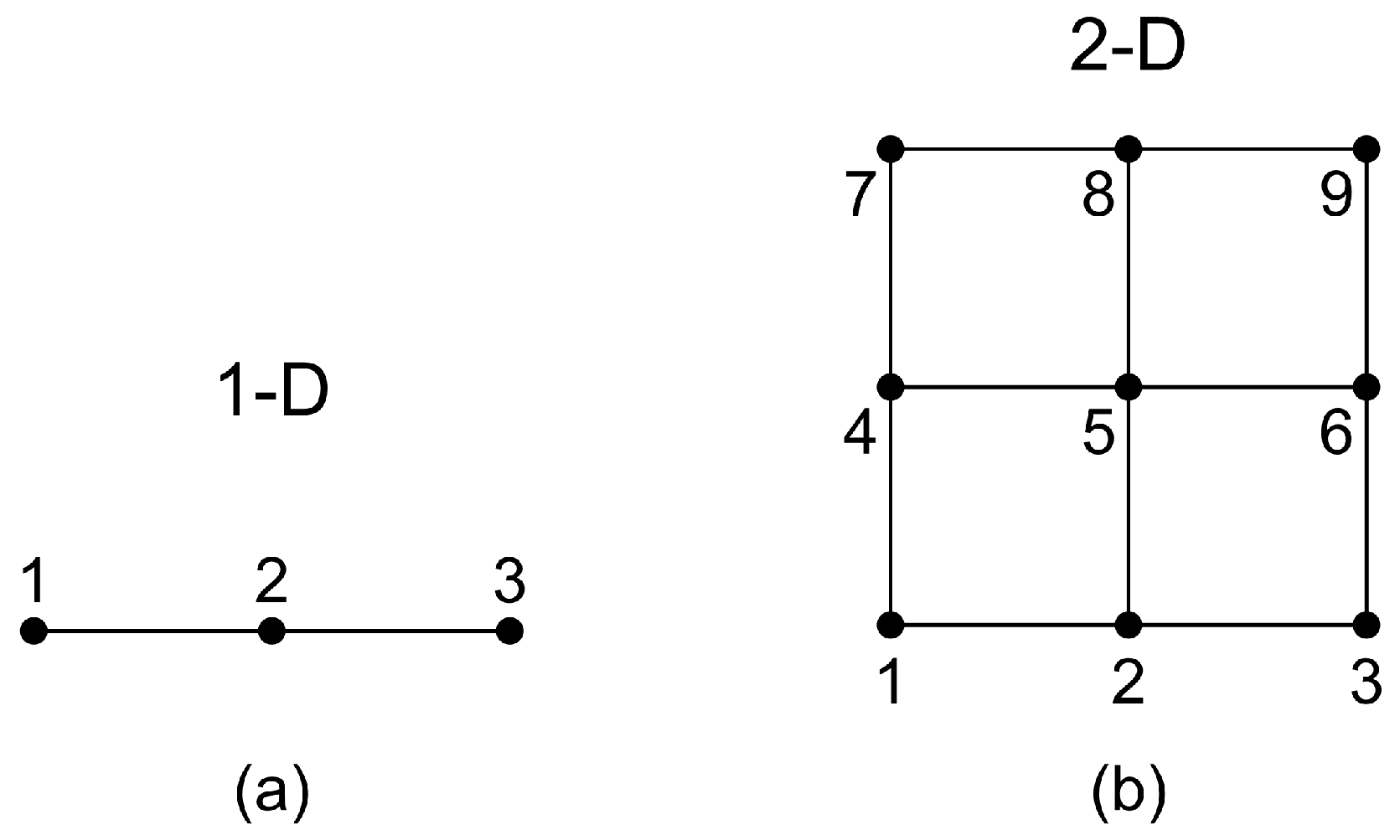
2. Tensor Product Elements
2.1. General Expressions
2.2. Quadratic Interpolation
3. Traditional Transfinite Elements
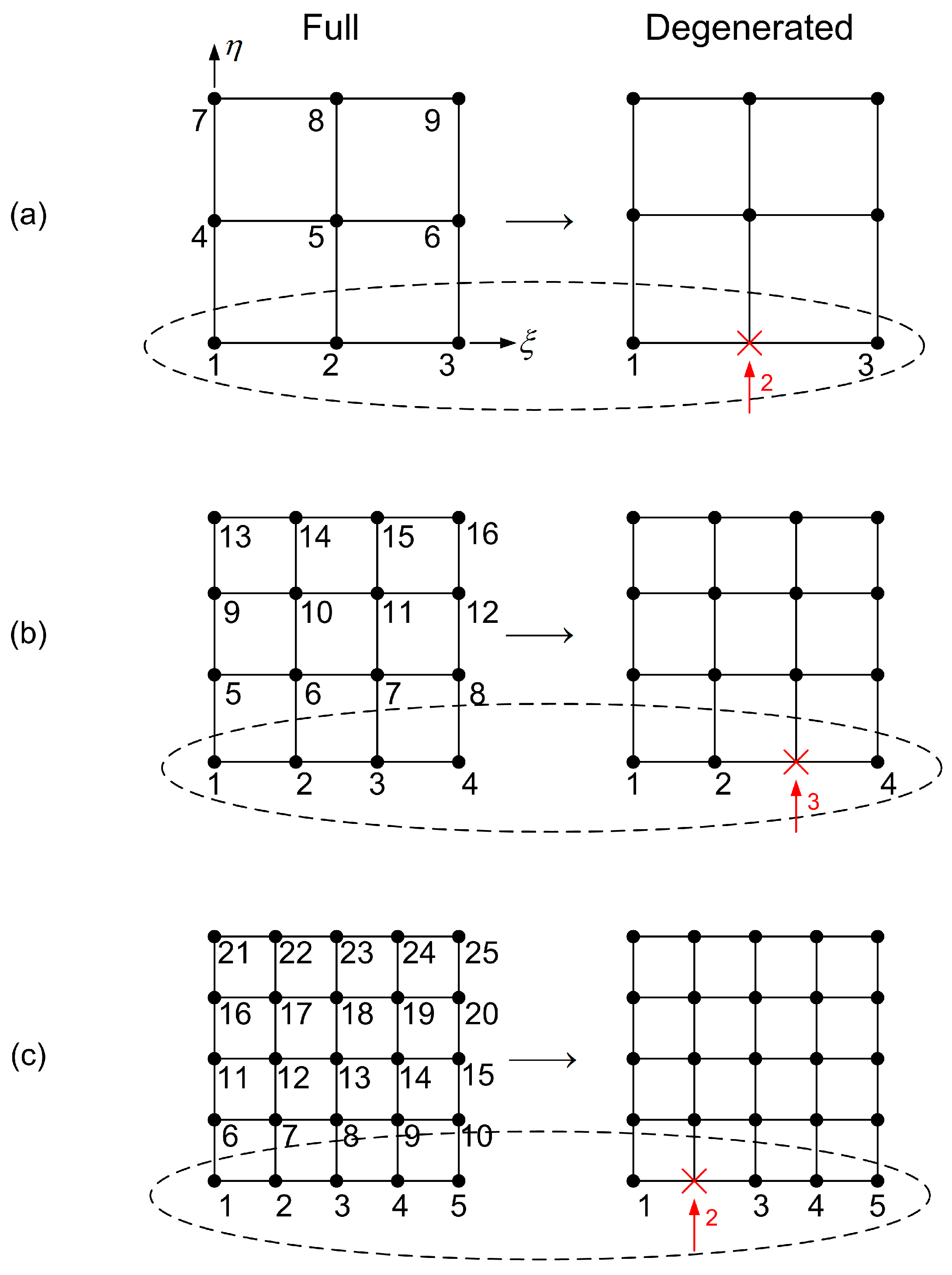
4. T-Meshed Patch Elements: Constraints and Elimination
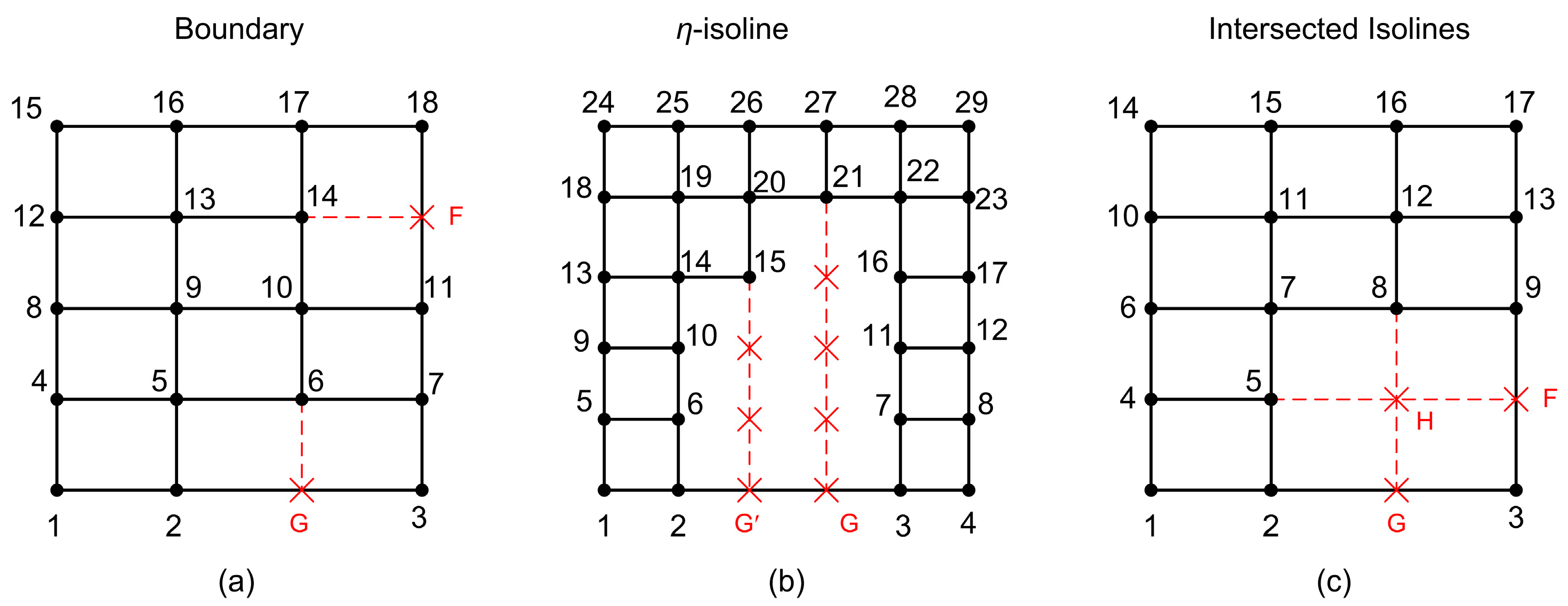
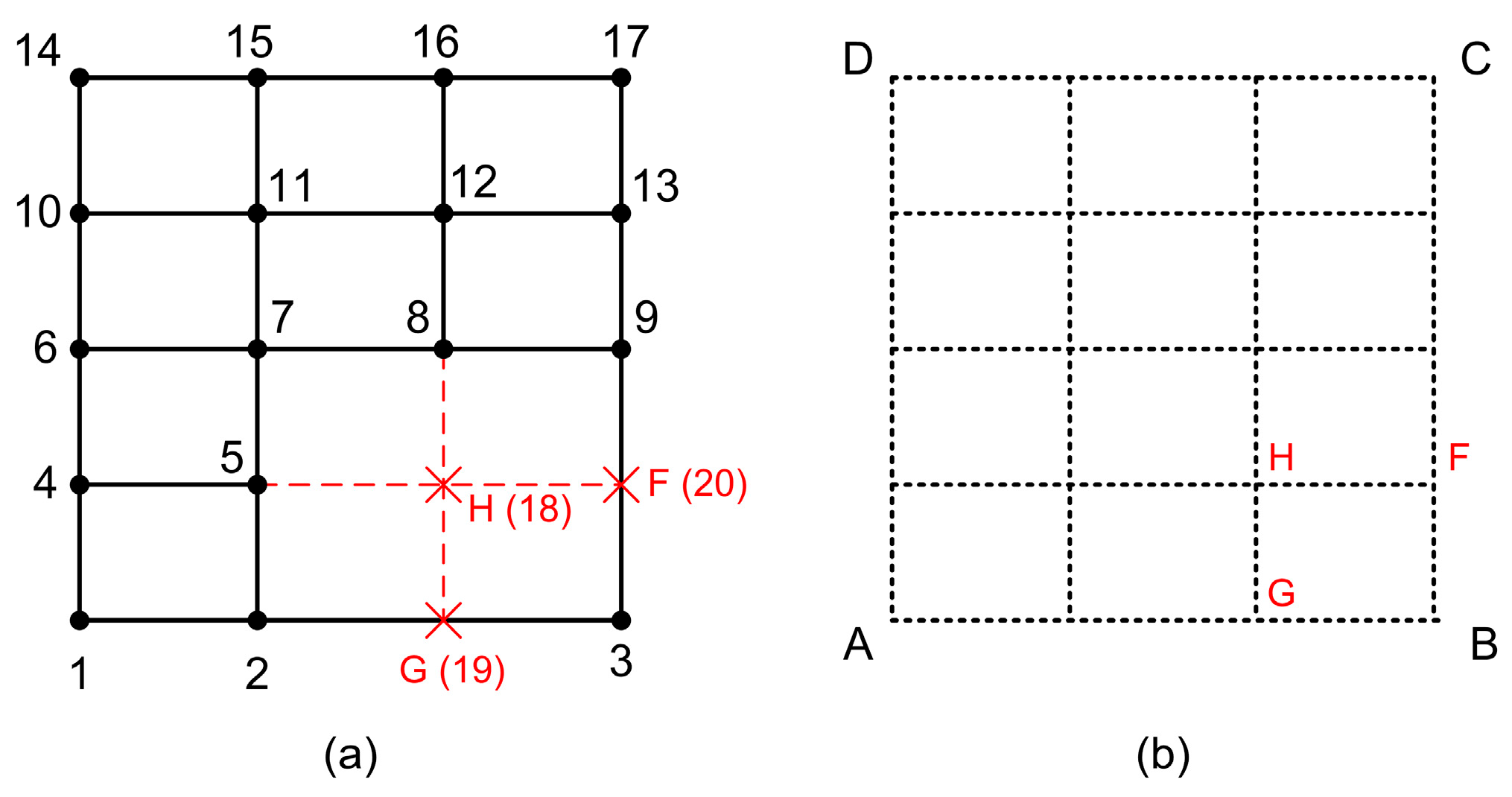
- Elements where the missing nodes belong to the boundary of the patch (e.g., nodes G and F as illustrated in Figure 4a).
- Elements with hanging internal nodes (denoted by a red cross ) that belong to the extension of isolines in only one direction (e.g., in Figure 4b these isolines are directed toward the -direction).
- Elements with hanging internal nodes that belong to the intersection of two isolines (e.g., node H as illustrated in Figure 4c).
- Technique 1: Eliminate H by considering it within the projector but ignoring it within the projector , i.e., considering the trial function along the horizontal isoline to be defined by the nodes (4, 5, and F). However, this trick cannot be applied to complicated T-meshes.
- Technique 2: Interpolate the nodal value at H once along a horizontal and another time, along the vertical isoline passing through H and then, consider the mean average value of these interpolations. Therefore, it is possible to eliminate the auxiliary node H, as later shown in Section 5.5.
5. Constraints
5.1. Quadratic Polynomials and Linear Constraints
5.2. Cubic Polynomials and Quadratic Constraints
5.3. Quartic Polynomials and Cubic Constraints
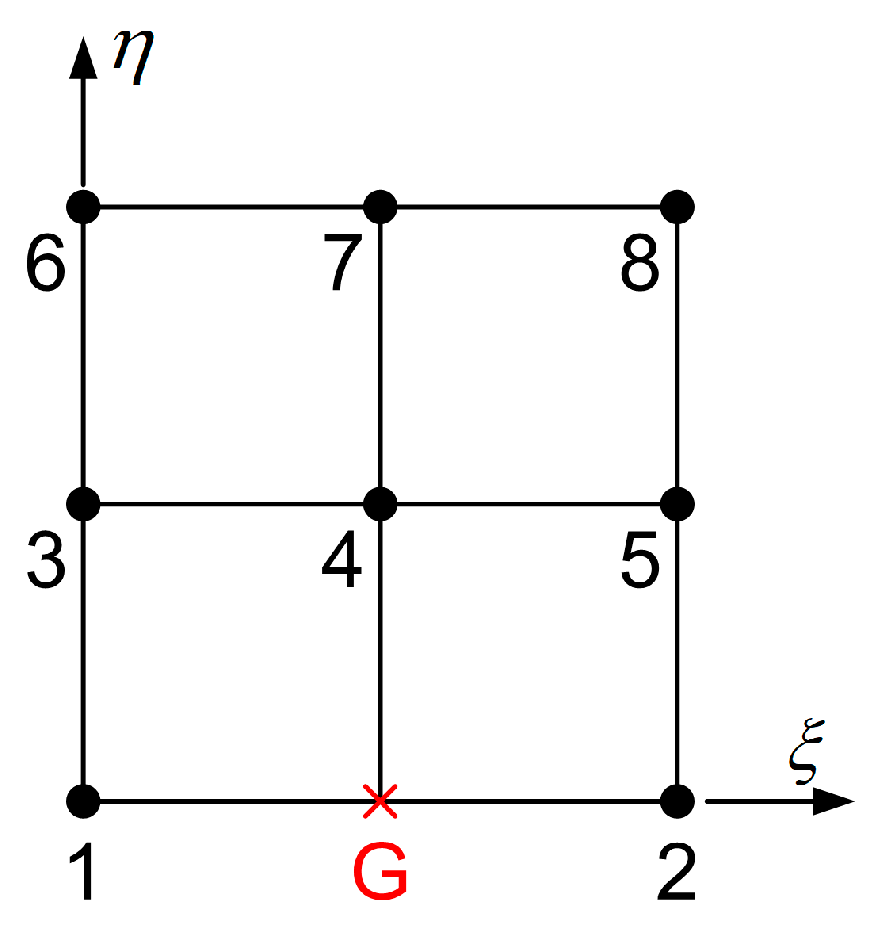
5.4. Implementation of an Eight-Node Transfinite Element
5.4.1. Approach 1: Transfinite Interpolation
5.4.2. Approach 2: Successive Node Elimination from an Initial Tensor Product
5.5. Elimination of Internal Nodes
6. Construction of the 17-Node and 18-Node T-Mesh Elements
6.1. Approach 1 to Derive T-Mesh Elements
6.1.1. General Remarks
6.1.2. The 17- and 18-Node Elements
Transfinite Elements Using 18 Nodal Points
- The two artificial values on the boundary () are eliminated;
- The one in the interior () remains.
Transfinite Elements Using 17 Nodal Points
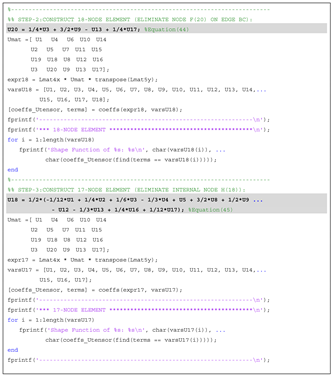
6.2. Approach 2 to Derive the 17-Node and 18-Node T-Mesh Elements
6.2.1. The 18-Node Element
6.2.2. The 17-Node Element
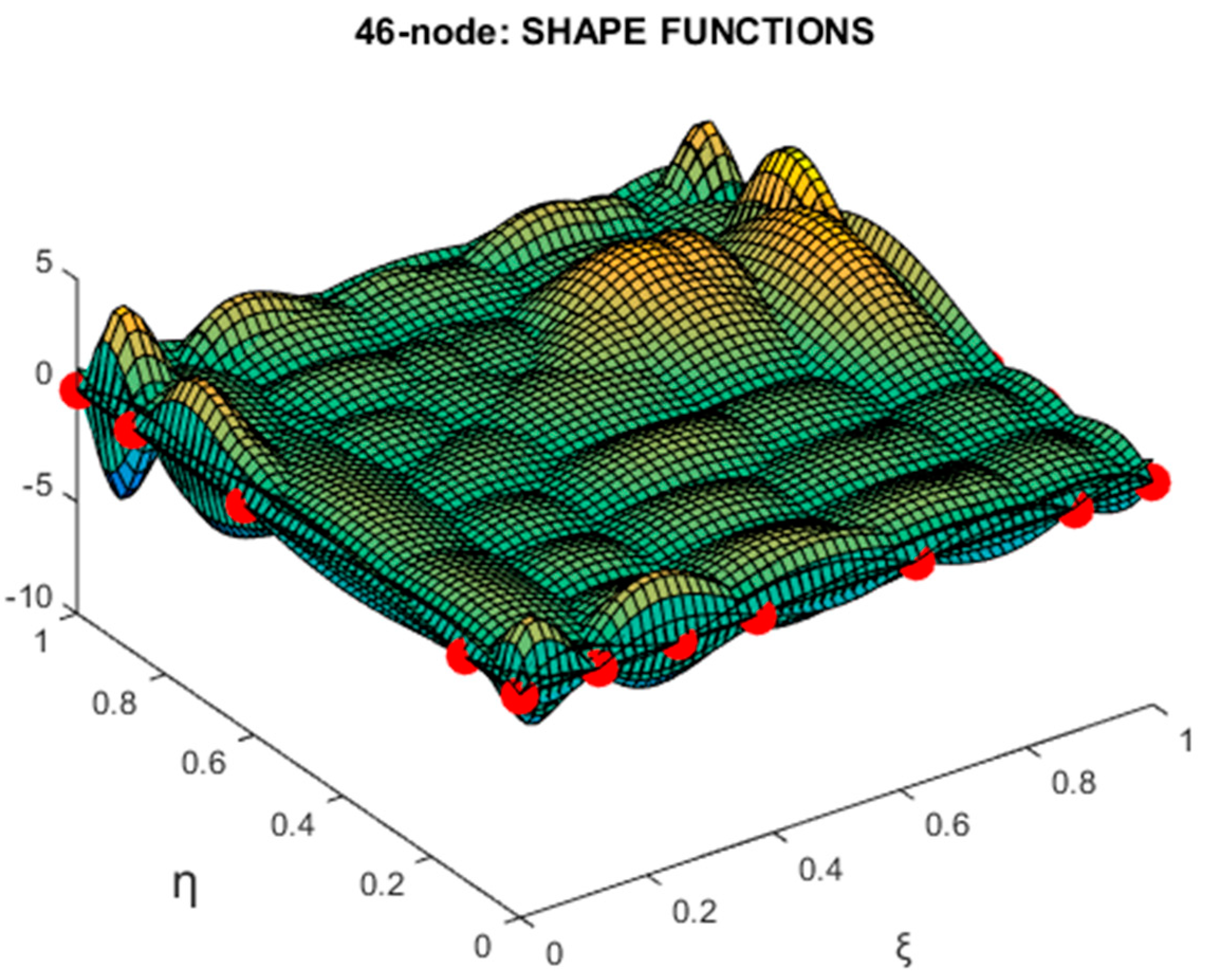
7. 46-Node T-Element
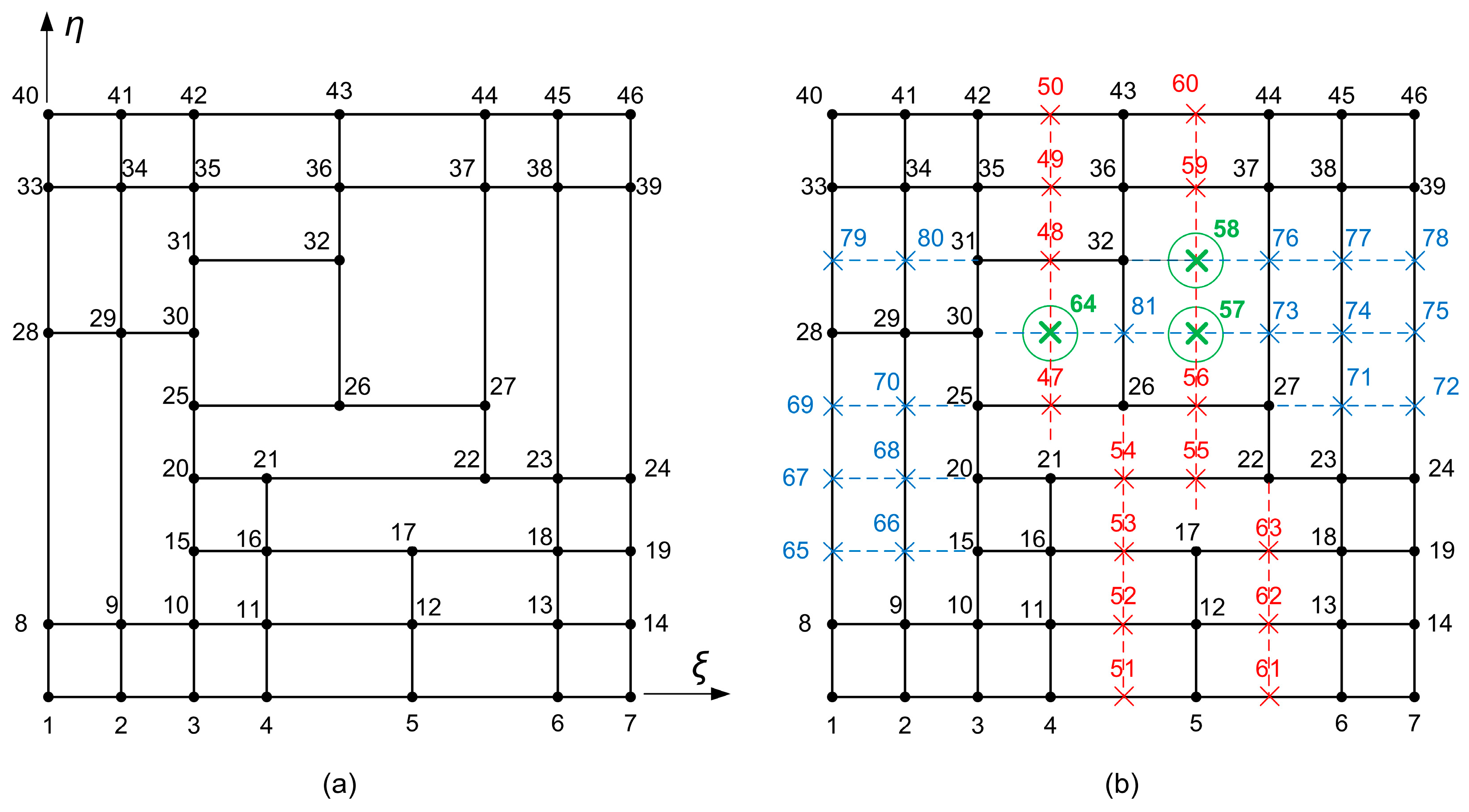
7.1. Description of the Stations
| Is it possible to number the auxiliary secondary nodes in a clever way so that they appear only twice in the Boolean sum? |
- Station H1 at , which is defined by the seven nodes , is described by a set of seven non-uniform Lagrange polynomials. All the involved nodes are primary.
- Station H2 at , which is defined by the seven nodes (), is again described by a set of seven non-uniform Lagrange polynomials. All the involved nodes are primary.
- Station H3 at , which is defined by the seven nodes , is described by a set of seven non-uniform Lagrange polynomials. Note that the first two nodes are secondary and are required to complete the support on the left part of station H3, whereas the auxiliary (background) nodes 53 and 63 are not required because they are between existing supports.
- Station H4 at , which is defined by the seven nodes , is described by a set of seven non-uniform Lagrange polynomials. Note that the first two nodes are secondary.
- Station H5 at , which is defined by the seven nodes , is described by a set of seven non-uniform Lagrange polynomials. Note that here, in addition to the first secondary nodes , additional auxiliary nodes are used to complete the support on the right side of the station.
- Station H6 at , which is defined by the seven nodes , of which the last four are secondary, is described by a set of seven non-uniform Lagrange polynomials.
- Station H7 at , which is defined by the nodes , of which five are secondary, is described by a set of seven non-uniform Lagrange polynomials.
- Station H8 at , which is defined by the nodes , is described by a set of seven non-uniform Lagrange polynomials. All the involved nodes are primary.
- Station H9 at , which is defined by the seven nodes , is described by a set of seven non-uniform Lagrange polynomials. All the involved nodes are primary.
- One may observe that all the above trial functions are non-uniform polynomials of the same degree 7, but this is an accidental event (which does not occur for the vertical stations).
- Regarding the vertical stations we have the following trial functions
- Station V1 at , which is defined by the five nodes , is described by a set of five non-uniform Lagrange polynomials. All the involved nodes are primary.
- Station V2 at , which is defined by the five nodes , is described by a set of five non-uniform Lagrange polynomials. All the involved nodes are primary.
- Station V3 at , which is defined by the nine nodes , is described by a set of nine uniform Lagrange polynomials. All the involved nodes are primary, and it is the only station which involves the maximum allowable number of nine primary nodes.
- Station V4 at , which is defined by the eight nodes , of which the last four are secondary, is described by a set of eight non-uniform Lagrange polynomials.
- Station V5 at , which is defined by the eight nodes , of which the first four are secondary, is described by a set of right non-uniform Lagrange polynomials.
- Station V6 at , which is defined by the seven nodes , of which the last four are secondary, is described by a set of seven non-uniform Lagrange polynomials. Note the big gap between the secondary nodes and .
- Station V7 at , which is defined by the seven nodes , of which the first three are secondary, is described by a set of seven non-uniform Lagrange polynomials. Note the big gap between and .
- Station V8 at , which is defined by the six nodes , is described by a set of six non-uniform Lagrange polynomials. Note that all the involved nodes are primary, while there is a big gap between and .
- Station V9 at , which is defined by the six nodes , is described by a set of six non-uniform Lagrange polynomials. Note that all the involved nodes are primary, while there is a big gap between and .
7.2. Imposition of Linear Constraints at Secondary Nodes
7.2.1. Approach 1
7.2.2. Approach 2
- If the auxiliary DOFs clearly belongs to a single station ( or ), then we interpolate in terms of the nodal values associated with this specific station. All of the auxiliary nodes, except for three, belong to this category (see below).
- If the auxiliary DOFs does not clearly belong to a single station but to the intersection of two sections, then we interpolate in both directions, using the mean average of the two values (one for the horizontal and the other for the vertical section). For the configuration of Figure 10, the relevant nodes (for averaging like Equation (36)) are 57, 58, and 64.
- For example, considering the non-uniform Lagrange polynomials based on the nodal points (1, 2, 3, 4, 5, 6, 7) on the bottom edge AB of the quadrilateral patch, the nodal values at the points 51 and 61 are eliminated in terms of the primary nodal values of the same edge by the linear relationships:
- Similar constraints, such as those of Equation (57), are obtained for the 17 (i.e., not all the 18) isolines and for all the secondary nodes except for (57, 58, and 64), which belong to two isolines simultaneously. As already mentioned, for the latter three secondary nodes, we take the mean average of the two constraints as previously shown in Equation (36).
- Since the secondary nodes are a linear combination of the primary ones (a portion given by Equation (57)), we can eventually find a numerical matrix (of size 35 × 46), according to Equation (54). Obviously, when Equation (54) is considered in the tensor product of the 81 terms, this will be eventually expressed in terms of the 46 primary variables only (i.e., the vector ). The procedure is very similar to that for a smaller mesh (see Section 6.2.2), which was described in detail through a MATLAB® computer program in Appendix A.
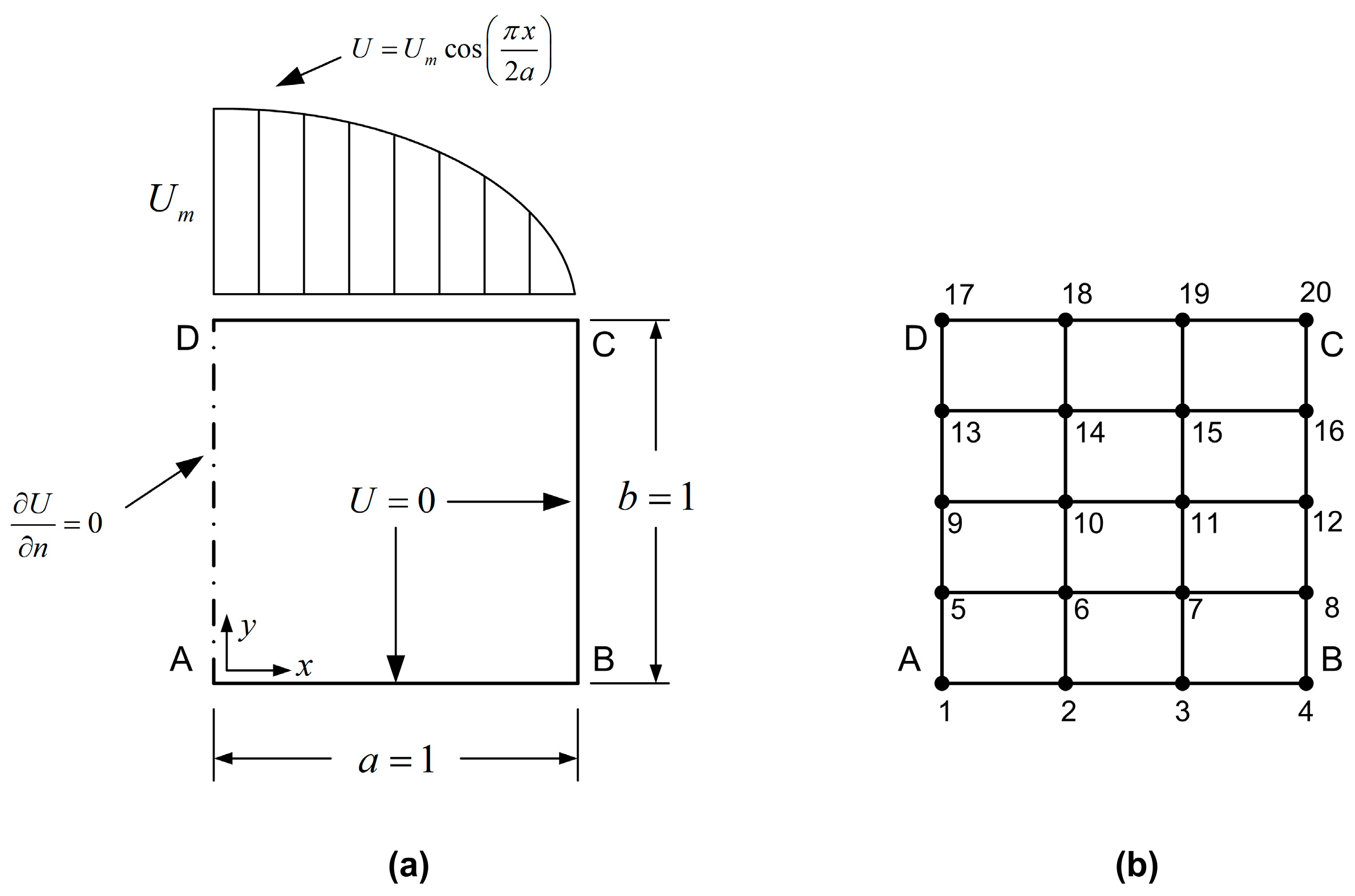
8. Numerical Verification
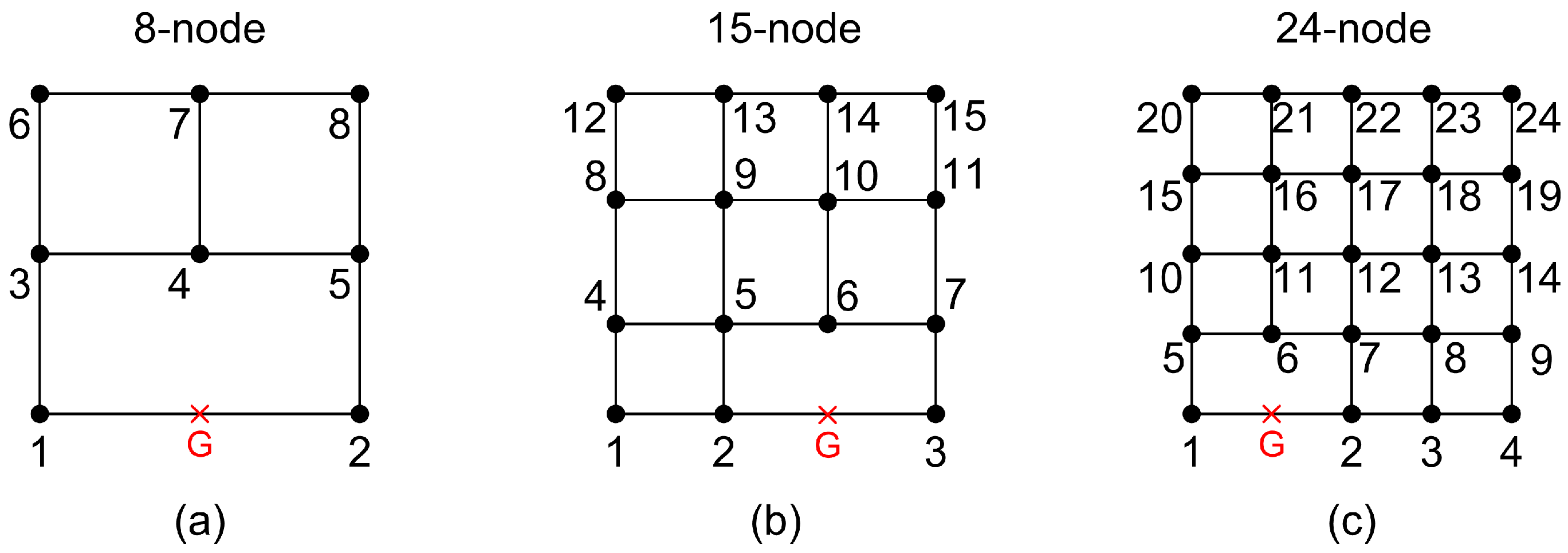
- The eight-node element, illustrated in Figure 5a, is quadratic regarding the blending functions, as well as the stations, except for the bottom edge 1-2, where it is linear.
- The 21-node transfinite element, illustrated in Figure 2, has quadratic blending functions and is quartic along each station (horizontal or vertical).
- The 20-node tensor-product element, illustrated in Figure 12b, has the previously mentioned degrees: , for both blending and trial functions along stations.
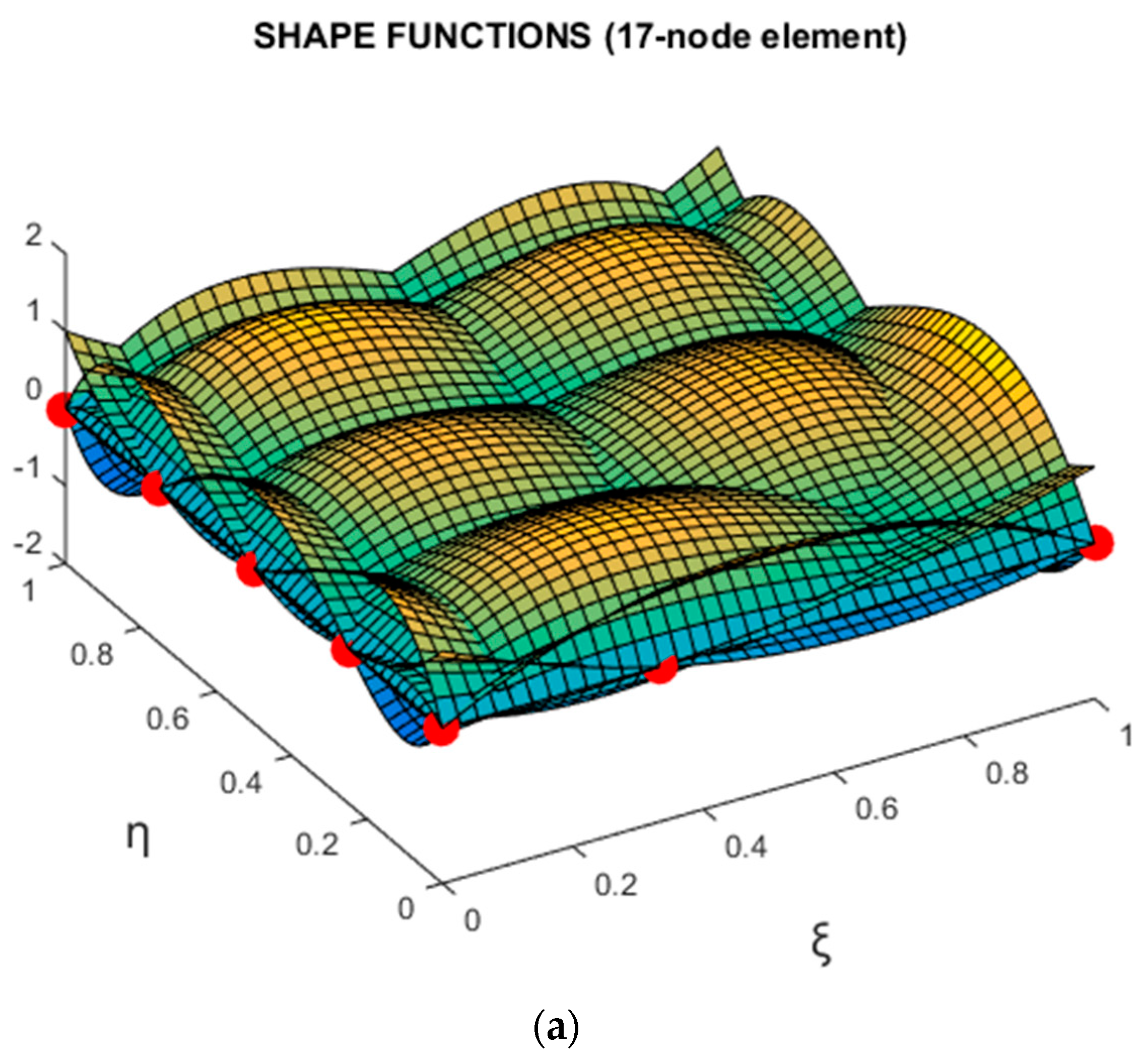
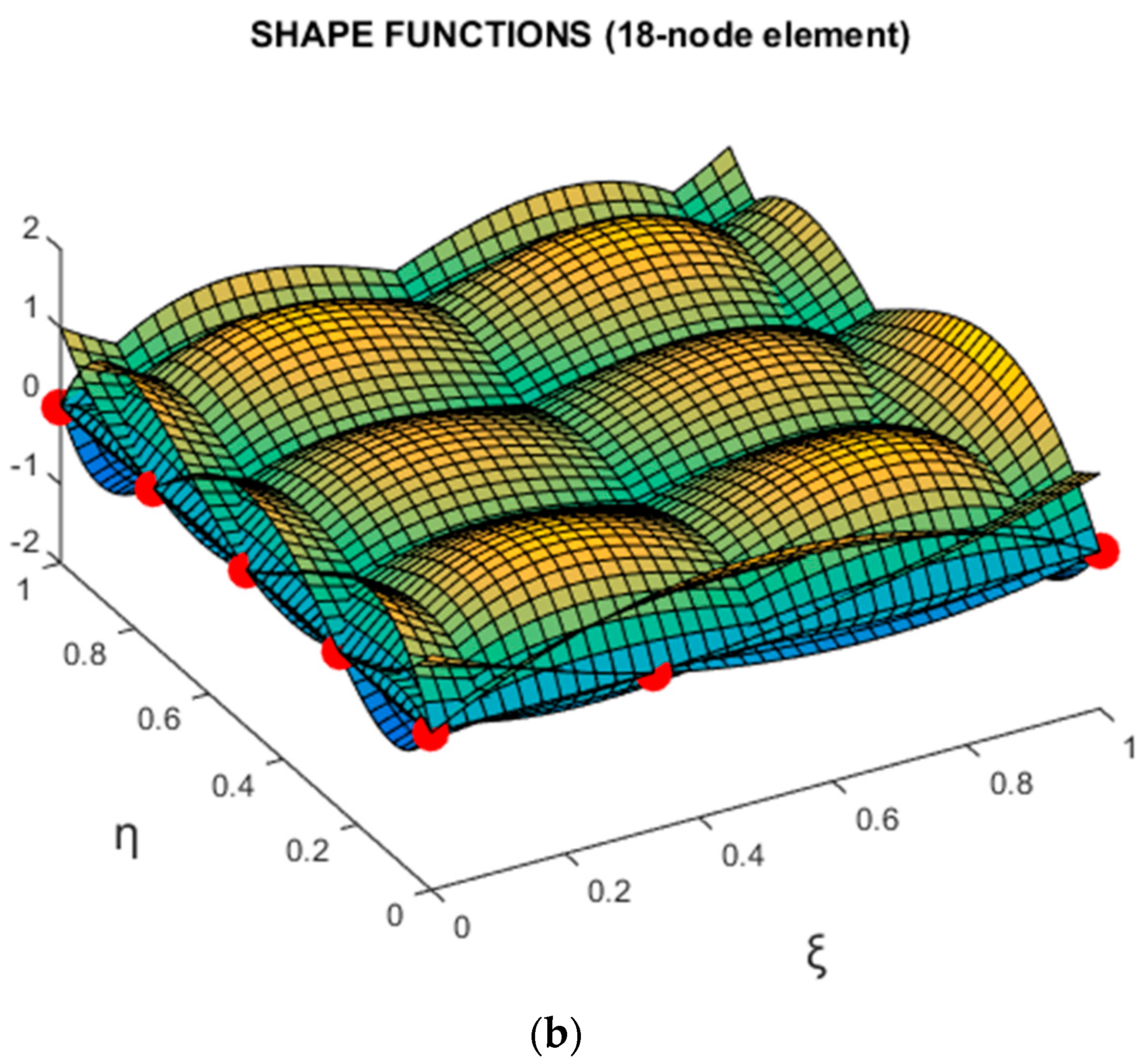
- The 18-node transfinite element, illustrated in Figure 8a, includes 17 black-colored nodes (numbered 1 to 17), plus the red-colored node H (18). The degrees for blending functions are . Horizontal stations are interpolated by cubic polynomials except for the bottom edge AB (with nodes 1-2-3) on which the trial function is non-uniform quadratic. Vertical stations are interpolated by quartic polynomials except for the edge BC (nodes 3-9-13-17) on which interpolation is non-uniform cubic.
- The 17-node transfinite element, illustrated in Figure 8a, includes the 17 black-colored nodes (numbered 1 to 17). The characteristics of this element are the same with the abovementioned 18-node transfinite element, apart from the fact that the DOFs associated with node H (18) have been eliminated using Equation (45).
- The 46-node transfinite element, illustrated in Figure 10a, has been fully described in Section 7, whereas its set of shape functions are explicitly given in Appendix B.
- The accuracy of the eight-node transfinite element is acceptable;
- The accuracy of the traditional 21-node transfinite element is excellent;
- The accuracy in the 17-, 18-, and 20-node transfinite elements is acceptable and very similar;
- The additional constraints to generate 18- or 17-node elements from a 20-node one decreases the accuracy;
- The constraints on internal secondary nodes are worse regarding the accuracy;
- The accuracy of the complicated 46-node transfinite T-element is the best of all, which is also expected since it features the largest number of nodes/DOFs and thus, also the most versatile ansatz.
9. Discussion
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Shape Functions of 17-, 18-, and 19-Node T-Mesh Elements


 in which one may recognize the three coefficients involved in Equation (18), which also refers to node G (19) on the bottom edge of the T-element shown in Figure 8a.
in which one may recognize the three coefficients involved in Equation (18), which also refers to node G (19) on the bottom edge of the T-element shown in Figure 8a.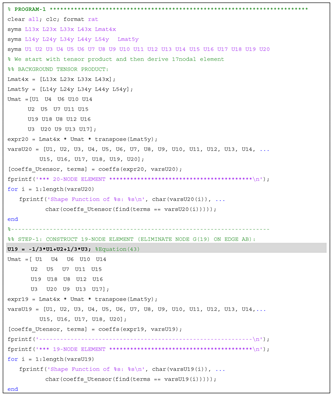
Appendix B. Global Shape Functions of the 46-Node T-like Element
References
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Bathe, K.-J. Finite Element Procedures, 2nd ed.; Bathe, K.-J., Ed.; Prentice Hall: Watertown, MA, USA, 2014. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
- Taig, I.C. Structural Analysis by the Matrix Displacement Method; Report Number SO 17 based on work performed ca. 1957; Technical Reports; British Aircraft Corporation: Preston, UK; Warton Aerodrome: Preston, UK; English Electric Aviation Limited: Preston, UK, 1957. [Google Scholar]
- Brebbia, C.A.; Ferrante, A.J. Computational Methods for the Solution of Engineering Problems, 3rd ed.; Pentech Pr.: London, UK, 1986. [Google Scholar]
- Szabó, B.; Babuška, I. Finite Element Analysis; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Rønquist, E.M.; Patera, A.T. A Legendre spectral element method for the Stefan problem. Int. J. Numer. Methods Eng. 1987, 24, 2273–2299. [Google Scholar] [CrossRef]
- Babuska, I.; Szabo, B.A.; Katz, I.N. The p-Version of the Finite Element Method. SIAM J. Numer. Anal. 1981, 18, 515–545. [Google Scholar] [CrossRef]
- Szabó, B.; Düster, A.; Rank, E. The p-Version of the Finite Element Method. In Encyclopedia of Computational Mechanics; Stein, E., Borst, R., Hughes, T.J.R., Eds.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- El-Zafrany, A.; Cookson, R.A. Derivation of Lagrangian and Hermitian shape functions for quadrilateral elements. Int. J. Numer. Methods Eng. 1986, 23, 1939–1958. [Google Scholar] [CrossRef]
- Pozrikidis, C. Introduction to Finite and Spectral Element Methods Using MATLAB, 2nd ed.; CRC Press: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- de Boor, C. A Practical Guide to Splines; rev ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Eisenträger, S.; Kapuria, S.; Jain, M.; Zhang, J. On the Numerical Properties of High-Order Spectral (Euler-Bernoulli) Beam Elements. Z. Angew. Math Mech. 2023, 103, e202200422. [Google Scholar] [CrossRef]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Eisenträger, S.; Eisenträger, J.; Gravenkamp, H.; Provatidis, C.G. High order transition elements: The xNy-element concept, Part II: Dynamics. Comput. Methods Appl. Mech. Eng. 2021, 387, 114145. [Google Scholar] [CrossRef]
- Gordon, W.J.; Hall, C.A. Transfinite element methods: Blending-function interpolation over arbitrary curved element domains. Numer. Math. 1973, 21, 109–129. [Google Scholar] [CrossRef]
- Cavendish, J.C.; Gordon, W.J.; Hall, C.A. Ritz-Galerkin approximations in blending function spaces. Numer. Math. 1976, 26, 155–178. [Google Scholar] [CrossRef]
- Cavendish, J.C.; Gordon, W.J.; Hall, C.A. Substructured macro elements based on locally blended interpolation. Int. J. Numer. Methods Eng. 1977, 11, 1405–1421. [Google Scholar] [CrossRef]
- Coons, S.A. Surfaces for Computer-Aided Design of Space Forms; Technical Reports; Massachusetts Institute of Technology: Cambridge, MA, USA, 1967. [Google Scholar]
- Provatidis, C.G. Two-dimensional elastostatic analysis using Coons-Gordon interpolation. Meccanica 2011, 47, 951–967. [Google Scholar] [CrossRef]
- Provatidis, C.G. Precursors of Isogeometric Analysis: Finite Elements, Boundary Elements, and Collocation Methods; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Provatidis, C.G. Free vibration analysis of two-dimensional structures using Coons-patch macroelements. Finite Elem. Anal. Des. 2006, 42, 518–531. [Google Scholar] [CrossRef]
- Duczek, S.; Saputra, A.A.; Gravenkamp, H. High Order Transition Elements: The xNy-Element Concept—Part I: Statics. Comput. Methods Appl. Mech. Eng. 2020, 362, 112833. [Google Scholar] [CrossRef]
- Provatidis, C.G. Solution of two-dimensional Poisson problems in quadrilateral domains using transfinite Coons interpolation. Commun. Numer. Methods Eng. 2004, 20, 521–533. [Google Scholar] [CrossRef]
- Provatidis, C.G. Eigenanalysis of Two-Dimensional Acoustic Cavities Using Transfinite Interpolation. J. Algorithms Comput. Technol. 2009, 3, 477–502. [Google Scholar] [CrossRef]
- Birkhoff, G.; Cavendish, J.C.; Gordon, W.J. Multivariate Approximation by Locally Blended Univariate Interpolants. Proc. Nat. Acad. Sci. USA 1974, 71, 3423–3425. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Zheng, J.; Bakenov, A.; Nasri, A. T-splines and T-NURCCs. ACM Trans. Graph. (TOG) 2003, 22, 477–484. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Evans, J.A.; Hughes, T.J.R.; Lipton, S.; Scott, M.A.; Sederberg, T.W. Isogeometric analysis using T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 229–263. [Google Scholar] [CrossRef]
- Dörfel, M.R.; Jüttler, B.; Simeon, B. Adaptive isogeometric analysis by local h-refinement with T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 264–275. [Google Scholar] [CrossRef]
- Wang, A.; Li, L.; Wang, W.; Du, X.; Xiao, F.; Cai, Z.; Zhao, G. Linear Independence of T-Spline Blending Functions of Degree One for Isogeometric Analysis. Mathematics 2021, 9, 1346. [Google Scholar] [CrossRef]
- EL-Fakkoussi, S.; Gouzi, M.B.; Elkhalfi, A.; Vlase, S.; Scutaru, M.L. Integrate the Isogeometric Analysis Approach Based on the T-Splines Function for the Numerical Study of a Liquefied Petroleum Gas (LPG) Cylinder Subjected to a Static Load. Appl. Sci. 2025, 15, 3102. [Google Scholar] [CrossRef]
- Guo, M.; Wang, W.; Zhao, G.; Du, X.; Zhang, R.; Yang, J. T-splines for isogeometric analysis of the large deformation of elastoplastic Kirchhoff–Love shells. Appl. Sci. 2023, 13, 1709. [Google Scholar] [CrossRef]
- Ayman-Mursaleen, M.; Nasiruzzaman, M.; Rao, N. On the Approximation of Szász-Jakimovski-Leviatan beta type integral operators enhanced by Appell polynomials. Iran. J. Sci. 2025, 1–10. [Google Scholar] [CrossRef]
- Khan, Q.; Suen, A. Comparative analysis of polynomials with their computational costs. arXiv 2024, arXiv:2411.00487. [Google Scholar]
- Provatidis, C.G. Transfinite patches for isogeometric analysis. Mathematics 2025, 13, 335. [Google Scholar] [CrossRef]
- Provatidis, C.G. Non-rational and rational transfinite interpolation using Bernstein polynomials. Int. J. Comput. Geom. Appl. 2022, 32, 55–89. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Provatidis, C.; Eisenträger, S. Macroelement Analysis in T-Patches Using Lagrange Polynomials. Mathematics 2025, 13, 1498. https://doi.org/10.3390/math13091498
Provatidis C, Eisenträger S. Macroelement Analysis in T-Patches Using Lagrange Polynomials. Mathematics. 2025; 13(9):1498. https://doi.org/10.3390/math13091498
Chicago/Turabian StyleProvatidis, Christopher, and Sascha Eisenträger. 2025. "Macroelement Analysis in T-Patches Using Lagrange Polynomials" Mathematics 13, no. 9: 1498. https://doi.org/10.3390/math13091498
APA StyleProvatidis, C., & Eisenträger, S. (2025). Macroelement Analysis in T-Patches Using Lagrange Polynomials. Mathematics, 13(9), 1498. https://doi.org/10.3390/math13091498







