Inverse Problem of Identifying a Time-Dependent Source Term in a Fractional Degenerate Semi-Linear Parabolic Equation
Abstract
1. Introduction
2. Preliminaries
2.1. Functional Spaces
2.2. Riemann–Liouville Kernel and Fractional Derivative
- (i)
- and .
- (ii)
- for all and .
- (iii)
- is decreasing in time t and
3. Weak Formulation and Uniqueness
4. Existence of Weak Solution
4.1. Time Discretization
4.2. A Priori Estimates
- (i)
- (ii)
- .
- (i)
- (ii)
- .
4.3. Existence
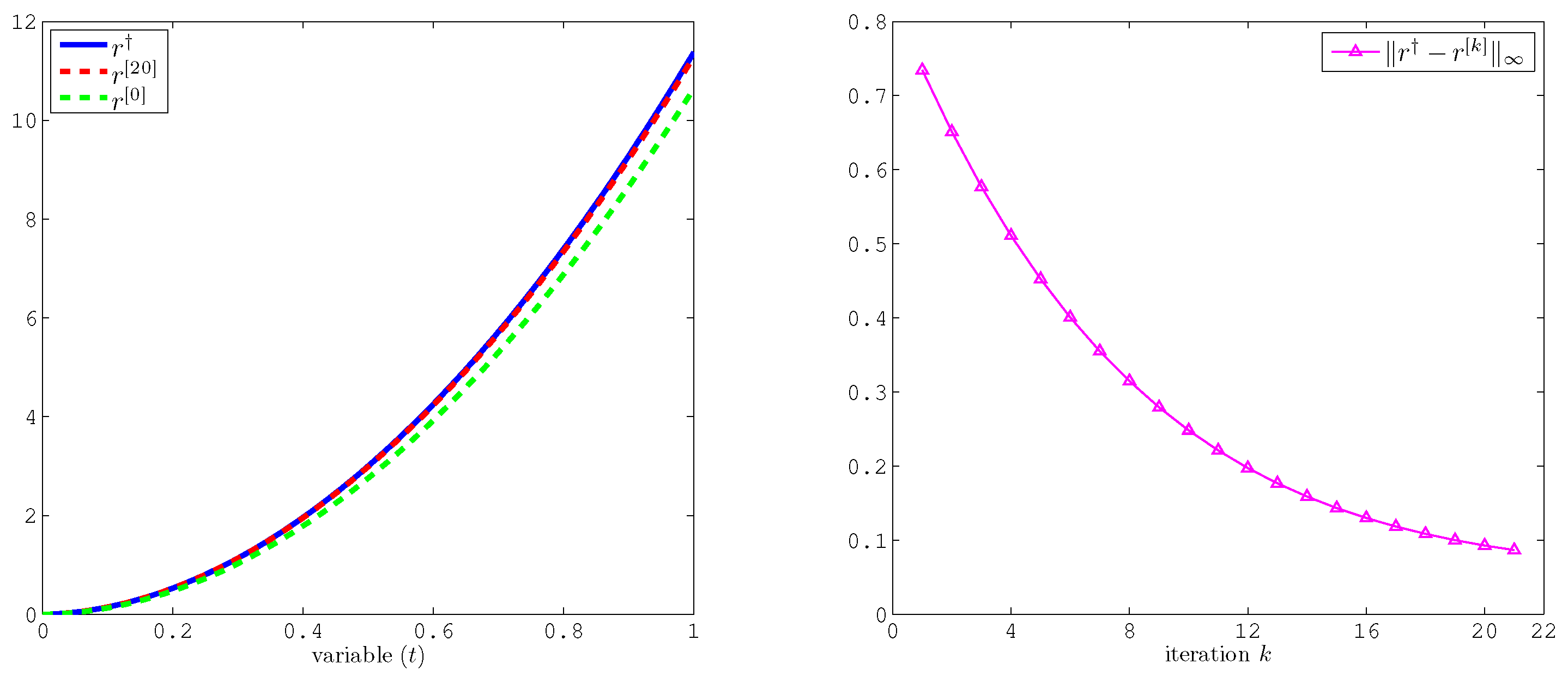
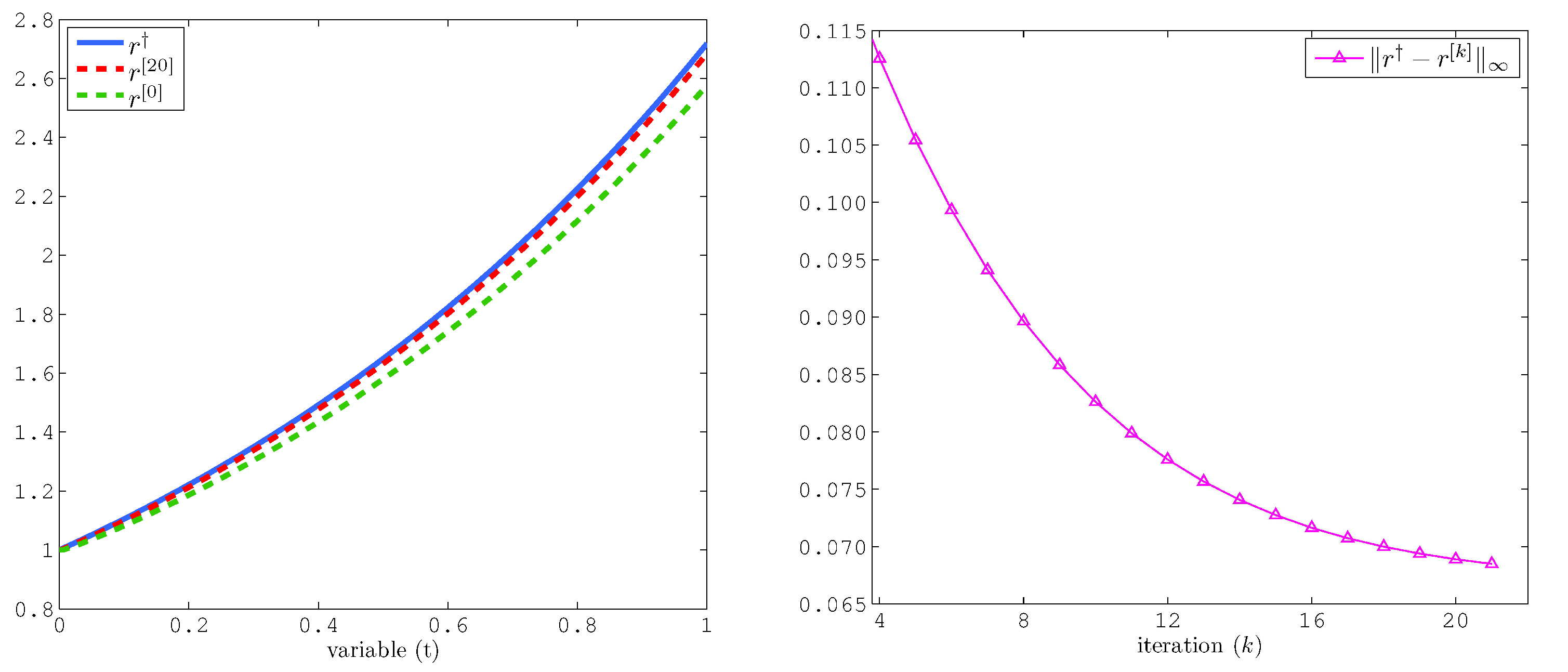
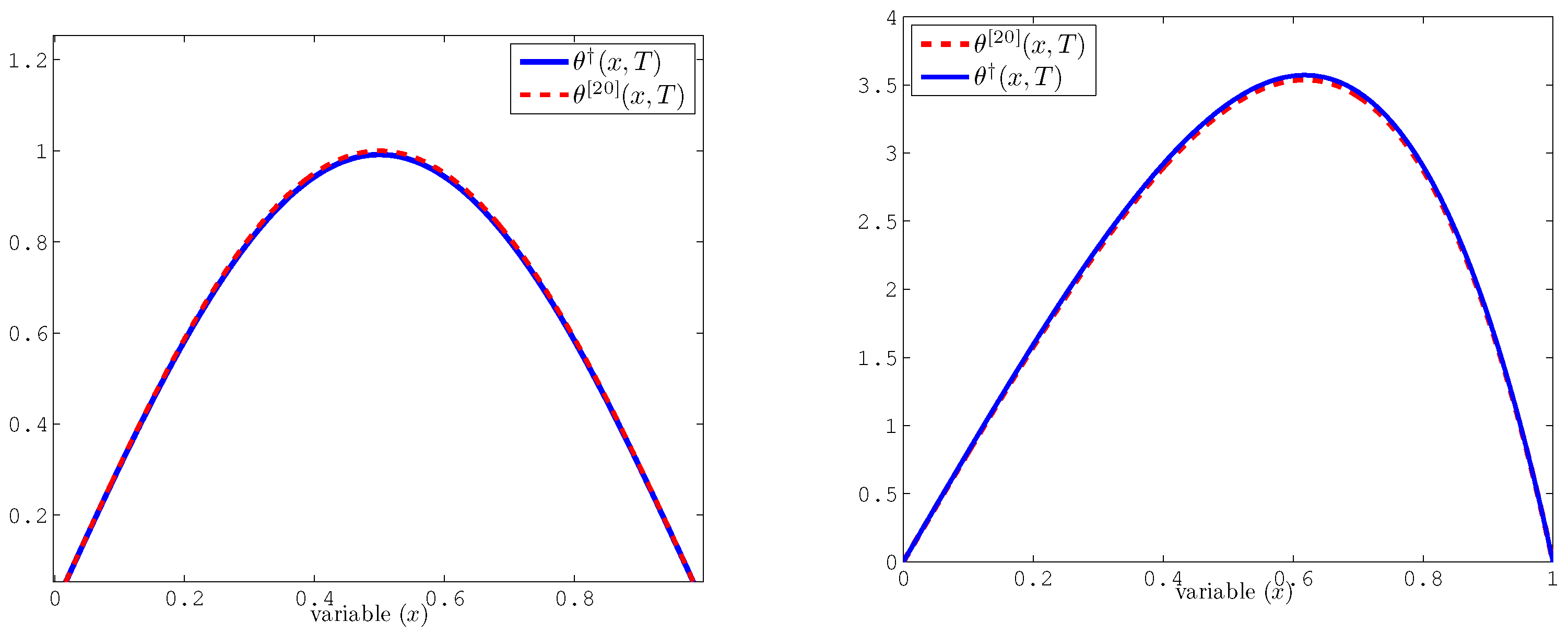
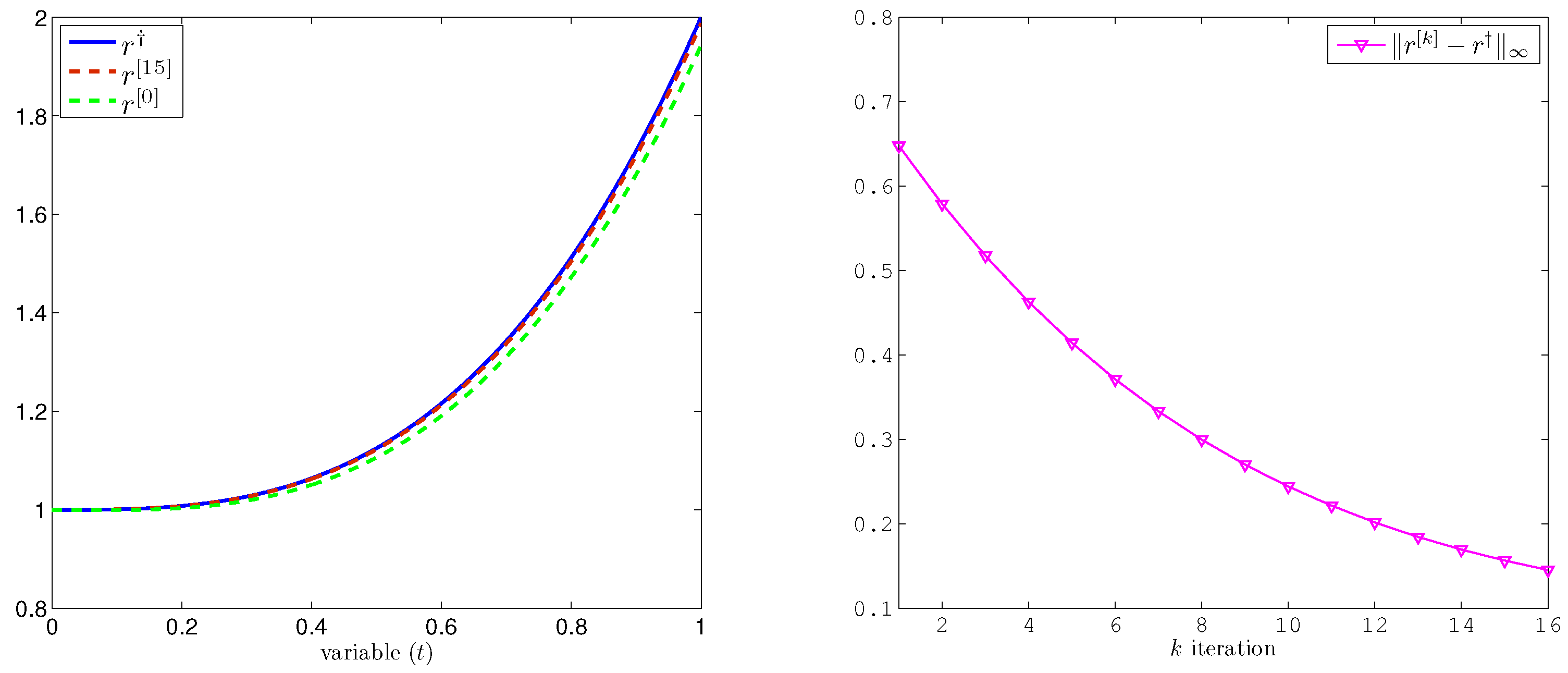
5. Numerical Reconstruction
| Algorithm 1 -Galerkin finite element method |
|
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buchot, J.-M.; Raymond, J.-P. A linearized model for boundary layer equations. In Optimal Control of Complex Structures: International Conference in Oberwolfach, 4–10 June 2000; Springer: Berlin/Heidelberg, Germany, 2001; pp. 31–42. [Google Scholar]
- Cannarsa, P.; Fragnelli, G.; Rocchetti, D. Controllability results for a class of one-dimensional degenerate parabolic problems in nondivergence form. J. Evol. Equ. 2008, 8, 583–616. [Google Scholar] [CrossRef]
- Martinez, P.; Raymond, J.-P.; Vancostenoble, J. Regional null controllability for a linearized Crocco-type equation. SIAM J. Control Optim. 2003, 42, 709–728. [Google Scholar] [CrossRef]
- Bertero, M.; Boccacci, P.; De Mol, C. Introduction to Inverse Problems in Imaging, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Mazaheri, M.; Mohammad Vali Samani, J.; Samani, H.M.V. Mathematical model for pollution source identification in rivers. Environ. Forensics 2015, 16, 310–321. [Google Scholar] [CrossRef]
- Zaporozhets, A.O.; Khaidurov, V.V. Mathematical models of inverse problems for finding the main characteristics of air pollution sources. Water Air Soil Pollut. 2020, 231, 563. [Google Scholar] [CrossRef]
- Tanaka, M.; Dulikravich, G.S. (Eds.) Inverse Problems in Engineering Mechanics; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Oldenburg, D.W.; Pratt, D.A. Geophysical inversion for mineral exploration: A decade of progress in theory and practice. Proc. Explor. 2007, 7, 61–95. [Google Scholar]
- Persova, M.G.; Soloveichik, Y.G.; Vagin, D.V.; Grif, A.M.; Kiselev, D.S.; Patrushev, I.I.; Ganiev, B.G. The design of high-viscosity oil reservoir model based on the inverse problem solution. J. Pet. Sci. Eng. 2021, 199, 108245. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Müller, S.; Kästner, M.; Brummund, J.; Ulbricht, V. A nonlinear fractional viscoelastic material model for polymers. Comput. Mater. Sci. 2011, 50, 2938–2949. [Google Scholar] [CrossRef]
- Oliveira, F.A.; Ferreira, R.M.; Lapas, L.C.; Vainstein, M.H. Anomalous diffusion: A basic mechanism for the evolution of inhomogeneous systems. Front. Phys. 2019, 7, 18. [Google Scholar] [CrossRef]
- Benabbes, F.; Boussetila, N.; Lakhdari, A. Two regularization methods for a class of inverse fractional pseudo-parabolic equations with involution perturbation. Fract. Differ. Calc. 2024, 14, 39–59. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L. An inverse problem of identifying the radiative coefficient in a degenerate parabolic equation. Chin. Ann. Math. 2014, 35, 355–382. [Google Scholar] [CrossRef]
- Durdiev, D.K.; Sultanov, M.A.; Rahmonov, A.A.; Nurlanuly, Y. Inverse Problems for a Time-Fractional Diffusion Equation with Unknown Right-Hand Side. Progr. Fract. Differ. Appl. 2023, 9, 639–653. [Google Scholar]
- Hasanoğlu, A.H.; Romanov, V.G. Introduction to Inverse Problems for Differential Equations; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Huzyk, N.M.; Pukach, P.Y.; Vovk, M.I. Coefficient inverse problem for the strongly degenerate parabolic equation. Carpathian J. Math. 2023, 15, 52–65. [Google Scholar]
- Isakov, V. Inverse Problems for Partial Differential Equations; Springer: New York, NY, USA, 2006; Volume 127. [Google Scholar]
- Jin, B.; Rundell, W. An inverse problem for a one-dimensional time-fractional diffusion problem. Inverse Probl. 2012, 28, 075010. [Google Scholar]
- Kaltenbacher, B.; Rundell, W. Inverse Problems for Fractional Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2023; Volume 230. [Google Scholar]
- Kirane, M.; Lopushansky, A.; Lopushanska, H. Inverse problem for a time-fractional differential equation with a time-and space-integral conditions. Math. Methods Appl. Sci. 2023, 46, 16381–16393. [Google Scholar] [CrossRef]
- Grimmonprez, M.; Slodička, M. Reconstruction of an unknown source parameter in a semilinear parabolic problem. J. Comput. Appl. Math. 2015, 289, 331–345. [Google Scholar] [CrossRef]
- Van Bockstal, K.; De Staelen, R.H.; Slodička, M. Identification of a memory kernel in a semilinear integrodifferential parabolic problem with applications in heat conduction with memory. J. Comput. Appl. Math. 2015, 289, 196–207. [Google Scholar]
- Bekakra, Y.; Bouziani, A. Rothe Time-discretization Method for Caputo Fractional Parabolic Equation. Lobachevskii J. Math. 2024, 45, 3873–3883. [Google Scholar] [CrossRef]
- Chattouh, A.; Saoudi, K.; Nouar, M. Rothe–Legendre pseudospectral method for a semilinear pseudoparabolic equation with nonclassical boundary condition. Nonlinear Anal. Model. Control 2022, 27, 38–53. [Google Scholar] [CrossRef]
- Slodička, M.; Šišková, K. An inverse source problem in a semilinear time-fractional diffusion equation. Comput. Math. Appl. 2016, 72, 1655–1669. [Google Scholar] [CrossRef]
- Wei, T.; Li, X.L.; Li, Y.S. An inverse time-dependent source problem for a time-fractional diffusion equation. Inverse Probl. 2016, 32, 085003. [Google Scholar] [CrossRef]
- Ruan, Z.; Wang, Z. Identification of a time-dependent source term for a time fractional diffusion problem. Appl. Anal. 2017, 96, 1638–1655. [Google Scholar] [CrossRef]
- Liu, S.; Feng, L.; Liu, C. A Fractional Tikhonov Regularization Method for Identifying a Time-Independent Source in the Fractional Rayleigh–Stokes Equation. Fractal Fract. 2024, 8, 601. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J. A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl. Numer. Math. 2014, 78, 95–111. [Google Scholar] [CrossRef]
- Ruan, Z.; Wan, G.; Zhang, W. Reconstruction of a space-dependent source term for a time fractional diffusion equation by a modified quasi-boundary value regularization method. Taiwan. J. Math. 2024, 1, 1–23. [Google Scholar] [CrossRef]
- Li, Z.; Deng, Z. A total variation regularization method for an inverse problem of recovering an unknown diffusion coefficient in a parabolic equation. Inverse Probl. Sci. Eng. 2020, 28, 1453–1473. [Google Scholar] [CrossRef]
- Klibanov, M.V.; Li, J.; Zhang, W. Convexification for an inverse parabolic problem. Inverse Probl. Sci. Eng. 2020, 28, 605–635. [Google Scholar] [CrossRef]
- Lv, X.; Feng, X. Identifying a Space-Dependent Source Term and the Initial Value in a Time Fractional Diffusion-Wave Equation. Mathematics 2023, 11, 1521. [Google Scholar] [CrossRef]
- Sidi, H.O.; Hendy, A.S.; Babatin, M.M.; Qiao, L.; Zaky, M.A. An inverse problem of Robin coefficient identification in parabolic equations with interior degeneracy from terminal observation data. Appl. Numer. Math. 2025, 212, 242–253. [Google Scholar] [CrossRef]
- Nouar, M.; Chattouh, A. On the source identification problem for a degenerate time-fractional diffusion equation. J. Math. Anal. 2024, 15, 84–98. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Yang, F.; Tian, F. The Landweber Iterative Regularization Method for Identifying the Unknown Source of Caputo-Fabrizio Time Fractional Diffusion Equation on Spherically Symmetric Domain. Symmetry 2023, 15, 1468. [Google Scholar] [CrossRef]
- Jiang, D.; Feng, H.; Zou, J. Quadratic convergence of Levenberg-Marquardt method for elliptic and parabolic inverse robin problems. ESAIM Math. Model. Numer. Anal. 2018, 52, 1085–1107. [Google Scholar] [CrossRef]
- Fragnelli, G.; Goldstein, G.R.; Goldstein, J.A.; Romanelli, S. Generators with interior degeneracy on spaces of L2 type. Electron. J. Differ. Equ. 2012, 2012, 1–30. [Google Scholar]
- Maes, F.; Van Bockstal, K. Existence and uniqueness of a weak solution to fractional single-phase-lag heat equation. Fract. Calc. Appl. Anal. 2023, 26, 1663–1690. [Google Scholar] [CrossRef]
- Alsaedi, A.; Ahmad, B.; Kirane, M. A survey of useful inequalities in fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 574–594. [Google Scholar] [CrossRef]
- Kačur, J. Method of Rothe in Evolution Equations. In Equadiff 6; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nouar, M.; Abdeledjalil, C.; Alsalhi, O.M.; Sidi, H.O. Inverse Problem of Identifying a Time-Dependent Source Term in a Fractional Degenerate Semi-Linear Parabolic Equation. Mathematics 2025, 13, 1486. https://doi.org/10.3390/math13091486
Nouar M, Abdeledjalil C, Alsalhi OM, Sidi HO. Inverse Problem of Identifying a Time-Dependent Source Term in a Fractional Degenerate Semi-Linear Parabolic Equation. Mathematics. 2025; 13(9):1486. https://doi.org/10.3390/math13091486
Chicago/Turabian StyleNouar, Maroua, Chattouh Abdeledjalil, Omar Mossa Alsalhi, and Hamed Ould Sidi. 2025. "Inverse Problem of Identifying a Time-Dependent Source Term in a Fractional Degenerate Semi-Linear Parabolic Equation" Mathematics 13, no. 9: 1486. https://doi.org/10.3390/math13091486
APA StyleNouar, M., Abdeledjalil, C., Alsalhi, O. M., & Sidi, H. O. (2025). Inverse Problem of Identifying a Time-Dependent Source Term in a Fractional Degenerate Semi-Linear Parabolic Equation. Mathematics, 13(9), 1486. https://doi.org/10.3390/math13091486





