A Novel Hybrid Approach Using an Attention-Based Transformer + GRU Model for Predicting Cryptocurrency Prices
Abstract
1. Introduction
2. Prediction Models
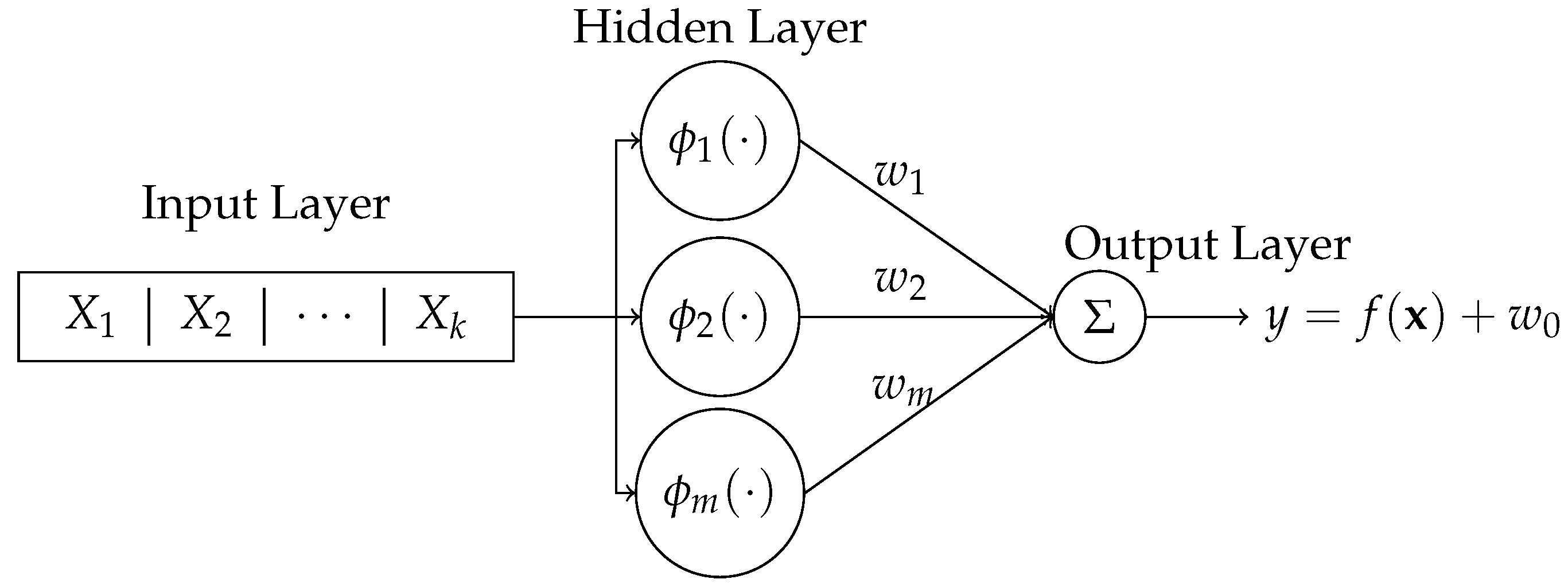
2.1. Radial Basis Function Network (RBFN)
2.2. General Regression Neural Network (GRNN) Model
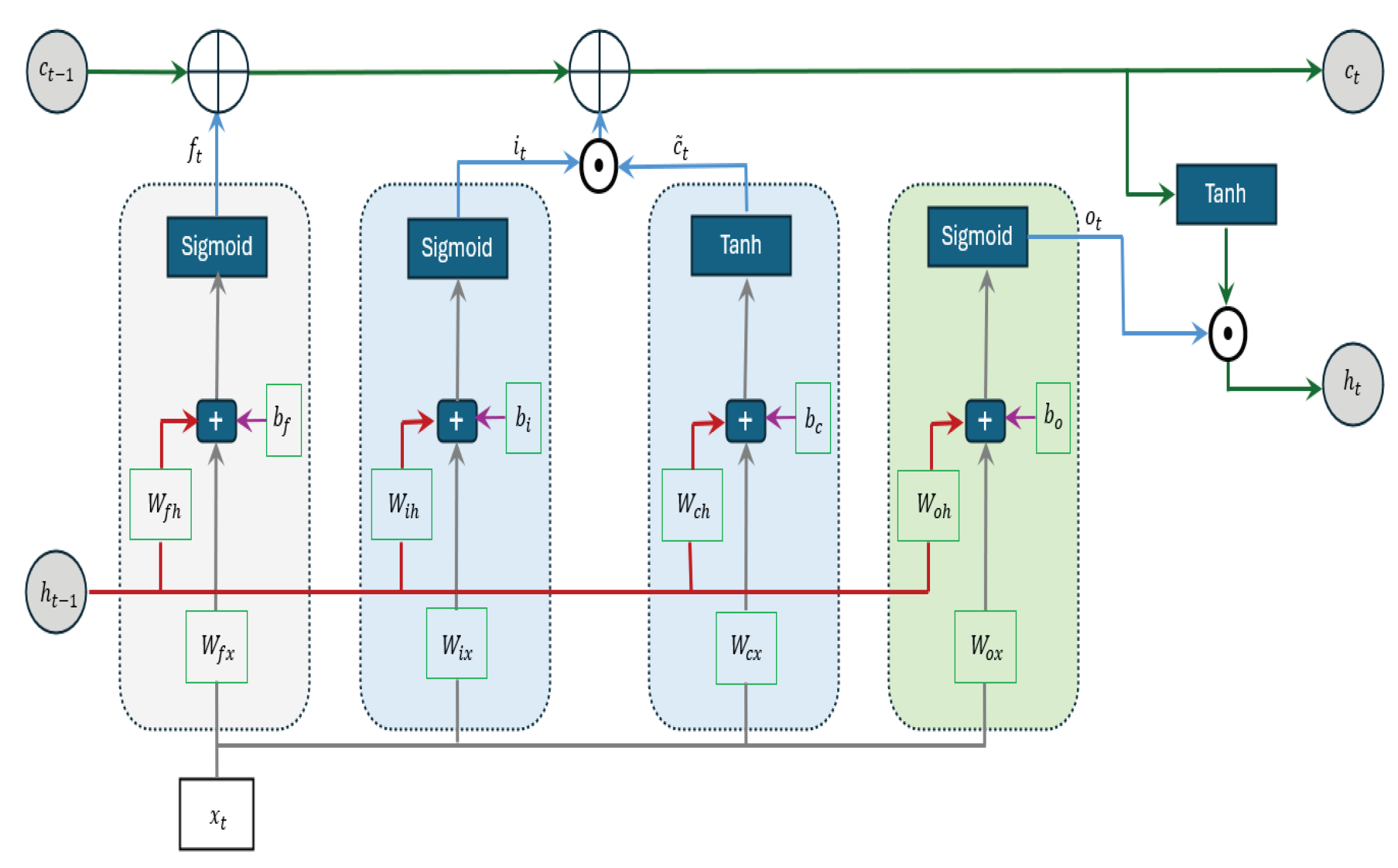
2.3. Long Short-Term Memory (LSTM) Model
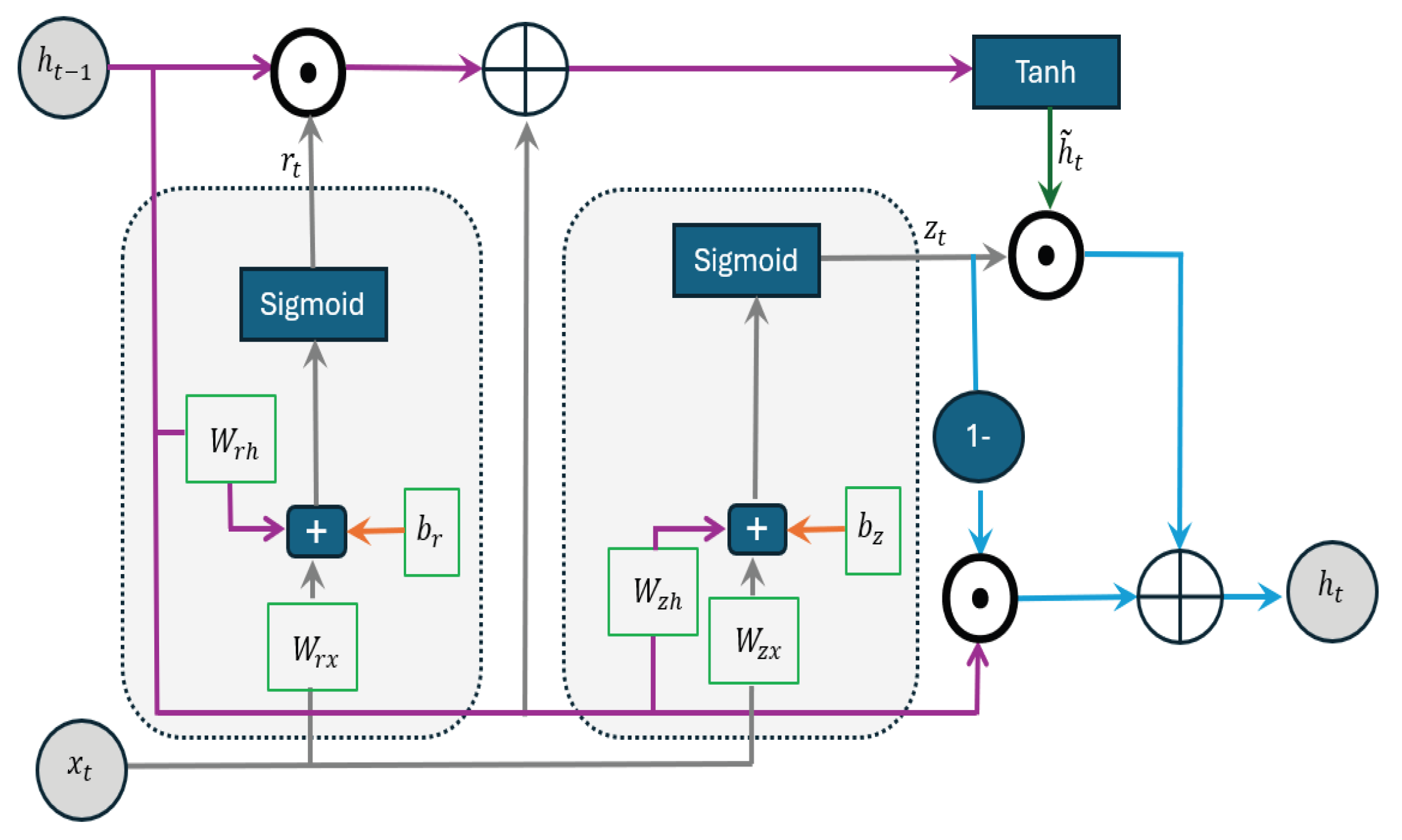
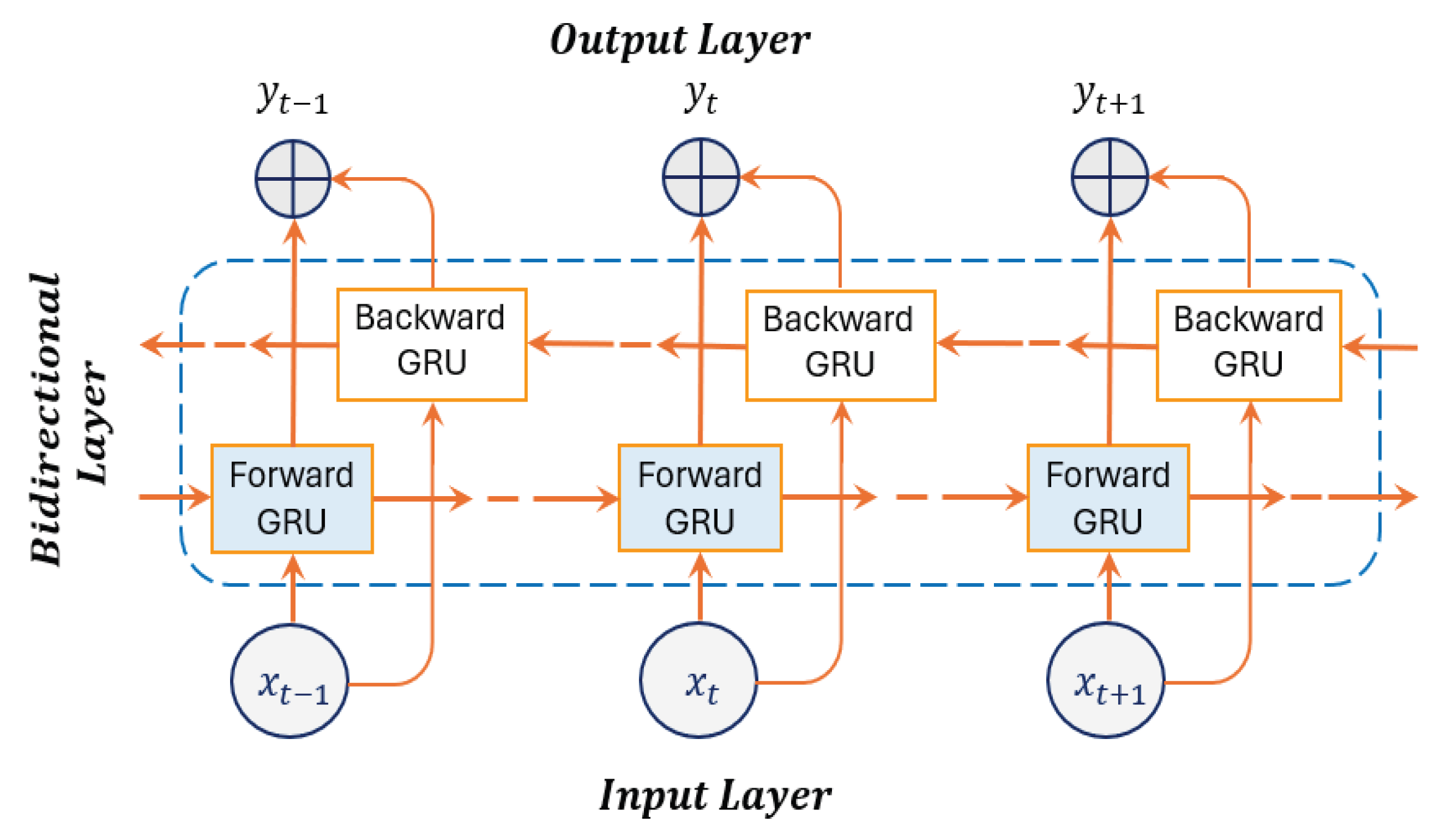
2.4. Gated Recurrent Unit (GRU) Model
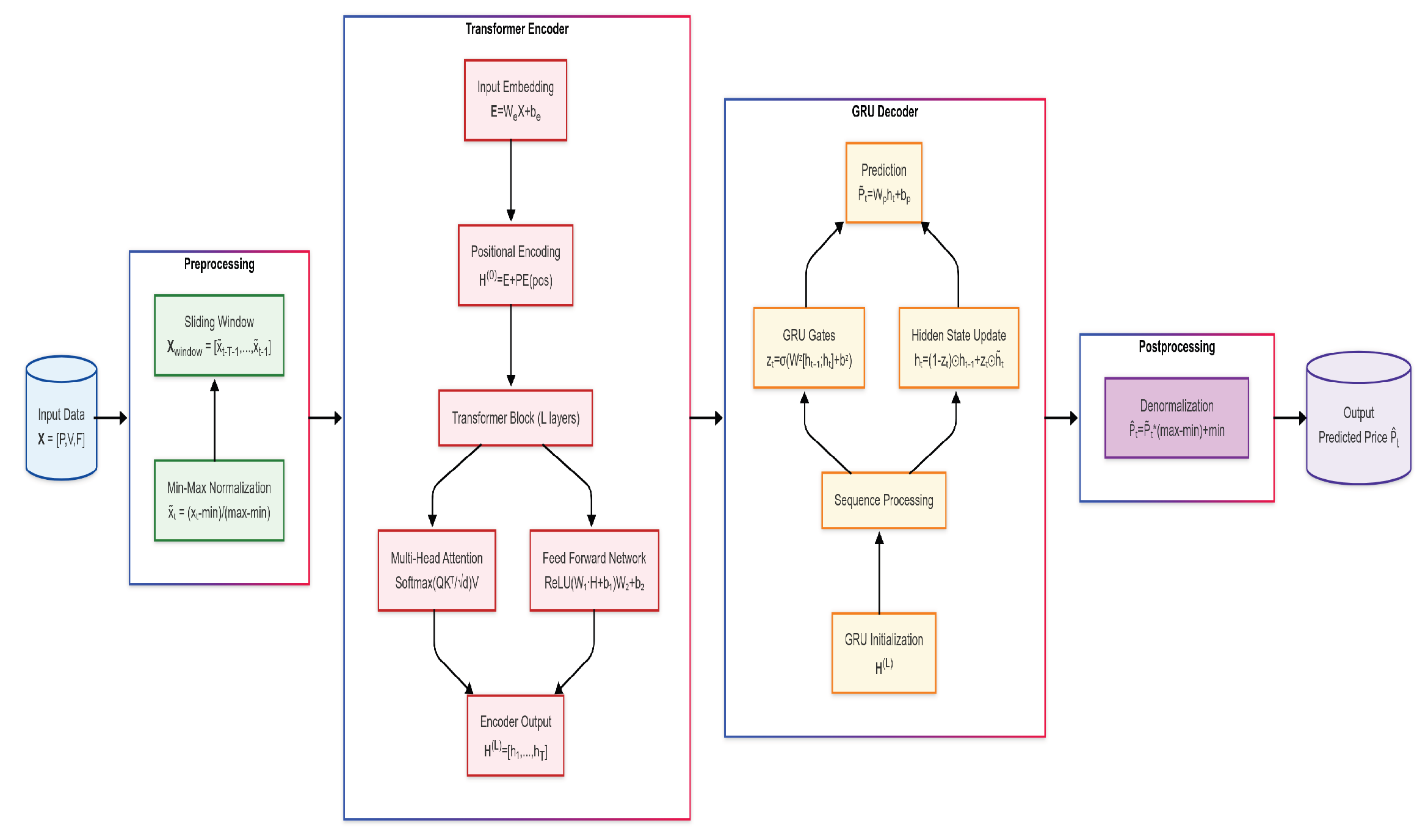
3. Hybrid Transformer + GRU Architecture
Step-by-Step Methodology
- 1.
- Input features: At each time i,where are the price of Bitcoin/Ethereum, exchange trading volume of Bitcoin/Ethereum, and Fear and Greed Index, respectively.
- 2.
- Preprocessing:
- 2.1.
- Normalization (Min–Max): Scale input features to the range using min–max normalization to ensure equal feature weighting.
- 2.2.
- Windowing: Split data into training and testing data and obtain a sliding window of values with fixed-length T (shape: ).
- 3.
- Encoder (Transformer):
- 3.1.
- Embedding layer: Project each into high-dimensional vectors dwhere , .
- 3.2.
- Positional encoding: Add time-order information to embeddings (positional encodings) using sine/cosine waves of varying frequencies.
- 3.3.
- Transformer layers: For each layer :
- 3.3.1.
- Multi-head self-attention: For each head m, split into h headswhere
- 3.3.2.
- Concatenate heads:where .
- 3.3.3.
- Residual connections and LayerNorm: In deeper layers, each module is wrapped with a residual connection followed by layer normalization, as follows:
- 3.3.4.
- Feedforward Network (FFN): Non-linear transformation of features:where and .
- 3.3.5.
- Second residual connections and LayerNorm:
- 4.
- Decoder (GRU with attention):
- 4.1.
- Sequence modeling: Process the Transformer’s final-layer output with GRU cells.The GRU equations:
- 4.2.
- Prediction: Use the final GRU hidden state to predict the price :where and .
- 5.
- Output (post-processing): Convert predictions back (denormalization) to original price scale.
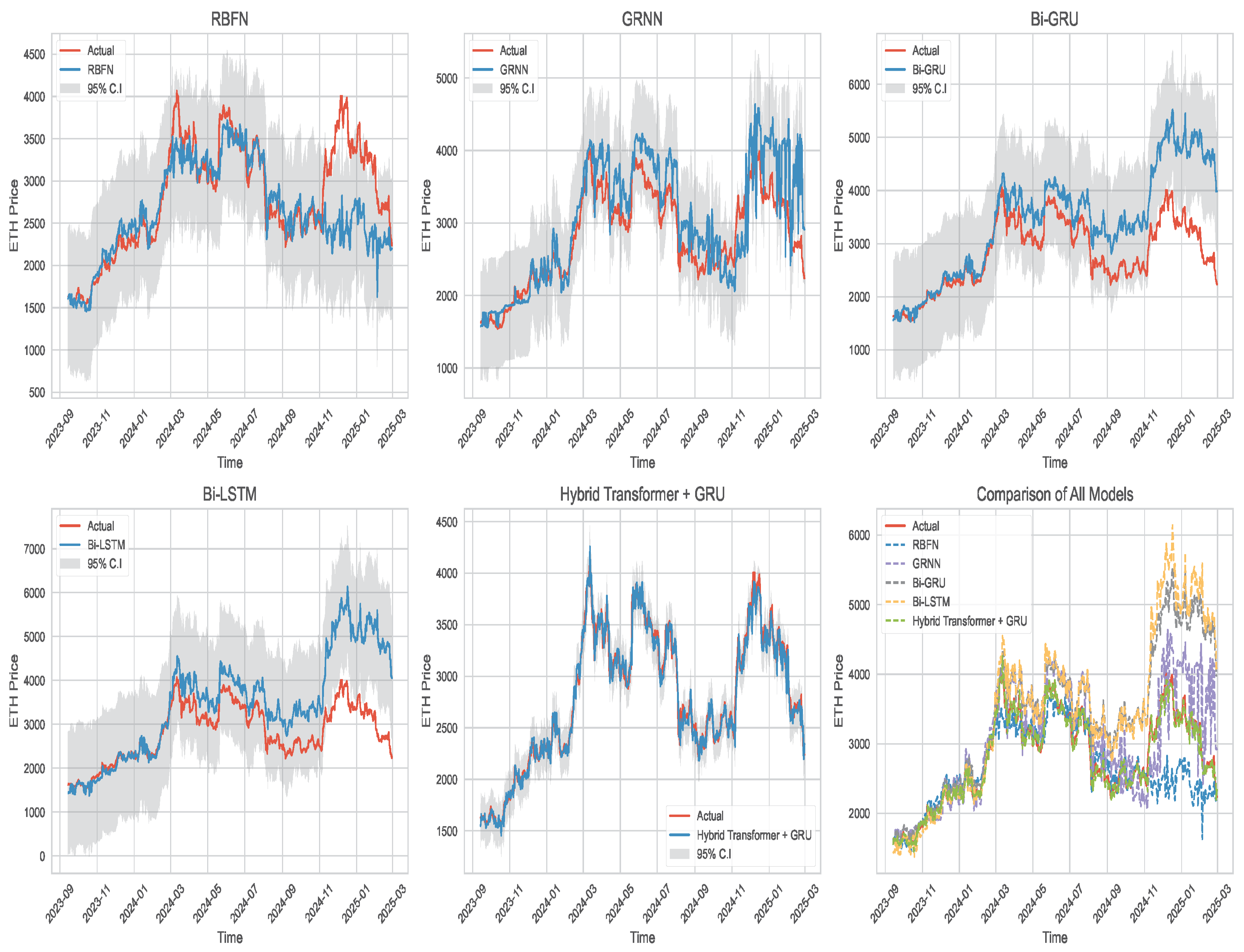
4. Exploratory Data Analysis
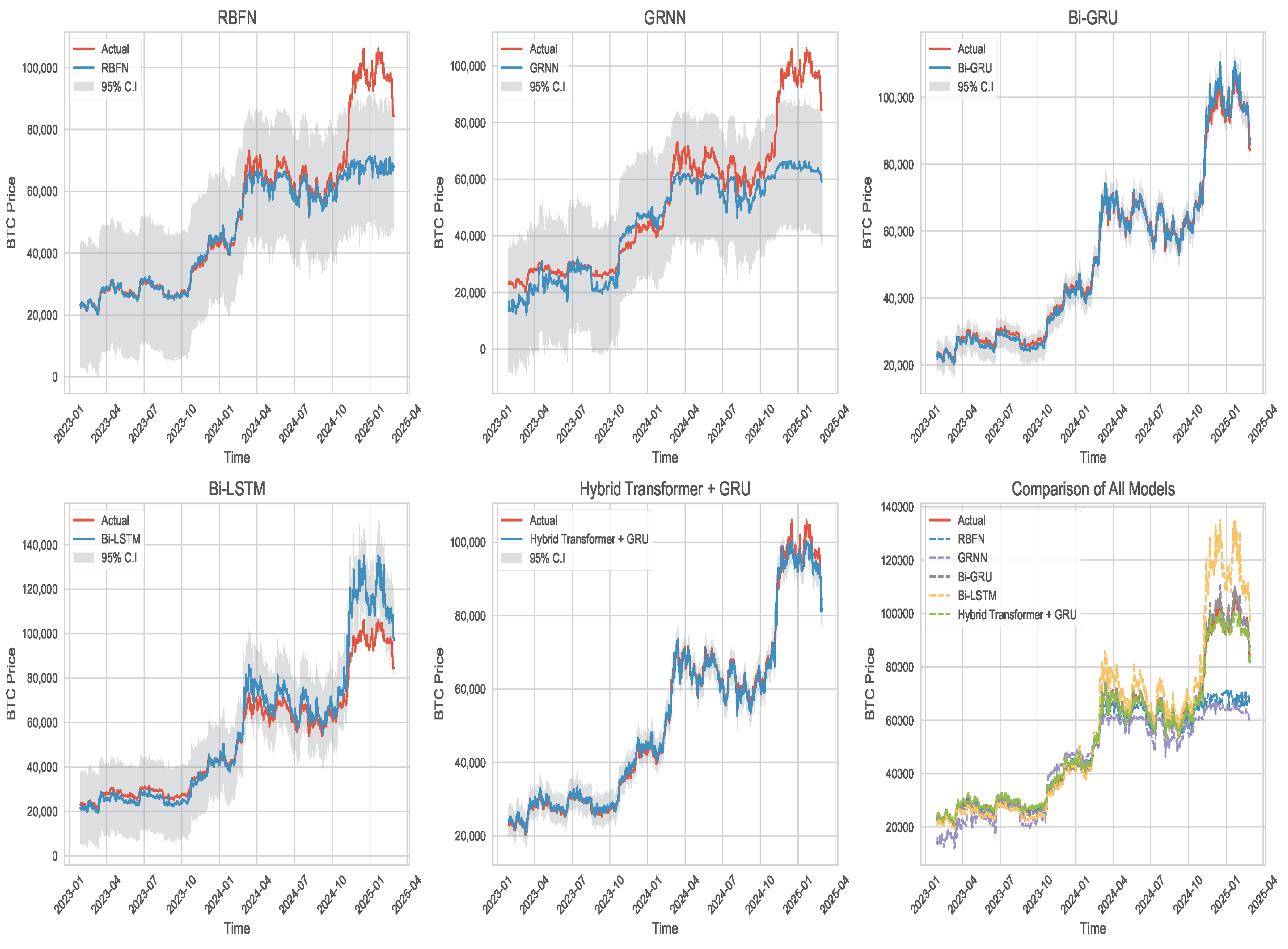
5. Conclusions and Recommendation
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Razi, M.A.; Athappilly, K. A comparative predictive analysis of neural networks (NNS), nonlinear regression and classification and regression tree (CART) models. Expert Syst. Appl. 2005, 29, 65–74. [Google Scholar] [CrossRef]
- Ślepaczuk, R.; Zenkova, M. Robustness of support vector machines in algorithmic trading on cryptocurrency market. Cent. Eur. Econ. J. 2018, 5, 186–205. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sun, W. Bitcoin price prediction using machine learning: An approach to sample dimension engineering. J. Comput. Appl. Math. 2020, 365, 112395. [Google Scholar] [CrossRef]
- Mahdi, E.; Leiva, V.; Mara’Beh, S.; Martin-Barreiro, C. A New Approach to Predicting Cryptocurrency Returns Based on the Gold Prices with Support Vector Machines during the COVID-19 Pandemic Using Sensor-Related Data. Sensors 2021, 21, 6319. [Google Scholar] [CrossRef]
- Akyildirim, E.; Goncu, A.; Sensoy, A. Prediction of cryptocurrency returns using machine learning. Ann. Oper. Res. 2021, 297, 3–36. [Google Scholar] [CrossRef]
- Makala, D.; Li, Z. Prediction of gold price with ARIMA and SVM. J. Phys. Conf. Ser. 2021, 1767, 012022. [Google Scholar] [CrossRef]
- Jaquart, P.; K¨opke, S.; Weinhardt, C. Machine learning for cryptocurrency market prediction and trading. J. Financ. Data Sci. 2022, 8, 331–352. [Google Scholar] [CrossRef]
- Mahdi, E.; Al-Abdulla, A. Impact of COVID-19 Pandemic News on the Cryptocurrency Market and Gold Returns: A Quantile-on-Quantile Regression Analysis. Econometrics 2022, 10, 26. [Google Scholar] [CrossRef]
- Qureshi, M.; Iftikhar, H.; Rodrigues, P.C.; Rehman, M.Z.; Salar, S.A.A. Statistical Modeling to Improve Time Series Forecasting Using Machine Learning, Time Series, and Hybrid Models: A Case Study of Bitcoin Price Forecasting. Mathematics 2024, 12, 3666. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Radial Basis Functions, Multi-Variable Functional Interpolation and Adaptive Networks (Technical Report); Memorandum 4148; Royal Signals and Radar Establishment (RSRE): Malvern, UK, 1988. [Google Scholar]
- Broomhead, D.S.; Lowe, D. Multivariable functional interpolation and adaptive networks. Complex Syst. 1988, 2, 321–355. [Google Scholar]
- Alahmari, S.A. Predicting the Price of Cryptocurrency Using Support Vector Regression Methods. J. Mech. Contin. Math. Sci. 2020, 15, 313–322. [Google Scholar] [CrossRef]
- Casillo, M.; Lombardi, M.; Lorusso, A.; Marongiu, F.; Santaniello, D.; Valentino, C. Sentiment Analysis and Recurrent Radial Basis Function Network for Bitcoin Price Prediction. In Proceedings of the IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; pp. 1189–1193. [Google Scholar] [CrossRef]
- Zhang, Y. Stock price behavior determination using an optimized radial basis function. Intell. Decis. Technol. 2025, 1–18. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Martínez, F.; Charte, F.; Rivera, A.J.; Frías, M.P. Automatic Time Series Forecasting with GRNN: A Comparison with Other Models. In Advances in Computational Intelligence, Proceedings of the 15th International Work-Conference on Artificial Neural Networks, IWANN 2019, Gran Canaria, Spain, 12–14 June 2019; Rojas, I., Joya, G., Catala, A., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; p. 11506. [Google Scholar] [CrossRef]
- Martínez, F.; Charte, F.; Frías, M.P.; Martínez-Rodríguez, A.M. Strategies for time series forecasting with generalized regression neural networks. Neurocomputing 2022, 49, 509–521. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- McNally, S.; Roche, J.; Caton, S. Predicting the Price of Bitcoin Using Machine Learning. In Proceedings of the 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP), Cambridge, UK, 21–23 March 2018; pp. 339–343. Available online: https://api.semanticscholar.org/CorpusID:206505441 (accessed on 27 April 2025).
- Liu, Y.; Gong, C.; Yang, L.; Chen, Y. DSTP-RNN: A dual-stage two-phase attention-based recurrent neural network for long-term and multivariate time series prediction. Expert Syst. Appl. 2020, 143, 113082. [Google Scholar] [CrossRef]
- Zoumpekas, T. Houstis, E.; Vavalis, M. ETH analysis and predictions utilizing deep learning. Expert Syst. Appl. 2020, 162, 113866. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Cryptocurrency forecasting with deep learning chaotic neural networks. Chaos Solitons Fractals 2019, 118, 35–40. [Google Scholar] [CrossRef]
- Ji, S.; Kim, J.; Im, H. A Comparative Study of Bitcoin Price Prediction Using Deep Learning. Mathematics 2019, 7, 898. [Google Scholar] [CrossRef]
- Uras, N.; Marchesi, L.; Marchesi, M.; Tonelli, R. Forecasting Bitcoin closing price series using linear regression and neural networks models. PeerJ Comput. Sci. 2020, 6, E279. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Deep learning forecasting in cryptocurrency high frequency trading. Cogn. Comput. 2021, 13, 485–487. [Google Scholar] [CrossRef]
- Cho, K.; Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Fethi, B.; Holger, S.; Bengio, Y. Learning phrase representations using RNN encoder- decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Jianwei, E.; Ye, J.; Jin, H. A novel hybrid model on the prediction of time series and its application for the gold price analysis and forecasting. Phys. A Stat. Mech. Its Appl. 2019, 527, 121454. [Google Scholar] [CrossRef]
- Dutta, A.; Kumar, S.; Basu, M. A gated recurrent unit approach to bitcoin price prediction. J. Risk Financ. Manag. 2020, 13, 23. [Google Scholar] [CrossRef]
- Tanwar, S.; Patel, N.P.; Patel, S.N.; Patel, J.R.; Sharma, G.; Davidson, I.E. Deep Learning-Based Cryptocurrency Price Prediction Scheme with Inter-Dependent Relations. IEEE Access 2021, 9, 138633–138646. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, Y.; Chen, H.; Pan, Y.; Jiang, Q. A Stacking Ensemble Deep Learning Model for Bitcoin Price Prediction Using Twitter Comments on Bitcoin. Mathematics 2022, 10, 1307. [Google Scholar] [CrossRef]
- Patra, G.R.; Mohanty, M.N. Price Prediction of Cryptocurrency Using a Multi-Layer Gated Recurrent Unit Network with Multi Features. Comput. Econ. 2023, 62, 1525–1544. [Google Scholar] [CrossRef]
- Hansun, S.; Wicaksana, A.; Khaliq, A.Q.M. Multivariate cryptocurrency prediction: Comparative analysis of three recurrent neural networks approaches. J. Big Data 2022, 9, 50. [Google Scholar] [CrossRef]
- Ferdiansyah, F.; Othman, S.H.; Radzi, R.Z.M.; Stiawan, D.; Sutikno, T. Hybrid gated recurrent unit bidirectional-long short-term memory model to improve cryptocurrency prediction accuracy. IAES Int. J. Artif. Intell. (IJ-AI) 2023, 12, 251–261. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Grigsby, J.; Wang, Z.; Qi, Y. Long-Range Transformers for Dynamic Spatiotemporal Forecasting. arXiv 2021, arXiv:2109.12218. [Google Scholar]
- Lezmi, E.; Xu, J. Time Series Forecasting with Transformer Models and Application to Asset Management. 2023. Available online: https://ssrn.com/abstract=4375798 (accessed on 27 April 2025).
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, Macao, 19–25 August 2023; pp. 6778–6786. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. arXiv 2020, arXiv:1907.00235. [Google Scholar]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A transformer-based framework for multivariate time series representation learning. In Proceedings of the KDD ’21: Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, Singapore, 14–18 August 2021; pp. 2114–2124. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. NeurIPS. arXiv 2021, arXiv:2106.13008. [Google Scholar]
- Castangia, M.; Grajales, L.M.M.; Aliberti, A.; Rossi, C.; Macii, A.; Macii, E.; Patti, E. Transformer neural networks for interpretable flood forecasting. Environ. Model. Softw. 2023, 160, 105581. [Google Scholar] [CrossRef]
- Nayak, G.H.H.; Alam, W.; Avinash, G.; Kumar, R.R.; Ray, M.; Barman, S.; Singh, K.N.; Naik, B.S.; Alam, N.M.; Pal, P.; et al. Transformer-based deep learning architecture for time series forecasting. Softw. Impacts 2024, 22, 100716. [Google Scholar] [CrossRef]
- Kristoufek, L. BitCoin meets Google Trends and Wikipedia: Quantifying the relationship between phenomena of the Internet era. Sci. Rep. 2013, 3, 3415. [Google Scholar] [CrossRef]
- Urquhart, A. What causes the attention of Bitcoin? Econ. Lett. 2018, 166, 40–44. [Google Scholar] [CrossRef]
- Kao, Y.S.; Day, M.Y.; Chou, K.H. A comparison of bitcoin futures return and return volatility based on news sentiment contemporaneously or lead-lag. N. Am. J. Econ. Financ. 2024, 72, 102159. [Google Scholar] [CrossRef]
- Mai, F.; Shan, J.; Bai, Q.; Sahne, W. How does social media impact Bitcoin value? A test of the silent majority hypothesis. J. Manag. Inf. Syst. 2018, 35, 19–52. [Google Scholar] [CrossRef]
- Garcia, D.; Schweitzer, F. Social signals and algorithmic trading of Bitcoin. R. Soc. Open Sci. 2015, 2, 150288. [Google Scholar] [CrossRef]
- Yan, K.; Li, Y. Machine learning-based analysis of volatility quantitative investment strategies for American financial stocks. Quant. Financ. Econ. 2024, 8, 364–386. [Google Scholar] [CrossRef]
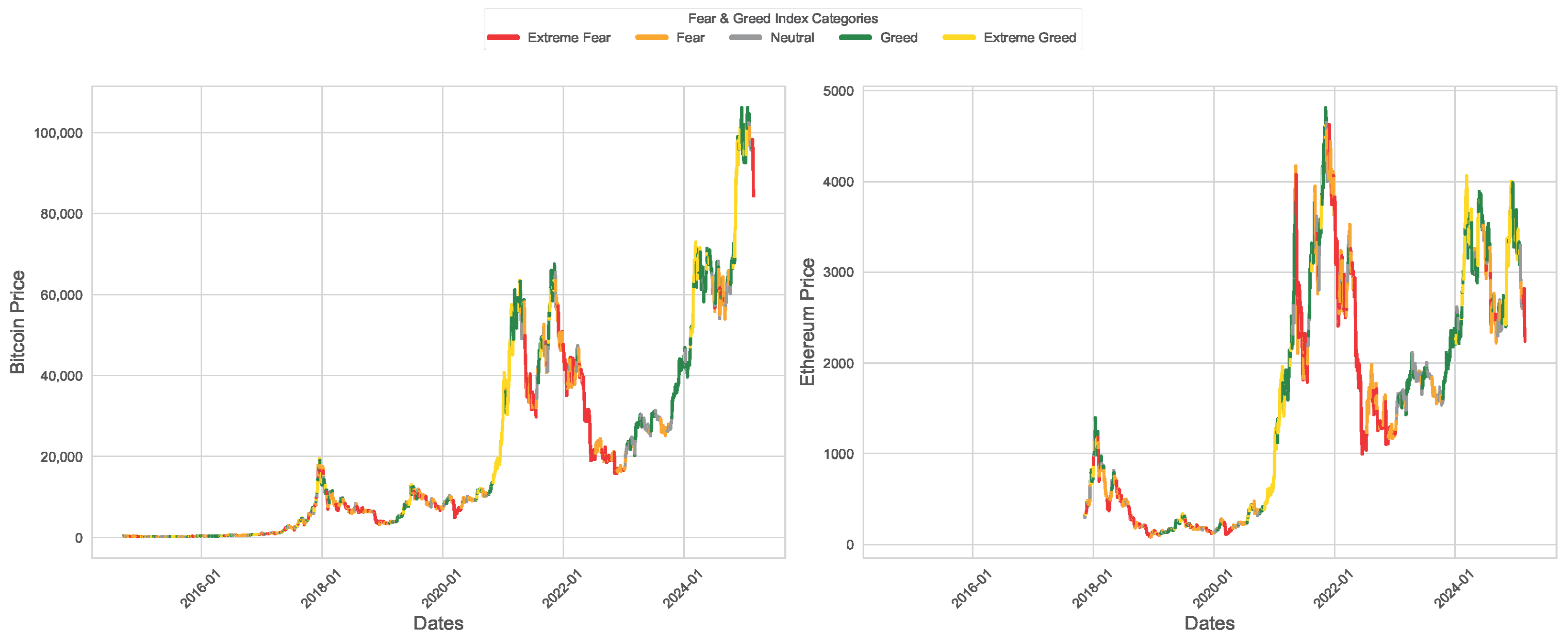
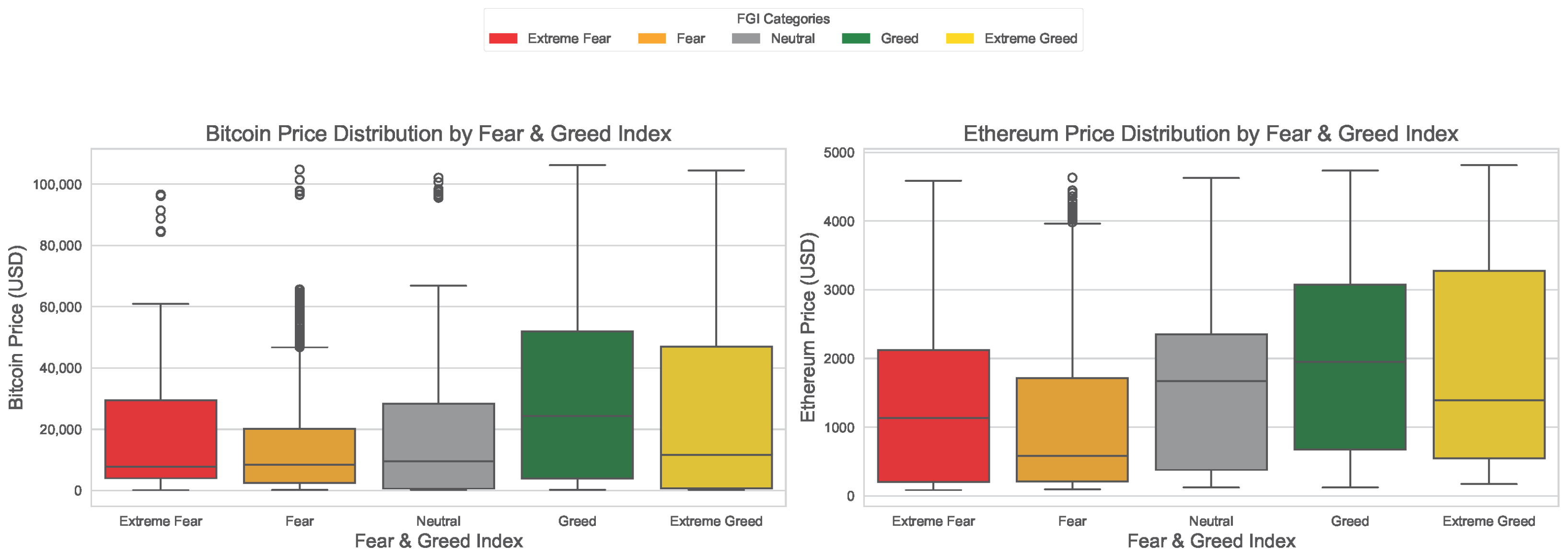
| Cryptocurrency | Start Date | End Date | Number of Records |
|---|---|---|---|
| Bitcoin | September 17, 2014 | February 28, 2025 | 3818 |
| Ethereum | November 09, 2017 | February 28, 2025 | 2669 |
| Model | MSE | RMSE | MAE | MAPE |
|---|---|---|---|---|
| RBFN | 13157.727 | 6928.640 | 9.479% | |
| GRNN | 13694.897 | 9179.342 | 15.857% | |
| BiGRU | 2087.692 | 1559.954 | 3.271% | |
| BiLSTM | 9046.889 | 5877.042 | 9.600% | |
| Hybrid Transformer + GRU | 1954.003 | 1419.972 | 2.825% |
| Model | MSE | RMSE | MAE | MAPE |
|---|---|---|---|---|
| RBFN | 203,541.169 | 451.155 | 288.453 | 9.362% |
| GRNN | 194,985.943 | 441.572 | 345.963 | 11.901% |
| BiGRU | 687,799.984 | 829.337 | 608.416 | 20.735% |
| BiLSTM | 907,844.180 | 952.809 | 675.427 | 22.640% |
| Hybrid Transformer + GRU | 11,344.686 | 106.511 | 78.809 | 2.755% |
| Model 1 | Model 2 | Wilcoxon Test | Raw p-Value | Bonferroni Corrected p-Value | Significant * |
|---|---|---|---|---|---|
| RBFN | GRNN | 38,606 | TRUE | ||
| RBFN | BiGRU | 47,196 | TRUE | ||
| RBFN | BiLSTM | 132,787 | 0.02894864 | 0.2894864 | FALSE |
| RBFN | Hybrid Transformer + GRU | 34,773 | TRUE | ||
| GRNN | BiGRU | 5058 | TRUE | ||
| GRNN | BiLSTM | 47,851 | TRUE | ||
| GRNN | Hybrid Transformer + GRU | 2604 | TRUE | ||
| BiGRU | BiLSTM | 20,834 | TRUE | ||
| BiGRU | Hybrid Transformer + GRU | 128,651 | 0.004209894 | 0.042098938 | FALSE |
| BiLSTM | Hybrid Transformer + GRU | 21,898 | TRUE |
| Model 1 | Model 2 | Wilcoxon Test | Raw p-Value | Bonferroni Corrected p-Value | Significant * |
|---|---|---|---|---|---|
| RBFN | GRNN | 47,616 | TRUE | ||
| RBFN | BiGRU | 20,411 | TRUE | ||
| RBFN | BiLSTM | 15,193 | TRUE | ||
| RBFN | Hybrid Transformer + GRU | 17,810 | TRUE | ||
| GRNN | BiGRU | 29,575 | TRUE | ||
| GRNN | BiLSTM | 26,767 | TRUE | ||
| GRNN | Hybrid Transformer + GRU | 5615 | TRUE | ||
| BiGRU | BiLSTM | 46,690 | TRUE | ||
| BiGRU | Hybrid Transformer + GRU | 4900 | TRUE | ||
| BiLSTM | Hybrid Transformer + GRU | 4839 | TRUE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdi, E.; Martin-Barreiro, C.; Cabezas, X. A Novel Hybrid Approach Using an Attention-Based Transformer + GRU Model for Predicting Cryptocurrency Prices. Mathematics 2025, 13, 1484. https://doi.org/10.3390/math13091484
Mahdi E, Martin-Barreiro C, Cabezas X. A Novel Hybrid Approach Using an Attention-Based Transformer + GRU Model for Predicting Cryptocurrency Prices. Mathematics. 2025; 13(9):1484. https://doi.org/10.3390/math13091484
Chicago/Turabian StyleMahdi, Esam, Carlos Martin-Barreiro, and Xavier Cabezas. 2025. "A Novel Hybrid Approach Using an Attention-Based Transformer + GRU Model for Predicting Cryptocurrency Prices" Mathematics 13, no. 9: 1484. https://doi.org/10.3390/math13091484
APA StyleMahdi, E., Martin-Barreiro, C., & Cabezas, X. (2025). A Novel Hybrid Approach Using an Attention-Based Transformer + GRU Model for Predicting Cryptocurrency Prices. Mathematics, 13(9), 1484. https://doi.org/10.3390/math13091484








