OWNC: Open-World Node Classification on Graphs with a Dual-Embedding Interaction Framework
Abstract
1. Introduction
- Imbalanced learning: It is common for the number of nodes with different labels to be imbalanced in the open-world setting due to the inherent diversity of the data. However, current models are ineffective in dealing with such imbalanced data.
- Too many or too few nodes from unseen classes: When dealing with too many or too few nodes from the unseen classes, the classification is usually less effective.
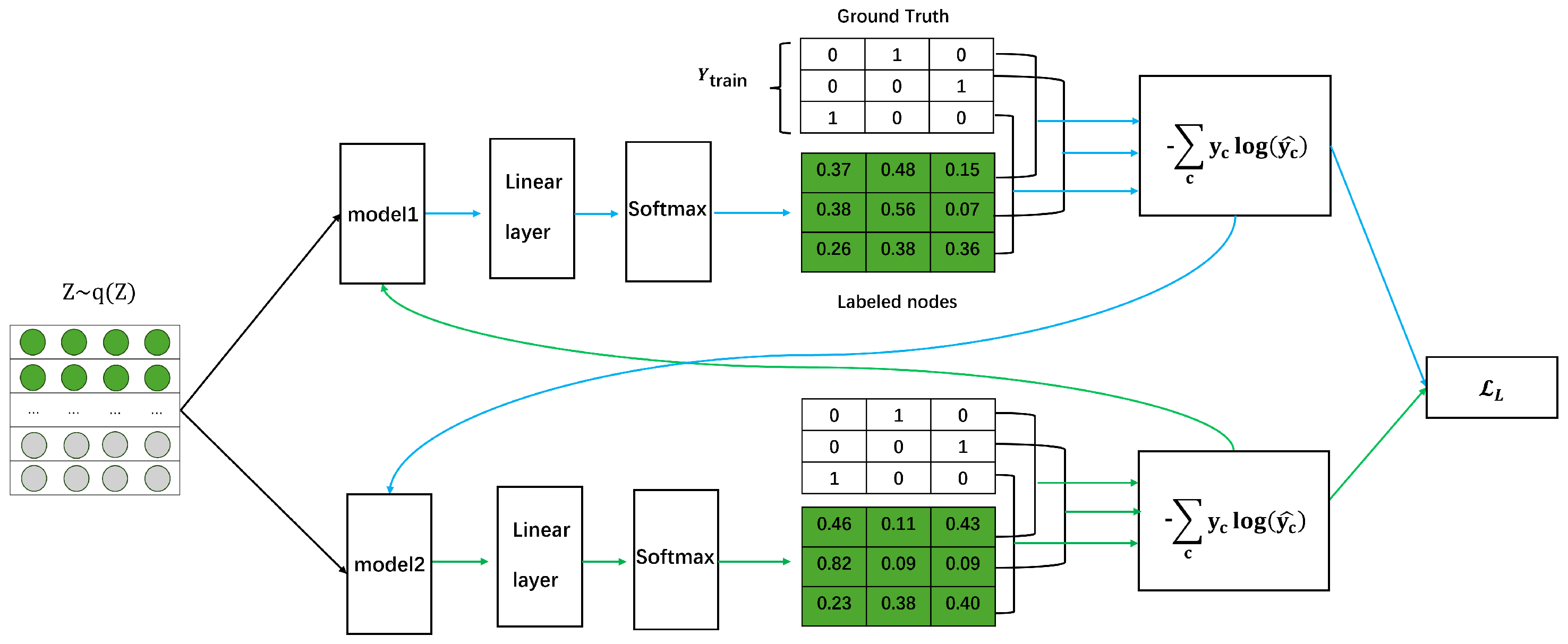
- We introduce a dual-embedding interaction training framework that enhances classification by effectively managing hard-to-learn samples, promoting model diversity through mutual sample selection, and reducing overfitting. These features collectively improve the model’s robustness and generalization, particularly in complex open-world scenarios.
- By integrating a GAN-based generator–discriminator architecture, our model maintains sensitivity to unseen classes, delivering strong performance regardless of whether there is a small or large number of nodes from unseen classes. This setup also mitigates imbalanced learning, further supporting the model’s ability to generalize.
- Our algorithm achieves significant performance improvements over state-of-the-art methods across three benchmark datasets, demonstrating its effectiveness in handling open-world node classification challenges.
2. Related Work
2.1. Open-World Learning
2.2. Graph Neural Networks
2.3. Co-Training Related Methods
2.4. Generator and Discriminator
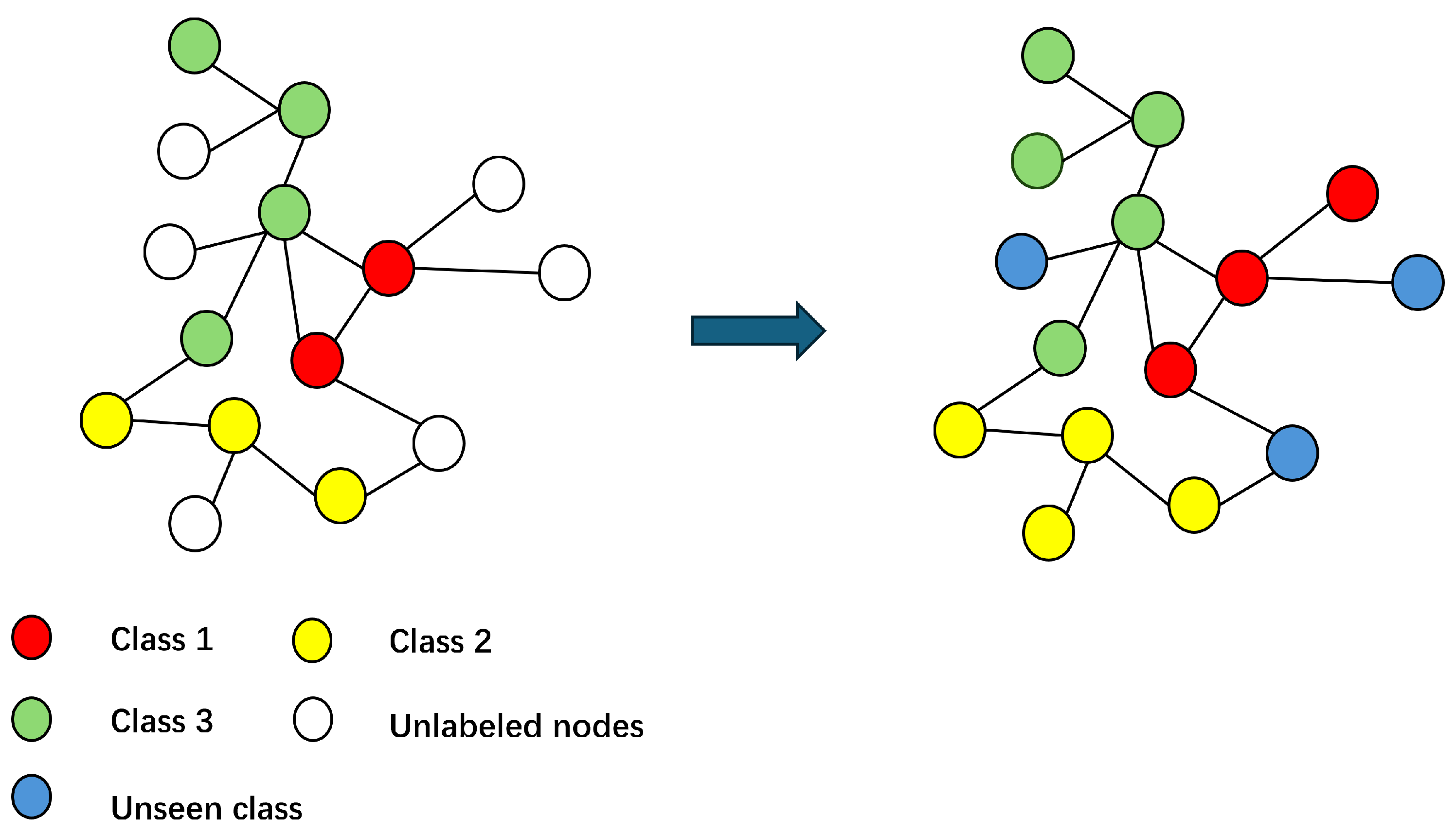
3. Problem Definition and Framework Structure
3.1. Problem Definition
3.2. Framework Structure
4. Framework Structure
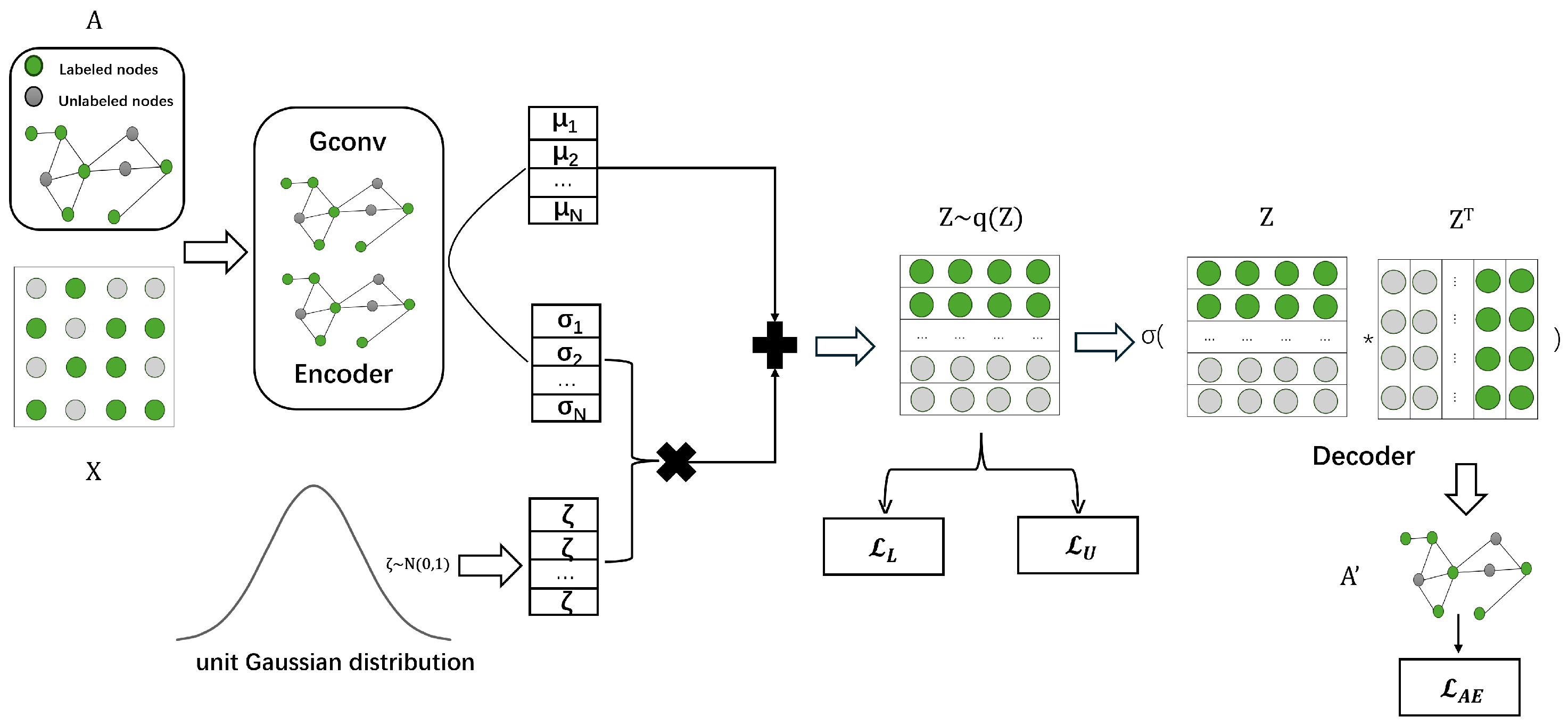
4.1. Open-World Classifier Learning
4.2. Graph Autoencoder Model
4.3. Labeled Loss Function
4.4. Unlabeled Loss
4.5. Open-World Node Classification
4.6. Algorithm Description
| Algorithm 1: OWNC algorithm |
| Date: : a graph with edges and node features; , , where S are the seen classes that appear in , and U are the unseen classes; C: the number of seen classes. Step: 1: // Graph Encoder Model 2: // For the first layer: 3: 5: 9: 11: 14: Obtain the label loss using Equation (10) 15: Obtain the unlabeled loss using Equation (17) 16: Back-propagate loss gradient using Equation (1) 17: |
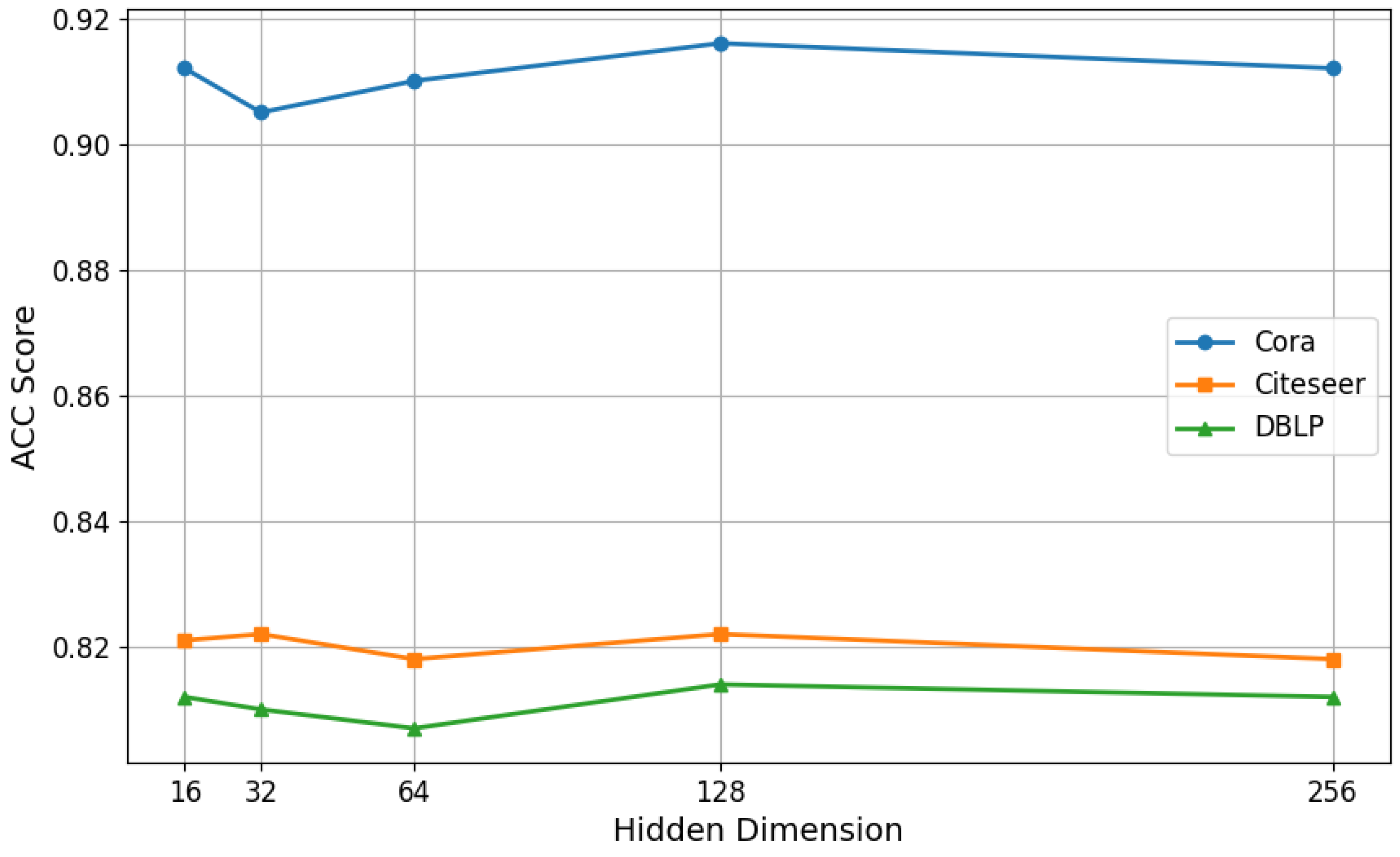
5. Experimental Setup
- OWNC¬D: A variant of OWNC with the dual-embedding interaction training framework module removed.
- OWNC¬G: A variant of OWNC with the GAN module removed.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph neural networks for social recommendation. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 417–426. [Google Scholar]
- Liu, S.; Grau, B.; Horrocks, I.; Kostylev, E. Indigo: Gnn-based inductive knowledge graph completion using pair-wise encoding. Adv. Neural Inf. Process. Syst. 2021, 34, 2034–2045. [Google Scholar]
- Innan, N.; Sawaika, A.; Dhor, A.; Dutta, S.; Thota, S.; Gokal, H.; Patel, N.; Khan, M.A.Z.; Theodonis, I.; Bennai, M. Financial fraud detection using quantum graph neural networks. Quantum Mach. Intell. 2024, 6, 7. [Google Scholar] [CrossRef]
- Zitnik, M.; Leskovec, J. Predicting multicellular function through multi-layer tissue networks. Bioinformatics 2017, 33, i190–i198. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Duvenaud, D.K.; Maclaurin, D.; Iparraguirre, J.; Bombarell, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional networks on graphs for learning molecular fingerprints. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Scheirer, W.J.; de Rezende Rocha, A.; Sapkota, A.; Boult, T.E. Toward open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1757–1772. [Google Scholar] [CrossRef]
- Wu, M.; Pan, S.; Zhu, X. Openwgl: Open-world graph learning. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 681–690. [Google Scholar]
- Zhang, Q.; Shi, Z.; Zhang, X.; Chen, X.; Fournier-Viger, P.; Pan, S. G2Pxy: Generative open-set node classification on graphs with proxy unknowns. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, Macao, China, 19–25 August 2023; pp. 4576–4583. [Google Scholar]
- Zhao, T.; Zhang, X.; Wang, S. Graphsmote: Imbalanced node classification on graphs with graph neural networks. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Jerusalem, Israel, 8–12 March 2021; pp. 833–841. [Google Scholar]
- Bendale, A.; Boult, T. Towards open world recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1893–1902. [Google Scholar]
- Xian, Y.; Lorenz, T.; Schiele, B.; Akata, Z. Feature generating networks for zero-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5542–5551. [Google Scholar]
- Fu, B.; Cao, Z.; Long, M.; Wang, J. Learning to detect open classes for universal domain adaptation. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XV 16. Springer: Cham, Switzerland, 2020; pp. 567–583. [Google Scholar]
- Jiang, L.; Zhou, Z.; Leung, T.; Li, L.J.; Fei-Fei, L. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2304–2313. [Google Scholar]
- Kumar, M.; Packer, B.; Koller, D. Self-paced learning for latent variable models. Adv. Neural Inf. Process. Syst. 2010, 23. [Google Scholar]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E.Y. Network representation learning with rich text information. In Proceedings of the IJCAI, Buenos Aires, Argentina, 25–31 July 2015; Volume 2015, pp. 2111–2117. [Google Scholar]
- Malach, E.; Shalev-Shwartz, S. Decoupling “when to update” from “how to update”. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Yu, X.; Han, B.; Yao, J.; Niu, G.; Tsang, I.; Sugiyama, M. How does disagreement help generalization against label corruption? In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 7164–7173. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mirza, M. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Radford, A. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Dhamija, A.R.; Günther, M.; Boult, T. Reducing network agnostophobia. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Oza, P.; Patel, V.M. C2ae: Class conditioned auto-encoder for open-set recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2307–2316. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Pan, S.; Wu, J.; Zhu, X.; Zhang, C.; Wang, Y. Tri-party deep network representation. In Proceedings of the International Joint Conference on Artificial Intelligence 2016, New York, NY, USA, 9–15 July 2016; pp. 1895–1901. [Google Scholar]
- Tang, J.; Zhang, J.; Yao, L.; Li, J.; Zhang, L.; Su, Z. Arnetminer: Extraction and mining of academic social networks. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 990–998. [Google Scholar]
- Shu, L.; Xu, H.; Liu, B. Doc: Deep open classification of text documents. arXiv 2017, arXiv:1709.08716. [Google Scholar]
- Ge, Z.; Demyanov, S.; Chen, Z.; Garnavi, R. Generative openmax for multi-class open set classification. arXiv 2017, arXiv:1707.07418. [Google Scholar]
- Xu, H.; Liu, B.; Shu, L.; Yu, P. Open-world learning and application to product classification. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 3413–3419. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards open set deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1563–1572. [Google Scholar]
- Yang, Z.; Cohen, W.; Salakhudinov, R. Revisiting semi-supervised learning with graph embeddings. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; pp. 40–48. [Google Scholar]
- Goodfellow, I. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part (Cybernetics) 1999, 29, 433–439. [Google Scholar]
- Van Der Maaten, L. Accelerating t-SNE using tree-based algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]



| Name | Nodes | Edges | Features | Classes |
|---|---|---|---|---|
| Cora | 2708 | 5429 | 1433 | 7 |
| CiteSeer | 3327 | 4732 | 3703 | 6 |
| Dblp | 17,716 | 105,734 | 1639 | 4 |
| Unseen Class = 1 | Unseen Class = 2 | Unseen Class = 3 | ||||
|---|---|---|---|---|---|---|
| Methods | ACC | F1 | ACC | F1 | ACC | F1 |
| GCN | 0.652 | 0.530 | 0.633 | 0.533 | 0.544 | 0.500 |
| GCN soft | 0.663 | 0.535 | 0.644 | 0.537 | 0.545 | 0.491 |
| GCN sigmoid | 0.729 | 0.554 | 0.658 | 0.549 | 0.509 | 0.456 |
| GCN-sigmoid threshold | 0.763 | 0.678 | 0.696 | 0.608 | 0.622 | 0.541 |
| GCN-softmax threshold | 0.771 | 0.776 | 0.737 | 0.673 | 0.631 | 0.622 |
| GCN-DOC | 0.787 | 0.756 | 0.775 | 0.739 | 0.673 | 0.697 |
| GCN openmax | 0.796 | 0.700 | 0.743 | 0.688 | 0.635 | 0.641 |
| OpenWGL | 0.833 | 0.835 | 0.790 | 0.781 | 0.778 | 0.752 |
| 0.855 | 0.855 | 0.820 | 0.800 | 0.556 | 0.655 | |
| OWNC | 0.916 | 0.911 | 0.901 | 0.867 | 0.891 | 0.824 |
| Unseen Class = 1 | Unseen Class = 2 | Unseen Class = 3 | ||||
|---|---|---|---|---|---|---|
| Methods | ACC | F1 | ACC | F1 | ACC | F1 |
| GCN | 0.665 | 0.505 | 0.531 | 0.453 | 0.374 | 0.382 |
| GCN softmax | 0.666 | 0.505 | 0.540 | 0.482 | 0.373 | 0.380 |
| GCN sigmoid | 0.572 | 0.407 | 0.491 | 0.375 | 0.344 | 0.382 |
| GCN-softmax threshold | 0.688 | 0.576 | 0.559 | 0.513 | 0.405 | 0.408 |
| GCN-sigmoid threshold | 0.732 | 0.658 | 0.570 | 0.533 | 0.600 | 0.599 |
| GCN-DOC | 0.675 | 0.617 | 0.715 | 0.658 | 0.664 | 0.587 |
| GCN openmax | 0.691 | 0.581 | 0.600 | 0.571 | 0.473 | 0.493 |
| OpenWGL | 0.700 | 0.654 | 0.753 | 0.618 | 0.723 | 0.496 |
| 0.733 | 0.632 | 0.780 | 0.660 | 0.493 | 0.404 | |
| OWNC | 0.822 | 0.793 | 0.868 | 0.778 | 0.873 | 0.716 |
| Unseen Class = 1 | Unseen Class = 2 | |||
|---|---|---|---|---|
| Methods | ACC | F1 | ACC | F1 |
| GCN | 0.584 | 0.532 | 0.441 | 0.391 |
| GCN softmax | 0.577 | 0.521 | 0.438 | 0.389 |
| GCN sigmoid | 0.592 | 0.539 | 0.436 | 0.388 |
| GCN-softmax threshold | 0.602 | 0.604 | 0.434 | 0.548 |
| GCN-sigmoid threshold | 0.610 | 0.556 | 0.441 | 0.392 |
| GCN_DOC | 0.698 | 0.632 | 0.588 | 0.542 |
| GCN openmax | 0.578 | 0.529 | 0.495 | 0.485 |
| OpenWGL | 0.743 | 0.742 | 0.760 | 0.753 |
| 0.751 | 0.700 | 0.716 | 0.654 | |
| OWNC | 0.811 | 0.816 | 0.794 | 0.788 |
| Unseen Class = 1 | Unseen Class = 2 | Unseen Class = 3 | ||||
|---|---|---|---|---|---|---|
| Methods | ACC | F1 | ACC | F1 | ACC | F1 |
| OWNC¬G | 0.913 | 0.902 | 0.889 | 0.842 | 0.884 | 0.813 |
| OWNC¬D | 0.790 | 0.800 | 0.796 | 0.784 | 0.810 | 0.764 |
| OWNC | 0.916 | 0.911 | 0.901 | 0.867 | 0.891 | 0.827 |
| Unseen Class = 1 | Unseen Class = 2 | Unseen Class = 3 | ||||
|---|---|---|---|---|---|---|
| Methods | ACC | F1 | ACC | F1 | ACC | F1 |
| OWNC¬G | 0.817 | 0.792 | 0.860 | 0.773 | 0.872 | 0.686 |
| OWNC¬D | 0.671 | 0.608 | 0.751 | 0.589 | 0.759 | 0.527 |
| OWNC | 0.822 | 0.793 | 0.868 | 0.778 | 0.873 | 0.716 |
| Unseen Class = 1 | Unseen Class = 2 | |||
|---|---|---|---|---|
| Methods | ACC | F1 | ACC | F1 |
| OWNC¬G | 0.801 | 0.808 | 0.776 | 0.762 |
| OWNC¬D | 0.654 | 0.655 | 0.660 | 0.646 |
| OWNC | 0.811 | 0.816 | 0.794 | 0.788 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, C. OWNC: Open-World Node Classification on Graphs with a Dual-Embedding Interaction Framework. Mathematics 2025, 13, 1475. https://doi.org/10.3390/math13091475
Chen Y, Wang C. OWNC: Open-World Node Classification on Graphs with a Dual-Embedding Interaction Framework. Mathematics. 2025; 13(9):1475. https://doi.org/10.3390/math13091475
Chicago/Turabian StyleChen, Yuli, and Chun Wang. 2025. "OWNC: Open-World Node Classification on Graphs with a Dual-Embedding Interaction Framework" Mathematics 13, no. 9: 1475. https://doi.org/10.3390/math13091475
APA StyleChen, Y., & Wang, C. (2025). OWNC: Open-World Node Classification on Graphs with a Dual-Embedding Interaction Framework. Mathematics, 13(9), 1475. https://doi.org/10.3390/math13091475






