A Mathematical Modeling of Time-Fractional Maxwell’s Equations Under the Caputo Definition of a Magnetothermoelastic Half-Space Based on the Green–Lindsy Thermoelastic Theorem
Abstract
1. Introduction
2. Basic Formulation of Mathematical Model
- (i)
- The half-space is sited on a rigid foundation to prevent the displacement of the material, and then we have this formulation:
- (ii)
- The bounding surface of the half-space is subjected to the following ramp-type heat:
- (iii)
- The magnetic intensity function and the electric intensity function must satisfy the continuity conditions around the bounding surface of the half-space as follows [6]:and
3. The Numerical Solutions and Results
4. Validation of Results
5. Conclusions
- The time-fractional parameter of Maxwell’s equations does not influence the temperature distribution.
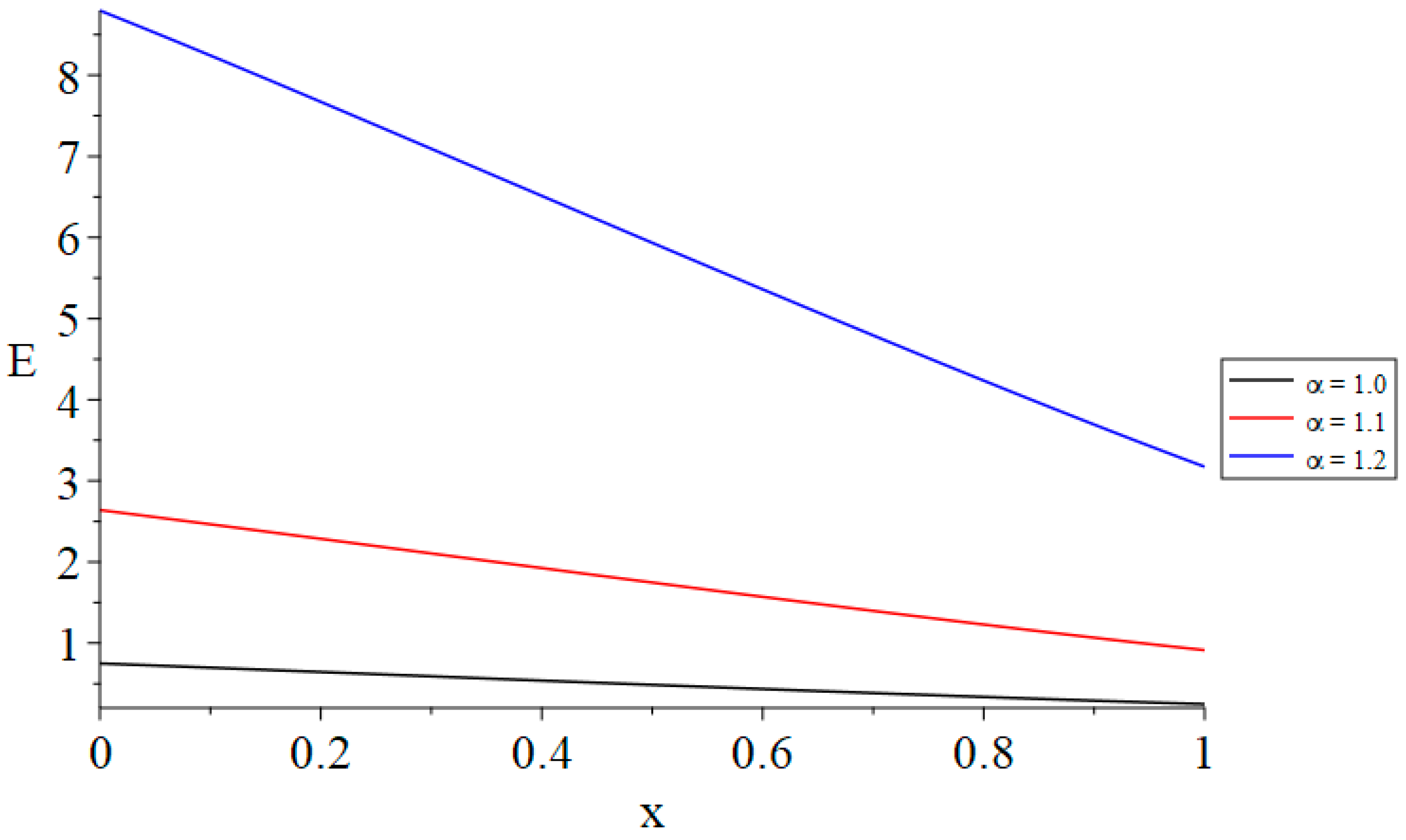
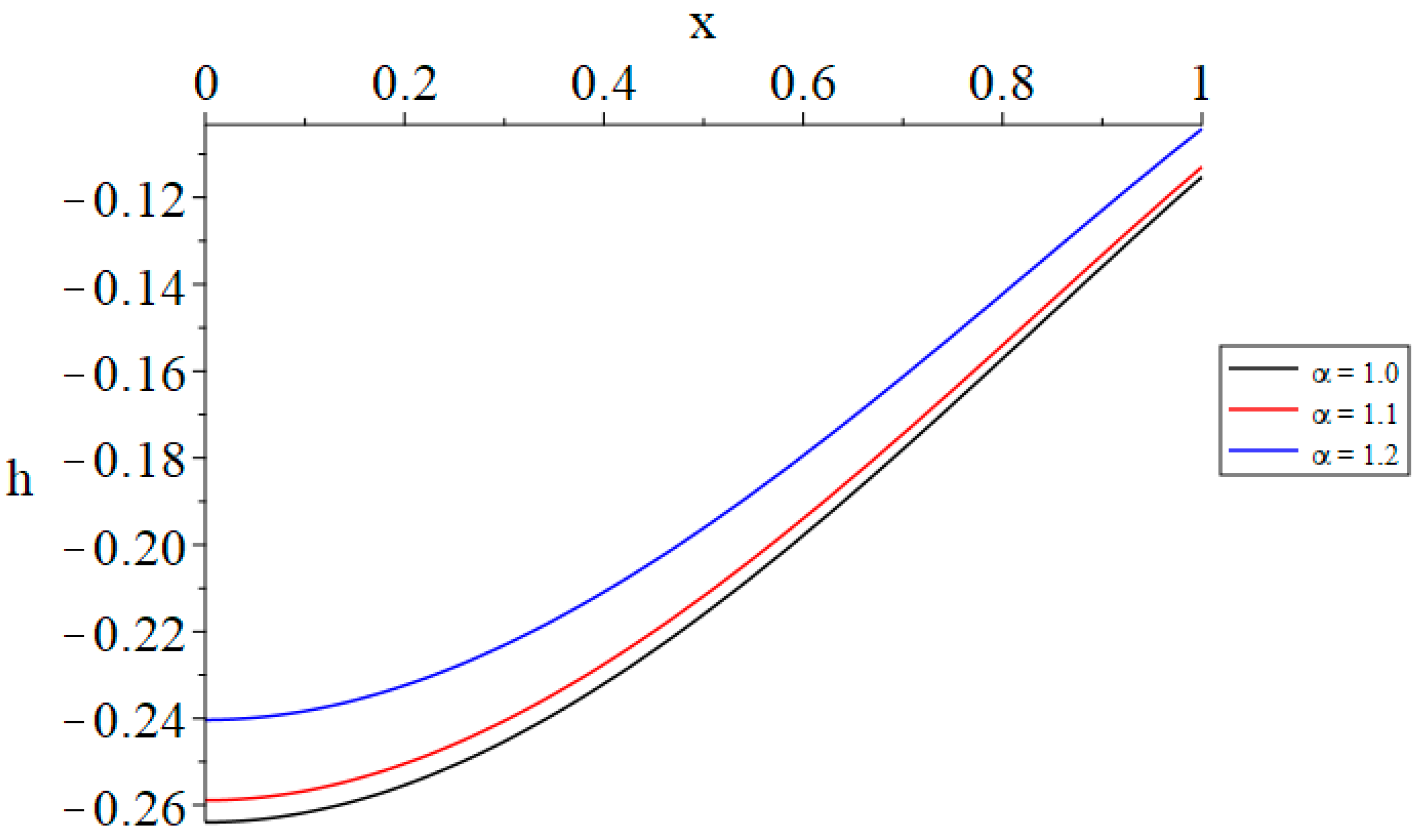
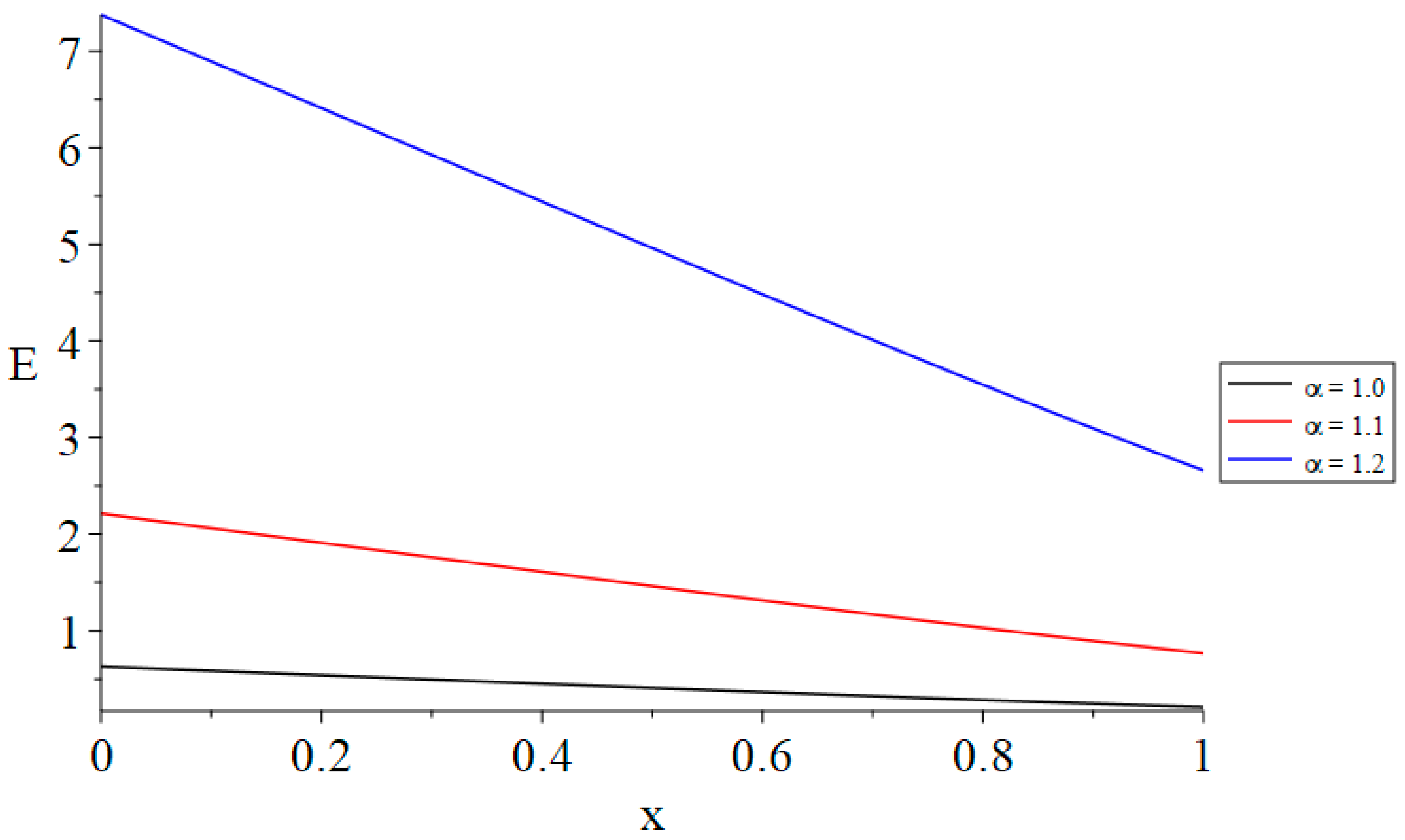
- The time-fractional parameter of Maxwell’s equations substantially influences the strain, displacement, stress, and induced magnetic and electric fields.
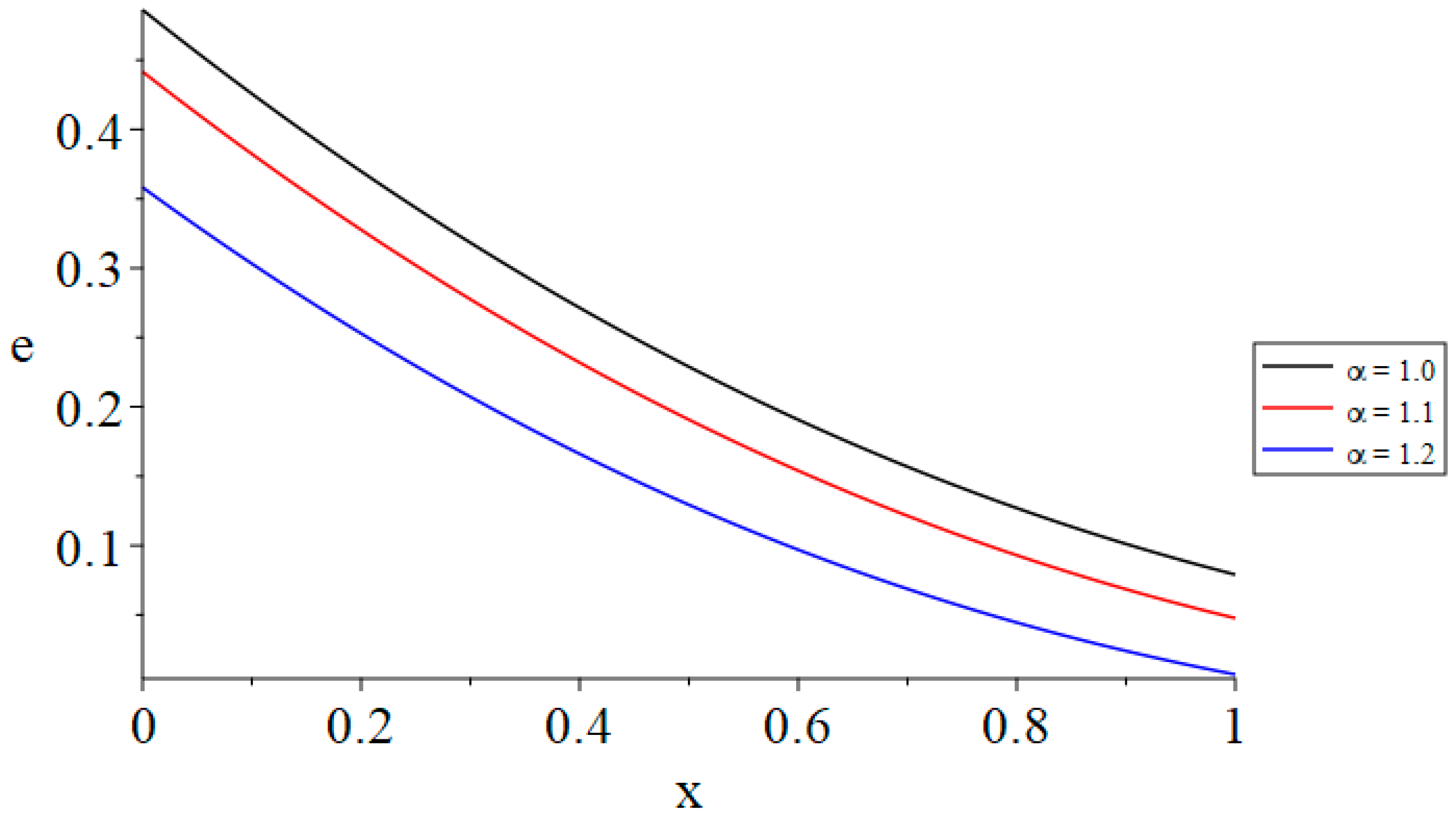
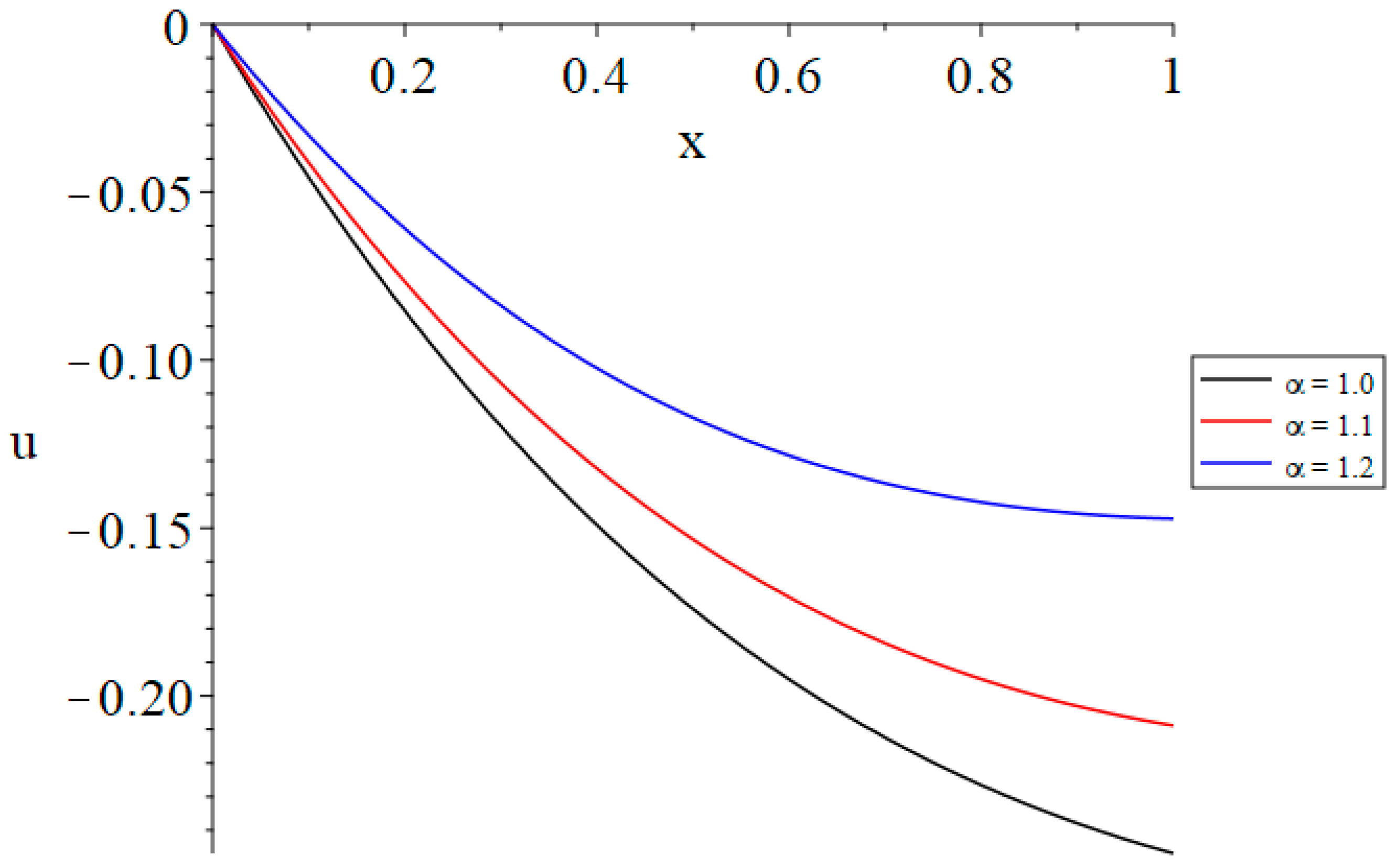
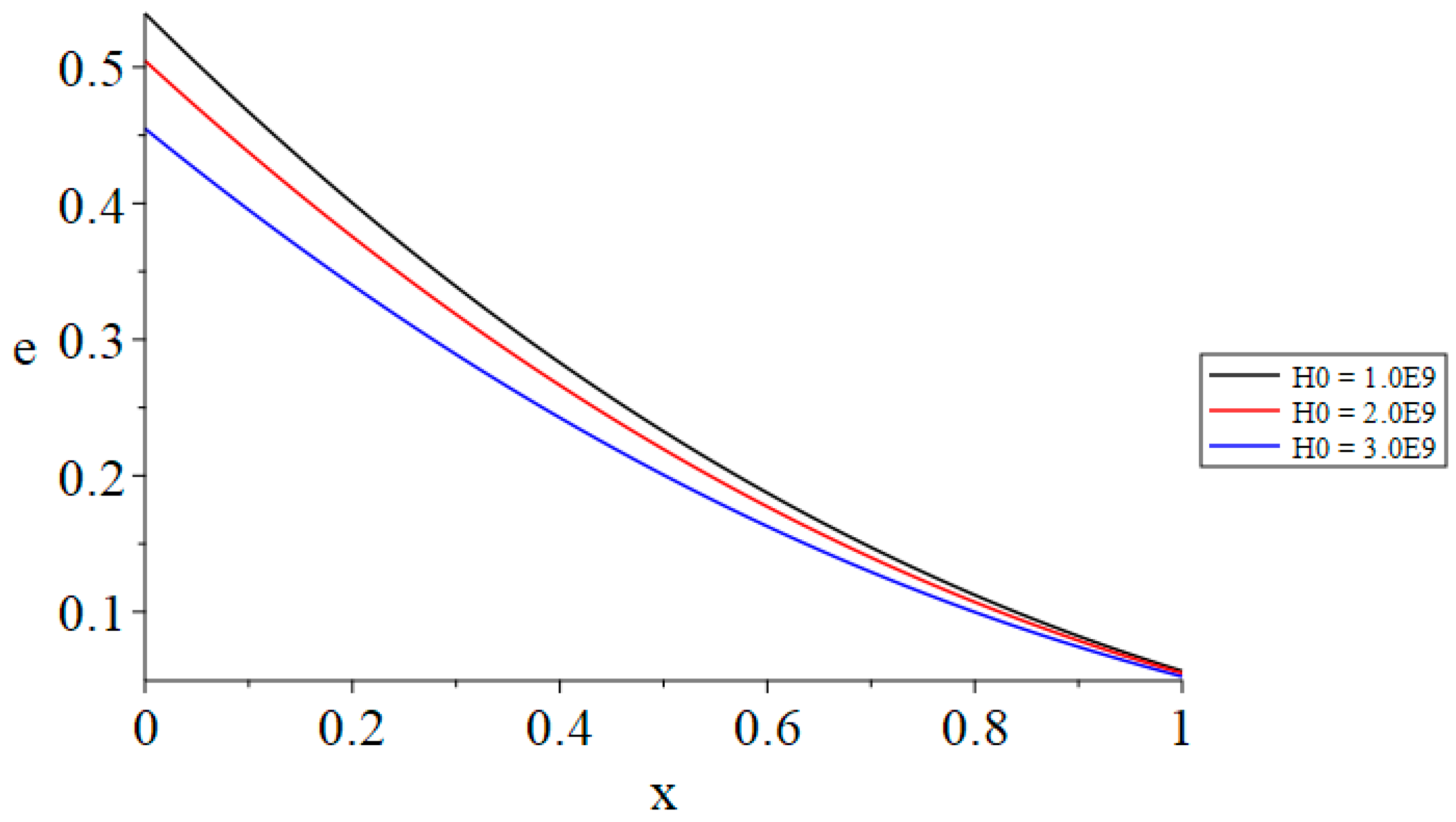
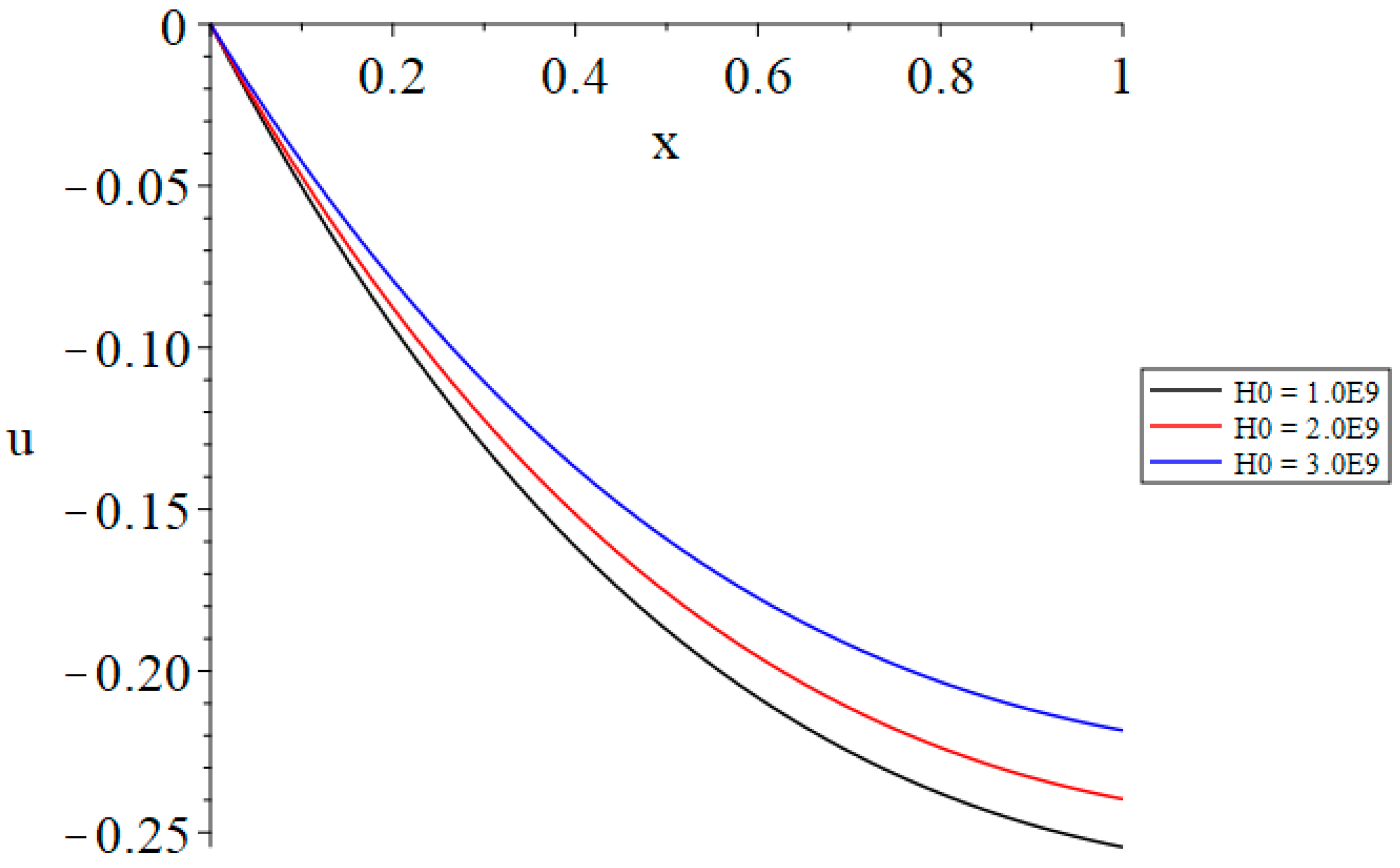
- Increasing the value of the time-fractional parameter of Maxwell’s equations results in a reduction in the volumetric dilatation, the absolute magnitude of the displacement, and the generated magnetic field.
- Increasing the value of the time-fractional parameter of Maxwell’s equations results in heightened stress and an augmented induced electric field.
- The time-fractional parameter of Maxwell’s equations acts as a barrier to deformation, displacement, and the induced magnetic field, while simultaneously catalyzing the created stress and electric field through the material.
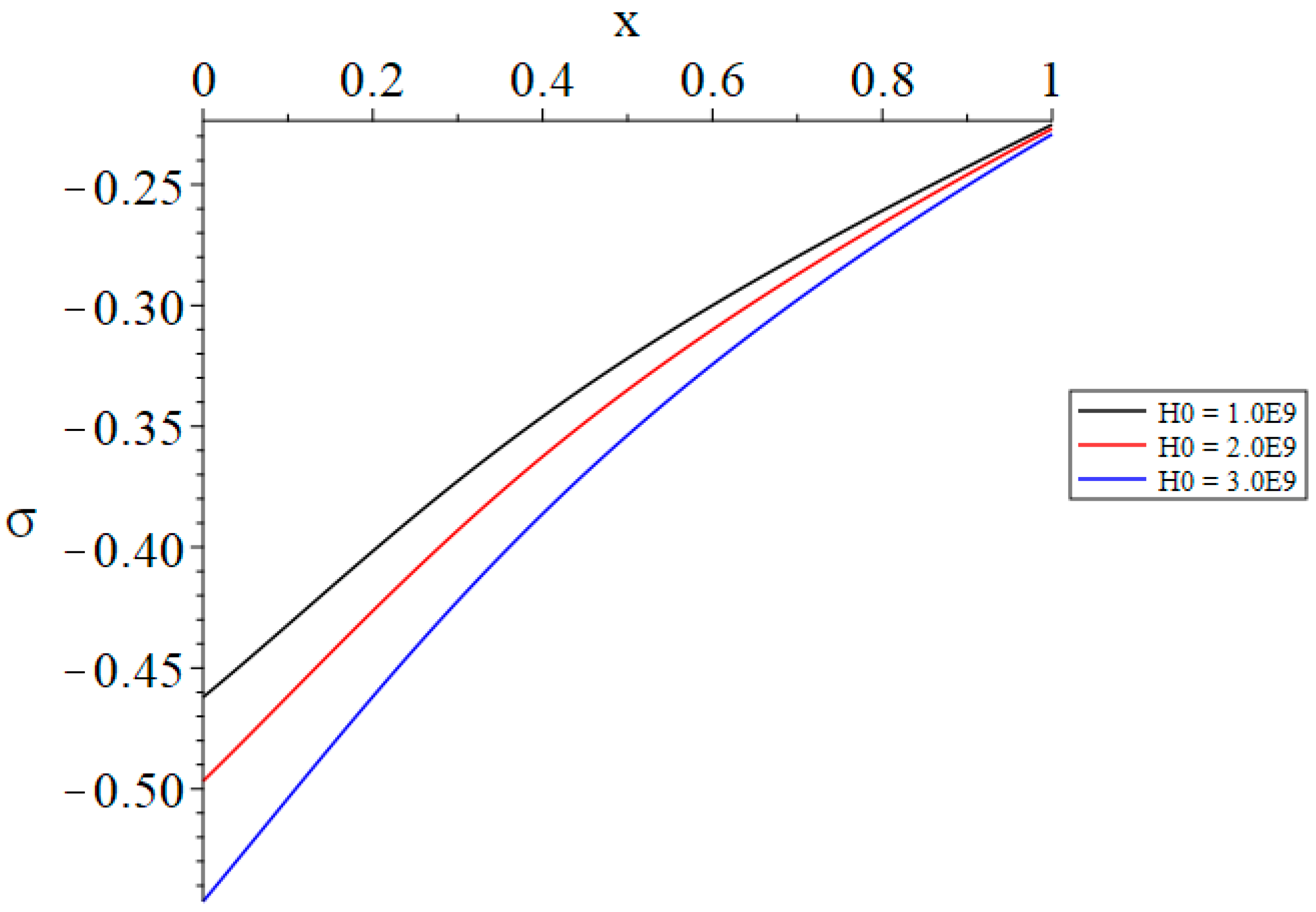
- The magnitude of the primary magnetic field substantially influences the distribution of the volumetric dilatation, displacement, stress, induced magnetic field, and induced electric field, but does not impact the temperature increase.
- The time-fractional parameter of Maxwell’s equations, ramp-time heat parameter, and primary magnetic field can be utilized to modulate the propagation of mechanical waves in magnetothermoelastic materials.
- The ramp-time heat parameter plays a vital role in the behavior of the thermal, mechanical, and electromagnetic waves.
Funding
Data Availability Statement
Conflicts of Interest
References
- Hetnarski, R.B.; Eslami, M.R.; Hetnarski, R.B.; Eslami, M.R. Basic laws of thermoelasticity. In Thermal Stresses—Advanced Theory and Applications; Springer: Cham, Switzerland, 2019; pp. 1–43. [Google Scholar]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Sherief, H.H.; Darwish, A.A. A short time solution for a problem in thermoelasticity of an infinite medium with a spherical cavity. J. Therm. Stress. 1998, 21, 811–828. [Google Scholar] [CrossRef]
- Othman, M.I. Relaxation effects on thermal shock problems in an elastic half-space of generalized magneto-thermoelastic waves. Mech. Mech. Eng. 2004, 7, 165–178. [Google Scholar]
- Sherief, H.H.; Yosef, H.M. Short time solution for a problem in magnetothermoelasticity with thermal relaxation. J. Therm. Stress. 2004, 27, 537–559. [Google Scholar] [CrossRef]
- Ezzat, M.A.; Youssef, H.M. Generalized magneto-thermoelasticity in a perfectly conducting medium. Int. J. Solids Struct. 2005, 42, 6319–6334. [Google Scholar] [CrossRef]
- Othman, M.I. Generalized Electromagneto-Thermoelastic Plane Waves by Thermal Shock Problem in a Finite Conductivity Half-Space with One Relaxation Time. Multidiscip. Model. Mater. Struct. 2005, 1, 231–250. [Google Scholar] [CrossRef]
- Abbas, I.A. Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method. Arch. Appl. Mech. 2009, 79, 41–50. [Google Scholar] [CrossRef]
- Othman, M.I.; Lotfy, K. Two-dimensional problem of generalized magneto-thermoelasticity with temperature dependent elastic moduli for different theories. Multidiscip. Model. Mater. Struct. 2009, 5, 235–242. [Google Scholar] [CrossRef]
- Ezzat, M.A.; Youssef, H.M. Generalized magneto-thermoelasticity for an infinite perfect conducting body with a cylindrical cavity. Mater. Phys. Mech. 2013, 18, 156–170. [Google Scholar]
- Sarkar, N. Generalized magneto-thermoelasticity with modified Ohm’s Law under three theories. Comput. Math. Model. 2014, 25, 544–564. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Karamany, A.S.; El-Bary, A.A. Electro-magnetic waves in generalized thermo-viscoelasticity for different theories. Int. J. Appl. Electromagn. Mech. 2015, 47, 95–111. [Google Scholar] [CrossRef]
- Othman, M.I.; Song, Y. Effect of the thermal relaxation and magnetic field on generalized micropolar thermoelasticity. J. Appl. Mech. Tech. Phys. 2016, 57, 108–116. [Google Scholar] [CrossRef]
- Lotfy, K.; Gabr, M. Electromagnetic field of Surface waves propagation in fiber-reinforced generalized thermoelastic medium. J. Niger. Math. Soc. 2017, 36, 239–286. [Google Scholar] [CrossRef]
- Sadeghi, M.; Kiani, Y. Generalized magneto-thermoelasticity of a layer based on the Lord–Shulman and Green–Lindsay theories. J. Therm. Stress. 2022, 45, 319–340. [Google Scholar] [CrossRef]
- Khader, S.; Marrouf, A.; Khedr, M. Influence of Electromagnetic Generalized Thermoelasticity Interactions with Nonlocal Effects under Temperature-Dependent Properties in a Solid Cylinder. Mech. Adv. Compos. Struct. 2023, 10, 157–166. [Google Scholar]
- Tiwari, R. Magneto-thermoelastic interactions in generalized thermoelastic half-space for varying thermal and electrical conductivity. Waves Random Complex Media 2024, 34, 1795–1811. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V. Fractional Calculus; Alpha Science International Limited: Oxford, UK, 2013. [Google Scholar]
- Li, C.; Cai, M. Theory and Numerical Approximations of Fractional Integrals and Derivatives; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Green, A.E.; Lindsay, K. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Sherief, H.H. Fundamental solution for thermoelasticity with two relaxation times. Int. J. Eng. Sci. 1992, 30, 861–870. [Google Scholar] [CrossRef]
- Sherief, H.H.; Helmy, K.A. A two-dimensional generalized thermoelasticity problem for a half-space. J. Therm. Stress. 1999, 22, 897–910. [Google Scholar]
- Ailawalia, P.; Priyanka. Effect of thermal conductivity in a semiconducting medium under modified Green-Lindsay theory. Int. J. Comput. Sci. Math. 2024, 19, 167–179. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, P.; Ma, J.; Liu, F. Dynamic response of thermoelasticity based on Green-Lindsay theory and Caputo-Fabrizio fractional-order derivative. Int. Commun. Heat Mass Transf. 2024, 159, 108334. [Google Scholar] [CrossRef]
- Karimipour Dehkordi, M.; Kiani, Y. Lord–Shulman and Green–Lindsay-based magneto-thermoelasticity of hollow cylinder. Acta Mech. 2024, 235, 51–72. [Google Scholar] [CrossRef]
- Kumar, P.; Prasad, R. An investigation of the thermomechanical effects of mode-I crack under modified Green–Lindsay theory. Arch. Appl. Mech. 2024, 94, 3157–3174. [Google Scholar] [CrossRef]
- Othman, M.I.; Said, S.M.; Gamal, E.M. A new model of rotating nonlocal fiber-reinforced visco-thermoelastic solid using a modified Green–Lindsay theory. Acta Mech. 2024, 235, 3167–3180. [Google Scholar] [CrossRef]
- Sharifi, H. Magneto–thermoelastic behavior of an orthotropic hollow cylinder based on Lord–Shulman and Green–Lindsay theories. Acta Mech. 2024, 235, 4863–4886. [Google Scholar] [CrossRef]
- Al-Lehaibi, E.A.; Youssef, H.M. The influence of the Caputo fractional derivative on time-fractional Maxwell’s equations of an electromagnetic infinite body with a cylindrical cavity under four different thermoelastic theorems. Mathematics 2024, 12, 3358. [Google Scholar] [CrossRef]
- Al-Lehaibi, E.A.; Youssef, H.M. State-Space Approach to the Time-Fractional Maxwell’s Equations under Caputo Fractional Derivative of an Electromagnetic Half-Space under Four Different Thermoelastic Theorems. Fractal Fract. 2024, 8, 566. [Google Scholar] [CrossRef]
- Almeida, R.; Tavares, D.; Torres, D.F. The Variable-Order Fractional Calculus of Variations; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Petrás, I. Fractional Derivatives, Fractional Integrals, and Fractional Differential Equations in Matlab; IntechOpen: London, UK, 2011. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Baleanu, D.; Golmankhaneh, A.K.; Golmankhaneh, A.K.; Baleanu, M.C. Fractional electromagnetic equations using fractional forms. Int. J. Theor. Phys. 2009, 48, 3114–3123. [Google Scholar] [CrossRef]
- Lazo, M.J. Gauge invariant fractional electromagnetic fields. Phys. Lett. A 2011, 375, 3541–3546. [Google Scholar] [CrossRef]
- Jaradat, E.; Hijjawi, R.; Khalifeh, J. Maxwell’s equations and electromagnetic Lagrangian density in fractional form. J. Math. Phys. 2012, 53, 033505. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Rivero, M.; Trujillo, J.J. From a generalised Helmholtz decomposition theorem to fractional Maxwell equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1036–1049. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Formulation of time-fractional electrodynamics based on Riemann-Silberstein vector. Entropy 2021, 23, 987. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Kestelyn, X.; Kharazian, E.; Grolet, A. Application of Normal Form Theory to Power Systems: A Proof of Concept of a Novel Structure-Preserving Approach. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024; pp. 1–5. [Google Scholar]
- Avazzadeh, Z.; Hassani, H.; Agarwal, P.; Mehrabi, S.; Javad Ebadi, M.; Hosseini Asl, M.K. Optimal study on fractional fascioliasis disease model based on generalized Fibonacci polynomials. Math. Methods Appl. Sci. 2023, 46, 9332–9350. [Google Scholar] [CrossRef]
- Alam, M.; Haq, S.; Ali, I.; Ebadi, M.; Salahshour, S. Radial basis functions approximation method for time-fractional fitzhugh–nagumo equation. Fractal Fract. 2023, 7, 882. [Google Scholar] [CrossRef]
- Machado, J.T.; Jesus, I.S.; Galhano, A.; Cunha, J.B. Fractional order electromagnetics. Signal Process. 2006, 86, 2637–2644. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of fractional order generalized thermoelasticity. J. Heat Transfer. 2010, 132, 061301. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of generalized thermoelasticity with fractional order strain. J. Vib. Control 2016, 22, 3840–3857. [Google Scholar] [CrossRef]
- Tzou, D.; Guo, Z.-Y. Nonlocal behavior in thermal lagging. Int. J. Therm. Sci. 2010, 49, 1133–1137. [Google Scholar] [CrossRef]
- Özisik, M.; Tzou, D. On the Wave Theory in Heat Conduction; ASME-Publications: New York, NY, USA, 1994. [Google Scholar]

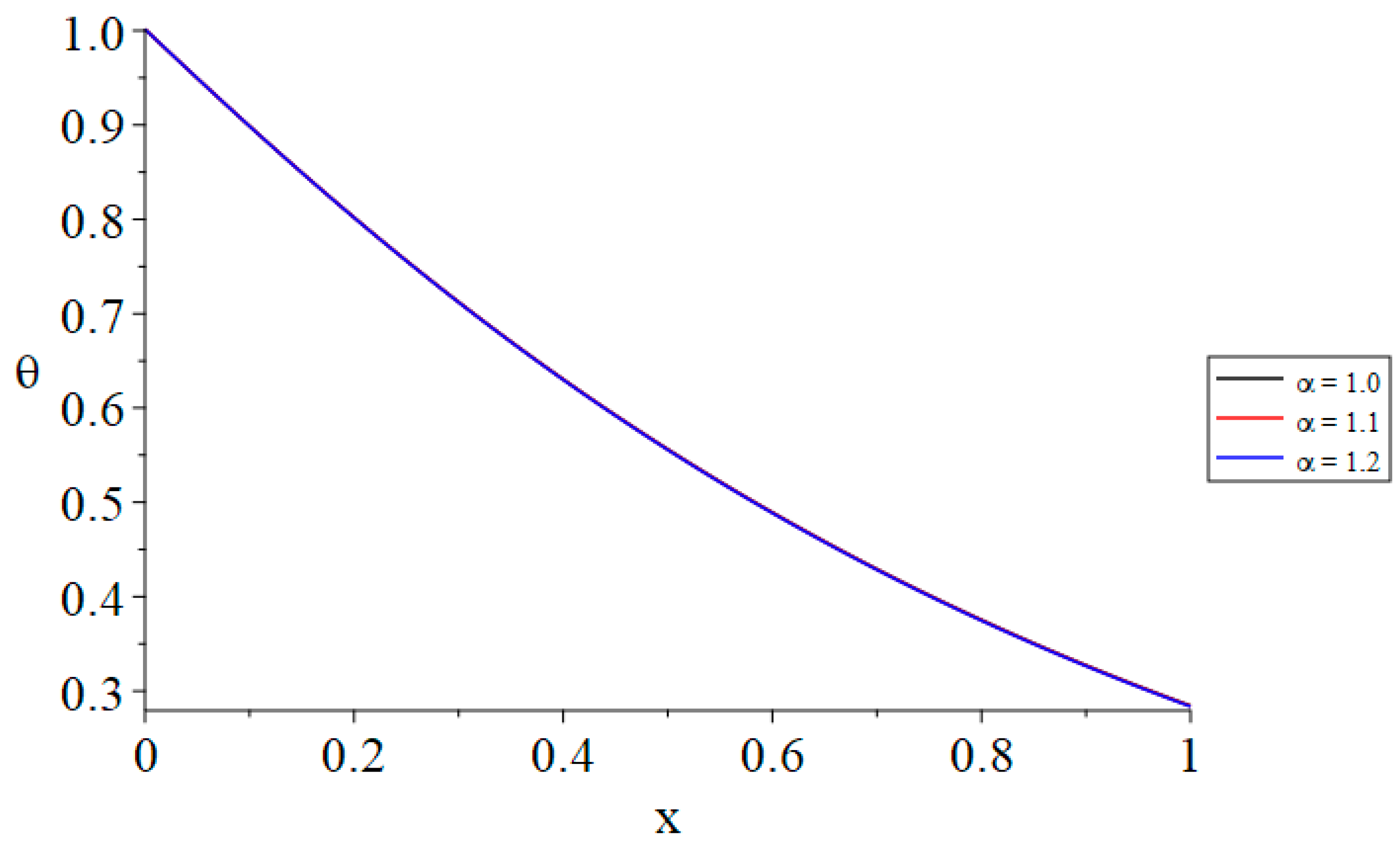
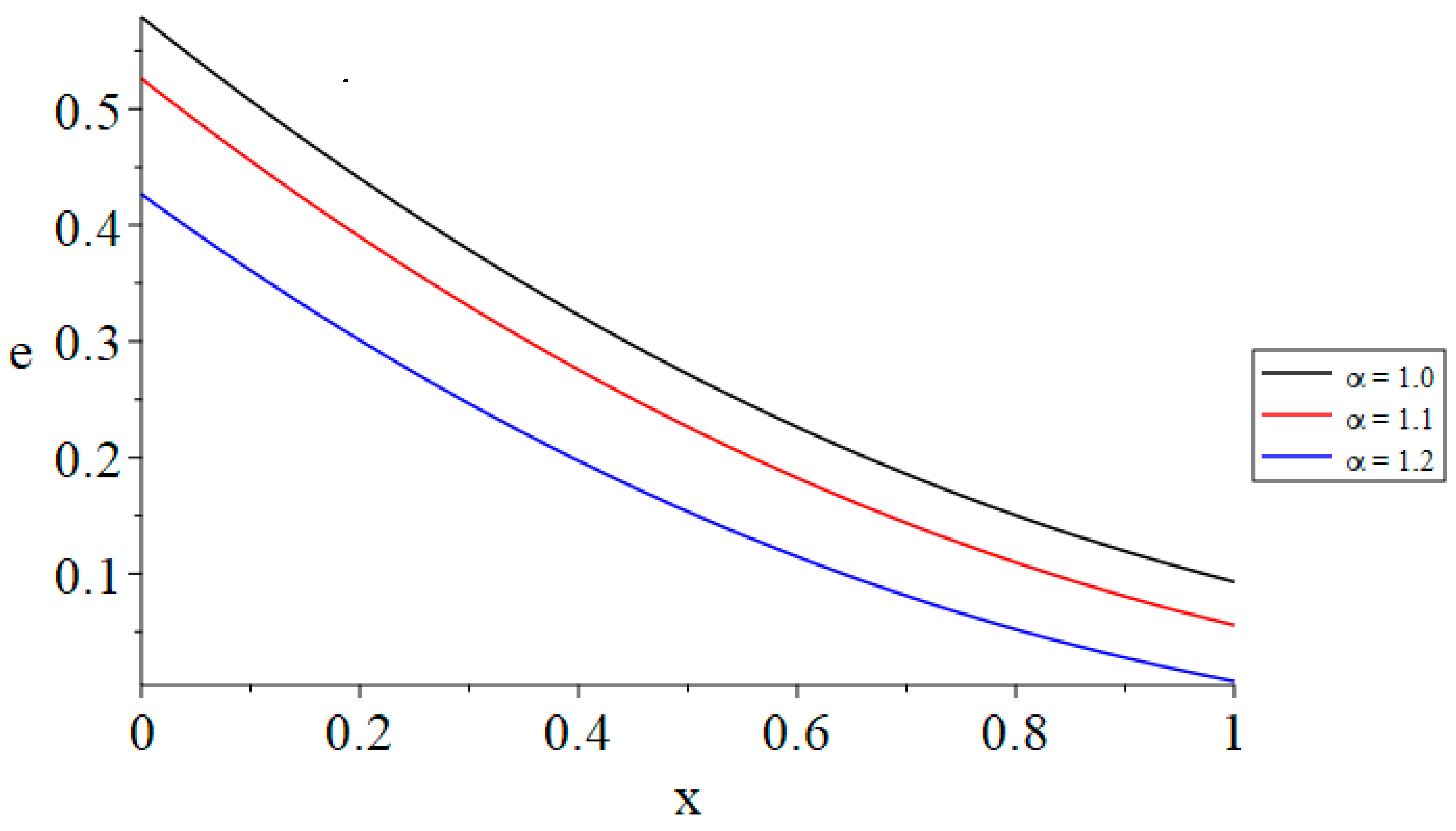

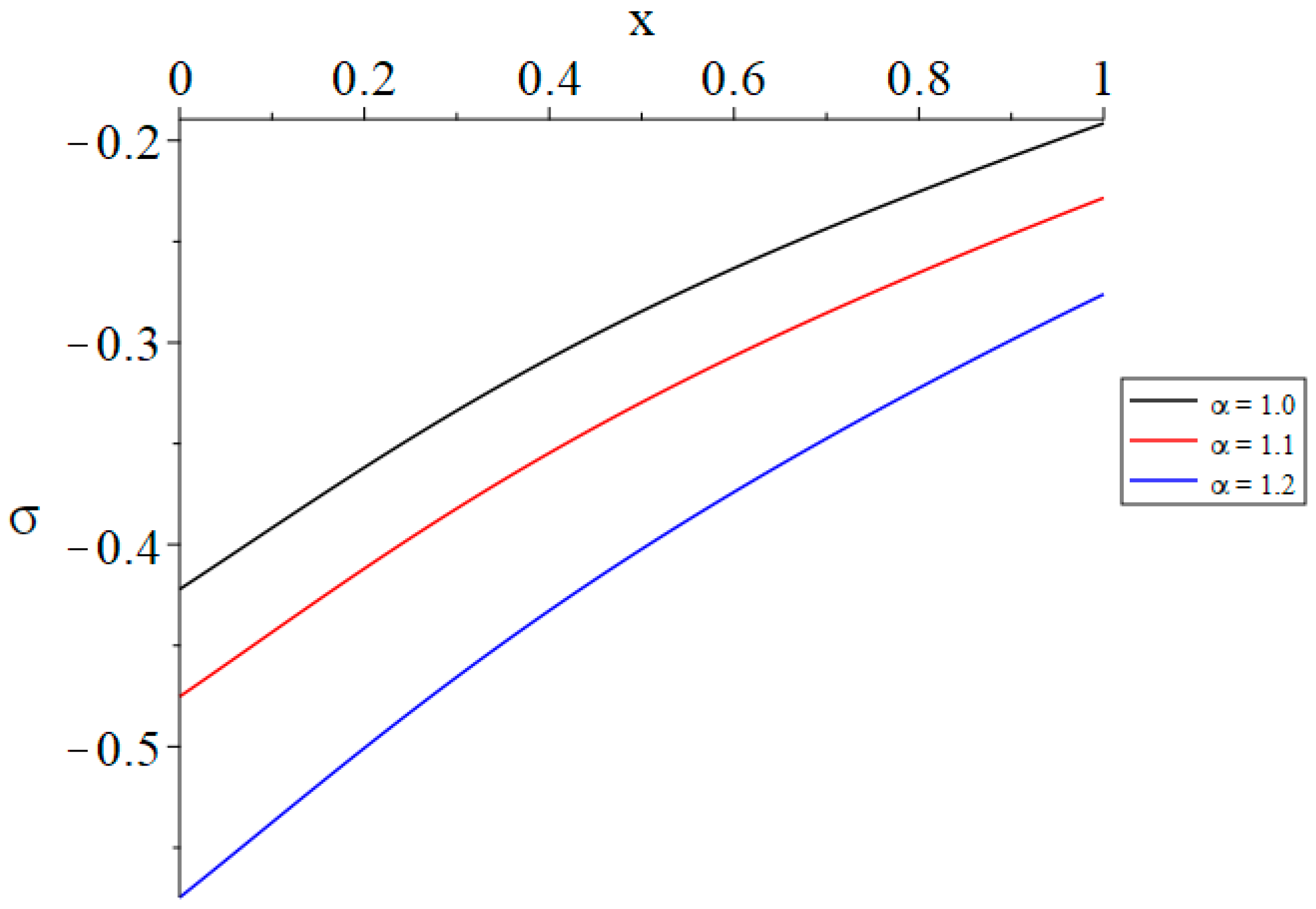
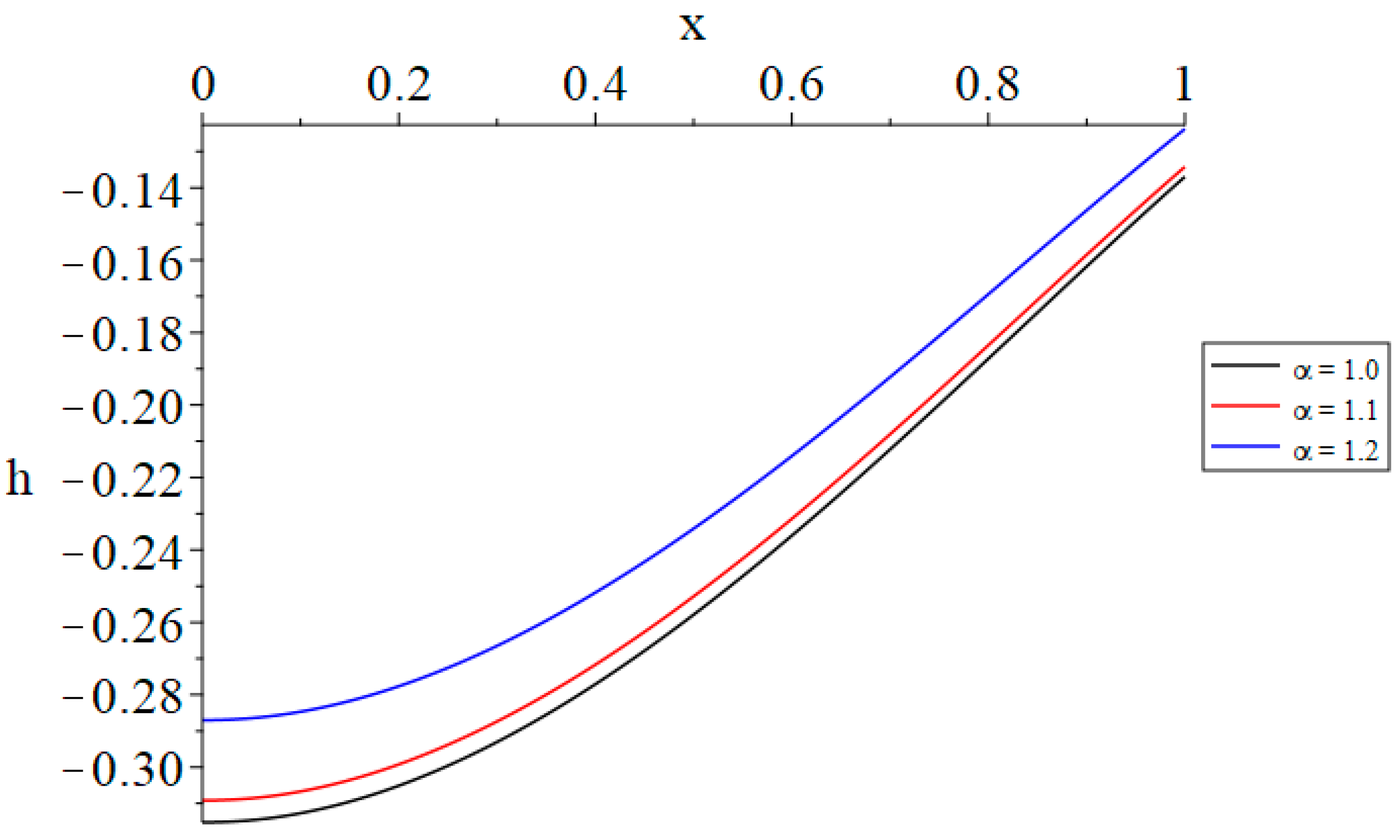
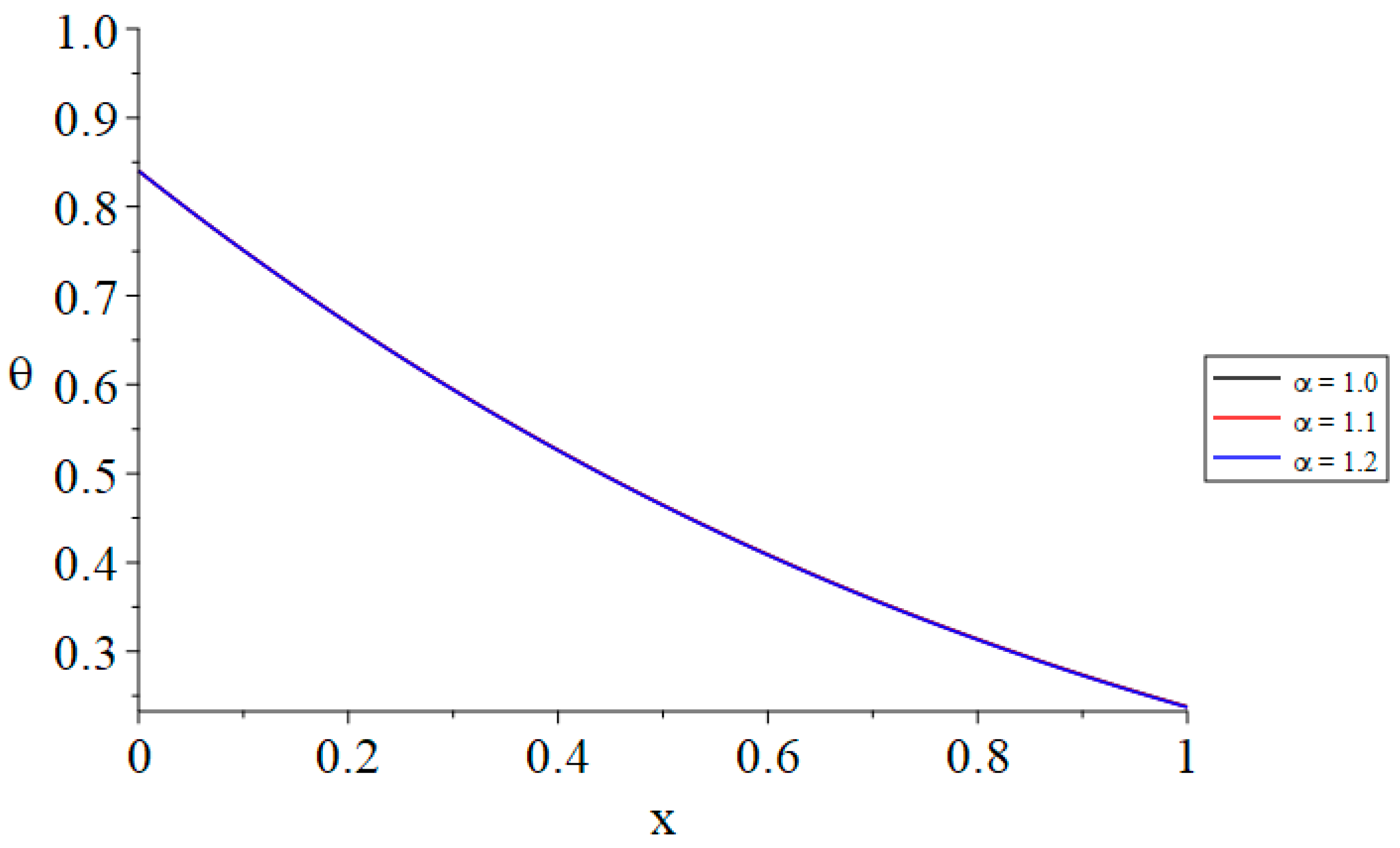




| θ(0, 1.0) | α = 1.0 | α = 1.1 | α = 1.2 |
|---|---|---|---|
| t = t0 = 1.0 | 1.0 | 1.0 | 1.0 |
| t(1.0) < t0(1.2) | 0.840 | 0.840 | 0.840 |
| e(0, 1.0) | α = 1.0 | α = 1.1 | α = 1.2 |
|---|---|---|---|
| t = t0 = 1.0 | 0.593 | 0.540 | 0.439 |
| t(1.0) < t0(1.2) | 0.498 | 0.453 | 0.368 |
| u(0, 1.0) | α = 1.0 | α = 1.1 | α = 1.2 |
|---|---|---|---|
| t = t0 = 1.0 | −0.29 | −0.23 | −0.16 |
| t(1.0) < t0(1.2) | −0.24 | −0.19 | −0.14 |
| σ(0, 1.0) | α = 1.0 | α = 1.1 | α = 1.2 |
|---|---|---|---|
| t = t0 = 1.0 | −0.408 | −0.462 | −0.563 |
| t(1.0) < t0(1.2) | −0.342 | −0.388 | −0.472 |
| h(0, 1.0) | α = 1.0 | α = 1.1 | α = 1.2 |
|---|---|---|---|
| t = t0 = 1.0 | −0.324 | −0.318 | −0.296 |
| t(1.0) < t0(1.2) | −0.272 | −0.267 | −0.248 |
| E(0, 1.0) | α = 1.0 | α = 1.1 | α = 1.2 |
|---|---|---|---|
| t = t0 = 1.0 | 0.764 | 2.686 | 8.939 |
| t(1.0) < t0(1.2) | 0.641 | 2.256 | 7.520 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Lehaibi, E.A.N. A Mathematical Modeling of Time-Fractional Maxwell’s Equations Under the Caputo Definition of a Magnetothermoelastic Half-Space Based on the Green–Lindsy Thermoelastic Theorem. Mathematics 2025, 13, 1468. https://doi.org/10.3390/math13091468
Al-Lehaibi EAN. A Mathematical Modeling of Time-Fractional Maxwell’s Equations Under the Caputo Definition of a Magnetothermoelastic Half-Space Based on the Green–Lindsy Thermoelastic Theorem. Mathematics. 2025; 13(9):1468. https://doi.org/10.3390/math13091468
Chicago/Turabian StyleAl-Lehaibi, Eman A. N. 2025. "A Mathematical Modeling of Time-Fractional Maxwell’s Equations Under the Caputo Definition of a Magnetothermoelastic Half-Space Based on the Green–Lindsy Thermoelastic Theorem" Mathematics 13, no. 9: 1468. https://doi.org/10.3390/math13091468
APA StyleAl-Lehaibi, E. A. N. (2025). A Mathematical Modeling of Time-Fractional Maxwell’s Equations Under the Caputo Definition of a Magnetothermoelastic Half-Space Based on the Green–Lindsy Thermoelastic Theorem. Mathematics, 13(9), 1468. https://doi.org/10.3390/math13091468






