Harmony Search Algorithm with Two Problem-Specific Operators for Solving Nonogram Puzzle
Abstract
1. Introduction
- Proposal of Novel HS-based Approaches:This study proposes two novel problem-specific operators tailored to the characteristics of nonogram puzzles, demonstrating the effective applicability of the Harmony Search (HS) algorithm to nonogram-solving.
- 2.
- Initially Confirmed Cell-Scanning Operator:The authors introduce an operator that efficiently reduces the search space and accelerates early-stage convergence by identifying and fixing cells whose states can be definitively confirmed at the initial phase of puzzle-solving.
- 3.
- Clue-Constrained Random Generation Operator:A random generation operator strictly adhering to row clues is proposed, significantly enhancing the validity of candidate solutions. This approach substantially reduces the search space, thereby dramatically decreasing computational burden and iteration counts.
- 4.
- Extensive Experimental Validation:Through extensive experimental evaluations using diverse benchmark nonogram puzzles, the authors validate that the proposed operators effectively improve the performance of the HS algorithm. Particularly, the Clue-Constrained Random Generation operator demonstrates high success rates and rapid convergence, even in complex puzzles.
- 5.
- Benchmark for Quantum Computing Applications:The authors suggest the Nonogram puzzle as a valuable benchmark problem for future quantum computing-based optimization research and propose the potential integration of the developed HS algorithm with quantum computing mechanisms.
2. Problem Definition and Optimization Modeling
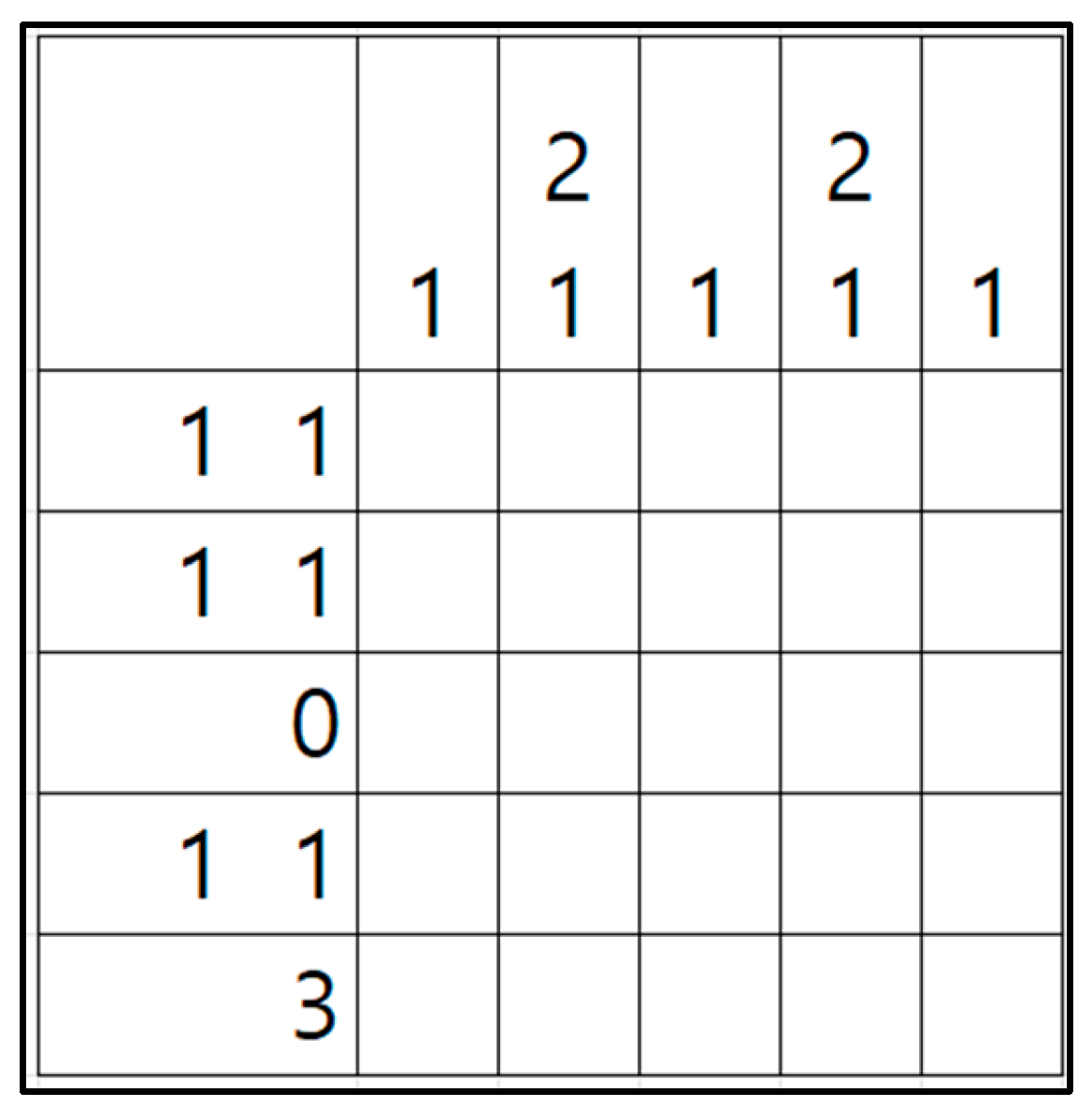
2.1. Problem Definition of Nonogram
2.2. Optimization Modeling
- Calculate the error between the first value “1” of the converted decision variable and the first given clue “3”.
- Calculate the error between the second value “2” of the converted decision variable and the second given clue (0 because there is no second clue).Sum these two differences to obtain the total error. Thus, in this example, the total error score is calculated as .
3. Harmony Search Algorithm and Its Variants for Nonogram
3.1. Overview of the Harmony Search Algorithm
- Random Selection: Generates entirely new random solutions to increase search diversity.
- Memory Consideration: Selects elements from existing solutions stored in the harmony memory (HM) to create new solutions.
- Pitch Adjustment: Slightly modifies solutions from harmony memory to enhance local search around existing solutions.
- Initialization (Step 1): Hyperparameters are established, and the harmony memory is initialized, usually with random solutions.
- Improvisation (Step 2): New solutions are generated to improve harmony memory, probabilistically combining the three main operators (Random Selection, Harmony Memory Consideration, and Pitch Adjustment) based on hyperparameter settings from Step 1.
- Evaluation (Step 3): The newly generated solutions are evaluated using the objective function, assigning scores to each new harmony.
- HM update (Step 4): If the new solution’s score is better than the lowest-scoring solution currently in harmony memory, the new solution replaces the worst one in the harmony memory.
- Termination or Repeat (Step 5): If the termination condition (usually a maximum number of iterations) is not satisfied, return to Step 2 and repeat the process of solution generation, evaluation, and harmony memory update. Once the termination condition is satisfied, the best-scoring solution in the harmony memory is returned as the final solution.
3.2. Harmony Search Variants for Nonogram
3.2.1. Basic Version (Version A): This Version Utilizes Only Three Basic Operators (Random Selection, Memory Consideration, and Pitch Adjustment) of the Original HS Algorithm
- The operator of Random Selection generates random binary sequences of 1 s and 0 s equal to the number of cells per row. For example, for a problem with a column size of 5, a randomly generated solution might look like 11001.
- The operator of Memory Consideration randomly selects one solution from HM and adopts one of its decision variable values for generating a new harmony.
- The operator of Pitch Adjustment slightly modifies a solution selected via HM Consideration by flipping one randomly chosen bit (changing 1 to 0 or 0 to 1).
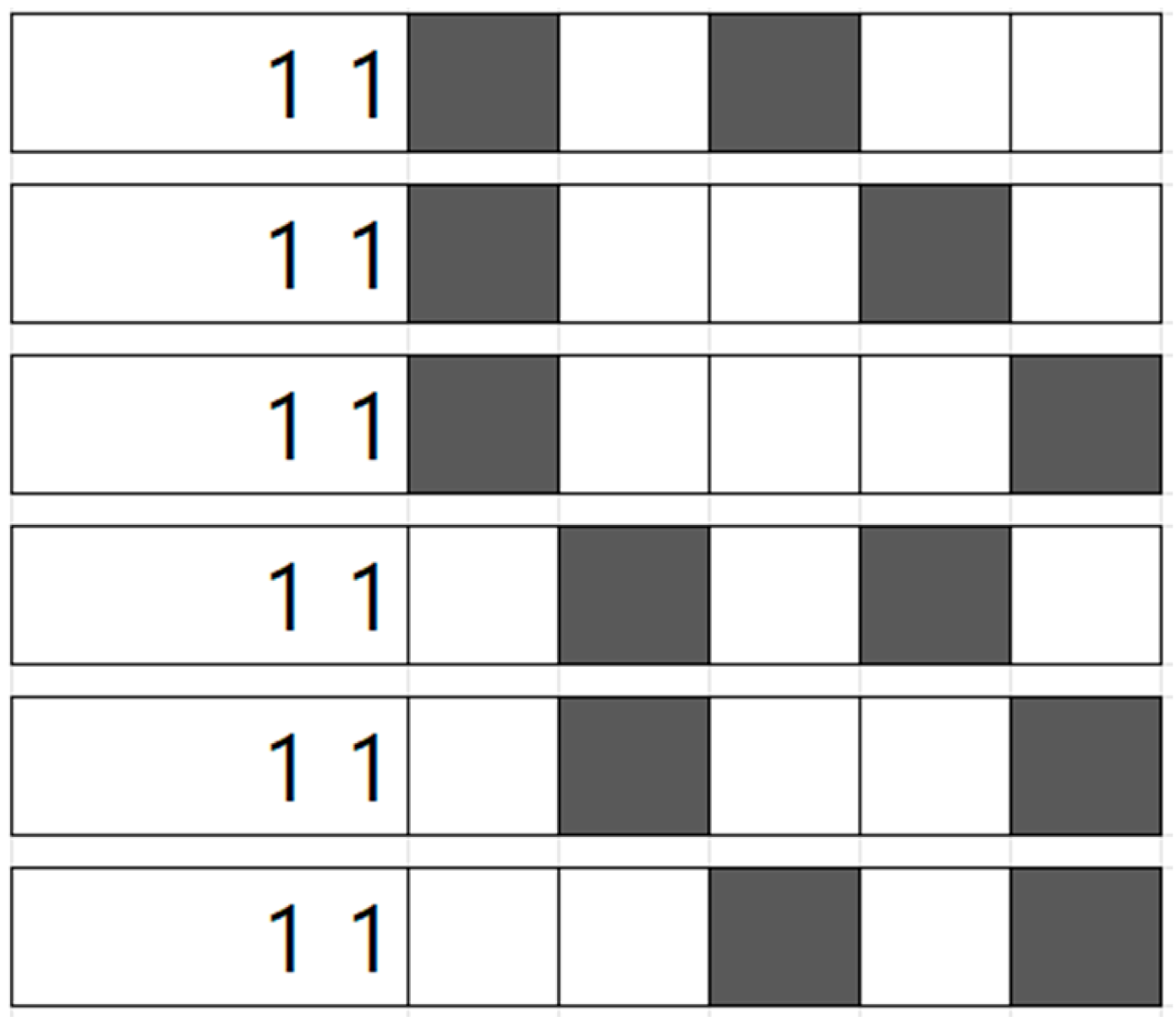
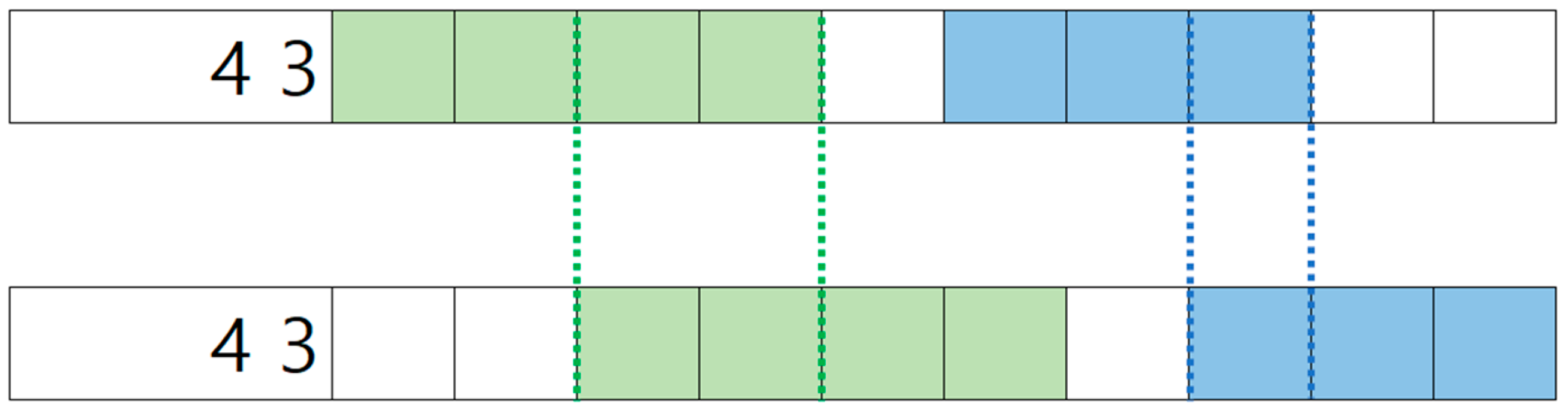
3.2.2. Initially Confirmed Cell-Scanning Version (Version B)
3.2.3. Clue-Constrained Random Generation Version (Version C)
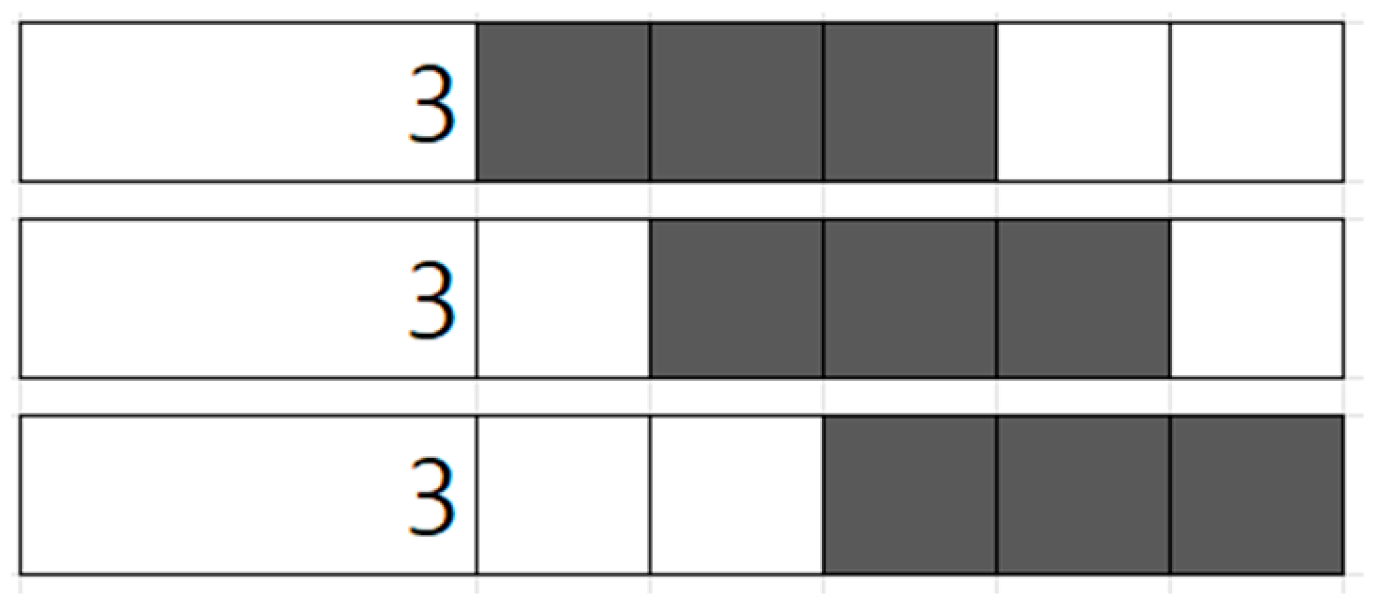
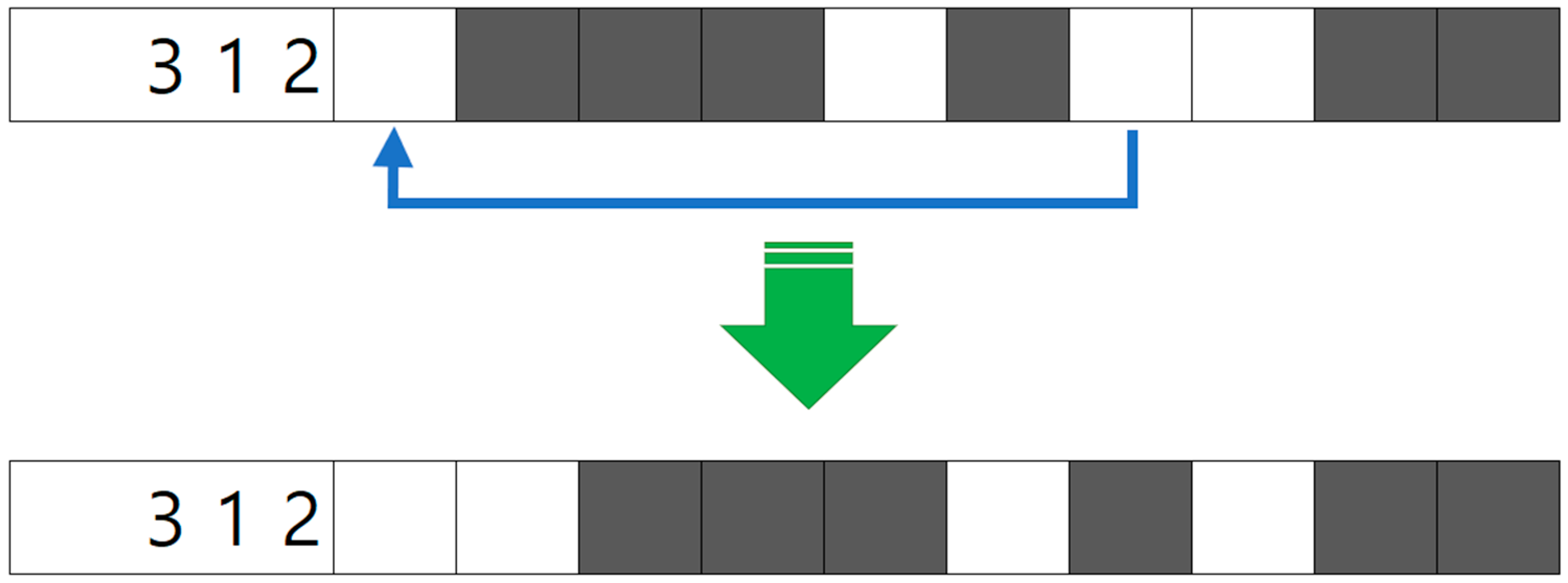
- Step 1: Initially, cells are filled according to the minimal arrangement dictated by the row clues. For example, given a 10 × 10 puzzle row with clues “3 1 2”, the minimal arrangement required to satisfy these clues is shown in Figure 10.
- 2.
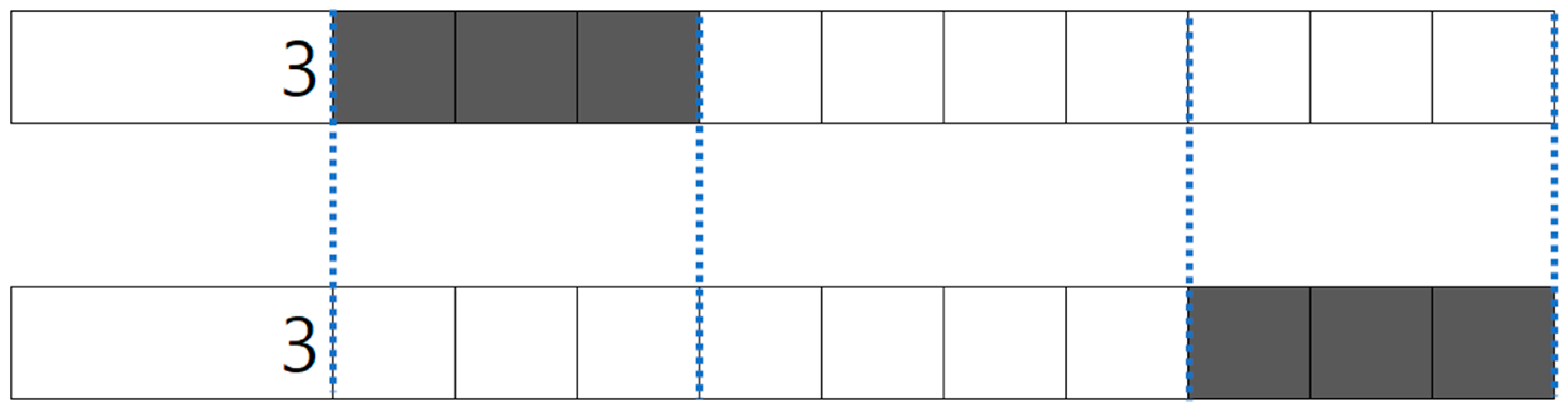
- Step 2: Next, the number and potential locations of extra white cells are determined. In the example from Step 1, eight cells are already occupied. Given the row size of 10, there are two remaining extra white cells. Extra white cells must be placed either at the ends of the row or between groups of black cells to maintain clue satisfaction. As illustrated in Figure 11, four potential positions for extra white cells are indicated by green arrows.
- 3.
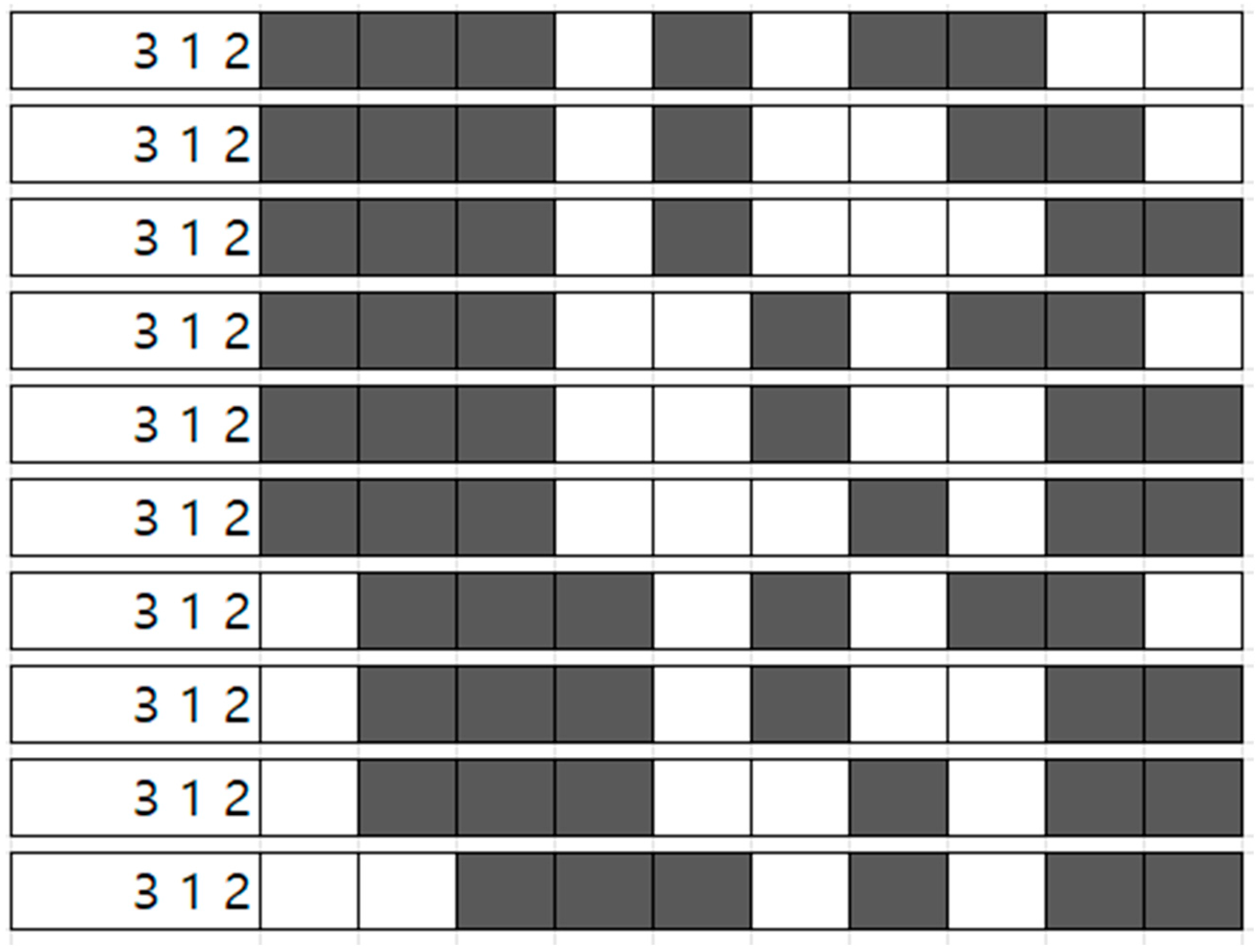
- Step 3: One of the identified positions from Step 2 is randomly selected to place an extra white cell. For example, if position #3 is chosen, the resulting configuration is updated accordingly, as depicted in Figure 12.
- Step 1: Extra white cell information is retrieved from the random generation operation. For the example of Figure 13, x3_extra_blank = [1,0,1,0].
- Step 2: One position among those with a non-zero number of extra white cells is randomly chosen. In this example, positions one and three are eligible. If position three is randomly chosen, one cell is removed from this position, updating the tracking variable to x3_extra_blank = [1,0,0,0].
- Step 3: Then, another position from the remaining positions (excluding the one just selected) is randomly chosen. If position one is chosen, one extra white cell is added to that position, updating the variable to x3_extra_blank = [2,0,0,0], as illustrated in Figure 14.
4. Experiments and Performance Analysis
- Improvement in Success Rate
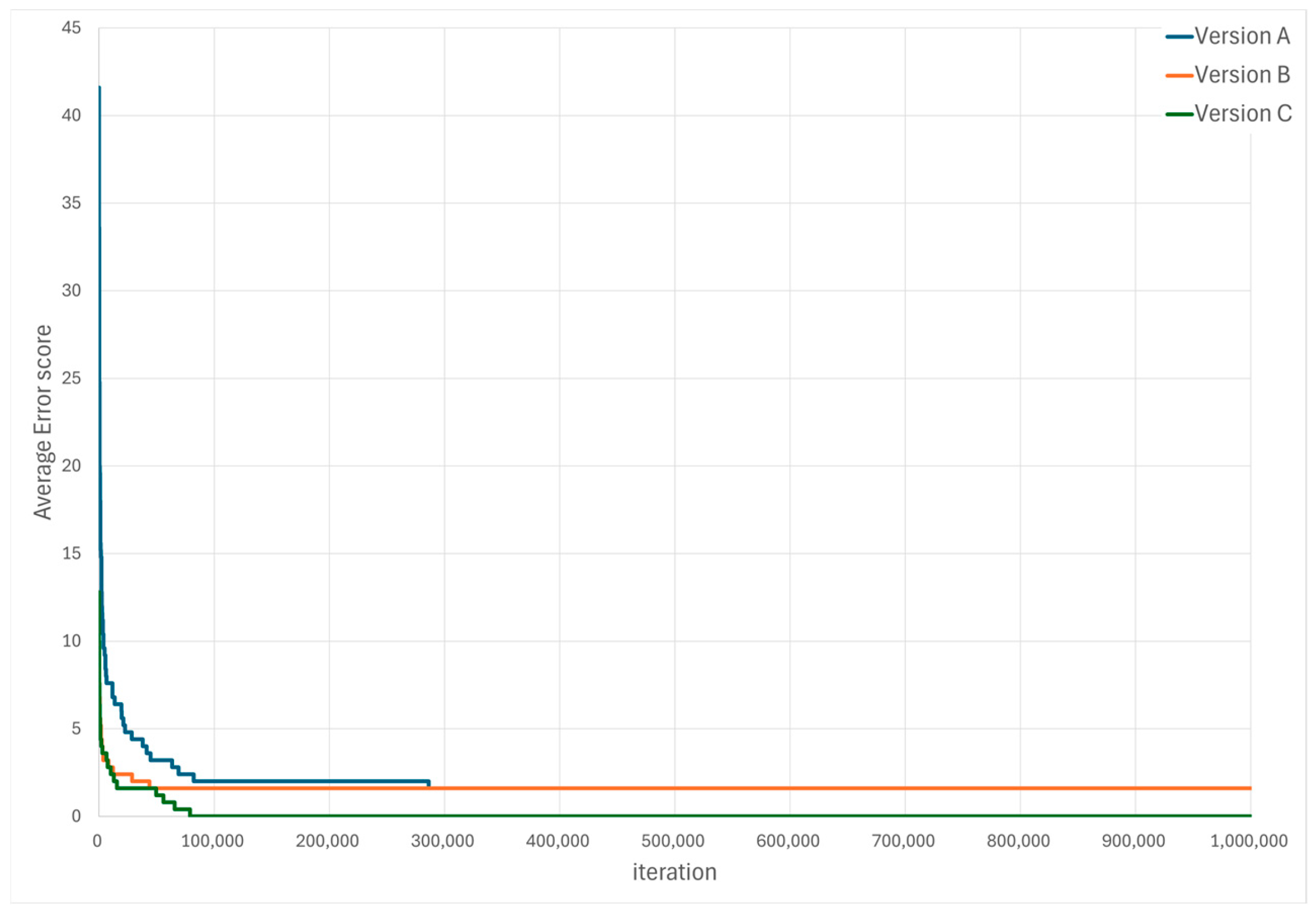
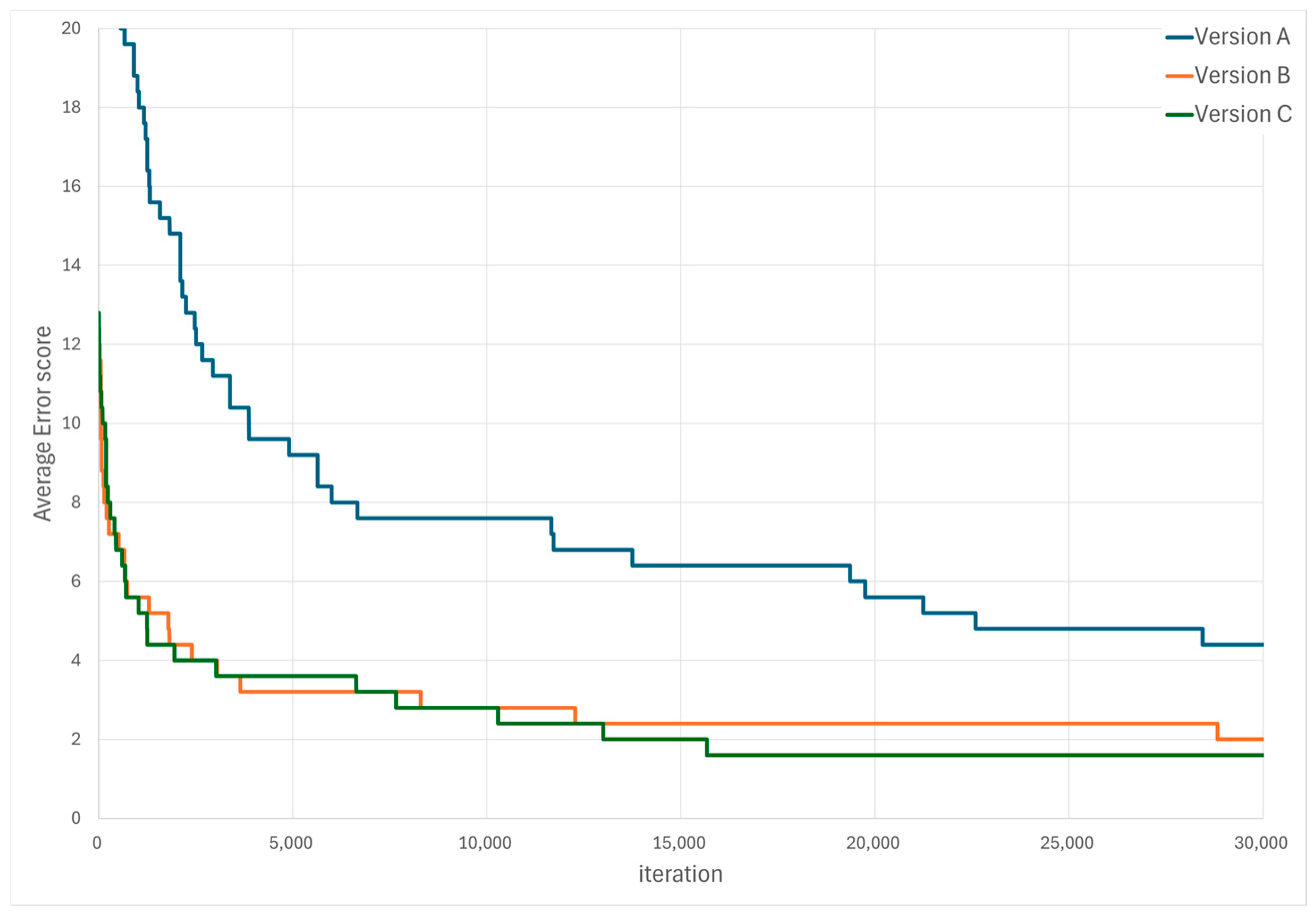
- For small puzzles (less than 10 × 10), all algorithm versions (A, B, C) showed high success rates, with Version C consistently maintaining the highest performance.
- For 10 × 10 puzzles, the original HS algorithm (Version A) rarely found solutions. However, the solving capability significantly improved for Versions B and C. Specifically, Version C successfully solved some challenging puzzles completely.
- Reduction in Average Iterations
- Version B showed reduced computational burden and improved convergence speed by pre-determining confirmed cells, effectively shrinking the search space.
- Version C drastically reduced the search space by constraining random generation within the row clues, significantly reducing the average number of iterations.
- While the performance of Versions B and C was similar for easier puzzles, Version C showed superior performance for puzzles of higher difficulty.
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ueda, N.; Nagao, T. NP-Completeness Results for Nonogram via Parsimonious Reductions; Tokyo Institute of Technology: Tokyo, Japan, 1996; pp. 1–8. [Google Scholar]
- Batenburg, K.J.; Kosters, W.A. Solving Nonograms by combining relaxations. Pattern Recognit. 2009, 42, 1672–1683. [Google Scholar] [CrossRef]
- Więckowski, J.; Shekhovtsov, A. Algorithms Effectiveness comparison in solving Nonogram boards. Procedia Comput. Sci. 2021, 192, 1885–1893. [Google Scholar] [CrossRef]
- Wu, I.C.; Sun, D.J.; Chen, L.P.; Chen, K.Y.; Kuo, C.H.; Kang, H.H.; Lin, H.H. An efficient approach to solving nonograms. IEEE Trans. Comput. Intell. AI Games 2013, 5, 251–264. [Google Scholar] [CrossRef]
- Batenburg, K.J.; Henstra, S.; Kosters, W.A.; Palenstijn, W.J. Constructing simple nonograms of varying difficulty. Pure Math. Appl. 2009, 20, 1–15. [Google Scholar]
- Tsai, J.T.; Chou, P.Y.; Fang, J.C. Learning intelligent genetic algorithms using Japanese nonograms. IEEE Trans. Educ. 2011, 55, 164–168. [Google Scholar] [CrossRef]
- Tsai, J.T. Solving Japanese nonograms by Taguchi-based genetic algorithm. Appl. Intell. 2012, 37, 405–419. [Google Scholar] [CrossRef]
- Yu, C.H.; Lee, H.L.; Chen, L.H. An efficient algorithm for solving nonograms. Appl. Intell. 2011, 35, 18–31. [Google Scholar] [CrossRef]
- Khan, K.A. Solving nonograms using integer programming without coloring. IEEE Trans. Games 2020, 14, 56–63. [Google Scholar] [CrossRef]
- Buades Rubio, J.M.; Jaume-i-Capó, A.; López González, D.; Moyà Alcover, G. Solving nonograms using neural networks. Entertain. Comput. 2024, 50, 100652. [Google Scholar] [CrossRef]
- Ruangwises, S. An improved physical ZKP for Nonogram and Nonogram color. J. Comb. Optim. 2023, 45, 122. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Geem, Z.W. Novel derivative of harmony search algorithm for discrete design variables. Appl. Math. Comput. 2008, 199, 223–230. [Google Scholar] [CrossRef]
- Saka, M.P.; Hasançebi, O.; Geem, Z.W. Metaheuristics in structural optimization and discussions on harmony search algorithm. Swarm Evol. Comput. 2016, 28, 88–97. [Google Scholar] [CrossRef]
- Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Del Ser, J.; Bilbao, M.N.; Salcedo-Sanz, S.; Geem, Z.W. A survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
- Kwon, T.Y.; Ma, S.S.; Huh, J.; Ahn, J.H. Optimizing steel arch bridge components using multi-objective harmony search. Structures 2025, 73, 108389. [Google Scholar] [CrossRef]
- Aderyani, F.R.; Mousavi, S.J. Machine learning-based rainfall forecasting in real-time optimal operation of urban drainage systems. J. Hydrol. 2024, 645, 132118. [Google Scholar]
- Zhang, Y.; Li, J. A Hybrid Heuristic Harmony Search Algorithm for the Vehicle Routing Problem with Time Windows. IEEE Access 2024, 12, 42083–42095. [Google Scholar] [CrossRef]
- Xie, G.; Xiong, Z.; Zhang, X.; Xie, R.; Guo, S.; Guizani, M. GAI-IoV: Bridging Generative AI and Vehicular Networks for Ubiquitous Edge Intelligence. IEEE Trans. Wirel. Commun. 2024, 23, 12799–12814. [Google Scholar] [CrossRef]
- Tang, W.; Gao, K.; Ma, Z.; Lin, Z.; Yu, H.; Huang, W.; Wu, N. Local search-based meta-heuristics combined with an improved K-Means++ clustering algorithm for unmanned surface vessel scheduling. Int. J. Prod. Res. 2025. [Google Scholar] [CrossRef]
- Etaati, A.; Bastam, M.; Ataie, E. Smart forest monitoring: A novel Internet of Things framework with shortest path routing for sustainable environmental management. IET Netw. 2024, 13, 528–545. [Google Scholar] [CrossRef]
- Gholami, M.; Arefi, A.; Hasan, A.; Li, C.; Muyeen, S.M. Enhancing energy autonomy of greenhouses with semi-transparent photovoltaic systems through a comparative study of battery storage systems. Sci. Rep. 2025, 15, 2213. [Google Scholar] [CrossRef] [PubMed]
- Pan, R. Plum: Prompt Learning Using Metaheuristics. Mater’s Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2024. [Google Scholar]
- Mitra, S.; Mahapatra, G.; Balas, V.E.; Chattaraj, R. Public Key Cryptography Using Harmony Search Algorithm. In Innovations in Infrastructure; Deb, D., Balas, V., Dey, R., Eds.; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Mokhtari, M.; Taghizadeh, M.; Mazare, M. Impedance control based on optimal adaptive high order super twisting sliding mode for a 7-DOF lower limb exoskeleton. Meccanica 2021, 56, 535–548. [Google Scholar] [CrossRef]
- Li, W.; Du, W.; Tang, W.; Pan, Y.; Zhou, J.; Lin, Z. Parallel algorithm of multiobjective optimization harmony search based on cloud computing. J. Algorithms Comput. Technol. 2017, 11, 301–313. [Google Scholar] [CrossRef]
- Sharma, P. Bone age estimation with HS-optimized Resnet and Yolo for child growth disorder. Expert Syst. Appl. 2025, 259, 125160. [Google Scholar] [CrossRef]
- Li, A.; Li, J.; Hu, Y.; Geng, Y.; Qiang, Y.; Zhao, J. A Dynamic Adaptive Ensemble Learning Framework for Noninvasive Mild Cognitive Impairment Detection: Development and Validation Study. JMIR Med. Inform. 2025, 13, e60250. [Google Scholar] [CrossRef]
- Manivannan, G.S.; Mani, K.; Rajaguru, H.; Talawar, S.V. Detection of Alcoholic EEG signal using LASSO regression with metaheuristics algorithms based LSTM and enhanced artificial neural network classification algorithms. Sci. Rep. 2024, 14, 21437. [Google Scholar] [CrossRef]
- Zamanidoost, Y.; Ould-Bachir, T.; Martel, S. OMS-CNN: Optimized Multi-Scale CNN for Lung Nodule Detection Based on Faster R-CNN. IEEE J. Biomed. Health Inform. 2025, 29, 2148–2160. [Google Scholar] [CrossRef]
- Kumar, M.G.; Kocharla, S.; Yaswanth, N.; Swamy, T.V.N.; Prasad, U.; Vamsee, T. EHA-LNN: Optimized light gradient-boosting machine enabled neural network for cancer detection using mammography. Biomed. Signal Process. Control 2025, 105, 107540. [Google Scholar]
- Saif, M.; Abdullah, R.; Adib, M.; Ahmed, A.A.; Omar, N.A.; Mostafa, S.A. Analysis of Objective Functions for Ribonucleic Acid Multiple Sequence Alignment Fusion Based on Harmony Search Algorithm. Fusion Pract. Appl. 2025, 17, 1–10. [Google Scholar]
- Geem, Z.W.; Tseng, C.L.; Park, Y. Harmony Search for Generalized Orienteering Problem: Best Touring in China. Lect. Notes Comput. Sci. 2005, 3612, 741–750. [Google Scholar]
- Navarro, M.; Corchado, J.M.; Demazeau, Y. MUSIC-MAS: Modeling a harmonic composition system with virtual organizations to assist novice composers. Expert Syst. Appl. 2016, 57, 345–355. [Google Scholar] [CrossRef]
- Koenderink, J.; van Doorn, A.; Wagemans, J. Picasso in the mind’s eye of the beholder: Three-dimensional filling-in of ambiguous line drawings. Cognition 2012, 125, 394–412. [Google Scholar] [CrossRef] [PubMed]
- Romero, V.M.; Tomes, L.L.; Yusiong, J.P.T. Tetris Agent Optimization Using Harmony Search Algorithm. Int. J. Comput. Sci. 2011, 8, 22–31. [Google Scholar]
- Geem, Z.W. Harmony Search Algorithm for Solving Sudoku. Lect. Notes Comput. Sci. 2007, 4692, 371–378. [Google Scholar]
- Lee, G.H.; Geem, Z.W. Harmony Search for Soving Nonogram Puzzle. J. Korean Inst. Intell. Syst. 2021, 31, 422–428. [Google Scholar]
- Batenburg, K.J.; Kosters, W.A. A reasoning framework for solving Nonograms. In International Workshop on Combinatorial Image Analysis; Springer: Berlin/Heidelberg, Germany, 2008; pp. 372–383. [Google Scholar]








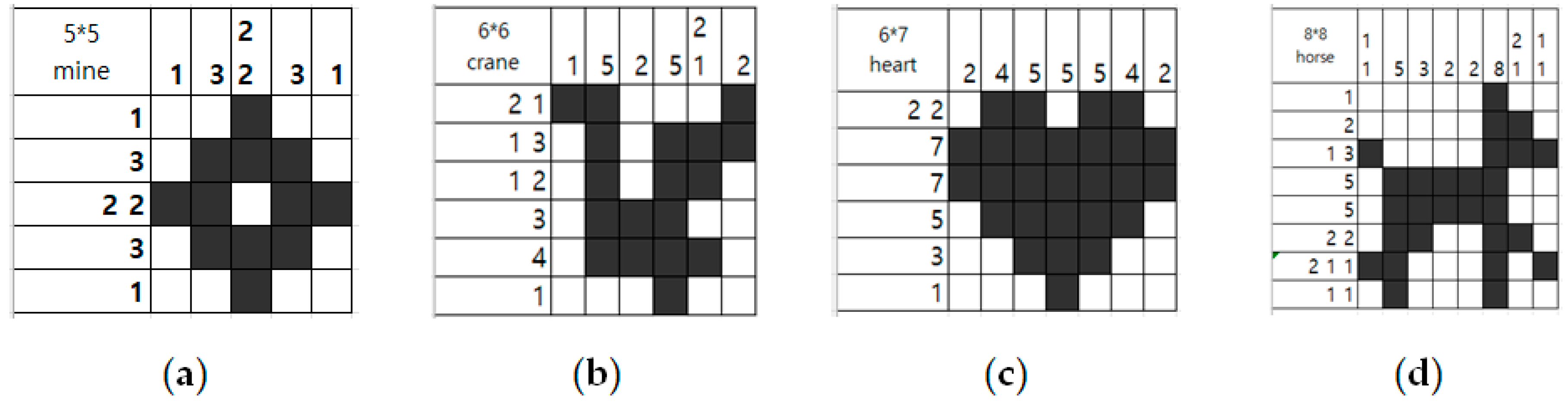


| Success Rate (out of 10 Trials) | Average Iteration (Function Evaluation) [Min–Max Range] | |||||||
|---|---|---|---|---|---|---|---|---|
| Puzzle Name | GA | HS Ver. A | HS Ver. B | HS Ver. C | GA | HS Ver. A | HS Ver. B | HS Ver. C |
| (a) Mine (5 × 5) | 10/10 | 10/10 | 10/10 | 10/10 | 2190 [270 ~6810] | 3222.2 [574 ~6192] | 1.0 [1~1] | 35.1 [1~237] |
| (b) Crane (6 × 6) | 10/10 | 10/10 | 10/10 | 10/10 | 7935 [2370 ~15,150] | 87,376.4 [7792 ~516,640] | 6740.5 [564 ~16,877] | 3933 [222 ~20,993] |
| (c) Heart (6 × 7) | 10/10 | 9/10 | 10/10 | 10/10 | 17,901 [3240 ~39,360] | 19,856.2 [6558 ~38,207] | 170.7 [4~463] | 101 [1~349] |
| (d) Horse (8 × 8) | 10/10 | 3/10 | 4/10 | 9/10 | 43,740 [15,240 ~122,520] | 500,291.3 [337,257 ~670,754] | 172,234 [124,671 ~243,174] | 28,121 [2891 ~57,043] |
| Success Rate (out of 10 Trials) | Average Iteration (Function Evaluation) [Min–Max Range] | |||||||
|---|---|---|---|---|---|---|---|---|
| Puzzle Name | GA | HS Ver. A | HS Ver. B | HS Ver. C | GA | HS Ver. A | HS Ver. B | HS Ver. C |
| (a) Sol | 0/10 | 0/10 | 0/10 | 1/10 | - | - | - | 385,592 [385,592 ~385,592] |
| (b) Note | 0/10 | 0/10 | 10/10 | 10/10 | - | - | 11,467.9 [5874 ~17,724] | 170,829.7 [28,453 ~426,283] |
| (c) Flower word | 0/10 | 0/10 | 0/10 | 1/10 | - | - | - | 122,062 [122,062 ~122,062] |
| (d) Leaf | 0/10 | 0/10 | 0/10 | 3/10 | - | - | - | 432,767.3 [314,904 ~585,708] |
| (e) Dog | 0/10 | 1/10 | 10/10 | 10/10 | - | 798,079 [798,079 ~798,079] | 13,062.1 [5874 ~17,724] | 100,865.4 [29,212 ~205,127] |
| (f) Mushroom cloud | 0/10 | 1/10 | 0/10 | 10/10 | - | 775,262 [775,262 ~775,262] | - | 20,087.7 [248 ~59,309] |
| (g) Tea | 0/10 | 2/10 | 0/10 | 6/10 | - | 603,041 [585,912 ~620,170] | - | 81,204.2 [30,448 ~173,770] |
| (h) TV | 0/10 | 1/10 | 9/10 | 5/10 | - | 771,885 [771,885 ~771,885] | 110,705.6 [48,405 ~240,562] | 143,291.2 [83,907 ~209,201] |
| (i) Snail | 0/10 | 0/10 | 10/10 | 10/10 | - | - | 36,689.5 [5691 ~179,136] | 124,208.2 [13,839 ~285,882] |
| (j) Scorpion | 0/10 | 0/10 | 0/10 | 8/10 | - | - | - | 122,928.1 [36,311 ~282,549] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.; Geem, Z.W. Harmony Search Algorithm with Two Problem-Specific Operators for Solving Nonogram Puzzle. Mathematics 2025, 13, 1470. https://doi.org/10.3390/math13091470
Lee G, Geem ZW. Harmony Search Algorithm with Two Problem-Specific Operators for Solving Nonogram Puzzle. Mathematics. 2025; 13(9):1470. https://doi.org/10.3390/math13091470
Chicago/Turabian StyleLee, Geonhee, and Zong Woo Geem. 2025. "Harmony Search Algorithm with Two Problem-Specific Operators for Solving Nonogram Puzzle" Mathematics 13, no. 9: 1470. https://doi.org/10.3390/math13091470
APA StyleLee, G., & Geem, Z. W. (2025). Harmony Search Algorithm with Two Problem-Specific Operators for Solving Nonogram Puzzle. Mathematics, 13(9), 1470. https://doi.org/10.3390/math13091470






