Detecting Clinical Risk Shift Through log–logistic Hazard Change-Point Model
Abstract
1. Introduction and Background
Change–Point Problems in Survival Analysis
- Introduce a novel hazard change–point model, namely the log–logistic hazard change–point model;
- Estimate the model parameters using the profile maximum likelihood estimation method and the Bayesian method, as well as compare the results for varying sample sizes and censoring levels;
- Show the suitability of the model to detect a change–point in two real–world datasets.
2. log–logistic Hazard Change–Point Model for Survival Analysis
3. Parameter Estimation Using PMLE
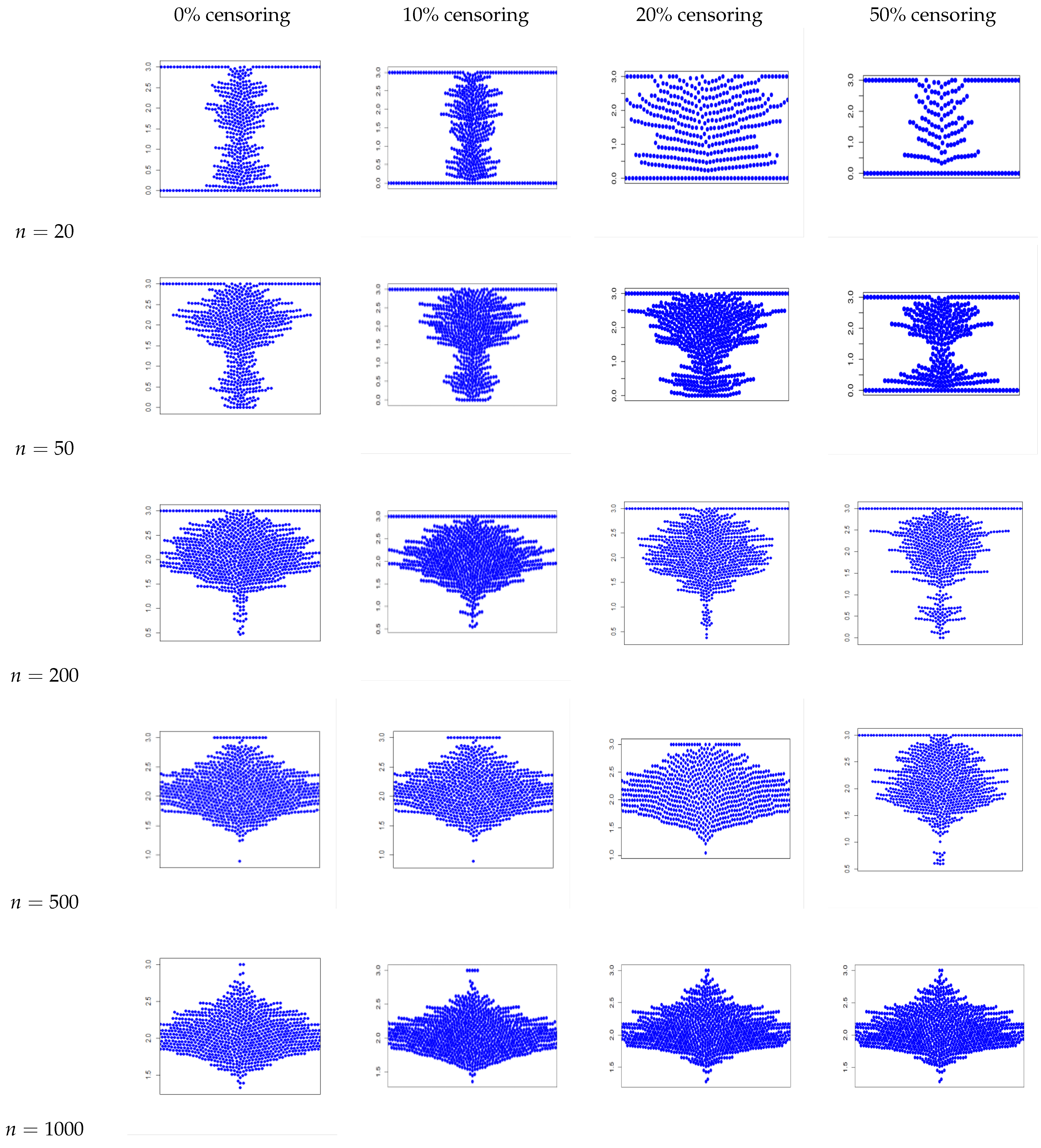
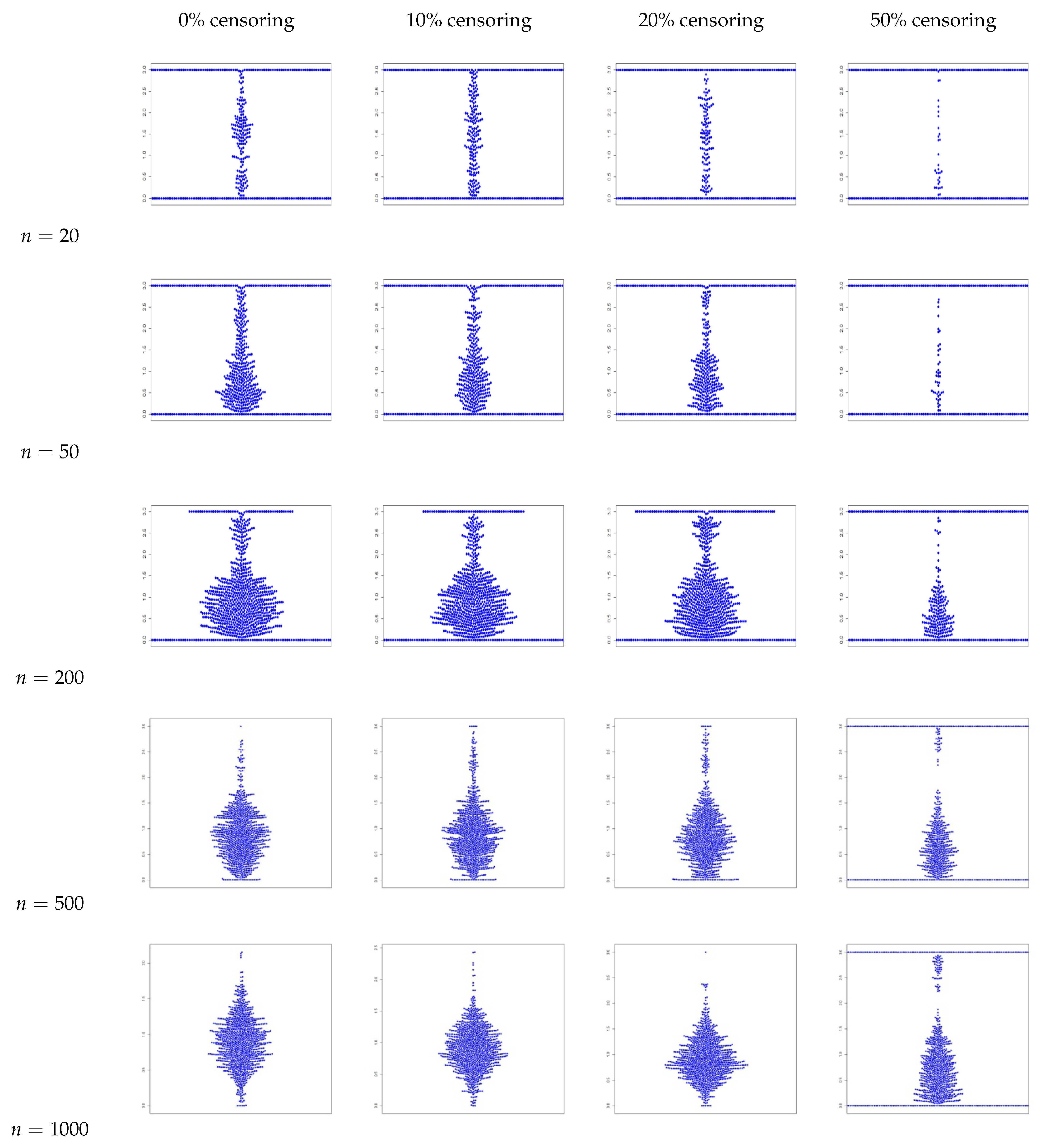
4. Simulation Study
Conclusion of the Simulation Study
- The estimators for , , and are consistently close to the true values across all sample sizes and censoring levels, with both bias and MSE decreasing as the sample size increases. This indicates that the estimators are approximately unbiased and consistent, even under high censoring. However, an increase in censoring percentage increases the MSE, because it introduces uncertainty due to missing information in the likelihood.
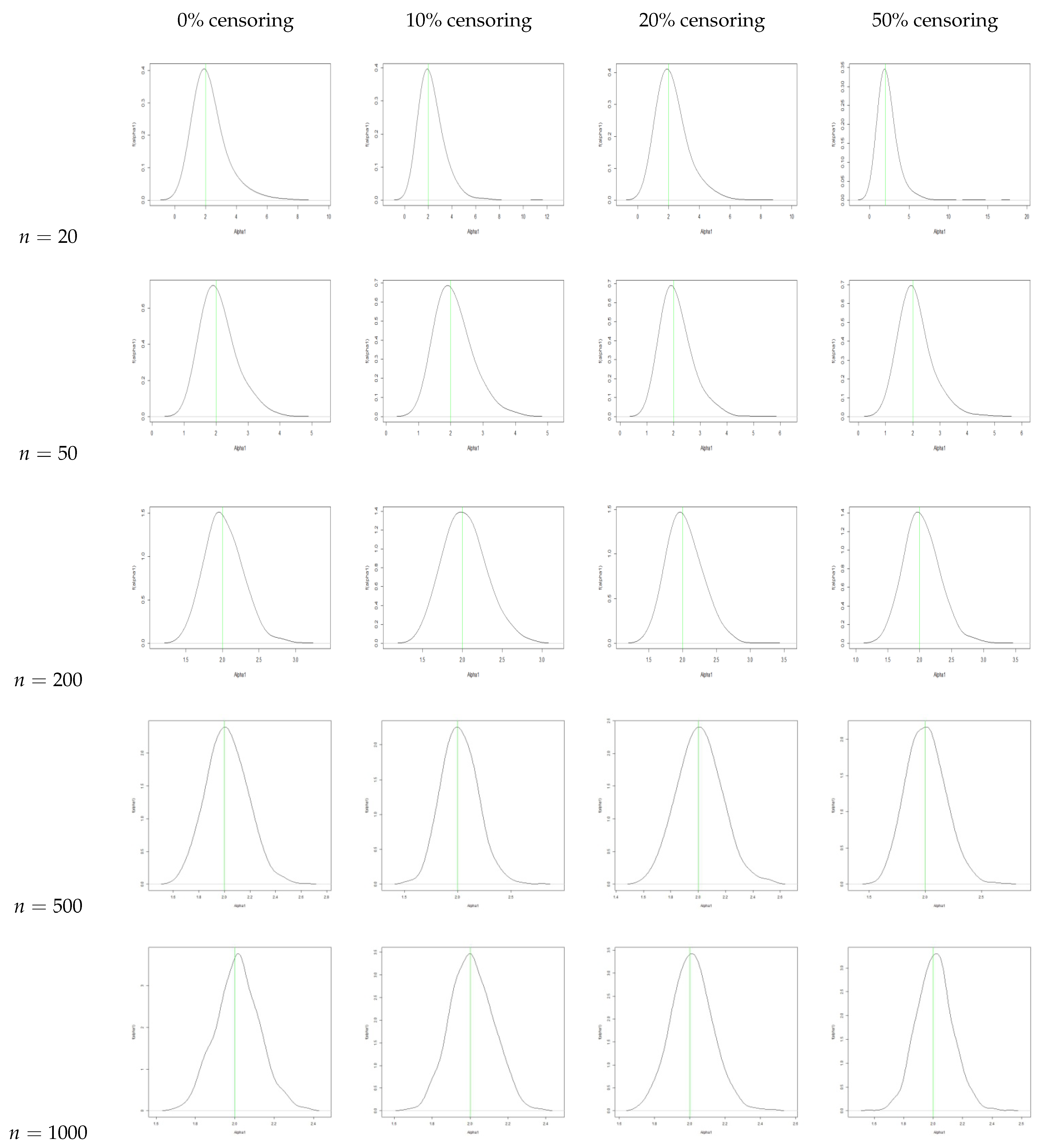
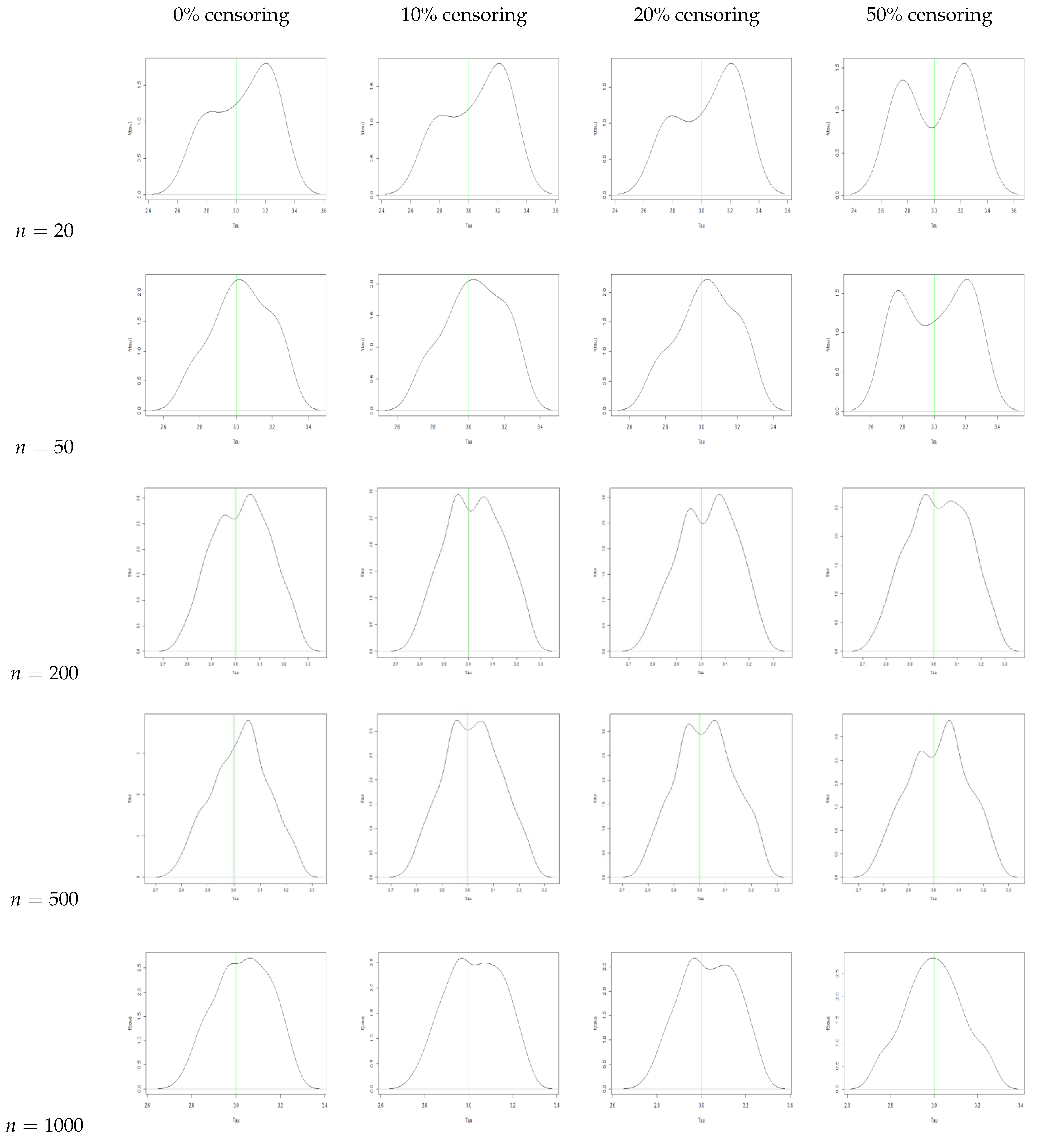
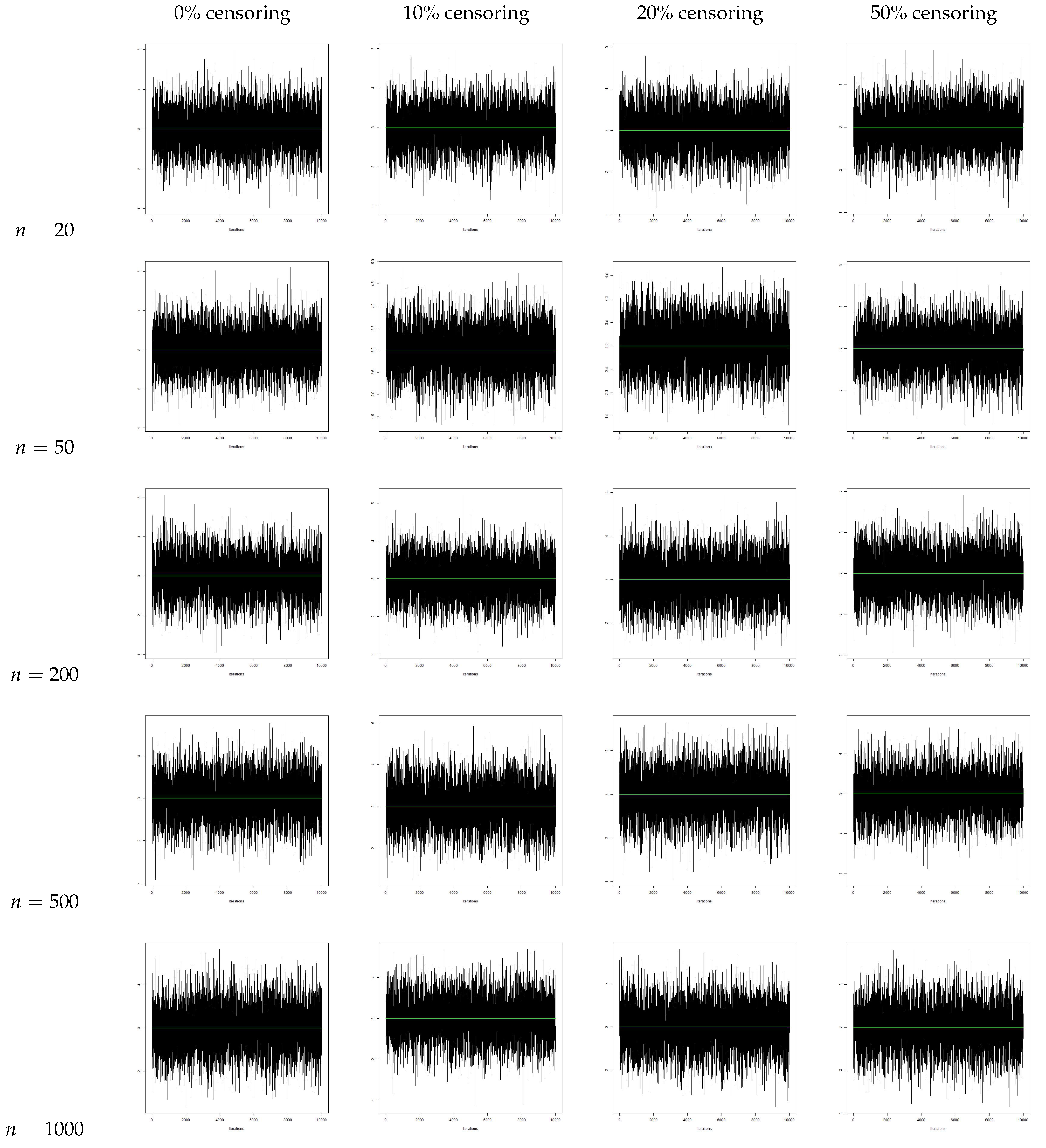
- We also plot the kernel density estimates to assess the normality. From Figure A4, Figure A5, Figure A6 and Figure A10, Figure A11, Figure A12, we see that the estimators are asymptotically normal. Here, in the case of 50% censoring when , we find that the kernel density estimator does not converge to normality at sample size 1000; however, the convergence can be achieved with a larger sample size.
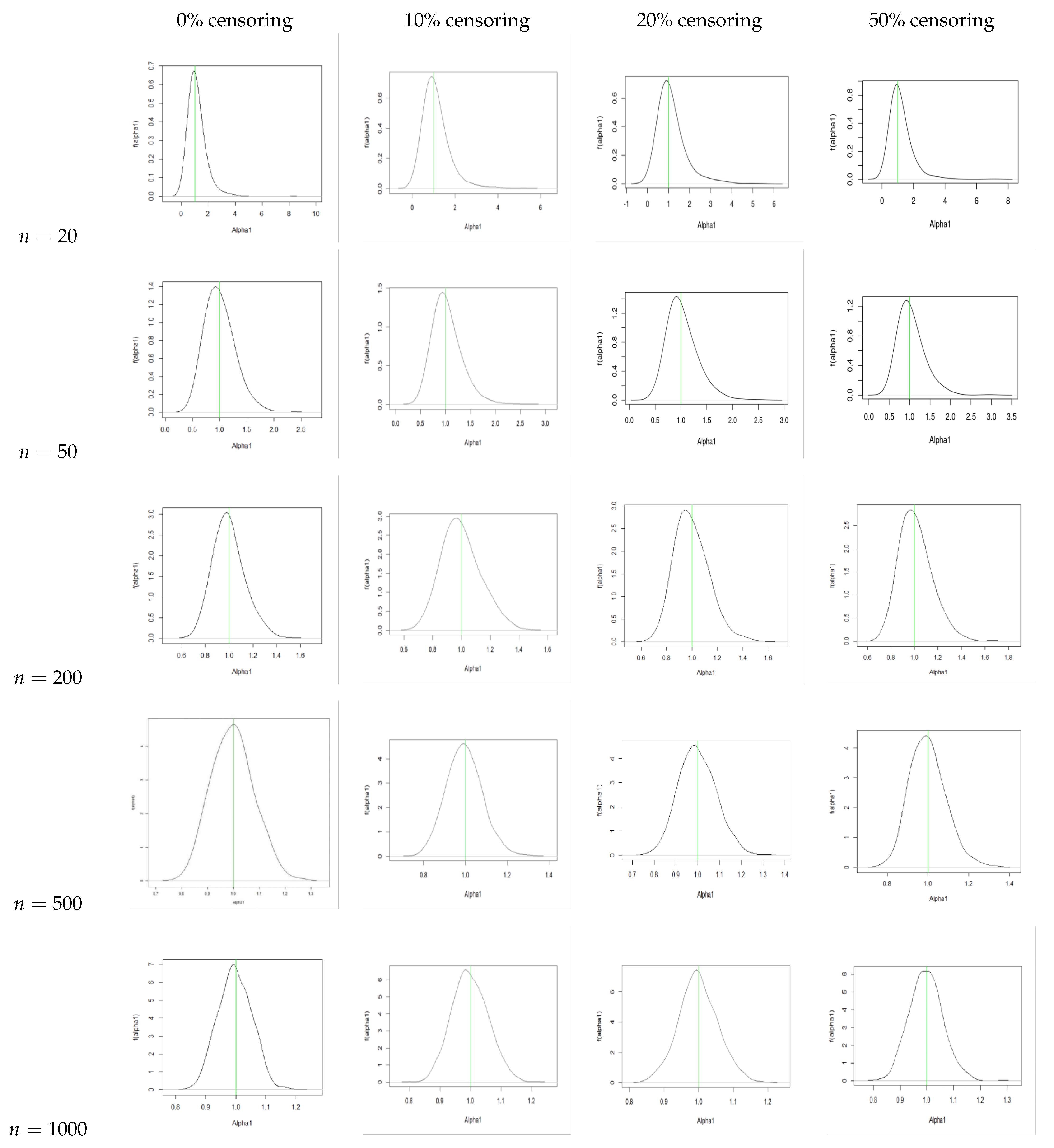
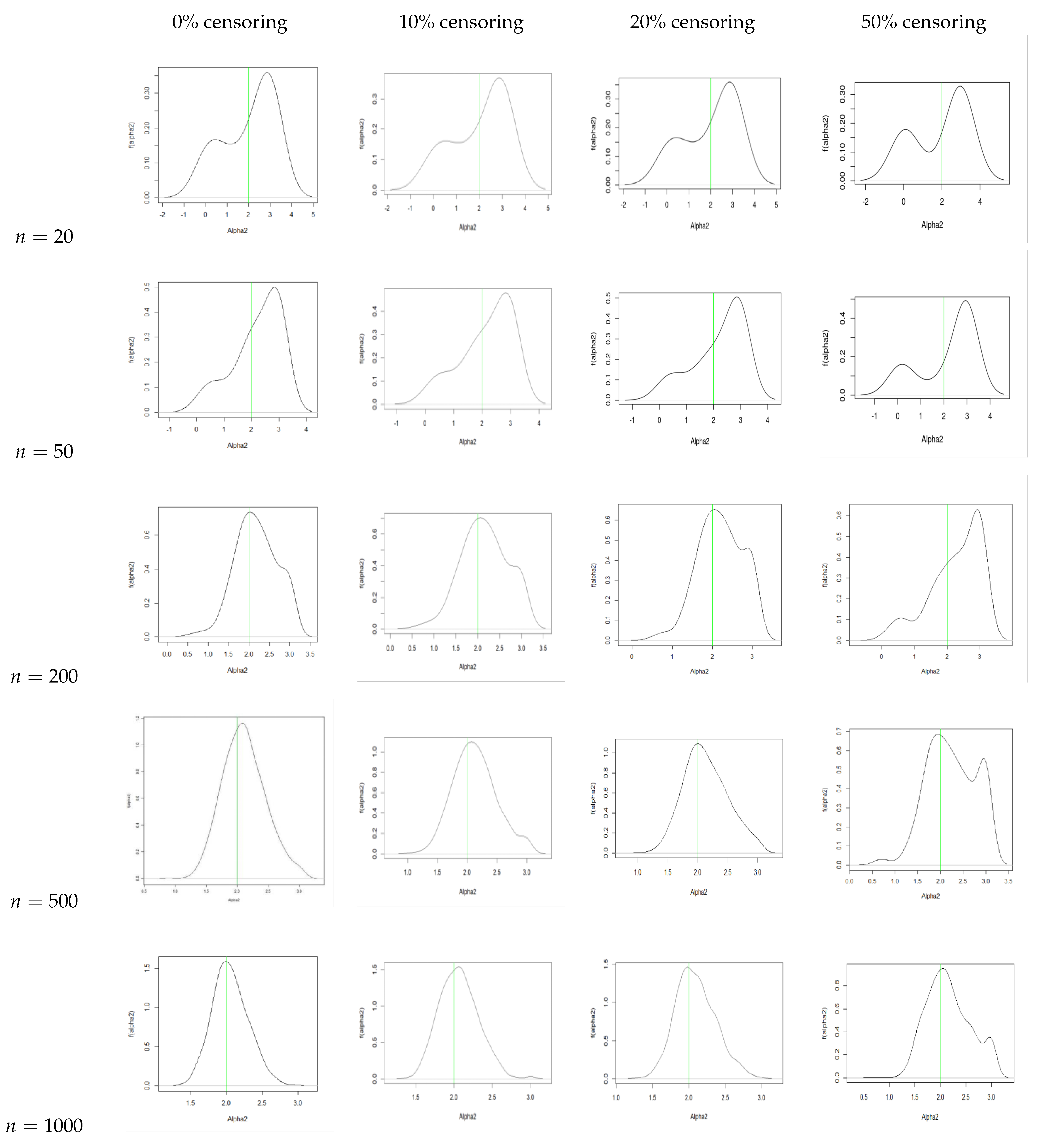
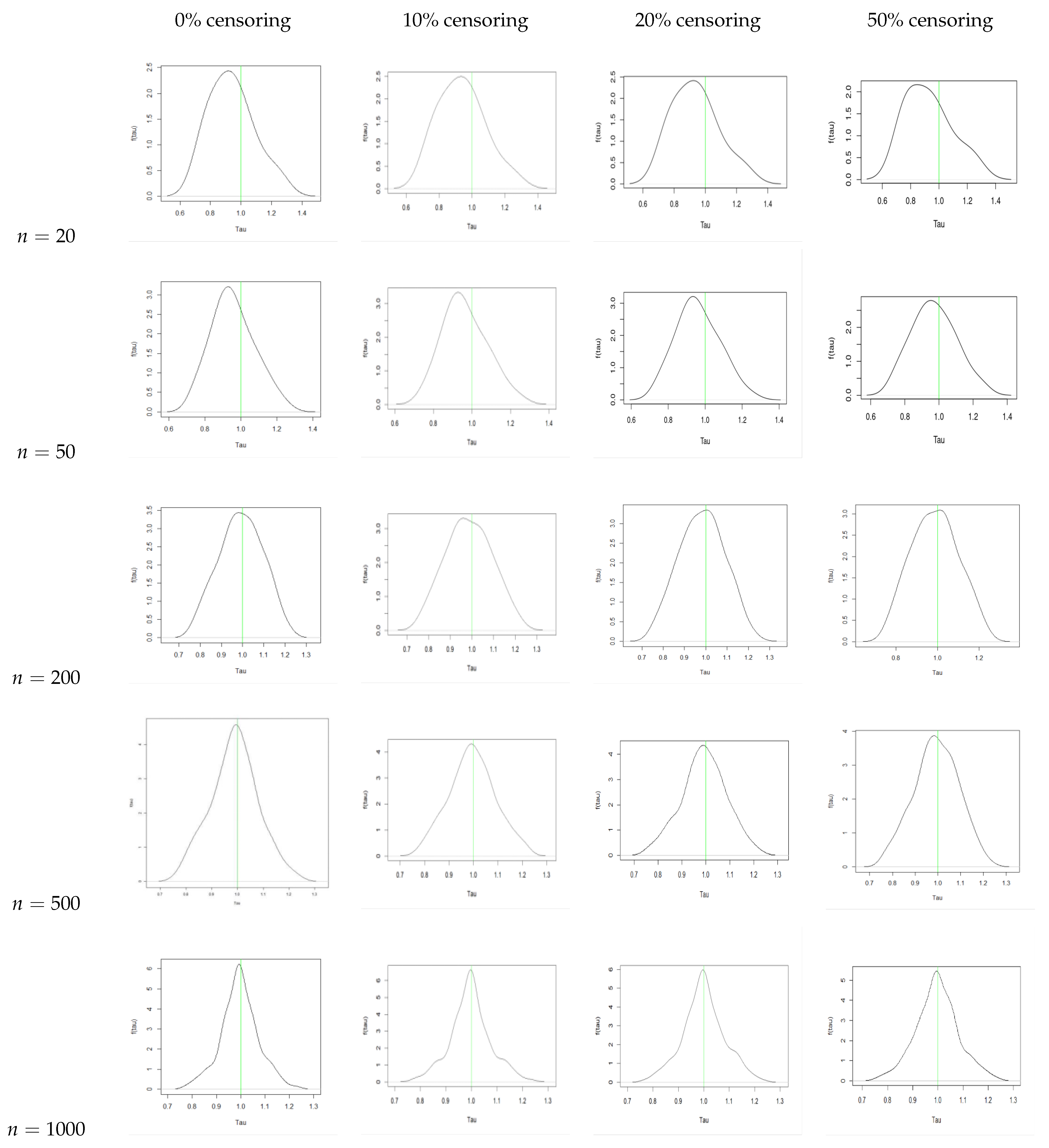
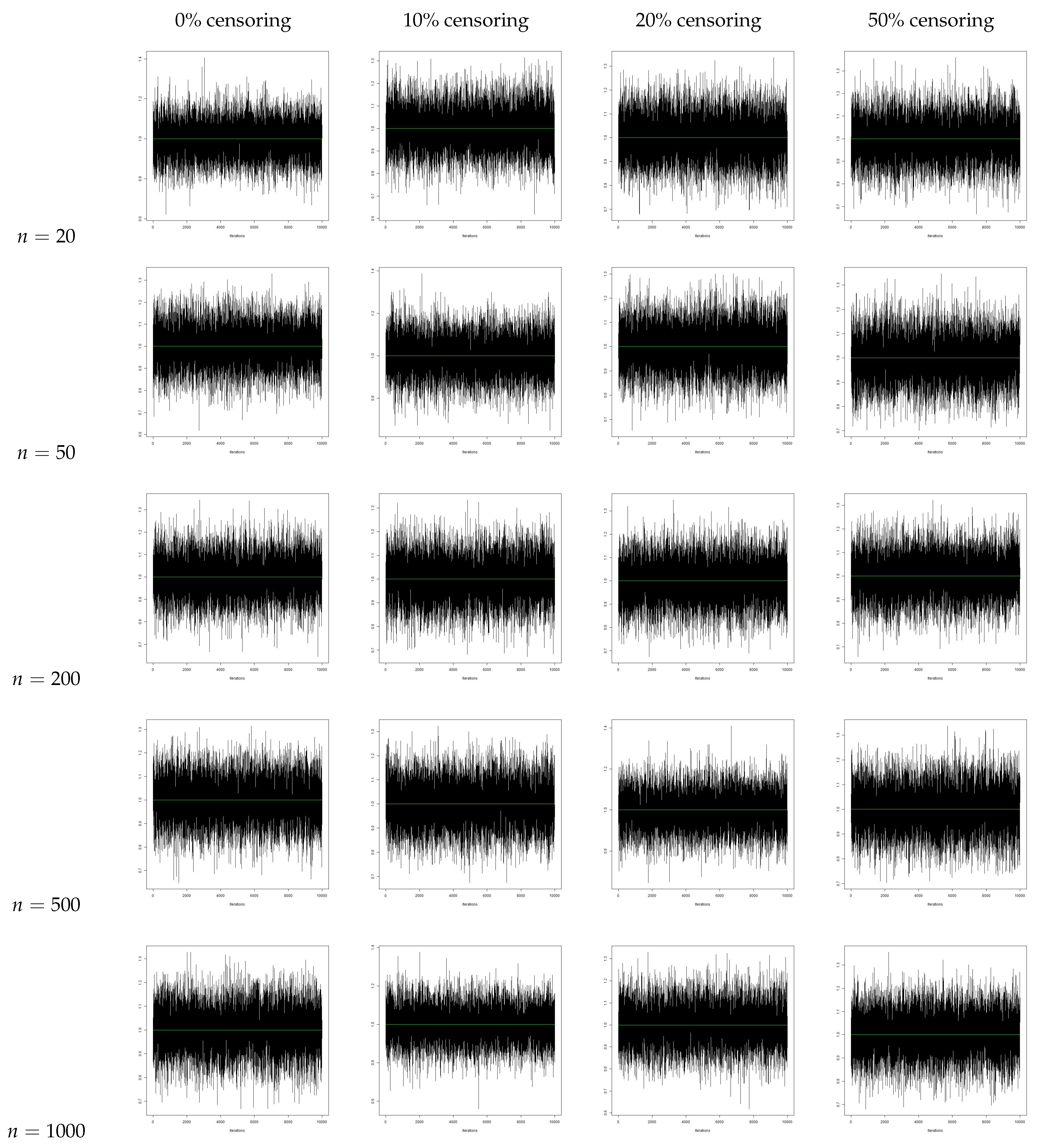
5. Bayesian Analysis
- First, generate a proposal from the proposal distribution .
- Next, compute the acceptance ratio, which is given as follows:
- Then, draw a random variable .
- If , accept the proposal and set ; otherwise, reject the proposal and set .
- With an increase in sample size, there is a reduction in the bias and the MSE for all three parameters.
- We observe that the AR increases with an increase in sample size. We also see that the AR is lower for the same sample size when we increase the censoring percentage. Hence, we can infer that censoring has a slight effect on the AR of the samples.
- From the traceplots, we see that there is no trend or fluctuation observed in any of the three parameters, indicating a good mix of the chain.
6. Data Analysis
- Model Evaluation Criteria and Goodness-of-Fit Measures
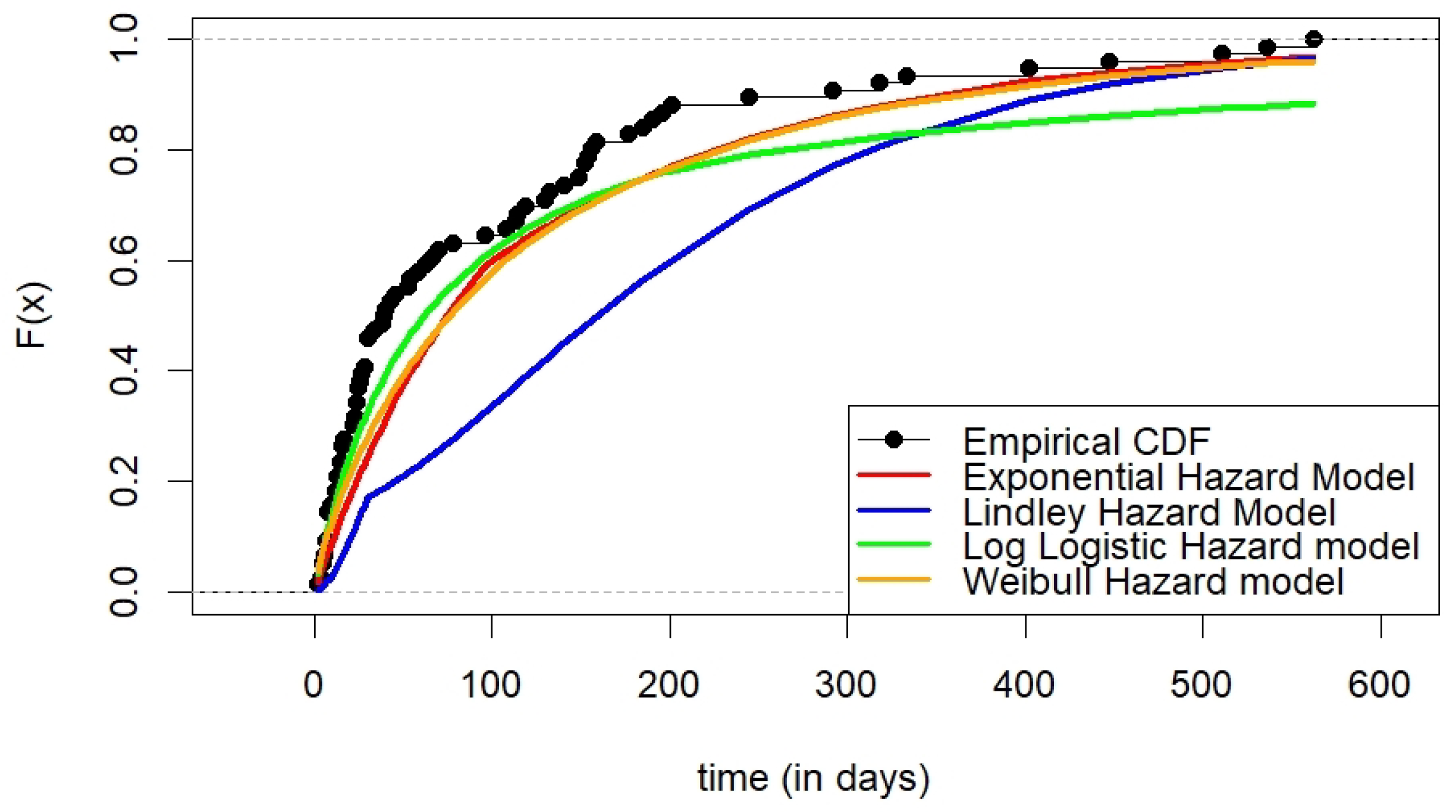
6.1. Kidney Catheter Data
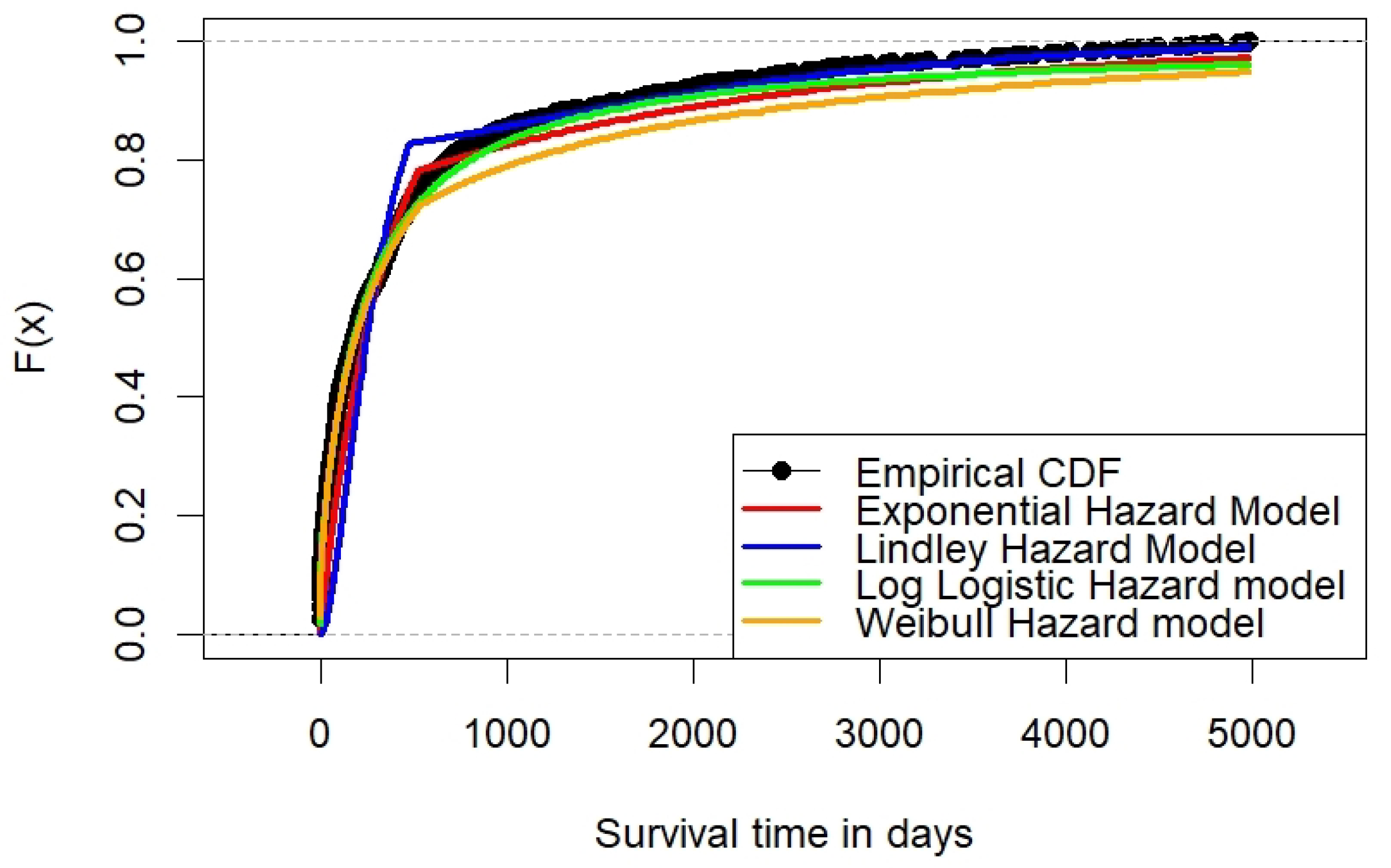
6.2. Acute Myeloid Leukemia
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AML | Acute Myeloid Leukemia |
| Probability Density Function | |
| GM | Generalized Moments |
| LL2 | 2-parameter log–logistic |
| Ex-LL | Extended log–logistic |
| MDPDEs | Minimum Density Power Divergence Estimators |
| AFT | Accelerated Failure Time |
| PMLE | Profile Maximum Likelihood Estimation |
| ML | Maximum Likelihood |
| CDF | Cumulative Distribution Function |
| MSE | Mean Square Error |
| MEV | Mean Estimated Value |
| M-H | Metropolis–Hastings |
| MCMC | Markov Chain Monte Carlo |
| AR | Acceptance Rate |
| LLHM | log–logistic Hazard Change-Point Model |
| EHM | Exponential Hazard Change-Point Model |
| LHM | Lindley Hazard Change-Point Model |
| WHM | Weibull Hazard Change-Point Model |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| Kolmogrov–Smirnov | |
| Anderson–Darling |
Appendix A






References
- Gupta, R.C.; Olcay, A.; Sergey, L. A study of log-logistic model in survival analysis. Biom. J. J. Math. Methods Biosci. 1999, 41, 431–443. [Google Scholar] [CrossRef]
- Steve, B. log–logistic regression models for survival data. J. R. Stat. Soc. Ser. C Appl. Stat. 1983, 32, 165–171. [Google Scholar]
- Muse, A.H.; Mwalili, S.; Oscar, N. On the log–logistic distribution and its generalizations: A survey. Int. J. Stat. Probab. 2021, 10, 93. [Google Scholar] [CrossRef]
- Lemonte, A.J. The beta log–logistic distribution. Braz. J. Probab. Stat. 2014, 28, 313–332. [Google Scholar] [CrossRef]
- Fahim, A.; Mahdi, S. Fitting the log–logistic distribution by generalized moments. J. Hydrol. 2006, 328, 694–703. [Google Scholar]
- Shoukri, M.M.; Mian, I.U.H.; Tracy, D.S. Sampling properties of estimators of the log-logistic distribution with application to Canadian precipitation data. Can. J. Stat. 1988, 16, 223–236. [Google Scholar] [CrossRef]
- De Santana, T.V.F.; Ortega, E.M.; Cordeiro, G.M.; Silva, G.O. The Kumaraswamy-log–logistic distribution. J. Stat. Theory Appl. 2012, 11, 265–291. [Google Scholar]
- Ramos, P.L.; Balakrishnan, N.; Zografos, K. The Zografos-Balakrishnan log–logistic distribution: Properties and applications. J. Stat. Theory Appl. 2013, 12, 275–290. [Google Scholar]
- Alfaer, N.M.; Gemeay, A.M.; Aljohani, H.M.; Afify, A.Z. The extended log–logistic distribution: Inference and actuarial applications. Mathematics 2021, 9, 1386. [Google Scholar] [CrossRef]
- Felipe, A.; Jaenada, M.; Miranda, P.; Pardo, L. Robust parameter estimation of the log–logistic distribution based on density power divergence estimators. arXiv 2023, arXiv:2312.02662. [Google Scholar] [CrossRef]
- Gaire, A.K.; Gurung, Y.B. Rayleigh generated log–logistic distribution properties and performance analysis. J. Turk. Stat. Assoc. 2024, 15, 13–28. [Google Scholar]
- Matthews, D.E.; Farewell, V.T. On Testing for a Constant Hazard against a Change-Point Alternative. Biometrics 1982, 38, 463–468. [Google Scholar] [CrossRef]
- Chang, I.S.; Chen, C.H.; Hsiung, C.A. Estimation in Change-Point Hazard Rate Models with Random Censorship. Lect. Notes-Monogr. Ser. 1994, 23, 78–92. [Google Scholar]
- Gijbels, I.; Gürle, U. Estimation of a Change-Point in a Hazard Function Based on Censored Data. Lifetime Data Anal. 2003, 9, 395–411. [Google Scholar] [CrossRef] [PubMed]
- Goodman, M.S.; Li, Y.; Tiwari, R.C. Detecting Multiple Change-Points in piece-wise Constant Hazard Functions. J. Appl. Stat. 2011, 38, 2523–2532. [Google Scholar] [CrossRef]
- Williams, M.R.; Kim, D.Y. A test for an Abrupt Change in Weibull Hazard Functions with Staggered Entry and Type-I Censoring. Commun. Stat. Theory Methods 2013, 42, 1922–1933. [Google Scholar] [CrossRef]
- Joshi, S.; Jose, K.K.; Bhati, D. Estimation of a Change-Point in the Hazard Rate of Lindley Model under Right Censoring. Commun. Stat. Simul. Comput. 2017, 46, 3563–3574. [Google Scholar] [CrossRef]
- Palmeros, O.; Villaseñor, J.A.; González, E. On computing estimates of a change–point in the Weibull regression hazard model. J. Appl. Stat. 2018, 45, 642–648. [Google Scholar] [CrossRef]
- Joshi, S.; Rattihalli, R.N. Estimation of parameters in a general hazard regression change–point model. J. Indian Stat. Assoc. 2019, 57, 19–40. [Google Scholar]
- Joshi, S.; Rattihalli, R.N. Estimation of Parameters in the Exponential-Lindley Hazard Change-Point Model. Adv. Intell. Syst. Comput. 2020, 1169, 345–356. [Google Scholar]
- Gierz, K.; Park, K. Detection of multiple change points in a Weibull accelerated failure time model using sequential testing. Biom. J. 2022, 64, 617–634. [Google Scholar] [CrossRef] [PubMed]
- Matloff, N. The Art of R Programming: A Tour of Statistical Software Design; No Starch Press: San Francisco, CA, USA, 2011. [Google Scholar]
- Lynch, S.M. Introduction to Applied Bayesian Statistics and Estimation for Social Scientists; Springer: New York, NY, USA, 2007; Volume 1. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Griffith, I.R.; Newsome, B.B.; Leung, G.; Block, G.A.; Herbert, R.J.; Danese, M.D. Impact of Hemodialysis Catheter Dysfunction on Dialysis and Other Medical Services: An Observational Cohort Study. Int. J. Nephrol. 2012, 8, 1179–1187. [Google Scholar] [CrossRef]
- Walter, R.B.; Othus, M.; Borthakur, G.; Ravandi, F.; Cortes, J.E.; Pierce, S.A.; Appelbaum, F.R.; Kantarjian, H.A.; Estey, E.H. Prediction of early death after induction therapy for newly diagnosed acute myeloid leukemia with pretreatment risk scores: A novel paradigm for treatment assignment. J. Clin. Oncol. 2011, 29, 4417–4423. [Google Scholar] [CrossRef] [PubMed]

| Censoring | MEV | Bias | MSE | MEV | Bias | MSE | MEV | Bias | MSE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 20 | 1.1166 | 0.1166 | 0.3426 | 2.1987 | 0.1987 | 1.2613 | 0.9383 | −0.0616 | 0.0225 |
| 50 | 1.0076 | 0.0076 | 0.0769 | 2.1770 | 0.1770 | 0.7837 | 0.9565 | −0.0434 | 0.0156 | |
| 200 | 0.9972 | −0.0028 | 0.0179 | 2.1079 | 0.1079 | 0.2890 | 0.9887 | −0.0112 | 0.0105 | |
| 500 | 0.9973 | −0.0027 | 0.0067 | 1.9134 | −0.0865 | 0.1290 | 0.9922 | −0.0077 | 0.0088 | |
| 1000 | 0.9981 | −0.0018 | 0.0031 | 2.0605 | 0.0605 | 0.0684 | 0.9960 | −0.0039 | 0.0062 | |
| 10% | 20 | 1.1175 | 0.1175 | 0.4022 | 2.1609 | 0.1609 | 1.2923 | 0.9388 | −0.0611 | 0.0222 |
| 50 | 1.0312 | 0.0312 | 0.0835 | 2.1525 | 0.1525 | 0.8102 | 0.9640 | −0.0359 | 0.0140 | |
| 200 | 0.9953 | −0.0046 | 0.0179 | 2.1294 | 0.1294 | 0.3024 | 0.9859 | −0.0140 | 0.0113 | |
| 500 | 0.9984 | −0.0015 | 0.0072 | 2.0645 | 0.0645 | 0.1477 | 0.9950 | −0.0050 | 0.0089 | |
| 1000 | 0.9995 | −0.0004 | 0.0034 | 2.0309 | 0.0309 | 0.0686 | 0.9966 | −0.0031 | 0.0063 | |
| 20% | 20 | 1.1421 | 0.1421 | 0.4310 | 2.2000 | 0.2000 | 1.3633 | 0.9374 | −0.0625 | 0.0239 |
| 50 | 1.0286 | 0.0286 | 0.0871 | 2.1937 | 0.1937 | 0.8994 | 0.9611 | −0.0388 | 0.0146 | |
| 200 | 0.9971 | −0.0028 | 0.0180 | 2.1383 | 0.1383 | 0.3371 | 0.9823 | −0.0176 | 0.0113 | |
| 500 | 0.9990 | −0.0009 | 0.0072 | 2.0972 | 0.0972 | 0.1522 | 0.9921 | −0.0078 | 0.0088 | |
| 1000 | 0.9995 | −0.0004 | 0.0031 | 2.0015 | 0.0015 | 0.0843 | 1.0000 | 0.0000 | 0.0068 | |
| 50% | 20 | 1.1863 | 0.1863 | 0.5001 | 2.2389 | 0.2389 | 1.8697 | 0.9289 | −0.0710 | 0.0296 |
| 50 | 1.0413 | 0.0413 | 0.1063 | 2.2263 | 0.2263 | 1.3949 | 0.9712 | −0.0288 | 0.0165 | |
| 200 | 0.9973 | −0.0027 | 0.0193 | 2.1904 | 0.1904 | 0.6604 | 0.9873 | −0.0126 | 0.0126 | |
| 500 | 1.0107 | 0.0107 | 0.0078 | 2.1628 | 0.1628 | 0.3369 | 0.9925 | −0.0074 | 0.0097 | |
| 1000 | 0.9992 | −0.0008 | 0.0038 | 1.9302 | −0.0697 | 0.2124 | 0.9976 | −0.0023 | 0.0072 | |
| Censoring | MEV | Bias | MSE | MEV | Bias | MSE | MEV | Bias | MSE | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 20 | 2.2831 | 0.2831 | 1.0149 | 1.2853 | 0.2853 | 1.9994 | 3.0450 | 0.0450 | 0.0397 |
| 50 | 2.0877 | 0.0877 | 0.3095 | 1.0913 | 0.0913 | 1.5068 | 3.0317 | 0.0317 | 0.0244 | |
| 200 | 2.0222 | 0.0222 | 0.0666 | 0.9105 | −0.0895 | 0.7233 | 3.0313 | 0.0313 | 0.0156 | |
| 500 | 2.0139 | 0.0139 | 0.0267 | 0.9184 | −0.0816 | 0.2782 | 3.0292 | 0.0292 | 0.0149 | |
| 1000 | 2.0098 | 0.0098 | 0.0129 | 0.9682 | −0.0318 | 0.1272 | 3.0135 | 0.0135 | 0.0120 | |
| 10% | 20 | 2.2886 | 0.2886 | 1.1477 | 1.2994 | 0.2994 | 2.0088 | 3.0485 | 0.0485 | 0.0413 |
| 50 | 2.1016 | 0.1016 | 0.3339 | 0.9163 | −0.0837 | 1.5001 | 3.0311 | 0.0311 | 0.0259 | |
| 200 | 2.0326 | 0.0326 | 0.0730 | 0.9180 | −0.0820 | 0.7256 | 3.0276 | 0.0276 | 0.0161 | |
| 500 | 2.0215 | 0.0215 | 0.0272 | 0.9453 | −0.0547 | 0.3060 | 3.0228 | 0.0228 | 0.0140 | |
| 1000 | 2.0095 | 0.0095 | 0.0114 | 1.0238 | 0.0238 | 0.1377 | 3.0199 | 0.0199 | 0.0124 | |
| 20% | 20 | 2.2438 | 0.2438 | 1.2129 | 1.2414 | 0.2414 | 2.0381 | 3.0471 | 0.0471 | 0.0424 |
| 50 | 2.1164 | 0.1164 | 0.3623 | 0.8776 | −0.1224 | 1.6715 | 3.0316 | 0.0316 | 0.0252 | |
| 200 | 2.0335 | 0.0335 | 0.0706 | 1.1176 | 0.1176 | 0.8812 | 3.0290 | 0.0290 | 0.0157 | |
| 500 | 2.0146 | 0.0146 | 0.0279 | 0.9209 | −0.0791 | 0.3597 | 3.0270 | 0.0270 | 0.0140 | |
| 1000 | 2.0141 | 0.0141 | 0.0135 | 0.9915 | −0.0085 | 0.1742 | 3.0233 | 0.0233 | 0.0138 | |
| 50% | 20 | 2.3193 | 0.3193 | 1.9843 | 1.5387 | 0.5387 | 2.4975 | 3.0267 | 0.0267 | 0.0523 |
| 50 | 2.0939 | 0.0939 | 0.3805 | 1.3016 | 0.3016 | 2.2389 | 3.0220 | 0.0220 | 0.0411 | |
| 200 | 2.0365 | 0.0365 | 0.0790 | 1.1406 | 0.1406 | 1.8872 | 3.0130 | 0.0130 | 0.0167 | |
| 500 | 2.0227 | 0.0227 | 0.0325 | 0.9288 | −0.0712 | 1.4062 | 3.0053 | 0.0053 | 0.0153 | |
| 1000 | 2.0084 | 0.0084 | 0.0149 | 1.0551 | 0.0551 | 0.9191 | 3.0004 | 0.0004 | 0.0150 | |
| AR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Censoring | Mean | Bias | MSE | Mean | Bias | MSE | Mean | Bias | MSE | ||
| 0% | 20 | 1.9973 | −0.0027 | 0.0640 | 0.9986 | −0.0014 | 0.0081 | 2.9879 | −0.0121 | 0.2465 | 0.9861 |
| 50 | 1.9979 | −0.0021 | 0.0637 | 1.0010 | 0.0010 | 0.0081 | 2.9895 | −0.0105 | 0.2444 | 0.9906 | |
| 200 | 2.0017 | 0.0017 | 0.0622 | 1.0008 | 0.0008 | 0.0080 | 2.9929 | −0.0071 | 0.2442 | 0.9948 | |
| 500 | 1.9994 | −0.0006 | 0.0617 | 1.0006 | 0.0006 | 0.0080 | 2.9932 | −0.0068 | 0.2430 | 0.9968 | |
| 1000 | 2.0005 | 0.0005 | 0.0612 | 0.9999 | −0.0001 | 0.0079 | 2.9954 | −0.0046 | 0.2427 | 0.9976 | |
| 10% | 20 | 1.9937 | −0.0063 | 0.0643 | 0.9986 | −0.0014 | 0.0082 | 2.9903 | −0.0097 | 0.2426 | 0.9776 |
| 50 | 1.9969 | −0.0031 | 0.0642 | 0.9989 | −0.0011 | 0.0082 | 2.9909 | −0.0091 | 0.2406 | 0.9827 | |
| 200 | 2.0031 | 0.0031 | 0.0634 | 1.0003 | 0.0003 | 0.0081 | 2.9952 | −0.0048 | 0.2391 | 0.9954 | |
| 500 | 1.9977 | −0.0023 | 0.0627 | 1.0001 | 0.0001 | 0.0080 | 2.9959 | −0.0041 | 0.2388 | 0.9961 | |
| 1000 | 1.9983 | −0.0017 | 0.0625 | 0.9999 | −0.0001 | 0.0080 | 2.9972 | −0.0028 | 0.2370 | 0.9968 | |
| 20% | 20 | 1.9964 | −0.0036 | 0.0631 | 0.9992 | −0.0008 | 0.0082 | 2.9913 | −0.0087 | 0.2451 | 0.9823 |
| 50 | 1.9980 | −0.0020 | 0.0628 | 0.9995 | −0.0005 | 0.0081 | 2.9933 | −0.0067 | 0.2408 | 0.9902 | |
| 200 | 1.998 | −0.002 | 0.0626 | 1.0004 | 0.0004 | 0.008 | 2.9950 | −0.0050 | 0.2404 | 0.9941 | |
| 500 | 1.9979 | −0.0021 | 0.0622 | 1.0001 | 0.0001 | 0.0080 | 3.0038 | 0.0038 | 0.2361 | 0.9956 | |
| 1000 | 2.0001 | 0.0001 | 0.0621 | 1.0000 | 0.0000 | 0.0080 | 3.0017 | 0.0017 | 0.2347 | 0.9965 | |
| 50% | 20 | 1.9939 | −0.0061 | 0.0624 | 0.9976 | −0.0024 | 0.0083 | 2.9773 | −0.0227 | 0.2421 | 0.9745 |
| 50 | 1.9947 | −0.0053 | 0.0630 | 0.9990 | −0.0010 | 0.0082 | 2.9912 | −0.0088 | 0.2413 | 0.983 | |
| 200 | 2.0005 | 0.0005 | 0.0630 | 1.0010 | 0.0010 | 0.0081 | 2.9919 | −0.0081 | 0.2391 | 0.9949 | |
| 500 | 1.9979 | −0.0021 | 0.0629 | 0.9999 | −0.0001 | 0.0079 | 3.0049 | 0.0049 | 0.2386 | 0.9955 | |
| 1000 | 1.998 | −0.002 | 0.0622 | 1.0000 | 0.0000 | 0.0078 | 2.9986 | −0.0014 | 0.2361 | 0.9965 | |
| Parameter | EHM | LHM | WHM | LLHM |
|---|---|---|---|---|
| 0.0092 | 0.0239 | 62.2149 | 0.0170 | |
| 0.0055 | 0.0088 | 143.7017 | 0.0155 | |
| 96.0000 | 30.0000 | 107.9997 | 201.0000 |
| Metrics | EHM | LHM | WHM | LLHM |
|---|---|---|---|---|
| AIC | 684.5601 | 696.1884 | 681.1359 | 677.3659 |
| BIC | 691.5523 | 703.1806 | 688.1281 | 684.3581 |
| -norm | 7.4771 | 16.4211 | 6.4272 | 5.1790 |
| -norm | 1.0032 | 2.0890 | 0.8541 | 0.6724 |
| statistic | 0.2174 | 0.3620 | 0.1810 | 0.1351 |
| test | 2.605 | 11.07 | 1.891 | 1.658 |
| asymptotic p-value | 0.04279 | 0.0000 | 0.1041 | 0.1413 |
| Parameter | EHM | LHM | WHM | LLHM |
|---|---|---|---|---|
| 0.0028 | 0.0066 | 0.01812 | 62.7735 | |
| 0.0004 | 0.0008 | 0.0085 | 232.6557 | |
| 527.0006 | 479.0017 | 534.9997 | 11.0000 |
| Metrics | EHM | LHM | WHM | LLHM |
|---|---|---|---|---|
| AIC | 10,783.44 | 13,692.67 | 12,224.05 | 12,180.56 |
| BIC | 10,798.29 | 13,707.52 | 12,238.9 | 12,195.41 |
| -norm | 71.4478 | 114.0331 | 22.5485 | 11.7279 |
| -norm | 2.7499 | 4.4937 | 0.9709 | 0.4706 |
| statistic | 0.1531 | 0.2586 | 0.0671 | 0.0397 |
| asymptotic p-value | 0.0000 | 0.0000 | 0.0015 | 0.1225 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadar, S.S.; Upadhyay, V.; Joshi, S. Detecting Clinical Risk Shift Through log–logistic Hazard Change-Point Model. Mathematics 2025, 13, 1457. https://doi.org/10.3390/math13091457
Nadar SS, Upadhyay V, Joshi S. Detecting Clinical Risk Shift Through log–logistic Hazard Change-Point Model. Mathematics. 2025; 13(9):1457. https://doi.org/10.3390/math13091457
Chicago/Turabian StyleNadar, Shobhana Selvaraj, Vasudha Upadhyay, and Savitri Joshi. 2025. "Detecting Clinical Risk Shift Through log–logistic Hazard Change-Point Model" Mathematics 13, no. 9: 1457. https://doi.org/10.3390/math13091457
APA StyleNadar, S. S., Upadhyay, V., & Joshi, S. (2025). Detecting Clinical Risk Shift Through log–logistic Hazard Change-Point Model. Mathematics, 13(9), 1457. https://doi.org/10.3390/math13091457






