Abstract
This study utilizes Computational Fluid Dynamics (CFD) to optimize the aerodynamic performance of a Formula 1 (F1) car diffuser, investigating the effects of vane placements, end-flap positions, and other structural modifications. Diffusers are critical in managing airflow, enhancing downforce, and reducing drag, directly influencing vehicle stability and speed. Despite ongoing advancements, the interaction between diffuser designs and turbulent flow dynamics requires further exploration. A Three-Dimensional k-Omega-SST RANS-based CFD methodology was developed to evaluate the aerodynamic performance of various diffuser configurations using Star CCM+. The findings reveal that adding lateral vane parallel to the divergence section improved high-intensity fluid flow distribution within the main channel, achieving 13.49% increment in downforce and 5.58% reduction in drag compared to the baseline simulation. However, incorporating an airfoil cross-section flap parallel to the divergence end significantly enhances the car’s performance, leading to a substantial improvement in downforce while relatively small increase in drag force. This underscores the critical importance of precise flap positioning for optimizing aerodynamic efficiency. Additionally, the influence of adding flaps underneath the divergence section was also analyzed to manipulate boundary layer separation to achieve improved performance by producing additional downforce. This research emphasizes the critical role of vortex management in preventing flow detachment and improving diffuser efficiency. The findings offer valuable insights for potential FIA F1 2023 undertray regulation changes, with implications for faster lap times and heightened competitiveness in motorsports.
Keywords:
computational fluid dynamics (CFD); Formula 1 (F1); fluid–solid interaction (FSI); aerodynamic optimization; F1 diffuser performance MSC:
76G25
1. Introduction
Recent advancements in high-performance computing has enabled F1 teams to aerodynamically enhance their cars without extensive need of wind tunnel testing. In real-world racing scenarios, the aerodynamically designed shape of the vehicle remains a decisive factor in determining overall performance. Furthermore, innovations in aerodynamic design have become pivotal in reducing drag, enhancing downforce, and ensuring vehicle stability at high speeds, emphasizing their critical role in modern motorsport engineering. [1]. In the realm of Formula 1 (F1), aerodynamics plays a crucial role, profoundly impacting a car’s speed, efficiency, and overall competitiveness. The sophisticated interaction of aerodynamic at the front and rear of the vehicle generates downforce, which improves grip, stability, and cornering speed while simultaneously reducing drag and tire wear, ultimately optimizing performance on the track [2,3]. Even a slight improvement in aerodynamic design can significantly influence a car’s performance, making it a vital area of focus for researchers and engineers striving to gain a competitive edge [4].
The aerodynamics performance of F1 cars is meticulously studied through both physical and virtual wind tunnel tests by every F1 car manufacturer in the industry. Computational Fluid Dynamics (CFD) has emerged as a high-fidelity approach, offering high-resolution insights into fluid flow by solving governing fluid flow equations. CFD provides accurate information comparable to expensive experimental testing, including wind tunnel tests [5]. Driven by Formula 1 regulations, budget caps, and FIA restrictions, CFD models have become more prevalent than experimental techniques, serving as a daily tool for aerodynamicists while reserving costly experimental methods for model validation [6].
F1 cars are equipped with various aerodynamic packages to enhance airflow and improve performance. Notably, the undertray or underbody of an F1 car generates approximately half of the overall car’s downforce, making it a crucial component [7]. Additionally, it has been reported that the undertray produces nearly nine times more downforce per unit of drag compared to the rear wings, further emphasizing its significance as a vital part of the aerodynamic package [8]. Despite its importance, undertray optimization has received limited attention. However, in recent years, researchers have focused on optimizing airflow around the car, recognizing the undertray’s vital role in enhancing overall performance and competitiveness.
Cooper et al. [9] conducted a wind tunnel test and CFD studies to investigate the aerodynamic contribution and flow physics of various diffuser components, examining the impact of ground clearance on diffuser performance. This study laid the foundation for understanding diffuser performance using a simplified Ahmed body. Additionally, Cooper et al. [10] proposed an analytical model to estimate the optimal length-to-area ratio for integrating a diffuser into a flat-bottomed car. Desai et al. [11] expanded on Cooper et al.’s [10] work by incorporating the wheel into their Ahmed body model and redefining the analytical framework. They investigated the behavior of the vortex generated by the tire when its position was varied, as well as its influence on the overall performance of the Ahmed body. Additionally, Khalighi et al. [12] conducted CFD and experimental studies on understanding the aerodynamic contribution of the undertray in downforce generation using a simplified Ahmed body.
Breslouer and George [13] conducted an aerodynamic study of Venturi-shaped diffusers using 0° and 9° diffuser angles on an Ahmed body, examining the effects of varying ground heights. Their results showed that diffusers with higher angles of attack outperformed those with lower angles. They also observed that the formation of longitudinal vortices at the rear end of the diffuser channel intensified with increasing angles of attack due to fluid flow separation but dissipated at higher ground clearance. Huminic et al. [14] demonstrated that a venturi-shaped diffuser in a simplified Ahmed body effectively reduces drag force and generates downforce. Katz [15] explained the role of diffusers in generating downforce and reducing drag. He provided intricate details about diffuser design, including optimal convergence and divergence surfaces, taper, and exit area, which are crucial for achieving optimal performance in F1 cars. Katz concluded that smoother fluid flow under the car could significantly reduce overall drag. Furthermore, he investigated vertical flaps and end plates on diffusers, finding that they reduce vortices at the exit, highlighting the importance of balanced design to achieve maximum performance. Toet [2] emphasized that the use of aerodynamically optimized shapes in F1 cars could be a new design solution and innovation for achieving maximum performance. Unni [16] emphasized the use of flaps in the rear of the diffuser without considering the tire geometry using CFD. However, Ehirim et al. [17] investigated the impact of adding flaps beneath the rear end of the diffuser on a simplified Ahmed body, while also analyzing the effects of increasing the expansion length and height. Similarly, Tian et al. [18] performed aerodynamic studies on the bus diffuser by varying the diffuser angle and channel numbers to reduce drag force.
Other studies, such as Asgar et al. [19], utilized CFD to simulate airflow around an F1 car’s undertray diffuser, investigating its aerodynamic performance by varying the pitch angle, height, and length. Their analysis employed a simplified diffuser geometry, excluding the car and tire geometry. Bhardwaj [20] also conducted similar studies to study the impact of ground effect diffusers on the aerodynamic performance of an Ahmed body using CFD. Chandra [21] utilized CFD to perform aerodynamic studies for the PACE F1 car, incorporating the effects of ground clearance, ride height, and diffuser geometry. Guerrero et al. [22] analyzed the wake effects on the F1 car bluff body and examined the effect of diffuser design on wake patterns, turbulence, and overall efficiency. Tohpati [23] studied the aerodynamics of the undertray on a Formula Student car using 2D and 3D CFD models, emphasizing the role of effective flow control through vortex generation to maintain flow attachment on the undertray walls, thereby enhancing downforce and reducing drag.
Based on the abovementioned studies [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23], it is evident that research on optimizing undertray diffusers for F1 cars is still in its nascent stages, particularly with regard to the ground effect under diverse aerodynamic configurations. Previous studies [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] have predominantly concentrated on simplified models, such as standalone undertrays, Formula Student/F1 car models, or Ahmed bodies, often neglecting the comprehensive dynamics of real-world scenarios. Moreover, these investigations have typically analyzed the effects of individual design parameters on diffuser performance, leaving the interaction and combined effects of multiple parameters largely unexplored. This limitation arises from the complexity of the problem, which demands sophisticated 3D CFD modeling and precise CAD models incorporating accurate turbulence physics to effectively study the aerodynamics. To overcome these challenges, it is essential to evaluate multiple design parameters simultaneously to identify the optimal combination for maximizing diffuser performance.
The primary objective of this research is to establish future regulatory guidelines for modifying the existing FIA Formula 1 2023 diffuser in compliance with FIA technical regulations to enhance the F1 car performance using Computational Fluid Dynamics (CFD). In this study, a robust 3D steady-state Reynolds-Averaged Navier–Stokes (RANS) CFD model has been set up to evaluate the performance of modified and baseline FIA F1 cars diffuser using Star CCM+. Performance sensitivity studies have been conducted by introducing lateral vanes parallel to the divergence wall, adding additional flaps beneath the divergence section, and increasing the number of flaps, along with testing various combinations of these modifications to achieve targeted improvements in overall F1 car performance.
This research addresses existing gaps in the study of undertray diffusers by providing a comprehensive analysis of the combined effects of multiple design parameters. The findings will offer valuable insights into diffuser optimization, serving as a foundation for future design strategies aimed at enhancing F1 car aerodynamics. The proposed guidelines will inspire race car designers and engineers to adopt innovative approaches to optimizing F1 performance through refined diffuser designs. By advancing the understanding of undertray diffuser dynamics, this work contributes to the ongoing evolution of Formula 1 technology, paving the way for faster, more efficient, and more competitive racing vehicles.
2. Materials and Methods
2.1. Governing Equations
In aerodynamic simulations of Formula 1 cars, Computational Fluid Dynamics (CFD) modeling relies on the governing equation for incompressible and isothermal fluid flow, which encompass the conservation of mass and momentum. These equations, collectively known as the incompressible Navier–Stokes (N-S) equations [24], provide a mathematical framework for describing fluid motion under the assumptions of incompressibility and negligible temperature gradients.
Additionally, to model the fluid–solid interaction (FSI) between the airflow and the diffuser structure, the conservation of displacement and stress tensors is considered. These principles are integral in fluid–structure interaction problems, where the mechanical behavior of the solid body is coupled with the fluid dynamics. The governing equations are thus extended as follows:
- Continuity Equation (Mass Conservation):
- Momentum Equation (Navier–Stokes):
To model the interaction between the fluid and the solid body (the diffuser), we use the conservation of displacement and stress tensors in the solid phase [27]. The stress tensor in the solid phase is defined as follows:
where is the stress tensor, is the displacement filed, is the pressure, and I is the identity matrix.
To solve these equations, a Finite Volume Method (FVM)-based numerical solver is employed, which discretizes the flow domain into control volumes. The governing equations are then solved iteratively over these volumes, using appropriate initial and boundary conditions to ensure numerical stability and convergence. These equations are solved behind the GUI of the Star CCM+ (Version 2023) software program commonly used for industrial CFD calculation.
2.2. Geometry
The baseline three-dimensional geometry was modeled using SolidWorks Premium (2023-2024) (a well-renowned commercial CAD and CAE package) based on FIA Formula 1 Technical Regulations [28]. Article 3.5 and RV-Floor-body were referenced when defining the maximum design volume of the floor for designing the undertray bottom surface [29]. The geometry was designed in accordance with the FIA standard procedures and guidelines. Figure 1 illustrates the modeled diffuser, which comprises six primary zones aligned with Article 3.5 of the FIA Technical Regulations [28]. These zones include the central and outer channels for airflow acceleration, side strakes to manage separation, Gurney flaps for pressure recovery, an upward ramp for expansion, and the transition zone interacting with the rear wing, all contributing to optimal aerodynamic efficiency [29].
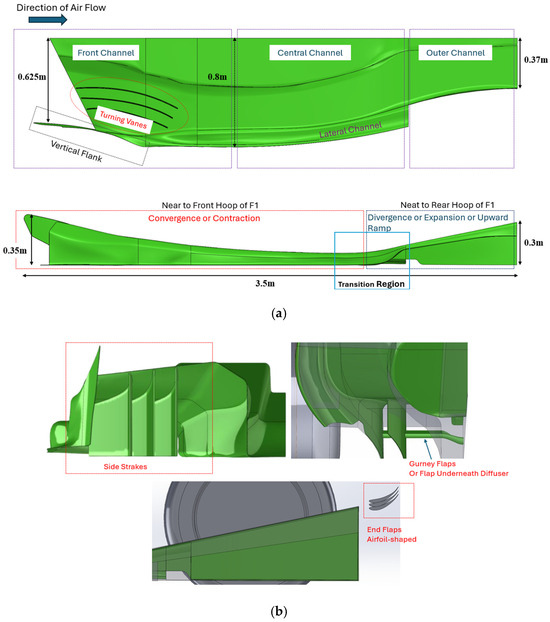
Figure 1.
Illustration of the modeled diffuser geometry, highlighting various structural components of the underbody with labeled dimensions: (a) outer, central, and front channel zones, lateral zone, vertical flank, turning or guiding vanes, contraction zone, and expansion zone; (b) side strakes, Gurney flaps or flaps beneath the diffuser, and the end-flaps with an airfoil shape.
The geometry was modeled using various advanced features available in SolidWorks. Smooth curves were generated through the surface loft feature, employing multiple surfaces across defined planes. To ensure continuity and smoothness during the lofting process, 3D spline curves were used to create the required sketches with high precision. Following the creation of the lofted surface, the “surface thicken” feature was applied to generate the solid bluff body, accurately representing the complete undertray structure of the F1 car.
The baseline diffuser model consists of a primary convergent/divergent channel, three strakes, and a fence, as shown in Figure 1 and Figure 2. The strakes and fence are specifically designed to isolate and redirect high-speed turbulent flow from the tire wake into the lateral channels, while guiding high-density flow away from the main channel. The design intent is to accelerate the flow within the Venturi tube-like section and subsequently decelerate it in the divergent section until it aligns with the free stream velocity. Plank location and gearbox geometry were not taken into consideration while modeling this undertray geometry.
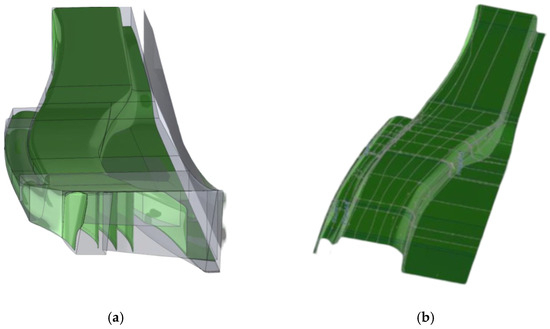
Figure 2.
Illustration of the modeled undertray with diffuser: (a) showing lateral vanes, and (b) rear view of the diffuser section.
2.3. Modifications in Diffuser Design
A total of six case studies have been investigated in this research on F1 diffuser optimization. Based on these studies, several modifications were made to the baseline geometry model, as shown and listed in below Table 1:

Table 1.
Case studies or modifications to our baseline diffuser model that were used in our research.
Table 1.
Case studies or modifications to our baseline diffuser model that were used in our research.
| Case Study | Description | ||
|---|---|---|---|
| CS-1 | Inclusion of lateral flow-guiding vanes in the divergent section (Figure 3a) | ||
| CS-2, 2.2, 2.3 | Addition of cambered airfoil-shaped flaps at the end of the divergent section to increase diffuser length. The end-flap position measure from the diffuser is as follows: | ||
| CS-2.3 | CS-2 | CS-2.2 | |
| Y = 0.32 m, X = 0.07 m | Y = 0.30 m, X = 0.07 m | Y = 0.28 m, X = 0.07 m | |
| CS-3 | Addition of flaps underneath the diffuser section (Figure 4a). | ||
| CS-4 | Combination of lateral vanes beneath the diffuser section (Figure 4b). | ||
| CS-5 | Addition of lateral vanes with slightly longer flaps beneath the diffuser section (Figure 5)—(CS-1 + CS-3). | ||
| CS-6 | Optimal combination from CS-4 and CS-5, incorporating flaps at the rear end of the diffuser section (CS-4 + CS-5 + CS-2). | ||
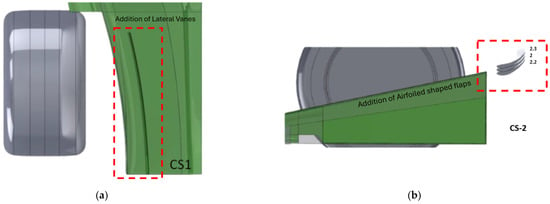
Figure 3.
F1 diffuser section with (a) lateral vanes (CS-1), and (b) airfoil-shaped flaps at the end of diffuser section (CS-2, 2.2, and 2.3).
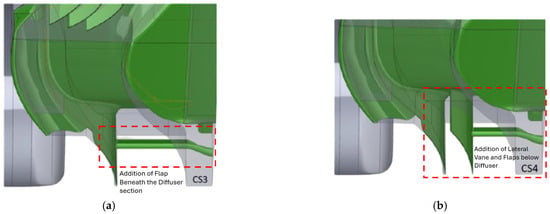
Figure 4.
F1 diffuser section with (a) flaps beneath the diffuser section (CS-3) and (b) combination of lateral vanes and flap below the diffuser section (CS-4).
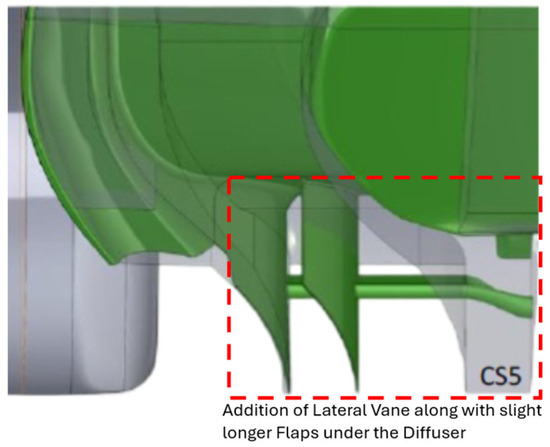
Figure 5.
F1 diffuser section with lateral vanes along with slightly longer flaps beneath the diffuser section.
2.4. CFD Methodology
The methodology used in this research to set up an virtual wind tunnel is based on Computational Fluid Dynamics (CFD), which comprises three main stages, namely Pre-Processing, Solver Setup, and Post-Processing, also illustrated in Figure 6.
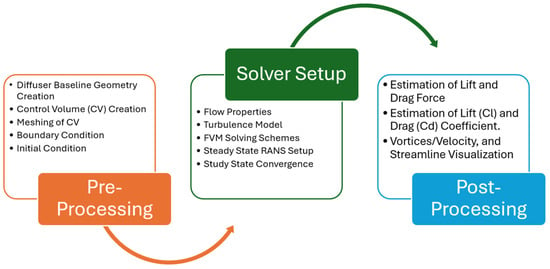
Figure 6.
CFD methodology illustrating the important used for optimizing the diffuser configuration which includes 1. Pre-Processing, 2. Solver Selection, and 3. Post-Processing.
Pre-Processing: The initial stage, a baseline diffuser geometry was modeled using CAD tool in compliance with FIA Formula 1 Technical Regulations. The computational domain or control volume or virtual wind tunnel boundaries was defined to capture the flow physics around the diffuser. The whole domain was discretized using high-quality unstructured meshing techniques, ensuring refinement in critical areas such as the diffuser channels and near-wall regions for accurate resolution of flow gradients using proper Y+ value (always below 1) near walls.
2.4.1. Computational Domain Creation
Due to center-plane symmetry of the undertray, only half the geometry of the undertray, including the tire, was modeled in SolidWorks Premium (2023-2024) to optimize computational resources usage, as discussed in Section 2.2 and Section 2.3. Analyzing the aerodynamics of an F1 car involves addressing fluid–solid interaction challenges, requiring the definition of boundaries for a virtual wind tunnel to study airflow interactions with the car’s solid components. The diffuser geometry, along with the tire, was subtracted from a rectangular computational domain to establish the necessary boundary conditions. To minimize the influence of boundary effects, the domain boundaries were positioned sufficiently far from the diffuser and tires. Furthermore, two local refinement zones were introduced to control mesh element density and accurately capture downstream wake patterns. The dimensions of the computational domain were adopted from the existing literature to ensure alignment with established methodologies [30] (Figure 7).
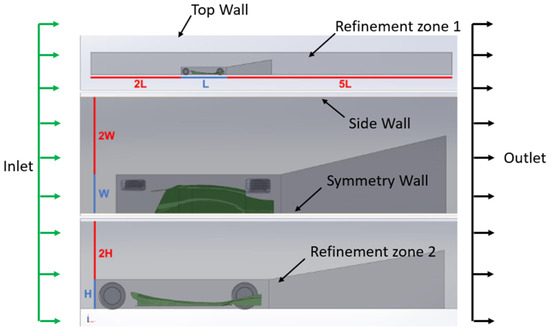
Figure 7.
Computational domain chosen for this CFD aerodynamic analysis of undertray.
2.4.2. Meshing
Numerical discretization, also known as meshing, involves the computational calculation of flow field fluxes using a Finite Volume Method (FVM)-based solver. A k-Omega SST model was employed, which requires low Y+ values (cells near surface walls). To ensure accuracy of fluid flow near the surface boundaries, a total thickness of 1.5 mm, 2 mm, and 3 mm was chosen with 13 inflation layers spread uniformly across the surface of the diffuser, tire, and base model, respectively. This approach maintained a Y+ value less than 1, using the following equation:
where is the first cell layer thickness near the wall in the mesh, x is the distance near wall to first cell layer, is the Reynolds number calculated using Equation (5), is the density of air, V is the velocity of fluid, L is the characteristic length, and is the dynamic viscosity of the fluid.
A polyhedral mesh was generated using Star CCM+ to achieve greater accuracy and a higher cell quality, as it causes less distortion compared to a tetrahedral mesh during 3D meshing. The Figure 8 and Figure 9 below illustrates the mesh used in this study.
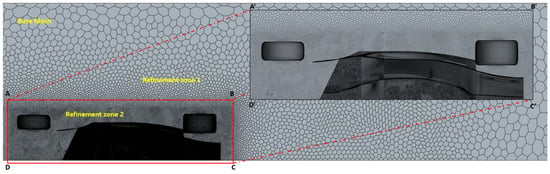
Figure 8.
Meshed computational model from top view representing the polyhedral base mesh, mesh refinement zone 1 and 2.
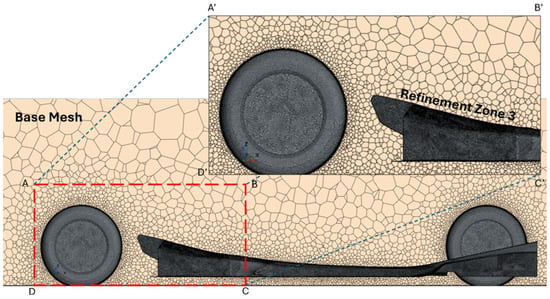
Figure 9.
Meshed computational model from side view considered for this study.
2.4.3. Initial and Boundary Conditions
The initial and boundary conditions are critical for solving complex governing fluid flow equations using Finite Volume Method (FVM) schemes in CFD. These conditions are essential for accurately replicating real-case scenarios and ensuring the validity of the simulation results. Properly defined initial and boundary conditions enable the model to closely mimic the actual airflow behavior around the undertray, providing reliable data for optimizing the diffuser’s aerodynamic performance. In this research, the properties of incompressible air were considered as the working fluid.
A velocity inlet condition was assigned to the inlet patch with a wind velocity of 50 m/s, a turbulent dissipation rate of 1.53 1/s, and a turbulent kinetic energy of 0.375 J/kg. No-slip conditions were applied to the diffuser, tire, and bottom ground walls. The top, side (left and right), and symmetry wall were assigned slip and symmetry boundary conditions, respectively. To mimic the moving tire physics, the bottom wall was configured as a moving boundary. A Multiple Reference Frame (MRF) approach was used to rotate the tires in the steady-state simulation by assigning an angular velocity of 218.723 rad/s. Outlet was assigned to zero atmospheric pressure outlet boundary condition. The Table 2 below provides other important specifications used for different boundaries:

Table 2.
Boundary condition specification for inlet, ground diffuser, and tire patch.
Solver Setup: A steady-state approach was used to evaluate the performance of F1 car’s diffuser based on the Reynolds-Averaged Navier–Stokes (RANS) equations solved via the Finite Volume Method (FVM). Key flow properties such as air density, viscosity, and inlet velocity were defined, along with an appropriate turbulence model, i.e., k−ω SST model (used in this study), to accurately capture boundary layer separation and vortex dynamics. Boundary conditions, including velocity inlets, pressure outlets, and no-slip walls, were applied similar to physical wind tunnel conditions. Solution convergence was closely monitored through residuals and force coefficients to ensure numerical stability and reliability.
2.4.4. Turbulent Solver and Solving Schemes
Equations (1) and (2) represent the continuity and momentum equations, respectively. To incorporate turbulence effects, the Reynolds-Averaged Navier–Stokes (RANS) equations are utilized. This method involves decomposing the instantaneous velocity into mean and fluctuating components, followed by taking the time average. The RANS equations, which effectively model the turbulence phenomena, are presented as follows:
where i and j are the position indices. The Reynolds stress term is represented by and is modeled using the eddy viscosity approach [24]. This is followed by the application of the Shear Stress Transport (SST) k-ω model, which accurately captures the boundary layer physics necessary for the correct simulation of turbulent flow behavior, adapted from the literature [31].
The turbulent nature of the wind was defined using the turbulence intensity () and the turbulence length scale (; L is the characteristics length), which were set to 0.0208 and 0.28, respectively. Steady-state simulation with K-Omega SST solver was deployed in this study. The k and Omega coefficient required for this model are computed using the following expression:
where U is the mean velocity of the flow, is the turbulence intensity, and is the length scale. A residual convergence criterion of 1 × 10−5 was established to minimize the imbalance between coefficients and to achieve higher accuracy. Lift and drag coefficients were assessed for each structural member for the baseline geometry of the diffuser. Subsequently, optimization was carried out based on modifications to the geometry.
Post-Processing: The lift and drag coefficients was evaluated for the diffuser. Advanced flow visualizations, including vortices, streamlines, and pressure distributions, were generated to analyze the flow behavior and assess the diffuser’s performance. These insights were used to refine and optimize the diffuser design.
This methodology was implemented to achieve a comprehensive evaluation and optimization of the diffuser, ensuring an optimal balance between aerodynamic lift and drag, contributing to improved performance in compliance with FIA technical standards.
3. Results
3.1. Mesh Sensitivity Study
A grid sensitivity analysis was conducted to achieve higher accuracy of aerodynamic force by maintaining a sufficient number of elements in the CFD model while using optimum computational resources. Five different meshes were generated, and the aerodynamic performance of the baseline undertray model with diffuser and tire geometry was measured. The meshing parameters were set with element sizes of 250 mm for the external flow domain, 100 mm for the wake region, 20 mm for the vehicle surface, and 10 mm for the tires.
A mesh independence study for the diffuser region was conducted using five progressively refined base mesh sizes: 10 mm, 7 mm, 5 mm, 4 mm, and 3 mm. The results, summarized in Table 3, reveals that the mesh with 4 mm grid size on the diffuser, comprising approximately 8.25 million cells, produced results nearly identical to the highly refined 3 mm mesh. Importantly, the 4 mm mesh achieved good accuracy in aerodynamic force predictions, i.e., drag force, while reducing computational time by 50%, as illustrated in Figure 10.

Table 3.
Diffuser’s grid sensitivity test results for five different mesh qualities obtained using CFD.
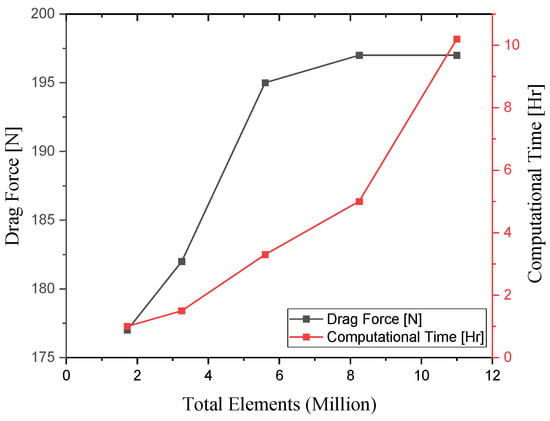
Figure 10.
Results obtained using mesh independent study illustrating the drag produced on refining the mesh and the computational time used for five different mesh qualities.
Based on these findings, the 4 mm base mesh was selected as the optimal configuration for subsequent simulations, balancing accuracy and computational resources (cost wise). It was also ensured that the Y+ values near the walls were adjusted below 1, as required for capturing turbulence flow physics. Figure 11 illustrates the Y+ values maintained along the length of the underbody for various structural components in our simulation, including the diffuser, front tire, rear tire, and floor. It demonstrates that Y+ values below 1 are achieved, ensuring accurate analysis of the aerodynamic properties of all components. These simulations were run on a standalone computer with the following specifications: Intel® Core™ i7-14700 processor, featuring 20 physical cores and 28 logical cores with a base clock speed of 2.10 GHz; 32 GB of RAM; and an NVIDIA GeForce RTX 4060 GPU. The simulation times were recorded accordingly.
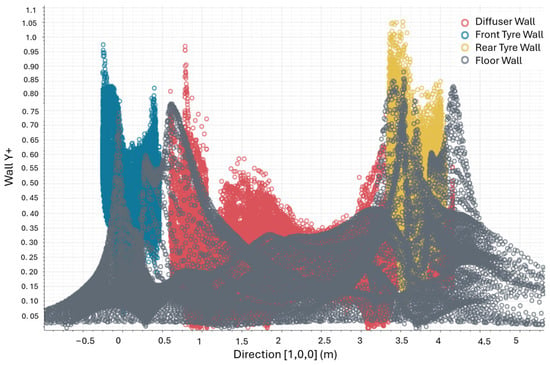
Figure 11.
Distribution of Y+ along the length of diffuser showing Local Y+ values maintained at wall less than 1 for front and rear tire, diffuser, and floor wall.
3.2. CFD Simulation Results
The aerodynamic performance of the diffuser, characterized by the coefficients of lift and drag, was evaluated using Computational Fluid Dynamics (CFD). Optimization studies were conducted on the baseline model by analyzing the effects of incorporating lateral vanes, flaps at the end section, and flaps beneath the diffuser section. Various other configurations were also examined. Although the geometric model encompasses the entire length of the floor as defined by the FIS regulations, the study focused on analyzing and enhancing the performance of the divergent section, commonly referred to as the diffuser.
3.2.1. Case Study 1 (CS-1): Influence of Lateral Vanes on Aerodynamic Performance
The results indicate that adding lateral vanes parallel to the divergence section of the diffuser significantly improves the car’s aerodynamic performance. Specifically, the addition of these vanes in diffuser results in a 13.49% increase in downforce, along with a 5.58% reduction in drag compared to baseline model, listed in Table 4. It was also observed that a small increment in downforce of 6.75% was generated on the rear tires walls; however, the drag remained the same on the front tire. Downforce refers to the negative lift force generated when the coefficient of lift becomes negative, commonly observed in aerodynamic simulations, particularly in vehicle dynamics.

Table 4.
Undertray’s aerodynamic performance on adding lateral vanes.
The velocity and vorticity contours demonstrate that the addition of lateral vanes effectively mitigates the intrusion of turbulent flow into the main divergent channel, caused by the aerodynamic influence of open rotating tires. While the vanes do not entirely redirect the turbulent wake into the lateral channel, they significantly attenuate the turbulent flow entering the primary diffuser region. This reduction in turbulence enhances the flow quality within the main channel, improving its aerodynamic efficiency, as shown below in Figure 12 and Figure 13.
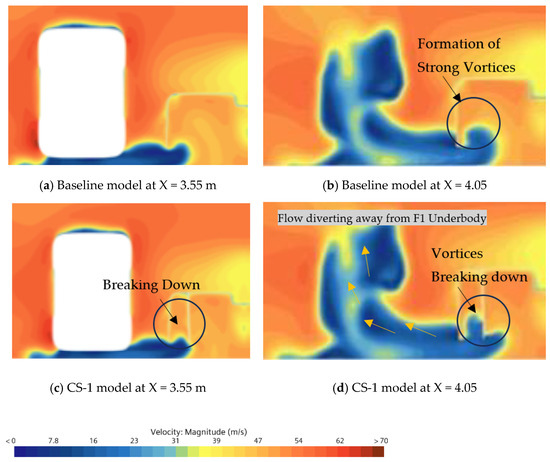
Figure 12.
Velocity contour comparison between Case Study 1 (c,d) with baseline model (a,b) at two different cut planes, X = 3.55 m (a,c) near front tire and X = 4.05 m (b,d) at rear side of front tire, showing breakdown of vortices and flow diverting away from F1 diffuser.
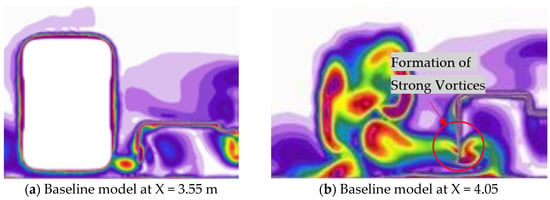
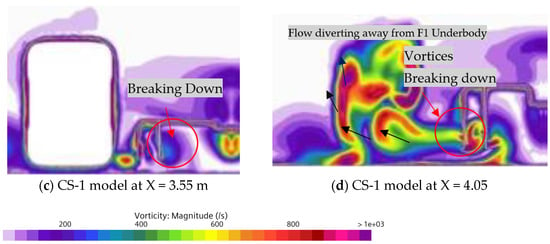
Figure 13.
Vorticity contour comparison between Case Study 1 (c,d) with baseline model (a,b) at two different cut planes, X = 3.55 m (a,c) near front tire and X = 4.05 m (b,d) at rear side of front tire, showing breakdown of vortices and flow diverting away from F1 diffuser.
Figure 12a,c compare the velocity contour our baseline model with CS-1 at X = 3.55 m, showing that the breakdown of vortices starts at the front tire, resulting in a slight reduction in drag force by 0.23% (see Table 4). However, with the addition of a single lateral vane, we observe a breakdown of vortices caused by the vane wall and incoming flow, leading to a 13.49% increase in downforce on the rear tire (see Table 4), as shown in Figure 12b,d. Due to the vane outward position, the flow is redirected away from the F1 car, highlighting the importance of using an undertray to optimize aerodynamic performance. Similar information is shown by vorticity contour in Figure 13.
3.2.2. Case Study 2 (CS-2): Influence of Varying End-Flap Height on Aerodynamic Performance
The influence of varying end-flap heights on aerodynamic performance was analyzed using a cambered airfoil with a chord length of 10 cm. Table 1 (See Section 2.3) and Figure 3b show the structural information and position of CS-2, 2.3, and 2.3. The findings indicate that incorporating a cambered airfoil significantly enhances the diffuser’s downforce. Positioning the flap at the end of the diffuser was found to be beneficial for achieving optimal aerodynamic performance.
The results demonstrate that increasing the height of the end-flap substantially improves downforce but also leads to a significant rise in drag force. Specifically, downforce increments of 21.83%, 20.53%, and 20.93% were observed for Case Studies 2, 2.3, and 2.3, respectively, with corresponding drag increases of 77.4%, 75.34%, and 72% compared to the baseline model, as shown in Table 5. Additionally, the flaps alone generated over 80 N of downforce, as listed in Table 6. The drag has increased but there is a possibility to explore this configuration in the context of considering its interaction with other vehicle components. The study showed that low velocities were observed on the upper section of the diffuser, while higher velocities and lower pressure values were noted on the suction side of the airfoil and diffuser, contributing to the generation of downforce, as illustrated in Figure 14. The low-pressure region on the flap’s suction side plays a crucial role in preventing flow detachment, thereby enhancing the undertray’s downforce performance. Additionally, the presence of the flap at the diffuser’s expansion aids in re-energizing the flow due to the suction effect created by the flap.

Table 5.
Undertray’s aerodynamic performance on varying the diffuser height.

Table 6.
Aerodynamic performance of end-flap.
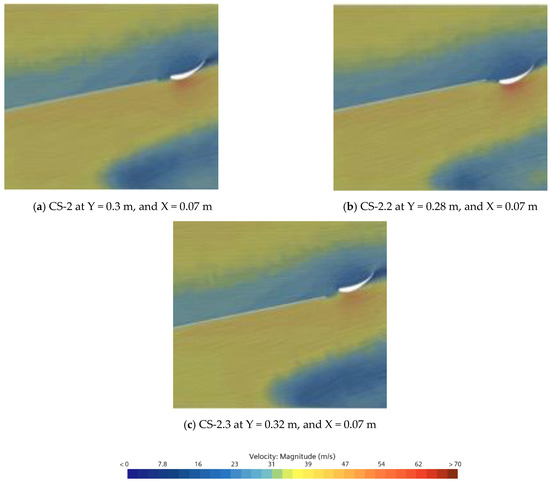
Figure 14.
Velocity contour showing flow physics variation on varying end-flap height, (a) CS-2, (b) CS-2.2, and (c) CS-2.3.
Increasing the end-flap height further improves downforce, which is essential for vehicle stability and handling, especially at high speeds. However, the corresponding rise in drag force highlights a trade-off, potentially impacting the vehicle’s overall aerodynamic efficiency and fuel consumption.
Optimizing the height and shape of the end-flap is therefore crucial to achieving a balance between enhanced downforce and reduced drag in Formula 1 aerodynamic design.
3.2.3. Case Study 3 (CS-3): Influence of Adding Flap Underneath the Diffuser
The impact of integrating cambered airfoil-shaped flaps of chord length 10 cm beneath the diffuser section on the aerodynamic performance of a Formula 1 car was also examined. Refer to Table 1 and Figure 4a for the structural information on CS3. This approach was adopted to mitigate the drag increase observed in previous cases where flaps were in direct contact with the free-stream flow. Positioning the flaps underneath the diffuser expansion allowed for more realistic results and facilitated the study of flow interaction with the ground.
The research findings demonstrate a significant improvement in aerodynamic performance at the rear section of the car, coupled with a substantial reduction in drag force. Specifically, adding flaps beneath the diffuser resulted in a 6.6% increase in downforce and a remarkable 44.45% reduction in drag, as detailed in Table 7. Additionally, the velocity contour revealed that the addition of flaps beneath the diffuser, with the central and lateral section precisely aligned with the inlet streamlines, exhibited minimal flow detachment near the trailing edge, also shown in Figure 15. This optimal alignment enabled a smoother flow regime, further enhancing aerodynamic performance.

Table 7.
Undertray’s aerodynamic performance on adding flaps underneath the diffuser.
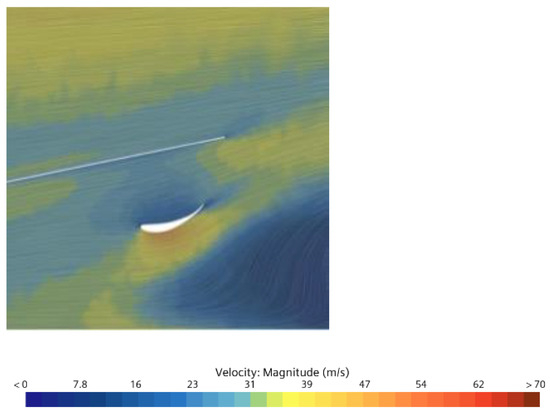
Figure 15.
Velocity contour showing influence of adding flap underneath diffuser on aerodynamic performance (CS-3).
From the flow structure perspective, the addition of this flap reduces the performance of the expansion at its exit zone due to an increase in high pressure on the pressure side of the flap. However, this loss is offset by the overall performance improvements introduced by the additional flap.
3.2.4. Case Study 4, 5, and 6 (CS-4, 5, 6): Influence on Performance on Adding Additional Structural Member Spontaneously
The effect of combining other structural features discussed in Section 3.2.1, Section 3.2.2 and Section 3.2.3 aimed to achieve better aerodynamic performance was also investigated in this research. Three different configurations were tested, namely CS-4, CS-5, and CS-6 (refer to Table 1 for design information).
The CS-4 and CS-5 configurations exhibited the lowest performance due to the poor fluid–solid interaction between the divergence and each flap, which resulted in more drag and caused a reduction in the performance of the diffuser (also illustrated in Figure 16a,b). In contrast, adding a flap in the lateral channel of the diffuser resulted in the production of additional downforce, while also creating a low-velocity zone (high pressure zone), leading to higher drag values. Furthermore, a significant changes were observed in flow field were observed due to the placement of an airfoiled cross-sectioned flap causing a suction effect creating this additional downforce.
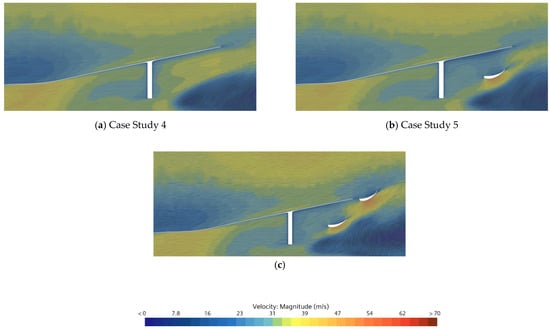
Figure 16.
Velocity contour representing flow around diffuser on adding different structural features, representing (a) Case Study 4, (b) Case Study 5, and (c) Case Study 6.
Incorporating double flaps, as illustrated in Figure 16 for the CS-6 configuration, resulted in significant performance improvements. This enhancement was attributed to the combined effect of both flaps, which increased the downforce while reducing the drag through their integrated geometrical design. This was also observed in CS-3, the configuration that improved the divergent exit section by enhancing suction through flow re-energization caused by the introduction of the flap. Furthermore, the presence of the lateral vane effectively organized the flow structures, as expected, isolating the turbulent wake from the rotating tire within the lateral channel.
A 200% enhancement in downforce was attained using the double flaps and a vertical vane in the diffuser design (CS-6); however, there was also a slight increase in drag by 60%, also listed in Table 8. The drag increase was expected due to the added elements creating more complex flow structures. However, the overall performance gains justify this trade-off. These findings underscore the importance of optimizing the structural features of diffusers to achieve a balance between downforce and drag, ultimately enhancing the overall aerodynamic performance.

Table 8.
Undertray’s aerodynamic performance after adding a combination of structural features.
Figure 17 presents the velocity contours from front plane at a X = 3.355 m, X = 4.05 m, and X = 4.25 m, illustrating the transversal velocity flow for the baseline geometry and the CS-5 and CS-6 diffuser designs configuration. A comparative analysis of Figure 17b,c reveals that the addition of extra flaps and vertical vanes effectively isolates the fluid flow away from the main channel, thereby mitigating interference effects on the floor flow structures. Moreover, the airfoil flaps provide supplementary downforce to the undertray, consequently enhancing the overall aerodynamic efficiency of the vehicle. This finding underscores the potential of diffuser design optimization to improve vehicle performance.
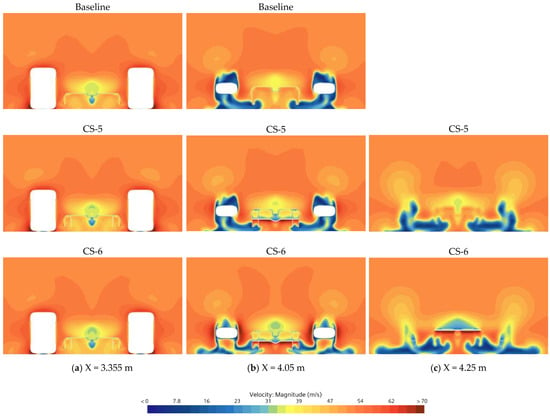
Figure 17.
Velocity contours at (a) X = 3.355 m, (b) X = 4.05 m, and (c) X = 4.25 m, illustrating the flow around the diffuser with added structural features, comparing the baseline model with the CS-5 and CS-6 designs.
3.2.5. Performance Comparison
The research findings concluded that the diffuser configuration with a vertical element and two flaps—one positioned underneath the diffuser and the other near the tail—corresponding to Case Study 6, delivered the best performance, as shown in Figure 18. Across the length of the floor, the downforce was observed to increase, while drag was significantly reduced, making this design the most efficient, as highlighted in Figure 19. Case Studies 2, 2.2, and 2.3 also demonstrated improvements in downforce and undertray performance. In contrast, Case Study Design 4, which incorporated only a vertical element, exhibited the poorest performance, represented in Figure 19 and Figure 20. Case Study Design 5 also produced a significant increase in downforce across the length of the undertray, as shown in Figure 19a.
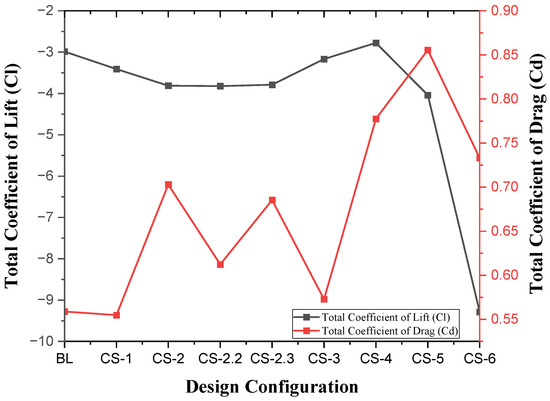
Figure 18.
Influence of adding structural features on the overall diffuser performance, i.e., lift and drag coefficient.
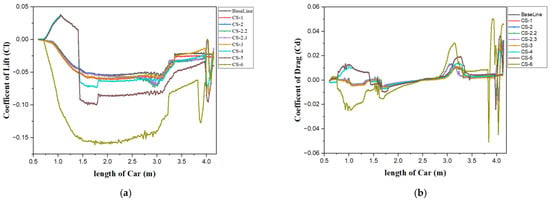
Figure 19.
Local variation in (a) lift and (b) drag coefficient across the length of floor for different design modifications studied in this research.
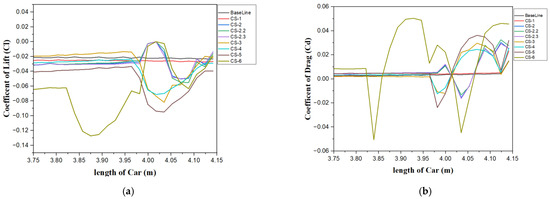
Figure 20.
Local variation in (a) lift (downforce) and (b) drag across the length of floor for different design modifications studied in this research.
Case Study Design 6 achieved a significantly higher downforce-to-drag ratio, underscoring the importance of these structural modifications. If adopted, these enhancements could greatly improve the aerodynamic efficiency, stability, and handling of F1 cars during competitions.
In the diffuser section, CS-6 generates the highest downforce; however, it also results in greater drag. The smallest improvement in downforce performance was observed in CS-1. CS-5 and CS-6 modifications were found to be the most effective diffuser modifications, as shown in Figure 20. Figure 20a clearly shows the interaction between various modifications, especially visible for CS-5 and CS-6.
4. Conclusions
This research demonstrates the significant potential of structural modifications to enhance the aerodynamic performance of Formula 1 (F1) car diffusers, focusing on configurations such as lateral vanes, end-flaps, and flaps beneath the diffuser section. The results highlight that the Case Study 6 (CS-6) configuration, which incorporates a vertical element and two strategically positioned flaps, achieved the best overall performance. This design produced a remarkable improvement in downforce while maintaining a reasonable trade-off with increased drag, essential for vehicle stability and handling at high speeds.
The study also emphasizes the critical role of vortex management and flow re-energization in optimizing diffuser performance. For instance, lateral vanes reduced turbulent wakes from rotating tires, while flaps strategically aligned with the flow streamlines minimized flow detachment and enhanced aerodynamic efficiency. These findings underscore the importance of balancing design elements to achieve optimal downforce-to-drag ratios.
Future work could focus on further exploring the interaction between diffusers and other aerodynamic components, such as underbody panels and rear wings, to achieve holistic aerodynamic optimization. Investigating the dynamic effects of structural changes during real-world racing conditions, including transient flow phenomena and multi-vehicle interactions, would also provide deeper insights. Leveraging CFD for the full car model and incorporating symmetric boundary conditions could enhance the accuracy of predictions, providing deeper insights into aerodynamic performance and guiding the development of next-generation F1 designs.
This research contributes valuable guidelines for diffuser optimization in compliance with FIA regulations, paving the way for more efficient, stable, and competitive F1 cars.
Author Contributions
E.P.N.: Investigation, Methodology, Software, Validation, Writing—original draft, Writing—review and editing. A.G.: Writing—review and editing M.M.: Conceptualization, Project administration, Supervision, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Oxford Brookes University, Oxford, United Kingdom.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors acknowledge the support of the research computing facilities at Oxford Brookes University, Oxford, United Kingdom, for CFD simulations and licensing is also secured by them.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nath, D.S.; Pujari, P.C.; Jain, A.; Rastogi, V. Drag reduction by application of aerodynamic devices in a race car. Adv. Aerodyn. 2021, 3, 1–20. [Google Scholar] [CrossRef]
- Toet, W. Aerodynamics and aerodynamic research in Formula 1. Aeronaut. J. 2013, 117, 1–26. [Google Scholar] [CrossRef]
- Aerodynamics in F1 | RacingNews365. Available online: https://racingnews365.com/aerodynamics-f1 (accessed on 28 July 2024).
- Aerodynamics in Formula 1: The Key to Speed and Performance by Raptor Sport Medium. Available online: https://medium.com/@raptorf1sport/aerodynamics-in-formula-1-the-key-to-speed-and-performance-9fe269cd81c9 (accessed on 28 July 2024).
- Ogawa, A.; Mashio, S.; Nakamura, D.; Masumitsu, Y.; Minagawa, M.; Nakai, Y. Aerodynamics Analysis of Formula One Vehicles. In Development Methodologies for Formula One Aerodynamics; Honda R&D Co., Ltd.: Haga, Japan, 2009. [Google Scholar]
- Driven by Simulation, a Regulations Overhaul Promises a New Era of Racing in Formula 1. Available online: https://mobile.engineering.com/amp/23449.html. (accessed on 28 July 2024).
- Poutiainen, A. Undertray Design and Development Procedure with CFD an Optimization Study of Different Undertray Designs with CFD Computations. Master’s Thesis, KTH, School of Engineering Sciences, Stockholm, Sweden, 2021. [Google Scholar]
- Aerodynamics Focus: The Undertray—Monash Motorsport. Available online: https://www.monashmotorsport.com/blog/aerodynamics-focus-the-undertray (accessed on 17 December 2024).
- Cooper, K.R.; Bertenyi, T.; Dutil, G.; Syms, J.; Sovran, G. The Aerodynamic Performance of Automotive Underbody Diffusers. SAE Tech. Pap. 1998, 107, 150–179. [Google Scholar] [CrossRef]
- Cooper, K.R.; Syms, J.; Sovran, G.; Cooper, K.R.; Syms, J.; Sovran, G. Selecting Automotive Diffusers to Maximise Underbody Downforce. SAE Tech. Pap. 2000, 109, 497–512. [Google Scholar] [CrossRef]
- Desai, S.S.; Lo, C.M.B.; George, A.R. A Computational Study of Idealized Bluff Bodies, Wheels, and Vortex Structures in Ground Effect. SAE Tech. 2008, 1, 0327. [Google Scholar] [CrossRef]
- Khalighi, B.; Zhang, S.; Koromilas, C.; Balkanyi, S.R.; Bernal, L.P.; Laccarino, G.; Moin, P. Experimental and Computational Study of Unsteady Wake Flow Behind a Bluff Body with a Drag Reduction Device. SAE Tech. Pap. 2001, 110, 1209–1222. [Google Scholar] [CrossRef]
- Breslouer, O.J.; George, A.R.; Breslouer, O.J.; George, A.R. Exploratory Experimental Studies of Forces and Flow Structure on a Bluff Body with Variable Diffuser and Wheel Configurations. SAE Tech. Pap. 2008, 1, 0326. [Google Scholar] [CrossRef]
- Huminic, A.; Huminic, G. Computational Study of Flow in the Underbody Diffuser for a Simplified Car Model. SAE Tech. Pap. 2010, 1, 0119. [Google Scholar] [CrossRef]
- Katz, J. Aerodynamics of race cars. Annu. Rev. Fluid. Mech. 2006, 38, 27–63. [Google Scholar] [CrossRef]
- Unni, T.P.A. Numerical Investigation on Aerodynamic Effects of Vanes and Flaps on Automotive Underbody Diffusers. SAE Tech. Pap. 2017, 1, 2163. [Google Scholar] [CrossRef]
- Ehirim, O.; Knowles, K.; Saddington, A.; Finnis, M. Passive Flow Control on a Ground-Effect Diffuser Using an Inverted Wing. SAE Int. J. Passeng. Cars-Mech. Syst. 2018, 11, 273–296. [Google Scholar] [CrossRef]
- Tian, J.; Liu, X.; Zhang, Y.; Chen, Q. Numerical Analysis of Underbody Diffusers with Different Angles and Channels. SAE Tech. Pap. 2019. [CrossRef]
- Asgar, A.; Khokhar, S.; Shirolkar, S.S. Design and Analysis of Undertray Diffuser For a Formula Style Racecar. Int. J. Res. Eng. Technol. 2015, 04, 202–210. [Google Scholar] [CrossRef]
- Bhardwaj, A. Analysis of Ground Effect Diffuser on a Race Car to Optimize Aerodynamic Performance. Int. J. Innov. Sci. Res. Technol. 2021. Available online: www.ijisrt.com (accessed on 29 July 2024).
- Chandra, S. CFD Analysis of PACE Formula-1 Car. Comput. Aided Des. Appl. 2011, 8, 1–14. [Google Scholar] [CrossRef]
- Guerrero, A.; Castilla, R. Aerodynamic Study of the Wake Effects on a Formula 1 Car. Energies 2020, 13, 5183. [Google Scholar] [CrossRef]
- (PDF) Design and Manufacture of an Aerodynamic Undertray for Formula Student. Available online: https://www.researchgate.net/publication/350639990_Design_and_Manufacture_of_an_Aerodynamic_Undertray_for_Formula_Student (accessed on 21 December 2024).
- Gupta, A.; Abderrahmane, H.A.; Janajreh, I. Flow analysis and sensitivity study of vertical-axis wind turbine under variable pitching. Appl. Energy 2024, 358, 122648. [Google Scholar] [CrossRef]
- (PDF) Flow Around a Cylinder: A Comparative Study of Immersed Boundary and Arbitrary Lagrangian-Eulerian (ALE) Methods in OpenFOAM. Available online: https://www.researchgate.net/publication/388279282_Flow_Around_a_Cylinder_A_Comparative_Study_of_Immersed_Boundary_and_Arbitrary_Lagrangian-Eulerian_ALE_Methods_in_OpenFOAM. (accessed on 22 April 2025).
- (PDF) Towards the Optimal Performance of Vertical Wind Turbine: Numerical Simulation and Experimental Validation. Available online: https://www.researchgate.net/publication/388278907_Towards_the_Optimal_Performance_of_Vertical_Wind_Turbine_Numerical_Simulation_and_Experimental_Validation (accessed on 22 April 2025).
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E. Computational Fluid-Structure Interaction: Methods and Applications; John Wiley & Sons, Publication: Hoboken, NJ, USA, 2013. [Google Scholar]
- 2023 FORMULA 1 TECHNICAL REGULATIONS; Fédération Internationale de l’Automobile: Paris, France, 2022.
- Federation Internationale de l’Automobile. Available online: https://www.fia.com/ (accessed on 16 March 2025).
- Marco, L. Best Practice Guidelines for Handling Automotive External Aerodynamics with Fluent; Marco Lanfrit: Darmstadt, Germany, 2025. [Google Scholar]
- Jakirlic, S.; Kutej, L.; Unterlechner, P.; Tropea, C. Critical Assessment of Some Popular Scale-Resolving Turbulence Models for Vehicle Aerodynamics. SAE Int. J. Passeng. Cars-Mech. Syst. 2017, 10, 235–250. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).