Abstract
Segmentation of retinal vessels from fundus images is critical for diagnosing diseases such as diabetes and hypertension. However, the inherent challenges posed by the complex geometries of vessels and the highly imbalanced distribution of thick versus thin vessel pixels demand innovative solutions for robust feature extraction. In this paper, we introduce DAF-UNet, a novel architecture that integrates advanced modules to address these challenges. Specifically, our method leverages a pre-trained deformable convolution (DC) module within the encoder to dynamically adjust the sampling positions of the convolution kernel, thereby adapting the receptive field to capture irregular vessel morphologies more effectively than traditional convolutional approaches. At the network’s bottleneck, an enhanced atrous spatial pyramid pooling (ASPP) module is employed to extract and fuse rich, multi-scale contextual information, significantly improving the model’s capacity to delineate vessels of varying calibers. Furthermore, we propose a hybrid loss function that combines pixel-level and segment-level losses to robustly address the segmentation inconsistencies caused by the disparity in vessel thickness. Experimental evaluations on the DRIVE and CHASE_DB1 datasets demonstrated that DAF-UNet achieved a global accuracy of 0.9572/0.9632 and a Dice score of 0.8298/0.8227, respectively, outperforming state-of-the-art methods. These results underscore the efficacy of our approach in precisely capturing fine vascular details and complex boundaries, marking a significant advancement in retinal vessel segmentation.
Keywords:
retinal vessel segmentation; deformable convolution; contextual feature fusion; U-Net architecture MSC:
68T99
1. Introduction
The geometric features of retinal vessels provide important insights into a patient’s health and aid in diagnosing diseases. Fundus images of diabetic patients often reveal lesion characteristics, including microaneurysms, hemorrhagic patches, and hard exudates, which assist physicians in early detection and diagnosis [1]. Glaucoma, which damages the optic nerve, also causes visible changes in the optic disc and surrounding blood vessels in fundus images, aiding in diagnosis and disease monitoring [2].
Computer-aided diagnosis (CAD) systems for retinal fundus images are an emerging technique that allows a physician to directly investigate the structure of the retina. Many diseases of the retina do not show symptoms in their early stage, while CAD systems enable early detection of subliminal lesions such as microaneurysms and hemorrhages to allow timely intervention and treatment [3]. There has thus been a drive toward developing more precise algorithms of retinal vessel detection to assist in early diagnosis of pathological conditions.
For example, there are two main challenges in the segmentation of fundus vessels, including the irregularity of vessel morphology and the imbalanced distribution of thick trunk vessels and tiny capillaries [4,5]. In addition, the structure of the retinal vessels presents a large diversity due to curvature, bifurcation, constriction, and dilation. Such variations are different for different patients and even for different regions from the same patient’s retina [6]. Vessel morphology can have high curvature, especially around the points of bifurcation or around areas containing lesions. Traditional methods of feature extraction cannot follow the path of blood vessels with irregular contours using a standard convolution operation and thus often result in segmentation breaks [7].
The vascular system of the fundus comprises both large trunk vessels and fine capillaries, which exhibit significant differences in distribution and morphological characteristics. In most fundus images, capillaries occupy a larger area compared to thick vessels. However, thick vessels typically occupy larger areas and are more prominent within the image [4]. Segmentation algorithms can easily detect thick vessels with high contrast and well-defined edges [8]. However, this inherent bias leads models to prioritize thicker vessels while neglecting finer capillaries. The imbalance in the number of thick and fine vessels may cause the model to disproportionately predict thicker vessels or, conversely, fail to adequately capture smaller capillaries. To address the challenge of feature extraction from irregular blood vessels, R2-Net introduces a recurrent residual convolutional network, replacing traditional conv+ReLU layers with RR blocks [9]. This approach enhances the model’s ability to capture features from both thick and fine vessels, mitigating the imbalance in vessel detection.
Similarly, the ladder network follows the residual structure inside the U-Net architecture. In Ladder-Net, the shared-weight residuals are combined with an encoder–decoder multi-group for feature extraction [10]. The whole network can be regarded as an integration of fully convolutional networks. The end-to-end network architecture, CE-Net, represents the architecture. Several pre-trained ResNet blocks are introduced in the feature encoder, and both the DAC module and RMP module are incorporated into a modified ResNet U-Net structure [11].
Deformable convolution has seen broad application in U-Net-based architectures. DU-Net, for instance, incorporates deformable convolutional layers in both the encoder and decoder, allowing the model to capture geometric variations more effectively by substituting traditional convolutional layers in the intermediate sections of the encoder and decoder [7]. To address the challenge of balancing thick and thin vessel segmentation, Yang et al. introduced a three-stage deep learning approach. Their model performs vessel segmentation through a sequence of stages: first segmenting thick vessels, then fine vessels, and, finally, fusing the segmented results [8].
In response to these challenges, we propose a deformable network with an integrated atrous-convolution feature pyramid to enhance retinal vessel segmentation performance. The main benefits of our approach are as follows:
- Adaptive Spatial Feature Extraction: By employing deformable convolution, the network dynamically adjusts its receptive field to capture structurally adaptive spatial information, which significantly enriches feature representation and allows for the precise delineation of complex vascular geometries.
- Enhanced Contextual Information Fusion: The contextual feature-extraction module, based on an advanced ASPP framework, leverages multi-scale atrous convolutions to integrate diverse contextual cues. This design enables the model to robustly detect vessels across varying scales and improve segmentation accuracy in regions with intricate vascular details.
- Robust Hybrid Loss Function: We introduce a novel hybrid loss function that synergistically combines pixel-level and segment-level losses. This formulation not only improves segmentation precision but also enhances the calibration of the model by addressing the challenges posed by the imbalanced distribution of thick and thin vessel pixels.
The rest of this paper is organized as follows: Section 2 reviews background knowledge in the relevant field, while Section 3 provides an in-depth description of the proposed methodology. Section 4 presents the experimental findings. Section 5 concludes the study, highlighting possible future research directions.
2. Related Work
2.1. U-Net and Its Improved Structure
The U-Net [12] is a special class of convolutional neural network. It was invented by Olaf Ronneberger et al. in 2015, and it was designed to effectively cope with medical image segmentation tasks when the number of training data was limited. The architecture employs a symmetric encoder–decoder structure. The encoder consists of successive convolutional layers followed by max-pooling operations, progressively reducing the spatial resolution of feature maps while increasing depth. Conversely, the decoder restores spatial resolution through upsampling operations (e.g., transposed convolutions) and reduces feature depth. Skip connections bridge encoder and decoder layers to preserve fine details, enabling precise localization in segmentation outputs. Since its introduction, U-Net has become a cornerstone architecture for medical image segmentation.
Subsequent advancements in U-Net have focused on optimizing its encoder, decoder, and core operations. A widely adopted strategy involves integrating pretrained backbone networks, such as ResNet [13], VGG [14], and DenseNet [15], into the encoder architecture. These models, pre-trained on large-scale datasets like ImageNet, enhance feature extraction capabilities by leveraging transfer learning. For example, ResNet’s residual connections effectively address vanishing gradient issues in deep networks, while DenseNet’s dense connections promote feature reuse through layer-wise concatenation, thereby improving information flow and gradient propagation. Beyond backbone adaptations, Dai et al. [7] introduced DU-Net, which replaces standard convolutions with deformable convolutions in both the encoder and the decoder. This innovation enables the network to dynamically adjust its receptive fields, allowing it to better adapt to irregular anatomical structures commonly encountered in medical imaging. This approach significantly improves the model’s ability to capture complex morphological features in retinal vascular segmentation tasks.
In parallel, hybrid techniques combining spatial-domain and transform-domain approaches have also shown effectiveness in enhancing robustness and performance in various signal processing tasks. For example, Raju et al. [16] proposed a robust video watermarking system based on SVD hybridization, demonstrating the benefit of multi-domain fusion, a concept also relevant to feature integration strategies in deep learning-based segmentation.
Further innovations address multi-scale feature fusion and contextual awareness. Zhuang [11] proposed LadderNet, a multi-path U-Net variant that interconnects multiple U-Net branches through lateral connections. This design facilitates hierarchical feature aggregation across different depths, while auxiliary supervision during training strengthens gradient propagation. Meanwhile, Gu et al. [12] developed CE-Net, which augments the encoder with a context extractor module combining dilated convolutions and channel attention. This module captures global contextual information while preserving local details, significantly improving performance on small or low-contrast lesions.
In addition, various multi-scale feature-extraction modules, including atrous convolution [17] and pyramid pooling [18], have been developed to enable the network to capture features of different scales, enhancing the capability of detecting multi-scale targets. Adaptive feature-extraction modules, such as deformable convolutional networks, dynamically allow the convolutional kernels to adaptively change their sampling positions with respect to the input image content. This yields a more flexible and robust way to handle deformations and complex structures [7]. In addition, some SPP modules have been added to the U-Net architecture to extract features from various receptive fields by performing multi-scale pooling, thereby enhancing the capture of contextual information in images.
SPP is usually used in the bottleneck between the encoder and decoder of U-Net. More specially, after several convolutional and downsampling layers in the encoder, the input image generates high-dimensional feature maps with much richer spatial and semantic information. Then the SPP module performs multi-scale pooling on these feature maps and preserves and fuses the multi-scale information. This is achieved by interpolating and concatenating the pooled feature maps, enhancing the model’s capability for target scale variance recognition and interpretation of intricately combined scenes [19]. The resultant fused multi-scale feature maps are further fed to the decoder, which rebuilds resolution through upsampling and convolution operations, while the skip connections integrate features from different stages of the encoder. This process yields segmentation results with high precision. Adding SPP to U-Net increases robustness and adaptability significantly. Consequently, it works very well on multi-scale image segmentation of complex structures. It finds wide applications in medical image processing and remote sensing image analyses since it therefore has wide applications and attracts much attention in.
2.2. Spatial Pyramid Pooling
Spatial pyramid pooling (SPP) was first proposed by Kaiming He et al. in 2014 [18], addressing the limitation of fixed input sizes in convolutional neural networks (CNNs). As illustrated in Figure 1b, SPP performs pooling operations at multiple scales on feature maps and concatenates the resulting pooled feature maps. This enables the network to accept input images of arbitrary size while preserving spatial information, thereby enhancing the detection of multi-scale targets.
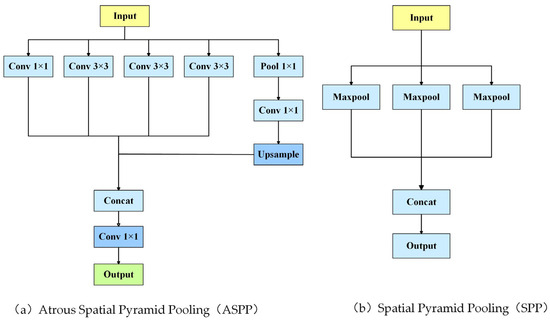
Figure 1.
ASPP and spp.
Atrous spatial pyramid pooling (ASPP) was introduced by Chen et al. in the DeepLab series in 2017 [20]. Instead of traditional pooling, ASPP employs atrous (dilated) convolution during the feature extraction process. Atrous convolution increases the receptive field by inserting dilations into the convolution kernel, allowing the network to capture a broader range of contextual information without adding parameters or increasing computational complexity. As shown in Figure 1a, ASPP applies multiple dilation rates to extract multi-scale features, which are then concatenated to improve the detection of multi-scale targets.
Techniques like SPP and ASPP have significantly enhanced the performance of CNNs in image segmentation and object detection tasks by enabling multi-scale feature extraction and fusion. SPP addresses the challenge of fixed input sizes, while ASPP extends the receptive field using dilated convolution, improving adaptability to multi-scale targets. As these methods have evolved, they have incorporated more contextual information and refined feature extraction strategies, driving advancements in both image segmentation and object detection techniques.
3. Method
We designed a deformable U-Net with an atrous-convolution feature pyramid (DAF-UNet) consisting of three parts: an encoder, an intermediate processing module, and a decoder. In contrast to U-Net, we use deformable convolution (DC) with residual structure to generate feature mapping. Unlike the general ASPP module, we designed a better feature fusion module and applied it to our U-Net.
3.1. Deformable Feature Extractor
A significant challenge in vessel segmentation lies in accurately modeling vessels of varying shapes and scales. Traditional approaches, such as manipulable filters and Frangi filters, rely on linear combinations of responses at different scales or orientations to capture vessel features, which may introduce bias [7]. Deformable convolutional networks tackle this issue by incorporating deformable convolutional layers into conventional neural network architectures. Inspired by deformable convolutional neural networks—which adaptively adjust receptive fields to capture diverse shapes and scales based on input features—this paper integrates deformable convolution within the proposed network.
In our proposed architecture, the conventional convolution blocks in the encoder—each originally composed of two convolution layers and one max-pooling layer—are replaced with a pre-trained ResNet-34 module. This module retains the first four residual blocks while omitting the average pooling and fully connected layers. ResNet-34 introduces shortcut connections that effectively mitigate gradient-vanishing and accelerate convergence, as illustrated in Figure 2.
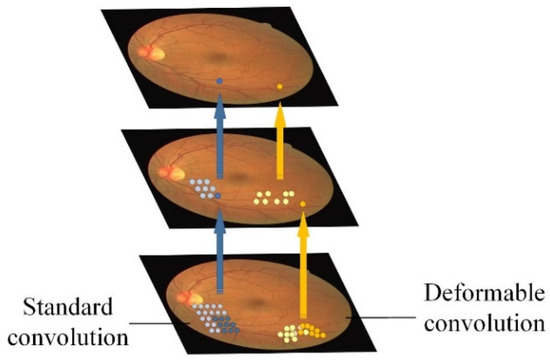
Figure 2.
Sampling process for standard convolution and DC.
To further enhance the network’s capacity for capturing spatial deformations, we integrated deformable convolution layers into the architecture. These layers adapt the spatial sampling locations of the convolution kernel by learning additional offset parameters. Specifically, for a 3 × 3 kernel, an extra offset field of dimension 2 × 32 (i.e., 18 parameters per spatial location) is generated, which allows the convolution to dynamically adjust its receptive field according to the underlying geometric structure of the input features. Moreover, if employing the modulated variant of deformable convolutions, a modulation scalar is learned for each offset, further refining the feature sampling process. This configuration—typically using 8 deformable groups to partition the offsets—enables the network to effectively model complex object deformations and variations in shape, thereby enhancing overall feature representation and detection performance.
Unlike standard convolution, which applies a fixed kernel position, deformable convolution introduces an offset, as illustrated in Figure 2, allowing the convolutional kernel to adapt its sampling positions. This adaptive positioning helps the network capture complex deformations and intricate geometric structures more effectively.
For an input feature map and a convolution kernel , the output of ordinary convolution is shown in Equation (1):
where denotes the value of the output feature map at position R denotes the sampling region of the convolution kernel, is the weight of the convolution kernel at position , and represents the value of the input feature map at the same position.
For a deformable convolution, the computation of the output introduces an offset that allows the sampling position of the convolution kernel to be dynamically adjusted. The output of the deformable convolution can be expressed as follows:
where is the convolution kernel at the position at which the offsets are learned by another offset-generating network. The other symbols are the same as those defined for an ordinary convolution.
The offset Δpn in a deformable convolution is learned and predicted by a specialized convolutional layer, as shown in Figure 3. This convolutional layer, is often referred to as an offset generation network (OGN). Specifically, this convolutional layer outputs feature maps of the same spatial dimensions as the input feature maps but with a different number of channels, and each value in these feature maps represents an offset at each position in the convolutional kernel.
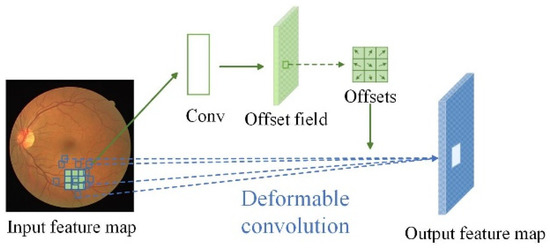
Figure 3.
Illustration of a 3 × 3 deformable convolution: The offset fields are derived from input patches and features, with a channel size of 2N, representing N two-dimensional offsets. The deformable convolution kernel maintains the same resolution as the current convolution layer, and both the convolution kernel and offsets are learned jointly.
Suppose the input feature map is and the weights of the offset generation network are , then the offset is calculated as shown in Equation (3):
where is a tensor with 2 × l × l channels, l × l is the size of the convolution kernel with two offsets (in the x and y directions) for each position, and is the weight of the offset-generating network which is a convolution kernel. * denotes the convolution operation.
Since the offset position is not necessarily an integer position, the value at that position needs to be obtained from the input feature map by bilinear interpolation.
Assuming that , where x′ and y′ are not integers, their values can be calculated by the bilinear interpolation formula of Equation (4):
where q is the input feature map with the four closest integer positions, and denotes the set of these positions.
Offset-generating networks learn spatial offsets from the input feature maps through convolutional operations and apply these offsets to the convolutional layers, allowing the convolutional kernel to adjust its sampling positions adaptively. This mechanism enables deformable convolution to better capture complex deformations and geometric structures, which is particularly advantageous in tasks requiring high-precision feature extraction, such as image segmentation.
It is important to ensure that the convolutional layer responsible for generating offsets maintains the same spatial resolution and dilation as the layer extracting features from the offset feature map. For the task of vascular segmentation, larger convolution kernels are more effective in capturing broader regions of the vascular image, while smaller kernels are more precise in extracting fine details of the vessel contours. Therefore, we utilize a large 7 × 7 convolutional kernel in the first DC layer to capture rough vascular regions, followed by smaller 3 × 3 kernels in subsequent layers to refine the contour details. This multi-scale deformable convolution (DC) approach, as proposed in this paper, yields better feature representations, leading to more precise vessel contouring and improved segmentation outcomes compared to single-scale DC.
Moreover, integrating DC within a residual network design in the encoder prevents gradient-vanishing and accelerates network convergence [13]. ResNet, while powerful, traditionally uses fixed-position sampling in its convolutional layers, which limits its ability to fully capture spatial context. In contrast, deformable convolution offers superior positional awareness, making it particularly suitable for segmentation tasks that demand high positional specificity. By capturing target boundaries and intricate details more accurately, DC enhances the perception of pixel positional information at every level, ultimately improving the accuracy of image segmentation [7].
3.2. Adaptive Dilated Fusion Block
ASPP faces two primary challenges in practical applications: (1) ASPP uses a fixed dilation rate, which can result in certain pixels falling within the receptive field being excluded from the convolution operation; and (2) the pooling operation in ASPP utilizes only a single pooling kernel, limiting its ability to segment images with significant scale variations. To address these challenges, we designed the adaptive dilated fusion block (ADFB), as shown in Figure 4.
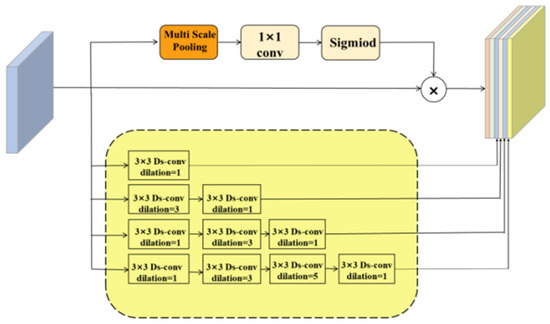
Figure 4.
Adaptive dilated fusion block (ADFB).
The fixed dilation rate in ASPP leads to the gridding effect [21]. This effect is due to the fact that in cavity convolution, as the cavity rate increases, there will be some pixels that fall into the receptive field that cannot participate in the convolution operation, thus leading to inadequate feature extraction.
To solve the problem that, due to the fact that ASPP has a fixed expansion rate, some pixels falling into the receptive field cannot participate in the convolution operation, and motivated by the Inception-ResNet-V2 block [22] and dilated convolution, a module combining a combination of dense and jump connections is proposed.
To determine the dilation rate for each layer, hybrid dilated convolution (HDC) [21] is employed to prevent the grid effect. For NNN convolutional layers with a kernel size of K × K and dilation rates (, , …, ), the objective of HDC is to ensure that the final receptive field of consecutive convolution operations fully covers a square region, with no gaps or unfilled edges. We define the “maximum distance between two non-zero values” as shown in Equation (5):
where = . The design goal is to make ≤ .
In accordance with this principle, the null rate of each layer is set as (3,1), (1,3,1), and (1,3,5,1), and the outputs of each layer are directly connected to each subsequent layer through dense connection, which can achieve the reuse of features and better transfer of gradient. And it can effectively solve the grid effect, as shown in Figure 5.
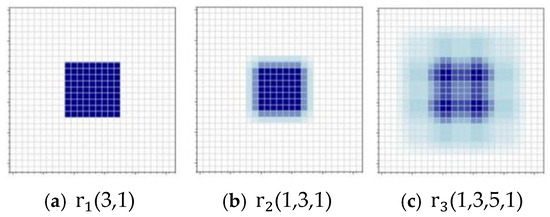
Figure 5.
Schematic diagram of the pixel points involved in the computation for each layer of null convolution. The size of the convolution kernel is 3 × 3, r is the size of the null rate, and all three layers of the null convolution eliminate the grid effect.
The second limitation of ASPP—its poor adaptability to varying object scales—is especially critical in medical image segmentation, where fine-grained structures (e.g., capillaries) coexist with larger anatomical features. To enhance multi-scale perception, ADFB incorporates a multi-scale pooling module (see Figure 6) using four parallel branches with receptive fields of size 2 × 2, 3 × 3, 5 × 5, and 6 × 6.
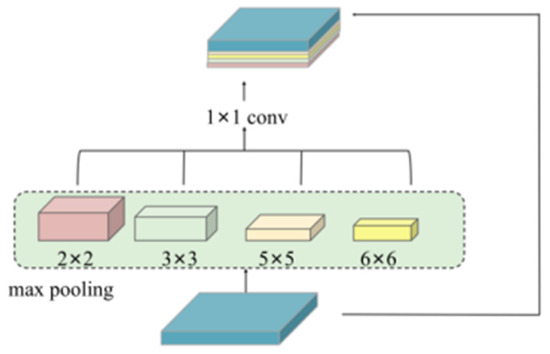
Figure 6.
Multi-scale pooling module (multi-scale pooling).
This design captures contextual information across diverse spatial resolutions. Additionally, deformable convolutions are integrated into the encoder, enabling adaptive receptive fields that adjust to object shapes and scales, thereby improving the model’s sensitivity to both global and local patterns.
3.3. Loss Function
3.3.1. Mixed Loss Function
Segment-wise loss function [23] definition: for each skeleton segment , the corresponding vascular pixels in I constitute a vascular segment . Then, to define each vessel segment the average vessel thickness of each vessel segment is expressed as follows:
To measure the inconstancy of thickness, each segment is assigned a search range to find the corresponding pixel in the probability map for comparison.
Then, for each vessel segment , the bivariate map lies within the search range . All vascular pixels within the search range form a vascular segment, denoted as . The mismatch ratio (mr) is measured by defining the mismatch ratio (mr) and The thickness incongruence is measured by defining the mismatch ratio (mr) to measure the thickness between the and thickness inconsistency, as follows:
The thinner the vessel, the smaller the , so, therefore, the mismatch ratio is more sensitive to thickness inconsistencies in thin vessels than in thick ones.
In order to construct segment-level losses, as in Equation (7), we define a weight matrix can be expressed as follows:
where is the weight of pixel S in the probability map. Then, we define the loss of each pixel :
where is the predicted probability value of p, and is the value of the p, the base truth value (0 for non-vesselized pixels and 1 for vesselized pixels). Based on thickness consistency measurements, an adaptive weight matrix has been developed to extend segment-level loss functions from pixel-wise losses. Thus, this uses hybrid loss functions which combine both the pixel-level loss and the fragment-level loss for the loss function, represented as follows:
where and are balancing coefficients that control the relative contributions of each loss term. The adaptive weight matrix, derived from thickness consistency metrics, helps to assign higher weights to regions where thickness deviations are more pronounced, thus ensuring that both thin and thick vessels are effectively learned. This combination of pixel-wise and segment-wise (fragment-level) loss terms enables the network to maintain fine-grained accuracy while preserving overall structural consistency, as represented in Equation (10).
3.3.2. Hyper-Parameter Selection
The proposed segment-level loss involves two hyper-parameters: the maximum length of skeleton segments (maxLength) and the radius of the searching range (r).The value of maxLength is determined based on thickness measurements derived from manual annotations. For each candidate value of maxLength, we partition into skeleton segments and derive the corresponding vessel segments .
Next, for each skeleton segment and its corresponding vessel segment , we define the thickness deviation as follows:
where is the radius at the skeleton pixel p, and is the average radius for the segment . The overall thickness deviation across all segments is then computed, and the optimal maxLength is chosen to minimize this total deviation.
Similarly, the radius r of the searching range is determined by evaluating thickness deviations over various candidate values of r and selecting the one that yields the smallest overall deviation. The final values of these two hyper-parameters, maxLength and r, are chosen based on their performance on the training set.
4. General Framework
The deformable U-Net with atrous-convolution feature pyramid in Figure 7 is composed of the encoder, the middle processing module, and the decoder. Such architecture adapts to the challenge of segmenting vessels of complex and varied shapes, especially during feature extraction. Addressed with the incorporation of deformable convolution and a residual structure, the challenge can be tackled.The challenge is addressed by incorporating deformable convolution and a residual structure, as outlined in Algorithm 1.
| Algorithm 1: DAF-UNet Workflow for Retinal Vessel Segmentation | |
| Input: Fundus image I | |
| Output: Segmentation mask Ŷ | |
| Step | Description |
| 1 | Preprocess I using CLAHE and gamma correction. |
| 2 | Convert to grayscale and resize to a fixed resolution. |
| 3 | Extract features using the encoder with deformable convolution layers. |
| 4 | Apply adaptive dilated fusion block (ADFB) at the bottleneck. |
| 5 | Fuse multi-scale context using the atrous spatial pyramid pooling (ASPP) module. |
| 6 | Decode features via the decoder path with skip connections. |
| 7 | Generate prediction map Ŷ. |
| 8 | Compute hybrid loss: |
| 9 | Backpropagate and update network parameters. |
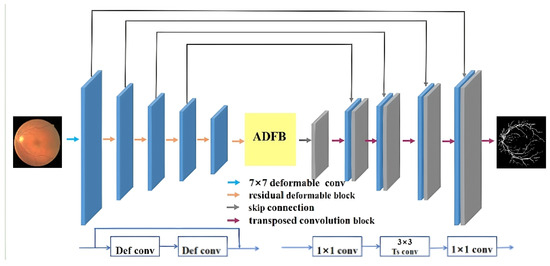
Figure 7.
Deformable U-Net with atrous-convolution feature pyramid for retinal vessel segmentation.
The intermediate processing module of the proposed ASPP module is different from the traditional one because it applies multi-scale pooling. This technique relates the original image to the outputs of the decoder at different layers, providing a more comprehensive feature representation. ADBF utilizes both dense and skip connections.
At the time of decoding, we substitute conventional upsampling operations with specialized decoder blocks that expand feature maps. Decoder blocks consist of 1 × 1 convolutions followed by 3 × 3 transposed convolutions.
The computational complexity of DAF-UNet can be analyzed in terms of its core architectural components. Assuming an input image of size H × W × C, and a convolutional kernel of size K × K producing M output channels, each convolutional operation has a time complexity of O(H′ × W′ × K2 × C × M).
Compared to standard convolutional operations, the deformable convolutional layers introduce learnable offset parameters, which enhance the network’s flexibility in modeling spatial deformations but add a modest increase in computational cost. Nevertheless, because these modules are applied selectively and efficiently, the overall complexity of DAF-UNet remains manageable and competitive with state-of-the-art segmentation networks.
With the rise of vision transformer (ViT)-based architectures in medical image analysis—such as Swin Transformer, TransUNet, and Swin-UNet—it is important to assess how DAF-UNet compares within this context.
While ViT-based models excel at capturing global dependencies through attention mechanisms, they often require substantial computational resources and large-scale datasets for optimal performance. In contrast, DAF-UNet achieves comparable or superior accuracy, especially in segmenting thin, irregular vessels, while maintaining a lighter computational footprint. This demonstrates that our combination of deformable convolution and ASPP-based multi-scale fusion effectively approximates the benefits of transformer-based global modeling in a more efficient manner.
Future work may consider integrating lightweight attention modules to further enhance the network’s performance while preserving its efficiency on medical imaging datasets.
To justify the network structure for general application in image segmentation tasks, many experiments have been conducted.
5. Experiments and Analysis of Their Results
5.1. Datasets
The selection of the DRIVE and CHASE_DB1 datasets for comparative experiments is driven by their complementary roles in evaluating retinal vessel segmentation algorithms: DRIVE, as the gold-standard benchmark with standardized adult retinal images (565 × 584 pixels) and expert annotations, ensures reproducibility and direct performance comparison across studies, while CHASE_DB1, comprising pediatric retinal images (700 × 605 pixels) captured with different imaging hardware, introduces heterogeneity in resolution, vascular morphology (e.g., finer vessels and pathological variations), and demographic profiles (children vs. adults). This combination rigorously tests model adaptability to scale variations, cross-device generalization (Canon vs. Sony cameras), and demographic shifts, while addressing clinical needs such as diabetic retinopathy screening across age groups. DRIVE’s predefined training-test splits validate supervised learning efficacy, whereas CHASE_DB1’s flexible partitioning challenges low-data robustness. Together, they expose algorithm limitations in handling illumination artifacts, subtle anatomical details, and hardware-induced biases, ensuring comprehensive validation of both technical robustness and clinical readiness for diverse real-world scenarios.
Digital Retinal Images for Vessel Extraction (DRIVE) dataset [4]: The DRIVE dataset consists of 40 high-resolution color retinal images, of which 20 are in the training set and 20 in the test set. All the images are of the same resolution: 565 × 584 pixels.
CHASE (CHASE_DB1) dataset [24]: CHASE_DB1 is a widely used retinal vessel segmentation dataset, often employed to assess the effectiveness of retinal image analysis algorithms. It comprises 20 high-resolution color retinal images with a resolution of 700 × 605 pixels.
The original RGB images were converted to single-channel format, resized to a fixed 1024 × 1024 resolution, and enhanced using contrast-limited adaptive histogram equalization (CLAHE) and gamma correction. Pixel values in the labels were normalized to optimize model learning. To further enrich the training dataset, images and labels were augmented with random flips. Finally, the preprocessed images and labels were resized to the target dimensions for the model to ensure high-quality, diverse training data.
5.2. Evaluation Metrics
To evaluate the method’s performance, the average Dice similarity coefficient (DSC), accuracy (ACC), and specificity (SP) were used as performance evaluation metrics in this experiment. These indicators are as follows:
where TP is the number of the true positive samples, TN is the number of the true negative samples, FP is the number of the false positive samples, and FN is the number of the false negative samples.
ACC = (TP + TN)/(TP + FP + TN + FN)
DSC = (2 × TP)/(2 × TP + FP + FN)
SP = TN/(TN + FP)
Experiments were conducted using PyCharm 2021.2.4 within the framework of PyTorch parameters for the experiment and established with an Adam optimizer set at a learning rate of 0.001, batch size of 2, and a weight decay of 0.00001.
5.3. Comparative Experiments
We carried out the comparative analyses on the DRIVE and CHASE_DB1 datasets to test performance disparity between our suggested network architectures and those that are widely accepted. As shown in Table 1, for the DRIVE dataset, our models performed better compared to the others in terms of ACC and Dice, with a high top score in correctness and overlap, demonstrating their skill in pixel-level segmentation.

Table 1.
Effect of comparison experiments on the DRIVE dataset.
Shifting focus to the CHASE_DB1 dataset, the outcomes are presented in Table 2, where our model, DAF-UNet, garnered the highest scores in specificity and Dice, underscoring its superiority in the domain of fundus vascular segmentation.

Table 2.
Effect of comparison experiments on the CHASE_DB1 dataset.
Figure 8 presents the qualitative comparison of retinal vessel segmentation results produced by different models, including U-Net, DU-Net, Residual U-Net, and the proposed DAF-UNet, alongside the ground truth annotations. It can be observed that while traditional U-Net and its variants (DU-Net and Residual U-Net) were capable of capturing the major vessel structures, they tended to struggle with the accurate delineation of fine capillaries, especially in peripheral regions.
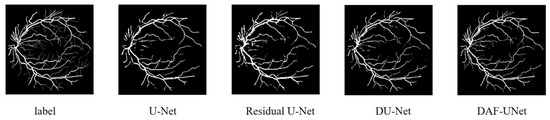
Figure 8.
Qualitative comparison of retinal vessel segmentation results produced by different models.
In contrast, the proposed DAF-UNet demonstrated superior segmentation performance, closely approximating the ground truth both in the continuity of major vessels and the preservation of thin vascular branches. The fine structures were more clearly delineated, and the vessel edges appeared smoother and more consistent across the entire image. Moreover, DAF-UNet exhibited stronger robustness to noise and background interference, which was particularly evident in regions where other models exhibited broken or missing vessel segments.
To rigorously evaluate the effectiveness of the proposed DAF-UNet over conventional models such as U-Net and DU-Net, we conducted a paired t-test using the Dice similarity coefficient (DSC) across test images in the DRIVE dataset, and the results are shown in Table 3.

Table 3.
Statistical significance analysis: paired t-test.
The resulting p-values for DAF-UNet vs. U-Net and DAF-UNet vs. DU-Net were 0.0021 and 0.0078, respectively—both well below the standard significance threshold (p < 0.05). These results confirm that the observed improvements were statistically significant and not due to random variation, thereby validating the superiority of DAF-UNet in segmentation accuracy.
These improvements can be attributed to the integration of the adaptive dilated fusion block (ADFB) and the multi-scale pooling mechanism, which enabled the model to more effectively capture and fuse contextual information at multiple spatial scales. As a result, DAF-UNet achieved a more holistic and precise representation of the retinal vasculature.
5.4. Ablation Experiments
Table 4 shows that replacing standard convolutions in the encoder with a pre-trained deformable ResNet architecture resulted in a large network performance increase while reducing the total number of parameters. Moreover, adding ADFB to the bottleneck architecture demonstrated large gains on all metrics at the expense of a limited increment in parameters. In addition, the customized loss function design coped with the intrinsic imbalance in blood vessel thickness, which was shown to be pretty effective for improving segmentation accuracy.

Table 4.
The ablation study conducted on the DRIVE dataset.
With the incorporation of these three improvements, the performance of this model was enhanced while reducing the number of parameters. Therefore, the results of ablation experiments turned out to be very effective evidence for the proposed network model in this paper. The introduction of this approach optimizes the model’s performance and underlines how each component acts to realize superior segmentation results.
6. Conclusions
In this paper, we propose an effective method for retinal vessel segmentation by integrating a residual dual-attention fusion network with a transformer-based encoder. Our approach demonstrated competitive performance on standard benchmark datasets, showcasing its capability to capture complex vascular structures while preserving fine-grained spatial information. Notably, our design shares conceptual alignment with recent work such as EnsUNet [26], which leverages the fusion of pre-trained models and attention mechanisms to enhance brain tumor segmentation performance. Inspired by such multi-branch integration strategies, our method employs a complementary fusion of deformable convolution and attention-based encoding to tackle the unique challenges of retinal imaging. Looking ahead, several promising directions can be pursued to further enhance the performance and applicability of our method. First, future research will focus on multi-class vessel segmentation, aiming to distinguish arteries, veins, uncertain regions, and background separately. This will provide more clinically relevant insights and support finer-grained ophthalmic diagnosis. Second, we plan to explore the lightweight design of the bottleneck modules, which will reduce computational complexity while preserving model accuracy—paving the way for deployment in real-time and resource-constrained environments. Lastly, special attention will be given to developing robust feature-extraction mechanisms for irregular vascular structures, as such vessels pose significant challenges due to their complex morphology and low contrast. Addressing these issues will substantially improve segmentation precision and generalization in diverse clinical scenarios.
Author Contributions
Conceptualization, Y.D.; Methodology, Y.D., M.Z. and S.-L.P.; Software, M.Z. and S.-L.P.; Validation, Y.D.; Formal analysis, R.Y. and M.Q.; Investigation, M.Q.; Resources, M.Q. and S.-L.P.; Data curation, R.Y.; Writing – original draft, R.Y.; Writing – review & editing, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China University Industry-University-Research Innovation Fund-Innovation project of new-generation information technology 2023 under Grant number 2023IT072.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wong, W.L.; Su, X.; Li, X.; Cheung, C.M.; Klein, R.; Cheng, C.Y.; Wong, T.Y. Global prevalence of age-related macular degeneration and disease burden projection for 2020 and 2040: A systematic review and meta-analysis. Lancet Glob. Health 2014, 2, e106–e116. [Google Scholar] [CrossRef] [PubMed]
- Weinreb, R.N.; Aung, T.; Medeiros, F.A. The pathophysiology and treatment of glaucoma: A review. JAMA 2014, 311, 1901–1911. [Google Scholar] [CrossRef] [PubMed]
- Doi, K. Computer-aided diagnosis in medical imaging: Historical review, current status and future potential. Comput. Med. Imaging Graph. 2007, 31, 198–211. [Google Scholar] [CrossRef] [PubMed]
- Fraz, M.M.; Remagnino, P.; Hoppe, A.; Uyyanonvara, B.; Rudnicka, A.R.; Owen, C.G.; Barman, S.A. An ensemble classification-based approach applied to retinal blood vessel segmentation. IEEE Trans. Biomed. Eng. 2012, 59, 2538–2548. [Google Scholar] [CrossRef] [PubMed]
- Fraz, M.M.; Remagnino, P.; Hoppe, A.; Uyyanonvara, B.; Rudnicka, A.R.; Owen, C.G.; Barman, S.A. Blood vessel segmentation methodologies in retinal images—A survey. Comput. Methods Programs Biomed. 2012, 108, 407–433. [Google Scholar] [CrossRef] [PubMed]
- Staal, J.; Abramoff, M.D.; Niemeijer, M.; Viergever, M.A.; van Ginneken, B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging 2004, 23, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Yang, X.; Wu, L.; Guo, J.; Li, M.; Liu, R.; Xu, L.; Lu, Z. Blood vessel segmentation using deep learning and conditional random field. In Proceedings of the 2017 IEEE 30th International Symposium on Computer-Based Medical Systems (CBMS), Thessaloniki, Greece, 22–24 June 2017; pp. 578–583. [Google Scholar]
- Li, H.; Xiong, W.; An, H.; Wang, S.; Tang, Y. A novel R2U-Net-based method for segmenting retinal vessels. In Proceedings of the 2019 IEEE International Conference on Big Data and Smart Computing (BigComp), Kyoto, Japan, 27 February–2 March 2019; pp. 121–124. [Google Scholar]
- Zhuang, X. LadderNet: Multi-path networks based on U-Net for medical image segmentation. arXiv 2018, arXiv:1810.07810. [Google Scholar]
- Gu, Z.; Cheng, J.; Fu, H.; Zhou, K.; Hao, H.; Zhao, Y.; Liu, J. CE-Net: Context encoder network for 2D medical image segmentation. IEEE Trans. Med. Imaging 2019, 38, 2281–2292. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Raju, K.; Murthy, A.S.D.; Rao, B.C.; Bhargavi, S.; Rao, G.J.; Madhu, K.; Saikumar, K. A Robust And Accurate Video Watermarking System Based On SVD Hybridation For Performance Assessment. Int. J. Eng. Trends Technol. 2020, 68, 19–24. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016; pp. 1–13. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 346–361. [Google Scholar]
- Edupuganti, V.G.; Chawla, A.; Kale, A. Automatic Optic Disk and Cup Segmentation of Fundus Images Using Deep Learning. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 2227–2231. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding Convolution for Semantic Segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar] [CrossRef]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Yan, Z.; Yang, X.; Cheng, K.T. Joint Segment-Level and Pixel-Wise Losses for Deep Learning Based Retinal Vessel Segmentation. IEEE Trans. Biomed. Eng. 2018, 65, 1912–1923. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Liu, L.; Fang, H. Study Group Learning: Improving Retinal Vessel Segmentation Trained with Noisy Labels. IEEE Trans. Med. Imaging 2023, 42, 1234–1246. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road extraction by deep residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Laouamer, I.; Aiadi, O.; Kherfi, M.L.; Cheddad, A.; Amirat, H.; Laouamer, L.; Drid, K. EnsUNet: Enhancing brain tumor segmentation through fusion of pre-trained models. In International Congress on Information and Communication Technology; Springer Nature: Singapore, 2024; pp. 163–174. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).