CNN-Based End-to-End CPU-AP-UE Power Allocation for Spectral Efficiency Enhancement in Cell-Free Massive MIMO Networks
Abstract
1. Introduction
1.1. Related Works
1.2. Heuristic-Based Power Allocation Methods
1.3. CNN-Based Power Allocation
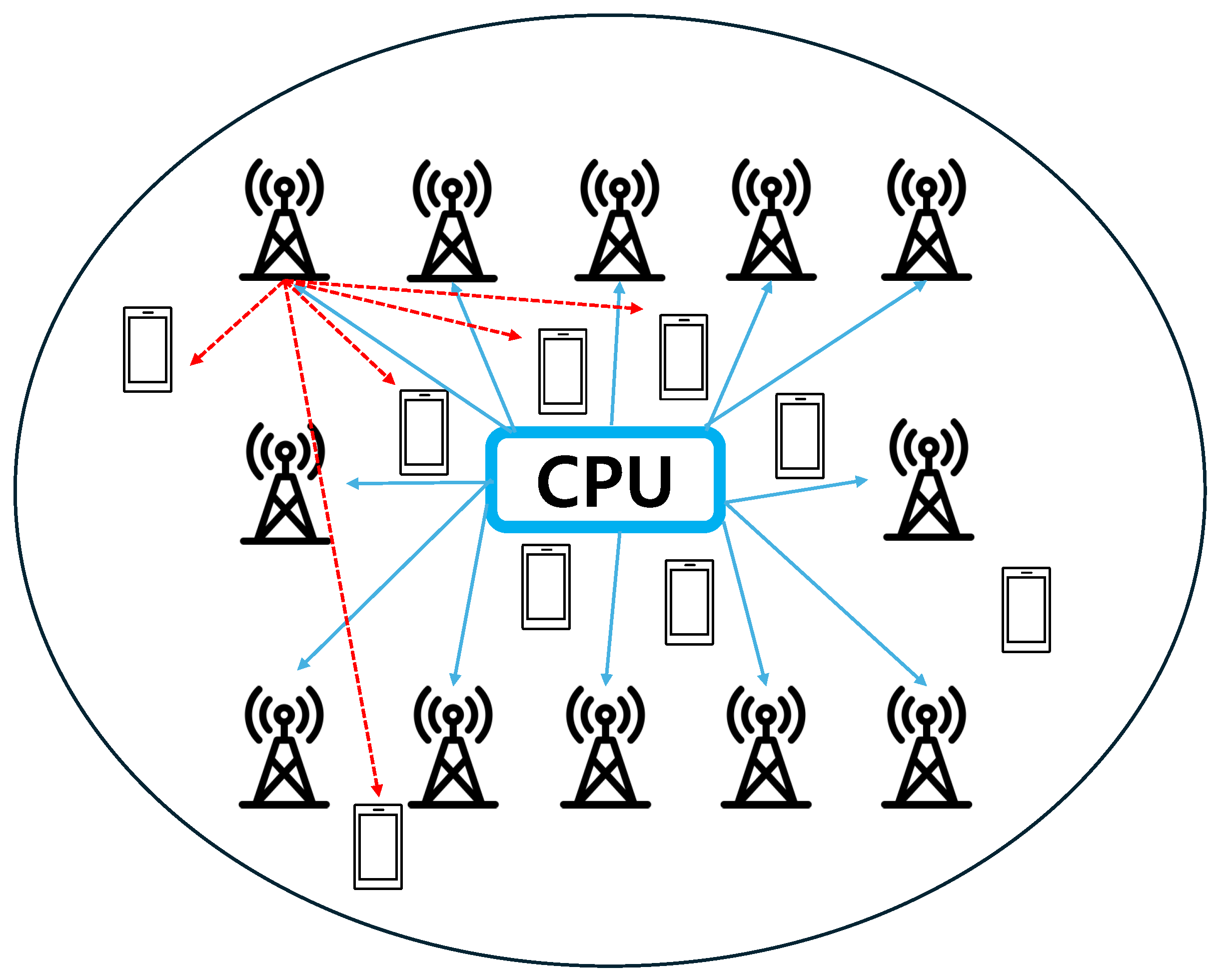
2. System Model
2.1. Network Architecture
2.2. Channel Model
2.3. Problem Formulation
3. Proposed CNN-Based Power Allocation Method
3.1. Motivation for Using CNN
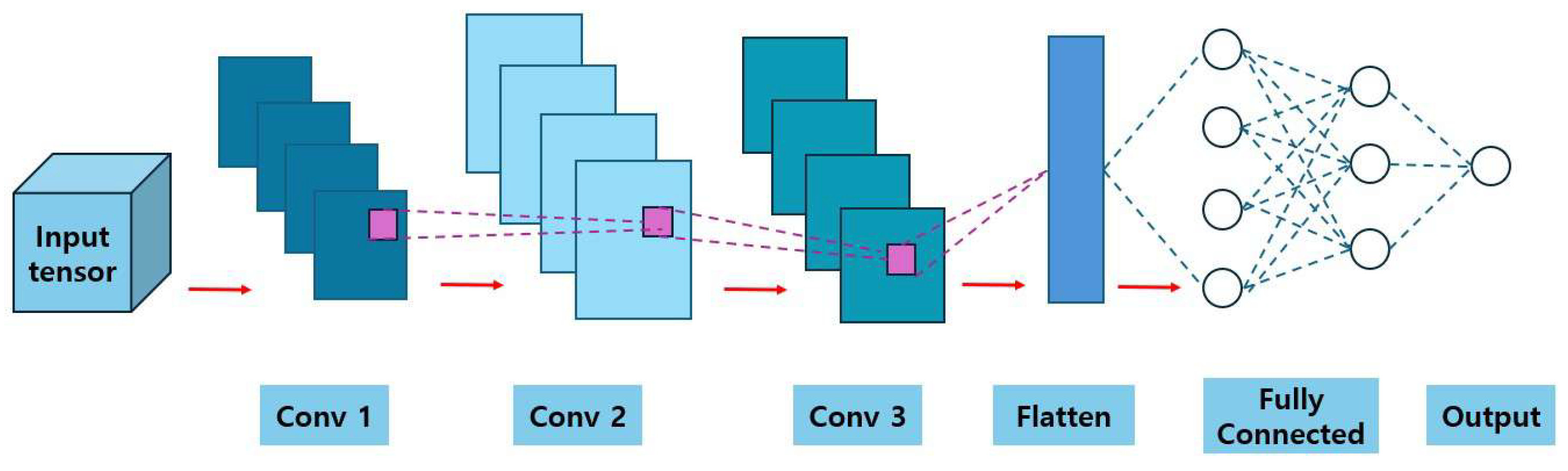
3.2. CNN Model Architecture and Feature Definition
3.3. CNN Training and Optimization Objective
3.4. Context-Aware Power Inference via CNN
4. Simulation Setup
4.1. Simulation Parameters
4.2. Comparison Methods
4.3. Evaluation Metrics
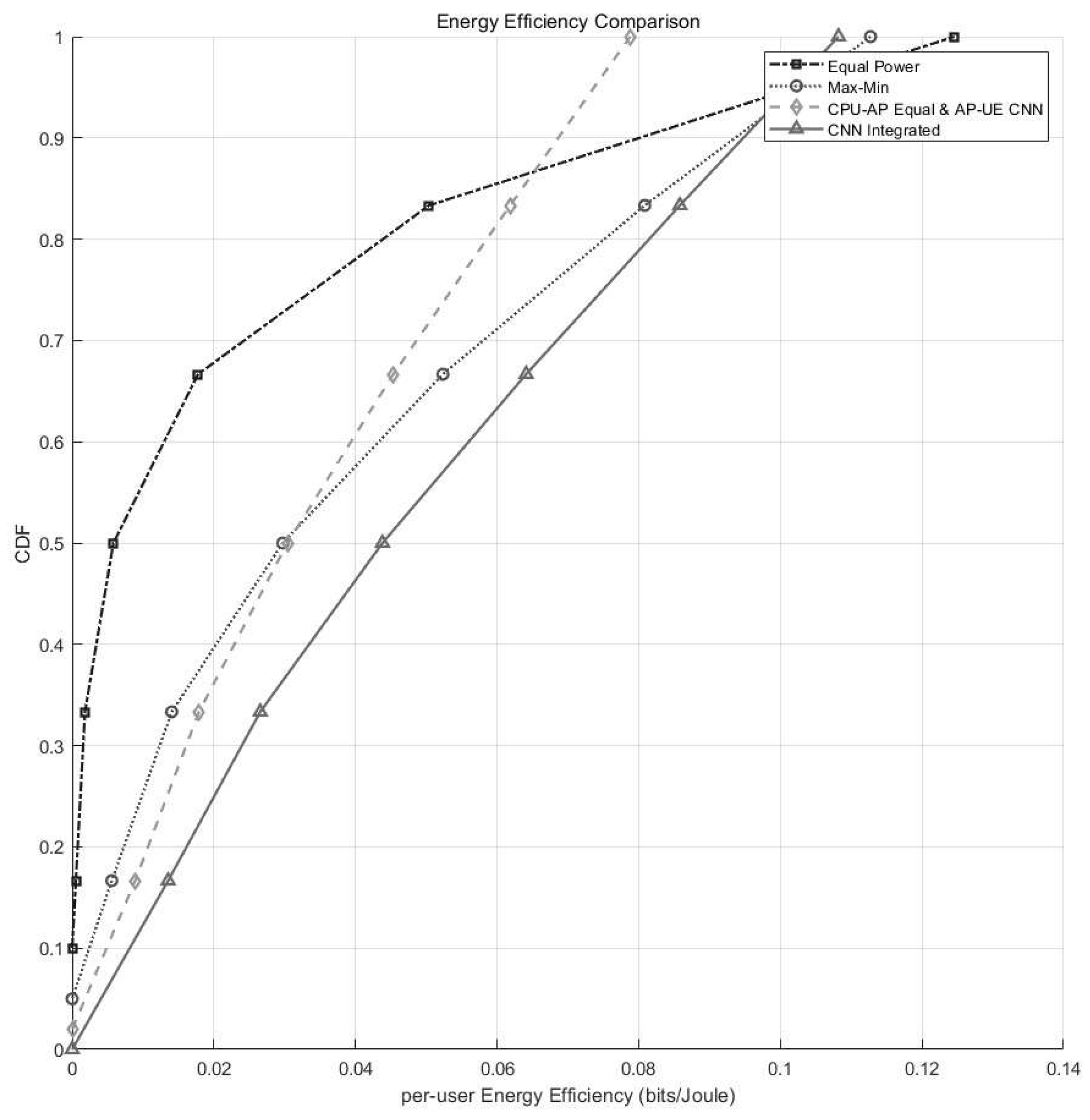
5. Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed CNN Model Description
- Channel gain magnitudes (from APs to UEs)
- AP–UE distances
- Interference estimates
- Initial SINR values.
- Conv1: channels, kernel, ReLU activation, batch normalization
- Conv2: channels, kernel, ReLU activation, batch normalization
- Flatten: Converts the 3D feature map to 1D vector of size
- FC1: Fully connected layer with 1024 neurons, ReLU
- Dual output heads:
- –
- Head 1: → CPU-to-AP power vector
- –
- Head 2: → AP-to-UE power matrix.
- Optimizer: Adam
- Learning rate:
- Batch size: 32
- Epochs: 50
- Loss function: Dual MSE loss with regularization (see Equation (7))
- Supervision: Optimal power values derived from max–min optimization.
References
- Ghosh, A.; Maeder, A.; Baker, M.; Chandramouli, D. 5G Evolution: A View on 5G Cellular Technology Beyond 3GPP Release 15. IEEE Access 2019, 7, 127639–127651. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO: Uniformly great service for everyone. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 201–205. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO Versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef]
- Imoize, A.L.; Obakhena, H.I.; Anyasi, F.I.; Sur, S.N. A Review of Energy Efficiency and Power Control Schemes in Ultra-Dense Cell-Free Massive MIMO Systems for Sustainable 6G Wireless Communication. Sustainability 2022, 14, 11100. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F.; Li, K.; Chen, R.; Yang, Y.; Wang, J. Deep Reinforcement Learning for Resource Allocation in Massive MIMO. In Proceedings of the 2021 29th European Signal Processing Conference (EUSIPCO), Virtual, 27–30 September 2021; pp. 1611–1615. [Google Scholar] [CrossRef]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency. Found. Trends Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Kim, D.; Lee, I.H. Deep Learning-Based Power Control Scheme for Perfect Fairness in Device-to-Device Communication Systems. Electronics 2020, 9, 1606. [Google Scholar] [CrossRef]
- Vaziri, A.; Moghaddam, P.S.; Shoeibi, M.; Kaveh, M. Energy-Efficient Secure Cell-Free Massive MIMO for Internet of Things: A Hybrid CNN–LSTM-Based Deep-Learning Approach. Future Internet 2025, 17, 169. [Google Scholar] [CrossRef]
- Cui, Z.; Tan, F. Power Allocation Based on CNN and Long Short-Term Memory Networks in Massive MIMO Systems. In Proceedings of the 12th International Conference on Computer Engineering and Networks, Haikou, China, 4–7 November 2022; Liu, Q., Liu, X., Cheng, J., Shen, T., Tian, Y., Eds.; Springer Nature: Singapore, 2022; pp. 441–447. [Google Scholar]
- Murshed, R.U.; Ashraf, Z.B.; Hridhon, A.H.; Munasinghe, K.; Jamalipour, A.; Hossain, M.F. A CNN-LSTM-Based Fusion Separation Deep Neural Network for 6G Ultra-Massive MIMO Hybrid Beamforming. IEEE Access 2023, 11, 38614–38630. [Google Scholar] [CrossRef]
- Van Chien, T.; Nguyen Canh, T.; Björnson, E.; Larsson, E.G. Power Control in Cellular Massive MIMO with Varying User Activity: A Deep Learning Solution. IEEE Trans. Wirel. Commun. 2020, 19, 5732–5748. [Google Scholar] [CrossRef]
- Perdana, R.H.Y.; Nguyen, T.V.; An, B. Deep Learning-based Power Allocation in Massive MIMO Systems with SLNR and SINR Criterions. In Proceedings of the 2021 Twelfth International Conference on Ubiquitous and Future Networks (ICUFN), Jeju Island, Republic of Korea, 17–20 August 2021; pp. 87–92. [Google Scholar] [CrossRef]
- Malhotra, S.; Yashu, F.; Saqib, M.; Mehta, D.; Jangid, J.; Dixit, S. Deep Reinforcement Learning for Dynamic Resource Allocation in Wireless Networks. arXiv 2025, arXiv:2502.01129. [Google Scholar]
- Shen, Y.; Shi, Y.; Zhang, J.; Letaief, K.B. Graph Neural Networks for Scalable Radio Resource Management: Architecture Design and Theoretical Analysis. IEEE J. Sel. A Commun. 2021, 39, 101–115. [Google Scholar] [CrossRef]
- Interdonato, G.; Björnson, E.; Ngo, H.Q.; Frenger, P.; Larsson, E.G. Ubiquitous Cell-Free Massive MIMO Communications. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 197. [Google Scholar] [CrossRef]
- Hamdi, R.; Driouch, E.; Ajib, W. Resource Allocation in Downlink Large-Scale MIMO Systems. IEEE Access 2016, 4, 8303–8316. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sun, H.; Chen, X.; Shi, Q.; Hong, M.; Fu, X.; Sidiropoulos, N.D. Learning to optimize: Training deep neural networks for wireless resource management. In Proceedings of the 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Patil, V.T.; Deore, S.S. Deep Learning-Driven IoT Defence: Comparative Analysis of CNN and LSTM for DDoS Detection and Mitigation. J. Inf. Secur. Appl. 2023, 10, 951. [Google Scholar] [CrossRef]
- He, H.; Wen, C.K.; Jin, S.; Li, G.Y. Deep Learning-Based Channel Estimation for Beamspace mmWave Massive MIMO Systems. IEEE Wirel. Commun. Lett. 2018, 7, 852–855. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]


| Feature | CNN–LSTM [8] | CNN–LSTM [9] | CNN–LSTM [10] | Proposed CNN |
|---|---|---|---|---|
| Target Application | CF-mMIMO IoT | Massive MIMO | UM-MIMO Beamforming | CF-mMIMO |
| CPU-to-AP Optimization | No | No | No | Yes |
| AP-to-UE Optimization | Yes | Yes | No | Yes |
| Temporal Modeling | Yes (LSTM) | Yes (LSTM) | Yes (LSTM) | No |
| Input Features | CSI, SE/EE, time series | Location, CSI | CSI sequences | CSI, distance, SINR, interference |
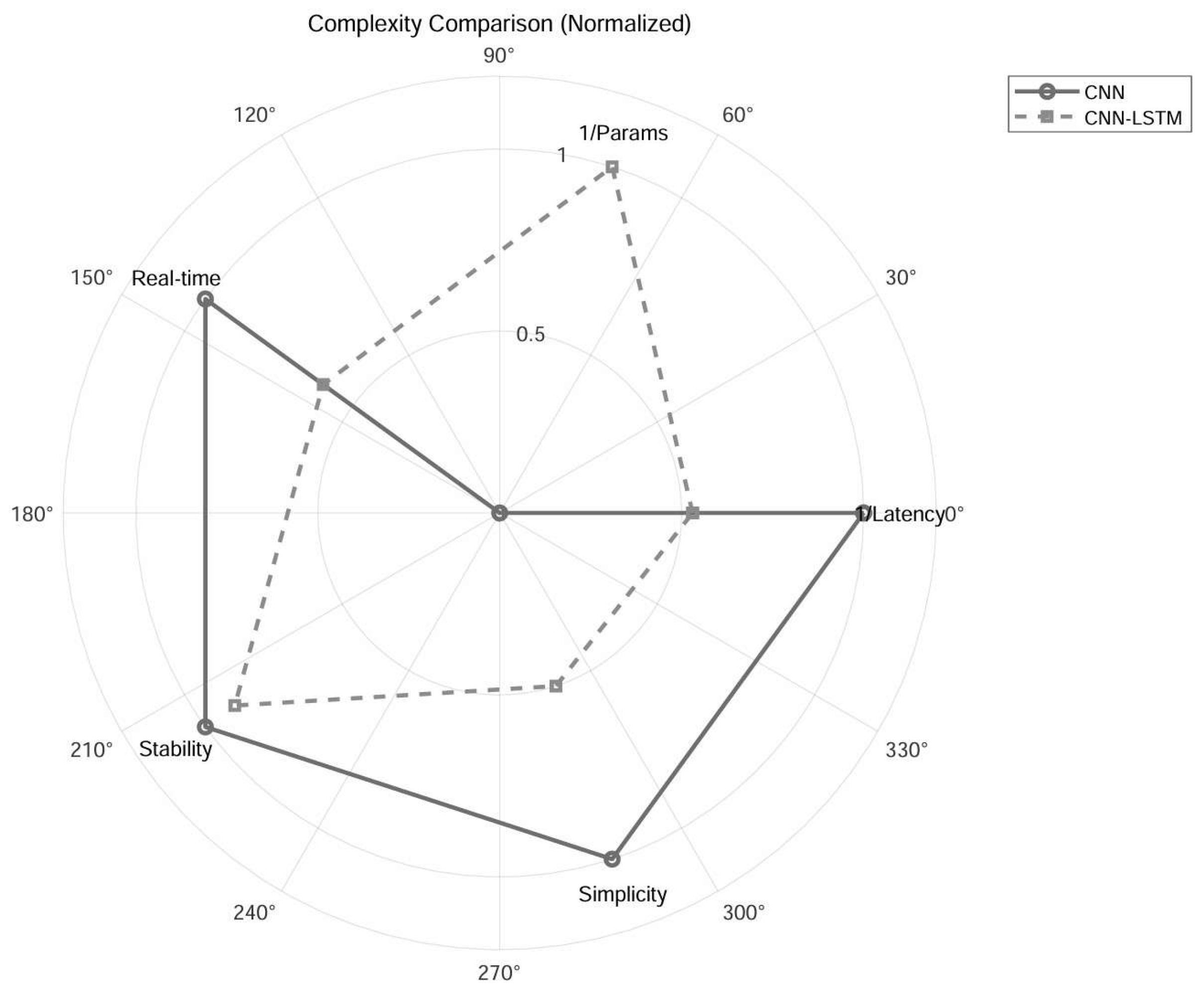
| Model Complexity | High | Moderate | High | Low |
| Real-Time Suitability | No | No | No | Yes |
| End-to-End Control | Partial | Partial | – | Yes |
| Model | Parameter Count | Inference Time (ms) |
|---|---|---|
| CNN | 34.7M | 9.68 |
| CNN–LSTM | 9.8M | 18.29 |
| Parameter | Value |
|---|---|
| Number of APs (M) | 64 |
| Number of UEs (K) | 20 |
| System Bandwidth (B) | 10 KHz |
| Noise Power Density () | −174 dBm/Hz |
| Path Loss Model | , where |
| Channel Model | Rayleigh fading |
| UE Distribution | Clustered in high-density regions |
| AP Transmission Power () | 200 mW |
| CPU Transmission Power () | 10 W |
| Minimum SINR Threshold () | 0 dB |
| CNN Training Epochs | 1000 |
| CNN Learning Rate |
| Method | Avg SE (bps/Hz) | Std SE | Avg EE (bits/J) | Std EE |
|---|---|---|---|---|
| Equal Power | 2.93 | 0.67 | 0.042 | 0.009 |
| Max-Min | 3.58 | 0.54 | 0.050 | 0.007 |
| Stage-wise CNN | 4.06 | 0.49 | 0.061 | 0.005 |
| Proposed CNN | 4.28 | 0.46 | 0.075 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.-J.; Yu, J.-H.; Seo, S.-H.; Choi, S.-G.; Jeong, H.-Y.; Kim, J.-E.; Baek, M.-S.; You, Y.-H.; Song, H.-K. CNN-Based End-to-End CPU-AP-UE Power Allocation for Spectral Efficiency Enhancement in Cell-Free Massive MIMO Networks. Mathematics 2025, 13, 1442. https://doi.org/10.3390/math13091442
Choi Y-J, Yu J-H, Seo S-H, Choi S-G, Jeong H-Y, Kim J-E, Baek M-S, You Y-H, Song H-K. CNN-Based End-to-End CPU-AP-UE Power Allocation for Spectral Efficiency Enhancement in Cell-Free Massive MIMO Networks. Mathematics. 2025; 13(9):1442. https://doi.org/10.3390/math13091442
Chicago/Turabian StyleChoi, Yoon-Ju, Ji-Hee Yu, Seung-Hwan Seo, Seong-Gyun Choi, Hye-Yoon Jeong, Ja-Eun Kim, Myung-Sun Baek, Young-Hwan You, and Hyoung-Kyu Song. 2025. "CNN-Based End-to-End CPU-AP-UE Power Allocation for Spectral Efficiency Enhancement in Cell-Free Massive MIMO Networks" Mathematics 13, no. 9: 1442. https://doi.org/10.3390/math13091442
APA StyleChoi, Y.-J., Yu, J.-H., Seo, S.-H., Choi, S.-G., Jeong, H.-Y., Kim, J.-E., Baek, M.-S., You, Y.-H., & Song, H.-K. (2025). CNN-Based End-to-End CPU-AP-UE Power Allocation for Spectral Efficiency Enhancement in Cell-Free Massive MIMO Networks. Mathematics, 13(9), 1442. https://doi.org/10.3390/math13091442







